1 Introduction

In Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometry, the measured signal results from induced charge on the FT-ICR trap detection electrodes caused by synchronous motion of ions in a static magnetic field. Ion motion synchronization is produced by radiofrequency-sweep excitation of ion cyclotron motion and results in a separate, synchronous ion cloud for each m/z. It is well known that during excitation and detection, ions undergo complex three-dimensional motion. For an ideal hyperbolic Penning trap, the motion in the plane perpendicular to the magnetic field is a combination of cyclotron and magnetron motions. Magnetron motion is induced by the radial component of the trap electric field and the axial magnetic field and is manifested as a modulation of the center of ion cyclotron rotation at a frequency typically ten thousand times smaller than the cyclotron frequency. In a hyperbolic trap and spatially homogeneous magnetic field, ions synchronized during cyclotron excitation continue to be synchronized indefinitely in the absence of collisions with neutrals and ion–ion interactions due to complete decoupling of cyclotron, magnetron, and axial oscillations. In an actual ICR trap, the three modes of motion are coupled and the cyclotron and magnetron frequencies depend on the axial oscillation amplitude, resulting in ion cloud dephasing and “comet” structure formation. Ion cloud dephasing results from accumulated phase difference in the measured (cyclotron minus magnetron) motion for ions with different z-oscillation amplitude in an ion cloud, which can be evaluated for any ion trap by calculating the radial electric field dependence on axial z-coordinate. After some time, the phase difference across the original cloud becomes 2π, corresponding to the head of the comet reaching the tail and resulting in complete loss of signal from the cloud. FT-ICR MS resolving power is proportional to the duration of synchronous motion and is, therefore, limited by the time needed for dephasing to take place, which depends on ion trap geometry and magnetic field homogeneity. Higher magnetic field strength results in smaller difference in measured cyclotron frequencies of ions in each cloud and smaller rate of phase difference accumulation.

The described phenomena are observed by particle-in-cell computer modeling of ion clouds dynamics what became possible after introducing the new approaches in modeling of ion motion in FT ICR cell such as particle–particle [14] and particle in cell [1, 15, 16], which have succeeded in accounting for various experimentally observed FT-ICR MS aspects, as in [10]. Previous approaches based on single-ion calculations and two-ion simulations [11–13] could not predict and describe these phenomena. For a cubic cell (in contrast to the cell with hyperbolic potential) and small ion number, comet structures form, leading to disappearance of the ICR signal after about 1 s at 7 T (extending prior simulations at 1 T [1]) corresponding to mass resolution in accordance with the expression for FT-ICR resolution as a function of observation period (see Figure 1 and Supplementary Material S1, which can be found in the electronic version of this article). Moreover, this phenomenon takes place at only small number of ions in the cell. As for the prior 1 T simulations (see Supplementary Material S1), above a critical ion number, ions of the same m/z move synchronously independent of their z-amplitude.

Figure 1
figure 1

Simulated x-y and y-z projections of ion clouds taken at 0.3 s after excitation (top) and time-domain ICR signals (bottom, 0.5 s of duration) for 5000 singly charged ions, m/z = 500, at 7 T Left: Cubic cell. Right: Quadrupolar trapping potential with excitation and detection electric fields taken from the cubic cell

Full size image

In this work, we have determined the dependence of minimum number, N, of ions in the cloud for onset of coalescence on magnetic field strength (B), cyclotron radius (R), ion mass (m), and difference between ion masses (m2 – m1), for two ion ensembles of different m/z and equal abundance, excited to the same nominal cyclotron radius. Empirical expressions for N as a function of each of the above listed experimental parameters are presented.

2 Methods

The present supercomputer simulations begin from previously developed computer code based on a Particle-in-Cell algorithm for calculation of electric forces acting on individual ion in an ion cloud from other ions in the cloud, from the field of trap electrodes, and from image charges on these electrodes [1]. Briefly, the ion density distribution is determined at every node of the mesh by dividing the total charge extrapolated to that particular node by the ions contained in the volume of each elementary cube of the mesh. By use of a direct fast Fourier transform (FFT) Poisson solver with the trap boundary conditions, corresponding to DC and rf potentials on the trap electrodes, the charge density on each grid point is converted into potentials at those points, and electric field is determined from the spatial derivatives of the potentials. The electric field at an individual ion position is calculated by interpolating the electric fields from the nearest grid points based on the same weighting algorithm as for charge projection to each grid point. The mathematical description of the whole procedure for solving the Poisson equation by the FFT method is described in [1]. The particle positions and velocities for the next time-step are calculated with the Boris integrator [1, 7, 8]. We used two grid resolutions: 32 × 32 × 32 and 64 × 64 × 64. For computational simplicity, we chose either a 1 × 1 × 1 or 2 × 2 × 2 in. cubic cell. The number of time steps for one cyclotron period was 50 or 100 depending on the magnetic field strength. The number of stored snapshots per simulation was determined from the snapshot repetition rate, namely, after every 13,560 steps. For the simulation results presented in Supplementary Material S5, snapshots were recorded for every 10 steps. The number of ions ranged from 10,000 to 1,000,000. For some simulations, ions with 10 charges were used. All simulations are based on spatially homogeneous static magnetic field, with coherent cyclotron motion induced by single-frequency resonant dipolar excitation. rf Amplitude, V p-p  = 10 V, was used for excitation. Excitation duration, Texc, to a final radius, R = 6 mm (for all plots except supplementary material S3) was determined from R = A V p-p Texc/B [6], and A = 300 (cm V–1 s–1) (determined empirically). For coalescence simulations, m/z and mass differences, (m2 – m1)/z were: m = 100, 100.3 Da, z = 1; m = 500, 500.3 Da, z = 1; m = 499.95, 500.05 Da, z = 1; m = 999.95, 1000.05, 1000.15 Da, z = 1; (cyt C m/z ≈ 512, z = 23). The present simulations are based on cubic ICR cell geometry. However, prior simulations based on a capacity matrix method inside the particle-in-cell code approach yield ion clouds of the same shape in rectangular and cylindrical cells. Simulations were performed with either the Moscow State Regatta supercomputer or a Florida State University Dell station. Computation time depends on processor type, ion mass-to-charge ratio, magnetic field strength, ion number, and particle-in-cell mesh spacing. For example, a 0.25 s time-domain signal requires ~5,000,000 computational steps. For 100,000 ions of m/z ~500 at 7 T, and a 64 × 64 × 64 PIC mesh, computation requires ~5 d by use of one core of 3 GHz Xeon processor. The progression from independent motion to collective motion modes of ion clouds was observed from a series of simulations with different number of trapped ions and other parameters fixed.

3 Results and Discussion

3.1 Coalescence

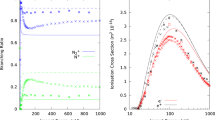
When two ion clouds with small m/z difference coherently rotate in their cyclotron orbits, collective motion of the two clouds occurs due to Coulomb interaction [2], ultimately resulting in phase locking when the mutual E × B drift velocity exceeds the ion cyclotron velocity difference between the clouds. The measured mass spectrum then contains only one m/z averaged peak rather than two peaks at their respective mass-to-charge ratios. Here, a systematically varied set of simulations enables a quantitative description of coalescence development as a function of the number of ions (N) in the interacting clouds, magnetic field strength (B), cyclotron radius (R), mass (m), and mass difference. Modeling was performed for ions trapped in 25.4 and 50.8 mm cubic cells. Simulations for the 25.4 mm cell (ion cloud initial radius at Z = 0 is ~2 mm (for an ellipsoidal ion cloud), post-excitation ion cyclotron orbital radius, R = 6 mm (i.e.; ~50% of the cubic cell inscribed radius), reveal the following relationships (Figure 2 and Supplementary Material S2):

$$ {\text{N}} = {2}00,000\;{{\text{B}}^{{2}}}\left( {{\text{m}} = {1}00.{15}\;{\text{Da}},\;{\text{z}} = {1},\;{{\text{m}}_{{2}}}--{{\text{m}}_{{1}}} = 0.{3}} \right) $$
(1)
$$ {\text{N}} = {1}0,000\;{{\text{B}}^{{2}}}\left( {{\text{m}} = {5}00.{15}\;{\text{Da}},\;{\text{z}} = {1},\;{{\text{m}}_{{2}}}--{{\text{m}}_{{1}}} = 0.{3}} \right) $$
(2)
$$ {\text{N}} = {3},000\;{{\text{B}}^{{2}}}\left( {{\text{m}} = {5}00\;{\text{Da}},\;{\text{z}} = {1},\;{{\text{m}}_{{2}}}--{{\text{m}}_{{1}}} = 0.{1}} \right) $$
(3)

Here and elsewhere, \( m = \left( {{{\text{m}}_{{1}}} + {{\text{m}}_{{2}}}} \right)/{2} \).

Figure 2
figure 2

Minimum number of ions at which FT-ICR peak coalescence takes place as a function of magnetic field strength, for equally abundant ions of m/z = 100 and 100.3 in a 25.4 mm cubic ICR cell. The smooth curve represents an analytical formula that approximately matches the simulated onsets. (In all simulations, coalescence appears to occur entirely during detection, but could possibly begin during excitation. We cannot distinguish between these possibilities because the excitation period is too short for clouds to separate from each other

Full size image

We recently developed an expression relating the minimum number of ions required to induce coalescence as a function of magnetic field B, mass m, mass difference (m2 – m1) and ion cyclotron radius R for ion clouds of arbitrary form:

$$ N = \frac{2}{\nu }\frac{{R{B^2}({m_2} - {m_1})/m}}{{km}} $$
(4)

in which k is the Coulomb force constant, \( {\text{k}} = {1}/{4}\pi {\varepsilon_0} = {8}.{9}\;{1}{0^{{9}}}{\text{N}}\;{\text{m}}/{{\text{C}}^{{2}}} \), and ν is a coefficient derived from the form of cloud interaction potential [3].

The cloud shape for our simulations is usually ellipsoidal. For a 25.4 mm cubic cell, the ellipse has semi-axes a and b = 4a, and the numerically calculated interaction potential is ν = 0.274/a2, so that

$$ N = 7.3\frac{{{a^2}R{B^2}({m_2} - {m_1})/m}}{{km}} $$
(5)

which may be rewritten as

$$ {\text{N}} = {4}.{87}\;{1}{0^{{8}}}{{\text{a}}^{{2}}}{\text{R}}\;{{\text{B}}^{{2}}}\left( {{{\text{m}}_{{2}}} - {{\text{m}}_{{1}}}} \right)/{\text{m}}^{{2}} $$
(6)

in which R is in mm, for [(m1+ m2)/2z] and [(m/z)2 – (m/z)1] m in Da, z = 1, B is in tesla, and N is the total number of ions in both clouds (each interacting cloud has the same ion number).

From this formula we obtain (assuming a ≈ 2 mm and R ≈ 6 mm)

$$ {\text{N}}\left( {{1}00.{15}/0.{3}} \right) = {283},{4}00\;{{\text{B}}^{{2}}} $$
(7)
$$ {\text{N}}\left( {{5}00.{15}/0.{3}} \right) = {12},{32}0\;{{\text{B}}^{{2}}} $$
(8)
$$ {\text{N}}\left( {{5}00/0.{1}} \right) = {4},{1}00\;{{\text{B}}^{{2}}} $$
(9)

which agrees well with the simulation results.

From the simulation for a 50.8 mm cubic cell (Supplementary Material S3):

$$ {\text{N}} = {8}00,000\;{\text{R}}\left[ {\text{cm}} \right]{\text{for}}\;{\text{ions}}\;{\text{of}}\;m/z\;499.95\;{\text{and}}\;500.05\;{\text{at}}\;{\text{B}} = {7}\;{\text{T}} $$
(10)
$$ {\text{Radius}}\;{\text{of}}\;{\text{cloud}}\;{\text{taken}}\;{\text{from}}\;{\text{simulation}}\;{\text{is}}\;{\text{a}} = {2}.{2}\;{\text{mm}}. $$
(11)

For the 50.8 mm cell, the ion cloud spreads more axially than radially. For an ellipsoidal cloud with semi-axes a and b = 8a in a 50.8 mm cell and by use of Equation (4) (as for 1:1:4 ellipsoids in the 25.4 mm cell) we obtain ν and an expression for N:

$$ N = 13.6\frac{{{a^2}R{B^2}({m_2} - {m_1})/m}}{{km}} $$
(12a)
$$ {\text{or}}\;{\text{N}} = {84},{235}\;{\text{R}}\left[ {\text{mm}} \right] $$
(12b)

Thus, the analytic description [3] is in good agreement with our numerical simulations. Analytic estimation shows that the coalescence condition depends not only on B, R, m, and (m2 – m1), but also on the shape and size of the interacting clouds, which depend on the cell geometry and the number of ions in the trap and may distort the dependence on B, R, m, and (m2 – m1).

3.2 Coalescence Threshold and Frequency Shifts

Close inspection of the simulations used to generate the data in Figure 2 and Supplementary Material S2 reveals complex and unstable progression from independent cloud rotation to coalescence (Figures 3, 4 and 5 and Supplementary Material S4). Figure 3 (B = 7 T, m/z ≈ 500, (m2 – m1)/z = 0.1, detection period = 0.5 s) and Supplementary Material S4 (B = 1 T, m/z ≈ 100, (m2 – m1)/z = 0.3, detection period = 0.5 s), displayed frequencies of two ion clouds of different m/z as a function of the total number of ions, 2*N. At small N, two distinct mass spectral peaks of different frequencies are evident, whereas at large N values, the two resonances coalesce into a single peak at a frequency close to the average cyclotron frequencies of both clouds. For intermediate N values, a third peak much broader than the other two appears. The broadening corresponds to instability of cloud coherence (see Figures 4 and 5). In Figure 4 (B = 7 T, m/z ≈ 100, (m2 – m1)/z = 0.3) two independent clouds become coupled during the detection period, starting ~0.03 s after excitation. In Figure 5 (B = 7 T, m/z ≈ 500, (m2 – m1)/z = 0.1), two initially coupled clouds become independent. After excitation, ion clouds have similar radius and phase. If the total ion population of a cloud is close to the limit, 2*N, coalescence is unstable. Thus, if mutual Coulomb interaction results in loss of some ions, an initially bound joint ion cloud separates into independent ion clouds of different m/z, as seen in Figure 5 starting at ~0.15 s after excitation.

Figure 3
figure 3

Top: Effective cyclotron frequencies of equally abundant ions of m/z = 499.94 and 500.05 as a function of the number of charges, N, at (25.4 mm cubic cell B = 7 T. Bottom: Simulated FT-ICR mass spectra for N = 100,000, 720,000, and 900,000.

Full size image
Figure 4
figure 4

Top: x-y projections of ion clouds for two initially independently orbiting equally abundant ion clouds. Note the redistribution of ions and comet tail formation for ions of lower m/z. (B = 1 T, N = 325,000 charges, m/z = 100 and 100.3, 25.4 mm cubic cell). Bottom: Time-domain ion signal (left) and corresponding FT-ICR mass spectrum (right). In Fgures 4,5 and in Supplementary material S6 lower m/z cloud are in blue; with higher m/z in red.

Full size image
Figure 5
figure 5

Top: x-y projections of ion clouds for two initially synchronously orbiting ion clouds of m/z = 499.95 and 500.05. Bottom: Time-domain ion signal (left) and corresponding FT-ICR mass spectrum (right). (B = 7 T, 725,000 charges, 25.4 mm cubic cell

Full size image

At the coalescence threshold, we observe ion cyclotron frequency shifts due to changes in the number of charges in the ion clouds, a trend that persists until the abrupt onset of coalescence. Analysis of the cyclotron motion in the simulations used to construct supplementary material S4 (B = 1 T) reveals decreasing frequency, (ν as in Equation (4)) of the m/z = 100 cloud (the faster moving mass), which is approximated by

$$ \nu \left( {\text{Hz}} \right) = - {2}.{4}\;{1}{0^{{--{4}}}}{\text{N}} + {152936} $$
(13)

Cloud dephasing for the slower (m/z =100.3) orbiting cloud begins at lower ion number (150,000 ions), so we fit only the first six data points:

$$ \nu \left( {\text{Hz}} \right) = - {2}.{2}\;{1}{0^{{--{7}}}}{\text{N}} + {153398} $$
(14)

Similarly, at 7 T for m/z 500 (Figure 3), we see a clear decrease in frequency of the faster moving ions of m/z = 499.95.

$$ \nu \left( {\text{Hz}} \right) = - {1}.{3}\;{1}{0^{{ - {5}}}}{\text{N}} + {214985} $$
(15)

Dephasing of the slower cloud (m/z = 500.05) begins with 725,000 ions in the two clouds, so we fit only the first 6 points:

$$ \nu \left( {\text{Hz}} \right) = - {5}\;{1}{0^{{--{7}}}}{\text{N}} + {21494}0 $$
(16)

Remarkably, the frequency shift of the faster moving clouds is consistently ~1000 times greater than for the slower moving cloud. We can explain the increased frequency shift of smaller m/z ions by stronger Coulomb interaction effect for them because they are outside of larger m/z cloud and experience the action of Coulomb force from it.

An analytic description of ion cyclotron frequency versus ion number can be taken from [4]. We consider an ion trap with potential

$$ {\Phi_0}\left( {x,y,z} \right) = {V_{{trap}}}\left( {\gamma + \frac{a}{{2{\alpha^2}}}\left( {2{z^2} - {x^2} - {y^2}} \right)} \right) $$
(17)

in which V trap is the applied trapping voltage, a is the trap diameter, and γ and α are cell geometry constants. The resulting detected cyclotron frequency is

$$ \omega = \frac{{qB}}{m} - \frac{{2GtV}}{B} $$
(18)

in which G is the trap geometry factor) Addition of the ion–ion interaction potential (we use the potential of a uniformly charged ellipsoid) [4] gives:

$$ \omega = \frac{{qB}}{m} - \frac{{2GtV}}{B} - \frac{{q\rho {G_i}}}{{{\varepsilon_0}B}} $$
(19)

in which Gi is the geometry factor for an ellipsoidal ion cloud, ρ is ion cloud density; and ε0 is vacuum permittivity). Eq. 19 predicts a linear decrease in ion cyclotron frequency with increasing ion number (density). Thus, the observed linear frequency shifts are in good agreement with the theoretical description.

3.3 Ion Cloud Motion During Coalescence and Ion Cloud Shape

Visualization of the detailed interaction between coalescing ion clouds helps to understand the underlying physics and to build accurate and predictive analytical models. Figure in Supplementary Material S5 shows a series of ion cloud snapshots that represent three different m/z clouds (m/z 999.95 in green, 1000.05 in red, and 1000.15 in blue) in a 7 Tesla magnetic field and 50.8 mm cubic cell during one cyclotron period under complete coalescence conditions (part A of Figure in Supplementary Material S5, 102,000 ions per cloud) and partially coalesced conditions (part B of Figure in Supplementary Material S5, 34,000 ions per cloud). Note that the ions of different m/z in coalesced clouds do not mix (i.e., ions of each m/z maintain separate coherence inside the coalesced cloud). Further, note that in part A of Figure in Supplementary Material S5, each of the three coalesced clouds completes one revolution around the cloud axis during each cyclotron rotation, and that the three m/z clouds are positioned such that ions of higher m/z are always closer to the center of rotation. This redistribution takes place after cyclotron excitation that excites ions of all m/z to the same radius.

Ion cloud shape is important because it influences the onset of coalescence [3]. Figure in Supplementary Material S6 shows the progression of ion cloud shape as a function of ion number for ions of m/z = 499.95 and 500.05 at 7 T in a 50.8 mm cubic cell, and 1 V trapping potential, at a post-excitation initial ICR orbital radius of 6 mm. The ion cloud shape corresponds to an elongated ellipsoid (x2/a2 + y2/b2 + z2/c2 = 1) that progresses from a = b < c, in which a ≈ 2.2 mm and c ≈ 10 mm for 100,000 ions to a ≈ 4 mm, b ≈ 6 mm, and c ≈ 20 mm for a coalesced cloud of 900,000 ions, which is near the cell capacity limit for 1 V trap potential. Note that all of our simulations proceed from an ellipsoidal initial ion distribution, and that no subsequent significant change of ion cloud shape was observed. A more accurate definition of initial ion cloud shape would require simulation of ion injection and capture.

3.4 Coalescence for an Isotopic Cluster of Cytochrome c

The analytical description presented above considers coalescence of two equal-abundance ion clouds. However there are typically many (up to 50,000) interacting clouds and the practical limitation of resolving power associated with coalescence may be different from the threshold predicted by the formulas derived from simulation of just two interacting clouds. In Figure 6, we show simulated coalescence of the more realistic case of the 23+ charge state isotopic cluster of cytochrome c, with relative isotopic abundances calculated from Molecular Weight Calculator [9] and each isotope peak color-coded as in Figure 6b.

Figure 6
figure 6

x-y Projections of ion clouds (left), and simulated time-domain ICR signals (top and right) and FT-ICR mass spectra (middle) for the Cytochrome c isotopic distribution (m/z ≈ 512, z = 23+) ion clouds, for different total ion numbers. Color-coding for members of the natural abundance isotopic distribution (individual peaks separated by m/z = 0.043) is shown at the bottom of the Figure. (B = 7 T ; 0.3 s detection; >100 steps per shortest cyclotron period; 0.0004 sec, 50 V p-p excitation potential “chirp” excitation to yield post-excitation ICR orbital radius of 10 mm; 5 V trapping potential

Full size image

Note that the individual m/z clouds initially rotate at equal cyclotron radius, but as the number of ions increases, the radius of each cloud changes so that lower m/z (faster) clouds have larger radius than higher m/z (slower) clouds and eventually only one ion cyclotron resonance frequency is observed. This behavior is similar to that from data in Supplementary Material S5, in which three different m/z clouds coalesced. Figure 6a also shows that higher ion number in the isotopic cluster results in increased rate of ion cloud dephasing and noticeably impacts the calculated spectrum if the number of charges in the isotopic cluster exceeds 100,000. Coalescence is first observed if the number of charges exceeds 350,000, in good agreement with the value predicted by Eq. 4 for m/z = 512, m/z difference of 0.043, B = 7 T, and an initially ellipsoidal cloud (a = b = 4 mm and c = 4a).

Comparison of the calculated signal magnitude (Figure 6a, top) with snapshots of ion cloud position for a noncoalesced isotopic cluster (100,000 charges) shows that the maximum signal magnitude corresponds to constructive interference of the isotopes, which occurs periodically when the clouds tend to converge at one azimuthal angle [5]. Typical FT-ICR excitation results in equal ion cyclotron radius at all m/z [6], which requires each pair of different m/z clouds to pass through each other at their respective ICR difference frequency. For example, the monoisotopic cloud for a singly-charged peptide at m/z 1000 will pass through the 13 C1 cloud ~100 times during a 1 s detection period. Our modeling shows that ion clouds adopt an ellipsoidal structure with length determined by the number of ions (charges). If ion density inside a cloud approaches the Brillouin limit [2], the ion potential energy is independent of ion position in the cloud, so that a small ion cloud will spread throughout a larger cloud during their interaction and will continue to be axially dispersed after emerging from the larger cloud. Axial dispersion causes ion cyclotron motion dispersion and loss of ions after multiple passes, and is manifested as a loss of low abundance components of the simulated cytochrome c isotopic cluster (Figure 6).

4 Conclusions

Dependence of coalescence on magnetic field is not easily measured with a single instrument because the magnetic field must be varied. The most practical recourse is to make realistic simulations of ion cloud behavior in magnetic fields of different intensity. The present simulations show that mass resolution stays constant at a given magnetic field strength with increasing ion number until a critical number N is reached, triggering the abrupt onset of coalescence. We have determined the dependence of N on magnetic field strength (B), cyclotron radius (R), ion mass (m), and difference between ion masses (m2 – m1) for two ion ensembles of different m/z and equal abundance, excited to the same nominal cyclotron radius. We find that N depends approximately quadratically on magnetic field strength in the range 1–21 Tesla, as does dynamic range. Dependences on cyclotron radius and (m2 – m1) are linear, and N depends on m as 1/m2. Empirical expressions for coalescence as a function of each of the above listed experimental parameters are presented. A recent analytical theory of ion cloud coalescence [3] agrees well with our simulation results. In this manuscript, we demonstrate that simulated ion cloud interactions based on a very simple physical model [2, 3] predicts quite well the dependences of mass resolution on practical experimental parameters (magnetic field strength, number of ions, dynamic range, mass-to-charge ratio, m/z separation between two or more ion clouds, cyclotron radius, etc.). Those dependences are difficult to separate in actual experiments: e.g., one cannot vary the magnetic field from 1 to 21 T with a given FT-ICR mass spectrometer. Thus, the present results serve to develop and guide intuition for experimentalists. Moreover, the behavior at a given magnetic field strength can predict what will happen at another magnetic field strength, as in Gross et al.’s [17] use of “scaled” results at 1 T to predict behavior at higher field.