Identification of boundary conditions of railway bridges using artificial neural networks

Abstract

This article presents a study that aims to identify the boundary conditions of a railway bridge using system identification and artificial neural networks. Vibrations generated by three different train types recorded during a 24-h long measurement campaign is used to identify the modal frequencies and mode shapes of a single-span 50 m long railway bridge. Frequency Domain Decomposition and Stochastic Subspace Identification with Covariance methods were used to identify the modal properties from the recorded vibrations and the effect of the used Operational Modal Analysis on the identified modal properties was evaluated. An initial finite-element (FE) model based on the design drawings was not able to replicate the observed dynamic behavior of the bridge. Using a sensitivity analysis, the key parameters of the finite-element model that impact the vibration frequencies of the bridge was determined. 300 finite-element models were created by changing the values of these key parameters within their effective range and were used to identify the relationship between these parameters and the vibration frequencies using Artificial neural networks (ANNs). Leveraging this relationship, the values of the FE model parameters that minimizes the error between the measured and computed frequencies was determined. As a result, the mean error between the computed and the identified vibration frequencies was reduced from 27.3% for the initial model to 3.0% for the updated model. The study indicates that boundary conditions are among the most influential parameter on the dynamic behavior of bridges and can deviate significantly from the simplistic models generally used in the FE models.

1 Introduction

Evaluation of the current state of existing bridge infrastructure remains a challenge for the engineering community. Use of numerical models under various loads is one of the most common methods to evaluate the state of the bridge under serviceability and ultimate limit states. While numerical models based solely on design drawings might be representative of the structure immediately after its construction, they may not necessarily simulate the behavior of an existing bridge constructed decades earlier, because the key parameters affecting the behavior of an existing bridge can vary significantly over time due to aging and deterioration. In particular, the boundary conditions are susceptible to such variations due to effects, such as increased friction between the superstructure, the bearings and the abutments and piers. System identification, which consists of determining the key parameters of a structure and revising its finite-element (FE) model, provide an attractive option to ensure that the FE model can accurately simulate the behavior of the bridge and its boundary conditions. Monitoring the dynamic behavior of the bridge and calibrating the FE model such that the observed dynamic behavior can be simulated is a common method used for system identification. The modal parameters that are inherent characteristics of the structure can be identified from the recorded vibrations and can be used as indicators to evaluate the current state of the structures [1, 2]. In early research, to identify the modal characteristic of the structures, forced vibration tests (input–output) were conducted using different excitation equipment, such as shakers or impact hammers [3]. The difficulties and costs of conducting this type of test on large structures encouraged researchers to develop methods that could be applied more efficiently leading to the development of the Operational Modal Analysis (OMA) methods. OMA uses the ambient vibrations that are generated by sources such as wind and traffic and is also known as output-only method, because it does not use an input excitation [4, 5].

Once the modal parameters of the structure are identified from the recorded vibrations using OMA, the next step of the system identification process requires updating the FE model of the structure to minimize the difference between the computed and identified parameters. For this, various computational methods have been developed and applied on different bridge types [6,7,8,9,10,11,12]. Of the available numerical methods for FE model updating, Artificial Neural Networks (ANNs) was successfully implemented in several model updating studies and was recognized as a powerful tool. ANNs are known as robust computing tools to find complex and hidden relationships in a data set, where an explicit formula is difficult to obtain, if not impossible. Hasancebi and Dumlupinar [13] employed ANN to develop an efficient technique for FE model updating of an aged concrete bridge. The network was trained using data sets from non-linear and linear analyses separately. This study demonstrated that ANN can be used reliably for model updating and prediction of structural parameters under a high level of complexity and uncertainties. Park et al. [14] evaluated the boundary conditions of a steel girder bridge using neural networks through laboratory and field tests. They used ANN to find the relationships between bridge response and the constraining effect of the boundary condition with a focus on the rotational stiffness at the boundaries of the FE model. Zapico et al. [15] used ANNs for the FE model updating of a small steel frame, where the network was employed to establish the relationship between key structural parameters and the natural frequencies. Chang et al. [16] proposed a model updating method and applied it on a suspension bridge using an adaptive neural network. They used an iterative procedure to reduce the differences between the predicted and measured frequencies, where the model updating process and training the network were updated repeatedly until obtaining a satisfactory agreement between the computed and measured responses.

Due to the significance of the boundary conditions on the bridge behavior, several studies focused on the boundary conditions of the bridges during the FE model updating process and reported that the in-situ conditions can differ significantly from the design drawings. Hester al. [17] studied the boundary conditions of a steel girder short-span highway bridge. The study revealed the real behavior of the support as pinned–pinned due to the friction on the bridge bearings, as opposed to the pinned-roller as suggested by the design drawings. Dilena et al. [18] applied FE model updating to identify the boundary conditions of a damaged reinforced concrete bridge. To represent both sliding and fixed constraining effects of boundary conditions, each support was modeled using an additional linear elastic spring acting along the bridge longitudinal direction, and then a sensitivity analysis was conducted to identify the relationship between spring stiffness and natural frequencies. Brownjohn et al. [19] evaluated the strengthening and refurbishing of a highway bridge by model updating and dynamic testing. To reflect the structural change of the bridge after refurbishment, the abutments were modeled with rotational stiffness rather than free-to-rotate pin supports as indicated in the design drawings.

This article presents a holistic system identification study starting from the measurement campaign conducted on a simply supported single-span railway bridge to the calibration of its FE model using ANNs. The main purpose of the study is to identify the boundary conditions of the bridge and quantify the deviation of the identified boundary conditions from the ideal conditions specified in the design drawings. The bridge is a 50-m long bridge single-span beam bridge located on the Ofot line (Ofotbanen) in Northern Norway and is part of a vital railroad that carries the iron ores mined in Kiruna, Sweden to the harbor in Narvik, Norway. This bridge is exposed to various types of train crossings, ranging from lightweight maintenance vehicles to heavy-haul trains carrying the iron ores. In the OMA process, the free vibrations recorded after the crossing of three types of trains, which are significantly different from each other as far as their mass is concerned, are used to identify the vertical and transverse modes of using FDD and the SSI–COV methods. The impact of the vibration source and the OMA algorithm used in the modal parameter identification process was evaluated and discussed.

The FE model of the bridge was then developed and calibrated using ANNs with special focus on the boundary conditions. First, sensitivity analyses were conducted to identify the parameters that significantly impact the dynamic response of the bridge. A set of sample FE models replicating a wide range of the critical modeling parameters selected randomly from their effective ranges were created. Although the boundary conditions were designed as simple pin and roller supports, the rotational stiffness at both supports and the translational stiffness at the roller support is also included in the FE model updating process to ensure that potential variations in the boundary conditions were reflected in the final model A data set containing the values of the modeling parameters and the computed modal parameters was thus created. This data set was then used as the training data for an ANN to learn the invisible patterns between the bridge parameters and the bridge responses. Various networks consisting of different hidden layers and processing elements are tested. The modal parameters of the bridge identified from the field response were then fed into the trained ANN to estimate the values of the modeling parameters that represent the current condition of the bridge. It is shown that the boundary conditions can vary significantly from the design assumptions and these variations can be captured successfully by utilizing the predictive capabilities of ANNs.

2 Bridge description, instrumentation, and vibration measurements

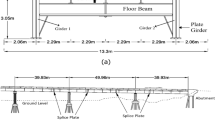
The Norddal bridge is a single-span, prestressed T-beam concrete bridge located on the Ofot line (Ofotbanen), which is part of a vital railroad that carries the iron ore mined in Kiruna, Sweden to the harbor in Narvik, Norway. As such, the bridge is exposed to very high axel loads from the iron ore trains crossing the bridge regularly. Figure 1a depicts the cross section of the bridge deck, which is a double tee section with a width of 6.6 m and a total depth of 2.5 m. A pair of elastomeric bearings installed at the top of each abutment supports the superstructure; Fig. 1b.

Fig. 1

a Cross section of the Norddal Bridge (all dimensions are in cm) and b detailed view of the bridge abutments

The instrumentation deployed on the bridge consists of five triaxial micro–electro-mechanical systems (MEMS) accelerometers and data loggers to record the vibration data. The accelerometers were attached to the steel plates using very strong magnets. The steel plates were, in turn, mounted on the concrete on the bridge deck using high strength epoxy, as shown in Fig. 2. The location of the five accelerometers on the bridge deck is presented in Fig. 3. Of the five accelerometers, one was placed at the mid-span (S3 in Fig. 3) effectively dividing the bridge into half. Two of the remaining accelerometers were placed 4.45 m away from each abutment (S1 and S5). The fourth accelerometer (S4) was placed approximately in the middle of the two accelerometers that are placed at the mid-span (S3) and one of the abutments (S5). The final accelerometer (S2) was then placed at 1/3 of the distance between the accelerometer at the other abutment (S1) and S3. A non-symmetrical sensor setup was used in the measurements to be able to obtain more information close to the abutments on one side while having evenly spaced sensors on the other side provides better information about the overall behavior of the bridge. Vibrations were recorded continuously on the bridge for a 24-h period in August 2020 with a sampling frequency of 250 Hz.

Fig. 2

Triaxial accelerometers on the bridge deck

Fig. 3

Location of the acceleration sensors on the bridge deck

Vibrations induced by three different train types were recorded during the measurement campaign: loaded iron ore trains, unloaded iron ore trains carrying the empty wagons, and lightweight maintenance vehicles used for regular track maintenance. The iron ore trains are composed of 68 wagons with four axels on each wagon (i.e., a total of 292 axes) and have a total length of approximately 700 m. The axel load for the loaded iron ore trains is specified as 30 tons. The length of each wagon is approximately 10 m; thus, the maximum number of wagons that are on the bridge at the same time is five. As such, the fully loaded iron ore train adds around 600t to the total mass of the bridge, while the total mass of the bridge itself is approximately 1100t. Thus, the total mass of the bridge increases by approximately 50% when the train is on the bridge potentially impacting the vibration frequencies of the bridge [20]. On the other hand, the lightweight maintenance vehicles, which generally consist of just one locomotive, have a mass that is insignificant compared to the total mass of the bridge. Figure 4 presents the time variation of accelerations recorded during the crossing of each train type and indicates the relative length and mass of the iron ore trains and the lightweight maintenance vehicles.

Fig. 4

Vertical acceleration time histories at the midspan of the bridge through different train crossings

In total, 23 train-induced excitations caused by eight loaded iron ore trains (designated by even numbers between T-9910 and T-9924), seven unloaded iron ore trains (designated by odd numbers between T-9909 and T-9921), and eight lightweight maintenance vehicles (designated by LW-1 to LW-8) were recorded during the measurement campaign and used in the identification of the modal properties of the bridge.

In addition to the train-induced vibrations, ambient vibrations were also recorded during the 24-h measurement campaign.

The measured accelerations were first de-trended to remove any drift in the signals. The data was then filtered by a 4th order Butterworth bandpass filter with the cutoff frequencies at 0.1 Hz and 25.0 Hz, which are out of the frequency range of interest for the modal identification process.

3 Identification of modal parameters using operational modal analysis

The recorded accelerations were then used to identify the modal parameters of the bridge via operational modal analysis (OMA). Over the two last decades, OMA procedures have developed rapidly, and the forced vibration tests have been replaced by OMA in many engineering applications [21]. Accordingly, a variety of OMA algorithms have been developed and numerous studies have been conducted on modal parameter identification of bridges using different OMA techniques to compare their performance and to evaluate their accuracy. The theoretical basis of the OMA techniques has been studied and developed in both frequency- and time-domain approaches. OMA methods in the frequency-domain identify the modal parameters using the power spectrum density (PSD) functions of output responses. In frequency-domain methods, measured signals are transformed from the time domain into the frequency domain through the Fourier transform. The peak picking (PP), frequency domain decomposition (FDD), and the enhanced frequency domain decomposition (EFDD) methods can be mentioned as the most common techniques in the frequency domain [22]. The time-domain approach is based on analysis of the time history response or the correlation functions and arguably tends to provide more accurate and better results specifically in the case of a large number of closely spaced modes [23]. Several OMA techniques in the time domain have been developed and successfully applied to identify the modal parameters of bridge structures, such as natural excitation technique (NEXT), stochastic subspace identification (SSI), auto-regressive moving average (ARMA), and eigensystem realization algorithm (ERA) [24, 25]. Different output-only frequency and time-domain system identification algorithms have been applied to extract the modal parameter of the bridge structures, such as the golden gate suspension bridge [26], the Sutong bridge [27], the Millau Viaduct [28], and the Humber bridge [29].

OMA techniques are performed under principal assumptions of stationary excitation, system linearity, lightly damped structure, and broadband white noise input signals with a Gaussian distribution that has a constant power spectrum density [25, 30]. In general, ambient vibrations are preferred for OMA applications as they, in general, satisfy these principal assumptions. However, the ambient vibrations are often affected by noise and the results extracted from OMA techniques using ambient vibrations highly depend on the signal noise ratio (SNR) [23]. The monitored bridge is in a remote area with no roads and traffic in the vicinity and the only ambient vibration source is the wind, which had a very low intensity during the measurement campaign. Therefore, the recorded ambient vibration has very low acceleration amplitudes and suffers from very low signal-to-noise ratios (SNRs). In the absence of satisfactory SNR from the ambient vibrations, the train-induced vibrations provide an opportunity for a reliable basis for the modal identification. Figure 5 shows an overview of different types of vibrations recorded on a railway bridge before, during and after a train crossing. Window 1 in Fig. 5 shows the forced vibrations induced by the train, while window 3 depicts the ambient vibrations. Indicated by window 2 in Fig. 5 is the free decay portion that commences immediately after the train leaves the bridge and ends when the train induced vibrations are completely damped out. The modal identification based on the vibrations during the forced vibration phase of the train crossing (i.e., window 1 in Fig. 5) are prone to contamination from the forcing frequency of the train and, possibly, the increase in the mass of the bridge due to the train mass. Furthermore, the train induced vibrations violates the basic assumptions of the OMA methods as the input excitation is non-stationary [23, 31]. To identify the modal parameters and to minimize the contamination of the frequency content of the bridge dynamic response, the free decay response that starts immediately after the train leaves the bridge (window 2 in Fig. 5) provides an attractive alternative that is used as a reliable excitation source to identify the modal parameters [31,32,33] and is used in this study.

Fig. 5

Types of different vibrations recorded on a railway bridge before, during and after a train crossing

Even though evaluation of just one free decay response induced by a random train can provide an initial insight into the bridge modal parameters, statistical analysis of the identified modal parameters from a set of excitations induced by different train types provides a more reliable set of modal parameters. Therefore, the modal identification is performed separately on all the 23 train crossings recorded during the measurement campaign.

To determine the length of the window that defines the free decay response (window 2 in Fig. 5) that will be used in the modal identification process, a sensitivity study on the effect of the length of the free decay on the identified modal frequencies proposed first by Ulker and Karoumi [34] was used. Accordingly, the length of the free-decay response was varied between 2 and 20 s and the identified frequencies were monitored. A 7-s window starting from the moment the train leaves the bridge was determined to be the optimum window for modal identification. Use of shorter data led to instabilities in the identified frequencies while using longer data resulted in the contamination of the data with noise due to the low SNR of the ambient vibration, which started to creep into the window when data longer than 7 s was used.

Acceleration measurements were analyzed using stochastic subspace identification with covariance (SSI–COV) [35] and Frequency Domain Decomposition (FDD) techniques [36] to evaluate the variation in the identified modal parameters with the OMA algorithm used. In the application of the SSI–COV technique, the stabilization diagram is used to identify the modal parameters. In the stabilization diagram, the physical modes appear with consistent frequencies, while spurious modes tend to be more scattered and show erratic behavior. This diagram is very valuable in separating the true system poles from the spurious numerical poles. Corresponding poles to a model order are compared with those of the former model order to recognize the stable or unstable poles which are determined and plotted with different symbols [37]. In this study, to build the stabilization diagrams, a series of modal parameters are identified across the frequency range by increasing the model orders from 0 to 70. If the change in the frequency and the damping ratio of the two consecutive model orders were within 1% and 5% of each other, respectively, and the modal assurance criterion (MAC) of the mode shapes was higher than 98%, these poles were assumed to be stable poles. If the poles did not meet these criteria, the first one was discarded and the second one was compared to the subsequent pole. Regarding the FDD method, the basic concepts behind this method in the form of Complex Mode Indication Function (CMIF) have been proposed by Shih et al. [38], and a complete definition of this method was developed by Brinckler [36]. Identification of the modal parameters using the FDD method was performed by Complex Mode Indicator Function (CMIF) that shows the resonant peaks and returns the singular values (SV) of the cross-power spectrums as a function of frequency.

Figure 6a, b shows the stabilization diagrams for the SSI–COV method and CMIF plots used in the FDD method obtained using the free decay of the vertical accelerations after the passage of loaded iron ore (T-9924), unloaded iron ore (T-9919), and lightweight maintenance (TW-8) trains, respectively. Also plotted in Fig. 6 are the indicated modal peaks corresponding to the first three modes of the bridge in the vertical direction.

Fig. 6

a Stabilization diagram from the SSI–COV algorithm and b CMIF plots associated with the FDD technique for the free decay of the vertical accelerations induced by different train types

A total of six modes of interest, three in the vertical direction and three in the transverse direction, were identified from a total of 23 train crossings. However, a minority of the train crossings did not provide enough information for identification all the mode shapes. Of the 138 cases (6 modes and 23 train crossings) investigated, FDD could successfully identify 126 cases (91.3% success rate), while SSI–COV could successfully identify 125 cases (90.5% success rate). Although the lightweight maintenance vehicles created much lower excitations compared to the iron trains, this did not hinder the modal identification process as the identification process was equally successful for all three train types considered.

Table 1 and Fig. 7 provide a comparative overview of the identified mean frequencies and the associated standard deviation for different train types and OMA algorithms. The transverse mode shapes are identified using the prefix “T” in the mode shape name in Table 1, while the vertical modes shapes have the prefix “V” followed by the number of the mode in that direction. The mean frequencies summarized indicate that the mass of the train that induces the free decay used in the modal identification process has a significant effect on the identified frequencies, particularly for the first mode in both directions. While the mean first vertical frequency is identified as 2.54 Hz using the FDD algorithm and the free decay from loaded iron ore trains, it increases to 2.93 Hz when the free decay from lightweight maintenance vehicle is used in the identification process. The impact of the train mass is much less pronounced for the second and third modes in each direction. In addition, the variation in the modal frequencies is much higher for the heavier trains compared to those identified from the lightweight train crossings. The identified frequencies for the first transverse and vertical modes are constant at 2.93 and 3.41 Hz, respectively, for all eight cases of lightweight train crossings leading to a standard deviation of 0.0 (Fig. 7b). On the other hand, the frequencies vary from one loaded train crossing to another as indicated by the standard deviation in parentheses for each mode shape in Table 1. This can be attributed to the impact of the train mass on the vibration frequency of the bridge. The lightweight maintenance vehicle has an insignificant mass compared to the mass of the bridge and, thus, the identified frequency is virtually equal to the natural frequency of the bridge and does not vary from one train crossing to the other. On the other hand, the mass of the loaded train and, to some extent, the unloaded train, is significant compared to that of the bridge leading to a shift in the vibration frequencies. Although a consistent method was used to extract the free decay data from the train crossings, it is likely that the impact of the train crossing on the free decay varies between the train crossings as it is impossible to eliminate the contamination of the free decay data from the forced vibrations, particularly when the mass of the train relative to the bridge is so high. This leads to a higher variation in the identified vibration frequencies for the unloaded and loaded trains compared to the lightweight maintenance vehicles.

Table 1 Mean and standard deviations (in parentheses) of the identified frequencies across different excitation cases and methods

Fig. 7

Identified natural frequencies through free decay responses after different train crossings (V vertical, T transverse), a SSI–COV method, b FDD method

The OMA algorithm used in the modal identification process also has an impact in the identified vibration frequencies as FDD and SSI–COV algorithms provide slightly different vibration frequencies. However, the variation is not systematic as one algorithm provides higher frequencies for one mode, while it provides lower frequencies for the other mode rendering it difficult to make a general conclusion about the effect of the algorithm used in the identified modal properties. Furthermore, the variation in the identified frequencies using the two methods is not significant enough to warrant further evaluation.

The damping ratios of the first six modes of the bridge were identified using the SSI–COV method and summarized in Table 2, where the mean and standard deviation of damping values are presented. The range of identified damping ratios is between 1.2 and 5.77% for the first three modes in each of the vertical and transverse directions. The damping ratios identified using the excitations from the lightweight vehicles are lower compared to their counterparts from loaded and unloaded iron ore trains. This can be attributed to the fact that the damping ratio tends to increase with an increase in the amplitude of vibrations and lightweight vehicles produce lower vibration amplitudes compared to the other two train types. Since identification of the damping ratio is not the main aim of this study and considering the well-documented observation that there are higher levels of uncertainty associated with identification of damping ratios compared to frequencies and mode shapes using OMA [39,40,41] the identified damping ratio values were not evaluated in further detail.

Table 2 Modal damping ratios identified using the SSI–COV method for the first three vertical (V1–V3) and transverse (T1–T3) modes

Mode shapes arguably provide the most valuable information about the dynamic properties of the bridge, because they provide not only global information about the structure but also localized insight that assists in a better understanding of the dynamic behavior of the structure compared to the global information, such as the vibration frequencies [40]. Figures 8 and 9 present a comparison of the identified mode shapes using the SSI–COV and FDD techniques for all the train crossings, respectively. Each row in these figures illustrates one of the identified modes, while each of the first three columns depicts the mode shapes identified using each train crossing for one of the train types. The fourth column depicts the mean mode shapes identified for each train type to enable the comparison of the results from different excitation sources.

Fig. 8

Mode shapes identified using the SSI–COV method in a vertical direction, b transverse direction

Fig. 9

Mode shapes identified using the FDD method in a vertical direction, b transverse direction

To be able to evaluate the boundary conditions of the bridge objectively, the plotted modal displacements at the ends of the bridge were not assigned prescribed values but were computed by fitting a third-degree polynomial to the identified modal displacements at the five sensors.

Figures 8 and 9 show some variation in the mean mode shapes identified using the two algorithms from the different types of train crossings. To evaluate this variation quantitatively, modal assurance criterion (MAC) values between the mean mode shapes identified using the SSI–COV algorithm from the vibrations induced by lightweight maintenance vehicles and unloaded and loaded iron trains in the vertical direction were computed and plotted in Fig. 10.

Fig. 10

Correlation between the mean vertical mode shapes identified using from the free decay induced by lightweight maintenance vehicle and a unloaded iron ore train b loaded iron ore train the SSI–COV algorithm

The results indicate that, although the train type has a significant impact on the identified vibration frequencies, it does not affect the identified mode shapes significantly. Particularly for the first mode in both directions, whose frequencies were affected most by the train type, the mode shapes identified using free decay data induced by all three train types are essentially identical leading to a MAC value of 0.99. Only in the third mode, the excitation source led to a variation in the mode shapes but even for this mode, a relatively high MAC value was obtained for the two extreme cases, i.e., the loaded train and the lightweight maintenance vehicle (Fig. 10b). Although the results are presented only for the vertical modes in Fig. 10 for brevity, the MAC values obtained for the transverse modes identified from different train crossings were very similar to those for the vertical modes.

Figure 11 presents the correlation of the identified mode shapes in the vertical and transverse directions obtained using the FDD and SSI–COV method for the lightweight maintenance vehicles. The mode shapes identified using the two algorithms show very strong correlation, especially in the vertical direction. Only for the third mode in the transverse direction, the MAC value falls below 0.90. This deviation stems most likely from the complex vibration mechanisms of the higher mode modes, which can be governed by structural characteristics as well as measurement errors [23].

Fig. 11

Correlation between the mean mode shapes identified through the FDD and SSI–COV using the free vibration after the lightweight vehicle crossing; a vertical modes, b transverse modes

As a result of the comprehensive modal identification study carried out using three different excitation sources and two different algorithms, it was decided to use the modal parameters obtained using the free decay induced by lightweight maintenance vehicles in the next phase of the study. This decision is mainly based on the insignificant mass of the lightweight vehicle compared to the bridge mass leading to identified modal frequencies that are virtually identical to the natural frequencies of the bridge. Furthermore, the mode shapes were shown to be insensitive to the excitation source and, as such, each of the three excitation sources provide similar identified mode shapes. Finally, for the lightweight maintenance vehicle, the OMA algorithm used in the modal identification process was shown to have very little impact on the identified modal parameters. This observation is in accordance with previous studies, all of which reported minimal variation in the identified mode shapes and frequencies using various OMA algorithms [31, 40,41,42]. Therefore, the modal frequencies and the mode shapes identified using SSI–COV algorithm is used as the benchmark in the finite-element model updating process, although those from the FDD algorithm could have been chosen as the two algorithms provide essentially identical modal parameters.

4 Initial finite-element model

An initial FE model of the bridge was developed in the SAP2000 R21 computational environment based on the available design drawings and the information obtained from the in-situ observations. The bridge deck was modeled using linearly elastic Bernoulli beams discretized at every 1 m. Using the cross section provided in Fig. 1a, the moment of inertia of the deck in the transverse and vertical directions are computed as 5.46 m⁴ and 16.89 m⁴, respectively, while the cross-sectional area is equal to 6.81 m².

For simplicity, the parapets and other non-structural elements are not considered in FE modeling as they have virtually no effect on the stiffness of the bridge. The concrete class is considered C45/55 with an elasticity modulus of 36 GPa based on the available information in the design drawings. The unit weight of the prestressed concrete deck including all the reinforcements, tendons, and prestressing cables is assumed to be 25 KN/m³. In addition to the self-weight of the reinforced concrete, additional mass due to the non-structural elements such as ballast, sleepers, and parapets was also considered in the analysis. For this, a normalized mass parameter (C_m) defined as the ratio of the total bridge mass (i.e., self-weight of the bridge deck plus the additional mass of the non-structural elements) to the self-weight of the bridge deck is introduced. For the initial FE model, the mass of the non-structural elements was assumed to be 25% of the self-weight of the bridge deck, i.e., C_m = 1.25 was used in the initial model.

The boundary conditions were modeled according to the specifications in the design drawings. Figure 12 shows the springs used at both abutments to simulate the boundary conditions at the abutments. For the initial model, at both ends, the supports were modeled as free to rotate (i.e., KR_v = KR_t = 0). The spring stiffnesses in the translational and vertical directions were computed based on the specified material and geometric properties of the elastomeric bearings. According to the design specifications, the stiffness of the elastomeric bearings in the vertical direction (K_v) was computed to be 1.63 × 10⁶ kN/m, while, in the two horizontal directions, the stiffnesses (K_t and K_l) were computed as 2667 kN/m using the shear stiffness of the bearings.

Fig. 12

Overview of the boundary conditions of the numerical model with translational and rotational springs

As a result of the modal analysis, the frequencies of the first three modes in the vertical direction was computed to be 1.86 Hz, 7.31 Hz, and 16.01 Hz. These frequencies deviate up to 43% from the identified frequencies (Table 3) and indicate that the behavior of the bridge in the vertical direction is much stiffer compared to the model based on the design drawings as the frequencies identified from the recorded vibrations are much higher compared (Sect. 4) to their counterparts computed using the initial FE model. In the transverse direction, the frequencies of the first three modes were computed as 0.34 Hz, 0.62 Hz, 7.11 Hz from the initial FE model, respectively. These values are significantly lower than the observed frequencies of the bridge (Table 3) indicating that the initial FE model underestimates the stiffness of the bridge in the transverse direction. This is most likely due to the spring stiffness of the bearings in the horizontal direction that is based on the design values. Although the mode shapes in the vertical direction obtained from the FE model had a high correlation with the identified mode shapes, the significant discrepancy in the frequencies computed using the initial FE model and those identified from the recorded vibrations show that the initial FE model fails to capture the dynamic behavior of the bridge indicating the need for updating the finite-element model.

Table 3 Measured and computed frequencies using initial and updated FE models and values of the key parameters for both models

5 Selection of updating parameters and sensitivity analysis

One of the most critical steps of finite-element model updating process is the identification of the structural parameters that will be used in the process. Depending on the complexity of the FE model there are several parameters, either material or geometric, that can potentially be used in the FE model updating process. However, not each of these potential parameters necessarily impact the dynamic response of the bridge significantly. Therefore, identification of the parameters that significantly affect the bridge response not only reduces the computational cost but also improves the accuracy of the final FE model. In this section, a parametric study that is carried out to determine the parameters that significantly impact the dynamic response of the bridge is summarized.

5.1 Boundary conditions

The boundary conditions, arguably, is the most complex part of the FE model of a structure, especially for a single-span beam bridge. Although often modeled as idealized roller or hinge supports for simplicity, the actual behavior of the boundary conditions can be more complex. In addition, actual boundary conditions tend to alter during the bridge service life due to aging or deterioration. For example, the friction between the superstructure and the substructure as well as the shear keys located at the ends of the abutments can create a very effective restraint in translational directions that are assumed to be free in simplified numerical models. To account for these effects, the translational springs are defined in three perpendicular directions with different spring stiffnesses, K_v, K_t, K_l, where three perpendicular directions are designated as ‘v’, ‘t’ and ‘l’ corresponding to vertical, transverse, and longitudinal directions, respectively. In addition, although the bridge supports are designed to be free to rotate, there are several potential factors that can create rotational stiffness at the ends of the bridge, such as continuity of the railway track and the ballast. To be able to consider the potential effect of these factors on the dynamic behavior of the bridge, two rotational springs, one for the rotation about the transverse axis, KR_t, and one for the rotation about the vertical axis, KR_v, is introduced to the model (Fig. 12). The first of these springs, KR_t, is likely to impact the vertical modes, while the latter, KR_v, can impact the transverse and longitudinal modes.

To determine the influence of the spring stiffnesses on the modal parameters, the frequencies of the first six modes of the analytical model were recorded, while the value of the spring stiffness was modified until no significant change is observed in the modal frequencies. The results are presented in Figs. 13 and 14, for the translational and rotational springs, respectively. Figure 13 shows that the translational spring coefficients in the vertical and transverse directions significantly impact the vibration frequencies. On the other hand, the spring stiffness in the longitudinal direction has virtually no effect on the vibration frequencies. Based on these observations, the longitudinal spring stiffness was decided to be an insignificant parameter as far as finite-element model updating is concerned. In addition, Fig. 14 shows that the rotational stiffness about the vertical axis (KR_v) has virtually no impact on the frequencies of the bridge, while the KR_t impacts the frequencies in the vertical direction, particularly when the value of KR_t is in the range between 10⁵ and 10⁸ kNm/rad. Hence, the rotational stiffness about the vertical axis was not considered in the FE updating process and was set to be equal to zero.

Fig. 13

Change of the natural frequencies of the bridge FE model vs. translational stiffnesses; a vertical stiffness, b transverse direction, c longitudinal stiffness

Fig. 14

Change of the natural frequencies of the bridge FE model vs. rotational spring stiffnesses; a about the transverse axis, b about the vertical axis

Although the frequencies are observed to be sensitive to the rotational stiffness about the transverse axis (KR_t), this does not necessarily validate the inclusion of this parameter in the finite-element model, because the supports at the abutments were originally designed to rotate freely. However, the significant difference between the identified first mode frequency in the vertical direction (3.3 Hz) and that computed from the initial FE model (1.8 Hz) shows that the bridge is much stiffer in the vertical direction than the design assumptions used in the FE model suggests. As a test study, the initial FE model was modified to maximize the frequency of the vertical mode without considering the rotational stiffness. For this, the bridge was modeled using pin supports at the ends, i.e., all the translational springs were set to be infinitely rigid, the modulus of elasticity of concrete was set to be 54 GPa (50% higher than the design value) and the total mass of the bridge was set to be 1.15 times the self-weight of the concrete bridge deck. This model represents the extreme case, where the modulus of elasticity of concrete was set to arguably its maximum realistic value, while the total mass of the bridge was set to its minimum value. Here, it should be noted that, the total mass of the bridge includes the ballast, track, sleepers, and other non-structural elements. Adding the fact that all translational springs were set to be rigid, it is not possible to have a higher frequency from a model, where the ends of the bridge are free to rotate unless either the modulus of elasticity of concrete or the mass of the bridge is set to unrealistic values. As a result of the modal analysis of this extreme model, the frequency of the first vertical mode was computed to be 2.4 Hz, i.e., 27.5% lower than the identified frequency. Further evaluation of the results indicated that including a rotational stiffness about the translational axis at the abutments that simulate different mechanisms such as continuous nature of the railway and aging in the elastomeric bearings is the only option to reach the frequencies identified from the recorded vibrations. As such, this parameter was included in the finite-element model updating process.

5.2 Modulus of elasticity of concrete

Modulus of elasticity of (E_c) is another parameter that influences the stiffness of the structure and hence its modal parameters. To quantify the impact of E_c on the vibration frequencies in the vertical and transverse directions of the bridge, modal analyses were carried out for a range of E_c while keeping the other parameters constant at their design values. It should be highlighted that a single value of E_c is considered for whole the bridge in FE modeling. Any local variation in E_c is due to factors such as deterioration or non-homogenous characteristics of concrete is assumed to be insignificant as far as the global behavior of the bridge is concerned and not considered.

The modulus of elasticity of concrete is a highly variable parameter that is difficult to specify or predict. Conventionally, modulus of elasticity of concrete is expressed in terms of compressive strength in the design standards worldwide. More than 3000 data collected [43] on the relationship between the modulus of concrete and compressive strength of concrete depict the variability of E_c for a given concrete compressive strength. The experimental data shows that E_c varies between 18 and 45 GPa for a compressive strength of 45–50 MPa. Considering the potential increase in the modulus of elasticity of due to aging of the concrete material, upper bound value of the modulus of elasticity of concrete was assumed to be 54 GPa, while the lower bound value was chosen as 18 GPa. Figure 15 shows that vibration frequencies vary significantly with the modulus of elasticity of concrete indicating that this parameter needs to be considered in the finite-element model updating process.

Fig. 15

Variation of natural frequencies with the elasticity modulus of concrete

5.3 Mass of bridge deck

Apart from the stiffness of the structure, mass is the only other parameter that influences the vibration frequencies and the mode shapes of a structure. Although the self-mass of the bridge can be computed accurately and can safely be assumed to be constant during its lifetime, the additional mass on an existing bridge deck due to the trackbed including the ballast and sleepers and other nonstructural parts of the bridge cannot necessarily be computed with sufficient accuracy. In this article, a normalized mass parameter (C_m), defined as the ratio of the total mass of the bridge deck including all the non-structural elements to its self-weight is considered for simplicity. The range of (C_m) used in the sensitivity analysis was determined as 1.15–1.40 based on the site observations and previous experience. As shown in Fig. 16, the normalized bridge mass has an effect, albeit not as significant as some other parameters considered, on the vibration frequencies.

Fig. 16

Variation of natural frequencies with the normalized mass parameter (C_m)

As a result of the sensitivity analysis carried out, five parameters out of the eight investigated were determined to significantly affect the vibration frequencies of the Norddal bridge and were considered in the finite-element model updating process. These parameters are the translational spring coefficients in the vertical and transverse directions (K_v and K_t), rotational spring coefficient about the transverse axis (KR_t), the modulus of elasticity of concrete (E_c), and the normalized mass of the bridge (C_m). Furthermore, the effective range of the parameters, where the vibration frequencies are sensitive to the variations in the parameters were determined to be 1.15–1.40 for C_m, 18–54GPa for E_c, 10⁵–10¹⁰ for K_v and K_t, and 10⁵–10⁸ for KR_t.

6 Neural network-based model updating

Artificial neural networks (ANN) provide an attractive alternative for FE model updating, since it is a robust computing tool to find hidden and complex relationships between a set of data. ANN can learn from events, experiences, and existing patterns by capturing functional relationships between a set of inputs and outputs using the training data. A trained network can then classify and examine new data sets that are in the same characteristics as the training data set and make a prediction for patterns that are not considered during learning [16]. A typical feed-forward neural network consists of an input layer, and output layer and one or more hidden computational units (neurons) that are interconnected. One of the strengths of artificial neural networks is their ability to reproduce and perform nonlinear processes through nonlinear transformation of the weighted sum of inputs to produce an output making them a suitable choice for finite-element model updating tasks [13].

In the ANN-based FE updating of the Norddals bridge, the first six natural frequencies of the bridge identified from the recorded vibrations, three in the vertical direction and three in the transverse direction, (f_v1, f_v2, f_v3, f_t1, f_t2, f_t3), are used as the inputs, and the bridge parameters (K_v, K_t, KR_v, E, C_m) are the outputs of the network. The neural network-based model updating procedure consists of the following steps:

• 1. Determination of the updating parameters and their effective range.

• 2. Identification of the bridge modal parameters from the field test.

• 3. Generating a training data set by repeated FE analyses by randomly changing the values of the updating parameters in their effective range and obtaining the FE model frequency responses.

• 4. Choosing the suitable network and training the network by use of the training data set to learn the relationship between inputs (f_v1, f_v2, f_v3, f_t1, f_t2, f_t3) and outputs (K_v, K_t, KR_v, E, C_m).

• 5. Feeding the identified modal parameters of the bridge into the trained network and obtaining the predicted parameters.

• 6. Updating the FE model using the predicted parameters and analyzing the FE model to obtain the response of the updated model.

• 7. Comparison of the field-measured responses with simulated responses to quantify the accuracy of the updated model and the success of the updating process.

The following subsections present further details and implementation of the model updating process.

6.1 Generating the training data set and training the network

After performing the sensitivity analysis, five bridge parameters (K_v, K_t, KR_v, E, and C_m) are selected as the most important parameters affecting the natural frequencies and their effective range was determined. The best training process is performed with the use of a data set created by randomly selecting different combinations of updating parameters within their effective range as reported by Atalla and Inman [44]. The training data set used in this study was generated through 300 FE analysis, where the values of each parameter was selected randomly within the predetermined range for that parameter. The frequency response from each set of parameters was computed via FE analysis and a database was created.

Hadi [45] evaluated the application of neural networks to concrete structures using different learning algorithms of back-propagation. Backpropagation with Levenberg–Marquardt (LM) algorithm was found to be the most effective algorithm to use in the finite-element model updating of concrete structures. It has the advantage of spending fewer epochs and less time to converge compared to other algorithms. As such, Backpropagation with Levenberg–Marquardt algorithm was selected for the finite-element model updating of the Norddal bridge.

The most widely used network model in structural engineering applications is a multi-layered feed-forward neural network and a typical feed-forward neural network consists of an input layer, an output layer, and one or more hidden (inner) layers [46]. To choose the suitable network architecture, no specific recommendation is outlined in former studies that uses ANN for finite-element model updating and a trial-and-error approach is required to reach the most suitable network architecture. For this, ten different networks with one and two inner layers with different numbers of neurons varying from 8 to 12 were evaluated considering the set of network parameters listed below.

• Share of training sets: 80%.

• Share of cross-validation sets: 20%.

• Number of input layer neurons: 6.

• Number of output layer neurons: 5.

• Activation functions: Sigmoid, Relu function.

• Normalization range: (0.0–1.0).

• Termination rule: minimum cross validation error or maximum epoch.

All ten networks were trained using the training data set and subsequently the identified frequencies from the recorded vibrations were fed into the networks. FE model of the bridge was updated based on each network’s output and the simulated and measured bridge responses were then compared to quantify the performance of the network. The best performance of the network is obtained with one hidden layer including eight neurons. Hence, the architectural form of the network 6–8–5 illustrated in Fig. 17 was found to minimize the error between the identified and estimated vibration frequencies. Furthermore, the activation function of Sigmoid had a better performance in predicting the vibration frequencies compared to the Relu activation function.

Fig. 17

Network architecture used for the model updating process

To evaluate the success of the training algorithm, the prediction error between the training and test samples are plotted in Fig. 18. The results show that the ANN model does not suffer from overfitting as indicated by the difference between the training and testing errors.

Fig. 18

Prediction errors between training and test samples

6.2 Estimation of the updated parameters using the trained ANN

After training the ANN, the identified frequencies from the crossing of the lightweight vehicle using the SSI–COV algorithm are introduced to the trained network as input and the predicted parameters (K_v, K_t, KR_t, E, C_m), which are outputs of the trained network, are obtained and presented in Table 3. The FE model is updated according to these parameters and a modal analysis was performed. The first six natural frequencies of the updated FE model are presented in Table 3 and compared to the identified modal frequencies from the lightweight maintenance vehicle crossings using the SSI–COV algorithm. Also presented in Table 3 are the vibration frequencies computed using the initial FE model based on the design drawings and design material properties. The model updated using the ANN provides very good estimates of the identified vibration frequencies. For the six modes, i.e., the first three modes in the vertical and transverse directions, the average error between the identified and estimated frequencies from the updated model is 3.0% with a maximum error of 8.2% for the second transverse mode (Table 3). On the contrary, the average error between the identified frequencies and those computed using the initial FE model is 27.3% with a maximum of 43.8% observed for the first vertical mode.

Table 3 also shows that, the identified frequencies are much higher compared to those estimated using the initial model in the vertical direction while being much lower than the same in the transverse direction. This indicates that the spring coefficient in the transverse direction used in the initial FE model is much higher compared to the real behavior. This should be expected as infinite stiffness was used as this spring coefficient in the initial FE model, while a finite stiffness coefficient (1.485e6 kN/m) is predicted by the ANN. The bearing stiffness in the transverse direction at the abutments is estimated to be 550 times higher than the shear stiffness of the bearing (1.485e6 kN/m vs. 2667 kN/m). This discrepancy is most likely due to the shear keys that are often used to prevent excessive movements in the transverse direction. However, the details of the shear keys were not available in the design drawings rendering it impossible to compute a realistic value to use in the initial FE model. Therefore, the spring in the transverse direction was modeled using the shear stiffness of the bearing, while the updating process using ANN provided a realistic estimate of the spring coefficient. This observation illustrates the importance of system identification of bridges using recorded vibrations, particularly in the transverse direction, where the estimation of the stiffness provided by the shear keys is often not straightforward. Furthermore, the shear stiffness of the elastomeric bearings provided by the manufacturer does not account for the presence of the vertical load, which is generally very significant, which may lead to a potential underestimation of this stiffness.

Figure 19 depicts the mode shapes identified from the vibration measurements together with their counterparts obtained from the updated FE model. For each mode shape, the modal assurance criterion (MAC) value between the identified and computed mode shapes is also presented. In addition, the MAC values between the identified and computed mode shapes for the first three modes in each direction is plotted in Fig. 20. Except for the third vertical mode and the second transverse mode, the MAC value is over 0.975 indicating a very strong correlation between the identified and computed mode shapes. For these two modes, i.e., the second transverse mode and the third vertical mode, the MAC values are 0.907 and 0.873, respectively, still indicating a very good correlation. The reason for the relatively lower MAC values for these modes can be identified from Fig. 19 as the discrepancy between the mode shapes at the boundaries indicating, once more, the significance of the boundary conditions in the FE model. Attempts to increase the MAC value for these two mode shapes by calibrating the boundary conditions, particularly the translational spring constants in the transverse and vertical directions, led to a decrease in the MAC value for the other mode shapes and a higher discrepancy in the identified and computed vibration frequencies. Hence, it was decided to use the bridge parameters estimated using the ANN as the final parameters. Finally, the cross-correlation between the different modes in both directions indicated by the off-diagonal terms in Fig. 20 are virtually zero providing further assurance that the identified and computed mode shapes have a very strong correlation.

Fig. 19

Comparison of the numerical and field-measured mode shapes for bridge B1; a vertical direction, b transverse direction

Fig. 20

Correlation between analytical and experimental mode shapes using MAC; a vertical direction, b transverse direction

Also plotted in Fig. 19 are the mode shapes obtained from the initial model that is based solely on the design drawings. The improvement in the estimated modal frequencies (Table 3) and the mode shapes through the modal updating process is evident both in the vertical and the transverse directions. The differences between the updated model, initial model and the field-measured mode shapes are especially striking for the first and second transverse modes. In the initial model, the design value for the shear stiffness of the elastomeric bearings, which is a relatively low value is used. As such, the first and second transverse mode shapes are close to a rigid body motion of the deck sliding on the bearings. However, the mode shapes identified from the measured vibrations show a very different response that can be captured by the updated model.

The discrepancy between the updated model and identified mode shapes for the third vertical and second transverse modes plotted in Fig. 19 at the boundaries deserves further attention. A closer look at the mode shapes at the third vertical mode shape (MAC = 0.873) reveal that the identified and computed mode shapes from the updated model are quite close to each other within the first 45 m of the bridge (0–45 m range). However, the two shapes diverge from each other significantly in the final 5 m of the bridge. The sensor locations plotted in Fig. 3 show that there are no sensors in this region, where the discrepancy between the two shapes is highest. In other words, the modal displacements for the identified mode shape in this region are not measured quantities. Instead, they are predicted using a cubic spline function based on the identified modal displacements at the five discrete sensor locations depicted in Fig. 3. On the other hand, the modal displacements from the updated numerical model are computed at a much higher resolution. Focusing only on the region of the bridge, where the sensors are located, i.e., between 5 and 45 m (Fig. 3), the two mode shapes are observed to be in quite a good agreement. However, the lack of sensors closer to the edges lead to the discrepancies at the boundaries amplified by the cubic spline interpolation at these locations.

The second transverse mode shape in Fig. 19 provides a more striking example. The identified mode shape and that computed using the updated numerical model provide a perfect match between the 5 and 45 m of the bridge, i.e., between the two edge sensors (number one and five in Fig. 3). However, the two mode shapes diverge from each other in the first and final 5 m of the bridge, where the identified mode shape is predicted by a spline function. This observation highlights the importance of the spatial resolution of sensors used in the measurements. In particular, placing sensors as close to the edges of the bridge as possible to minimize the uncertainties associated with the use of the spline functions is crucial for reliable mode shape identification.

The estimated normalized mass by the ANN (C_m = 1.302) indicates that mass of the non-structural parts such as ballast and sleepers is approximately 30% of the self-weight of the bridge deck. Furthermore, the modulus of elasticity of concrete was estimated to be 32.71 GPa. As mentioned in Sect. 5.2, the modulus of elasticity of concrete has a very high uncertainty due to the nature of concrete and can be sensitive to several factors, such as temperature and humidity. Therefore, the estimated value can be considered within the acceptable range for C45 concrete as evidenced by the experimental data provided in [43] and does not necessarily provide any information regarding the condition of the bridge.

6.3 Dynamic response under loaded iron ore train

To be able to evaluate the efficacy of the updated model to emulate the dynamic response of the bridge under loaded iron ore trains, a moving load analysis was conducted. The accelerations computed from the moving load model were compared with those recorded during a train crossing. The iron ore train was modeled as a series of moving loads that is equal to the axle load of the loaded train, i.e., 300 kN. The iron ore train has, in total, 256 axles and its total length is approximately 800 m. The speed of the train crossing recorded on site was not known. However, the speed limit on the bridge is 50 km/h and it was assumed this speed represents the reality successfully. As such, the dynamic analysis on the updated model was run with a train speed of 50 km/h.

The acceleration response at the mid-span from the field measurements and the updated numerical model is depicted in Fig. 21. The field-measured and numerical responses are, in general, in good agreement with each other. This is even though the numerical model considers neither the vehicle bridge interaction as the train loads is modeled as moving loads nor the track irregularities that can impact the acceleration response of the bridge. Here, it should be noted that modeling the vehicle bridge interaction and the track irregularities is beyond the scope of this study, because the current study focuses mainly on the modal response of the bridge. The dynamic analysis results provided are only to show that the updated numerical model provides reasonable acceleration response compared to the field-measured response.

Fig. 21

Acceleration response at the mid-span measured on-site and obtained from updated numerical model

7 Conclusions

This study aims to identify the modal parameters of a single-span prestressed concrete railway bridge and update its FE model using artificial neural networks so that the FE model replicate the observed behavior, particularly its boundary conditions. The research was divided into two main parts: (i) the identification of the modal parameters of the bridge from the free decay responses caused by various train-induced excitations including 23 different train crossings categorized into three groups according to the train type using FDD and SSI–COV algorithms (ii) FE model updating with a focus on constraining effect of the boundary conditions represented by both translational and rotational stiffness at the supports to establish a more accurate FE model. Artificial Neural Network (ANN) was used to identify the relationship between the FE model response of the bridge and the key bridge parameters. This relationship was then used to estimate the values of these key bridge parameters using the identified vibration frequencies. The following conclusions can be drawn from the conducted study:

• The identified frequencies show a significant variance, specifically for higher modes, from one train crossing to another. In addition, a higher standard deviation was observed for identified frequencies using the loaded iron ore train crossings, while the identified frequencies using the lightweight vehicle crossings showed lower discrepancies. Although the vibrations during the free decay phase of the train crossings were used for modal identification, the influence of the mass of the train on the identified natural frequencies can be clearly observed causing a reduction in the vertical and transverse modal frequencies.

• The mean identified natural frequencies using the different OMA algorithms (FDD and SSI–COV) were in good agreement, with a difference of less than 3% in most cases. The variation in the frequencies from one train crossing to the other identified using the FDD algorithm was relatively larger compared to that from the SSI–COV algorithm.

• Furthermore, FDD and SSI–COV algorithms provided similar mode shapes for all the investigated mode shapes with MAC values higher than 0.90. Considering the similarity of the identified frequencies and mode shapes, it can be concluded that FDD and SSI–COV provide very similar estimates of the modal parameters.

• The mean identified mode shapes from different train types are, in general, close to each other indicating that mode shapes can be reliably extracted from a population of train crossings for simply supported bridges.

• Even though the bridge is completely straight with no skewness in plan and the main direction of the loading exerted by the train loading is vertical, the vibrations in the transverse direction had sufficient energy to enable identification of the mode shapes in the transverse direction.

• Due to influence of the additional mass of the train on the identified frequencies, it is concluded that the results from the lightweight maintenance vehicle crossing are more likely to be close to the modal parameters of the bridge compared to the identified parameters from loaded and unloaded iron ore train crossings.

• The sensitivity analysis and the modal updating process conducted highlighted the importance of the boundary conditions on the modal parameters of the bridge. More specifically, the boundary conditions that are often assumed to be free such as the rotational stiffness at the abutments may deviate from the assumed value due to different mechanisms, such as continuous nature of the railway and aging in the elastomeric bearings. Consideration of these parameters in the modal updating process can prove to be crucial to be able to simulate the observed behavior of the bridge.

• In the transverse direction, the behavior of the bridge was shown to be very sensitive to the stiffness provided by the shear action in the elastomeric bearing and the shear keys, which are very difficult to compute from product descriptions and design drawings only. Using recorded vibrations and the identified modal parameters to estimate this stiffness was instrumental in simulating the behavior of the bridge in the transverse direction.

• By updating the key parameters using ANN, a finite-element model that can reliably simulate the observed behavior of the bridge as demonstrated by the very low error between the identified and estimated modal frequencies and the high MAC values was obtained.

• The identified mode shapes can be vulnerable to uncertainties at the boundaries if the outermost sensors are not placed close enough to the edges of the bridge. These uncertainties can be amplified by the use of spline functions to increase the spatial resolution of the identified mode shapes.

• Supplementing the acceleration measurements by measuring other structural response parameters such as the displacements at the abutments during the train crossings is likely to provide further insight into the critical boundary conditions and should be considered in future studies.