Morelli-Włodarczyk cobordism and examples of rooftop flips

Abstract

We introduce the notion of rooftop flip, namely a small modification among normal projective varieties which is modeled by a smooth projective variety of Picard number 2 admitting two projective bundle structures. Examples include the Atiyah flop and the Mukai flop, modeled respectively by $\mathbb {P}^1\times \mathbb {P}^1$ and by $\mathbb {P}\left( T_{\mathbb {P}^2}\right)$. Using the Morelli-Włodarczyk cobordism, we prove that any smooth projective variety of Picard number 1, endowed with a ${\mathbb C}^*$-action with only two fixed point components, induces a rooftop flip.

1 Introduction

The relation between birational geometry and ${\mathbb C}^*$-actions has been deeply studied over the years (see for instance [19, 20] and in recent years [16]). One famous example for instance is the notion of Morelli-Włodarczyk cobordism (cf. [22, Definition 2], see Definition 2.3), introduced to study birational maps among normal projective varieties which are realized as geometric quotients by a ${\mathbb C}^*$-action. This algebraic version of cobordism has been used to prove the Weak factorization conjecture (see [22]).

On the other hand, the relation between birational maps and ${\mathbb C}^*$-actions becomes evident in the example of the Atiyah flop (see [19, Sect. 1.3]). Consider the ${\mathbb C}^*$-action on ${\mathbb C}^4$ given by

$$\begin{aligned} t \cdot \left( x_0,x_1,y_0,y_1\right) =\left( tx_0,tx_1,t^{-1}y_0,t^{-1}y_1\right) , \end{aligned}$$

where $t\in {\mathbb C}^*$ and $(x_0,x_1,y_0,y_1)\in {\mathbb C}^4$. The GIT quotient ${\mathbb C}^4\rightarrow {\mathbb C}^4\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ is the affine cone over the Segre embedding of $\mathbb {P}^1 \times \mathbb {P}^1$. The variety ${\mathbb C}^4 \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ has a cone singularity at the origin, which can be resolved by blowing-up the vertex of the cone. The exceptional divisor $\mathbb {P}^1\times \mathbb {P}^1$ of the blow-up can be contracted in two different ways, producing two smooth varieties $X_1$ and $X_2$, which are isomorphic on the complement of a closed subset of codimension equal to 2. The resulting birational map $X_1 \dashrightarrow X_2$ is called the Atiyah flop and ${\mathbb C}^4$ is an example of cobordism associated to it. The following picture summarizes the example:

One may generalize this example by considering a similar ${\mathbb C}^*$-action on ${\mathbb C}^{n+1}$ (see for instance [22, Example 1]), or allowing also weights different from $\pm 1$ (cf. [1, Sect. 3]): the resulting birational map is called the Atiyah flip. In the above construction of the Atiyah flop, the varieties $X_1$ and $X_2$ are defined using the two projective $\mathbb {P}^1$-bundle structures on $\mathbb {P}^1 \times \mathbb {P}^1$. Smooth projective varieties with two different projective bundle structures have been already studied in the literature (see for instance [14]): in particular, in [16, Lemma 4.4] the authors have constructed a correspondence between them and smooth projective varieties of Picard number 1 admitting a ${\mathbb C}^*$-action having only two fixed point components.

Motivated by the example of the Atiyah flop and its connection with a variety admitting two projective bundle structures, we introduce the notion of rooftop flip. Given a smooth projective variety $\Lambda$ of Picard number 2 admitting two projective bundle structures,

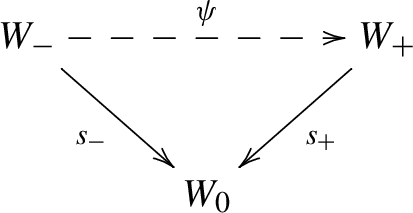
a rooftop flip modeled by $\Lambda$ (see Definition 3.12) is a commutative diagram between normal quasi-projective varieties

where $\psi$ is a small modification and $s_{\pm }$ are small contractions, which can be resolved by a common divisorial contraction

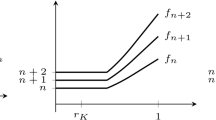
whose exceptional loci over $W_0$ behave fiberwise as in Diagram 1.

In this setting, the Atiyah flop is a rooftop flip modeled by $\mathbb {P}^1\times \mathbb {P}^1$. As we will see, the class of rooftop flips includes classical birational transformations: the Atiyah flip is a rooftop flip modeled by $\mathbb {P}^m\times \mathbb {P}^l$, and the Mukai flop (see [6, 21]) is a rooftop flip modeled by $\mathbb {P}\left( T_{\mathbb {P}^2}\right)$. In the paper we discuss the definition of rooftop flip and its connection with smooth projective varieties having a ${\mathbb C}^*$-action with only two fixed point components. Our main result is the following:

Theorem 1.1

Given a smooth projective variety $\Lambda$ of Picard number 2 with two projective bundle structures, there exists a rooftop flip modeled by $\Lambda$.

1.1 Outline

In Sect. 2 we recall some notions regarding ${\mathbb C}^*$-actions on smooth polarized pairs and we recall the definition of Morelli-Włodarczyk cobordism (see Definition 2.3).

We begin Sect. 3 by focusing on the case of ${\mathbb C}^*$-actions whose associated fixed point locus consists only of 2 connected components; such varieties are called drums (see Definition 3.3) and they are constructed upon the choice of a triple $(Y,{\mathcal L}_-,{\mathcal L}_+)$, where Y is a smooth projective variety of Picard number 2 admitting two projective bundle structures, and ${\mathcal L}_{\pm }$ are semiample line bundles on Y. We then introduce and discuss the notion of rooftop flip (see Definition 3.12), and we state our main result, namely Theorem 1.1. We conclude by revisiting the example of Atiyah flip and prove that it is indeed a rooftop flip (see Sect. 3.3).

In Sect. 4 we prove Theorem 1.1. The idea of the proof is to view our case as a restriction of the Morelli-Włodarczyk cobordism associated to the Atiyah flip. We conclude by deducing that the drum structure on the smooth quadric hypersurface induces a rooftop flip modeled by $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$ (see Corollary 4.6).

2 Preliminaries

2.1 Notation

We work over ${\mathbb C}$. In this paper X will be a smooth projective variety. We denote by $\rho _X:= \dim {\mathop {\mathrm{N^1}}\nolimits }(X)$ the Picard number of X, where ${\mathop {\mathrm{N^1}}\nolimits }(X)$ is the finite-dimensional real vector space of Cartier divisors modulo numerical equivalence. Given V a finite-dimensional vector space, by $\mathbb {P}\left( V\right)$ we mean the space of one-dimensional quotients of V. The standard ${\mathbb C}^*$-action by homoteties is denoted by ${\mathbb C}^*_h$, with coordinate h. For sake of notation, by t we will denote the coordinate of a ${\mathbb C}^*$-action which does not act by homoteties. By a contraction we mean a proper surjective morphism with connected fibers. A birational contraction f is small if . By a flip we mean a D-flip as in [5, Definition 5.1.4].

2.2 ${\mathbb C}^*$-actions on smooth projective varieties

In this section we collect some preliminaries about ${\mathbb C}^*$-actions on smooth projective varieties. We refer to [16, Sect. 2] for a detailed discussion.

Let X be a smooth projective variety endowed with a ${\mathbb C}^*$-action. By $X^{{\mathbb C}^*}$ we denote the fixed point locus of the action, and by ${\mathcal Y}$ its set of connected components, namely:

$$X^{{\mathbb C}^*}=\bigsqcup _{Y \in {\mathcal Y}} Y.$$

By [7, Main Theorem], the subvarieties $Y\in {\mathcal Y}$ are smooth and irreducible.

For any $Y\in {\mathcal Y}$, we define the Białynicki-Birula cells as

$$\begin{aligned} X^{\pm }(Y):=\left\{ x\in X:\lim _{t\rightarrow 0}t^{\pm 1}\cdot x\in Y\right\} . \end{aligned}$$

The sink (resp. source) of the ${\mathbb C}^*$-action is the unique component $Y_-\in {\mathcal Y}$ (resp. $Y_+\in {\mathcal Y}$) such that $X^-(Y_-)$ (resp. $X^+(Y_+)$) are dense subsets of X. As noticed in [16, Remark 2.5], the uniqueness of the sink and the source follows from the well-known Białynicki-Birula Theorem (see [2] for the original exposition).

Definition 2.1

A ${\mathbb C}^*$-action is equalized at $Y\in {\mathcal Y}$ if for every point $p\in \left( X^-(Y)\cup X^+(Y)\right) \setminus Y$ the isotropy group of the ${\mathbb C}^*$-action at p is trivial. Moreover, a ${\mathbb C}^*$-action is equalized if it is equalized at every fixed point component $Y\in {\mathcal Y}$.

Let L be an ample line bundle on X. Consider the induced ${\mathbb C}^*$-action on L; by [11, Proposition 2.4 and the subsequent Remark], a linearization of L exists. For any $Y\in {\mathcal Y}$, the induced action of ${\mathbb C}^*$ on the fibers of $L|_{Y}$ is by multiplication with a character, which we denote by $\mu _L(Y) \in {\mathbb Z}$. Since L is ample, one may show (see for instance [16, Remark 2.12]) that

$$\begin{aligned} \mu _L(Y_-)=\min _{Y\in {\mathcal Y}}\mu _L(Y), \qquad \mu _L(Y_+)=\max _{Y\in {\mathcal Y}}\mu _L(Y). \end{aligned}$$

By a ${\mathbb C}^*$-action on a smooth polarized pair (X, L) we mean a non-trivial ${\mathbb C}^*$-action on a smooth projective variety X and a linearization of the ample line bundle L.

Definition 2.2

Let X be a smooth projective variety and let $L\in \mathop {\textrm{Pic}}\nolimits (X)$ be ample. The bandwidth of the ${\mathbb C}^*$-action on (X, L) is defined as

$$\begin{aligned} |\mu _L|:=\mu _L(Y_+)-\mu _L(Y_-). \end{aligned}$$

2.3 Morelli-Włodarczyk cobordism

We recall the notion of Morelli-Włodarczyk cobordism: it was first introduced by Morelli in the case of toric varieties (see [12]), and then generalized by Włodarczyk (see [22]).

Definition 2.3

Let $X_1,X_2$ be birationally equivalent normal varieties. The Morelli–Włodarczyk cobordism between $X_1$ and $X_2$ is a normal variety B, endowed with a ${\mathbb C}^*$-action such that

$$\begin{aligned} \begin{aligned} B_+&=\{p\in B\mid \lim _{t\rightarrow 0} tp \text { does not exists}\},\\ B_-&=\{p\in B\mid \lim _{t\rightarrow \infty } tp \text { does not exists}\} \end{aligned} \end{aligned}$$

are non-empty open subsets of B, such that there exist geometric quotients $B_-/{\mathbb C}^*$ and $B_+/{\mathbb C}^*$ satisfying

$$\begin{aligned} B_-/{\mathbb C}^*\simeq X_1 \dashrightarrow X_2\simeq B_+/{\mathbb C}^*, \end{aligned}$$

where the birational equivalence is realized by the open subset $(B_-\cap B_+)/{\mathbb C}^*$ contained in $B_{\pm }/{\mathbb C}^*$.

We stress that the notation in the above definition is slightly different from the original one (cf. [22, Definition 2]), in particular the role on $B_-$ and $B_+$ are switched. The reason behind this apparent misleading decision is that in this setting it will be less confusing in the forthcoming sections to keep track of the ±-signs.

3 Smooth drums and rooftop flips

3.1 Smooth drums

We refer to [16, Sect. 4] for details.

Set-up 3.1

Let Y be a smooth projective variety such that $\rho _Y=2$, admitting two projective bundle structures $p_{\pm }:Y\rightarrow Y_{\pm }$, with $Y_{\pm }$ smooth. Let $L_{\pm }$ be very ample line bundles on $Y_{\pm }$, and set ${\mathcal L}_{\pm }:=p_{\pm }^*L_{\pm }$. Suppose that $\mathop {\textrm{deg}}\nolimits ({\mathcal L}_{\mp }|_{F_{\pm }})=1$, where $F_\pm$ denotes a fiber of $p_\pm$. Let $\pi : \mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)\rightarrow Y$ be the associated projective bundle.

Lemma 3.2

In the situation of Set-up 3.1, ${\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1)$ is globally generated, and there exists a contraction, birational onto the image,

$$\begin{aligned} \phi =\phi _{{\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1)}:\mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right) \longrightarrow \mathbb {P}\left( {{\,\textrm{H}\,}}^0\left( \mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+), {\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1)\right) \right) . \end{aligned}$$

Proof

The global generation of ${\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1)$ is immediate. Let us prove that the morphism

$$\begin{aligned} \phi : \mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right) \rightarrow \mathbb {P}\left( {{\,\textrm{H}\,}}^0(Y_-,L_-)\oplus {{\,\textrm{H}\,}}^0(Y_+,L_+)\right) , \end{aligned}$$

associated to evaluation of sections is a contraction, birational onto the image. Consider the sections $\sigma _{\pm }: Y\rightarrow \mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right)$ associated to the quotients ${\mathcal L}_-\oplus {\mathcal L}_+\rightarrow {\mathcal L}_{\pm }$. The compositions $\phi \circ \sigma _{\pm }$ coincide with the bundle maps $p_{\pm }$, in particular they have connected fibers. On the other hand the restriction of $\phi$ to $\mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right) {\setminus } \left( \sigma _-(Y)\cup \sigma _+(Y)\right)$ is an isomorphism onto the image. $\square$

Definition 3.3

The image $X:=\phi \left( \mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)\right)$ is called the drum constructed upon the triple $(Y,{\mathcal L}_-,{\mathcal L}_+)$.

We can summarize the above construction by means of the following diagram:

Theorem 3.4

[16, Lemma 4.4] A drum X is smooth if and only if the following conditions are satisfied:

• ${\mathop {\textrm{Nef}}\nolimits }(Y)=\langle {\mathcal L}_-,{\mathcal L}_+ \rangle$;

• $p_\pm : Y\rightarrow Y_\pm$ has a projective bundle structure;

• $\mathop {\textrm{deg}}\nolimits ({\mathcal L}_{\mp }|_{F_{\pm }})=1$, where $F_\pm$ denotes a fiber of $p_\pm$.

Remark 3.5

Notice that X comes with a natural ample line bundle L, which is the restriction of the hyperplane class in $\mathbb {P}\left( {{\,\textrm{H}\,}}^0(Y,{\mathcal L}_-\oplus {\mathcal L}_+)\right)$, such that $\phi ^*L={\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1)$.

Lemma 3.6

[16, Remark 4.2] In the situation of Set-up 3.1, there exists a ${\mathbb C}^*$-action on $(\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+),{\mathcal {O}}_{{\mathcal L}_-\oplus {\mathcal L}_+}(1))$ of bandwidth 1 with sink $\sigma _-(Y)$ and source $\sigma _+(Y)$, where $\sigma _{\pm }$ are the sections associated to the quotients ${\mathcal L}_-\oplus {\mathcal L}_+\rightarrow {\mathcal L}_{\pm }$. Moreover, the contraction $\phi$ is ${\mathbb C}^*$-equivariant, and the induced ${\mathbb C}^*$-action on (X, L) has bandwidth 1 with sink $Y_-$ and source $Y_+$.

Theorem 3.7

[16, Theorem 4.8] Let X be a smooth projective variety with $\rho _X=1$ different from the projective space and let L be an ample line bundle on X. Then (X, L) admits a ${\mathbb C}^*$-action of bandwidth 1 if and only if X is a smooth drum.

Remark 3.8

Consider the ${\mathbb C}^*$-action obtained by composing the induced action of $\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)$ with the morphism ${\mathbb C}^*\rightarrow {\mathbb C}^*$, $t\mapsto t^2$. The resulting action on $(X,{\mathcal {O}}_X(1))$ is not faithful, has bandwidth 2 and up to a character we may assume that $\mu _{{\mathcal {O}}_X(1)}(Y_{\pm })=\pm 1$. We obtain an induced action of ${\mathbb C}^*$ on ${{\,\textrm{H}\,}}^0(X,{\mathcal {O}}_X(1))^\vee$ of the form $t\cdot (v_-,v_+)=(tv_-,t^{-1}v_+)$, with $v_-\in {{\,\textrm{H}\,}}^0(Y_-,L_-)^\vee$, $v_+\in {{\,\textrm{H}\,}}^0(Y_+,L_+)^\vee$.

Example 3.9

Consider $Y_-=\mathbb {P}^m, Y_+=\mathbb {P}^l$, let $Y=\mathbb {P}^m \times \mathbb {P}^l$, and let $p_\pm$ be the projections onto the two factors of $\mathbb {P}^m \times \mathbb {P}^l$. Set $L_-={\mathcal {O}}_{\mathbb {P}^m}(1)$ and $L_+={\mathcal {O}}_{\mathbb {P}^l}(1)$. Then ${\mathcal L}_-={\mathcal {O}}_{\mathbb {P}^m \times \mathbb {P}^l}(1,0)$, ${\mathcal L}_+={\mathcal {O}}_{\mathbb {P}^m \times \mathbb {P}^l}(0,1)$, and we have a diagram of the form

We obtain that $X\simeq \mathbb {P}^{m+l+1}$, that is $\mathbb {P}^{m+l+1}$ is the drum constructed upon

$$\begin{aligned} \left( \mathbb {P}^m\times \mathbb {P}^l, {\mathcal {O}}_{\mathbb {P}^m\times \mathbb {P}^l}(1,0),{\mathcal {O}}_{\mathbb {P}^m\times \mathbb {P}^l}(0,1)\right) . \end{aligned}$$

Moreover, the ${\mathbb C}^*$-action on $(X,{\mathcal {O}}_X(1))$ given by

$$\begin{aligned} t \cdot \left[ x_0:\ldots :x_{m+l+1}\right] =\left[ tx_0:\ldots :t x_{m}:x_{m+1}:\ldots :x_{m+l+1}\right] . \end{aligned}$$

has bandwidth 1, with sink $\mathbb {P}^m=\left\{ x_{0}=\ldots =x_{m}=0\right\}$ and source $\mathbb {P}^l=\left\{ x_{m+1}=\ldots =\right.$$\left. x_{m+l+1}=0\right\}$.

Finally, let $\hat{X}$ be the affine cone over X and consider the induced ${\mathbb C}^*$-action of Remark 3.8. We obtain that

$$\begin{aligned} B_-=\hat{X}\setminus Z(y_0,\ldots ,y_{m}),\qquad B_+=\hat{X}\setminus Z(x_0,\ldots ,x_{l}), \end{aligned}$$

where we denote by $y_0,\ldots ,y_{m}$ (resp. $x_0,\ldots ,x_{l}$) the coordinates on which ${\mathbb C}^*$ acts with positive (resp. negative) weights, and $B_{\pm }$ the non-empty open subsets of Definition 2.3. Moreover there exists a birational map among the geometric quotients $\psi : B_-/{\mathbb C}^*\dashrightarrow B_+/{\mathbb C}^*$ which, as we will see in Sect. 3.3, is a rooftop flip modeled by $\mathbb {P}^m\times \mathbb {P}^l$.

Example 3.10

Consider the ${\mathbb C}^*$-action on $\mathbb {P}^{2n+1}$ defined as follows:

$$\begin{aligned} t \cdot \left[ x_0:\ldots :x_{2n+1}\right] =\left[ tx_0:\ldots :tx_n: x_{n+1}:\ldots :x_{2n+1}\right] . \end{aligned}$$

Let $Q^{2n} \subset \mathbb {P}^{2n+1}$ be the smooth quadric hypersurface defined by the equation $x_0x_{n+1}+x_1x_{n+2}+\ldots +x_nx_{2n+1}=0$. By construction $Q^{2n}$ is ${\mathbb C}^*$-invariant and its fixed point locus consists only of the sink and the source, which are respectively:

$$\begin{aligned} Y_-=\left\{ x_{n+1}=\ldots =x_{2n+1}=0\right\} \simeq \mathbb {P}^n, \qquad Y_+=\left\{ x_0=\ldots =x_n=0\right\} \simeq (\mathbb {P}^n)^\vee , \end{aligned}$$

where the duality between $Y_-$ and $Y_+$ is provided by the non-degenerate quadratic form defining $Q^{2n}$. Since the ${\mathbb C}^*$-action on $(Q^{2n},{\mathcal {O}}_{Q^{2n}}(1))$ has bandwidth 1, using Theorem 3.7 we argue that $Q^{2n}$ is a smooth drum. By [18, Proposition 1.9], the smooth projective variety of Picard number 2 associated to this drum is

where the two projective bundle structures are induced by the well known description $\mathbb {P}\left( T_{\mathbb {P}^n}\right) =\left\{ (p,H)\in \mathbb {P}^n\times (\mathbb {P}^n)^\vee \mid p\in H\right\}$. Let us briefly explain this fact; let X be the smooth drum associated to $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$. Then $X \subset \mathbb {P}^{2n+1}$ and, by Remark 3.6, the sink and the source of the ${\mathbb C}^*$-action on X are respectively $\mathbb {P}^n$, $(\mathbb {P}^n)^\vee$. Write $\mathbb {P}^n=\mathbb {P}\left( V\right)$, $(\mathbb {P}^n)^\vee =\mathbb {P}\left( V^\vee \right)$, with V a complex vector space of dimension $n+1$. By construction the drum X of $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$ is an hypersurface in $\mathbb {P}\left( V\oplus V^\vee \right)$. A point in $\mathbb {P}\left( V\oplus V^\vee \right)$ belongs to X if it is the class of a vector $p+ h\in V\oplus V^\vee$ such that $h(p)=0$. Algebraically this says that X is given by a nondegenerate quadratic equation, hence we conclude.

Following Remark 3.8, consider the induced ${\mathbb C}^*$-action on $\hat{Q}^{2n}\subset {\mathbb C}^{2n+2}$ obtained by the restriction of the action $t\cdot (v_-,v_+)=(tv_-,t^{-1}v_+)$, with $v_-\in {\mathbb C}^{n}$, $v_+\in {\mathbb C}^{n}$.

As we will see in Corollary 4.6, there exists a birational map $\psi : \hat{Q}^{2n}\cap B_-/{\mathbb C}^*\dashrightarrow \hat{Q}^{2n}\cap B_+/{\mathbb C}^*$, which is a rooftop flip modeled by $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$. For $n=2$ this is the classic Mukai flop (see [6, 21]).

Remark 3.11

To our understanding, the only known examples of smooth drums are constructed upon a smooth projective variety Y admitting two projective bundle structures such that $Y_\pm$ are rational homogeneous varieties, i.e. quotient of semisimple linear algebraic groups by parabolic subgroups. Except for a non-homogeneous sporadic example appearing in [17] (see also [9, Sect. 2]), in all the known examples Y is also a rational homogeneous variety. In [14, Remark 3.3] there is a complete classification of rational homogeneous varieties with Picard number 2 admitting two projective bundle structures. The corresponding smooth drums X constructed from a rational homogeneous variety Y are well-known in literature: they are smooth projective horospherical varieties classified by Pasquier, see [18, Theorem 0.1].

3.2 Rooftop flips

Definition 3.12

Consider a normal projective variety $\Lambda$ with $\rho _{\Lambda }=2$ admitting two projective bundle structures:

A small modification $\psi : W_- \dashrightarrow W_+$ between normal quasi-projective varieties is called a rooftop flip modeled by $\Lambda$ if the following hold:

• (1) There are small contractions $s_\pm : W_{\pm }\rightarrow W_0$, with $W_0$ a normal quasi-projective variety,

  

  such that, denoting by $Z_\pm \subset W_\pm$ their exceptional loci, the restrictions $s_\pm |_{Z_\pm }: Z_\pm \rightarrow Z_0 \subset W_0$ are smooth and the fibers are $\Lambda _\pm$-bundles.

• (2) There is a resolution

  

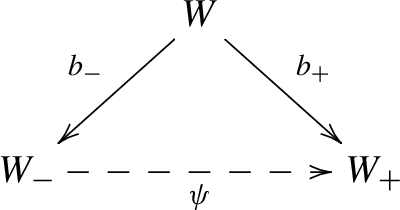
  such that $Z:=b_\pm ^{-1}(Z_\pm ) \subset W$ is a divisor, and $b_\pm |_Z: Z \rightarrow Z_\pm$ defines projective bundle structures on Z.

• (3) For any $z_0 \in Z_0$ we have that $b^{-1}_\pm |_{s^{-1}_\pm (z_0)}=p_\pm ^{-1}$:

  

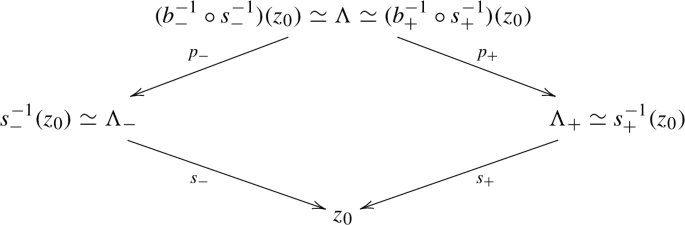
The reason behind the choice of the name  “rooftop” , is motivated by the form of the last diagram above. Moreover, the term   “roof”  has been already used in the literature (see for instance [10, Definition 0.1]) to denote certain varieties with two projective bundles structures.

Remark 3.13

A birational map $\chi : X_-\dashrightarrow X_+$ between smooth projective varieties is a K-equivalent simple map if there exists a resolution of indeterminacy

by a smooth projective variety $\widetilde{X}$ such that $f_{\pm }$ are smooth blow-ups and $f^*_-K_{X_-}=f^*_+K_{X_+}$. Let us notice that the notion of rooftop flip is similar to a characterization of K-equivalent simple maps done in [10, Theorem 0.2]. However, in a rooftop flip the fibers of the double projective bundle structure may have different dimensions, in contrast to the case of K-equivalent simple map where by construction they are the same. With this in mind, rooftop flips modeled by $\mathbb {P}^m\times \mathbb {P}^m$ and by $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$ are examples of K-equivalent simple maps (see for instance [10, Examples 5.1, 5.2]).

Remark 3.14

Given a ${\mathbb C}^*$-action on a polarized pair (X, L), one may construct several geometric quotients which parametrize different ${\mathbb C}^*$-invariant open subsets of stable points (see for instance [15, Construction 1]). Moreover, as noticed in [15, Remark 2.13] there exist birational maps among those geometric quotients; in particular, if X is smooth and the ${\mathbb C}^*$-action is equalized, the birational maps among the geometric quotients can be blow-ups, blow-downs and Atiyah flips (see [15, Theorem 1.1 (1)]). More generally, as noticed in [3, Remark 11.1.2], the birational maps associated to ${\mathbb C}^*$-actions on smooth varieties factorize as locally toric flips, whose local models have been described by Morelli and Włodarczyk (see [22]). If we want to see other type of flips as maps induced by ${\mathbb C}^*$-actions, we must consider ${\mathbb C}^*$-actions on singular varieties. For instance, in [4], the autors show that the Cremona transformation of [8] is induced by an action of ${\mathbb C}^*$ on a certain singular variety, and the birational map among the geometric quotients factorizes as a blow-up, a Mukai flop and a blow-down.

We can now state our main result, which we will prove in Sect. 4:

Theorem 3.15

Let X be a smooth drum constructed upon $(Y,{\mathcal L}_-,{\mathcal L}_+)$, and denote by $\hat{X}$ its affine cone. Then there exist a rooftop flip

$$\psi : \hat{X}\cap B_-/{\mathbb C}^*\dashrightarrow \hat{X}\cap B_+/{\mathbb C}^*$$

modeled by Y.

3.3 Atiyah rooftop flips

In this section we show that the Atiyah flip is in particular a rooftop flip modeled by $\mathbb {P}^{m}\times \mathbb {P}^{l}$. Let us recall that such example can be also easily described using toric geometry; in particular the birational map is induced by two different subdivisions of a cone. We refer to [1, Sect. 3] for a detailed discussion from the toric point of view.

Set-up 3.16

Let $V_-$ and $V_+$ denote the complex vector spaces of dimension respectively $m+1$ and $l+1$, with $l,m\ge 1$, and set $V:=V_-\oplus V_+$. Consider the ${\mathbb C}^*$-action on V having weight $-1$ on $V_-$ and weight 1 on $V_+$. There is an induced ${\mathbb C}^*$-action on $V^\vee$ given by $t\cdot v= \left( t v_-,t^{-1}v_+\right)$, where $v=\left( v_-,v_+\right) \in V^\vee$. We will frequently abuse notation by writing $V_{-}$ (resp. $V_+$) for $V_-\times \{0\}$ (resp. $\{0\}\times V_+$).

Fig. 1

A picture of the ${\mathbb C}^*$-action on $V^\vee$

Remark 3.17

The restriction of the ${\mathbb C}^*$-action on $V^\vee$ defined in Set-up 3.16 to $V_-^\vee$ (resp. $V_+^\vee$) coincides with ${\mathbb C}^*_h$-action on $V^\vee _-$ (resp. $V^\vee _+$) by homoteties.

The fixed point locus of this action on $V^\vee$ given in Set-up 3.16 coincides with the origin. We can consider the induced ${\mathbb C}^*$-action of the coordinate ring of $V^\vee$, namely ${\mathbb C}[V^\vee ]={\mathbb C}\left[ y_0,\ldots ,y_m,x_0,\ldots ,x_l\right]$. The GIT-quotient

$$\begin{aligned} V^\vee \rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*:=\mathop {\textrm{Spec}}\nolimits {\mathbb C}[V^\vee ]^{{\mathbb C}^*} \end{aligned}$$

is the affine cone over the Segre embedding of $\mathbb {P}\left( V_-\right) \times \mathbb {P}\left( V_+\right) \simeq \mathbb {P}^m \times \mathbb {P}^l$, therefore singular at the origin of $V_-^\vee \otimes V_+^\vee$.

Remark 3.18

Under the notation of Definition 2.3, we have that

$$\begin{aligned}&B_- \simeq V^\vee \setminus \left\{ y_0=\ldots =y_m=0\right\} ,\\&B_+\simeq V^\vee \setminus \left\{ x_0=\ldots =x_l=0\right\} . \end{aligned}$$

In particular $B_{\pm }$ are non-empty open subsets of stable points under the ${\mathbb C}^*$-action, therefore we have two geometric quotients $B_{\pm }\rightarrow B_{\pm }/{\mathbb C}^*$.

Lemma 3.19

The geometric quotients $B_-/{\mathbb C}^*$ and $B_+/{\mathbb C}^*$ are birational, and the exceptional locus of the birational map $\psi : B_-/{\mathbb C}^*\dashrightarrow B_+/{\mathbb C}^*$ is $\mathbb {P}\left( V_-\right)$. In particular, $\psi$ is a small modification.

Proof

Notice that $B_-/{\mathbb C}^*$ and $B_+/{\mathbb C}^*$ are birational since they contain the open subset $\left( B_-\cap B_+\right) /{\mathbb C}^*\ne \emptyset$. Let us study the exceptional locus of $\psi$. It suffices to show that $V_-^\vee \setminus 0\subset B_-$ (then $\mathbb {P}\left( V_-\right) \subset B_-/{\mathbb C}^*$) and that $V_-^\vee {\setminus } 0\not \subset B_+$. Let $p\in \mathbb {P}\left( V_-\right)$, and consider the associated line $\hat{p}$ in $V_-^\vee$ passing through the origin. Then $\hat{p}=\left( hv_-,0\right)$, for $h\in {\mathbb C}^*_h$ and $v_-\in V_-^\vee$. For any point $q\in \hat{p} {\setminus } 0$ we have that that $\lim _{t\rightarrow \infty } t\cdot q$ does not exist, hence every point q of $\hat{p}\setminus 0$ belongs to $B_-$. By Remark 3.17, the restriction of the ${\mathbb C}^*$ on $V_-^\vee {\setminus } 0$ coincides with the action by homoteties, so we have that $p\in B_-/{\mathbb C}^*$. On the other hand it is easy to see that $\lim _{t\rightarrow 0} t\cdot q$ exists, hence $q\notin B_+$. Finally $\psi$ is a small modification since $\mathop {\textrm{codim}}\nolimits _{B_-/{\mathbb C}^*} \text {Exc}(\psi )\ge 2$. $\square$

Corollary 3.20

The exceptional locus of $\psi ^{-1}: B_+/{\mathbb C}^*\dashrightarrow B_-/{\mathbb C}^*$ is $\mathbb {P}\left( V_+\right)$.

Remark 3.21

Let $\beta : W\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ be the blow-up of $V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ along the origin. Then the exceptional divisor is $\mathbb {P}\left( V_-\right) \times \mathbb {P}\left( V_+\right)$.

Lemma 3.22

The blow-up $\beta : W\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ can be factorized through $b_{\pm }: W\rightarrow B_{\pm }/{\mathbb C}^*$ and the small contractions $s_{\pm }: B_{\pm }/{\mathbb C}^*\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ with exceptional loci $\mathbb {P}(V_{\pm })$.

Proof

There exist two natural birational morphisms $s_{\pm }: B_{\pm }/{\mathbb C}^*\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$, isomorphisms over the set of points which are semistable but not stable. From this it follows that $\mathop {\textrm{Exc}}\nolimits (s_{\pm })=\mathbb {P}\left( V_{\pm }\right)$, so $s_{\pm }$ are small contractions. Moreover, since W is birational to $V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$, which is birational to $B_{\pm }/{\mathbb C}^*$, we conclude there exist birational maps $b_{\pm }: W\dashrightarrow B_{\pm }/{\mathbb C}^*$, defined over $W{\setminus } \left( \mathbb {P}\left( V_-\right) \times \mathbb {P}\left( V_+\right) \right)$. Since the exceptional locus has codimension one, $b_{\pm }$ are morphisms. Let us prove that $b_{\pm }\circ s_{\pm }=\beta$. For sake of simplicity, let us consider $b_-\circ s_-$. It is immediate to notice that $b_-^{-1}(s_-^{-1}(0))=b_-^{-1}(\mathbb {P}\left( V_-\right) )=\mathbb {P}\left( V_-\right) \times \mathbb {P}\left( V_+\right) =\beta ^{-1}(0)$. $\square$

We summarize the above construction by means of the diagram

and its restriction to the exceptional loci:

Theorem 3.23

The birational map $\psi :B_-/{\mathbb C}^*\dashrightarrow B_+/{\mathbb C}^*$ is a rooftop flip modeled by $\mathbb {P}\left( V_-\right) \times \mathbb {P}\left( V_+\right)$.

Proof

We verify that each condition of Definition 3.12 is satisfied. (1) follows from Lemmas 3.19, 3.22. Thanks to Remark 3.21, (2) is satisfied. Finally for (3) we have that $Z_0$ is the origin, and thanks to Lemma 3.22 we conclude.

Corollary 3.24

The geometric quotients $B_{\pm } /{\mathbb C}^*$ are smooth, and the rooftop flip $\psi : B_-/{\mathbb C}^*\dashrightarrow B_+/{\mathbb C}^*$ is in particular a small ${\mathbb {Q}}$-factorial modification.

Proof

Since the non-empty open subset $B_{\pm }$ are smooth, and ${\mathbb C}^*$ acts freely on them, using [13, Corollary p.199] we obtain that $B_{\pm }$ are ${\mathbb C}^*$-principal bundles over $B_{\pm }/{\mathbb C}^*$, hence they are smooth. $\square$

4 Proof of the main result

This section is devoted to prove Theorem 3.15; we will adapt the example of Atiyah flip explained in Sect. 3.3 in greater generality.

Set-up 4.1

Let X be a smooth drum constructed upon a triple $(Y,{\mathcal L}_-,{\mathcal L}_+)$ (cf. Section 3.1). Let $\hat{X}$ be the affine cone over X, contained in the affine space $V^\vee :=V_-^\vee \oplus V_+^\vee$, where

$$\begin{aligned} V_-:={{\,\textrm{H}\,}}^0(Y_-,L_-), \qquad V_+:={{\,\textrm{H}\,}}^0(Y_+,L_+). \end{aligned}$$

Consider the ${\mathbb C}^*$-action on $V^\vee$ given by $t\cdot v=\left( t v_-,t^{-1}v_+\right)$, where $v=\left( v_-,v_+\right) \in V^\vee$.

Notice that the ${\mathbb C}^*$-action on $V^\vee$ is the one described in Remark 3.8. Consider the restriction of the ${\mathbb C}^*$-action on $V^\vee$ to $\hat{X}$; there exists a GIT quotient $\hat{X}\rightarrow \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$, singular at the origin. Moreover we can also consider the intersection $\hat{X}\cap B_{\pm }$, which are non-empty open subsets of stable points giving geometric quotients $\pi _{\pm }:\hat{X}\cap B_{\pm }\rightarrow \hat{X}\cap B_{\pm }/{\mathbb C}^*$.

Proposition 4.2

There exists a small modification

$$\begin{aligned} \psi : \hat{X}\cap B_-/{\mathbb C}^*\dashrightarrow \hat{X}\cap B_+/{\mathbb C}^*, \end{aligned}$$

whose exceptional locus is $Y_-$.

Proof

The existence of such a birational map is immediate after noticing that $\hat{X}\cap B_-\cap B_+$ is open and non-empty. Let us prove that the exceptional locus of $\psi$ is $Y_-$. It suffices to show that

$$\begin{aligned} (\hat{X}\cap B_-/{\mathbb C}^*) \cap \mathbb {P}\left( V_-\right) =Y_-. \end{aligned}$$

Notice that the $\supset$ inclusion is trivial, so let us focus on the $\subset$ inclusion. Let $p\in (\hat{X}\cap B_-/{\mathbb C}^*) \cap \mathbb {P}\left( V_-\right)$, and let $\hat{p}=(hv_-,0)$ the corresponding line in $V_-^\vee$ through the origin, with $h\in {\mathbb C}^*_h$. The preimage $\pi ^{-1}_-(p)$ is a closed orbit ${\mathbb C}^*\cdot q$ such that $\lim _{t\rightarrow \infty } t\cdot q$ does not exist, hence ${\mathbb C}^*\cdot q=\left\{ (tv_-,v_+)\mid t\in {\mathbb C}^*\right\}$. Since p belongs to the intersection, ${\mathbb C}^*\cdot q=\left\{ (tv_-,0)\mid t\in {\mathbb C}^*\right\}$. Therefore since the restriction to $V^\vee _-$ of the ${\mathbb C}^*$action on $V^\vee$ coincides with the ${\mathbb C}^*_h$-action on $V^\vee _-$ by homoteties, we have that $\hat{p}={\mathbb C}^*\cdot q$. Moreover $\hat{X}\cap V_-^\vee =\hat{Y}_-$, therefore $p\in Y_-$. Since $\mathop {\textrm{codim}}\nolimits _{\hat{X}\cap B_{\pm }/{\mathbb C}^*} (Y) \ge 2$, we conclude. $\square$

Corollary 4.3

The exceptional locus of the birational map $\psi ^{-1}$ is $Y_+$.

Consider the blow-up $\beta : W\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ along the vertex of the affine cone $V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$, as in Proposition 3.21, with exceptional divisor $\mathbb {P}(V_-)\times \mathbb {P}(V_+)$.

Let $R:=\overline{\beta ^{-1}((\hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*){\setminus } 0)}$ be the strict transform of $\hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ under $\beta : W\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$. We abuse notation by denoting with $b_{\pm }: R\rightarrow \hat{X}\cap B_{\pm }/{\mathbb C}^*$ the restriction of the blow-up $b_{\pm }: W\rightarrow B_{\pm }/{\mathbb C}^*$. Notice that $R\simeq \overline{b_{\pm }^{-1}((\hat{X}\cap B_{\pm }/{\mathbb C}^*) {\setminus } \hat{Y}_{\pm })}$, where again we abuse notation by denoting with $s_{\pm }: \hat{X}\cap B_{\pm } \rightarrow \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ the restriction of $s_{\pm }: B_{\pm }/{\mathbb C}^*\rightarrow V^\vee \mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$. We obtain a diagram:

Proposition 4.4

It holds that $b_{\pm }^{-1}(Y_{\pm })\simeq Y$.

Proof

We proceed by steps. First, let us denote by $X/{\mathbb C}^*$ the geometric quotient of $\left( X,L\right)$ under the ${\mathbb C}^*$-action, defined over the set of stable points $X\setminus \left( Y_-\cup Y_+\right)$ (see [15, Proposition 2.9])

• Step 1 We want to prove that $Y\simeq X/{\mathbb C}^*$. Thanks to [16, Remark 4.2], the contraction $\phi :\mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right) \rightarrow X$ is ${\mathbb C}^*$-equivariant, in particular the geometric quotients of $(\mathbb {P}\left( {\mathcal L}_-\oplus {\mathcal L}_+\right) ,{\mathcal {O}}_{\mathbb {P}({\mathcal L}_-\oplus {\mathcal L}_+)}(1))$ and (X, L) with respect to the ${\mathbb C}^*$-action are isomorphic. Since the former is a $\mathbb {P}^1$-bundle on Y, and therefore its geometric quotient is isomorphic to Y, we conclude.

• Step 2 We show that the GIT quotient $\hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ is the affine cone over Y. Let us recall that by ${\mathbb C}^*_h$ we denote the natural ${\mathbb C}^*$-action on the affine space $V^\vee$ given by the homoteties. We claim that

  $$\begin{aligned} \left( \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^* \setminus 0\right) /{\mathbb C}^*_h\simeq Y. \end{aligned}$$

  To this end, let us note that the two ${\mathbb C}^*$-actions commute over the open subset of the points stable under both the ${\mathbb C}^*$ and the ${\mathbb C}^*_h$ actions. Therefore we have that

  $$\begin{aligned} \left( \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^* \setminus 0\right) /{\mathbb C}^*_h \simeq \left( \hat{X} \setminus \left( \hat{Y}_- \cup \hat{Y}_+\right) \right) /\left( {\mathbb C}^*_h \times {\mathbb C}^*\right) . \end{aligned}$$

  (1)

  Notice that

  $$\begin{aligned} \frac{\hat{X} \setminus \left( \hat{Y}_- \cup \hat{Y}_+\right) }{{\mathbb C}^*_h}=\frac{\left( \hat{X} \setminus 0\right) \setminus \left( \left( \hat{Y}_- \setminus 0\right) \cup \left( \hat{Y}_+ \setminus 0\right) \right) }{{\mathbb C}^*_h}\simeq X \setminus \left( Y_- \cup Y_+\right) \end{aligned}$$

  and that

  $$\begin{aligned} \left( X \setminus \left( Y_- \cup Y_+\right) \right) /{\mathbb C}^*=X/{\mathbb C}^* \simeq Y. \end{aligned}$$

  Then the right-hand side of (1) is isomorphic to Y and we conclude.

• Step 3 We want to prove that $\beta ^{-1}(0)=Y$. It follows immediately after recalling that we are considering the restriction of the blow-up map to $\hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$, whose base of the cone is precisely Y.

• Step 4 We show that $s_{\pm } \circ b_{\pm }=\beta$ and that $s_{\pm }^{-1}(0)\simeq Y$. The first claim follows directly from Lemma 3.22. Since $s_{\pm }: B_{\pm }/{\mathbb C}^*\rightarrow \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ are small contractions whose exceptional locus is $\mathbb {P}(V_{\pm })\cap \hat{X}=Y_{\pm }$ by Proposition 4.2, we conclude.

$\square$

We can now prove Theorem 3.15:

Proof of Theorem 3.15

We verify each condition of Definition 3.12 is satisfied.

• (1) Using Proposition 4.2, the birational map $\psi : \hat{X}\cap B_-/{\mathbb C}^*\dashrightarrow \hat{X}\cap B_+/{\mathbb C}^*$ is a small modification with exceptional locus $Y_-$. The exceptional loci of $s_{\pm }: \hat{X}\cap B_{\pm }/{\mathbb C}^*\rightarrow \hat{X}\mathbin {/\hspace{-3.33328pt}/}{\mathbb C}^*$ are $Y_{\pm }$ and the restriction $s_{\pm }|_{Y_{\pm }}: Y_{\pm } \rightarrow 0$ are precisely $Y_{\pm }$-bundles.

• (2) If we consider the resolution $b_{\pm }: R\rightarrow \hat{X}\cap B_{\pm }/{\mathbb C}^*$ we have that $Y=b^{-1}_{\pm }(Y_{\pm })$ is a divisor in R, and $Y\rightarrow Y_{\pm }$ defines two projective bundle structures by construction.

• (3) In this case $Z_0=0$, and we know that $s^{-1}_{\pm }(0)\simeq Y_{\pm }$. Moreover $(b_{\pm }^{-1}\circ s_{\pm }^{-1})(0)\simeq Y$ by Proposition 4.4, hence we conclude.

$\square$

Corollary 4.5

The geometric quotients $\hat{X}\cap B_{\pm } /{\mathbb C}^*$ are smooth and in particular the rooftop flip $\psi : \hat{X}\cap B_-/{\mathbb C}^*\dashrightarrow \hat{X}\cap B_+/{\mathbb C}^*$ is a small ${\mathbb {Q}}$-factorial modification.

Proof

Since the affine variety $\hat{X}$ has only a singularity at the origin, $\hat{X}\cap B_{\pm }$ is smooth. Moreover, the ${\mathbb C}^*$-action is free on $\hat{X}\cap B_{\pm }$, therefore using [13, Corollary p.199] $\hat{X}\cap B_{\pm }$ is a ${\mathbb C}^*$-principal bundle over $\hat{X}\cap B_{\pm }/{\mathbb C}^*$, hence they are also smooth. By definition $\psi$ is in particular a small ${\mathbb {Q}}$-factorial modification. $\square$

We conclude by using Theorem 3.15 to show that the smooth drum $Q^{2n}\subset \mathbb {P}^{2n+1}$ induces a rooftop flip modeled by $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$. Notice that for $n=2$ this is the famous Mukai flop (see [6, 21]):

Corollary 4.6

Let $Q^{2n}\subset \mathbb {P}^{2n+1}$ be the smooth quadric hypersurface, viewed as the smooth drum constructed upon $\left( \mathbb {P}\left( T_{\mathbb {P}^n}\right) , p^{*}_-{\mathcal {O}}_{\mathbb {P}^n}(1), p^{*}_+{\mathcal {O}}_{(\mathbb {P}^n)^\vee }(1)\right)$ (cf. Example 3.10). Then the small modification

$$\begin{aligned} \psi : \hat{Q}^{2n}\cap B_-/{\mathbb C}^* \dashrightarrow \hat{Q}^{2n}\cap B_+/{\mathbb C}^* \end{aligned}$$

is a rooftop flip modeled by $\mathbb {P}\left( T_{\mathbb {P}^n}\right)$.