Abstract
We link small modifications of projective varieties with a \({\mathbb {C}}^*\)-action to their GIT quotients. Namely, using flips with centers in closures of Białynicki-Birula cells, we produce a system of birational equivariant modifications of the original variety, which includes those on which a quotient map extends from a set of semistable points to a regular morphism. The structure of the modifications is completely described for the blowup along the sink and the source of smooth varieties with Picard number one with a \({\mathbb {C}}^*\)-action which has no finite isotropy for any point. Examples can be constructed upon homogeneous varieties with a \({\mathbb {C}}^*\)-action associated to short grading of their Lie algebras.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In classical Mumford’s Geometric Invariant Theory (GIT), [20], quotients of projective varieties by reductive group actions are determined by the choice of a linearization of an ample line bundle which yields the set of semistable points, an open subset of the original variety on which the quotient is defined as a morphism; thus GIT requires passing to quasiprojective varieties.
However, if the group in question is \({\mathbb {C}}^*\) the complement of the set of semistable points is a union of closures of Białynicki-Birula cells, whose structure is well understood, see [6]. One may then ask if there is a natural equivariant compactification of the set of semistable points on which the quotient map extends to a regular morphism. This requires a good understanding of the equivariant birational modifications of varieties with a \({\mathbb {C}}^*\)-action.
The relation of birational geometry with the theory of quotients of \({\mathbb {C}}^*\)-actions has been acknowledged since the early days of the Minimal Model Program or Mori Theory; see the contributions by Thaddeus and Reid [25, 27] (see also [5, Remark 11.1.2, p. 46]) which focused on describing birational transformations in terms of variation of stability conditions yielding geometric quotients. This concept gave rise to the notions of Mori Dream Space (MDS) introduced in [12], and total coordinate—or Cox—ring (see [2]), whose spectrum gives, as GIT quotients, small \({\mathbb {Q}}\)-factorial modifications of an MDS.
Włodarczyk in [28] used \({\mathbb {C}}^*\)-actions to prove the Weak Factorization Conjecture, which asserts that a birational map of smooth projective varieties can be factored as a sequence of blowups and blowdowns in smooth centers. The key tool in his work was the notion of birational cobordism, constructed by Morelli in the toric case [19]. This is a quasiprojective variety with a \({\mathbb {C}}^*\)-action, containing two open equivariant subsets admitting quotients to two birationally equivalent varieties; see [1, 29] for a broader view on this topic.
In the present paper we deal with equivariant birational modifications of smooth projective varieties with a \({\mathbb {C}}^*\)-action. When the action is equalized, which means that no point has finite isotropy, after blowing up the source and the sink of the action (see Sect. 2.1 for definitions) we obtain a variety which admits a system of small \({\mathbb {Q}}\)-factorial \({{\mathbb {C}}}^*\)-equivariant modifications (cf. Sect. 4). Some of these modifications are compactifications of sets of stable points which are \({\mathbb {P}}^1\)-bundles over the respective quotients (Proposition 2.16). Each of these modifications is a projective version of a cobordism associated to the natural birational map between a pair of GIT quotients. Namely, each of the varieties that we construct is a \({{\mathbb {C}}}^*\)-equivariant compactification of a cobordism. Its boundary consists of two divisors—that are the source and the sink of the action—which are birationally equivalent varieties in Włodarczyk’s construction of the cobordism. Roughly speaking, cobordisms represent birational maps, and we study here their birational modifications.
More precisely, the main results of the paper can be summarized in the following statement (see Sects. 2.1, 2.2 for notation and definitions of the concepts involved). For clarity of exposition, we state here only the case in which the extremal fixed point components are positive dimensional. Our arguments work also in the remaining cases; a complete description can be found in Sect. 4.
Theorem 1.1
Let X be a smooth complex projective variety of Picard number one admitting a nontrivial \({{\mathbb {C}}}^*\)-action. Assume that the action is equalized of criticality r, and that its extremal fixed point components \(Y_0,Y_r\) are not isolated points. Denote by  , \(i=0,\dots ,r-1\), the corresponding geometric quotients. Then:
, \(i=0,\dots ,r-1\), the corresponding geometric quotients. Then:
-
(1)
The varieties
 are smooth and the natural birational maps
are smooth and the natural birational maps 
are flips.
-
(2)
The blowup \(X^\flat \) of X along \(Y_0\), \(Y_r\) is a Mori dream space.
-
(3)
Given a pair (i, j) of indices \(i,j\in \{0,\dots ,r\}\), \(i\leqslant j\), there exists a unique small \({\mathbb {Q}}\)-factorial modification X(i, j) of \(X^\flat \) that is smooth and admits a \({{\mathbb {C}}}^*\)-action with extremal fixed point components
 ,
,  .
. -
(4)
Every small \({\mathbb {Q}}\)-factorial modification of \(X^\flat \) is constructed as above.
Note that in the above statement we are using the word flip to refer to a D-flip, for a certain \({\mathbb {Q}}\)-divisor  (see [12, Definition 1.9]). More concretely, we will see that the flips appearing in our description are compositions of a smooth blowup and a smooth blowdown (Sect. 3). In order to prove the previous statement we will describe completely the small modifications among the varieties X(i, j), showing that they can be written as a composition of \({{\mathbb {C}}}^*\)-equivariant flips, whose restriction to the extremal fixed point components are the flips described in Part (1) of the theorem (Sect. 4).
(see [12, Definition 1.9]). More concretely, we will see that the flips appearing in our description are compositions of a smooth blowup and a smooth blowdown (Sect. 3). In order to prove the previous statement we will describe completely the small modifications among the varieties X(i, j), showing that they can be written as a composition of \({{\mathbb {C}}}^*\)-equivariant flips, whose restriction to the extremal fixed point components are the flips described in Part (1) of the theorem (Sect. 4).
Outline: We start the paper with a section of preliminaries on \({{\mathbb {C}}}^*\)-actions and their GIT quotients; we also include some results on \({{\mathbb {C}}}^*\)-invariant linear systems on the variety X and its blowup \(X^{\flat }\) along its extremal fixed point components. Section 3 contains the technical core of the paper: we construct some \({{\mathbb {C}}}^*\)-equivariant flips of varieties admitting an equalized \({{\mathbb {C}}}^*\)-action with codimension one sink and source, relating them to flips of these extremal fixed point components (Theorem 3.1). By applying recursively Theorem 3.1, we prove Theorem 1.1 in Sect. 4, describing completely the movable cone of the variety \(X^\flat \) of the statement and its Mori chamber decomposition. Finally we illustrate our results by showing how to construct examples of equalized \({{\mathbb {C}}}^*\)-actions in the framework of representation theory and rational homogeneous spaces (Sect. 5). In particular we revisit some examples of equalized \({{\mathbb {C}}}^*\)-actions of small bandwidth, previously presented in [21].
2 Preliminaries
2.1 Actions of complex tori
We will introduce here some notation and conventions on \({{\mathbb {C}}}^*\)-actions. We refer to [4, 9, 21] for further details.
2.1.1 Fixed point components
Given a \({{\mathbb {C}}}^*\)-action on a proper complex algebraic variety X, we denote by \(X^{{{\mathbb {C}}}^*}\) the fixed locus of the action, and by  the set of irreducible fixed point components of the action, so that we may write
the set of irreducible fixed point components of the action, so that we may write

Among these components there are two distinguished ones, called sink and source of the action, defined by the property of containing, respectively, the limiting points
where \(x\in X\) is a general point. If X is smooth and projective, which will be mostly our case, every  is smooth (cf. [14]).
is smooth (cf. [14]).
2.1.2 Linearizations and weight maps
Given a \({{\mathbb {C}}}^*\)-action on a normal projective variety X as above, and given a line bundle  , one may find a linearization of the \({{\mathbb {C}}}^*\)-action on it (cf. [15]), so that for every
, one may find a linearization of the \({{\mathbb {C}}}^*\)-action on it (cf. [15]), so that for every  , \({{\mathbb {C}}}^*\) acts on \(L_{|Y}\) by multiplication with a character
, \({{\mathbb {C}}}^*\) acts on \(L_{|Y}\) by multiplication with a character  , that we call weight of the linearization on Y. It is well known that any two linearizations differ by a character of
, that we call weight of the linearization on Y. It is well known that any two linearizations differ by a character of  , so that for every line bundle L there exists a unique linearization (called normalized) whose weight at the sink is equal to zero. By fixing an isomorphism
, so that for every line bundle L there exists a unique linearization (called normalized) whose weight at the sink is equal to zero. By fixing an isomorphism  , this linearization defines a map
, this linearization defines a map  , sending every fixed point component to its weight.
, sending every fixed point component to its weight.
Abusing notation we will denote with the same symbols line bundles and the Cartier divisors defining them, and use the additive notation for the group operation in  . Note that
. Note that
for every  , \(k\in {{\mathbb {Z}}}\),
, \(k\in {{\mathbb {Z}}}\),  . In particular we may extend this definition to \({\mathbb {Q}}\)-divisors in X, by setting
. In particular we may extend this definition to \({\mathbb {Q}}\)-divisors in X, by setting

2.1.3 Actions on polarized pairs
A \({{\mathbb {C}}}^*\)-action on a projective variety X, endowed with the weight map \(\mu _L\) determined by an ample \({\mathbb {Q}}\)-divisor L, will be referred to as a \({{\mathbb {C}}}^*\)-action on the \({\mathbb {Q}}\)-polarized pair (X, L). In this case one may denote by
the weights \(\mu _L(Y)\),  , ordered increasingly, and set
, ordered increasingly, and set

In analogy with the case of Morse theory, the values \(a_i\) will be called the critical values; the number r will be called the criticality of the \({{\mathbb {C}}}^*\)-action. It is well known that the minimum and maximum of these values are achieved at the sink and the source of the action, respectively, so that, \(Y_0,Y_r\) are respectively the sink and the source of the action and, in particular, \(a_0=0\). The value \(\delta =a_r\) is called the bandwidth of the \({{\mathbb {C}}}^*\)-action on (X, L).
2.1.4 The Białynicki-Birula decomposition
Let X be a proper variety admitting a \({{\mathbb {C}}}^*\)-action as above. Given  , we denote by
, we denote by

the Białynicki-Birula cells of the action and their closures; we refer to [9] for a complete account on the Białynicki-Birula decomposition and its applications, and to [4] for the original reference. When considering the action of \({{\mathbb {C}}}^*\) on a \({\mathbb {Q}}\)-polarized pair (X, L) as above, we will write

and, for notational reasons, we also set \(B^\pm _i=\varnothing \) for  .
.
If X is smooth, the normal bundle of Y in X splits into two subbundles, on which \({{\mathbb {C}}}^*\) acts with positive and negative weights, respectively

We will often use the notation

The action of \({{\mathbb {C}}}^*\) on \(X^{\pm }(Y)\) is equivariantly isomorphic to the induced action on the bundles  (see [9, Theorem 4.2] and [4] for the original exposition).
(see [9, Theorem 4.2] and [4] for the original exposition).
2.1.5 Equalized actions
We say that the action of \({{\mathbb {C}}}^*\) on a proper variety X is equalized at  if for every
if for every  the isotropy group of the \({{\mathbb {C}}}^*\)-action on x is trivial. Note that in the smooth case, the definition of equalization presented here coincides with the one introduced in [26, Definition 1.6]:
the isotropy group of the \({{\mathbb {C}}}^*\)-action on x is trivial. Note that in the smooth case, the definition of equalization presented here coincides with the one introduced in [26, Definition 1.6]:
Lemma 2.1
Let X be a smooth variety supporting a \({{\mathbb {C}}}^*\)-action. The action is equalized if and only if the weights of the action on  are all equal to \(\pm 1\) for every fixed point component
are all equal to \(\pm 1\) for every fixed point component  .
.
Proof
It follows from the existence, for every  , of the \({{\mathbb {C}}}^*\)-equivariant isomorphisms
, of the \({{\mathbb {C}}}^*\)-equivariant isomorphisms  . \(\square \)
. \(\square \)
Moreover, the equalization hypothesis implies that the closure of any 1-dimensional orbit is a smooth rational curve, whose L-degree may be computed in terms of the weights at its extremal points. The following statement follows from the AM vs. FM formula presented in [26]:
Lemma 2.2
(AM vs. FM) Let (X, L) be a \({\mathbb {Q}}\)-polarized pair, with X smooth, supporting an equalized action of  , and let C be the closure of a 1-dimensional orbit, whose sink and source are denoted by \(x_-\) and \(x_+\). Then C is a smooth rational curve of L-degree equal to \(\mu _L(x_+)-\mu _L(x_-)\).
, and let C be the closure of a 1-dimensional orbit, whose sink and source are denoted by \(x_-\) and \(x_+\). Then C is a smooth rational curve of L-degree equal to \(\mu _L(x_+)-\mu _L(x_-)\).
Proof
The smoothness follows from the Białynicki-Birula decomposition (see [9, Theorem 4.2]), while the degree statement is precisely [26, Corollary 3.2 (c)].\(\square \)
2.1.6 B-type actions and bordisms
Following [21], a \({{\mathbb {C}}}^*\)-action on a proper algebraic variety X whose extremal fixed point components \(Y_0,Y_r\) have codimension one is called a B-type action. In the case in which X is projective and smooth, by the Białynicki-Birula decomposition, the restriction maps  , \(j=0,r\), are surjective; we will say that the \({{\mathbb {C}}}^*\)-action is a bordism (cf. [21, Definition 3.8]) if the restriction maps
, \(j=0,r\), are surjective; we will say that the \({{\mathbb {C}}}^*\)-action is a bordism (cf. [21, Definition 3.8]) if the restriction maps  , \(j=0,r\), fit into two short exact sequences:
, \(j=0,r\), fit into two short exact sequences:

The following equivalence, which is a consequence of [10, Theorem 3] has been proved in [21, Corollary 3.7].
Lemma 2.3
Let X be a smooth projective variety admitting a \({{\mathbb {C}}}^*\)-action of B-type. The action of \({{\mathbb {C}}}^*\) on X is a bordism if and only if \(\nu ^\pm (Y)\geqslant 2\) for every inner fixed point component Y.
2.1.7 The blowup of a \({{\mathbb {C}}}^*\)-variety along the extremal fixed point components
Examples of B-type \({{\mathbb {C}}}^*\)-actions can be constructed by considering any \({{\mathbb {C}}}^*\)-action on a proper variety smooth at its extremal fixed point component \(Y_0,Y_r\). If the action is equalized at \(Y_0,Y_r\), then the blowup \(X^\flat \) of X along \(Y_0,Y_r\) inherits a \({{\mathbb {C}}}^*\)-action that is of B-type (see [21, Lemma 3.10]). As we will see later on, there is a deep relation among the birational geometry of \(X^{\flat }\) and the birational geometry of the GIT quotients of X. In order to describe precisely this relation we will need to study certain linear systems on \(X^{\flat }\). Let us first introduce some notation.
Notation 2.4
We denote by \(\beta :X^\flat \rightarrow X\) the blowup of X along \(Y_0,Y_r\), and by  , \(i=0,r\), its exceptional divisors. For every \(\tau _-,\tau _+\in {{\mathbb {R}}}\) satisfying that \(0\leqslant \tau _-\leqslant \tau _+\leqslant \delta \) we introduce the following \({{\mathbb {R}}}\)-divisor:
, \(i=0,r\), its exceptional divisors. For every \(\tau _-,\tau _+\in {{\mathbb {R}}}\) satisfying that \(0\leqslant \tau _-\leqslant \tau _+\leqslant \delta \) we introduce the following \({{\mathbb {R}}}\)-divisor:

We may now state the following lemma, that will be very important later on.
Lemma 2.5
Let (X, L) be a \({\mathbb {Q}}\)-polarized pair, with X smooth, admitting a \({{\mathbb {C}}}^*\)-action, equalized at the sink and the source. For every \(m\in {{\mathbb {N}}}\), \(\tau _-,\tau _+\in {\mathbb {Q}}\) such that  , \(0\leqslant \tau _-\leqslant \tau _+\leqslant \delta \), \(m\tau _\pm \in {{\mathbb {Z}}}\), the map \(\beta ^*\) induces an isomorphism
, \(0\leqslant \tau _-\leqslant \tau _+\leqslant \delta \), \(m\tau _\pm \in {{\mathbb {Z}}}\), the map \(\beta ^*\) induces an isomorphism

where \({{\,\mathrm{H}\,}}^0(X,mL)_k\) is the eigenspace of \({{\,\mathrm{H}\,}}^0(X,mL)\) on which \({{\mathbb {C}}}^*\) acts with weight k.
Proof
Note that \(\beta ^*\) induces a \({{\mathbb {C}}}^*\)-equivariant embedding of  into \({{\,\mathrm{H}\,}}^0(X,mL)\). In order to determine its image we use [8, Lemma 2.17] (that describes locally the invariant sections of a line bundle along a fixed point component), that allows us to identify \({{\,\mathrm{H}\,}}^0(X,mL)_k\) with the set of sections of mL vanishing with multiplicity k at \(Y_0\), and with multiplicity \(m\delta -k\) at \(Y_r\), that is with
into \({{\,\mathrm{H}\,}}^0(X,mL)\). In order to determine its image we use [8, Lemma 2.17] (that describes locally the invariant sections of a line bundle along a fixed point component), that allows us to identify \({{\,\mathrm{H}\,}}^0(X,mL)_k\) with the set of sections of mL vanishing with multiplicity k at \(Y_0\), and with multiplicity \(m\delta -k\) at \(Y_r\), that is with  . Then the statement follows by pulling back this identification to \(X^\flat \) via \(\beta \).\(\square \)
. Then the statement follows by pulling back this identification to \(X^\flat \) via \(\beta \).\(\square \)
The importance of this lemma relies on the fact that it allows us to describe the base loci of divisors in \(X^\flat \) in terms of the closures of the Białynicki-Birula cells defined in (2.1). Let us start by introducing the following notation:
Notation 2.6
In the setup of Lemma 2.5, let \(0=a_0<\dots <a_r\) be the critical values of the action. For every \(i,j\in \{0,\dots ,r\}\) (see Fig. 1) we set

We denote by  the closure of
the closure of  . For every \(\tau \in [0,\delta ]\cap {\mathbb {Q}}\), we set
. For every \(\tau \in [0,\delta ]\cap {\mathbb {Q}}\), we set

This notation is set so that, given rational numbers \(\tau _-\leqslant \tau _+\) in \([0,\delta ]\), we have

In particular we can state:
Corollary 2.7
Let (X, L) be as in Lemma 2.5. For every \(\tau _-,\tau _+\in [0,\delta ]\cap {\mathbb {Q}}\), \(\tau _-\leqslant \tau _+\), and for \(m\gg 0\) such that \(m\tau _-,m\tau _+\in {{\mathbb {Z}}}\), the following hold:

Proof
The first equality is obtained from the fact that, by definition,

For the second equality, in view of Lemma 2.5, we are left to check that any point  does not belong to
does not belong to  .
.
In order to do so, we assume, for instance, that  and let \(C\subset X^\flat \) be the closure of the unique 1-dimensional \({{\mathbb {C}}}^*\)-orbit having y as sink. Denoting by \(C'\) the strict transform of C in X, and being \(m\gg 0\), we may assume that
and let \(C\subset X^\flat \) be the closure of the unique 1-dimensional \({{\mathbb {C}}}^*\)-orbit having y as sink. Denoting by \(C'\) the strict transform of C in X, and being \(m\gg 0\), we may assume that  , so that the \({{\mathbb {C}}}^*\)-equivariant morphism
, so that the \({{\mathbb {C}}}^*\)-equivariant morphism
is surjective. In particular the surjectivity is inherited by the corresponding \({{\mathbb {C}}}^*\)-eigenspaces, so that we have a surjective map

Applying now Lemma 2.5 we have a surjective map

By the choice of y, \(mL(\tau _-,\tau _+)\) has positive degree on C, and the result follows.\(\square \)
2.2 GIT-quotients of torus actions
Following Mumford’s Geometric Invariant Theory (GIT), given a reductive group G acting on a variety X, one may consider the problem of describing all the possible proper geometric and semi-geometric quotients of G-invariant open subsets of X. In the case in which X is normal and proper, and \(G={{\mathbb {C}}}^*\) the problem was treated in [7], and the solution was written in terms of the ordered set of fixed point components of X.
Although we will not need the results of [7] in full generality, we recall the description introduced there, since it provides a very clear geometric insight on the construction of the quotients we will work with.
Let X be a proper normal complex algebraic variety with a nontrivial action of \({{\mathbb {C}}}^*\). As shown in [7], there exists a unique partial order \(\preceq \) on  satisfying that \(Y\preceq Y'\) if \(X^+(Y')\cap X^-(Y)\ne \varnothing \), that is, if there exists an orbit converging to a point of Y when t goes to \(\infty \), and to a point of \(Y'\) when t goes to 0. Note that we have deliberately inverted the order appearing in [7], in order to make it compatible with the weights of the fixed point components with respect to positive line bundles: in fact, if L is a nef \({\mathbb {Q}}\)-divisor in X, the AM vs. FM formula [26, Corollary 2.3], \(Y\preceq Y'\) implies that \(\mu _L(Y)\leqslant \mu _L(Y')\).
satisfying that \(Y\preceq Y'\) if \(X^+(Y')\cap X^-(Y)\ne \varnothing \), that is, if there exists an orbit converging to a point of Y when t goes to \(\infty \), and to a point of \(Y'\) when t goes to 0. Note that we have deliberately inverted the order appearing in [7], in order to make it compatible with the weights of the fixed point components with respect to positive line bundles: in fact, if L is a nef \({\mathbb {Q}}\)-divisor in X, the AM vs. FM formula [26, Corollary 2.3], \(Y\preceq Y'\) implies that \(\mu _L(Y)\leqslant \mu _L(Y')\).
Definition 2.8
A semi-section of the action is a partition  satisfying that
satisfying that

A section of the action is a semi-section such that  and
and  .
.
The following statement is a reformulation of [7, Theorem 2.1]:
Proposition 2.9
Let X be a normal projective variety admitting a \({{\mathbb {C}}}^*\)-action as above. Given a semi-section  of the action, and denoting by U the open set
of the action, and denoting by U the open set  , there exists a semi-geometric quotient of U by the induced action of \({{\mathbb {C}}}^*\). Furthermore, if the semi-section is a section, then the quotient of U by \({{\mathbb {C}}}^*\) is geometric.
, there exists a semi-geometric quotient of U by the induced action of \({{\mathbb {C}}}^*\). Furthermore, if the semi-section is a section, then the quotient of U by \({{\mathbb {C}}}^*\) is geometric.
In this paper we will consider only a certain type of sections and semi-sections, whose quotients will not only be proper, but projective, since they will be standard GIT quotients of X. The construction is the following.
Construction 2.10
Let (X, L) be a \({\mathbb {Q}}\)-polarized pair with a nontrivial \({{\mathbb {C}}}^*\)-action, and denote by \(0=a_0<\dots <a_r=\delta \) the critical values of the action. We obtain a semi-section (respectively a section) of the action choosing an index \(i\in \{0,\dots ,r\}\) (resp. \(i\in \{0,\dots ,r-1\}\)), and setting

(resp.  ,
,  ). Let us denote by \(X^\mathrm{ss}(i,i)\) (resp. \(X^\mathrm{ss}(i,i\,{+}\,1)\)) the open set
). Let us denote by \(X^\mathrm{ss}(i,i)\) (resp. \(X^\mathrm{ss}(i,i\,{+}\,1)\)) the open set  , and by
, and by  (resp.
(resp.  ) the corresponding proper semi-geometric (resp. geometric) quotients. See Fig. 2.
) the corresponding proper semi-geometric (resp. geometric) quotients. See Fig. 2.
Definition 2.11
For every rational number \(\tau \in {\mathbb {Q}}\cap [0,\delta ]\), we define a graded algebra and a homogeneous ideal

where the subindex \(m\tau \) denotes the direct summand of \({{\,\mathrm{H}\,}}^0(X,mL)\) of \({{\mathbb {C}}}^*\)-weight equal to \(m\tau \), and \({{\,\mathrm{H}\,}}^0(X,mL)\) is set to be zero if  .
.
The construction of the varieties  ,
,  can be then described in terms of the original linearization of L by means of Mumford’s Geometric Invariant Theory (cf. [20, Amplification 1.11, p. 40]), as follows.
can be then described in terms of the original linearization of L by means of Mumford’s Geometric Invariant Theory (cf. [20, Amplification 1.11, p. 40]), as follows.
Proposition 2.12
Let (X, L) be a \({\mathbb {Q}}\)-polarized pair with a nontrivial \({{\mathbb {C}}}^*\)-action with critical values \(0=a_0<\dots <a_r=\delta \). Then:
-
for every \(i=0,\dots ,r\), we have

-
for every \(i=0,\dots ,r-1\), and every \(\tau \in (a_i,a_{i+1})\cap {\mathbb {Q}}\), we have

Definition 2.13
In the above situation, we will call the varieties  ,
,  the GIT-quotients of the pair (X, L) by the action of \({{\mathbb {C}}}^*\).
the GIT-quotients of the pair (X, L) by the action of \({{\mathbb {C}}}^*\).
Remark 2.14
Note that, since the intersection of all the open sets \(X^\mathrm{ss}(i,i\,{+}\,1)\) is nonempty, the varieties  are birationally equivalent. Moreover, the natural birational maps among them fit in the following commutative diagram, whose diagonal arrows are contractions:
are birationally equivalent. Moreover, the natural birational maps among them fit in the following commutative diagram, whose diagonal arrows are contractions:

Note also that, by construction,  ,
,  , and, since
, and, since  for every
for every  , the fibers of the diagonal morphisms are weighted projective spaces (standard projective spaces if the action is equalized).
, the fibers of the diagonal morphisms are weighted projective spaces (standard projective spaces if the action is equalized).
We observe also that the equalization hypothesis implies that the geometric quotients of X are \({{\mathbb {C}}}^*\)-principal bundles.
Lemma 2.15
Let (X, L) be a \({\mathbb {Q}}\)-polarized pair with a nontrivial equalized \({{\mathbb {C}}}^*\)-action with critical values \(0=a_0<\dots <a_r=\delta \). The geometric quotients  , \(i=0,\dots ,r-1\), are \({{\mathbb {C}}}^*\)-principal bundles. In particular, if X is smooth, then its geometric quotients by \({{\mathbb {C}}}^*\) are smooth.
, \(i=0,\dots ,r-1\), are \({{\mathbb {C}}}^*\)-principal bundles. In particular, if X is smooth, then its geometric quotients by \({{\mathbb {C}}}^*\) are smooth.
Proof
We take an affine open covering \(\{U_i\}\) of  such that the inverse image of every \(U_i\) is an affine \({{\mathbb {C}}}^*\)-scheme. It is enough to show that \(\pi _i^{-1}(U_i)\rightarrow U_i\) is a \({{\mathbb {C}}}^*\)-principal bundle for every i, and since by Lemma 2.1 we know that the action of \({{\mathbb {C}}}^*\) has trivial stabilizers, this is a corollary of Luna Slice Theorem (see [20, Corollary on p. 199]).\(\square \)
such that the inverse image of every \(U_i\) is an affine \({{\mathbb {C}}}^*\)-scheme. It is enough to show that \(\pi _i^{-1}(U_i)\rightarrow U_i\) is a \({{\mathbb {C}}}^*\)-principal bundle for every i, and since by Lemma 2.1 we know that the action of \({{\mathbb {C}}}^*\) has trivial stabilizers, this is a corollary of Luna Slice Theorem (see [20, Corollary on p. 199]).\(\square \)
In particular, one may construct a different compactification of \(X^\mathrm{ss}(i,i\,{+}\,1)\) by considering the natural action of \({{\mathbb {C}}}^*\) on \({{\mathbb {P}}}^1\) and considering the variety

where  if and only if
if and only if  ,
,  for some \(t\in {{\mathbb {C}}}^*\). Intuitively \({\widehat{X}}(i,i\,{+}\,1)\) is constructed by adding to \(X^\mathrm{ss}(i,i\,{+}\,1)\) two sections corresponding to the limit points of the action when t goes to 0 and infinity. The variety \({\widehat{X}}(i,i\,{+}\,1)\) is a \({{\mathbb {P}}}^1\)-bundle, projectivization of a decomposable rank two vector bundle on
for some \(t\in {{\mathbb {C}}}^*\). Intuitively \({\widehat{X}}(i,i\,{+}\,1)\) is constructed by adding to \(X^\mathrm{ss}(i,i\,{+}\,1)\) two sections corresponding to the limit points of the action when t goes to 0 and infinity. The variety \({\widehat{X}}(i,i\,{+}\,1)\) is a \({{\mathbb {P}}}^1\)-bundle, projectivization of a decomposable rank two vector bundle on  , and it is birationally equivalent to X by construction. The following statement describes when the natural map \(X\dashrightarrow {\widehat{X}}(i,i\,{+}\,1)\) is a small modification:
, and it is birationally equivalent to X by construction. The following statement describes when the natural map \(X\dashrightarrow {\widehat{X}}(i,i\,{+}\,1)\) is a small modification:
Proposition 2.16
Let (X, L) be a \({\mathbb {Q}}\)-polarized pair with a nontrivial equalized B-type \({{\mathbb {C}}}^*\)-action with critical values \(0=a_0<\dots <a_r=\delta \), and let \(i\in \{0,\dots ,r-1\}\) satisfy:

Then X is \({{\mathbb {C}}}^*\)-equivariantly isomorphic in codimension one to \({\widehat{X}}(i,i\,{+}\,1)\).
Proof
Note first that the rational map \(X\dashrightarrow {\widehat{X}}(i,i\,{+}\,1)\) is defined on \(X^\mathrm{ss}(i,i\,{+}\,1)\), and, by the B-type hypothesis, it is also defined on every point of \(Y_0\cup Y_r\) that lies in the boundary of an orbit contained in \(X^\mathrm{ss}(i,i\,{+}\,1)\). In other words, the map is defined in

Since the hypothesis \((\dagger )\) implies that each of the varieties \(\overline{X^{\pm }(Y)}\) has codimension at least two (see [9, Theorem 4.2]), it follows that \(X\dashrightarrow {\widehat{X}}(i,i\,{+}\,1)\) is defined in codimension one.\(\square \)
3 Small modifications of B-type actions and bordisms
In this section we consider the case of a \({\mathbb {Q}}\)-polarized pair (X, D), with X smooth, admitting a B-type equalized action, and we will show how to construct, under some assumptions, two \({{\mathbb {C}}}^*\)-equivariant small \({\mathbb {Q}}\)-factorial modifications of X which are smooth and of smaller criticality,  ,
,  , having indeterminacy locus \(B^+_1\), \(B^-_{r-1}\), respectively. The construction is an extension of the one described in [21, Section 8] in the particular case of bandwidth three actions. The main result we will show is the following:
, having indeterminacy locus \(B^+_1\), \(B^-_{r-1}\), respectively. The construction is an extension of the one described in [21, Section 8] in the particular case of bandwidth three actions. The main result we will show is the following:
Theorem 3.1
Let X be a smooth projective variety and D be an ample \({\mathbb {Q}}\)-divisor on X, such that (X, D) admits a B-type equalized action of \({{\mathbb {C}}}^*\), of criticality \(r\geqslant 2\) and critical values \(0,a_1,\dots ,a_r\). Assume moreover that \(\nu ^-(Y)>1\) for every fixed point component Y of weight \(a_1\). Then there exists a smooth projective variety  together with a B-type equalized \({{\mathbb {C}}}^*\)-action, and a \({{\mathbb {C}}}^*\)-equivariant small modification
together with a B-type equalized \({{\mathbb {C}}}^*\)-action, and a \({{\mathbb {C}}}^*\)-equivariant small modification  , such that:
, such that:
-
the indeterminacy locus of \(\psi ^-\) is \(B^+_1\);
-
the \({\mathbb {Q}}\)-divisor
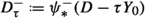 is ample for every \(\tau \in (a_1,a_2)\cap {\mathbb {Q}}\);
is ample for every \(\tau \in (a_1,a_2)\cap {\mathbb {Q}}\); -
 has critical values \(0,a_2-\tau ,\dots ,a_r-\tau \), and criticality \(r-1\).
has critical values \(0,a_2-\tau ,\dots ,a_r-\tau \), and criticality \(r-1\).
Moreover, the map \(\psi ^-\) sends isomorphically the fixed point components in X of weight \(a_i\), \(i\geqslant 2\), to the fixed point components of weight \(a_i-\tau \) in  , and preserves \(\nu ^\pm \) on these components.
, and preserves \(\nu ^\pm \) on these components.
Remark 3.2
Note that, by composing the action of \({{\mathbb {C}}}^*\) with the inversion map \(t\mapsto t^{-1}\) (an operation that exchanges the sink and the source of the action), the above statement implies that if \(\nu ^+(Y)>1\) for every fixed point component of weight \(a_{r-1}\), there exists a small \({{\mathbb {C}}}^*\)-equivariant modification  onto a smooth variety admitting a B-type equalized action, whose indeterminacy locus is \(B^-_{r-1}\), such that the \({\mathbb {Q}}\)-divisor
onto a smooth variety admitting a B-type equalized action, whose indeterminacy locus is \(B^-_{r-1}\), such that the \({\mathbb {Q}}\)-divisor  is ample for every \(\tau \in (a_{r-2},a_{r-1})\cap {\mathbb {Q}}\), and such that the critical values of
is ample for every \(\tau \in (a_{r-2},a_{r-1})\cap {\mathbb {Q}}\), and such that the critical values of  are \(0,a_1-\tau ,\dots ,a_{r-2}-\tau \).
are \(0,a_1-\tau ,\dots ,a_{r-2}-\tau \).
The situation of Theorem 3.1 may be represented as follows. We consider in \({\text {N}^1}(X)\) the affine plane  of classes of the form \(D-\tau _-Y_0-(\delta -\tau _+)Y_r\), \(\tau _-,\tau _+\in {{\mathbb {R}}}\). The region
of classes of the form \(D-\tau _-Y_0-(\delta -\tau _+)Y_r\), \(\tau _-,\tau _+\in {{\mathbb {R}}}\). The region  meets
meets  on an edge passing by \(D^-_{a_1}=D-a_1Y_0\) and
on an edge passing by \(D^-_{a_1}=D-a_1Y_0\) and  on an edge passing by \(D^+_{a_{r-1}}=D-(\delta -a_{r-1})Y_r\). Each wall-crossing corresponds to a flip. We have represented the intersections of the cones with
on an edge passing by \(D^+_{a_{r-1}}=D-(\delta -a_{r-1})Y_r\). Each wall-crossing corresponds to a flip. We have represented the intersections of the cones with  in Fig. 3; a more complete description will be provided in Sect. 4.
in Fig. 3; a more complete description will be provided in Sect. 4.
The proof will be done in three steps. We will start by showing in Sect. 3.1, by means of Nakano Contractibility Theorem, that  exists as a compact complex manifold (Corollary 3.7). Then we will proof in Sect. 3.2 that
exists as a compact complex manifold (Corollary 3.7). Then we will proof in Sect. 3.2 that  is projective, by analyzing the restriction of
is projective, by analyzing the restriction of  to the extremal fixed point components of X and relating them to the geometric quotients of X. Finally, in Sect. 3.3, we will check that
to the extremal fixed point components of X and relating them to the geometric quotients of X. Finally, in Sect. 3.3, we will check that  satisfies all the properties required in the statement.
satisfies all the properties required in the statement.
3.1 Existence of  as a complex manifold
as a complex manifold
Let us start by studying the variety \(B^+_1\), which will be indeterminacy locus of  , and proving that it is a projective bundle over \(Y_1\), in the sense that the irreducible components of \(B^+_1\) are projective bundles over the irreducible components of \(Y_1\). Note that \(Y_1\) is not assumed to be irreducible, and in fact it may have irreducible component of different dimensions (see Remark 3.4 below). We will also identify the normal bundle to \(B^+_1\) in X.
, and proving that it is a projective bundle over \(Y_1\), in the sense that the irreducible components of \(B^+_1\) are projective bundles over the irreducible components of \(Y_1\). Note that \(Y_1\) is not assumed to be irreducible, and in fact it may have irreducible component of different dimensions (see Remark 3.4 below). We will also identify the normal bundle to \(B^+_1\) in X.
Proposition 3.3
Let X be a smooth projective variety, and D be an ample \({\mathbb {Q}}\)-divisor on X, such that (X, D) admits an equalized B-type \({{\mathbb {C}}}^*\)-action, of criticality \(r\geqslant 2\). Then \(B^+_1\subset X\) is the disjoint union of the varieties \(B^+(Y)\),  , \(\mu _D(Y)=a_1\), and each \(B^+(Y)\) is a projective bundle over Y, of relative dimension \(\nu ^+(Y)\). Moreover, denoting by \(p:B^+(Y)\rightarrow Y\) the natural projection, and by F a fiber of p we have
, \(\mu _D(Y)=a_1\), and each \(B^+(Y)\) is a projective bundle over Y, of relative dimension \(\nu ^+(Y)\). Moreover, denoting by \(p:B^+(Y)\rightarrow Y\) the natural projection, and by F a fiber of p we have

Remark 3.4
One may construct examples in which \(Y_1\) has components of different dimensions. For instance, the variety  (where \(Q^{n-1}\) denotes a smooth \((n\,{-}\,1)\)-dimensional quadric) admits an equalized \({{\mathbb {C}}}^*\)-action of bandwidth 3 such that \(Y_0\) and \(Y_3\) are two isolated points, and both \(Y_1\) and \(Y_2\) are the union of a point and \(Q^{n-3}\) (see [26, Theorem 3.6 (2)]). If we consider the blowup of X along \(Y_0\) and \(Y_3\) we obtain an equalized B-type \({{\mathbb {C}}}^*\)-action with \(B^{+}_1\), \(B^{+}_2\) still reducible with two irreducible components.
(where \(Q^{n-1}\) denotes a smooth \((n\,{-}\,1)\)-dimensional quadric) admits an equalized \({{\mathbb {C}}}^*\)-action of bandwidth 3 such that \(Y_0\) and \(Y_3\) are two isolated points, and both \(Y_1\) and \(Y_2\) are the union of a point and \(Q^{n-3}\) (see [26, Theorem 3.6 (2)]). If we consider the blowup of X along \(Y_0\) and \(Y_3\) we obtain an equalized B-type \({{\mathbb {C}}}^*\)-action with \(B^{+}_1\), \(B^{+}_2\) still reducible with two irreducible components.
Proof of Proposition 3.3
Note that, since X is smooth and the action is of B-type, then, by the Białynicki-Birula Theorem (see for instance [21, Theorem 2.8]) \(X^-(Y_0)\) is isomorphic to a line bundle over \(Y_0\); in particular, two components of the form \(B^+(Y)\subset B^+_1\) do not intersect and we may write

Let \(Y\subset Y_1\) be an irreducible component. Consider the set  which is isomorphic, by the Białynicki-Birula decomposition (see Sect. 2.1), to the open set
which is isomorphic, by the Białynicki-Birula decomposition (see Sect. 2.1), to the open set

where \(s_0\) denotes the zero section of  . On the other hand, a similar argument shows that
. On the other hand, a similar argument shows that  is isomorphic to the open set
is isomorphic to the open set

where \(s'_0\) denotes the zero section of  . This is a \({{\mathbb {C}}}^*\)-principal bundle over \(B^+(Y)\cap Y_0\), so its projection to \(B^+(Y)\cap Y_0\) is a geometric quotient, whose fibers are the orbits of the action of \({{\mathbb {C}}}^*\). Since the action is equalized, \({{\mathbb {C}}}^*\) acts homothetically on
. This is a \({{\mathbb {C}}}^*\)-principal bundle over \(B^+(Y)\cap Y_0\), so its projection to \(B^+(Y)\cap Y_0\) is a geometric quotient, whose fibers are the orbits of the action of \({{\mathbb {C}}}^*\). Since the action is equalized, \({{\mathbb {C}}}^*\) acts homothetically on  , therefore we get
, therefore we get

Note that \(B^+(Y)\) can be written as the union of two open sets, \(X^+(Y)\), and  , and the smoothness of \(B^+(Y)\) follows.
, and the smoothness of \(B^+(Y)\) follows.
We consider now the blowup \(B^{+}(Y)^{\flat }\) of \(B^+(Y)\) along Y; it is a \({{\mathbb {P}}}^1\)-bundle over  with two sections: one is the exceptional divisor of the blowup, and the other is the strict transform of \(B^+(Y)\cap Y_0\); this tells us that \(B^{+}(Y)^{\flat }\) can be written as
with two sections: one is the exceptional divisor of the blowup, and the other is the strict transform of \(B^+(Y)\cap Y_0\); this tells us that \(B^{+}(Y)^{\flat }\) can be written as  , where
, where  is the conormal bundle of the first section in \(B^{+}(Y)^{\flat }\). Since the normal bundle of the exceptional divisor
is the conormal bundle of the first section in \(B^{+}(Y)^{\flat }\). Since the normal bundle of the exceptional divisor  in the blowup \(B^{+}(Y)^{\flat }\) is
in the blowup \(B^{+}(Y)^{\flat }\) is  , it follows that
, it follows that

From this it easily follows that

Let \(F\simeq {{\mathbb {P}}}^{\nu ^+(Y)}\) be a fiber of p, and let \(x_1\) be the intersection point \(F\cap Y\). We will show that  for every line \({{\mathbb {P}}}^1\subset F\) passing by \(x_1\); the results will then follow from [23, Theorem 3.2.1].
for every line \({{\mathbb {P}}}^1\subset F\) passing by \(x_1\); the results will then follow from [23, Theorem 3.2.1].
Given such a line \({{\mathbb {P}}}^1\), we set  , and compute the splitting type of the bundle
, and compute the splitting type of the bundle  by using the vector bundle version of the AM vs FM formula [21, Lemma 2.17]. Since the action is equalized, the splitting type can be obtained as the set of differences of the weights of the action on the vector spaces
by using the vector bundle version of the AM vs FM formula [21, Lemma 2.17]. Since the action is equalized, the splitting type can be obtained as the set of differences of the weights of the action on the vector spaces  ,
,  , and it is a straightforward computation that these weights are, respectively \(\bigl ((-1)^{\nu ^-(Y)}\bigr )\), \(\bigl (0^{\nu ^-(Y)}\bigr )\), with the exponent denoting the occurrence of \(-1\) and 0, respectively. \(\square \)
, and it is a straightforward computation that these weights are, respectively \(\bigl ((-1)^{\nu ^-(Y)}\bigr )\), \(\bigl (0^{\nu ^-(Y)}\bigr )\), with the exponent denoting the occurrence of \(-1\) and 0, respectively. \(\square \)
Let us now denote by \(b:X'\rightarrow X\) the blowup of X along \(B^+_1\) and by E its exceptional divisor, which is the disjoint union of the divisors  ,
,  , \(\mu _D(Y)=a_1\); recall also the varieties \(V^\pm (Y)\), for every
, \(\mu _D(Y)=a_1\); recall also the varieties \(V^\pm (Y)\), for every  , defined in (2.3). The following statement describes E and its irreducible components.
, defined in (2.3). The following statement describes E and its irreducible components.
Proposition 3.5
Let (X, D) be as in Proposition 3.3. Then

Proof
We will show that for every irreducible component \(Y\subset Y_1\) we have

Using Proposition 3.3, given a fiber F of \(p:B^+(Y)\rightarrow Y\), we have that  , hence \(E_Y\) is a \({{\mathbb {P}}}^{\nu ^+(Y)}\)-bundle over a variety Z, and Z is necessarily a \({{\mathbb {P}}}^{\nu ^-(Y)-1}\)-bundle over Y, i.e. we have a Cartesian square
, hence \(E_Y\) is a \({{\mathbb {P}}}^{\nu ^+(Y)}\)-bundle over a variety Z, and Z is necessarily a \({{\mathbb {P}}}^{\nu ^-(Y)-1}\)-bundle over Y, i.e. we have a Cartesian square

whose maps are projective bundles. Now we note that, since \(B^+(Y)\) is isomorphic to \(X^+(Y)\) in a neighborhood of Y, then  , and we have a diagram composed of two Cartesian squares
, and we have a diagram composed of two Cartesian squares

In particular, the composition of the two upper horizontal arrows is an isomorphism, that is \(Z\simeq V^-(Y)\), and the statement follows.\(\square \)
Since \(B^+_1\) is \({{\mathbb {C}}}^*\)-invariant, then the action of \({{\mathbb {C}}}^*\) on X extends to \(X'\). This action is of B-type by construction, and its sink which we denote by \(Y_0'\) is the strict transform of \(Y_0\) via b. Since \(B^+_1\) intersects \(Y_0\) transversally, it follows that \(Y_0'\) is the blowup of \(Y_0\) along \(B^+_1\cap Y_0\). We have shown in the proof of Proposition 3.3 (see equation (3.1)) that for each component \(Y\subset Y_1\) we have that  . We will describe now the exceptional locus \(E_Y\cap Y_0'\) of \(b_{|Y_0'}\).
. We will describe now the exceptional locus \(E_Y\cap Y_0'\) of \(b_{|Y_0'}\).
Corollary 3.6
Let \((X, D)\) be as in Proposition 3.3, let \(Y\subset Y_1\) be an irreducible component of \(Y_1\), and \(E_Y\) be the corresponding irreducible component of the exceptional divisor E of the blowup \(b:X'\rightarrow X\). Moreover, let \(\Gamma \simeq {{\mathbb {P}}}^{\nu ^+(Y)-1}\) be any fiber of \(V^+(Y)\rightarrow Y\). Then

Proof
Under the identification \(B^+(Y)\cap Y_0=V^+(Y)\) we may write

Since \({\Gamma }\) is a projective subspace of a fiber of \(B^+(Y)\rightarrow Y\), the first equality holds. Projectivizing the above isomorphism, the inclusion  fits into a commutative diagram consisting of two Cartesian squares
fits into a commutative diagram consisting of two Cartesian squares

This implies that

Corollary 3.7
Let X be a smooth projective variety, and D be an ample \({\mathbb {Q}}\)-divisor on X, such that (X, D) admits an equalized B-type \({{\mathbb {C}}}^*\)-action, of criticality \(r\geqslant 2\). Let \(X'\) be the blowup of X along \(B^+_1\), with exceptional divisor E, and let \(Y_0'\subset X'\) be the strict transform of \(Y_0\) into \(X'\). Then there exists a proper map

which is the blowup of a smooth proper variety  along a subvariety isomorphic to \(V^-_1\), whose exceptional divisor is E. Moreover:
along a subvariety isomorphic to \(V^-_1\), whose exceptional divisor is E. Moreover:
-
\(b'_{|_E}\) is the natural projection
 .
. -
\(b'_{|Y'_0}\) is the smooth blowup of \(b'(Y_0')\) along \(V^-_1\), with exceptional divisor
 .
.
Proof
The divisor E is not necessarily connected, but we are not claiming yet that  is projective, so the statement is local: we will show that there exists a holomorphic contraction
is projective, so the statement is local: we will show that there exists a holomorphic contraction  that is a smooth blowup on an analytic neighborhood of every component \(E_Y\) of E, mapping
that is a smooth blowup on an analytic neighborhood of every component \(E_Y\) of E, mapping  onto a variety isomorphic to \(V^-(Y)\). Let us denote by \(F'\simeq {{\mathbb {P}}}^{\nu ^+(Y)}\) a fiber of the projective bundle \({\bar{p}}:E_Y \rightarrow V^-(Y)\). By the Nakano Contractibility Criterion [3, Theorem 3.2.8] for the first part of the statement it is enough to show that
onto a variety isomorphic to \(V^-(Y)\). Let us denote by \(F'\simeq {{\mathbb {P}}}^{\nu ^+(Y)}\) a fiber of the projective bundle \({\bar{p}}:E_Y \rightarrow V^-(Y)\). By the Nakano Contractibility Criterion [3, Theorem 3.2.8] for the first part of the statement it is enough to show that

This follows by noting that, by Proposition 3.5, \(F'\) is a section of \(E_Y \rightarrow B^+(Y)\) over its image, that we denote by F, and F is a fiber of \(p:B^+(Y)\rightarrow Y\) (see Proposition 3.5). By Proposition 3.3,  , and so the above equality follows by a straightforward computation.
, and so the above equality follows by a straightforward computation.
For the second part of the statement we note that, by Corollary 3.6, \(b'\) maps \(E_Y\cap Y_0'\) onto a subvariety of \(b'(Y_0')\) isomorphic to \(V^-(Y)\), for every component \(Y\subset Y_1\). The fact that \(b'_{|Y_0'}\) is again a smooth blowup follows again by Nakano’s Criterion and by the first part of Corollary 3.6.\(\square \)
Let us define the rational map  as follows:
as follows:

Its indeterminacy locus is \(B^+_1\) by construction. We will now prove that the \({{\mathbb {C}}}^*\)-action on \(X'\) descends to  , and identify the corresponding sink.
, and identify the corresponding sink.
Corollary 3.8
The map  induces a B-type equalized \({{\mathbb {C}}}^*\)-action on
induces a B-type equalized \({{\mathbb {C}}}^*\)-action on  , whose sink is isomorphic to
, whose sink is isomorphic to  .
.
Proof
The restriction of the \({{\mathbb {C}}}^*\)-action on \(X'\) to every component  is the fiber product of the natural action of \({{\mathbb {C}}}^*\) on \(B^+(Y)\) and \(V^-(Y)\). In particular, the fibers of \(b'\) are \({{\mathbb {C}}}^*\)-invariant, and the action descends to
is the fiber product of the natural action of \({{\mathbb {C}}}^*\) on \(B^+(Y)\) and \(V^-(Y)\). In particular, the fibers of \(b'\) are \({{\mathbb {C}}}^*\)-invariant, and the action descends to  .
.
Note that a priori we do not know if  is projective; by saying that the action of \({{\mathbb {C}}}^*\) on it is of B-type and equalized we mean that the sink and the source of the action are divisors, and that the isotropy group of every point in a 1-dimensional orbit is trivial.
is projective; by saying that the action of \({{\mathbb {C}}}^*\) on it is of B-type and equalized we mean that the sink and the source of the action are divisors, and that the isotropy group of every point in a 1-dimensional orbit is trivial.
The B-type property is clear since the extremal fixed point components of  are \(\psi ^-(Y_0)\) and \(\psi ^-(Y_r)\). In order to see that the action is equalized we observe that the image of E into
are \(\psi ^-(Y_0)\) and \(\psi ^-(Y_r)\). In order to see that the action is equalized we observe that the image of E into  is contained in the image of \(Y_0'\) (see Corollary 3.7); this implies that the 1-dimensional orbits of
is contained in the image of \(Y_0'\) (see Corollary 3.7); this implies that the 1-dimensional orbits of  do not meet \(b'(E)\), and so they are mapped isomorphically into X. In particular, the isotropy groups of the points in these orbits are trivial.
do not meet \(b'(E)\), and so they are mapped isomorphically into X. In particular, the isotropy groups of the points in these orbits are trivial.
In order to study the sink \(\psi ^-(Y_0)\) of  , we note first that the open subset \(X^\mathrm{ss}(1,2)\subset X\) maps isomorphically into \(X'\) and
, we note first that the open subset \(X^\mathrm{ss}(1,2)\subset X\) maps isomorphically into \(X'\) and  . By construction, the image \(\psi ^-(X^\mathrm{ss}(1,2))\) contains all the 1-dimensional orbits in
. By construction, the image \(\psi ^-(X^\mathrm{ss}(1,2))\) contains all the 1-dimensional orbits in  whose limit at \(\infty \) belongs to \(\psi ^-(Y_0)\); more precisely, we claim that for every point \(P\in \psi ^-(Y_0)\) there exists a unique orbit in \(\psi ^-(X^\mathrm{ss}(1,2))\) whose limit at \(\infty \) is P. This is obvious if
whose limit at \(\infty \) belongs to \(\psi ^-(Y_0)\); more precisely, we claim that for every point \(P\in \psi ^-(Y_0)\) there exists a unique orbit in \(\psi ^-(X^\mathrm{ss}(1,2))\) whose limit at \(\infty \) is P. This is obvious if  , so we are left to study the case in which P belongs to the complement of this set in \(\psi ^-(Y_0)\), which is isomorphic to
, so we are left to study the case in which P belongs to the complement of this set in \(\psi ^-(Y_0)\), which is isomorphic to  . Denoting by \(p:V^-_1\rightarrow Y_1\) the natural projection, given a point
. Denoting by \(p:V^-_1\rightarrow Y_1\) the natural projection, given a point  , by the Białynicki-Birula decomposition, there exists a unique orbit in \(X^\mathrm{ss}(1,2)\) whose limit at \(\infty \) is the point p(P) with tangent direction P. This completes the proof of the claim.
, by the Białynicki-Birula decomposition, there exists a unique orbit in \(X^\mathrm{ss}(1,2)\) whose limit at \(\infty \) is the point p(P) with tangent direction P. This completes the proof of the claim.
In particular, we have a bijective morphism from the quotient  to \(\psi ^-(Y_0)\), sending every orbit in \(X^\mathrm{ss}(1,2)\) to the limit at \(\infty \) of its image in
to \(\psi ^-(Y_0)\), sending every orbit in \(X^\mathrm{ss}(1,2)\) to the limit at \(\infty \) of its image in  ; this map is bijective by the above claim. Since \(\psi ^-(Y_0)\) is smooth (by Corollary 3.7) and
; this map is bijective by the above claim. Since \(\psi ^-(Y_0)\) is smooth (by Corollary 3.7) and  is normal, the map is an isomorphism.\(\square \)
is normal, the map is an isomorphism.\(\square \)
3.2 Projectivity of 
Let \(b:X'\rightarrow X\) be the blowup of X along \(B^+_1\), E the exceptional divisor and \(Y_0'\) the strict transform of \(Y_0\). In order to prove that the holomorphic map  provided by Corollary 3.7 is projective, we will show that it admits a supporting \({\mathbb {Q}}\)-divisor, i.e., there exists a nef \({\mathbb {Q}}\)-divisor on \(X'\) having intersection number zero exactly on the curves contracted by \(b'\):
provided by Corollary 3.7 is projective, we will show that it admits a supporting \({\mathbb {Q}}\)-divisor, i.e., there exists a nef \({\mathbb {Q}}\)-divisor on \(X'\) having intersection number zero exactly on the curves contracted by \(b'\):
Proposition 3.9
Under the assumptions of Theorem 3.1, the \({\mathbb {Q}}\)-divisor

is a supporting divisor of \(b'\).
The proof of this fact is done in two steps. First we show (Lemma 3.10) that the statement can be reduced to analyzing the behavior of this divisor in \(Y_0'\); then the proof is concluded by interpreting \(b'_{|Y_0'}\) as a resolution of the natural map among two geometric quotients of X.
Lemma 3.10
If \(D'_{|Y_0'}\) is a supporting \({\mathbb {Q}}\)-divisor for \(b'_{|Y_0'}\), then \(D'\) is a supporting \({\mathbb {Q}}\)-divisor for \(b'\).
Proof
The Mori cone of \(X'\) is generated by the numerical classes of \({{\mathbb {C}}}^*\)-invariant curves (cf. [26, Lemma 1.5]), that is by the classes of closures of 1-dimensional orbits and by the classes of curves contained in the fixed point components \(Y_i'\). Let us note that \(Y_i'=Y_i\) for \(i \geqslant 2\) and \(Y_1'=V_1^-\). It is easy to show, by using Lemma 2.2, that  if C is:
if C is:
-
the closure of an orbit having sink on \(Y'_i\), \(i\geqslant 1\); in this case \(D'\cdot C=b^*D\cdot C>0\) if \(i \geqslant 2\) and
 if \(i=1\);
if \(i=1\); -
the closure of an orbit having sink on \(Y'_0\), and source on \(Y'_i\), \(i\geqslant 2\), for which
 ;
; -
a curve contained in \(Y'_i\), \(i\geqslant 2\), for which we have
 .
.
Moreover  if C is the closure of an orbit joining \(Y'_0\) with \(Y'_1\), since, by Corollary 3.7,
if C is the closure of an orbit joining \(Y'_0\) with \(Y'_1\), since, by Corollary 3.7,  , hence
, hence  .
.
We are left to study the classes of curves contained in \(Y_1'=V^-_1\). We have shown (Corollary 3.5) that the exceptional divisor \(E\subset X'\) is a projective bundle over \(V^-_1\), containing \(V^-_1\) as a section. If \(C\subset V^-_1\) were an irreducible curve such that  , we could find an irreducible curve \(C'\) in \(Y_0' \cap E\) such that, for some positive integer m the cycle \(C'-mC\) would be numerically proportional to the class \([\ell ^-]\) of a line in a fiber of \(E\rightarrow V^-_1\). Since
, we could find an irreducible curve \(C'\) in \(Y_0' \cap E\) such that, for some positive integer m the cycle \(C'-mC\) would be numerically proportional to the class \([\ell ^-]\) of a line in a fiber of \(E\rightarrow V^-_1\). Since  , we would have
, we would have  , hence
, hence  and it would follow that \(C'\) is numerically proportional to \(\ell ^-\). Hence also C would be numerically proportional to \(\ell ^-\), and therefore contracted by the projection \(E\rightarrow V^-_1\), a contradiction.\(\square \)
and it would follow that \(C'\) is numerically proportional to \(\ell ^-\). Hence also C would be numerically proportional to \(\ell ^-\), and therefore contracted by the projection \(E\rightarrow V^-_1\), a contradiction.\(\square \)
Proof of Proposition 3.9
By means of Corollary 3.8, let us identify the sink of  with
with  . Consider the rational map
. Consider the rational map  . As shown in the proof of Corollary 3.8, this is the natural map among the geometric quotients
. As shown in the proof of Corollary 3.8, this is the natural map among the geometric quotients  ,
,  . In particular, it coincides with the restriction of the quotient map
. In particular, it coincides with the restriction of the quotient map  .
.
Since the action of X is of B-type (so its blowup along its sink and source is an isomorphism), by applying Proposition 2.12 and Lemma 2.5, the quotient map  is given by a linear system of the form \(|m(D-\tau Y_0-(\delta -\tau )Y_r)|\), for \(\tau \in {\mathbb {Q}}\cap (a_1,a_2)\), and m large enough and divisible. Therefore \(\psi ^-_{|Y_0}\) is given by a linear subsystem of \(|m(D-\tau Y_0)_{|Y_0}|\).
is given by a linear system of the form \(|m(D-\tau Y_0-(\delta -\tau )Y_r)|\), for \(\tau \in {\mathbb {Q}}\cap (a_1,a_2)\), and m large enough and divisible. Therefore \(\psi ^-_{|Y_0}\) is given by a linear subsystem of \(|m(D-\tau Y_0)_{|Y_0}|\).
Since this rational map is resolved via the blowup b, a supporting divisor of  will be of the form
will be of the form
for some \(r\in {\mathbb {Q}}\). Imposing that this divisor has degree zero on a curve contracted by \(b'\), we easily get \(r=\tau -a_1\). Then the statement follows by Lemma 3.10.\(\square \)
3.3 The fixed point components of 
First of all we note that, from the results in Sects. 3.1, 3.2, we already know that the rational map  has indeterminacy locus \(B^+_1\), and that it is \({{\mathbb {C}}}^*\)-equivariant with respect to an action on
has indeterminacy locus \(B^+_1\), and that it is \({{\mathbb {C}}}^*\)-equivariant with respect to an action on  that is of B-type and equalized. From Proposition 3.9 and applying \(b'_*\), we obtain that
that is of B-type and equalized. From Proposition 3.9 and applying \(b'_*\), we obtain that  is ample on
is ample on  , for every \(\tau \in {\mathbb {Q}}\cap (a_1,a_2)\). Then we are left with studying the fixed point components of
, for every \(\tau \in {\mathbb {Q}}\cap (a_1,a_2)\). Then we are left with studying the fixed point components of  , and their weights with respect to \(D^-_\tau \).
, and their weights with respect to \(D^-_\tau \).
Note that there exists a linearization of the \({{\mathbb {C}}}^*\)-action on the line bundle  satisfying that
satisfying that  . Then, by Lemma 2.2, we have that
. Then, by Lemma 2.2, we have that  for any fixed point component \(Y\ne Y_0\).
for any fixed point component \(Y\ne Y_0\).
The fixed components in  correspond isomorphically via \(\psi ^-\) to the fixed components in
correspond isomorphically via \(\psi ^-\) to the fixed components in  , that is to
, that is to  , and the ranks \(\nu ^\pm \) are obviously preserved by this correspondence. By definition, on each of these components we have
, and the ranks \(\nu ^\pm \) are obviously preserved by this correspondence. By definition, on each of these components we have
On the other hand the \(D^-_\tau \)-weight of the action at \(\psi ^-(Y_0)\) can be computed at its general point, for which
This finishes the proof of Theorem 3.1.
4 Equalized actions and Mori dream spaces
In this section we will show that, under some assumptions, the blowup of a smooth projective variety X supporting an equalized \({{\mathbb {C}}}^*\)-action is an MDS; we will study its movable cone, as well as its small \({\mathbb {Q}}\)-factorial modifications. Although our arguments should work in broader generality, for the sake of clarity we will stick to the case in which the Picard number of X is one. We will not assume that the sink and the source of the action are positive dimensional; in that particular case, our arguments provide a proof for Theorem 1.1. From now on we will work under the following assumptions:
Setup 4.1
X is a smooth projective variety of Picard number one,  is ample, and there exists an equalized \({{\mathbb {C}}}^*\)-action on X together with a linearization of the action on L. We will assume that X is not \({{\mathbb {P}}}^n\) endorsed with the faithful \({{\mathbb {C}}}^*\)-action that fixes a point and a disjoint hyperplane. We will denote by \(0=a_0<\dots <a_r=\delta \) the weights of the action on the fixed point components, by \(\beta :X^\flat \rightarrow X\) the blowup of X along the sink \(Y_0\) and the source \(Y_r\), and by \(Y^\flat _0,Y^\flat _r\subset X^\flat \) the corresponding exceptional divisors. Following [21, Lemma 3.10], the action of \({{\mathbb {C}}}^*\) on X extends equivariantly via \(\beta \) to a B-type action on \(X^\flat \).
is ample, and there exists an equalized \({{\mathbb {C}}}^*\)-action on X together with a linearization of the action on L. We will assume that X is not \({{\mathbb {P}}}^n\) endorsed with the faithful \({{\mathbb {C}}}^*\)-action that fixes a point and a disjoint hyperplane. We will denote by \(0=a_0<\dots <a_r=\delta \) the weights of the action on the fixed point components, by \(\beta :X^\flat \rightarrow X\) the blowup of X along the sink \(Y_0\) and the source \(Y_r\), and by \(Y^\flat _0,Y^\flat _r\subset X^\flat \) the corresponding exceptional divisors. Following [21, Lemma 3.10], the action of \({{\mathbb {C}}}^*\) on X extends equivariantly via \(\beta \) to a B-type action on \(X^\flat \).
Remark 4.2
We note that a variety X as in Setup 4.1 is rationally connected (see [21, Remark 2.3]), in particular  is torsion free, and
is torsion free, and  .
.
Remark 4.3
Saying that a variety X with Picard number one is not \({{\mathbb {P}}}^n\) together with the \({{\mathbb {C}}}^*\)-action with a fixed point and a fixed hyperplane is equivalent to say that neither the sink nor the source of the action are divisors (cf. [22, Lemma 6.3]). Note also that in the excluded case, \(X^\flat \) is the blowup of \({{\mathbb {P}}}^n\) along a point, which does not have nontrivial small \({\mathbb {Q}}\)-factorial modifications.
Before presenting our description of the birational geometry of \(X^\flat \), we will need some preliminary results on the fixed point components of X. Let us start by recalling the following statement (cf. [21, Lemma 2.6 (2), Lemma 3.10]):
Lemma 4.4
Let (X, L) be as in Setup 4.1. Then the \({{\mathbb {C}}}^*\)-action on \(X^\flat \) is a bordism if and only if  .
.
In the case in which the extended action on \(X^\flat \) is not a bordism, the fixed point components Y with \(\nu ^{\pm }(Y)=1\) are the “closest” to the sink and the source:
Lemma 4.5
Let (X, L) be as in Setup 4.1, and assume that \(Y_0\) (resp. \(Y_r\)) is a point. Then \(Y_1\) is irreducible and \(\nu ^+(Y_1)=1\) (resp. \(Y_{r-1}\) is irreducible and \(\nu ^-(Y_{r-1})=1\)). Moreover, for every other inner fixed point component Y we have \(\nu ^+(Y) >1\) (resp. \(\nu ^-(Y) >1\)).
Proof
If \(Y \subset Y_1\) is an irreducible component such that \(\nu ^+(Y)>1\), then there exists a positive dimensional family of invariant curves linking a point \(y \in Y\) and the point \(Y_0\). By bending-and-breaking, this family contains a non integral 1-cycle Z, which is necessarily \({{\mathbb {C}}}^*\)-invariant.
By means of Lemma 2.2, the equalization of the action implies that Z cannot be non-reduced and irreducible. On the other hand, if it were reducible the intersection point of two components would be a fixed point with a weight in between \(a_0\) and \(a_1\), a contradiction.
The proof is finished recalling [21, Lemma 2.6 (2)], which proves that there exists a unique irreducible fixed point component on which \(\nu ^+\) is equal to 1.\(\square \)
Remark 4.6
Let us denote by I(X, L) the set of indices \(\{0,\dots ,r\}\) satisfying the hypothesis \((\dagger )\) of Proposition 2.16. The above two lemmas imply that if (X, L) is as in Setup 4.1, then

In particular, by Proposition 2.16, for every \(i\in I(X,L)\) we have a small modification \({\widehat{X}}(i,i\,{+}\,1)\) of \(X^\flat \) that is a \({{\mathbb {P}}}^1\)-bundle over  .
.
4.1 The movable cone of \(X^\flat \) and its stable base locus decomposition
Recall that, given a \({\mathbb {Q}}\)-divisor  on a normal variety Y, the stable base locus of D (see [17, Definition 2.1.20]) is defined as
on a normal variety Y, the stable base locus of D (see [17, Definition 2.1.20]) is defined as

A \({\mathbb {Q}}\)-divisor  on a normal variety Y is called movable if \({{\mathbb {B}}}(D)\) has codimension at least two. If
on a normal variety Y is called movable if \({{\mathbb {B}}}(D)\) has codimension at least two. If  , then being movable is a numerical property and we can define the movable cone of Y, denoted
, then being movable is a numerical property and we can define the movable cone of Y, denoted  , as the convex cone in \({\text {N}^1}(Y)\) generated by the classes of movable divisors. Furthermore, we may decompose
, as the convex cone in \({\text {N}^1}(Y)\) generated by the classes of movable divisors. Furthermore, we may decompose  in chambers on whose interior the stable base locus is constant; this is called the stable base locus (SBL) decomposition of the movable cone Y (see, for instance, [13, Section 4.1.3]).
in chambers on whose interior the stable base locus is constant; this is called the stable base locus (SBL) decomposition of the movable cone Y (see, for instance, [13, Section 4.1.3]).
Note that, for a variety X in the situation of Setup 4.1, as in Remark 4.2, we have that  , hence it makes sense to talk about
, hence it makes sense to talk about  and its SBL decomposition; this is the goal of this Section.
and its SBL decomposition; this is the goal of this Section.
Let us start by describing  . For simplicity we will focus on the case in which the action is a bordism (i.e.
. For simplicity we will focus on the case in which the action is a bordism (i.e.  for \(i=0,r\)), an we will discuss later how the same arguments apply in the non-bordism case.
for \(i=0,r\)), an we will discuss later how the same arguments apply in the non-bordism case.
Proposition 4.7
In the situation of Setup 4.1, assuming that  , \(i=0,r\), then the movable cone of \(X^\flat \) is simplicial:
, \(i=0,r\), then the movable cone of \(X^\flat \) is simplicial:

Proof
The divisor \(L(0,\delta )=\beta ^*L\) is semiample, hence movable. On the other hand, by Corollary 2.7,  , for \(m\gg 0\). Each irreducible component of
, for \(m\gg 0\). Each irreducible component of  is either the source or has codimension in X equal to \(\nu ^-(Y)\) for an inner fixed point component Y. By Remark 4.3, Lemmas 4.4 and 2.3, none of these components is a divisor and L(0, 0) is movable. A similar proof shows that \(L(\delta ,\delta )\) is movable, so we get an inclusion
is either the source or has codimension in X equal to \(\nu ^-(Y)\) for an inner fixed point component Y. By Remark 4.3, Lemmas 4.4 and 2.3, none of these components is a divisor and L(0, 0) is movable. A similar proof shows that \(L(\delta ,\delta )\) is movable, so we get an inclusion

On the other hand, we consider the numerical classes of the following curves:
-
the closure \(C_{{\text {gen}}}\) of the general \({{\mathbb {C}}}^*\)-orbit in \(X^\flat \);
-
a line \(C_i\) in a fiber of the projective bundle \(\beta :Y_i^\flat \rightarrow Y_i\), \(i=0,r\).
The loci of the deformations of these curves have codimension 0 and 1, respectively, hence their intersection number with every class in  must be nonnegative. Since, by Lemma 2.2, we have
must be nonnegative. Since, by Lemma 2.2, we have  , and clearly
, and clearly

the above nonnegativity conditions can easily be rewritten as

and the statement follows.\(\square \)
Remark 4.8
The above proof shows that the dual of  in the case in which
in the case in which  is the cone generated by the classes \([C_{{\text {gen}}}],[C_0],[C_r]\). This follows from the fact that we have the following intersection numbers:
is the cone generated by the classes \([C_{{\text {gen}}}],[C_0],[C_r]\). This follows from the fact that we have the following intersection numbers:
\(\cdot \) | \(C_{{\text {gen}}}\) | \(C_0\) | \(C_r\) |
|---|---|---|---|
\(L(0,\delta )\) | \(\delta \) | 0 | 0 |
L(0, 0) | 0 | 0 | \(\delta \) |
\(L(\delta ,\delta )\) | 0 | \(\delta \) | 0 |
If this condition is not fulfilled, we need to add some extra classes of curves (whose deformation loci have codimension 1) to the set of generators of  . For instance, if
. For instance, if  , the deformations of a general irreducible \({{\mathbb {C}}}^*\)-invariant curve linking \(Y_1\) with \(Y_r\) (which has negative intersection with L(0, 0)) span a divisor in X, making L(0, 0) not movable.
, the deformations of a general irreducible \({{\mathbb {C}}}^*\)-invariant curve linking \(Y_1\) with \(Y_r\) (which has negative intersection with L(0, 0)) span a divisor in X, making L(0, 0) not movable.
More concretely, denoting by \(C_{1,r}\), \(C_{0,r-1}\) two irreducible \({{\mathbb {C}}}^*\)-invariant curve linking \(Y_1\) with \(Y_r\), and \(Y_0\) with \(Y_{r-1}\), respectively, an argument similar to the one in the previous proof gives:
-
If
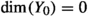 ,
,  , then
, then 
-
If
 ,
,  , then
, then 
-
If \(\dim (Y_0)=0\), \(\dim (Y_r)=0\), then

The position of the generators of (an affine slice of) the movable cone in each case has been represented in Fig. 4.
The SBL decomposition of  can be now read out of the following statement, that is a consequence of Corollary 2.7,
can be now read out of the following statement, that is a consequence of Corollary 2.7,
Corollary 4.9
For every \(\tau _-,\tau _+\in [0,\delta ]\cap {\mathbb {Q}}\), \(\tau _-\leqslant \tau _+\) we have

In particular, the chambers of the SBL decomposition of  can be described as follows. For every set of indices (i, j), \(0\leqslant i\leqslant j\leqslant r\), we set
can be described as follows. For every set of indices (i, j), \(0\leqslant i\leqslant j\leqslant r\), we set

The previous statement tells us that \(N_{i,j}\) is an SBL-chamber whenever it is contained in  , and this is the case for every (i, j), \(i< j\), except in the following two cases (see Remark 4.8 and Fig. 4):
, and this is the case for every (i, j), \(i< j\), except in the following two cases (see Remark 4.8 and Fig. 4):
-
\(Y_0\) is a point and \((i,j)=(0,1)\);
-
\(Y_r\) is a point and \((i,j)=(r-1,r)\).
4.2 The Mori chamber decomposition of \(X^\flat \)
We will now describe the Mori chamber decomposition of the movable cone of \(X^\flat \), which in general is only known to be a refinement of the stable base locus decomposition of the movable cone (see for instance [16, Remark 2.5]). In our case we will show:
Theorem 4.10
In the situation of Setup 4.1, the Mori chamber decomposition of \(X^\flat \) equals its SBL decomposition, that is, the Mori chambers of \(X^\flat \) are the sets  .
.
Note that if  (resp.
(resp.  ) then
) then  does not contain the chamber \(N_{0,1}\) (resp. \(N_{r-1,r}\)); in the case in which \(X^\flat \) is a bordism we have a chamber for every pair of indices \((i,j)\in \{0,\dots ,r\}^2\), \(i<j\). Let us set
does not contain the chamber \(N_{0,1}\) (resp. \(N_{r-1,r}\)); in the case in which \(X^\flat \) is a bordism we have a chamber for every pair of indices \((i,j)\in \{0,\dots ,r\}^2\), \(i<j\). Let us set

In order to prove Theorem 4.10 we will use a recursive argument that allows us to prove the following more detailed version of it:
Proposition 4.11
In the situation of Setup 4.1, for every  there exists a smooth projective variety X(i, j), with a B-type equalized \({{\mathbb {C}}}^*\)-action of criticality \(j-i\), and a \({{\mathbb {C}}}^*\)-equivariant small modification \(\varphi _{i,j}:X^\flat \dashrightarrow X(i,j)\) such that:
there exists a smooth projective variety X(i, j), with a B-type equalized \({{\mathbb {C}}}^*\)-action of criticality \(j-i\), and a \({{\mathbb {C}}}^*\)-equivariant small modification \(\varphi _{i,j}:X^\flat \dashrightarrow X(i,j)\) such that:
-
(i)
the indeterminacy locus of \(\varphi _{i,j}\) does not meet any inner fixed point component of L-weight \(a_k\), for \(i<k<j\);
-
(ii)
\(\varphi _{i,j}\) maps isomorphically the inner fixed point components of \(X^\flat \) of weights \(a_k\), \(i<k<j\) to the inner fixed point components of X(i, j), and preserves the values of \(\nu ^\pm \) on these components;
-
(iii)
 .
.
Proof
We start by setting  ,
,  .
.
By Corollary 4.9, any \({\mathbb {Q}}\)-divisor in \(\overline{N_{0,r}}\) is semiample, hence nef, so we may conclude that  . On the other hand, by the same corollary, movable \({\mathbb {Q}}\)-divisors outside of \(\overline{N_{0,r}}\) are not semiample, hence not ample, so the equality follows.
. On the other hand, by the same corollary, movable \({\mathbb {Q}}\)-divisors outside of \(\overline{N_{0,r}}\) are not semiample, hence not ample, so the equality follows.
Take  and assume that the statement holds for such a pair. We will show that if
and assume that the statement holds for such a pair. We will show that if  , then the statement is also true for \((i\,{+}\,1,j)\); an analogous argument yields that the result holds for \((i,j\,{-}\,1)\) when
, then the statement is also true for \((i\,{+}\,1,j)\); an analogous argument yields that the result holds for \((i,j\,{-}\,1)\) when  .
.
First of all, we note that assuming that  implies that either
implies that either
-
(a)
\(j-i\geqslant 3\), or
-
(b)
\(j-i=2\) and \(i<r-2\), or
-
(c)
\(i=r-2\), \(j=r\), and
 .
.
This follows from the description of  given in Proposition 4.7 and Remark 4.8, and of its SBL decomposition given at the beginning of this section.
given in Proposition 4.7 and Remark 4.8, and of its SBL decomposition given at the beginning of this section.
Now we use property (ii) to identify the inner fixed point components of X(i, j) with some inner fixed point components of \(X^\flat \); we also choose an ample \({\mathbb {Q}}\)-divisor  . By Lemma 2.2, the D-weights of the inner fixed point components of X(i, j) are \(a_{i+1}-\tau _-,\dots ,a_{j-1}-\tau _-\).
. By Lemma 2.2, the D-weights of the inner fixed point components of X(i, j) are \(a_{i+1}-\tau _-,\dots ,a_{j-1}-\tau _-\).
Since \(\nu ^{\pm }\) is preserved by \(\varphi _{i,j}\) on these inner fixed point components, by Lemmas 4.4, 4.5, it follows that, in each of the situations (a), (b), (c) described above, the pair (X(i, j), D) satisfies the hypotheses of Theorem 3.1. We then consider the smooth \({{\mathbb {C}}}^*\)-equivariant small modification  provided by that statement and set
provided by that statement and set

Let us now show that \(X(i\,{+}\,1,j)\) and \(\varphi _{i+1,j}\) satisfy the requirements of the proposition. Note that the induced \({{\mathbb {C}}}^*\)-action on \(X(i\,{+}\,1,j)\) is equalized of B-type by Theorem 3.1, so we are left to prove the properties (i), (ii), (iii).
By assumption, the indeterminacy locus of \(\varphi _{i,j}\) does not meet any fixed point component of L-weight \(a_k\), for \(i<k<j\). On the other hand, as stated in Theorem 3.1, the indeterminacy locus of \(\psi ^-\) does not meet any fixed point component of X(i, j) of D-weight \(a_{k}-\tau _-\), for \(i+1<k<j\), that correspond via \(\varphi _{i,j}\) to the fixed point components of \(X^\flat \) of L-weight \(a_{k}\), for \(i+1<k<j\), so (i) follows.
Property (ii) follows in a similar way: both \(\varphi _{i,j}\) and \(\psi ^-\) map isomorphically the fixed point components of D-weights \(a_{k}\), for \(i+1<k<j\).
For part (iii) we denote by \(Y_0^-\) the sink of X(i, j), and note that \(Y_0^-=(\varphi _{i,j})_*(Y_0)\). Then, by Theorem 3.1,
is ample on \(X(i+1,j)\), for every \(\tau \in (a_{i+1}-\tau _-,a_{i+2}-\tau _-)\). Since this holds for every \(L(\tau _-,\tau _+)\in N_{i,j}\), setting  , we conclude that \((\varphi _{i+1,j})_* L(\tau ',\tau _+)\) is ample on \(X(i+1,j)\) for every \(L(\tau ',\tau _+)\in N_{i+1,j}\).
, we conclude that \((\varphi _{i+1,j})_* L(\tau ',\tau _+)\) is ample on \(X(i+1,j)\) for every \(L(\tau ',\tau _+)\in N_{i+1,j}\).
On the other hand, since the Mori chamber decomposition is a refinement of the SBL decomposition, the ample cone of \(X(i\,{+}\,1,j)\) must be contained in \(N_{i+1,j}\), and we conclude that  .\(\square \)
.\(\square \)
We finish this section with some observations regarding the GIT quotients of the small modifications of \(X^\flat \). In the following statement we consider the set of indices I(X, L) introduced in Remark 4.6.
Corollary 4.12
In Setup 4.1, for every \(i\in I(X,L)\):
-
(i)
the closure of \(N_{i,i+1}\) is the nef cone of the \({{\mathbb {P}}}^1\)-bundle \({\widehat{X}}(i,i\,{+}\,1)\);
-
(ii)
the intersection

is the nef cone of the geometric quotient
 ;
; -
(iii)
the intersection
 equals
equals  .
.
Proof
First of all, as noted in Remark 4.6, for each such i the nef cone of \({\widehat{X}}(i,i\,{+}\,1)\) is the closure of one of the Mori chambers of \(X^\flat \), and the projection  corresponds to a facet of that chamber. On the other hand, by Proposition 2.12 and Lemma 2.5
corresponds to a facet of that chamber. On the other hand, by Proposition 2.12 and Lemma 2.5

which implies that \(L(\tau ,\tau )\) is a supporting \({\mathbb {Q}}\)-divisor of the rational contraction  . Since the only chamber containing \(L(\tau ,\tau )\) in its boundary is \(N_{i,i+1}\), we conclude that
. Since the only chamber containing \(L(\tau ,\tau )\) in its boundary is \(N_{i,i+1}\), we conclude that  , that is, (i).
, that is, (i).
Moreover,  must be the facet of \(\overline{N_{i,i+1}}\) containing \(L(\tau ,\tau )\), which is \(\overline{N_{i,i+1}}\cap C_{{\text {gen}}}^\perp \), and so (ii) follows.
must be the facet of \(\overline{N_{i,i+1}}\) containing \(L(\tau ,\tau )\), which is \(\overline{N_{i,i+1}}\cap C_{{\text {gen}}}^\perp \), and so (ii) follows.
In order to proof part (iii) we first note that the geometric quotients  \(i\in I(X,L)\), are all isomorphic in codimension one by construction, so we may conclude by showing that the extremal rays of
\(i\in I(X,L)\), are all isomorphic in codimension one by construction, so we may conclude by showing that the extremal rays of  do not correspond to small contractions. For simplicity let us consider only the left-hand side extremal ray R, and denote by
do not correspond to small contractions. For simplicity let us consider only the left-hand side extremal ray R, and denote by  the geometric quotient whose nef cone contains that ray; according to Remark 4.6 we have two situations: either \(i_0=0\), or \(i_0=1\).
the geometric quotient whose nef cone contains that ray; according to Remark 4.6 we have two situations: either \(i_0=0\), or \(i_0=1\).
If \(i_0=0\), the contraction  associated to the ray R is the projective bundle \(Y_0^\flat \rightarrow Y_0\). If else \(i_0=1\), the contraction
associated to the ray R is the projective bundle \(Y_0^\flat \rightarrow Y_0\). If else \(i_0=1\), the contraction  is divisorial: in fact by Lemma 4.5 in this case there is a unique component \(Y_1\) of weight \(a_1\), and \(\nu ^+(Y_1)=1\); therefore the subset of
is divisorial: in fact by Lemma 4.5 in this case there is a unique component \(Y_1\) of weight \(a_1\), and \(\nu ^+(Y_1)=1\); therefore the subset of  parametrizing orbits converging to \(Y_1\) at infinity is a divisor (by the Białynicki-Birula decomposition) that gets contracted onto
parametrizing orbits converging to \(Y_1\) at infinity is a divisor (by the Białynicki-Birula decomposition) that gets contracted onto  . \(\square \)
. \(\square \)
Remark 4.13
Similar arguments show that, for every \(i<j\), the geometric (resp. semigeometric) quotients of the small modification X(i, j) are the varieties  , \(i\leqslant k\leqslant j-1\) (resp.
, \(i\leqslant k\leqslant j-1\) (resp.  , \(i\leqslant k\leqslant j\)). In particular, the sink and the source of X(i, j) are
, \(i\leqslant k\leqslant j\)). In particular, the sink and the source of X(i, j) are  ,
,  .
.
Remark 4.14
In the case in which the sink of the action in X is a point, we have seen that the simplicial cone generated by \(L(0,0),L(0,a_1),L(a_1,a_1)\) is not contained in  . However, it is still contained in the pseudo-effective cone of \(X^\flat \), and the \({\mathbb {Q}}\)-divisors contained in it have a geometric interpretation.
. However, it is still contained in the pseudo-effective cone of \(X^\flat \), and the \({\mathbb {Q}}\)-divisors contained in it have a geometric interpretation.
In fact, the complete linear system of a large enough integral multiple of a \({\mathbb {Q}}\)-divisor in  has a fixed point component supported in the unique divisor \(\overline{X^-(Y_1)}\). In particular, the divisors of the form \(m L(\tau ,\tau )\), \(\tau \in {\mathbb {Q}}\cap (0,a_1)\), \(m\gg 0\), still define rational maps from \(X^\flat \) to the geometric quotient
has a fixed point component supported in the unique divisor \(\overline{X^-(Y_1)}\). In particular, the divisors of the form \(m L(\tau ,\tau )\), \(\tau \in {\mathbb {Q}}\cap (0,a_1)\), \(m\gg 0\), still define rational maps from \(X^\flat \) to the geometric quotient  , as we knew from GIT (see Proposition 2.12).
, as we knew from GIT (see Proposition 2.12).
5 Examples: equalized actions on rational homogeneous manifolds
The paper [21], in which the birational geometry of equalized \({{\mathbb {C}}}^*\)-actions of small bandwidth was considered, shows that important examples of equalized actions can be found using Representation Theory. Let us start this section by presenting some of these. As in Sect. 4, we will be interested in smooth projective varieties of Picard number one admitting an equalized nontrivial \({{\mathbb {C}}}^*\)-action. We will also consider a linearization of the action on the ample generator L of  and denote the bandwidth and the criticality of the action by \(\delta \) and r, respectively.
and denote the bandwidth and the criticality of the action by \(\delta \) and r, respectively.
First of all, we will introduce the notation that we will use to describe our varieties and actions.
Notation 5.1
Let G be a semisimple algebraic group, with Lie algebra \({{\mathfrak {g}}}\). We consider a Borel subgroup \(B\subset G\) and a Cartan subgroup \(H\subset B\subset G\), denote by \(\varPhi \) the root system of G with respect to H, by \(W=N_G(H)/H\) the Weyl group of G, by \(\Delta =\{\alpha _1,\dots ,\alpha _r\}\) the base of positive simple roots of \(\varPhi \) induced by \(B\supset H\), by \(\varPhi ^+\) the set of positive roots determined by B, and by  the Dynkin diagram of G. We will assume that
the Dynkin diagram of G. We will assume that  is connected, i.e., that the Lie algebra \({{\mathfrak {g}}}\) of G is simple (and we will say that G is a simple algebraic group), and that G is simply connected. In particular the lattice of characters
is connected, i.e., that the Lie algebra \({{\mathfrak {g}}}\) of G is simple (and we will say that G is a simple algebraic group), and that G is simply connected. In particular the lattice of characters  of H coincides with the lattice of weights of \({{\mathfrak {g}}}\), generated by the fundamental dominant weights \(\{\omega _1,\dots ,\omega _n\}\).
of H coincides with the lattice of weights of \({{\mathfrak {g}}}\), generated by the fundamental dominant weights \(\{\omega _1,\dots ,\omega _n\}\).
A fundamental weight \(\omega _i\) defines a representation \(V_{\omega _i}\) such that the unique closed G-orbit in the projectivization \({{\mathbb {P}}}(V_{w_i})\) is a rational homogeneous variety. This variety is completely determined by the choice of a node i in the Dynkin diagram  , hence we will denote it by
, hence we will denote it by  .
.
5.1 Examples with \(r=1\)
The first example of variety admitting an equalized action of Picard number one and criticality \(r=1\) is the projective space \({{\mathbb {P}}}^n\), together with the linear action that fixes the points of a hyperplane \(H\subset {{\mathbb {P}}}^n\) and a point \(P\notin H\). Other examples of this kind can be found within the class of horospherical varieties. Following [24], besides \({{\mathbb {P}}}^n\), smooth projective horospherical varieties of Picard number one are determined by the choice of some triples  , where
, where  is the Dynkin diagram of a simple Lie algebra and i, j are two nodes of the diagram. One requires the morphisms
is the Dynkin diagram of a simple Lie algebra and i, j are two nodes of the diagram. One requires the morphisms  ,
,  to be projective bundles, denotes by
to be projective bundles, denotes by  the pullbacks of the ample generators of
the pullbacks of the ample generators of  ,
,  , and constructs the associated horospherical variety as the contraction of the decomposable \({{\mathbb {P}}}^1\)-bundle
, and constructs the associated horospherical variety as the contraction of the decomposable \({{\mathbb {P}}}^1\)-bundle  via the corresponding tautological line bundle
via the corresponding tautological line bundle  (see [21, Section 4] for details). The variety in question inherits a \({{\mathbb {C}}}^*\)-action induced by the natural one on
(see [21, Section 4] for details). The variety in question inherits a \({{\mathbb {C}}}^*\)-action induced by the natural one on  , which has \(\delta =r=1\); its (extremal) fixed point components are, clearly,
, which has \(\delta =r=1\); its (extremal) fixed point components are, clearly,  ,
,  . Table 1 contains the complete list of these varieties, and Fig. 5 the description of their movable cones.
. Table 1 contains the complete list of these varieties, and Fig. 5 the description of their movable cones.
5.2 Examples with \(r=2\)
By [26, Theorem 4.1], the only smooth projective varieties admitting an equalized action of bandwidth two with isolated extremal fixed points are the smooth quadrics, \(\mathrm{B}_n(1)\), \(\mathrm{D}_n(1)\).
If X is a rational homogeneous space of Picard number one and L is the ample generator of  , examples in which \(r=2\) can be found among adjoint varieties. Let us recall that, given a simple Lie algebra \({{\mathfrak {g}}}\), its adjoint variety is the unique closed orbit of the action of the adjoint group of \({{\mathfrak {g}}}\) on \({{\mathbb {P}}}({{\mathfrak {g}}}^\vee )\). In [21, Section 7] all the possible adjoint varieties admitting an equalized \({{\mathbb {C}}}^*\)-action with \(\delta =r=2\) have been described in terms of short gradings of Lie algebras (see Table 2).
, examples in which \(r=2\) can be found among adjoint varieties. Let us recall that, given a simple Lie algebra \({{\mathfrak {g}}}\), its adjoint variety is the unique closed orbit of the action of the adjoint group of \({{\mathfrak {g}}}\) on \({{\mathbb {P}}}({{\mathfrak {g}}}^\vee )\). In [21, Section 7] all the possible adjoint varieties admitting an equalized \({{\mathbb {C}}}^*\)-action with \(\delta =r=2\) have been described in terms of short gradings of Lie algebras (see Table 2).
We have represented the movable cones of these varieties in Fig. 6. Note that the arguments in [21, Section 6] provide, for every smooth projective variety X together with an equalized action with \(\delta =r=2\) and non-isolated extremal fixed points, two small modifications of \(X^\flat \) that are \({{\mathbb {P}}}^1\)-bundles. They correspond, in the language introduced here, to the varieties X(0, 1) and X(1, 2), whose nef cones are the two triangular chambers in the right hand side of Fig. 6.
5.3 Examples with \(r=3\)
A complete list of smooth projective varieties admitting an equalized action of bandwidth three with isolated fixed points is known (see [21, 26]). In the case of Picard number one the varieties in question are all rational homogeneous and they can be described in terms of special Cremona transformations and Severi varieties (that appear as the inner fixed point components \(Y_1,Y_2\) of the action). Their complete list is given in Table 3.
In [21] it has been shown that the blowup of such a variety along the sink and the source admits a small modification which is a decomposable \({{\mathbb {P}}}^1\)-bundle (over the blowup of a projective space along a Severi variety). Again, the nef cone of this \({{\mathbb {P}}}^1\)-bundle is the closure of the triangular chamber represented in Fig. 7, and the small modification from \(X^\flat \) onto it is a composition of two (commuting) flips of the type described in Sect. 3.
5.4 Rational homogeneous examples with arbitrary criticality
A description of \({{\mathbb {C}}}^*\)-actions on rational homogeneous varieties of Picard number one has been given in [11], with particular attention to the actions of minimal bandwidth. The author describes also when these actions are equalized. For the reader’s convenience we include here some elementary facts that belong to that paper.
Let i be a node of the connected Dynkin diagram  of a group G as in Notation 5.1, and set
of a group G as in Notation 5.1, and set  ,
,  . In order to study \({{\mathbb {C}}}^*\)-actions on (X, L), we note first that we may always assume that the action extends to the action of H in X by means of a homomorphism \(\jmath :{{\mathbb {C}}}^*\rightarrow H\). The fixed points of the action of H on X, as well as the weights of the action on L and on the tangent spaces of X at those points, can be written in terms of \(\varPhi \) and W, so that we may compute the \({{\mathbb {C}}}^*\)-weights of L and \(T_X\) by means of the induced map
. In order to study \({{\mathbb {C}}}^*\)-actions on (X, L), we note first that we may always assume that the action extends to the action of H in X by means of a homomorphism \(\jmath :{{\mathbb {C}}}^*\rightarrow H\). The fixed points of the action of H on X, as well as the weights of the action on L and on the tangent spaces of X at those points, can be written in terms of \(\varPhi \) and W, so that we may compute the \({{\mathbb {C}}}^*\)-weights of L and \(T_X\) by means of the induced map  . By choosing an isomorphism
. By choosing an isomorphism  , this map defines a grading of \({{\mathfrak {g}}}\), whose graded pieces are
, this map defines a grading of \({{\mathfrak {g}}}\), whose graded pieces are

One may then easily check that the relation among equalization and shortness of the grading found in [21, Section 5] holds for every X as above:
Proposition 5.2
The action of \({{\mathbb {C}}}^*\) on X is equalized if the induced \({{\mathbb {Z}}}\)-grading on X is short, that is \({{\mathfrak {g}}}_m=0\) for \(m\ne -1,0,1\).
A classical example of this kind is the case of the Grassmannian of i-dimensional subspaces of an \((n\,{+}\,1)\)-dimensional vector space V, which we denote by \(X=\mathrm{A}_n(i)\). A similar description can be done in the case of rational homogeneous varieties of type \(\mathrm{B}\), \(\mathrm{C}\) and \(\mathrm{D}\), and also in the exceptional cases, with the help of some representation-theoretical tools. We refer to [11] for details.
The line bundle L is, in this case, the Plücker line bundle, that provides the embedding of X into  . One may then construct equalized \({{\mathbb {C}}}^*\)-actions on X by choosing a decomposition
. One may then construct equalized \({{\mathbb {C}}}^*\)-actions on X by choosing a decomposition

and a \({{\mathbb {C}}}^*\)-action on V whose weight is 0 on \(V_0\) and 1 on \(V_1\). Setting  , and assuming, without loss of generality, that \(i\leqslant k\leqslant n-k+1\), one can then check that, for \(m>0\):
, and assuming, without loss of generality, that \(i\leqslant k\leqslant n-k+1\), one can then check that, for \(m>0\):

In particular \({{\mathfrak {g}}}_m=0\) for \(m>1\), that is, the grading is short. One may compute that the fixed point components of the action are

where we set \(\mathrm{A}_{r}(r+1)\) to be a point.
The \({{\mathbb {C}}}^*\)-weights of L on these components will be \(0,1,\dots ,i-1,i\), respectively. Note that our result provides a description of the Mori chamber decomposition of the movable cone of \(\mathrm{A}_n(i)^\flat \), which is not a Fano variety with the exception of the cases \(i=1,n\). In particular, these examples show that one may find, within the class of rational homogeneous spaces, equalized \({{\mathbb {C}}}^*\)-actions of arbitrary large criticality.
Note that will have isolated extremal fixed points in the following cases:
-
\(i=k<n+1-k\) (isolated sink),
-
\(i=k=n+1-k\) (isolated sink and source).
In the latter case the sink and the source of \(\mathrm{A}_n(i)^\flat \) can be both identified with the projectivization of the space of  matrices, and the birational map among them is known (we refer to [18] for details) to be induced by the inversion function. This description allows us to decompose the (projectivized) inversion function as a sequence of a blowup, \((n+1)/2-2\) flips, and a blowdown.
matrices, and the birational map among them is known (we refer to [18] for details) to be induced by the inversion function. This description allows us to decompose the (projectivized) inversion function as a sequence of a blowup, \((n+1)/2-2\) flips, and a blowdown.
Change history
15 September 2022
Missing Open Access funding information has been added in the Funding Note.
References
Abramovich, D., Karu, K., Matsuki, K., Włodarczyk, J.: Torification and factorization of birational maps. J. Amer. Math. Soc. 15(3), 531–572 (2002)
Arzhantsev, I., Derenthal, U., Hausen, J., Laface, A.: Cox Rings. Cambridge Studies in Advanced Mathematics, vol. 144. Cambridge University Press, Cambridge (2015)
Beltrametti, M.C., Sommese, A.J.: The Adjunction Theory of Complex Projective Varieties. De Gruyter Expositions in Mathematics, vol. 16. de Gruyter, Berlin (1995)
Białynicki-Birula, A.: Some theorems on actions of algebraic groups. Ann. Math. 98, 480–497 (1973)
Białynicki-Birula, A., Carrell, J.B., McGovern, W.M.: Algebraic Quotients. Torus Actions and Cohomology. The Adjoint Representation and the Adjoint Action. Encyclopaedia of Mathematical Sciences, vol. 131. Springer, Berlin (2002)
Białynicki-Birula, A., Świȩcicka, J.: Complete quotients by algebraic torus actions. In: Carrell, J.B. (ed.) Group Actions and Vector Fields. Lecture Notes in Mathematics, vil. 956, pp. 10–22. Springer, Berlin (1982)
Białynicki-Birula, A., Świȩcicka, J.: Generalized moment functions and orbit spaces. Amer. J. Math. 109(2), 229–238 (1987)
Buczyński, J., Wiśniewski, J.A., Weber, A.: Algebraic torus actions on contact manifolds (2018). arXiv:1802.05002 (to appear in J. Differ. Geom.)
Carrell, J.B.: Torus actions and cohomology. In: Białynicki-Birula, A., et al. (eds.) Algebraic Quotients. Torus Actions and Cohomology. The Adjoint Representation and the Adjoint Action, pp. 83–158. Encyclopaedia of Mathematical Sciences, vol. 131. Springer, Berlin (2002)
Carrell, J.B., Sommese, A.J.: Some topological aspects of \(\mathbb{C}^*\)-actions on compact Kähler manifolds. Comment. Math. Helv. 54(4), 567–582 (1979)
Franceschini, A.: Minimal bandwidth \(\mathbb{C}^*\)-actions on generalized Grassmannians (2020). arXiv:2012.00498 (To appear in Rendiconti del Circolo Mat. di Palermo Series 2)
Hu, Y., Keel, S.: Mori dream spaces and GIT. Mich. Math. J. 48, 331–348 (2000)
Huizenga, J.: Birational geometry of moduli spaces of sheaves and Bridgeland stability. In: Coskun, I., et al. (eds.) Surveys on Recent Developments in Algebraic Geometry. Proceedings of Symposia in Pure Mathematics, vol. 95. American Mathematical Society, Providence (2017)
Iversen, B.: A fixed point formula for action of tori on algebraic varieties. Inv. Math. 16(3), 229–236 (1972)
Knop, F., Kraft, H., Luna, D., Vust, T.: Local Properties of Algebraic Group Actions. In: Kraft, H., et al. (eds.) Algebraische Transformationsgruppen und Invariantentheorie. DMV Seminar, vol. 13, pp. 63–75. Birkhäuser, Basel (1989)
Laface, A., Massarenti, A., Rischter, R.: On Mori chamber and stable base locus decompositions. Trans. Amer. Math. Soc. 373(3), 1667–1700 (2020)
Lazarsfeld, R.: Positivity in Algebraic Geometry. Vol. I. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, vol. 48. Springer, Berlin (2004)
Michałek, M., Monin, L., Wiśniewski, J.A.: Maximum likelihood degreee, complete quadrics, and \(\mathbb{C}^*\)-action. SIAM J. Appl. Algebra Geom. 1(5), 60–85 (2021)
Morelli, R.: The birational geometry of toric varieties. J. Algebraic Geom. 5(4), 751–782 (1996)
Mumford, D., Fogarty, J., Kirwan, F.: Geometric Invariant Theory. 3rd edn. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 34. Springer, Berlin (1994)
Occhetta, G., Romano, O.A., Solá Conde, L.E., Wiśniewski, J.A.: Small bandwidth \(\mathbb{C}^*\)-actions and birational geometry (2019). arXiv:1911.12129 (To appear in J. Algebraic Geom.)
Occhetta, G., Solá Conde, L.E., Romano, E.A., Wiśniewski, J.A.: High rank torus actions on contact manifolds. Selecta Math. 27(10), (2021)
Okonek, Chr., Schneider, M., Spindler, H.: Vector Bundles on Complex Projective Spaces. Progress in Mathematics, vol. 3. Birkhäuser, Boston (1980)
Pasquier, B.: On some smooth projective two-orbit varieties with Picard number 1. Math. Ann. 344(4), 963–987 (2009)
Reid, M.: What is a flip? (1992). http://homepages.warwick.ac.uk/staff/Miles.Reid/3folds
Romano, E.A., Wiśniewski, J.A.: Adjunction for varieties with a \(\mathbb{C}^*\) action. Transf. Groups. https://doi.org/10.1007/s00031-020-09627-8
Thaddeus, M.: Geometric invariant theory and flips. J. Amer. Math. Soc. 9(3), 691–723 (1996)
Włodarczyk, J.: Birational cobordisms and factorization of birational maps. J. Algebraic Geom. 9(3), 425–449 (2000)
Włodarczyk, J.: Simple constructive weak factorization. In: Abramovich, D., et al. (eds.) Algebraic Geometry—Seattle 2005. Part 2. Proceedings of Symposia in Pure Mathematics, vol. 80.2, pp. 957–1004. American Mathematical Society, Providence (2009)
Acknowledgements
The authors would like to thank Joachim Jelisiejew for his valuable help with questions regarding GIT. The third author would like to thank Fran Presas for the inspiring conversations about Morse theory 20 years ago.
Funding
Open access funding provided by Università degli Studi di Trento within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first and third authors were supported by the PRIN project “Geometria delle varietà algebriche”. The second and fourth authors were supported by the Polish National Science Center project 2016/23/G/ST1/04282. The second author was supported by Associazione Amici di Claudio Demattè.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Occhetta, G., Romano, E.A., Solá Conde, L.E. et al. Small modifications of Mori dream spaces arising from \(\mathbb {C}^*\)-actions. European Journal of Mathematics 8, 1072–1104 (2022). https://doi.org/10.1007/s40879-022-00540-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-022-00540-w




 are smooth and the natural birational maps
are smooth and the natural birational maps 
 ,
,  .
.
 ,
, 



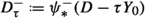 is ample for every
is ample for every  has critical values
has critical values 
 as a complex manifold
as a complex manifold .
. .
.
 if
if  ;
; .
.
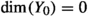 ,
,  , then
, then 
 ,
,  , then
, then 


 .
. .
.
 ;
; equals
equals  .
.

