Abstract
In this paper we start the study of Schur analysis for Cauchy–Fueter regular quaternionic-valued functions, i.e. null solutions of the Cauchy–Fueter operator in \({\mathbb {R}}^4\). The novelty of the approach developed in this paper is that we consider axially regular functions, i.e. functions spanned by the so-called Clifford-Appell polynomials. This type of functions arises naturally from two well-known extension results in hypercomplex analysis: the Fueter mapping theorem and the generalized Cauchy–Kovalevskaya (GCK) extension. These results allow one to obtain axially regular functions starting from analytic functions of one real or complex variable. Precisely, in the Fueter theorem two operators play a role. The first one is the so-called slice operator, which extends holomorphic functions of one complex variable to slice hyperholomorphic functions of a quaternionic variable. The second operator is the Laplace operator in four real variables, that maps slice hyperholomorphic functions to axially regular functions. On the other hand, the generalized CK-extension gives a characterization of axially regular functions in terms of their restriction to the real line. In this paper we use these two extensions to define two notions of rational function in the regular setting. For our purposes, the notion coming from the generalized CK-extension is the most suitable. Our results allow to consider the Hardy space, Schur multipliers and their relation with realizations in the framework of Clifford-Appell polynomials. We also introduce two notions of regular Blaschke factors, through the Fueter theorem and the generalized CK-extension.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Fueter mapping theorem and the generalized Cauchy–Kovalevskaya (GCK) extension are two main tools in quaternionic, and more generally, in Clifford analysis, both allowing one to get axially regular functions, i.e. null solutions of the Cauchy–Fueter operator in \( {\mathbb {R}}^4\), starting from analytic functions of one real or complex variable.
The Fueter mapping theorem is a two-steps procedure giving an axially regular function starting from a holomorphic function of one complex variable. This is achieved by using two operators. The first one is the so-called slice operator that extends holomorphic functions of one complex variable to slice hyperholomorphic functions. The theory of slice hyperholomorphic functions is nowadays well developed, see [23, 24]. The second operator is the Laplace operator in four real variables which maps slice hyperholomorphic functions to axially regular functions. On the other hand, the generalized CK-extension is defined in terms of powers of \( {\underline{x}} \partial _{x_0}\), where \(x_0\) and \( {\underline{x}}\) are the real and imaginary parts of a quaternion, respectively.
The two maps are not the same: the generalized CK-extension is an isomorphism, whereas the Fueter map is only surjective. In [31] a connection between the two extension operators has been proved. Furthermore, in [31] the authors showed that although for the exponential, trigonometric and hyperbolic functions the two extension maps coincide, the two maps differ in most cases, for example when acting on the rational functions.
In the framework of rational functions, we recall that in [18, 38] it is explained how the state space theory of linear systems gave rise to the notion of realization, which is a representation of a rational function. In the complex setting a realization in a neighbourhood of the origin is defined as
where A, B, C and D are matrices of suitable dimensions. Moreover, the inverse of a realization is still a realization when D is square and invertible, as well as the sum and the product of two realizations of compatible sizes. See [18] and the beginning of Sect. 3 in the present paper.
In this paper we shall introduce the counterpart of the realization theory in the regular setting through the Fueter theorem and the generalized CK-extension. The main obstacles to achieve this goal are
-
a suitable replacement of monomials in the framework of axially regular functions,
-
an appropriate product between axially regular functions.
In order to explain how to overcome these issues, we fix the following notations. The set \({\mathbb {H}}\) of real quaternions is defined as:
where the imaginary units satisfy the relations
We can also write a quaternion as \(x=x_0+ {\underline{x}}\), where we denoted by \(x_0\) its real part and by \( {\underline{x}}:=e_1x_1+e_2x_2+e_3x_3\) its imaginary part. The conjugate of a quaternion \(x \in {\mathbb {H}}\) is defined as \(x=x_0- {\underline{x}}\) and its modulus is given by \(|x|= \sqrt{x {\bar{x}}}=\sqrt{x_0^2+x_1^2+x_2^2+x_3^2}\). By the symbol \({\mathbb {S}}\) we denote the sphere of purely imaginary unit quaternions defined as
We observe that if \(I \in {\mathbb {S}}\) then \(I^{2}=-1\). This means that I is an imaginary unit and that
is an isomorphic copy of the complex numbers.
In quaternionic analysis, the Taylor expansion of a regular function is given in terms of the well-known Fueter polynomials, which play the role of the monomials \(x_0^{\alpha _1}x_1^{\alpha _1} \ldots x_n^{\alpha _n}\) in several real variables. An easy way to describe regular functions is through axially regular functions, see [46]. Indeed, for axially regular functions a simpler approach than the one of Fueter polynomials is available: the approach of the Clifford-Appell polynomials.
These polynomials are defined as
and they were investigated in [21, 22]. We note that they arise as the action of the Fueter map on the monomials \(x^k\), \(x \in {\mathbb {H}}\), see [30]. Any axially regular function in a neighbourhood of the origin can be written as a power series in terms of the polynomials \( {\mathcal {Q}}_m(x)\) of the form
As we discussed above, another issue is the fact that one needs a suitable product between axially regular functions, since the pointwise product evidently spoils the regularity. A well known product between regular functions is the so-called CK-product. This product is defined for regular functions f and g as
In [10] a CK-product between Clifford-Appell polynomials is performed. Precisely, it is given by
The drawback of the previous formula is the presence of the constant \(c_k\), depending on the degree k, which makes the formula unsuitable for some types of computations.
In [32] a new kind of product is defined between axially regular functions: the so-called generalized CK-product. This gives a more natural formula for the multiplication of the Clifford-Appell polynomials:
Another advantage of the generalized CK-product is that it is a convolution (also called Cauchy product) of the coefficients of the Clifford-Appell polynomials.
The polynomials \( {\mathcal {Q}}_m(x)\) are also useful to define a counterpart of the Hardy space in the quaternionic unit ball for axially regular functions. This space consists of functions of the form (1.2) which satisfy the condition \( \sum _{n=0}^\infty |f_n|^2 <\infty \). In this context, the reproducing kernel of the Hardy space is given by
The notion of Clifford-Appell polynomials and generalized CK-product paved the way to provide a definition of Schur multipliers in this setting.
In the literature, Schur multipliers are related to several applications: inverse scattering (see [12, 13, 20, 26]), fast algorithms (see [42, 43]), interpolation problems (see [33]) and several other ones.
In complex analysis a function s defined in the unit disk \( {\mathbb {D}}\) is a Schur multiplier if and only if the kernel
is positive definite in the open unit disk. Recently a generalization of Schur multipliers in the slice hyperholomorphic setting has been provided, see [3, 5]. The notion we shall consider in this paper is the following: a quaternionic-valued function S defined in the unit ball is a Schur multiplier if and only if the kernel
is positive definite in the unit ball of \({\mathbb {R}}^4\).
With this definition, most of the characterizations of Schur multipliers can be adapted to the non-commutative framework of Clifford-Appell polynomials. We note that in the quaternionic matrix case, being a Schur function is not equivalent to taking contractive values; see [4, (62.38) p. 1767].
As a particular example of Schur multiplier, we define the so-called Clifford-Appell Blaschke factor by
with \(a \in {\mathbb {H}}\), such that \(|a|<1\). Another and different notion of Blaschke factor is given by applying the Fueter map to the slice hyperholomorphic Blaschke factor. Nevertheless, these two regular notions of Blaschke factor are not equivalent.
The paper is divided into eight parts besides the present introduction. In Sect. 2 we recall some key notions in hypercomplex analysis and we state the Fueter mapping theorem and the generalized CK-extension. In Sect. 3 we provide the notion of axially rational regular function by using the Fueter mapping theorem. In Sect. 4 we define the counterpart of rational function in the regular setting by using the generalized CK-extension, and we prove some properties of regular rational functions. In Sect. 5 we define the Hardy space in this framework. In Sect. 6 we give the definition of Schur multipliers by means of the Clifford-Appell polynomials, and we give several characterizations of such. In Sect. 7 we prove a co-isometric realization of Schur multiplier. Section 8 is devoted to study a particular example of the Schur multiplier: the Blaschke factor. Finally, in Sect. 9 we provide another notion of axially regular Blaschke factor through the Fueter map.
2 Preliminaries
2.1 Quaternionic-valued functions
In the quaternionic setting there are various classes of functions generalizing holomorphic functions to quaternions, but in past few years two classes are the most studied: the slice hyperholomorphic functions and the regular functions. In this section we revise their definitions and their main properties.
First of all we recall the following:
Definition 2.1
We say that a set \(U \subset {\mathbb {H}}\) is axially symmetric if, for every \(u+Iv \in U\), all the elements \(u+Jv\) for \(J \in {\mathbb {S}}\) are contained in U.
The type of sets defined above are designed to work in class of functions in the next definition.
Definition 2.2
Let \(U \subset {\mathbb {H}}\) be an axially symmetric open set and let
A function \(f:U \rightarrow {\mathbb {H}}\) of the form
is left (resp. right) slice hyperholomorphic if \(\alpha \) and \( \beta \) are quaternionic-valued functions and satisfy the so-called "even-odd" conditions i.e.
Moreover, the functions \( \alpha \) and \( \beta \) satisfy the Cauchy-Riemann system
The set of left (resp. right) slice hyperholomorphic functions on U is denoted by \(\mathcal{S}\mathcal{H}_L(U)\) (resp. \(\mathcal{S}\mathcal{H}_R(U)\)). If the functions \( \alpha \) and \( \beta \) are real-valued functions, then we say that the slice hyperholomorphic function f is intrinsic, and the class of instrinsic functions is denoted by \( {\mathcal {N}}(U)\).
We observe that the pointwise product of two slice hyperholomorphic functions is not slice hyperholomorphic. However it is possible to define a product that preserves the slice hyperholomorphicity.
Definition 2.3
Let \(f=\alpha _0+I\beta _0\), \(g=\alpha _1+I\beta _1 \in \mathcal{S}\mathcal{H}_L(U)\). We define their \(*\)-product as
Let \(f=\alpha _0+\beta _0I\), \(g=\alpha _1+\beta _1I \in \mathcal{S}\mathcal{H}_R(U)\). We define their \(*\)-product as
Definition 2.4
Let \(f=\alpha _0+I\beta _0 \in \mathcal{S}\mathcal{H}_L(U)\). We define its left slice hyperholomorphic conjugate as \(f^c= \overline{\alpha _0}+I \overline{\beta _0}\) and its symmetrisation as \(f^s=f^c * f=f*f^c\). The left slice hyperholomorphic reciprocal is defined as \(f^{-*}=(f^s)^{-1}f^c\).
Let \(f=\alpha _0+\beta _0I \in \mathcal{S}\mathcal{H}_R(U)\). We define its right slice hyperholomorphic conjugate as \(f^c= \overline{\alpha _0}+\overline{\beta _0}I \) and its symmetrisation as \(f^s=f^c * f=f*f^c\). The right slice hyperholomorphic reciprocal is defined as \(f^{-*}=f^c(f^s)^{-1}\).
Another well studied class of quaternionic-valued functions is given by the Cauchy–Fueter regular (regular, for short) functions, see [19, 27, 35].
Definition 2.5
Let \( U \subset {\mathbb {H}}\) be an open set and let \(f:U \rightarrow {\mathbb {H}}\) be a function of class \( {\mathcal {C}}^1\). We say that the function f is (left) regular if
\({\mathcal {D}}\) is the so-called Cauchy–Fueter operator.
Example
The fundamental example of regular functions is given by the so-called Fueter variables defined as
A way to characterize regular functions is the well-known CK-extension, see [19, 27, 34]. An arbitrary regular function f is uniquely obtained by considering its restriction to the hyperplane \(x_0=0\). Precisely, we define the CK-extension of a function \(f({\underline{x}})\), which is real analytic in a set \({\tilde{U}}\subset {\mathbb {R}}^3\) (in the real variables \(x_1,x_2,x_3\)), as the function defined in a suitable open set \(U\subseteq \mathbb H\cong {\mathbb {R}}^4\), \(U\supset {{\tilde{U}}}\) given by
The pointwise product of regular functions is clearly not regular. Indeed, the product of two Fueter variables is a counter-example proving this fact. For this reason, a suitable product between regular functions is established, and since it is based on the CK-extension it is called CK-product, see [19].
Definition 2.6
Let f, g be two regular functions, then their CK-product is defined as
where the product at the right hand side is the pointwise product of two real analytic functions in \(x_1,x_2,x_3\) which are the restrictions of f and g to \(x_0=0\).
We recall that for \(a_1\),...,\(a_n \in {\mathbb {H}}\) the symmetrized product is defined as
where \(S_n\) is the set of all permutations of the set \(\{1,\ldots ,n\}\). By making the symmetrized product of the Fueter polynomials, we get
We observe that \( \xi ^{\nu }\) is the CK-extension of \(x^{\nu }=x_1^{\nu _1}x_2^{\nu _2}x_2^{\nu _2}\) and so it is in fact \( \xi ^{\nu }=\xi _1^{\nu _1} \odot \xi _2^{\nu _2} \odot \xi _3^{\nu _3}\).
Every regular function in neighbourhood of the origin can be written in the following way
The CK-product of the basis \(\xi ^{\nu }\) si given by
Thus the CK-product of two functions written in the form (2.3) in neighbourhood of the origin can be computed via the convolution (also called Cauchy product, see [36]) of the coefficients along the Fueter polynomials.
A subset of regular functions is the right quaternionic space of the axially regular functions. These functions are defined below:
Definition 2.7
Let U be an axially symmetric slice domain in \( {\mathbb {H}}\). We say that a function \(f:U \rightarrow {\mathbb {H}}\) is axially regular, if it is regular and it is of the form
where the functions A and B are quaternionic valued and satisfy the even-odd conditions (2.1). We denote by \( \mathcal{A}\mathcal{M}(U)\) the set of axially regular functions on U.
The set of axially regular functions constitutes the “building blocks” to define a regular functions in the sense of the result below, see [27].
Theorem 2.8
Let \(U \subseteq {\mathbb {H}}\) be an axially symmetric open set. Then every regular function \( f:U \rightarrow {\mathbb {H}}\) can be written as
where \(f_k(x)\) are functions of the form
where \(A_{k,j}\) and \(B_{k,j}\) satisfy conditions (2.1) and \({\mathcal {P}}_{k,j}( {\underline{x}})\) form a basis for the space of spherical regular functions of degree k, which has dimension \(m_k\).
2.2 Fueter theorem and generalized CK-extension
We now recall how to induce slice hyperholomorphic functions from holomorphic intrinsic functions.
Definition 2.9
An open connected set in the complex plane is an intrinsic complex domain if it is symmetric respect the real-axis.
Definition 2.10
A holomorphic function \(f(z)= \alpha (u,v)+i \beta (u,v)\) is intrinsic if is defined in an intrinsic complex domain D and \(\overline{f(z)}=f({\bar{z}})\). We denote the set of holomorphic intrinsic functions on D by \( {\mathcal {H}}(D)\).
Remark 2.11
Slice hyperholomorphic intrinsic functions defined on
are induced by intrinsic holomorphic functions defined in \(D \subset {\mathbb {C}}\), by the so-called slice operator defined in the following way
which consists of replacing the complex variable \(z=u+iv\) by the quaternionic variable \(x=x_0+ {\underline{x}}\) and the complex unit i is replaced by \(I:= \frac{{\underline{x}}}{|{\underline{x}}|}\).
Real analytic functions in one variable can be extended to slice hyperholomorphic functions in a suitable open set. In fact, let \( {\tilde{D}}:= D \cap {\mathbb {R}}\). We denote by \( {\mathcal {A}}({\tilde{D}})\) the space of real-valued analytic functions defined on \({\tilde{D}}\) with a unique holomorphic extension to the set D. The holomorphic extension map is defined as \(C=\exp (iv \partial _u)\). With this notation, we can define the slice regular extension map as \(S_1=S \circ C= \exp ({\underline{x}} \partial _{x_0})\).
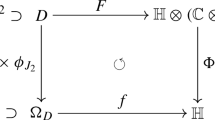
Theorem 2.12
We have the isomorphism,
and the following commutative diagram

Remark 2.13
A slice operator can be defined also for right slice hyperholomorphic functions and a result similar to Theorem 2.12 is valid in this case.
In quaternionic analysis the main tools to transform analytic functions of one real or complex variable into axially regular functions are the Fueter mapping theorem (see [37]) and the Cauchy–Kovalevskaya (CK) extension (see [27]).
Theorem 2.14
(Fueter mapping theorem) Let \(f_{0}(z)= \alpha (u,v)+i \beta (u,v)\) be a holomorphic function defined in a domain (open and connected) D in the upper-half complex plane and let \(\Omega _D\) as before. Then the operator S defined in (2.4) maps the set of holomorphic functions to the set of slice hyperholomorphic functions. Moreover, the function
is axially regular, where \(\Delta := \partial _{x_0}^2+\partial _{x_1}^2+\partial _{x_2}^2+\partial _{x_3}^2\) is the Laplace operator in the four real variables \(x_{\ell }\), \( \ell =0,1,2,3\).
Remark 2.15
The Fueter theorem was extended to the Clifford setting in 1957 by M. Sce, in the case of odd dimensions, see [44]. In this case, the Laplace operator \(\Delta \) is replaced by \( \Delta _{n+1}^{\frac{n-1}{2}}\), where \( \Delta _{n+1}\) is the Laplacian in \(n+1\) dimensions and n is odd, so in this case we are dealing with a differential operator. The proof of M. Sce in the Clifford setting is just a particular case of the computations in a generic quadratic algebra, see [44] and its translation with commentaries in [25]. In 1997, T. Qian showed that the Fueter-Sce theorem can be also proved in even dimensions. In this case the operator \(\Delta _{n+1}^{\frac{n-1}{2}}\) is a fractional operator, see [40, 41].
Theorem 2.16
(Generalized CK-extension, [27]) Let \({\tilde{D}} \subset {\mathbb {R}}\) be a real domain and consider an analytic function \(f_0(x_0) \in {\mathcal {A}}({\mathbb {R}}) \otimes {\mathbb {H}}\). Then there exists a unique sequence \( \{f_{j}(x_0)\}_{j=1}^\infty \subset {\mathcal {A}}( {\mathbb {R}}) \otimes {\mathbb {H}}\) such that the series
is convergent in an axially symmetric 4-dimensional neighbourhood \( \Omega \subset {\mathbb {H}}\) of D and its sum is a regular function i.e., \((\partial _{x_0}+\partial _{{\underline{x}}})f(x_0, {\underline{x}})=0\).
Furthermore, the sum f is formally given by the expression
where \(J_{\nu }\) is the Bessel function of the first kind of order \(\nu \).
The function in (2.5) is known as the generalized CK-extension of \(f_0\), and it is denoted by \(GCK[f_0](x_{0}, {\underline{x}})\).
This extension operator defined an isomorphism between right modules:
whose inverse is given by the restriction operator to the real line, i.e. \(GCK[f_0](x_0,0)=f_0(x_0)\).
A match between the generalized CK-extension and the Fueter theorem has been found in [31, Thm. 4.2]:
Theorem 2.17
Let \(f(u+iv)=\alpha (u,v)+i\beta (u,v)\) be an intrinsic holomorphic function defined on an intrinsic complex domain \(\Omega _2 \subset {\mathbb {C}}\). Then we have
2.3 Clifford-Appell polynomials
In this subsection we recall the definition and the main properties of the Clifford-Appell polynomials, see [21, 22]. These are defined by
where
The polynomials \( {\mathcal {Q}}_m(x)\) satisfy the Appell property
An interesting feature of the Clifford-Appell polynomials is that they come from the application of the Fueter map to the monomials \(x^m\). In particular, see [30], we have the formula
Since the polynomials \({\mathcal {Q}}_m(x)\) are axially regular and
we get that
The fact that the coefficients of the polynomials \({\mathcal {Q}}_m(x)\) satisfy the relation
implies the inequality
The Clifford-Appell polynomials are a basis for axially regular functions, see [10, Thm. 3.1].
Theorem 2.18
Let us consider \( \Omega \subset {\mathbb {H}}\) be an axially symmetric slice domain containing the origin. Let f be an axially regular function on \(\Omega \). Then there exist \( \{a_k\}_{k \in {\mathbb {N}}_0} \subset {\mathbb {H}}\) such that
In [32] the authors defined a new product among regular functions which is more useful in the set of axially regular functions than the CK-product.
Definition 2.19
Let \(f(x_0, {\underline{x}})\) and \(g(x_0, {\underline{x}})\) be axially regular functions. We define
Definition 2.20
Let \(f(x_0, {\underline{x}})\) be an axially regular function then we define
The previous definition introduces the multiplicative inverse of the generalized CK-product, indeed
This product fits perfectly with the product of Clifford-Appell polynomials. Indeed we have
Remark 2.21
If we consider two axially regular functions f and g expanded in convergent series
then their generalized CK-product is given by
Thus the generalized CK-product is a convolution (also called Cauchy product, see [36]) on the coefficients along the Clifford-Appell polynomials.
Remark 2.22
It is clear that
Remark 2.23
As we explained in the Introduction, formula (1.3) is unsuitable for some computations because of the presence of the constants. To have a more natural product, in [8] the authors introduced the polynomials
In this way formula (1.3) can be written as
However, the polynomials \(P_n(x)\) do not satisfy the Appell property like the one in (2.7). Moreover, the CK-product is not a convolution on the coefficients of the polynomials \( P_m(x)\). Thus the product (2.11) looks the best option to work in the set of axially regular functions.
3 Axially rational regular functions through the Fueter theorem
We start by recalling that any \({\mathbb {C}}^{N \times M}\)-valued rational function R(z), without a pole at the origin can be written in the form
where D, C, A and B are matrices of suitable sizes. Formula (3.1) is known in the literature with the name of realization (centred at the origin). It is well-known that the inverse of the function R(z) is still a realization. Indeed, if we assume \(N=M\) and D being an invertible matrices one has the following formula
Moreover the product of two different realizations \(R_\ell (z)=D_\ell +zC_\ell (I-zH_\ell )^{-1}B_\ell \) of suitable sizes is given by
where
The sum of two realizations it is a realization as well. This follows as a special case of the product since
The aim of this section is to introduce a notion of realization in the framework of axially regular functions. As we explained in the previous section, there are two possible ways to extend analytic functions of one complex variable to the regular setting. As we will see, the two approaches do not coincide for rational functions.
We start by studying the notion of axially rational function by means of the Fueter theorem. To this end we need to recall the notion of rational slice hyperholomorphic functions and their characterisation, [3, Thm. 4.6].
These functions arise from the study of the counterpart of state space equations in the slice hyperholomorphic setting, see [3].
Theorem 3.1
Let r be a \( {\mathbb {H}}^{N \times N}\)-valued function, slice hyperholomorphic in a neighbourhood \(\Omega \) of the origin. Then, we have
-
1.
r(x) is a rational function from \(\Omega \cap {\mathbb {R}}\) to \({\mathbb {H}}^{N\times N}\).
-
2.
There exist matrices A, B and C, of appropriate dimensions, such that
$$\begin{aligned} r(x)= D+ xC*(I-xA)^{-*}B. \end{aligned}$$(3.2) -
3.
The function r can be expanded in series as follows
$$\begin{aligned} r(x)= D+ \sum _{n=1}^\infty x^n C A^{n}B, \end{aligned}$$for suitable matrices A, B, C, D.
Remark 3.2
It is important to note that the formula (3.2) is formally identical to that one in the classical complex case; however, when expanded, it gives
This shows that the formula is very unconventional, because the term \(|x|^2\) is involved.
Remark 3.3
If we consider two functions \(r_1\), \(r_2\) admitting realizations of the form (3.2) of appropriate sizes, then \(r_1*r_2\) can be written in the form (3.2). Similarly the function \(r_1+r_2\) admits a realization of the form (3.2).
Now, we define the first notion of axially rational regular function of this paper:
Definition 3.4
A quaternionic valued function \( \breve{r}= \Delta r\) is called rational axially regular in a neighborhood of the origin if r satisfies one of the equivalent statements in Theorem 3.1.
We now prove some equivalent statements on rational axially regular functions:
Theorem 3.5
Let r be an \({\mathbb {H}}^{M \times N}\)-valued rational slice hyperholomorphic in a neighbourhood of the origin. Then the following conditions are equivalent
-
1.
\( \breve{r}(x)= \Delta r(x)\) is a rational axially regular function.
-
2.
\( \breve{r}(x)\) can be written as
$$\begin{aligned} \breve{r}(x)=-4(C- {\bar{x}}CA)Q_x(A)^{-2}AB, \end{aligned}$$where \(Q_x(A)= |x|^2 A^2-2 x_0A + I\) and A, B, C are quaternionic matrices of appropriate sizes
-
3.
\( \breve{r}\) can be expanded as follows
$$\begin{aligned} \breve{r}(x)= E+ \sum _{n=1}^\infty (n+1)(n+2) {\mathcal {Q}}_n(x) CA^{n+1}B, \end{aligned}$$where \(E:=-4CAB\) and \({\mathcal {Q}}_n(x)\) are the Clifford-Appell polynomials.
Proof
We start by showing that \(1) \Longleftrightarrow 2)\). By Definition 3.4 we know that a function \( \breve{r}\) is a rational axially regular function if there exists a rational slice hyperholomorphic function r such that
By Theorem 3.1 we know a characterization of rational slice hyperholomorphic functions, thus we can apply the Laplace operator to the entries \(r_{\ell j}\) of the rational slice hyperholomorphic function r, i.e.
where \({\mathcal {Q}}_x(a):=|x|^2a^2-2x_0a+1\) and a, b, c and d represent the quaternionic entries of the matrices A, B, C and D.
To simplify the computations we set
Then, we have
For \(1 \le i \le 3\) we have
Finally, we get
Since \(2x_0=x+ {\bar{x}}\) we obtain
Therefore, we get
We get the result with \(A=a\) and appropriate matrices B, C and D.
Now, we show the relation \(1) \Longleftrightarrow 3)\). By Theorem 3.1 we know that we can expand a rational slice hyperholomorphic function r as
Now, we consider the generic quaternions a, b, c and d that represent the entries of the quaternionic matrices A, B, C and D. We apply the Laplace operator in four real variables to the entries of (3.3), which are denoted by \(r_{\ell j}\), and we get
By formula (2.8) we deduce that for \(n \ge 2\) we have \( \Delta (x^n)=-2(n-1)n {\mathcal {Q}}_{n-2}(x).\) This implies that
We get the result with \(A=a\) and appropriate matrices B, C and D. \(\square \)
Remark 3.6
If we restrict to the case \(x \in {\mathbb {R}}\) in Theorem 3.5 we can write the axially regular function \(\breve{r}\) as
Remark 3.7
The rational axially regular functions defined in this section admit a realization as proved in Theorem 3.5, however they have some limitations. For example, if one performs the generalized CK-product of two rational axially regular functions then, in general, one does not get a rational axially regular function in the sense of Definition 3.4.
In particular, to preserve algebraic properties similar to those of the complex realizations we need to find an alternative definition of a rational axially regular function.
4 Axially rational regular function through the generalized CK-extension
In this section we propose another notion of rational axially regular, different from the one in Definition 3.4. The new notion makes use of the generalized CK-extension. The main advantage is that we can prove some main algebraic properties of realizations.
The idea of the definition comes from the standard equivalent statements given in Theorem 3.1 in the case of slice hyperholomorphic functions, but using the product \(\odot _{GCK}\) instead of the \(*\)-product since we are in the set of regular functions.
Definition 4.1
An \( {\mathbb {H}}^{M \times N}\)-valued function r is called (left) rational axially regular in a neighborhood of the origin if it can be represented in the form
This notion arises by considering the counterpart of the state space equations in the regular hyperholomorphic setting. Let us consider the following quaternionic linear system
where A, B, C and D are matrices of appropriate sizes with quaternionic entries and \( U:=\{u_n\}_{n \in {\mathbb {N}}_0}\) is a given sequence of vectors with quaternionic entries, and of suitable size. In the complex setting the “transfer function” of the system is defined by taking the \( {\mathcal {Z}}\)-transform which, in this framework, can be defined as
We observe that the \({\mathcal {Z}}\)-transform is right linear, since
Furthermore \( {\mathcal {Z}}(U)\) is an axially regular function, see Theorem 2.18. Another important property of the \( {\mathcal {Z}}\)-transform is the following. If we set
then if \(u_0=0\) we have
However, in the regular setting a “transfer function” cannot be defined by taking the \( {\mathcal {Z}}\)-transform like in the complex case. The transfer function matrix-valued of the system (4.2) is the axially regular function
where \({\mathcal {Y}}(x)\) and \({\mathcal {U}}(x)\) are the GCK-extensions of the \( {\mathcal {Z}}\)-transforms of \( y_n\) and of \(u_n\), respectively. We now give the counterpart of the classical realization for the transfer function.
Theorem 4.2
Let A, B, C, D and \( \{u_n\}_{n \in {\mathbb {N}}_0}\) be defined as above. Then we have
Proof
We start by considering the system (4.2) on the real line, where A, B, C and D are replaced by given quaternionic numbers a, b, c and d. Now, we suppose that \( \{u_n\}_{n \in {\mathbb {N}}_{0}}\) is a given sequence of real numbers:
Let \(x_0 \in {\mathbb {R}}\). By applying the real-valued \( {\mathcal {Z}}\)-transform defined as
where \(U= \{u_n\}_{n \in {\mathbb {N}}_0}\) we get
Each element of the above system is commutative, thus we have
All the functions involved in (4.4) are analytic on the real line, so we can use the generalized CK-extension (see Theorem 2.16) to get axially regular function in the variable x. Thus by Definition 2.19 we have
By substituting the first equation in the second one of the above system we get
Finally, by the definition of the function H(x) we obtain
In order to get a matrix valued-function it is sufficient to replace a, b, c and d, respectively, with the matrices A, B, C, D of suitable size and with quaternionic entries. Then we get the axially regular function
\(\square \)
Proposition 4.3
Let r be a quaternionic valued slice hyperholomorphic function and let \(\partial _{x_0}^2r_{| {\mathbb {R}}}\) be a rational function in the real variable \(x_0\). Then we have
where D, C, B and A are quaternionic matrices of suitable sizes.
Proof
By hypothesis we know that \( \partial _{x_0}^2 r|_{{\mathbb {R}}}\) is rational. This implies that we can write
By Theorem 2.17 we know that
We replace the quaternionic matrices A, B, C, D with the respective entries a, b, c and d. Now, by Definitions 2.19 and 2.20 we obtain
This implies the following equality for the entries \(r_{\ell j}\) of the \({\mathbb {H}}^{M \times N}\)-valued function r
The thesis follows by absorbing the constant \(-2\) in the matrices. \(\square \)
A relation between the two different notions of rational axially regular functions is discussed in the next result.
Proposition 4.4
A function which is rational axially regular according to Definition 3.4 is also rational according to Definition 4.1.
Proof
In Definition 3.4 we suppose that the function r is rational slice hyperholomorphic, so its restriction to the real line is a rational function and thus also the function \(\partial _{x_0}^2r_{| {\mathbb {R}}}\) is rational. The statement follows by Proposition 4.3. \(\square \)
4.1 Algebraic properties of rational axially regular functions
We now show that the notion of rational axially regular function given in Definition 4.1 is the most suitable one to extend to the Clifford-Appell framework the classical properties that hold for classical rational functions.
We begin by observing that a function which is a linear combination of the polynomials \({\mathcal {Q}}_{\ell }(x)\) admits a realization.
Lemma 4.5
Let M(x) be the \({\mathbb {H}}^{N \times N}\)-valued function defined as
Then
where \(D= M_0\) and
Proof
The assertion follows from the formula
\(\square \)
Lemma 4.6
Let us consider two axially regular realizations of the following form
which are \( {\mathbb {H}}^{M \times N}\) and \( {\mathbb {H}}^{N \times R}\)-valued, respectively. The generalized CK-product \(r_1 \odot _{GCK} r_2\) is a \( {\mathbb {H}}^{M \times R}\)-valued function, which can be written as
where \(U:= \begin{pmatrix} I &{}&{} 0\\ 0 &{}&{} I \end{pmatrix}\).
Given realizations of the two rational \( {\mathbb {H}}^{M \times N}\)-valued functions \(r_1\) and \(r_2\), then a realization of the the sum \(r_1+r_2\) is given by
Proof
We start by proving the formula for the generalized CK-product between \(r_1\) and \(r_2\). We have
Then, by setting \( {\mathcal {A}}:= I- {\mathcal {Q}}_1(x)A_1\), \( {\mathcal {B}}:=- {\mathcal {Q}}_1(x)B_1C_2\) and \( {\mathcal {C}}=I- {\mathcal {Q}}_1(x)A_2\) we get
Now we observe that
The above formula implies that
To show the formula for \(r_1(x)+r_2(x)\) it is enough observe that
and to apply the formula for \(r_1 \odot _{GCK} r_2\). \(\square \)
Lemma 4.7
Let us consider the following \( {\mathbb {H}}^{N \times N}\) rational axially regular function
where A, B, C and D are matrices with quaternionic entries and of appropriate sizes and such that D is invertible. Then the generalized CK-inverse of r admits the following realization
where \({\tilde{A}}:= A-BD^{-1}C.\)
Proof
We have to show
Then we have
Now, we observe that
This implies that
This proves the statement. \(\square \)
For a generic axially regular function written in the form
we define the operator
which plays the role of the backward shift operator.
Now, we prove five conditions that characterize rational axially regular functions.
Theorem 4.8
The following conditions are equivalent
-
(1)
A rational axially regular function can be written as
$$\begin{aligned} r(x)= D+C \odot _{GCK} (I- {\mathcal {Q}}_1(x)A)^{-\odot _{GCK}} \odot _{GCK} ({\mathcal {Q}}_1(x)B), \end{aligned}$$(4.6)where \(D_1\), \(C_1\), \(A_1\) and \(B_1\) are quaternionic matrices of suitable size.
-
(2)
The function r can be written as a series converging in a neighbourhood of the origin
$$\begin{aligned} r(x)=\sum _{k=0}^\infty {\mathcal {Q}}_k(x) r_k \qquad r_{k}= {\left\{ \begin{array}{ll} D \qquad k=0\\ CA^kB \qquad k \ge 1. \end{array}\right. } \end{aligned}$$(4.7) -
(3)
The right linear span \( {\mathcal {M}}(r)\) of the columns of the functions \( R_0r\), \(R_0^2 r, \ldots \) is finite dimensional.
Proof
We start proving \((1) \Longleftrightarrow (2)\). We show the implication by considering the quaternionic entries of the matrices A, B, C and D, that we denote by a, b, c and d, respectively. By Definition 2.20 we have
Since the generalized CK-extension is a right-linear operator and by (2.9) we get
Now, we show that \((1) \Longrightarrow (3)\). Firstly, we observe that
By iterating similar computations we have
This means that the right liner span \( {\mathcal {M}}(r)\) is included in the span of the columns of the function \(C \odot _{GCK} (I- {\mathcal {Q}}_1(x)A)^{-\odot _{GCK}}\). Therefore the span \( {\mathcal {M}}(r)\) is finite dimensional.
Now, we prove that \((3) \Longrightarrow (1)\). Since (4) is in force there exists an integer \(m_0 \in {\mathbb {N}}\) such that for every \(m \in {\mathbb {N}}\) and \(v \in {\mathbb {H}}^q\), there exist vectors \(u_1, \ldots , u_{m_0}\) such that
Now, we denote by E the \( {\mathbb {H}}^{p \times m_0q}\)-valued slice hyperholomorphic function
Now, by (4.8), there exists a matrix \(A \in {\mathbb {H}}^{m_0q \times m_0q}\) such that
By the definition of the operator \(R_0\), see (4.5), we have
This implies that
Therefore, we have
Moreover, we have also that
The definition of the operator \( R_0\) and formula (4.9) implies that
Then we have that r(x) is of the form (4.6). \(\square \)
Remark 4.9
A different type of regular rational functions was previously considered in [16]. In that paper the authors studied a notion of rational hyperholomorphic function in \( {\mathbb {R}}^4\) by means of the Fueter variables and the CK-product. Precisely, they define the counterpart of rational function in the regular setting as
where \(A_i\), \(B_i\) (with \(i=1,2,3\)) are constants matrices with entries in the quaternions and of appropriate dimensions. We observe that the function R is Fueter regular in a neighbourhood of the origin.
A different notion of rational regular function of axial type was considered in [8]. They defined a rational axially regular as
where the matrices A, B, C and D are quaternionic matrices of suitable sizes. The main issue with the previous notion of rational axially regular is that it is not possible to write an expansion in series like the one in (4.7).
In this table we summarize the notions of rational functions in the hyperholomorphic setting that appear in the literature
Setting | Realization | Series |
|---|---|---|
Slice hyperholomorphic | \(D+ C*(I-xA)^{-*}*(pB)\) | \(\sum _{n=0}^\infty x^n C A^{n}B\) |
Monogenic | \(D+ C\odot (I- \xi _1 A_1-\xi _2A_2-\xi _3A_3)^{- \odot }\) | |
\(\odot (\xi _1 B_1+ \xi _2B_2+\xi _3B_3)\) | \(\sum _{n=0}^\infty \sum _{|\nu |=n} \xi ^{\nu } R_{\nu }\) | |
Axially regular (CK) | None | \(\sum _{k=0}^\infty P_k(x) CA^kB\) |
Axially regular (GCK) | \(D+C \odot _{GCK} (I- {\mathcal {Q}}_1(x)A)^{-\odot _{GCK}}\) | |
\( \odot _{GCK} ({\mathcal {Q}}_1(x)B)\) | \(\sum _{k=0}^\infty {\mathcal {Q}}_k(x) CA^kB\) |
where \(R_{\nu }:=\frac{(|\nu |-1)!}{\nu !} C\begin{pmatrix} \nu _1 A^{\nu -e_1}&\,&\nu _2 A^{\nu -e_2}&\,&\nu _3 A^{\nu -e_3} \end{pmatrix}B\).
5 Hardy space
Positive definite functions and kernels and their associated reproducing kernel Hilbert spaces are important in complex analysis, stochastic process and machine learning, see [2, 45, 47]. In the quaternionic setting these notions are considered e.g. in [5, 15].
Definition 5.1
A quaternionic-valued function \({\mathcal {K}}(u,v)\), with u and v in some set \(\Omega \) is called positive definite if
-
it is Hermitian:
$$\begin{aligned} {\mathcal {K}}(u,v)=\overline{{\mathcal {K}}(v,u)} \qquad \forall u,v \in \Omega . \end{aligned}$$(5.1) -
for every \(N \in {\mathbb {N}}\), every \(u_1, \ldots , u_N \in \Omega \) and \(c_1, \ldots , c_N \in {\mathbb {H}}\) it holds that
$$\begin{aligned} \sum _{\ell ,j =1}^N {\bar{c}}_\ell {\mathcal {K}}(u_{\ell }, u_j) c_j \ge 0. \end{aligned}$$(5.2)
From (5.1) it is clear that for any choice of the variables, the sum in (5.2) is a real number.
Associated with \( {\mathcal {K}}(u,v)\) there exists a uniquely defined reproducing kernel quaternionic (right)-Hilbert space \( {\mathcal {H}}({\mathcal {K}})\).
Definition 5.2
A quaternionic Hilbert space \( {\mathcal {H}}({\mathcal {K}})\) of quaternionic valued functions defined on a set \( \Omega \) is called reproducing kernel quaternionic Hilbert space if
-
for every \(v \in \Omega \) and \(c \in {\mathbb {H}}\) the function \( u \mapsto {\mathcal {K}}(u,v)c\) belongs to \( {\mathcal {H}}({\mathcal {K}})\),
-
for every \(f \in {\mathcal {H}}({\mathcal {K}})\), \(u \in \Omega \) and \(c \in {\mathbb {H}}\) it holds that
$$\begin{aligned} {\bar{c}}f(v)= \langle f(.), {\mathcal {K}}(.,v)c \rangle _{{\mathcal {H}}({\mathcal {K}})}. \end{aligned}$$
It is possible to characterize a function belonging to \( {\mathcal {H}}({\mathcal {K}})\), see next result originally proved in [15, Prop. 9.4]
Lemma 5.3
Let us a consider the space \( {\mathcal {H}}({\mathcal {K}})\) a reproducing kernel quaternionic Hilbert space, with reproducing kernel the function \( {\mathcal {K}}(u,v)\). Then, a function f belongs to \( {\mathcal {H}}( {\mathcal {K}})\) if and only if there exists a constant \( M>0\) such that
In the previous equality \(M:= \Vert f \Vert _{{\mathcal {H}}({\mathcal {K}})}\).
An example of reproducing kernel quaternionic Hilbert space is the Hardy space.
The aim of this section is to recall and study the main properties of the Hardy space defined through the Clifford-Appell polynomials. This space was already considered in [32], but in this paper we show more properties. We denote by \( {\mathbb {B}}\) the unit ball in \( {\mathbb {R}}^4\)
To state the next result we introduce the notation
Lemma 5.4
The function
is absolutely convergent for x, \(y \in {\mathbb {B}}\).
Proof
The convergence follows by (2.10), indeed we have
By the behaviour of the geometric series (5.4) converges if x, \(y \in {\mathbb {B}}\). \(\square \)
By using the generalized CK-inverse, we have the following result.
Lemma 5.5
The function \({\mathcal {K}}(x,y)\), introduced in (5.3), for x, \(y \in {\mathbb {B}}\), can be written as
where the generalized CK-extension is with respect to the variable x.
Proof
We set \( \alpha (y):={\mathcal {Q}}_1^{m \odot _{GCK}}(y)\) and we recall that \( {\mathcal {Q}}_1(x)=GCK[x_0^m]\). Then we get
Since x, \(y \in {\mathbb {B}}\) we can write
\(\square \)
Definition 5.6
The kernel in (5.3) is associated with a reproducing kernel Hilbert space called Hardy space. This will be denoted by \( {\textbf{H}}_2({\mathbb {B}})\).
Following [32] we recall a characterization of the Hardy space
Theorem 5.7
The Hardy space \( {\textbf{H}}_2({\mathbb {B}})\) consists of functions of the form
where the coefficients satisfy the following condition
The norm of a function f in the Hardy space is given by \( \Vert f \Vert _{{\textbf{H}}_2({\mathbb {B}})}=\sum _{m=0}^\infty |f_m|^2.\)
Remark 5.8
Other different types of Hardy space can be studied in the noncommutative setting. For example, in [16] the authors studied the so-called Drury-Averson space. The reproducing kernel of this space is given by
The convergence of the previous sum is guaranteed if x, y belong the ellipsoid \( {\mathcal {E}}:=\{x \in {\mathbb {R}}^4 \,: \, 3x_0^2+x_1^2+x_2^2+x_3^2 <1\}\).
In [8], the authors use the axially regular kernel defined by
where x, \(y \in \mathcal {E'}:=\{x \in {\mathbb {R}}^4\,: \, 9x_0^2+x_1^2+x_2^2+x_3^2 <1\}\). The function defined in (5.5) is a reproducing kernel of the Hardy space defined in terms of the polynomials \(P_{n}(x)\), see (4.10). We observe that the kernel (5.5) differs from the one used in this paper since we use another type of Clifford-Appell polynomials, see (2.6). Moreover, we make use of the GCK-product.
Finally, another hypercomplex setting where to consider the Hardy space is the slice hyperholomorphic framework, see [3, 5]. In this case the reproducing kernel is
All the reproducing kernels and domains of the different Hardy spaces (or Drury-Averson) in the non commutative settings are summarized in the following table.
Setting | Reproducing kernel | Domain |
|---|---|---|
Slice hyperholomorphic | \(\sum p^n {\bar{q}}^n\) | \({\mathbb {B}}\) |
Monogenic | \(\sum _{m=0} \sum _{|\nu |=m} \frac{|\nu |!}{\nu !} \xi (x)^\nu {\overline{\xi }}^{\nu }(y)\) | \({\mathcal {E}}\) |
Axially regular (CK) | \( \sum _{m=0}^\infty P_1(x)^{m \odot _{CK}} \overline{P_1(y)}^{m \odot _{CK}}\) | \(\mathcal {E'}\) |
Axially regular (GCK) | \( \sum _{m=0}^\infty {\mathcal {Q}}_1(x)^{m\odot _{GCK}}\overline{{\mathcal {Q}}_1(y)}^{m\odot _{GCK}}\) | \({\mathbb {B}}\) |
We recall from [32] that the counterpart of shift operator in our framework is given by
In [32, Thm. 6.8] the authors proved that the adjoint of the previous operator is the so-called backward-shift operator and it is defined in the following way
Lemma 5.9
The operator defined in (5.7) for functions in \( {\textbf{H}}_2({\mathbb {B}})\) coincides with \( R_0f\) introduced in (4.5).
Proof
Let us consider the axially regular function on \({\mathbb {B}}\)
This implies that
Therefore, we have that
\(\square \)
Lemma 5.10
Let \(f \in {\textbf{H}}_2({\mathbb {B}})\). The operator \({\mathcal {M}}_{{\mathcal {Q}}_1}\) is an isometry in the Hardy space. Moreover, we have
Proof
It is easy to prove that the shift operator is an isometry on the Hardy space. By formula (5.7) we have
\(\square \)
Now we can define the point evaluation map in the Hardy space as \(Cf=f(0)\). The adjoint operator is defined as \(C^{*}u= {\mathcal {K}}(.,0)u=u\). Then by the equality (5.8) we get
Remark 5.11
A structural equality like the one in (5.9) is also obtained in the framework of Clifford-Appell polynomials in [8] but with the operator of multiplication by \(P_1\).
In this table we sum up the main structural identities in the quaternionic setting.
Setting | Structural identity |
|---|---|
Slice hyperholomorphic | \(I- {\mathcal {M}}_{p}{\mathcal {M}}^{*}_p=C^*C\) |
Regular | \(I- {\mathcal {M}}_{\xi } {\mathcal {M}}^{*}_{\xi }=C^*C\) |
Axially regular (CK) | \(I- {\mathcal {M}}_{P_1} {\mathcal {M}}^{*}_{P_1}=C^{*}C.\) |
Axially regular (GCK) | \(I- {\mathcal {M}}_{{\mathcal {Q}}_1} {\mathcal {M}}^{*}_{{\mathcal {Q}}_1}=C^{*}C.\) |
6 Schur multipliers
We recall that, in the complex setting, a Schur multiplier is a function s that satisfies one of the following conditions, see [1].
Theorem 6.1
The following are equivalent
-
1.
The function s is analytic and contractive in the open unit disk.
-
2.
The function s is defined in \( {\mathbb {D}}\) and the operator of multiplication by s is a contraction from the Hardy complex Hardy space into itself.
-
3.
The function s is defined in \( {\mathbb {D}}\) and the kernel
$$\begin{aligned} k_s(z,w)= \sum _{n=0}^\infty z^n(1- s(z)\overline{s(w)}) {\overline{w}}^n= \frac{1-s(z)\overline{s(w)}}{1-z {\bar{w}}} \end{aligned}$$is positive definite in the open unit disk.
In the literature Schur multipliers are related to several research directions: inverse scattering (see [12, 13, 20, 26]), fast algorithms (see [42, 43]), interpolation problems (see [33]) among others.
In [3, 5] the authors defined a counterpart of the Schur multipliers in the quaternionic setting by using the theory of slice hyperholomorphic functions. Also in this framework it is possible to show a list of equivalent conditions characterising Schur multipliers, see [5, Thm. 6.2.5].
In [17] Schur multipliers were introduced in the regular setting using the Cauchy–Kovalevskaya product and series of Fueter polynomials. Precisely, a function \({\textbf{S}}\) is a Schur multiplier in the regular setting if the kernel
is positive.
Inspired from this definition, we give the definition of Schur multipliers in the present framework. We note that in [8] Schur multipliers have been defined in the axially regular setting by using the polynomials defined in (4.10) and the CK-product but, as we discussed in the previous sections, the description via the CGK-product and the polynomials \({\mathcal {Q}}_{n}(x)\) has more advantages.
Definition 6.2
A function \(S: {\mathbb {B}} \rightarrow {\mathbb {H}}\) is a Schur multiplier if the kernel
is positive in \( {\mathbb {B}} \times {\mathbb {B}}\).
The reproducing kernel Hilbert space with reproducing kernel \(K_S(x,y)\) will be denoted by \( {\mathcal {H}}(S)\). This space was first introduced in [28, 29].
In this paper we use the following notion for the multiplicative operator
Definition 6.3
Let \(S: {\mathbb {B}} \rightarrow {\mathbb {H}}\) be a generic function. The left \(\odot _{GCK}\)-multiplication operator by S is defined as
If we consider a function regular in the unit ball \({\mathbb {B}}\) and written in the form \(f(x)=\sum _{k=0}^\infty {\mathcal {Q}}_k(x)f_{k}\), with \(f_k \in {\mathbb {H}}\), we can write the operator \( {\mathcal {M}}_S\) in the following way
Remark 6.4
In order to define the operator \( {\mathcal {M}}_S\) we need to request that the function S has a restriction to the real axis which is real analytic. Moreover, we observe that since if the operator \( {\mathcal {M}}_S\) maps \( {\textbf{H}}_2({\mathbb {B}})\) into itself, then we have that \( S={\mathcal {M}}_S\) belongs to the Hardy space \( {\textbf{H}}_2({\mathbb {B}})\).
Theorem 6.5
A function \(S: {\mathbb {B}} \rightarrow {\mathbb {H}}\) is a Schur multiplier if and only if the operator \( {\mathcal {M}}_S\) is a contraction on \( {\textbf{H}}_2({\mathbb {B}})\).
Proof
Let us start by supposing that the operator \({\mathcal {M}}_S\) is a contraction. By the formula of the reproducing kernel of Hardy space, see formula (5.3), and (6.1) we obtain
By using the reproducing kernel property we have that
This formula implies that
Now, we consider a function \(f \in {\textbf{H}}_2({\mathbb {B}})\) of the form
Therefore, we have
Since the operator \( {\mathcal {M}}_S\) is a contraction we have that \(\langle (I- {\mathcal {M}}_S {\mathcal {M}}_S^{*}) f, f \rangle _{ {\textbf{H}}_2({\mathbb {B}})}\) is non negative. this implies that the quadratic form defined in (6.4) is non negative, then the kernel \(K_S\) is positive.
Now, we suppose that the kernel \( {\mathcal {K}}_S\) is positive on \( {\mathbb {B}} \times {\mathbb {B}}\). Firstly, we observe that the function defined in (6.2) belongs to \( {\textbf{H}}_2({\mathbb {B}})\) for each fixed \(y \in {\mathbb {B}}\), since the operator \( {\mathcal {M}}_S^{*}\) maps \( {\textbf{H}}_2({\mathbb {B}})\) to \( {\textbf{H}}_2({\mathbb {B}})\). This implies that the following operator
is well defined. It is possible to consider an extension by linearity of the previous operator to functions f of the form (6.3). Such type of functions are dense in \( {\textbf{H}}_2({\mathbb {B}})\), and so we get that we can extend by continuity the operator T to all of \( {\textbf{H}}_2({\mathbb {B}})\). Using this density argument and formula (6.4), where instead of the operator \( {\mathcal {M}}_S^{*}\) we consider the operator T, by the positivity of \( {\mathcal {K}}_S\) we get that T is a contraction on \( {\textbf{H}}_2({\mathbb {B}})\). Now, we compute the adjoint of the operator T. Let \(c_1\), \(c_2 \in {\mathbb {H}}\) and \(y_1\), \(y_2 \in {\mathbb {B}}\), then we get
Thus we get that \(T^{*}= {\mathcal {M}}_S\). Since the operator T is a contraction also its adjoint is a contraction. This implies that the operator \( {\mathcal {M}}_S\) is a contraction. \(\square \)
Another characterization of Schur multipliers is the following.
Theorem 6.6
A function \(S: {\mathbb {B}} \rightarrow {\mathbb {H}}\) is a Schur multiplier if and only if S belongs to \( \mathcal{A}\mathcal{M}({\mathbb {B}})\) and for all \( n\ge 0\) we have
where \(L_n\) is the lower triangular Toeplitz matrix given by
Proof
We assume that S is a Schur multiplier. Computations similar to those done in (6.2) show that for S written as in (6.5) we have, for all \( k \ge 0\), that
which extends by linearity to
If we set \( {\textbf{f}}:=[f_0, \ldots , f_n]^T\) and by the shape of the matrix \(L_n\) we get
By Theorem 6.5 we know that \( {\mathcal {M}}_S\) is a contraction on \({\textbf{H}}_2({\mathbb {B}})\) (thus also \({\mathcal {M}}_S^{*}\)), hence (6.6) is nonnegative for every \( {\textbf{f}} \in {\mathbb {H}}^{n+1}\). This means \(I_{n+1}- L_{n}L_{n}^{*}\) is positive definite.
Conversely, we assume that \(I_{n+1}-L_nL^{*}_n \ge 0\), for each \(n \ge 1\). By (6.6) we have that the operator \( {\mathcal {M}}_S^{*}\) acts contractively on functions of the form \(\sum _{k=0}^\infty {\mathcal {Q}}_k(x) f_k\). However, this type of functions are dense in \( {\textbf{H}}_2({\mathbb {B}})\), then the operators \( {\mathcal {M}}_S\) and \( {\mathcal {M}}_S^{*}\) are contractions. The thesis follows by Theorem 6.5. \(\square \)
Lemma 6.7
Let \(S_1\), \(S_2\) and S be Schur multipliers. Then we have the following equalities
-
(1)
\({\mathcal {M}}_{S_1} {\mathcal {M}}_{S_2}= {\mathcal {M}}_{S_1 \odot _{GCK} S_2}\)
-
(2)
\( {\mathcal {M}}_{{\mathcal {Q}}_1} {\mathcal {M}}_{S}= {\mathcal {M}}_{S}{\mathcal {M}}_{{\mathcal {Q}}_1}.\)
Proof
-
(1)
We observe that \(S_1 \odot _{GCK} S_2\) is an axially regular function with an expansion in series in terms of the polynomials \( \{{\mathcal {Q}}_{n}(y)\}_{n \ge 0}\). Then we get
$$\begin{aligned} {\mathcal {M}}_{S_1} {\mathcal {M}}_{S_2}(f)= & {} {\mathcal {M}}_{S_1}( S_2 \odot _{GCK}f)\\= & {} (S_1 \odot _{GCK} S_2)\odot _{GCK} f\\= & {} {\mathcal {M}}_{S_1 \odot _{GCK} S_2} \end{aligned}$$ -
(2)
Let us consider a function \(f=\sum _{n=0}^\infty {\mathcal {Q}}_n(x) \alpha _n\), with \( \{\alpha _n\}_{n \in {\mathbb {N}}_0} \in {\mathbb {H}}\). Then by the fact that the generalized CK-product is a convolution product and (5.6) we have
$$\begin{aligned} {\mathcal {M}}_{{\mathcal {Q}}_1} {\mathcal {M}}_{S}(f)= & {} {\mathcal {Q}}_1 \odot _{GCK} ({\mathcal {M}}_Sf)\\= & {} {\mathcal {Q}}_1 \odot _{GCK} \left( S \odot _{GCK} f\right) \\= & {} {\mathcal {Q}}_1 \odot _{GCK} \left( \sum _{n=0}^\infty ({\mathcal {Q}}_n(x) \odot _{GCK} S) \alpha _n\right) \\= & {} \sum _{n=0}^\infty ({\mathcal {Q}}_{n+1} \odot _{GCK} S)(x) \alpha _n\\= & {} {\mathcal {M}}_S \left( \sum _{n=0}^\infty {\mathcal {Q}}_{n+1}(x)\alpha _n\right) \\= & {} {\mathcal {M}}_S({\mathcal {Q}}_1 \odot _{GCK} f)\\= & {} {\mathcal {M}}_S{\mathcal {M}}_{{\mathcal {Q}}_1}(f). \end{aligned}$$
\(\square \)
Now, we show the counterpart of Schwarz’s lemma for Schur multipliers in this framework.
Theorem 6.8
Let S be a Schur multiplier, and assume that \(S(0)=0\). We set \(S(x)= (S^{(1)} \odot _{GCK}{\mathcal {Q}}_1 )(x)\). Then \(S^{(1)}\) is a Schur multiplier.
Proof
Since by hypothesis \(S(0)=0\) we have that \(1= {\mathcal {K}}_S(x,0) \in {\mathcal {H}}(S)\) and \( {\mathcal {K}}_S(0,0)=1=\Vert 1 \Vert _{{\mathcal {H}}(S)}\). Hence by Lemma 5.3 (with the function \(f \equiv 1\)) we have that
in \( {\mathbb {B}}\). By Definition 6.2 we have that
Since \( {\mathcal {Q}}_0(x)= {\mathcal {Q}}_0(y)=0\) we have that
By changing index to the first sum we get
This implies that
Therefore, by Definition 6.2 we get the thesis. \(\square \)
Finally, we conclude this section with a characterization of the space \( {\mathcal {H}}(S)\). The proof is as in the classic case, see [9, 14].
Theorem 6.9
Let S be a Schur multiplier. Then
endowed with the norm
where \(\pi \) is the orthogonal projection on \(\hbox {Ker}(\sqrt{I- {\mathcal {M}}_S {\mathcal {M}}^{*}_S})\).
7 Realizations of Schur multipliers
In the case of holomorphic and slice hyperholomorphic functions the realizations and the Schur multiplier are related to each other, see [3, 5], respectively. The aim of this section is to get a similar results in the framework of Clifford-Appell polynomials.
We start by recalling the following notion.
Definition 7.1
A realization is called observable, or closely outer-connected, if the pair \((C,A) \in {\mathbb {H}}^{N \times N} \times {\mathbb {H}}^{M \times M}\) is observable, i.e.
Theorem 7.2
Let us consider a function \(S: {\mathbb {B}} \rightarrow {\mathbb {H}}\). Then S is a Schur multiplier if and only if there exists a right quaternionic Hilbert space \( {\mathcal {H}}(S)\) and a coisometric operator
such that
where
If we assume that (C, A) are closely outer-connected, then the realization S is unique up to an an isometry of right quaternionic Hilbert spaces.
By Theorem 4.8 we can write the Schur multiplier S of the previous theorem as
In order to show the previous theorem we need to show some technical lemmas. We will use the following notation \(\Gamma _S:=I- {\mathcal {M}}_S {\mathcal {M}}_S^{*}\). We recall that for h, \(g \in {\textbf{H}}_2({\mathbb {B}})\) we have the following relations
see for instance [6, 34]. To show the next results we use a similar method applied in [11], suitably adapted.
Lemma 7.3
Let S be a Schur multiplier. Then for \(x_1\), \(x_2 \in {\mathbb {B}}\) we have the following equality
Proof
First of all we observe that by (5.7) we have
and
By formulas (7.5), (7.7) and (7.8) we have that
Now, by the second point of Lemma 6.7 and Definition 6.2 we get
\(\square \)
In the next result we will use the following notation
Note that \(\omega _yu\) is well defined since \({\mathcal {M}}_{Q_1}\) is a bounded operator from \({\textbf{H}}_2({\mathbb {B}})\) into itself.
Lemma 7.4
The right vector subspace of \(( {\mathcal {H}}(S) \oplus {\mathbb {H}}) \times ( {\mathcal {H}}(S) \oplus {\mathbb {H}})\) spanned by the pairs
where
defines an isometric relation R
with dense domain.
Proof
Firstly we show that the relation R is an isometry. Precisely, we have to show that
where \(u_1\), \(u_2\), \(v_1\), \(v_2 \in {\mathcal {H}}(S)\) and \(y_1\), \(y_2 \in {\mathbb {B}}\). We can write relation (7.9) as
By using Lemma 7.3 we write the term on the right hand side of (7.10) in the following way
We can write the term on the left hand side as
By Definition 6.2 we observe that
This implies that
Then by using
we can write (7.12) in the following way
Since (7.11) and (7.13) are equal we get that the relation R is an isometry.
Now, we show that the relation R has a dense domain. Let us consider \((\omega _0, \omega _1) \in {\mathcal {H}}(S) \times {\textbf{H}}_2({\mathbb {B}})\) be orthogonal to the domain of R, where
with \(f_{0}:= \sqrt{\Gamma _S} h \in {\mathcal {H}}(S)\), \(h \in {\textbf{H}}_2({\mathbb {B}})\). If we first consider \(u=0\) we get \(v_0=0\). If now we consider that \(v=0\) from the orthogonality of \(\omega _0\) and \( \omega _1\) we get
By formula (7.6), (5.7) and the reproducing kernel property of \( {\textbf{H}}_2({\mathbb {B}})\) we have
By combining (7.14) and (7.15) we get
This implies that \(f_0(x)=0\). This concludes the proof. \(\square \)
Proposition 7.5
The relation R is the graph of a densely defined isometry. Moreover, its extension to \( {\mathcal {H}}(S) \oplus {\mathbb {H}}\) is defined as
Then
Proof
First we prove that R is the graph of a densely defined isometry. By definition, the domain R is the set of \(U \in {\mathcal {H}}(S) \otimes {\mathbb {H}}\) such that there exists \(V \in {\mathcal {H}}(S) \oplus {\mathbb {H}}\) such that \((U,V) \in R\). By Lemma 7.4 we know that R has a dense domain. Thus we introduce a densely defined operator W such that \(WU=V\). Now, we assume that there exists \(V_1\) and \(V_2\) such that \(TU=V_1\) and \(TU=V_2\). Then if \((U,V_1) \in R\) and \((U,V_2) \in R\) then \((0, V_1-V_2) \in R\). Since by Lemma 7.4 we know that the relation R is an isometry we get \( \Vert 0\Vert = \Vert V_1-V_2 \Vert \). This implies that \(V_1=V_2\). Therefore W is a densely defined isometry. As in the complex Hilbert spaces, it extends to an everywhere defined isometry.
Now, we compute the operator T. Let \(y \in {\mathbb {B}}\) and \(u \in {\textbf{H}}_2({\mathbb {B}})\) and we assume that \(B^*= {\hat{B}}\) is bounded from \( {\mathcal {H}}(S)\) to \( {\mathcal {H}}(S)\) then we have
On one side, for \(g \in {\mathcal {H}}(S)\), by the reproducing kernel property we have
On the other side we have that
Now, we set \(Ag= \sqrt{\Gamma _S}h\), with h being not unique. By formula (7.5) and the reproducing kernel property of the space \( {\textbf{H}}_2({\mathbb {B}})\) we have
By putting together (7.17) and (7.18) we get
By formula (2.12) we get
Similarly, we compute the operator Bv, for \(v \in {\textbf{H}}_2({\mathbb {B}})\). We have that
On one side we get
On the other side we have
Now we set \(Bv:= \sqrt{\Gamma _S} h\). Therefore, by using formula (7.5) and the reproducing kernel of the space \( {\textbf{H}}_2({\mathbb {B}})\) we obtain
By putting together formula (7.19) and (7.20) we obtain
Now we compute the operator B. To do this we note that
for every \(u \in {\mathbb {H}}_2({\mathbb {B}})\). Then, for \(f \in {\mathcal {H}}(S)\) we have
Hence we have \( C(f)=f(0)\). Finally, it is obvious that \(D=S(0)\). \(\square \)
Proof of Theorem 7.2
We observe that the pair (C, A) is closely outer connected, see (7.15) and (7.16). A generic function \(f \in {\mathcal {H}}(S)\) can written with the following power series
We have the expression for the coefficients of f
Then we obtain
Finally we apply this formula to Bv, where \(v \in {\textbf{H}}_2({\mathbb {B}})\), then we get
Now, we show the converse. We assume that the function S has the form (7.2) with coefficients defined (7.3). First of all we show the following formula for x, \(y \in {\mathbb {B}}\)
where the function U is defined as
Then we have
Since the operator matrix (7.1) is coisometric we have that
These imply that we can write formula (7.23) in the following way
Now, we observe that
and
By inserting (7.25) and (7.26) in (7.24) we get the expression (7.21). Now, from (7.21) we obtain that
By making the generalized CK multiplication of the formula (7.21) from the left with \( {\mathcal {Q}}_n(x)\) and on the right by \( \overline{{\mathcal {Q}}_n(y)}\) we get
These imply that
Therefore we have that \( {\mathcal {K}}_S(x,y)\) is positive define in \( {\mathbb {B}}\), therefore by Definition 6.2 the function S is a Schur multiplier.
Now, we have to show the uniqueness of the claim. Let us consider two different closely outer-connected coisometric realizations of S defined in the following way
where \( {\mathcal {H}}_1(S)\) and \( {\mathcal {H}}_2(S)\) are different right quaternionic Hilbert spaces. In order to show that \(S_1\) and \(S_2\) are equivalent we have to prove that there exists an unitary map \(W: {\mathcal {H}}_1(S) \oplus {\mathbb {H}} \rightarrow {\mathcal {H}}_2(S) \oplus {\mathbb {H}}\) such that the following diagram is commutative

This means that we have to show the following equalities
The last relation is obvious, because by Proposition 7.5 we know that \(D_1=D_2=S(0)\). In order to show the other relations, we observe that by (7.27) we have
where \(U_1\) and \(U_2\) are defined as in (7.22). Then, it follows that for nay m, \(n \in {\mathbb {N}}_0\) we get
Since the pairs \((C_1,A_1)\) and \((C_2, A_2)\) are closely outer connected we get that the following relation
is a densely defined isometric relation in \({\mathcal {H}}_1(S) \times {\mathcal {H}}_2(S)\) with dense range. Therefore it is the graph of a unitary map U such that
If we consider \(m=0\) in (7.29) we get
Using another time (7.29) we obtain
Since the pairs \((C_1, A_1)\) and \((C_2,A_2)\) are closely outer-connected we get
Now, using (7.30) and (7.31) we get
By the fact that the pair \((C_1,A_1)\) is closely outer connected we get \(WB_1=B_2\). This concludes the proof. \(\square \)
8 Blaschke product: through the GCK-extension
In complex analysis the Blaschke factor is defined as
These kind of functions are very important in the study of invariant subspaces and interpolation, see [33, 39]. In [7] a Blaschke factors and an interpolation problem in the slice hyperholomorphic setting were studied.
Definition 8.1
Let \(a \in {\mathbb {H}}\), \(|a|<1\). The function
is called a slice hyperholomorphic Blaschke factor at a.
Remark 8.2
By the definition of \(*\)-product we have that
This implies that we can write the Blaschke factor at a as
Similarly to the holomorphic case also in the slice hyperholomorphic setting it is possible to have a series expansion at the origin of the Blaschke factor at a.
Proposition 8.3
Let \(a \in {\mathbb {B}}\). Then it holds that
A regular counterpart of the Blaschke factor is given in [16] for the quaternionic Arverson space. Precisely, it is given by
where \( \xi ^\nu \) are the Fueter polynomials defined in (2.2). In this section we introduce and study the Blaschke products in the framework of the Clifford-Appell polynomials.
Definition 8.4
Let \(a \in {\mathbb {H}}\) and \(|a|<1\). The function
is called Clifford-Appell-Blaschke factor at a.
This definition leads to the following result.
Proposition 8.5
Let \(a \in {\mathbb {H}}\) and \(|a|<1\). The Clifford-Appell-Blaschke factor \( {\mathcal {B}}_a\) is an axially regular function in \( {\mathbb {B}}\).
Remark 8.6
The Clifford-Appell-Blaschke factor in the Clifford-Appell setting can be deduced as a particular example of Schur multiplier. Precisely, if we consider
where \(a \in {\mathbb {B}}\), by formula (7.4) we get
It is interesting to note that our definition leads to a series expansion of the Clifford-Appell-Blaschke factor in terms of Clifford-Appell polynomials.
Proposition 8.7
Let a, \(x \in {\mathbb {B}}\). Then it holds that
Proof
We start by observing that
By Definition 8.4 we get
This concludes the proof. \(\square \)
The result above implies the following.
Theorem 8.8
Let \(a \in {\mathbb {H}}\), \(|a|<1\). Then the Clifford-Appell-Blaschke factor \({\mathcal {B}}_a\) maps the unit ball \({\mathbb {B}}\) into itself.
Proof
We have to show that if \(|x| <1\) than \(| {\mathcal {B}}_a(x)|<1\). By Proposition 8.7 and the fact that in particular \( | {\mathcal {Q}}_n(x)| < |x|^n\), we have
To prove that \(| {\mathcal {B}}_a(x)| <1\) we have to prove that \(|a|+|x| <1-|a||x|\), which is equivalent to \(|a|+|x| <1+|a||x|\). Taking the square we get
The previous inequality follows from \(|x|<1\) and \(|a| <1\). \(\square \)
Theorem 8.9
Let \( {\mathcal {B}}_a\) be a Clifford-Appell-Blaschke factor. The operator
is an isometry from \( {\textbf{H}}_2({\mathbb {B}})\) into itself.
Proof
We start by considering the functions \(f(x)= {\mathcal {Q}}_u(x) h\) and \(g(x)= {\mathcal {Q}}_v(x) k\), where u, \(v \in {\mathbb {N}}_0\) and h, \(k \in {\mathbb {H}}\). We prove
By Theorem 8.7 and using f and g defined as above, we have
and
We begin by considering the case \(u=v\), we have
Now, we consider the case \(u < v\), we have that
and
It follows that
The case \(v<u\) follows by using similar arguments. By continuity for f \(g \in {\textbf{H}}_2({\mathbb {B}})\) we get
This concludes the proof. \(\square \)
9 Blaschke factor through the Fueter map
Another way to define the Blaschke factor in the regular setting is to apply the Fueter map to the slice hyperholomorphic Blaschke factor.
Definition 9.1
Let \(a \in {\mathbb {H}}\), \(|a|<1\). Let \(B_a(x)\) be the slice-hyperholomorphic Blaschke factor at a. The Fueter-Blaschke factor at a is defined as \( \Delta B_a(x)=\breve{B}_a(x)\).
Theorem 9.2
Let \(a \in {\mathbb {H}}\) and \(|a|<1\). Then the Fueter-Blaschke factor can be written as
Proof
We apply the Laplace operator in four real variables to the slice hyperholomorphic Blaschke product, see (8.1). By formula (3.3) with \(c=1\) we get
Now, we have to compute
We set
We start performing the derivation of G(x) with respect to \(x_0\), we get
and
Now, we perform the computations with respect to the variables \(x_i\), with \(1 \le i \le 3\), we get
and
These computations imply that
Therefore we have
Finally, by putting together (9.1) and (9.2) we have
\(\square \)
Theorem 9.3
Let \(a \in {\mathbb {H}}\), then we have
Proof
By Proposition 8.3 and from the fact that \(\Delta (x^n)=-2n (n-1){\mathcal {Q}}_{n-2}(x)\) for \(n\ge 2\) we get
\(\square \)
Theorem 9.4
Let \(a \in {\mathbb {H}}\) and \(|a|<1\). Then the Fueter-Blaschke factor \(\breve{B}_a(x)\) satisfy the following properties
-
1.
it maps the unit ball \( {\mathbb {B}}\) into itself.
-
2.
it has a zero at \(x= \frac{a}{|a|^2}\).
Proof
-
1.
We have to show that if \(|x|<1\) then \(|\breve{B}_a(x)|<1\). By Theorem 9.3 and the fact that \(| {\mathcal {Q}}_n(x)| < |x|^n \) we get
$$\begin{aligned} |\breve{B}_a(x)|< & {} 2 \sum _{n=1}^\infty (n+1)(n+2) | {\mathcal {Q}}_n(x)| |a|^{n+2} \left( |a|+ \frac{1}{|a|}\right) \\< & {} |a|^2\sum _{n=1}^\infty (n+1)(n+2) |xa|^n \left( |a|+ \frac{1}{|a|}\right) . \end{aligned}$$Now from the fact that \( \sum _{n=1}^\infty n^2|xa|^n=- \frac{|xa|(|xa|+1)}{(|ax|-1)^3}\) and \( \sum _{n=1}^\infty n|xa|^n=- \frac{|xa|}{(|ax|-1)^2}\) we get
$$\begin{aligned}{} & {} |a|^2\sum _{n=1}^\infty (n+1)(n+2) |xa|^n \left( |a|+ \frac{1}{|a|}\right) \\{} & {} =\left( - \frac{|a|^2|xa|(1+|xa|)}{(|xa|-1)^3}+3 \frac{|a|^2 |ax|}{(|ax|-1)^2}-2 \frac{|a|^2|xa|}{(|xa|-1)}\right) \left( \frac{|a|^2+1}{|a|}\right) \\{} & {} = \frac{2|x||a|^2(1+|a|^2)(3|x||a|-3-|x|^2|a|^2)}{(|xa|-1)^3}. \end{aligned}$$Now, since x, \(a \in {\mathbb {B}}\) we get
$$\begin{aligned} \frac{2|x||a|^2(1+|a|^2)(3|x||a|-3-|x|^2|a|^2)}{(|xa|-1)^3}< \frac{2(1+|a|^2)|x|^2|a|^2}{(1-|x| |a|)^3}. \end{aligned}$$To finish the proof we have to show that
$$\begin{aligned} \frac{2(1+|a|^2)|x|^2|a|^2}{(1-|x| |a|)^3}<1. \end{aligned}$$Since \( \frac{1}{1+|a|^2}<1\) we have to prove that
$$\begin{aligned} \frac{2|x|^2 |a|^2}{(1-|x||a|)^3} <1. \end{aligned}$$This is equivalent to show the following inequality
$$\begin{aligned} 3|x| |a| < 1+|x|^3|a|^3+|x|^2|a|^2. \end{aligned}$$The previous inequality is verified for all x, \(a \in {\mathbb {B}}\).
-
2.
By Theorem 9.2 to study the zero of the function \( \breve{B}_a\) we need to study the zeros of the polynomial \(1- {\bar{x}} {\bar{a}}\). It is obvious that the zeros of the previous polynomials are given by \(x= {\bar{a}}^{-1}= \frac{a}{|a|^2}\).
\(\square \)
Remark 9.5
The Fueter-Blaschke factor at a does not satisfy an isometry property like the one showed in Proposition 8.9.
References
Alpay, D.: The Schur Algorithm. Reproducing Kernel Spaces and System Theory. American Mathematical Society, Providence (2001). (Translated from the 1998 French original by Stephen S. Wilson, Panoramas et Syntheses. [Panoramas and Syntheses])
Alpay, D.: An Advanced Complex Analysis Problem Book. Topological Vector Spaces, Functional Analysis, and Hilbert Spaces of Analytic Functions. Birkhäuser, Basel (2015)
Alpay, D., Colombo, F., Sabadini, I.: Schur functions and their realizations in the slice hyperholomorphic setting. Integr. Equ. Oper. Theory 72(2), 253–289 (2012)
Alpay, D., Colombo, F., Sabadini, I.: Schur analysis in the quaternionic setting: the Fueter regular and the slice regular case. In: Alpay, D. (ed.) Handbook of Operator Theory, vol. 2, pp. 1745–1786. Springer, Basel (2015)
Alpay, D., Colombo, F., Sabadini, I.: Slice Hyperholomorphic Schur Analysis. Operator Theory: Advances and Applications, vol. 256, p. xii+362. Cham, Birkhäuser/Springer (2016)
Alpay, D., Colombo, F., Sabadini, I.: Realizations of holomorphic and slice hyperholomorphic functions: the Krein space case. Indag. Math. 31(4), 607–628 (2020)
Alpay, D., Colombo, F., Sabadini, I.: Pontryagin-de Branges-Rovnyak spaces of slice hyperholomorphic functions. J. Anal. Math. 121, 87–125 (2013)
Alpay, D., Colombo, F., Diki, K., Sabadini, I.: On a polyanalytic approach to noncommutative de Branges-Rovnyak spaces and Schur analysis. Integr. Equ. Oper. Theory 93(4), 38 (2021)
Alpay, D., Dewilde, P., Dym, H.: Lossless inverse scattering and reproducing kernels for upper triangular operators. In: Gohberg, I. (ed.) Extension and Interpolation of Linear Operators and Matrix Functions. Operator Theory: Advances and Applications, vol. 47, pp. 61–135. Birkhäuser, Basel (1990)
Alpay, D., Diki, K., Sabadini, I.: Fock and Hardy spaces: Clifford Appell case. Math Nachr. 295(5), 834–860 (2022)
Alpay, D., Dijksma, A., Rovnyak, J., De Snoo, H.: Schur Functions, Operator Colligations, and Reproducing Kernel Pontryagin Spaces. Operator Theory: Advances and Applications, vol. 96. Birkhäuser Verlag, Basel (1997)
Alpay, D., Dym, H.: Hilbert spaces of analytic functions, inverse scattering and operator models. Integr. Equ. Oper. Theory 7(5), 589–641 (1984)
Alpay, D., Dym, H.: Hilbert spaces of analytic functions, inverse scattering and operator models, II. Integr. Equ. Oper. Theory 8(2), 145–180 (1985)
Alpay, D., Dym, H.: On applications of reproducing kernel spaces to the Schur algorithm and rational J-unitary factorization. In: Gohberg, I. (ed.) I. Schur Methods in Operator Theory and Signal Processing. Operator Theory: Advances and Applications, vol. 18, pp. 89–159. Birkhäuser Verlag, Basel (1986)
Alpay, D., Shapiro, M.: Reproducing kernel quaternionic Pontryagin spaces. Integr. Equ. Oper. Theory 50(4), 431–476 (2004)
Alpay, D., Shapiro, M., Volok, D.: Rational hyperholomorphic functions in \({{\mathbb{R} }}^4\). J. Funct. Anal. 221(1), 122–149 (2005)
Alpay, D., Shapiro, M., Volok, D.: Reproducing kernel spaces of series of Fueter polynomials. In: Operator Theory in Krein Spaces and Nonlinear Eigenvalue Problems. Operator Theory: Advances and Applications, vol. 162, pp. 19–45. Birkhäuser, Basel (2006)
Bart, H., Gohberg, I., Kaashoek, M.: Minimal Factorization of Matrix and Operator Functions. Operator Theory: Advances and Applications, vol. 1. Birkhäuser Verlag, Basel (1979)
Brackx, F., Delanghe, R., Sommen, F.: Clifford analysis. Pitman Res. Not. Math. 76 (1982)
Bruckstein, A.M., Kailath, T.: Inverse scattering for discrete transmission-line models. SIAM Rev. 29(3), 359–389 (1987)
Cação, I., Falcão, M.I., Malonek, H.: Hypercomplex polynomials, Vietoris’ rational numbers and a related integer numbers sequence. Complex Anal. Oper. Theory 11(5), 1059–1076 (2017)
Cação, I., Falcao, M.I., Malonek, H.R.: Laguerre derivative and monogenic Laguerre polynomials: an operational approach. Math. Comput. Model. 53(5–6), 1084–1094 (2011)
Colombo, F., Sabadini, I., Struppa, D.C.: Noncommutative Functional Calculus. Progress in Mathematics, vol. 289. Birkhäuser/Springer, Basel (2011)
Colombo, F., Sabadini, I., Struppa, D.C.: Entire Slice Regular Functions. SpringerBriefs in Mathematics, Springer, Cham (2016)
Colombo, F., Sabadini, I., Struppa, D.C.: Michele Sce’s Works in Hypercomplex Analysis. A Translation with Commentaries. Birkhäuser/Springer, Basel (2020)
Constantinescu, T., Sayed, A., Kailath, T.: Inverse scattering experiments, structured matrix inequalities, and tensor algebra. Linear Algebra Appl. 343(344), 147–169 (2002). (Special issue on structured and infinite systems of linear equations)
Delanghe, R., Sommen, F., Soucek, V.: Clifford Algebra and Spinor-Valued Functions. A Function Theory for the Dirac Operator. Mathematics and Its Applications, vol. 53. Kluwer Academic Publishers Group, Dordrecht (1992)
de Branges, L., Rovnyak, J.: Canonical models in quantum scattering theory. In: Wilcox, C. (ed.) Perturbation Theory and its Applications in Quantum Mechanics, pp. 295–392. Wiley, New York (1966)
de Branges, L., Rovnyak, J.: Square Summable Power Series. Holt, Rinehart and Winston, New York (1966)
Diki, K., Krausshar, R.S., Sabadini, I.: On the Bargmann-Fock-Fueter and Bergman-Fueter integral transforms. J. Math. Phys. 60(8), 083506 (2019)
De Martino, A., Diki, K., Guzmán Adán, A.: On the connection between the Fueter mapping theorem and the Generalized CK-extension. Results Math. 78(2), 55 (2023)
De Martino, A., Diki, K., Guzmán, Adán. A.: The Fueter-Sce mapping and the Clifford-Appell polynomials. Proc. Edinb. Math. Soc. (2) 66(3), 642–688 (2023)
Dym, H.: Hermitian block Toeplitz matrices, orthogonal polynomials, reproducing kernel Pontryagin spaces, interpolation and extension. In: Gohberg, I. (ed.) Orthogonal Matrix-Valued Polynomials and Applications (Tel Aviv, 1987–88). Operator Theory: Advances and Applications, vol. 34, pp. 79–135. Birkhäuser, Basel (1988)
Gheondea, A.: Reproducing kernel Kreĭn spaces. In: Alpay, D. (ed.) Operator Theory, pp. 311–343. Springer, Basel (2015)
Gürlebeck, K., Habetha, K., Sprößig, W.: Holomorphic Functions in the Plane and n-dimensional Space. Birkhäuser, Basel (2008)
Fliess, M.: Matrices De Hankel. J. Math. Pures Appl. 53(9), 197–222 (1974)
Fueter, R.: Die Funktionentheorie der Differentialgleichungen \(\Delta u=0\) und \(\Delta \Delta u=0\) mit vier reellen Variablen. Comment. Math. Helv. 7(1), 307–330 (1934)
Kalman, R.E., Falb, P.L., Arbib, M.A.K.: Topics in Mathematical System Theory. McGraw-Hill, New-York (1969)
Rudin, W.: Functional Analysis. International Series in Pure and Applied Mathematics, McGraw-Hill International Editions, New-York (1991)
Qian, T.: Generalization of Fueters result to \({{\mathbb{R} }}^{n+1}\). Rend. Mat. Acc. Lincei 9, 111–117 (1997)
Qian, T., Li, P.: Singular Integrals and Fourier Theory on Lipschitz Boundaries, p. xv+306. Science Press Beijing, Beijing; Springer, Singapore, (2019)
Sayed, A.H., Kailath, T.: Fast algorithms for generalized displacement structures and lossless systems. Linear Algebra Appl. 219, 49–78 (1995)
Sayed, A.H., Kailath, T.: A look-ahead block Schur algorithm for Toeplitz-like matrices. SIAM J. Math. Anal. 16, 388–414 (1995)
Sce, M.: Osservazioni sulle serie di potenze nei moduli quadratici. Atti Accad. Naz. Lincei. Rend. CI. Sci. Fis. Mat. Nat. 23, 220–225 (1957)
Schölkopf, B., Tsuda, K., Vert, J.P.: Kernel Methods in Computational Biology. MIT Press, Cambridge (2004)
Sommen, F.: Special functions in Clifford analysis and axial symmetry. J. Math. Anal. Appl. 130(1), 110–133 (1988)
Steinwart, I., Christmann, A.: Support Vector Machines. Springer, New York (2008)
Funding
Open access funding provided by SCELC, Statewide California Electronic Library Consortium.
Author information
Authors and Affiliations
Contributions
All authors had the same role in the research and writing of the manuscript.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alpay, D., Colombo, F., De Martino, A. et al. On axially rational regular functions and Schur analysis in the Clifford-Appell setting. Anal.Math.Phys. 14, 41 (2024). https://doi.org/10.1007/s13324-024-00902-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-024-00902-5
Keywords
- Clifford-Appell polynomials
- Rational functions
- Blaschke factor
- Schur analysis
- Generalized Cauchy–Kovalevskaya extension