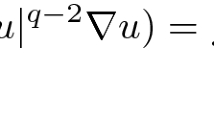Abstract
In this paper we study a Dirichlet double phase problem with a parametric superlinear right-hand side that has subcritical growth. Under very general assumptions on the data, we prove the existence of at least two nontrivial bounded weak solutions to such problem by using variational methods and critical point theory. In contrast to other works we do not need to suppose the Ambrosetti–Rabinowitz condition.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider the following Dirichlet double phase problem
where \(\Omega \subseteq \mathbb {R}^N\), \(N\ge 2\), is a bounded domain with Lipschitz boundary \(\partial \Omega \), \(1<p<N\), \(p<q<p^*\) and \(0\le \mu (\cdot )\in L^\infty (\Omega )\) with \(p^*=\frac{Np}{N-p}\), \(\lambda >0\) is a parameter and \(f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}\) is a Carathéodory function that satisfies subcritical growth and a certain behavior at \(\pm \infty \).
The operator involved is the so-called double phase operator defined by
with \(W^{1, \mathcal {H}}_0(\Omega )\) being an appropriate Musielak-Orlicz Sobolev space, see its Definition in Sect. 2. It is clear that (1.2) reduces to the p-Laplacian if \(\mu \equiv 0\) and to the (q, p)-Laplacian if \(\inf _\Omega \mu \ge \mu _0>0\). Moreover, the double phase operator is related to the two-phase integral functional \(J:W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}\) given by
Zhikov [24] was the first who introduced and studied functionals of type (1.3) whose integrands change their ellipticity according to a point in order to provide models for strongly anisotropic materials. It is clear that the integrand of (1.3) has unbalanced growth. The main characteristic of (1.3) is the change of ellipticity on the set where the weight function is zero, that is, on the set \(\{x\in \Omega :\, \mu (x)=0\}\). In other words, the energy density of (1.3) exhibits ellipticity in the gradient of order q on the points x where \(\mu (x)\) is positive and of order p on the points x where \(\mu (x)\) vanishes. We also refer to the book of Zhikov-Kozlov-Oleĭnik [25]. Functionals of the form (1.3) have been studied by several authors with respect to regularity of local minimizers, see, for example, the works of Baroni-Colombo-Mingione [1,2,3], Colombo-Mingione [9, 10] and for nonautonomous integrals, the recent work of De Filippis-Mingione [12].
The main objective of our work is to apply an abstract critical point theorem to problem (1.1) in order to get two nontrivial bounded weak solutions with different energy sign. In addition, we give a precise interval to which the solutions belong. Our paper can be seen as an extension of a work of the first two authors recently published in [22]. The differences to [22] are twofold: First, in [22] the operator is the well-known (q, p)-Laplacian and so the function space is a usual Sobolev space. Second, we are able to weaken the assumptions on f in our paper. Indeed, in contrast to [22] and lots of other works in this direction we do not need to assume that f fulfills the usual Ambrosetti–Rabinowitz condition, which says, that there exist \(\tilde{\mu }>q\) and \(M>0\) such that

for a. a. \(x\in \Omega \) and for all \(|s|\ge M\). Instead of (AR) we suppose that the primitive of f is q-superlinear at \(\pm \infty \) (see (H2)(ii)) and we have another behavior near \(\pm \infty \), see (H2)(iii). Both conditions are weaker than (AR) and they also imply that f is \((q-1)\)-superlinear at \(\pm \infty \). Note that we do not need any behavior of f or its primitive near the origin, see Theorem 3.4.
The abstract critical point theorem we used is due to Bonanno-D’Aguì [4, see Theorem 2.1 and Remark 2.2] and was applied in the same paper to the p-Laplace problem
in order to get two nontrivial solutions of (1.4).
Finally we would like to mention related works dealing with multiplicity results for (p, q)-Laplacians or double phase problems via different methods, like truncation techniques, comparison principles, critical point theory, Nehari manifold treatment and so on. We refer to the papers of Bonanno-D’Aguì-Livrea [5] (general nonhomogeneous operators), Bonanno-D’Aguì-Winkert [6] (nondifferentiable functions), Chinnì-Sciammetta-Tornatore [7] (anisotropic (p, q)-equations), Colasuonno-Squassina [8] (double phase eigenvalue problems), Gasiński-Winkert [14, 15] (convection and superlinear problems), Liu-Dai [17] (Nehari manifold treatment), Papageorgiou-Winkert [20] (subdiffusive and equidiffusive (p, q)-equations), Perera-Squassina [21] (Morse theory for double phase problems), see also the references therein.
The paper is organized as follows. In Sect. 2 we recall some facts about Musielak-Orlicz Sobolev spaces and state the abstract critical point theorem mentioned above, see Theorem 2.4. Then, in Sect. 3 we formulate our hypotheses, state and prove our main result, see Theorem 3.4 and we consider some consequences for special cases of (1.1), see Corollaries 3.5 and 3.6, especially when f is nonnegative and independent of x.
2 Preliminaries
In this section we recall some preliminary facts and tools which are needed in the sequel. To this end, let \(\Omega \subseteq \mathbb {R}^N\), \(N\ge 2\) be a bounded domain with Lipschitz boundary \(\partial \Omega \). For \(1\le r\le \infty \) we denote by \(L^{r}(\Omega )\) and \(L^r(\Omega ;\mathbb {R}^N)\) the usual Lebesgue spaces equipped with the norm \(\Vert \cdot \Vert _r\) and for \(1\le r<\infty \), \(W^{1,r}(\Omega )\) and \(W^{1,r}_0(\Omega )\) stand for the Sobolev spaces endowed with the norms \(\Vert \cdot \Vert _{1,r}\) and \(\Vert \cdot \Vert _{1,r,0}=\Vert \nabla \cdot \Vert _r\), respectively.
Let \(1<p<\infty \). From the Sobolev embedding theorem we know that for any \(\ell \in [1,p^*]\) we have the continuous embedding \(W^{1,p}_0(\Omega )\rightarrow L^{\ell }(\Omega )\) with best constant \(c_{\ell }>0\), that is,
It is clear that the embedding in (2.1) is compact if \(\ell <p^*\). Suppose that \(\ell <p^*\). Then, from Hölder’s inequality and (2.1), we obtain
with \(|\Omega |\) being the Lebesgue measure of \(\Omega \) in \(\mathbb {R}^N\).
Let
Then we can find an element \(x_0 \in \Omega \) such that the ball with center \(x_0\) and radius \(R>0\) belongs to \(\Omega \), that is,
We set
and
In the following we use the subsequent assumptions:
-
(H1)
\(1<p<N\), \(p<q<p^*\) and \(0\le \mu (\cdot )\in L^\infty (\Omega )\), where \(p^*\) is the critical Sobolev exponent to p given by \(p^*=\frac{Np}{N-p}\).
Let \(M(\Omega )\) be the space of all measurable functions \(u:\Omega \rightarrow \mathbb {R}\) and let \(\mathcal {H}:\Omega \times [0,\infty )\rightarrow [0,\infty )\) be the nonlinear function defined by
Then, the Musielak-Orlicz space \(L^\mathcal {H}(\Omega )\) is defined by
equipped with the Luxemburg norm
where the modular function \(\rho _{\mathcal {H}}\) is given by
Furthermore, we define the seminormed space
which is endowed with the seminorm
The Musielak-Orlicz Sobolev space \(W^{1,\mathcal {H}}(\Omega )\) is defined by
equipped with the norm
where \(\Vert \nabla u\Vert _\mathcal {H}=\Vert \,|\nabla u|\,\Vert _{\mathcal {H}}\). The completion of \(C^\infty _0(\Omega )\) in \(W^{1,\mathcal {H}}(\Omega )\) is denoted by \(W^{1,\mathcal {H}}_0(\Omega )\). We know that \(L^{\mathcal {H}}(\Omega )\), \(W^{1,\mathcal {H}}(\Omega )\) and \(W^{1,\mathcal {H}}_0(\Omega )\) are reflexive Banach spaces and we can equip the space \(W^{1,\mathcal {H}}_0(\Omega )\) with the equivalent norm
see Proposition 2.18(ii) of Crespo-Blanco-Gasiński-Harjulehto-Winkert [11].
The norm \(\Vert \cdot \Vert _{\mathcal {H}}\) and the modular function \(\rho _\mathcal {H}\) are related as follows, see Liu-Dai [17, Proposition 2.1].
Proposition 2.1
Let (H1) be satisfied, let \(y\in L^{\mathcal {H}}(\Omega )\) and let \(\rho _{\mathcal {H}}\) be defined by (2.7). Then the following hold:
-
(i)
If \(y\ne 0\), then \(\Vert y\Vert _{\mathcal {H}}=\lambda \) if and only if \( \rho _{\mathcal {H}}(\frac{y}{\lambda })=1\);
-
(ii)
\(\Vert y\Vert _{\mathcal {H}}<1\) (resp. \(>1\), \(=1\)) if and only if \( \rho _{\mathcal {H}}(y)<1\) (resp. \(>1\), \(=1\));
-
(iii)
If \(\Vert y\Vert _{\mathcal {H}}<1\), then \(\Vert y\Vert _{\mathcal {H}}^q\le \rho _{\mathcal {H}}(y)\le \Vert y\Vert _{\mathcal {H}}^p\);
-
(iv)
If \(\Vert y\Vert _{\mathcal {H}}>1\), then \(\Vert y\Vert _{\mathcal {H}}^p\le \rho _{\mathcal {H}}(y)\le \Vert y\Vert _{\mathcal {H}}^q\);
-
(v)
\(\Vert y\Vert _{\mathcal {H}}\rightarrow 0\) if and only if \( \rho _{\mathcal {H}}(y)\rightarrow 0\);
-
(vi)
\(\Vert y\Vert _{\mathcal {H}}\rightarrow +\infty \) if and only if \( \rho _{\mathcal {H}}(y)\rightarrow +\infty \).
We have the following embedding results for the spaces \(L^{\mathcal {H}}(\Omega )\) and \(W^{1,\mathcal {H}}_0(\Omega )\), see [11, Proposition 2.16].
Proposition 2.2
Let (H1) be satisfied. Then the following embeddings hold:
-
(i)
\(L^{\mathcal {H}}(\Omega ) \hookrightarrow L^{r}(\Omega )\) and \(W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow W^{1,r}_0(\Omega )\) are continuous for all \(r\in [1,p]\);
-
(ii)
\(W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow L^{r}(\Omega )\) is continuous for all \(r \in [1,p^*]\);
-
(iii)
\(W^{1, \mathcal {H}}_0(\Omega )\hookrightarrow L^{r}(\Omega )\) is compact for all \(r \in [1,p^*)\);
-
(iv)
\(L^{\mathcal {H}}(\Omega ) \hookrightarrow L^q_\mu (\Omega )\) is continuous;
-
(v)
\(L^{q}(\Omega ) \hookrightarrow L^{\mathcal {H}}(\Omega )\) is continuous.
Let \(A:W^{1, \mathcal {H}}_0(\Omega )\rightarrow W^{1, \mathcal {H}}_0(\Omega )^*\) be the nonlinear map defined by
for all \(u,\varphi \in W^{1, \mathcal {H}}_0(\Omega )\), where \(\langle \,\cdot ,\,\cdot \,\rangle \) is the duality pairing between \(W^{1, \mathcal {H}}_0(\Omega )\) and its dual space \(W^{1, \mathcal {H}}_0(\Omega )^*\). The operator \(A:W^{1, \mathcal {H}}_0(\Omega )\rightarrow W^{1, \mathcal {H}}_0(\Omega )^*\) has the following properties, see Liu-Dai [17].
Proposition 2.3
Let hypotheses (H1) be satisfied. Then, the operator A defined in (2.8) is bounded, continuous, strictly monotone and of type \(({{\,\textrm{S}\,}}_+)\), that is,
imply \(u_n\rightarrow u\) in \(W^{1, \mathcal {H}}_0(\Omega )\).
We refer to the books of Harjulehto-Hästö [16], Musielak [18] and the papers of Colasuonno-Squassina [8], Crespo-Blanco-Gasiński-Harjulehto-Winkert [11] and Liu-Dai [17] for more information about Musielak-Orlicz Sobolev spaces and double phase operators.
Let X be a Banach space and \(X^*\) its topological dual space. Given \(\varphi \in C^1(X)\) we say that \(\varphi \) satisfies the Cerami-condition (C-condition for short), if every sequence \(\{x_n\}_{n\in \mathbb {N}}\subseteq X\) such that \(\{\varphi (u_n)\}_{n\ge 1} \subseteq \mathbb {R}\) is bounded and
admits a strongly convergent subsequence.
The following theorem is used in our proofs and can be found in the paper of Bonanno-D’Aguì [4, see Theorem 2.1 and Remark 2.2].
Theorem 2.4
Let X be a real Banach space and let \(\Phi \), \(\Psi :X \rightarrow \mathbb {R}\) be two functionals of class \(C^1\) such that \(\displaystyle \inf _X \Phi (u) = \Phi (0) = \Psi (0) = 0\). Assume that there are \(r \in \mathbb {R}\) and \(\tilde{u} \in X\), with \(0< \Phi (\tilde{u}) < r\), such that
and, for each
the functional \(I_{\lambda } = \Phi - \lambda \Psi \) satisfies the C-condition and it is unbounded from below. Moreover, \(\Phi \) is supposed to be coercive.
Then, for each \(\lambda \in \tilde{\Lambda }\), the functional \(I_{\lambda }\) admits at least two nontrivial critical points \(u_{\lambda ,1}\), \(u_{\lambda ,2}\in X\) such that \(I_\lambda (u_{\lambda ,1})< 0 < I_\lambda (u_{\lambda ,2})\).
3 Main result
In this section we formulate and prove our main results concerning the existence of nontrivial bounded weak solutions to problem (1.1). First, we state the hypotheses on the nonlinearity \(f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}\). We suppose the following conditions:
-
(H2)
\(f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}\) is a Carathéodory function satisfying the following conditions:
-
(i)
There exist \(\ell \in (q,p^*)\) and constants \(\kappa _1, \kappa _2>0\) such that
$$\begin{aligned} |f(x,s)| \le \kappa _1+\kappa _2|s|^{\ell -1} \end{aligned}$$for a. a. \(x\in \Omega \) and for all \(s\in \mathbb {R}\);
-
(ii)
If \(F(x,s)=\int _0^sf(x,t)\,\textrm{d}t\), then
$$\begin{aligned} \lim _{s\rightarrow \pm \infty } \frac{F(x,s)}{|s|^q}=+\infty \end{aligned}$$uniformly for a. a. \(x\in \Omega \);
-
(iii)
There exists
$$\begin{aligned} \zeta \in \left((\ell -p)\frac{N}{p},p^*\right) \end{aligned}$$such that
$$\begin{aligned} 0<\zeta _0 \le \liminf _{s\rightarrow \pm \infty }\, \frac{f(x,s)s-qF(x,s)}{|s|^ \zeta } \end{aligned}$$uniformly for a. a. \(x\in \Omega \).
-
(i)
Remark 3.1
Note that (H2)(ii) and (H2)(iii) imply that
uniformly for a. a. \(x\in \Omega \).
Remark 3.2
Due to Remark 3.1 we know that \(f(x,\cdot )\) is \((q-1)\)-superlinear at \(\pm \infty \). Our conditions are weaker than the Ambrosetti–Rabinowitz condition (AR-condition for short). Indeed, instead of the AR-condition, we suppose hypotheses (H2)(ii) and (H2)(iii) which are less restrictive. Consider the function
where \(1<\beta _1<p\) and \(1<\beta _2<q\), then we see that f satisfies (H2) but fails to satisfy the AR-condition.
The energy functional \(I_\lambda :W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}\) of (1.1) is given by
for all \(u\in W^{1, \mathcal {H}}_0(\Omega )\). It is clear that \(I_\lambda \in C^1\) and the critical points of \(I_\lambda \) are the weak solutions of (1.1). Next, we introduce the functionals \(\Phi ,\,\Psi :W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}\) defined by
for all \(u\in W^{1, \mathcal {H}}_0(\Omega )\). We have that \(I_\lambda = \Phi (u)-\lambda \Psi (u)\) and all these functionals are of class \(C^1\), where their derivatives are given by
for all \(u,v\in W^{1, \mathcal {H}}_0(\Omega )\).
First, we obtain the following proposition.
Proposition 3.3
Let hypotheses (H1) and (H2) be satisfied. Then the functional \(I_{\lambda }:W^{1, \mathcal {H}}_0(\Omega )\rightarrow \mathbb {R}\) satisfies the C-condition.
Proof
Let \(\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1, \mathcal {H}}_0(\Omega )\) be a sequence such that
From (3.3) we get
for all \(h\in W^{1, \mathcal {H}}_0(\Omega )\) with \(\varepsilon _n\rightarrow 0^+\). Choosing \(h=u_n\in W^{1, \mathcal {H}}_0(\Omega )\) in (3.4) gives
for all \(n\in \mathbb {N}\). From (3.2) we have
Adding (3.5) and (3.6) and recalling that \(p<q\), we derive
for some \(c_2>0\) and for all \(n\in \mathbb {N}\).
Hypotheses (H2)(i) and (H2)(iii) imply that we can find \(c_3 \in (0,\zeta _0)\) and \(c_{4}>0\) such that
for a. a. \(x\in \Omega \) and for all \(s\in \mathbb {R}\). Using (3.8) in (3.7) leads to

Hence

Note that \(p < N\). From hypothesis (H2)(iii) it is clear that we may assume that \(\zeta<\ell <p^*\). Then we can find \(t\in (0,1)\) such that
Using the interpolation inequality (see Papageorgiou-Winkert [19, p. 116]), we have

This combined with (3.9) and Proposition 2.2(ii) results in

with some \(c_{6}>0\). Testing (3.4) with \(h=u_n\in W^{1, \mathcal {H}}_0(\Omega )\) we obtain
From Proposition 2.1(iii), (iv) and (H2)(i) as well as (3.11) we arrive at
for some \(c_7>0\) and for all \(n\in \mathbb {N}\).
From (3.10) and (H2)(iii) it follows
Then, from (3.12) and (3.13) we obtain that
Hence there exists a subsequence, not relabeled, such that
If we use \(h=u_n-u\in W^{1, \mathcal {H}}_0(\Omega )\) in (3.4), pass to the limit as \(n\rightarrow \infty \) and use (3.14), we obtain
The \(({{\,\textrm{S}\,}}_+)\)-property of A (see Proposition 2.3) implies that \(u_n\rightarrow u\) in \(W^{1, \mathcal {H}}_0(\Omega )\). This shows that \(I_\lambda \) satisfies the C-condition. \(\square \)
Now we are ready to formulate our main existence result.
Theorem 3.4
Let hypotheses (H1), (H2) be satisfied and let \(\xi , \eta >0\) be two constants with \(\xi >\eta \) such that
where \(\kappa _1, \kappa _2\), \(\ell \), R and K are given in (H2)(i), (2.3) and (2.6), respectively. Then, for each
problem (1.1) has at least two nontrivial bounded weak solutions \(u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )\) such that \(I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )\).
Proof
Let \(\Phi \) and \(\Psi \) be as given in (3.1). First we see that \(\Psi \) and \(\Phi \) fulfill all the required regularity properties in Theorem 2.4. Indeed, \(\Phi \) is coercive due to Proposition 2.1(iv) and the functional \(I_\lambda \) is unbounded from below because of (H2)(ii). Also we see that
It is clear that the interval \(\Lambda \) is nonempty due to assumption (3.16). Hence, we can fix \(\lambda \in \Lambda \) and we set
where \(c_{p^*}\) is the best constant of the embedding \(W^{1,p}_0(\Omega )\hookrightarrow L^{p^*}(\Omega )\). Next, we define the function
where \(x_0\in \Omega \) is such that \(B(x_0,R)\subseteq \Omega \), see (2.4). It is easy to see that \(\tilde{u}\in W^{1, \mathcal {H}}_0(\Omega )\).
Step 1 \(0<\Phi (\tilde{u})<r\)
Using the representations of \(\omega _R\) in (2.5) and R in (2.6) we obtain
From the definition of r and (3.19) we see that we have to show that
Assume (3.20) is not true, so let us suppose that
From the growth condition of f in (H2)(i) we derive that
Using (3.21) and (3.22) along with \(\xi >\eta \) we have that
This is a contradiction to (3.16). Therefore, (3.20) holds, so we have shown that \(0<\Phi (\tilde{u})<r\).
Step 2 We need to verify the validity of condition (2.9) for r and \(\tilde{u}\) defined in (3.17) and (3.18), respectively.
The representation of r in (3.17) gives
From the growth condition in (H2)(i), (2.2) and (3.23) we derive that
On the other hand, using (3.15), we get that
Combining (3.24), (3.16), (3.19) and (3.25) gives
This proves Step 2.
From Steps 1 and 2 and Proposition 3.3 we see that all the conditions in Theorem 2.4 are satisfied and so we conclude that problem (1.1) has at least two nontrivial weak solutions \(u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )\) such that \(I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )\). From Gasiński-Winkert [13, Theorem 3.1] we know that \(u_\lambda , v_\lambda \in L^{\infty }(\Omega )\). \(\square \)
Let us now consider the special case when f is nonnegative and independent of x. We suppose the following conditions:
-
(H3)
\(f:\mathbb {R}\rightarrow \mathbb {R}\) is a continuous function with \(f(s)\ge 0\) for all \(s\in \mathbb {R}\) satisfying the following conditions:
-
(i)
There exist \(\ell \in (q,p^*)\) and constants \(\kappa _1, \kappa _2>0\) such that
$$\begin{aligned} f(s) \le \kappa _1+\kappa _2|s|^{\ell -1} \end{aligned}$$for all \(s\in \mathbb {R}\);
-
(ii)
If \(F(s)=\int _0^sf(t)\,\textrm{d}t\), then
$$\begin{aligned} \lim _{s\rightarrow \infty } \frac{F(s)}{s^q}=+\infty ; \end{aligned}$$ -
(iii)
There exists
$$\begin{aligned} \zeta \in \left((\ell -p)\frac{N}{p},p^*\right) \end{aligned}$$such that
$$\begin{aligned} 0<\zeta _0 \le \liminf _{s\rightarrow \infty }\, \frac{f(s)s-qF(s)}{s^ \zeta }. \end{aligned}$$
-
(i)
The next result is a consequence of Theorem 3.4.
Corollary 3.5
Let hypotheses (H1), (H3) be satisfied and let \(\xi , \eta >0\) be two constants with \(\xi >\eta \) such that
where \(\kappa _1, \kappa _2\), \(\ell \), R and K are given in (H3)(i), (2.3) and (2.6), respectively. Then, for each
problem (1.1) has at least two nontrivial bounded weak solutions \(u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )\) such that \(I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )\) and \(u_\lambda , v_\lambda \ge 0\).
Proof
We are going to apply Theorem 3.4. First, we point out that, since f is nonnegative, we have \(F(t)\ge 0\) for all \(t\in \mathbb {R}\). So (3.15) is satisfied. In addition, we know that
see (2.5). From (3.27) and (3.26) we see that (3.16) is fulfilled as well. Then, applying Theorem 3.4, for each
problem (1.1) has at least two nontrivial bounded weak solutions \(u_\lambda , v_\lambda \in W^{1, \mathcal {H}}_0(\Omega )\) such that \(I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )\). Testing the corresponding weak formulation with \(-u_\lambda ^-\in W^{1, \mathcal {H}}_0(\Omega )\) and \(-v_\lambda ^-\in W^{1, \mathcal {H}}_0(\Omega )\), respectively, shows that both are nonnegative, so \(u_\lambda , v_\lambda \ge 0\). \(\square \)
We get another result for nonnegative functions \(f:\mathbb {R}\rightarrow \mathbb {R}\).
Corollary 3.6
Let hypotheses (H1), (H3) be satisfied and suppose that
Then, for each
problem (1.1) has at least two nonnegative, nontrivial bounded weak solutions \(u_\lambda , v_\lambda \) \(\in W^{1, \mathcal {H}}_0(\Omega )\) such that \(I_\lambda (u_\lambda )<0<I_\lambda (v_\lambda )\).
Proof
Let \(\lambda \in \Lambda _2\) be fixed. Then we can find \(\xi >0\) such that
On the other hand condition (3.28) implies that
Hence, we can find a number \(\eta \in (0,\xi )\) such that
Then the assertion of the theorem follows from Corollary 3.5. \(\square \)
Finally, we want to give a concrete example for a function which fits in our setting.
Example 3.7
Let \(p=3\), \(N=4\) and \(q=4\), then \(1<p<N\) and \(p<q<p^*=12\). Let \(\Omega =B\left( 0,3^{\frac{1}{8}}\right) \subset \mathbb {R}^4\). Then \(\left| B\left( 0,3^{\frac{1}{8}}\right) \right| =\dfrac{3^{\frac{1}{2}}}{2} \pi ^2\). We consider the function
Then we have
For each
the problem
admits at least two nonnegative, nontrivial bounded weak solutions.
Indeed, if we put \(\kappa _1=15\), \(\kappa _2=20\), \(\ell =5\) and \(\xi =\left( \frac{15}{4}\right) ^{\frac{1}{4}} \) we observe that (H3) and (3.28) are satisfied. Moreover, due to Talenti [23], one has that
This gives
Then, the assertion follows from Corollary 3.6.
Availability of data and materials
Not applicable.
References
Baroni, P., Colombo, M., Mingione, G.: Harnack inequalities for double phase functionals. Nonlinear Anal. 121, 206–222 (2015)
Baroni, P., Colombo, M., Mingione, G.: Non-autonomous functionals, borderline cases and related function classes. St. Petersburg Math. J. 27, 347–379 (2016)
Baroni, P., Colombo, M., Mingione, G.: Regularity for general functionals with double phase. Calc. Var. Part. Diff. Eq. 57, 48 (2018)
Bonanno, G., D’Aguì, G.: Two non-zero solutions for elliptic Dirichlet problems. Z. Anal. Anwend. 35(4), 449–464 (2016)
Bonanno, G., D’Aguì, G., Livrea, R.: Triple solutions for nonlinear elliptic problems driven by a non-homogeneous operator. Nonlinear Anal. 197, 17 (2020)
Bonanno, G., D’Aguì, G., Winkert, P.: A two critical points theorem for non-differentiable functions and applications to highly discontinuous PDE’s. Pure Appl. Funct. Anal. 4(4), 709–725 (2019)
Chinnì, A., Sciammetta, A., Tornatore, E.: Existence of non-zero solutions for a Dirichlet problem driven by the \((p(x), q(x))\)-Laplacian. Appl. Anal. 101(15), 5323–5333 (2022)
Colasuonno, F., Squassina, M.: Eigenvalues for double phase variational integrals. Ann. Mat. Pura Appl. 195(6), 1917–1959 (2016)
Colombo, M., Mingione, G.: Bounded minimisers of double phase variational integrals. Arch. Ration. Mech. Anal. 218(1), 219–273 (2015)
Colombo, M., Mingione, G.: Regularity for double phase variational problems. Arch. Ration. Mech. Anal. 215(2), 443–496 (2015)
Crespo-Blanco, Á., Gasiński, L., Harjulehto, P., Winkert, P.: A new class of double phase variable exponent problems: existence and uniqueness. J. Diff. Eq. 323, 182–228 (2022)
De Filippis, C., Mingione, G.: Lipschitz bounds and nonautonomous integrals. Arch. Ration. Mech. Anal. 242, 973–1057 (2021)
Gasiński, L., Winkert, P.: Constant sign solutions for double phase problems with superlinear nonlinearity. Nonlinear Anal. 195, 9 (2020)
Gasiński, L., Winkert, P.: Existence and uniqueness results for double phase problems with convection term. J. Diff. Eq. 268(8), 4183–4193 (2020)
Gasiński, L., Winkert, P.: Sign changing solution for a double phase problem with nonlinear boundary condition via the Nehari manifold. J. Diff. Eq. 274, 1037–1066 (2021)
Harjulehto, P., Hästö, P.: Orlicz Spaces and Generalized Orlicz Spaces. Springer, Cham (2019)
Liu, W., Dai, G.: Existence and multiplicity results for double phase problem. J. Diff. Eq. 265(9), 4311–4334 (2018)
Musielak, J.: Orlicz Spaces and Modular Spaces. Springer-Verlag, Berlin (1983)
Papageorgiou, N.S., Winkert, P.: Applied Nonlinear Functional Analysis. De Gruyter, Berlin (2018)
Papageorgiou, N.S., Winkert, P.: On a parametric nonlinear Dirichlet problem with subdiffusive and equidiffusive reaction. Adv. Nonlinear Stud. 14(3), 565–591 (2014)
Perera, K., Squassina, M.: Existence results for double-phase problems via Morse theory. Commun. Contemp. Math. 20(2), 14 (2018)
Sciammetta, A., Tornatore, E.: Two positive solutions for a Dirichlet problem with the \((p, q)\)-Laplacian. Math. Nachr. 293(5), 1004–1013 (2020)
Talenti, G.: Best constant in Sobolev inequality. Ann. Mat. Pura Appl. 110, 353–372 (1976)
Zhikov, V.V.: Averaging of functionals of the calculus of variations and elasticity theory. Izv. Akad. Nauk SSSR Ser. Mat. 50(4), 675–710 (1986)
Zhikov, V.V., Kozlov, S.M., Oleĭnik, O.A.: Homogenization of Differential Operators and Integral Functionals. Springer-Verlag, Berlin (1994)
Acknowledgements
The first two authors are members of the Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). The second author was financially supported by FFR2021. The third author was financially supported by GNAMPA and thanks the University of Palermo for the kind hospitality during a research stay in May/June 2022.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
Not applicable.
Corresponding author
Ethics declarations
Conflict of interest
The author(s) declare that they have no competing interest.
Ethical approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sciammetta, A., Tornatore, E. & Winkert, P. Bounded weak solutions to superlinear Dirichlet double phase problems. Anal.Math.Phys. 13, 23 (2023). https://doi.org/10.1007/s13324-023-00783-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-023-00783-0
Keywords
- Critical point theory
- Double phase operator
- Location of the solutions
- Parametric problem
- Superlinear nonlinearity