1 Introduction

In the standard Hele-Shaw free boundary problem for fluid with zero surface tension, the pressure, or velocity potential, satisfies Laplace’s equation in the fluid region, is constant on its boundary and the normal velocity of the interface is given by the gradient of the velocity potential in the normal direction. This simply formulated, but nonlinear, two-dimensional free boundary problem has a remarkable variety of applications occurring over a wide range of lengthscales including oil recovery, flow in porous media and injection moulding. Because of this, and with its rich mathematical structure becomingly increasingly evident, Laplacian growth, as it is also known, has attracted much attention in the literature e.g. [9]. As a consequence, powerful mathematical techniques, naturally formulated in terms of complex variables, have been developed leading to the derivation of a variety of exact solutions for Laplacian growth. These formulations include the Polubarinova–Galin equation [8, 20], Richardson’s demonstration of an infinity of conservation laws for the moments of the fluid [21], and a formulation in terms of the Schwarz function for the free boundary e.g. [4].

The mathematical problem in which Laplace’s equation is replaced by Poisson’s equation has received less attention, despite having important applications. When the right hand side of Poisson’s equation is constant the model is equivalent to the evaporation of thin liquid films [2]. Moment-based methods were used by [2] to derive exact solutions, some of which displayed typical Laplacian growth type cusp formation on the boundary.

When the upper plate of a Hele-Shaw cell is raised or lowered, the thickness of the thin gap between the plates is time-dependent and this leads to the pressure inside the blob satisfying Poisson’s equation with a time-dependent right-hand side. This time-dependence can be scaled out, so that the right-hand side becomes constant. Shelley et al. [22] studied this variable-gap Hele-Shaw problem and showed when the upper plate is raised instability arises, this being analogous to the evaporation case of [2]. Shelley et al. [22] examined the existence and regularity of solutions and found exact and numerical solutions with and without surface tension, including examples illustrating bubble fission and cusp formation. The multiply connected problem has been tackled by Crowdy and Kang [3]. They used associated quadrature domain identities to find explicit solutions which demonstrate that the usual well-posed ‘squeeze’ case for singly connected domains can break down in finite time in the multiply connected case. Another physical manifestation of Poisson growth is the debonding of adhesively joined surfaces e.g. [12]. The thin gap between the surfaces acts like a Hele-Shaw cell and air fingers penetrate the adhesive as the surfaces are separated.

In addition to Laplacian growth, several authors, e.g. [10, 13, 14], have considered other elliptic PDEs governing the interior of the fluid, as occurs, for example, in flow of fluid in inhomogeneous porous media. Few explicit solutions are known for these more general elliptic operators, one difficulty being their lack of conformal invariance.

The Poisson growth problem is formulated in Sect. 2 and its associated Schwarz function equation derived. This equation is then used to derive the moment evolution equations, a Polubarinova–Galin type equation and an associated Baiocchi-type transformation. Examples of explicit solutions are given in Sect. 3. The case when the right hand side of Poisson’s equation is linear in one of the space variables is considered in Sect. 4. The Schwarz function equation is derived and used to find an exact solution consisting of a propagating circular blob with time-dependent radius.

2 Schwarz function formulation of the free boundary problem

2.1 Derivation of Schwarz function equation

Consider the free boundary problem for a domain \(\Omega (t)\) in the \((x,y)\)-plane

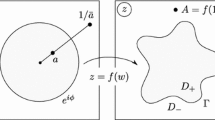
$$\begin{aligned} \nabla ^2 \phi&= -\beta +Q(x,y),\quad \mathrm{in}\quad \Omega (t),\nonumber \\ \phi&= 0\quad \mathrm{and}\quad v_n={\partial \phi /{\partial n}}\quad \mathrm{on}\quad \partial \Omega (t). \end{aligned}$$
(1)

Here \(\beta \) is a constant, \(Q\) represents any hydrodynamic singularities that are present (e.g. point sources or sinks), \(\phi \) is a real velocity potential such that \(\mathbf{u}=\nabla \phi \) is the velocity field, and \(v_n\) is the normal velocity of the boundary \(\partial \Omega (t)\). The task is to find the evolution of the free boundary \(\partial \Omega (t)\), which may be finite or infinite and singly or multiply-connected, given some initial boundary shape \(\partial \Omega (0)\). The problem is illustrated in Fig. 1.

Fig. 1
figure 1

The Poisson growth problem with point source \(Q\)

Full size image

Equation (1) implies that \(\nabla .\mathbf{u}=-\beta \); that is, depending on the sign of \(\beta \) there is a source (\(\beta <0\)) or sink (\(\beta >0\)) distributed uniformly over the extent of the fluid blob. The free boundary problem (1) is a generalisation of the standard Laplacian growth or Hele-Shaw problem (\(\beta =0\)) and is referred to here as the Poisson growth problem.

Introducing \(z=x+i y\) and defining \(\phi =\psi -\beta z{\bar{z}}/4\), it follows that \(\nabla ^2\psi =0\) and so \(\psi \) can be considered the real part of an analytic function \(w\). Let \(g(z,t)\) be the Schwarz function of the free boundary \(\partial \Omega (t)\) i.e. \(g(z,t)\) is an analytic function in the neighbourhood of \(\partial \Omega \) such that \(g(z,t)={\bar{z}}\) on \(\partial \Omega \) [5]. Since \(\phi =\psi -\beta z{\bar{z}}/4\) it follows that on \(\partial \Omega (t)\)

$$\begin{aligned} {\bar{v}}=\partial _z w-\beta {\bar{z}}/2=\partial _z w-\beta g/2, \end{aligned}$$
(2)

where \(v\) is the complex velocity field. It is known e.g. [1] that the boundary conditions on \(\partial \Omega (t)\) imply \(2{\bar{v}}={\partial _t g}\). Combining this with (2) gives

$$\begin{aligned} 2\partial _z w={\partial _t g}+\beta g=e^{-\beta t}{\partial _t}\left( ge^{\beta t} \right) \!, \end{aligned}$$
(3)

Equation (3) is referred to as the Schwarz function equation for Poisson growth. Lacey [11] discusses the behaviour of Schwarz function singularities in the case of Hele-Shaw flow with a time-dependent gap for the case when there is no hydrodynamic forcing. In particular he derives an explicit solution for the behaviour of an elliptical blob being squeezed between the plates of a Hele-Shaw cell.

Strictly, the derivation of (3) applies on the free boundary only, but by analytic continuation it applies everywhere in the fluid blob \(\Omega (t)\) where the terms of (3) are defined. If \(\beta =0\) then (3) reduces to the well-known Schwarz function relation governing Laplacian growth e.g. [4]. Since the nature of the singularities of \(g\) and \(w\) in (3) are independent of \(\beta \), an immediate implication is that solutions of the Poisson growth free boundary problem share the same geometries as the standard Hele-Shaw problem although they will in general have different evolution.

As noted in [7] there is a connection between the Poisson growth problem and the behaviour of a blob of fluid in a rotating Hele-Shaw cell of constant width. This is immediately evident by comparing the Schwarz function equations in each case. In the latter case the flow is subject to a centrifugal potential and has Schwarz function equation [15]

$$\begin{aligned} 2\partial _z w={\partial _t g}+\omega \partial _z(zg)\!, \end{aligned}$$
(4)

where \(\omega \) is the rotation parameter. Rescaling \(z\) by the factor \(\exp (\beta t)\) in (3) and choosing \(\omega =\beta \) gives (4).

2.2 Moments

Suppose \(Q(x,y)=Q\delta (x,y)\) where \(Q\) is constant, so that there is a point source of constant strength \(Q\) at the origin. Define the \(k\)th moment as

$$\begin{aligned} M_k=\int \!\!\!\int _{\Omega (t)} z^k dA,\quad k=0,1,2\cdots . \end{aligned}$$
(5)

Using the complex form of Green’s theorem and (3) gives

$$\begin{aligned} {\partial _t M}_k&= {1\over {2i}}\oint _{\partial \Omega (t)} z^k{\partial _t g}\,dz\nonumber \\&= -{\beta \over {2i}}\oint _{\partial \Omega (t)} z^k{ g}\,dz+{1\over {i}}\oint _{\partial \Omega (t)}z^k {\partial _z w}\,dz \nonumber \\&= -\beta M_k+Q\delta _{k0}. \end{aligned}$$
(6)

[2, 22] obtained the same evolution equations for the moments in the absence of point sources by direct integration of (1). More generally [7], write down an expression for the evolution of the integral of a harmonic function \(u(z)\) integrated over the fluid domain in a variable-gap Hele-Shaw cell.

2.3 Polubarinova-Galian type equation

Denoting the moving boundary \(z(s,t)\), where \(s\) is an arc-length parameter, the normal velocity of the boundary is

$$\begin{aligned} v_n=\mathrm{Im}({\bar{z}}_tz_s )=\partial _n\phi =\partial _n (\psi -\beta z{\bar{z}}/4). \end{aligned}$$
(7)

The complexified normal vector on \(\partial \Omega \) is \(-iz_s\) and \(\nabla =2\partial _{\bar{z}}\) in conjugate coordinates. Hence \(\partial _n z{\bar{z}}=2\mathrm{Im}({\bar{z}}z_s)\), and (7) becomes

$$\begin{aligned} \mathrm{Im}\left[ ({\bar{z}}_t+(\beta /2){\bar{z}})z_s \right] =\partial _n\psi =\partial _s\psi ^*, \end{aligned}$$
(8)

where \(\psi ^*\) is the harmonic conjugate of \(\psi \). If there is a point source of strength \(Q\) inside the fluid blob at \(z=0\) then on \(\partial \Omega \), \(\partial _s\psi ^*>0\) and \(Q\theta /2\pi =\psi ^*=s\) may be used to parameterise the boundary giving

$$\begin{aligned} \mathrm{Im}\left[ ({\bar{z}}_t+(\beta /2){\bar{z}})z_\theta \right] =Q/2\pi . \end{aligned}$$
(9)

Equation (9) is of the type derived by [8, 20], and reduces to their equations when \(\beta =0\).

2.4 A related Baiocchi-type transform

Define the real function \(\Psi \), the Schwarz potential, by

$$\begin{aligned} \Psi ={z{\bar{z}}\over 4}-{1\over 4}\int ^zg dz-{1\over 4}\overline{\int ^zg dz}. \end{aligned}$$
(10)

Note that \(\nabla ^2\Psi =1\) in \(\Omega \) and \(\Psi _z=\Psi _{\bar{z}}=0\) on \(\partial \Omega \) which, in turn, implies \(\Psi =\partial \Psi /\partial n=0\) on \(\partial \Omega \). Applying the operator \(e^{-\beta t}({\partial _t}e^{\beta t}.)\) to (10) and using (3) gives

$$\begin{aligned} {\partial _t \Psi }+\beta \Psi&= {\beta \over 4} z{\bar{z}}-\mathfrak {R}w, \nonumber \\&= {\beta \over 4} z{\bar{z}}-\psi , \nonumber \\&= -\phi . \end{aligned}$$
(11)

When \(\beta =0\) this reduces to the standard Baiocchi transform for Hele-Shaw free boundary flow e.g. [4].

3 Examples

3.1 Circular blob

The boundary of a circle of radius \(a(t)\) and centre \(z=0\) has Schwarz function \(g=a^2/z\). If the fluid region, which lies inside the circle, has no hydrodynamic singularities (i.e. \(Q=0\)) then \(w\) is analytic everywhere inside \(\Omega (t)\). Comparing the behaviour of the singular terms in (3) gives

$$\begin{aligned} {d\over {dt}}a^2+\beta a^2=0, \end{aligned}$$
(12)

or, \(A(t)=A(0) \exp (-\beta t)\) where \(A(t)=\pi a^2\) is the area of the circular blob. That is, the blob remains circular and centred at the origin with its area either increasing or decreasing exponentially according to the sign of \(\beta \). Alternatively this result follows directly from (6) with the realization \(M_0\equiv A\) or from (9) using \(z=a(t)e^{i\theta }\).

3.2 Stability of a circular blob and bubble

Let \(z=a(\zeta +\epsilon \zeta ^n)\), where \(a=a(t)\) and \(\epsilon =\epsilon (t)\) are real time-varying positive parameters with \(0<\epsilon \ll 1\), be a map from the interior of the unit \(\zeta \)-disk to the interior of a perturbed circular blob of radius \(a\). In polar coordinates the boundary of the blob is given by \(r=a(1+\epsilon \cos (n-1)\theta )+\mathcal {O}(\epsilon ^2)\), \(0\le \theta < 2\pi \), and so \(\epsilon \) measures the amplitude of a sinusoidal perturbation to the circular boundary. The interest here is on the growth or decay of \(\epsilon (t)\) with time. Since \(\bar{\zeta }=\zeta ^{-1}\) on the boundary of the blob, the Schwarz function of the blob boundary has behaviour as \(z\rightarrow 0\)

$$\begin{aligned} g(z,t)&= {\epsilon a^{n+1}\over {z^n}}+{{a^2(1+\epsilon ^2 n)}\over z}+{\mathcal O}(1), \nonumber \\&\approx {\epsilon a^{n+1}\over {z^n}}+{{a^2}\over z}+{\mathcal O}(1), \end{aligned}$$
(13)

where the approximation \(\epsilon ^2\ll n^{-1}\) has been used. For a point source of strength \(Q\) at \(z=0\), the Schwarz function equation (3) becomes \({\partial _t g}+\beta g=Q/\pi z\) as \(z\rightarrow 0\). Considering coefficients of the singular terms \(z^{-1}\) and \(z^{-n}\) in (3) using (13) gives two coupled ODEs for \(\epsilon (t)\) and \(a(t)\)

$$\begin{aligned} \begin{aligned} {d\over {dt}}(a^2)+\beta a^2&={Q\over \pi }, \\ {d\over {dt}}(\epsilon a^{n+1})+\beta \epsilon a^{n+1}&=0. \end{aligned} \end{aligned}$$
(14)

Combining (14) into a single equation for \(\epsilon \) gives

$$\begin{aligned} {d\epsilon \over {dt}}+{\epsilon \over 2}(n+1)\left[ {Q\over {\pi a^2}}-{(n-1)\over {(n+1)}}\beta \right] =0. \end{aligned}$$
(15)

Thus the flow is stable when \(Q>\beta \pi a^2\). This criteria is equivalent to saying that stability follows when the blob expands in area since \(Q\) is the area flux due to a point source while \(\beta \pi a^2\) is the rate of area loss due to the Poisson term. When \(Q=0\) the blob is unstable if \(\beta >0\) as also found by [22].

A similar analysis for a perturbed circular bubble in an infinite fluid (as opposed to a finite blob of fluid) using the map \(z=a(\zeta ^{-1}+\epsilon \zeta ^n)\) from the interior of the unit \(\zeta \)-disk to the exterior of the perturbed bubble and considering singular behaviour as \(z\rightarrow \infty \) shows that a bubble is stable if \(Q<\beta \pi a^2\).

3.3 Limaçon

Consider the time-dependent map from the interior of the unit \(\zeta \)-circle to the limaçon-shaped fluid blob given by

$$\begin{aligned} z=a\zeta +b\zeta ^2, \end{aligned}$$
(16)

where \(a(t)\) and \(b(t)\) are real, time-dependent parameters to be found. A point source of strength \(Q\) is located at the origin and hence \(\partial _z w\rightarrow Q/2\pi z+{\mathcal O}(1)\) as \(z\rightarrow 0\). From (16) as \(z\rightarrow 0\) [see also (13)]

$$\begin{aligned} g= {a^2 b\over {z^2}}+{{a^2+2b^2}\over z} +{\mathcal O} (1). \end{aligned}$$
(17)

Substituting (17) into (3) and comparing the singular behaviour of terms \({\mathcal O}(z^{-1})\) and \({\mathcal O}(z^{-2})\) gives the following pair of coupled ODEs for \(a(t)\) and \(b(t)\)

$$\begin{aligned} \begin{aligned} {d\over {dt}}(a^2b)+\beta a^2 b&=0, \\ {d\over {dt}}(a^2+2b^2)+\beta (a^2+2b^2)&={Q\over \pi }. \end{aligned} \end{aligned}$$
(18)

Note that (18) implies the existence of a steady state with \(b=0\) and \(a^2=Q/\pi \beta \) provided \(\mathrm{sgn}(Q\beta )>0\). This corresponds to a circular blob of radius \(\sqrt{Q/\pi \beta }\) in which the point source \(Q\) balances that due to a uniform sink \(\beta \pi a^2\). Figure 2 shows the evolution of an initial limaçon with \(\beta =1\) (i.e. ‘evaporation’) with and without the presence of a point source at the origin. In both cases the mass flux owing to the distributed sink causes the limaçon to shrink. When \(Q>0\) the shrinkage is halted as \(t\rightarrow \infty \) when the sink balances the mass source \(Q\) and the blob approaches a circle. When \(Q=0\) (Laplacian growth) the problem is ill-posed and the limaçon forms a cusp singularity (i.e. becoming a cardioid) in finite time.

Fig. 2
figure 2

Evolution of a limaçon-shaped fluid blob with \(a(0)=1\), \(b(0)=.31\) for \(\beta =1\). On the left the initial limaçon shrinks toward a circular blob shape as \(t\rightarrow \infty \). This is the case when there is a point source of strength \(Q/\pi =.195\) at the origin of the circle. On the right is the case when there is no point source present (\(Q=0\)) and the blob begins to shrink forming a cusp singularity in finite time \(t\approx .265\)

Full size image

3.4 A finger solution

Let

$$\begin{aligned} z=d(t)-\log \zeta +2(1-\lambda (t)) \log \left( {{1+a(t)\zeta }\over 2}\right) \!, \end{aligned}$$
(19)

where \(a\), \(d\) and \(\lambda \) are real time-dependent parameters, be a map from the interior of the unit \(\zeta \) disk to a finger of length \(d\) occupying the fraction \(\lambda \) of a channel of width \(2\pi \). For the map to be well-defined it is required that \(|a(t)|<1\). The fluid speed as \(\mathrm{Re}(z)\rightarrow \infty \) is unity.

The Schwarz function of the finger boundary is

$$\begin{aligned} g=d(t)+(2\lambda -1)\log \zeta +2(1-\lambda ) \log \left( {{\zeta +a}\over 2}\right) \!, \end{aligned}$$
(20)

which, as \(z\rightarrow \infty \), has behaviour

$$\begin{aligned} g\rightarrow (1-2\lambda ) z+2\lambda d -4\lambda (1-\lambda ) \log 2+2(1-\lambda )\log a+{\mathcal O}(z^{-1})\!. \end{aligned}$$
(21)

The Schwarz function (20) has a logarithmic singularity at \(\zeta =-a\) and because there are no point sources or sinks in the fluid, there are no singularities of the type \((z-z(-a))^{-1}\) in \(\partial _z w\), and hence (3) implies \(z(-a)=const\) or

$$\begin{aligned} d-\log |a| +2(1-\lambda ) \log \left( {{1-a^2}\over 2}\right) =const. \end{aligned}$$
(22)

As \(z\rightarrow \infty \), \(\partial _z w=1\) and (21) combined with (3) yields, considering terms of \({\mathcal O}(z)\),

$$\begin{aligned} {d \lambda \over {dt}}+\beta \lambda =\beta /2\!, \end{aligned}$$
(23)

and considering \({\mathcal O}(1)\) terms

$$\begin{aligned} \left( {d\over {dt}}+\beta \right) \left[ 2\lambda d-4\lambda (1-\lambda )\log 2+2(1-\lambda )\log |a|\right] =2. \end{aligned}$$
(24)

An immediate feature implied by (23) is that when \(\beta >0\) a steady state is reached with \(\lambda =1/2\). That is, the Poisson growth term selects the finger width to be precisely half the width of the channel. This is consistent with observations which show that \(\lambda =1/2\) is the preferred finger width in the Laplacian growth, or Hele-Shaw, problem where it is known as a Saffman–Taylor finger. Much theoretical effort has been made in seeking to explain selection of the half-width finger in Laplacian growth. This effort has either focussed on surface tension in providing the selection mechanism e.g. [17, 23], or, more recently, through the nonlinear stability (without surface tension) of the time-evolving fingers [16]. The result here is consistent with that of [16] in that the Poisson term provides a perturbation to the evolving finger, permitting the half-width finger to be selected. Here, for large times, (24) implies the steady finger has length \(d=2/\beta -\log (a/2)\) where \(a\rightarrow 1\) provided \(\beta \ll 2\). A plot of an evolving finger given by (19) with \(\beta =0.2\) is shown in Fig. 3, where the time-dependent parameters have been found by solving ODEs (22), (23) and (24) numerically.

Fig. 3
figure 3

Evolution of a Poisson growth Saffman–Taylor finger, with \(\beta =0.2\), in a channel of width \(2\pi \). The finger propagates to the right with the interface shown at times 5, 10, 20 and 40, and the initial values of the parameters are \(d(0)=0\), \(\lambda (0)=0.45\) and \(a(0)=0.01\)

Full size image

If \(\beta <0\) the finger solution breaks down in finite time as it either becomes an infinitely thin finger when \(\lambda (0)<1/2\), or occupies the full width of the channel if \(\lambda (0)>1/2\).

3.5 Application to the geometry of valleys

The case when \(\beta >0\) is of possible relevance to the geometry of valleys cut by groundwater seepage [18]. The flow of groundwater in sandy soil is governed by

$$\begin{aligned} \nabla ^2 h^2=-{2P\over K}, \end{aligned}$$
(25)

where \(h(x,y)\) be the elevation of the water table above some impermeable layer, \(K>0\) is the constant sand conductivity and \(P>0\) is the rate of precipitation (assumed constant over a timescale of many tens of years). Assuming the valley geometry is related to the local water table depth [18], its shape is governed by a Poisson growth problem (1) with \(Q=0\) and \(\beta >0\) proportional to \(P/K\). As discussed in Sect. 3.4 this means that an individual valley in a periodic array tends to a steady shape with, for sufficiently small \(P\), \(a\approx 1\) and \(\lambda =1/2\), so that, from (19), the valley boundary is given by \(x=d+\log (\cos y)\) i.e. a Saffman–Taylor finger. This is precisely the same boundary derived by [18] who used arguments based on field measurements which relate the flux of groundwater to the curvature of the valley finding excellent agreement between this theoretically predicted valley shape and field observations. While this close comparison is appealing, it is not clear that the assumption that the valley geometry is directly related to the local water table depth holds. In fact it seems likely that the general valley geometry problem is more complicated with the shape of the valley being determined by both a Poisson growth problem for the groundwater depth outside the valley itself, and a Laplacian growth problem inside the valley governing erosion of the valley walls [19]. This is an area of current investigation.

4 Linear variation in the mass forcing

Consider the case in which the governing equation inside a finite fluid blob is

$$\begin{aligned} \nabla ^2 \phi =8\gamma x, \end{aligned}$$
(26)

where \(\gamma >0\) is a constant. This might occur, for example, when the ‘evaporation’ rate varies linearly in a particular direction and is such that when \(x\) changes sign the forcing goes from mass loss to mass injection. This may occur, for example, in a Hele-Shaw cell when the upper plate is tilted about the axis \(x=0\), although in this scenario the LHS is no longer the Laplacian operator–see [6].

Proceeding as in Sect. 2, let

$$\begin{aligned} \phi =\psi +{\gamma \over 2} z{\bar{z}}(z+{\bar{z}}), \end{aligned}$$
(27)

where \(\psi \) is harmonic and is the real part of an associated complex analytic potential \(w\). Thus, the complex velocity is

$$\begin{aligned} {\bar{v}}=\partial _z w+\gamma (2z{\bar{z}}+{\bar{z}}^2). \end{aligned}$$
(28)

The boundary condition \(2{\bar{v}}={\partial _t g}\) and (28) combine to give the following Schwarz function relation valid on \(\partial \Omega \)

$$\begin{aligned} {\partial _t g}-4\gamma z g-2\gamma g^2=2\partial _z w, \end{aligned}$$
(29)

which, again, by analytic continuation can be extended throughout \(\Omega \).

An exact solution is now described for (29): consider a circular blob of radius \(a(t)\) centred on the \(\mathrm{Re} (z)\)-axis at \(z=b(t)\) with no hydrodynamic sources. The Schwarz function for the boundary of this blob is

$$\begin{aligned} g=b+{a^2\over {z-b}}. \end{aligned}$$
(30)

Taking the time derivative of (30) and substituting into (29) and equating coefficients of the singular terms of \({\mathcal O}(z-b)^{-1}\) and \({\mathcal O}(z-b)^{-2}\) gives the following pair of coupled ODEs for \(a(t)\) and \(b(t)\)

$$\begin{aligned} {d a\over {dt}}&= 4\gamma a b, \nonumber \\ {d b\over {dt}}&= 2\gamma a^2. \end{aligned}$$
(31)

By inspection (31) represents a circular blob translating in the positive direction. The radius of the blob decreases if it is centred in the region \(x<0\) and increases if \(x>0\). An exact solution to (31) is obtained by differentiating the equation for \(d b/dt\) in (31) with respect to time and then substituting for \(a{d a/dt}\) using the other equation of (31) to find an differential equation in \(b\) alone which is, after integrating once,

$$\begin{aligned} {d b\over {dt}}=4\gamma b^2+C, \end{aligned}$$
(32)

where \(C\) is constant. Once \(d b/dt\) is known the area of the circular blob \(\pi a^2\) can be found from (31) i.e. \(a^2={d b/dt}/2\gamma \). At \(t=0\) let \(a=a_0>0\) and \(b=b_0\).

If \(b_0^2>a_0^2/2\) then (32) gives

$$\begin{aligned} b=-d_0 \mathrm{coth} \left[ 4d_0\gamma t-\mathrm{coth}^{-1}\left( b_0/d_0\right) \right] \!, \end{aligned}$$
(33)

where \(d_0=\sqrt{ b_0^2-a_0^2/2}\). The solution (33) behaves differently according to the sign of \(b_0\): (i) For \(b_0>0\) (33) implies \(b(t)\rightarrow \infty \) in the finite time \(t^*=\mathrm{coth}^{-1}\left( b_0/d_0\right) /4\gamma d_0\). In this case the problem is ill-posed with the blob propagating infinite distance and becoming infinitely large at \(t=t^*\). (ii) For \(b_0<0\), as \(t\rightarrow \infty \), \(b\rightarrow -d_0\) monotonically (i.e. \(b\) approaches \(-d_0\) smoothly from below) and \( a(t)^2=2d_0^2 \mathrm{cosech}^2\left[ 4d_0\gamma t-\mathrm{coth}^{-1}\left( b_0/d_0\right) \right] \rightarrow 0\) as \(t\rightarrow \infty \). This corresponds to a diminishing circular blob which ‘evaporates’ completely as it approaches \(x=-d_0\) as \(t\rightarrow \infty \).

If \(b_0^2<a_0^2/2\) then the solution to (32) is

$$\begin{aligned} b=e_0 \mathrm{tan} \left[ 4 e_0d_0\gamma t+\mathrm{tan}^{-1}\left( b_0/e_0\right) \right] \!, \end{aligned}$$
(34)

where \(e_0=\sqrt{a_0^2/2-b_0^2}\). In this case if \(b_0<0\) then the blob initially shrinks while propagating toward positive \(x\), before crossing into the region \(x>0\) where it begins to grow eventually becoming unbounded in size in finite time \(t^{**}=[\pi /2-\mathrm{tan}^{-1}(b_0/e_0)]/(4\gamma e_0 d_0)\). An example showing the behaviour of \(a(t)\) and \(b(t)\) of a circular blob first decreasing in size and then increasing once its centre crosses \(x=0\) is shown in Fig. 4.

Fig. 4
figure 4

Behaviour of the blob radius \(a(t)\) and centre \(x=b(t)\) subject to a linearly varying mass forcing with initial conditions \(a(0)=1\) and \(b(0)=-0.7\). Here \(\gamma =1/2\)

Full size image

5 Conclusions

The Poisson growth problem has been formulated in terms of the Schwarz function of the free boundary for the cases when the right hand side is either constant or varies linearly in one space direction. Simple examples of exact solutions have been derived. Although not presented here, it is straightforward to find the Schwarz function equation when the right hand side of Poisson’s equation depends only on the radial coordinate \(r^2=z{\bar{z}}=zg\) on \(\partial \Omega \), in which case a trivial solution is a non-translating circular blob with time-dependent area. It is of interest to explore the possibility of formulating Schwarz function equations and finding explicit solutions for other forms of functional dependence of the right hand side of Poisson’s equation.