1 Introduction

During an aircraft certification process, it needs to be proved that flutter velocity is outside of the flight envelope for all significant aircraft configurations and altitudes. A certain safety margin is prescribed by an airworthiness authority. The flutter velocity determination process, known as flutter analysis, is very time-consuming. The process is well described in [1] for Light Sport Aircraft. In the event that the flutter velocity is not high enough, a modification of the aircraft must be performed to increase the flutter velocity or suppress the flutter occurrence. Modification of an aircraft structure can be carried out using passive or active methods. The modification is then followed by another flutter analysis for verification of this modification.

The passive methods include a change of inertia, stiffness, damping, or geometrical characteristics of the aircraft structure. The typical method of a change in inertia characteristic is the control surface mass balance that completely suppresses the occurrence of flutter [2]. The modification of the stiffness characteristic would require a disproportionately large increase in the cross-sectional properties of the aircraft's primary structure to increase the flutter velocity. The change in damping consists of the installation of control surface dampers or the use of a dissipative material in the aircraft structure. The second approach requires accurate damping models implemented in the analysis [3]. An aircraft geometry is rarely changed to increase the velocity of the flutter or suppress its effect. For instance, the aerodynamic balancing of the control surface [2], which can be achieved by modifying the geometry of the control surface, does not offer a significant increase in flutter velocity. In addition, each of the passive methods works just for a certain type of flutter, which is given by eigen-modes present in the flutter response.

The active methods generate additional damping forces to suppress the flutter. They are also called active flutter suppression methods. In contrast to passive methods, active methods can be tuned against any type of flutter. In addition, the active flutter suppression system is also often used for gust load alleviation [4]. The damping forces are produced by extracting energy from the airflow or by adding energy to the airflow. The extraction of the energy is realized by one or more control surfaces driven by an actuator [5], usually a servo-actuator. Another possibility is to change the external shape of the lifting surface using piezoelectric actuators [6] or active fiber composite patches [7]. The energy extraction by a control surface is not suitable in some cases, e.g. large inertia of the control surface, where the actuator response can be too slow to damp the oscillations. Thus, a method based on adding energy to the airflow has been developed. It uses the so-called active flow control actuators, which maintain fast response and high efficiency under complex flow conditions. The flow control actuators, such as the blowing and suction actuator [8] or the synthetic jet actuator [9], have been widely investigated. These actuators require a sufficiently powerful energy source on board of the aircraft. Regardless of which actuator is used, it is driven by a controller which represents the control law. Usually, the control block is situated in a feedback loop. The controller operates based on an input control variable that is drawn from sensors on the aircraft structure. This input provides information about the dynamic response of the aircraft. The goal is then to design the control law, which drives the actuator to damp the unstable aircraft oscillations, e.g. flutter. Active flutter suppression was successfully realized and put into practice for military aircraft such as B-52 [10], F-4F Phantom [11], F-18 [12] or large civil aircraft like B-747 [13], B-787 [14]. However, it has not been used or even intended for Light Sport Aircraft so far.

This paper aims to use active flutter suppression in the category of Light Sport Aircraft (LSA hereinafter). This category encompasses aircraft which are aerodynamically controlled and carry up to two people. They are powered by a single reciprocating engine power plant, where the maximum take-off weight is given by certification specifications, but cannot exceed 600 kg. The design speed of LSA is usually not limited by regulation standards, and it usually reaches values from 250 km/h up to 350 km/h. Nowadays, producers do not have a problem passing certification criteria regarding the strength of the aircraft structure. However, it is difficult for them to pass the flutter certification criteria. Moreover, the vast majority of these aircraft are using a Rotax 912i engine with a power of 73 kW. However, the latest version of this engine, Rotax 916, reaches a maximum power of 160 kW. This will lead to a gradual increase in the design speed of upcoming aircraft. The producers of LSA often do not design mass-balanced control surfaces, and if they do, the counterweight has inadequate mass. When the flutter analysis shows that the flutter velocity is too low to pass the certification criteria, the producers have a problem adding or enlarging counterbalancing weights of control surfaces, especially for the rudder or elevator, due to the shift of the aircraft's centre of gravity. They seek other possibilities, such as increasing the stiffness of the primary structure. But this turns out to be a very inefficient way to increase flutter velocity for LSA aircraft.

The goal of this paper is to design a system of active flutter suppression that will be simple and feasible for aircraft in the LSA category, both financially and regarding airworthiness. The system will be based on a servo-actuator of a control surface that will generate additional damping forces. The main reason for this is that active flutter suppression by a control surface has already been realized and put into practice for several large civil or military aircraft. The solution presented here lies in splitting the control surface into two parts along the span. A pilot will control the first part using mechanical control consisting of rods and levers. This will be used only for the control of the aircraft. A controller-based actuator will drive the second part of the control surface. The control law will be designed to copy the deflection of the pilot-controlled control surface and, if any unstable aircraft oscillations occur, to damp them.

The presented solution of the control surface split is suitable for LSA aircraft due to the assured controllability of the aircraft in the case of malfunction of the active control system. This can be a strategic argument for the very first flight tests of such a system in this category. Any system of fly-by-wire or active flutter suppression has never been used in this category. The LSA airworthiness authority does not have a regulatory basis for it, neither does it expect a request for the certification of such a system. Thus, the controllability of the aircraft guaranteed by the conventional mechanical way can be very helpful during the very first certification process of an LSA aircraft equipped with such a system. LSA producers are usually very small companies, usually with an engineering group consisting of several employees who have no previous practical experience with fly-by-wire. Therefore, for the very first implementation of such a system in this category, keeping the mechanical control can be a strategic argument too. The paper also focuses on the simplicity of such a system, which lies in the design of the controller in such a way that an analog implementation might be possible. This may be more suitable for small-scale production common in this category of aircraft and to pass the certification of airworthiness. Moreover, the successful implementation of an active control system can later be extended to gust alleviation. Another advantage lies in the fact that the system can be designed to suppress those types of flutter where the most common passive prevention—mass balancing—is ineffective, e.g. for coupling of modes of a lifting surface torsion with a control surface rotation or for coupling of lifting surface bending and torsion modes.

Another goal of this paper is to damp a typical flutter for a given category of aircraft. Based on the authors' experience with flutter analysis of thirty-one LSA, typically the lowest flutter velocity is caused by the interaction of the following modes-1st vertical fuselage bending with 1st symmetric elevator rotation. This is the case in the vast majority of indicated flutter cases of this aircraft category. Thus, active damping of this flutter case will be the subject of this paper.

Finally, the ability to dampen the flutter will be examined for different ratios of span between the pilot and actuator-controlled parts of the control surface to determine the optimal span ratio.

2 Mathematical model

The mathematical model of the aircraft is based on the Light Sport Aircraft UFM-13 Lambada motor glider. The aircraft is an all-composite 15 m wing span structure with a T-tail for two people. The maximum take-off weight is 600 kg. This aircraft had two accidents caused by the flutter of the tailplane [15, 16]. Then, all control surfaces were balanced, followed by a ground vibration test, experimental measurement of the characteristic mass, and flutter analysis [17]. The results showed that even for the balanced elevator with a centre of gravity at 3% of the elevator chord, the flutter velocity is relatively low. The flutter here is caused by the interaction of 1st vertical fuselage bending mode with 1st Symmetric rotation of elevator mode in the free configuration of control.

2.1 Structural model

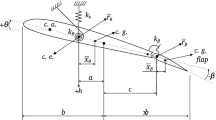
A structural model for the tailplane is developed using the finite element method (FEM). The tailplane model alone was chosen instead of the whole aircraft model because of the easier modal parameter tuning. The authors believe that this simplification does not affect the flutter cases considered in the paper. The model consists of massless beams, concentrated mass, and springs, with a total number of 42 independent nodes. The properties of the control surface merge with the properties of the lifting surface to one node by extension of the global coordinate system from standard 6 degree-of-freedom (DOF) to 9 DOF as follows:

$${\user2{q}} = \left\{ {\begin{array}{*{20}c} X & Y & Z & {RX} & {RY} & {RZ} & {RXX} & {RYY} & {RZZ} \\ \end{array} } \right\}^{T} ,$$
(1)

where \({\user2{q}}\) is the vector of independent coordinates; X, Y, and Z are translations of the lifting surface, RX, RY, and RZ denote rotations of the lifting surface and RXX, RYY, and RZZ denotes for control surface rotation. When only one DOF of the control surface is used per element, the other two have no physical meaning. Thus, their properties are set to zero. A boundary condition is the fixation of the free fuselage end, which is located half a meter behind the aircraft cockpit. The model visualisation is shown in Fig. 1. The global mass and stiffness matrix has a rank of 274.

Fig. 1
figure 1

Visualisation of structural (black) and aerodynamic (grey) tailplane model. Each structural node contains the concentrated mass element

Full size image

An update of the global stiffness matrix was carried out to fit the modal parameters of the model to the results of the ground vibration test (GVT) according to [18]. The eigen-frequencies of the updated structural model are presented in Table 1. The comparison of eigen-vectors using a Modal Assurance Criterion is in Fig. 2. Very small structural proportional damping was included in the model. The value of the damping ratio is equivalent to 1 × 10–4 of eigen-frequency.

Table 1 Comparison of tail-plane eigen-frequencies between the model (FEM) and the aircraft (GVT)
Full size table
Fig. 2
figure 2

Comparison of eigen-vectors by a Modal Assurance Criterion between the model (FEM Modes) and the aircraft (GVT Modes)

Full size image

2.2 Unsteady aerodynamic model

A strip theory with a Theodorsen unsteady aerodynamic model [19] was used for the aerodynamic forces. 17 strips were used for the stabilizer and 12 strips for the fin, one strip per each node. The unsteady aerodynamic forces of the fuselage are not simulated. The influence of the fuselage is negligible due to the small size and velocity range used in this category of aircraft. By performing calculations of flutter velocity with and without fuselage unsteady aerodynamic forces, simulated by Slender-Body theory in combination with the Doublet-Lattice method for lifting surfaces, the difference in flutter velocity was 2 × 10–3%.

The aerodynamic tools used here cannot provide a correct prediction of one specific T-tail flutter instability, which is caused by aeroelastic coupling between the vertical fin and horizontal stabilizer. This instability is governed by in plane dynamics and steady aerodynamic loading [20], which are not included in the aerodynamic model used.

The Theodorsen model has to be transformed purely into the time domain for the simulation of active flutter suppression. This was done by a Fourier transformation of the circulatory component of Theodorsen’s equations by means of a Duhamel integral. The circulatory component contains a so-called Theodorsen function, which is defined in the frequency domain. The Theodorsen equations for the lift, moment and hinge moment of the strip are formed by circulatory and non-circulatory terms as follows:

$${\user2{F}}_{{\user2{a}}} = {\user2{F}}_{{\user2{a}}}^{{{\user2{NC}}}} + {\user2{F}}_{{\user2{a}}}^{{\user2{C}}} ,$$
(2)

where Fa is the vector of Theodorsen unsteady aerodynamic forces, index NC is for the non-circulatory component and index C is for the circulatory component. The vector of the non-circulatory component of aerodynamic forces can be written in the following form:

$${{\user2{F}}}_{{\user2{a}}}^{{\user2{N}}{\user2{C}}}={{\user2{M}}}_{{\user2{A}}}\ddot{{\user2{q}}}+{{\user2{T}}}_{{\user2{A}}}\dot{{\user2{q}}}+{{\user2{K}}}_{{\user2{A}}}{\user2{q}},$$
(3)

where M is the mass matrix, T is the damping matrix, and K is the stiffness matrix, the bottom index A denotes the aerodynamic matrix. The circulatory component of aerodynamic forces is

$${{\user2{F}}}_{{\user2{a}}}^{{\user2{C}}}={\user2{A}} {C}_{(k)}{Q}_{(t)},$$
(4)

where A is a vector of aerodynamic influence coefficients, C(k) is the Theodorsen function, and Q(t) is a deformation vector, also denoted as a reference angle of attack. The deformation vector consists of the following elements

$${Q}_{(t)}=RZ+\frac{\dot{Y}}{v}+\frac{c}{v}\left(\frac{1}{2}-\frac{{x}_{e}}{c}\right)\dot{RZ}+\frac{{T}_{10}}{\pi }RZZ+\frac{c{T}_{11}}{2\pi v}\dot{RZZ},$$
(5)

in the local coordinate system of the strip, with v as the velocity of air flow, c as the semi-chord, \(x_{e}\) as the position of the elastic axis. T10 and T11 are Theodorsen constants of the control surface.

The term C(k) of Eq. (4) is in the frequency domain, and the term Q(t) is in the time domain. Therefore, for the transformation of Eq. (4) into a pure time domain, the Fourier transformation was used with respect to the rule of convolution represented by a Duhamel integral. In addition, according to [21] the Theodorsen and Wagner functions are related by means of the Fourier transformation pair \(\psi_{\left( t \right)} \Leftrightarrow {\text{C}}_{\left( k \right)}\). Thus, Eq. (4) can be transformed into the time domain as follows:

$${\user2{F}}_{{\user2{a}}}^{{\user2{C}}} = {\user2{A}}\left[ {Q_{{\left( {t = 0} \right)}} \psi_{\left( t \right)} + \int_{0}^{t} {\frac{{\partial Q_{\left( \tau \right)} }}{\partial \tau }} \psi_{{\left( {t - \tau } \right)}} d\tau } \right],$$
(6)

where t denotes the time and \(\tau\) the non-dimensional time.

An explicit expression of the Wagner function does not exist, so for a practical evaluation of the Duhamel integral, a Jones [22] second-order exponential approximation of the Wagner function is defined as \({\Phi }_{\left( t \right)}\) is used

$$\psi_{\left( t \right)} \dot{ = }{\Phi }_{\left( t \right)} = 1 - \alpha_{1} e^{{\left( { - \beta_{1} v t/c} \right)}} - \alpha_{2} e^{{\left( { - \beta_{2} v t/c} \right)}} .$$
(7)

with the Leishman [23] optimized coefficients \(\alpha_{1} = 0.2048, \alpha_{2} = 0.2952, \beta_{1} = 0.0557, \beta_{2} = 0.3330\). Due to this approximation, the Duhamel integral in Eq. (6) can be solved by the Edwards [24] state space model

$$\left[\begin{array}{c}\dot{{l}_{1}}\\ \dot{{l}_{2}}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -{\beta }_{1}{\beta }_{2}{\left(\frac{v}{c}\right)}^{2}& -\left({\beta }_{1}+{\beta }_{2}\right)\left(\frac{v}{c}\right)\end{array}\right]\left[\begin{array}{c}{l}_{1}\\ {l}_{2}\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]{Q}_{\left(t\right),}$$
(8)
$$y_{2} = \left[ {\begin{array}{*{20}c} {\left( {\frac{{\beta_{1} \beta_{2} }}{2}} \right)\left( \frac{v}{c} \right)^{2} } & {\left( {\alpha_{1} \beta_{1} + \alpha_{2} \beta_{2} } \right)\left( \frac{v}{c} \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {l_{1} } \\ {l_{2} } \\ \end{array} } \right] + \frac{1}{2}Q_{\left( t \right)} ,$$
(9)

where l is the aerodynamic lag that represents the delay in aerodynamic forces due to the previous behaviour in time \(\tau\), and \(y_{2}\) is the output of state space mode, respectively the product of the convolution. There is one Duhamel integral solved for each strip. The circulation component of the aerodynamic forces will then be

$${\user2{F}}_{{\user2{a}}}^{{\user2{C}}} = {\user2{A}} y_{2} .$$
(10)

2.3 Open-loop model

The equation of motion for the aeroelastic model is formed by the structural and aerodynamic model as follows:

$${\user2{M}}_{{\user2{s}}} \ddot{\user2{q}} + {\user2{T}}_{{\user2{s}}} \dot{\user2{q}} + {\user2{K}}_{{\user2{s}}} {\user2{q}} = {\user2{F}}_{{\user2{a}}} .$$
(11)

with the bottom index S denoting the structural matrix. By substituting from Eqs. (2) & (3), and transferring the non-circulatory part of aerodynamic forces to the left, we can obtain the following:

$${\user2{M}}{\ddot{q}} + {\user2{T}}{\dot{q}} + {\user2{Kq}} = {\user2{F}}_{{\user2{a}}}^{{\user2{C}}} ,$$
(12)

where \({\user2{M}} = {\user2{M}}_{{\user2{s}}} - {\user2{M}}_{{\user2{A}}}\), \({\user2{T}} = {\user2{T}}_{{\user2{s}}} - {\user2{T}}_{{\user2{A}}} ,\) \({\user2{K}} = {\user2{K}}_{{\user2{s}}} - {\user2{K}}_{{\user2{A}}}\). The circulatory part of the aerodynamic forces has to remain on the right side of Eq. (12), with respect to the Duhamel integral. It depends on the previous behaviour of the model and thus has to be solved in a feedback loop. Equation (12) is then transformed into a state space model, labelled S1 in Fig. 3, by substituting \(x_{1} = q,\) \(x_{2} = \dot{q},\) as follows:

$$\left[ {\begin{array}{*{20}c} {\dot{\user2{x}}_{{\mathbf{1}}} } \\ {\dot{\user2{x}}_{{\mathbf{2}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\user2{I}} \\ {{\user2{M}}^{ - 1} {\user2{K}}} & {{\user2{M}}^{ - 1} {\user2{T}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\user2{x}}_{{\mathbf{1}}} } \\ {{\user2{x}}_{{\mathbf{2}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\user2{M}}^{ - 1} } \\ \end{array} } \right]\;{\user2{F}}_{{\user2{a}}}^{{\user2{C}}} ,$$
(13)
$${\user2{y}}_{{\mathbf{1}}} = \left[ {\begin{array}{*{20}c} {\user2{I}} & {\mathbf{0}} \\ {\mathbf{0}} & {\user2{I}} \\ {{\user2{M}}^{ - 1} {\user2{K}}} & {{\user2{M}}^{ - 1} {\user2{T}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\user2{x}}_{{\mathbf{1}}} } \\ {{\user2{x}}_{{\mathbf{2}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {\mathbf{0}} \\ {{\varvec{M}}^{ - 1} } \\ \end{array} } \right]\;{\user2{F}}_{{\user2{a}}}^{{\user2{C}}} .$$
(14)

with the output \({\user2{y}}_{1}\) in the form of displacement, velocity, and acceleration for all DOF of the structural model.

$${\user2{y}}_{{\user2{1}}} = \left\{ {\begin{array}{*{20}c} {\user2{q}} & {\dot{\user2{q}}} & {\ddot{\user2{q}}} \\ \end{array} } \right\}^{T} .$$
(15)
Fig. 3
figure 3

Block diagram of the open-loop model

Full size image

The S1 output is rearranged in the feedback loop to form the deformation vector \({\user2{Q}}_{{\left( {\user2{t}} \right)}}\) given by Eq. (5), required as input to the Duhamel integral. This is carried out by the Reduction matrix R. The output of the Duhamel integral \({\user2{y}}_{2}\) is multiplied by the aerodynamic influence vector A, Eq. (5), to form the vector of the circulatory part of aerodynamic forces \({\user2{F}}_{{\user2{a}}}^{{\user2{C}}}\) respectively input to S1.

2.4 Verification of the open-loop model

The stability of the open-loop model is determined on the basis of an eigenvalue analysis

$$det\left| {{\user2{A}}_{{{\user2{sys}}}} - I\lambda } \right| = {\mathbf{0}},$$
(16)

where Asys is the system matrix of the open-loop state-space model developed by merging all elements according to Fig. 3. λ are the eigenvalues in the form of a complex conjugate pair that represents the frequency and damping of the flexible modes as.

$$\lambda = \omega \left( {\xi \pm i} \right).$$
(17)

with \(\omega\) as the frequency,\(\xi\) as the damping ratio and i as the complex unit. The roots with positive imaginary parts have a physical meaning. The eigenvalues with real roots only represent the aerodynamic lag state. The plots of damping and frequency against velocity are present in Fig. 4. The calculation carried out up to 170 m/s shows three flutter cases, summarized in the first row of Table 2. The Flutter Case No. 1 is caused by the interaction of mode 1-elevator rotation and mode 4—1st vertical fuselage bending and will be subject to active suppression. Flutter Case No. 2 is formed by the interaction of modes 7—Fin bending and 9—1st Elevator torsion. The last Flutter Case No. 3 is contributed to by modes 8—Symmetric stabilizer bending and 10—2nd Elevator torsion. A visualisation of eigen-shapes involved in the flutter is in the appendix.

Fig. 4
figure 4

Damping and frequency plot of the open-loop model

Full size image
Table 2 Flutter cases comparison
Full size table

The open-loop model verification was carried out by comparing the results obtained by Nastran. The Nastran flutter analysis uses the p-k method and the Küssner unsteady aerodynamic strip theory. The distribution and dimensions of the strips were the same as those used in the open-loop model. The Theodorsen function was calculated on the basis of the Bessel functions. Table 2 compares the results of the both  calculations. The computations lead to very similar results. The maximum deviation of flutter velocity for Flutter Case No. 1 is 3%, and for Flutter Cases No. 2 and No. 3 it is 1%.

3 Closed-loop model

An active element for flutter suppression is the elevator. It is divided into three parts, as shown in Fig. 5. The elevator split in the model is done by the zero control surface torsion stiffness for an element at the location of the split. The middle part of the control surface labeled as Elevator remains under direct pilot control by pure mechanical linkage. The two outboard parts of the control surface labelled Active control surface (ACS) are driven by the actuator and the control law. The stiffness of the actuator including a rod is simulated in the same way as for elevator control, that is, by a grounded spring. The minimum suitable ACS span is the subject of this paper. Thus, the ACS span is a variable, and the desired investigated configurations are shown in Table 3. An increment of ACS nodes for each configuration is one node on each side of the stabilizer in the direction from tip to root. The position of the actuator is always in the root node of the ACS.

Fig. 5
figure 5

Split elevator schematic. Black lines represent the contours of the aircraft and red lines represent the FEM model

Full size image
Table 3 ACS configuration
Full size table

3.1 Implementation of the active control surface to the model

A controller representing the control law is added to the feedback loop of the open-loop model. The controller generates a command for the actuator, which deflects the ACS. The deflection for ACS is used as input to the open-loop model. Thus the rotational DOF of ACS in the nodes where actuators are situated do not have their own dynamics but rotate on behalf of controller commands, i.e. actuator commands only. Therefore, to form the closed-loop model, the actuated DOF of the open-loop model are moved from the system matrix (independent DOF) to the input matrix (dependent DOF), in Eq. (13).

This is done by moving columns corresponding to the DOF of the ACS rotation where actuators are placed, for the state variable \(x_{1}\) and \(x_{2}\) of Eq. (13), from the system matrix to in front of the columns of the input matrix. Then, the corresponding rows are removed from the system and the input matrix. The same columns are also moved from the output matrix to in front of the columns of the feedthrough matrix in Eq. (14). However, the output and feed-through matrix rows corresponding to the rotation, velocity and acceleration of the actuated ACS DOF are overridden by zero values. Then, the elements of the state variables \(x_{1} ,x_{2}\) in Eq. (13), (14), corresponding to the removed rows of the system matrix, are also removed. The input vector of the state-space model in Eq. (13), (14), formed by \({\user2{F}}_{{\user2{a}}}^{{\user2{C}}}\), can be widened by the extra terms which represent the DOF of the rotation of the ACS and its first derivative. These are further labeled as \(\Theta ,\dot{\Theta }\) respectively and are governed by the controller and actuator. The output vector of Eq. (14) does not change, only the calculated rotation acceleration of the ACS will become zero as the only actuated DOF of the ACS was moved from the independent to the dependent DOF.

The actuator dynamics are simulated by adding a separate actuator model to the feedback of the closed-loop model. An input to the actuator model is commanded from the controller, and the output is formed by rotation and rotational speed of the ACS governed by actuator dynamics. The actuator model is as follows:

$$\dot{s} = \left[ { - 1/\tau_{s} } \right]s + \left[ {1/\tau_{s} } \right]u_{s}$$
(18)
$${\user2{y}}_{{\user2{s}}} = \left[ {\begin{array}{*{20}c} 1 \\ { - 1/\tau_{s} } \\ \end{array} } \right]s + \left[ {\begin{array}{*{20}c} 0 \\ { - 1/\tau_{s} } \\ \end{array} } \right]u_{s}$$
(19)

where s is the state variable, us is the input i.e. controller command. \(\tau_{s}\) is the actuator constant chosen so that the servo is fast enough to damp the flutter, in this case \(\tau_{s} = 0.01\) s. \(y_{s}\) denotes the output from the actuator as \(y_{s} = \left\{ {\Theta ,\dot{\Theta }} \right\}^{T}\). The actuator model output is set as the input to the open-loop model through a distribution matrix, where the proper arrangement of input vector DOF is performed.

The calculated flutter velocity for investigated configurations of the ACS span are given in Fig. 6. The dashed lines are for the open-loop model including the ACS with the actuator as a spring only. The solid lines are for a closed-loop model with implemented ASC as mentioned above, zero gain controller in the feedback loop, and the same spring for actuator stiffness as used for the open-loop model.

Fig. 6
figure 6

Flutter velocity for different configurations of the ACS span analysed. (The flutter velocities for zero ACS nodes correspond to those from Fig. 4.)

Full size image

The Flutter Case No.1 curves are identical for both models, except for the 12-node configuration, where the difference is 0.6 m/s. The flutter velocity is increasing with an increasing number of ACS nodes for this case. It is caused by the shrinking area of the elevator, thus the contribution of mode 1—elevator rotation-decreases.

Some modes involved in the Flutter Cases No. 2 and No. 3 of open-loop and zero gain closed-loop model are gradually substituted by other modes, as their eigen-frequencies vary with the increasing area of the ACS. Especially, this involves elevator torsion modes and ACS rotation modes, listed in Table 4. Eigen-frequencies of the modes not listed in the table change by less than about 1%, for all ACS configurations investigated. The modes participating in Flutter Case No. 2, i.e. 7 + 9, change to modes 7+ACS antisymmetric rotation. The change is marked by a filled circle in Fig. 6. For the Flutter Case No. 3, modes 8 + 10 are changed starting with the 4-node configuration to modes 8 + 11 (not marked in the plot). In addition, the modes are changed once again from a configuration marked by a filled triangle to modes 8+ACS symmetric rotation. As the ACS eigen-frequencies of the open-loop model drop with increasing number of the ACS nodes, see Table 4, the ACS modes begin to interact with modes of Flutter Cases No. 2 and No. 3 and substituting some of the original modes. This leads to a drop in the flutter velocity of the open-loop model.

Table 4 Open-loop eigen-frequencies of the ACS and elevator. The upper index is for zero gain closed-loop
Full size table

Nevertheless, the zero gain controller of the closed-loop model reinforces the actuator by holding it in the neutral position. This leads to an increase in the ACSs eigen-frequencies by about 7–20 Hz compared to the open-loop model, see Table 4—superscripts. Thus, the participation of the ACS modes in Flutter Cases No. 2 and No. 3 is significantly reduced or shifted to higher frequencies. This, in turn, leads to higher flutter velocities.

From a flutter velocity point of view, the open-loop case represents malfunctions such as the loss of actuator power. Meanwhile, the zero gain closed-loop case represents a malfunction such as the loss of control command or signal from the sensor. Nevertheless, the Flutter Case No.1 flutter velocity becomes critical for both, except for the 12-node configuration, where the critical velocity is given by the open-loop Flutter Case No. 3.

3.2 Controller design

The goal is to design a control law for active damping of the Flutter Case No.1 to be as simple as possible. The flutter is caused by the interaction of the modes of elevator rotation and 1st vertical fuselage bending, at a frequency of about 9 Hz. The control law should follow the pilot command in the stable regime and when unstable oscillations occur, it should damp them. Two parallel controllers in the feedback of the open-loop model were used for this purpose, see Fig. 7. The first, a band-pass controller, is used for the active damping of flutter, in a frequency span around the flutter frequency. The controller is defined by the equation

$$\Theta_{1} = G_{1} \frac{{\omega_{1}^{2} s}}{{s^{2} + 2\omega_{1} \xi s + \omega_{1}^{2} }}\left( {a_{1} .CV_{1} } \right),$$
(20)

where \({\Theta }\) is the output of the controller representing the rotation of the ACS, \(G\) is the gain, a is a constant and CV denotes the control variable.

Fig. 7
figure 7

Block diagram of the closed-loop model

Full size image

The second, a Butterworth 4-th-order low-pass controller, is used to track the pilot command, which is expected to occur in the low-frequency range. The controller is defined as follows

$$\Theta_{2} = G_{2} \left( {\frac{{\omega_{2}^{2} }}{{\left( {s - s_{1} } \right)\left( {s - s_{4} } \right)}}} \right)\left( {\frac{{\omega_{2}^{2} }}{{\left( {s - s_{2} } \right)\left( {s - s_{3} } \right)}}} \right)\left( {a_{2} .CV_{2} } \right),$$
(21)

where

$$s_{1} = \omega_{2} e^{{i\frac{5\pi }{8}}} ,$$
(22)
$$s_{2} = \omega_{2} e^{{i\frac{7\pi }{8}}} ,$$
(23)
$$s_{3} = \omega_{2} e^{{ - i\frac{7\pi }{8}}} ,$$
(24)
$$s_{4} = \omega_{2} e^{{ - i\frac{5\pi }{8}}} .$$
(25)

The design of the Band-pass controller was done for a fixed velocity of 20 m/s above the open-loop flutter velocity. Several types of control variables were analysed, such as acceleration, velocity, and position for vertical displacement of the stabilizer, torsion of the stabilizer, or elevator rotation. In addition, a linear combination of two different inputs was tested. The intended position of the sensor for the Band-pass controller is in the middle of the vertical tailplane only. The deformations of the vertical tailplane are primarily formed by the modes 1st vertical fuselage bending and the elevator rotation. Both modes produce almost the same deformation along the vertical tailplane span and are symmetric. Therefore, there is no rational reason for another sensor position. All controller constants were tuned by root locus analysis for each ACS configuration to obtain the best possible flutter-suppressing capability. The best results in suppressing flutter were obtained for the control variable in the form of elevator rotational velocity. The optimized controller constants for each configuration are listed in Table 5.

Table 5 Controller constants
Full size table

The 4 Hz Butterworth controller frequency \(\omega_{2}\) was chosen with respect to the maximum possible frequency produced by a pilot. The authors estimated the maximum frequency of pilot-induced impulse to control as 3.5 Hz. The chosen controller frequency is above the spectrum of manual control of the aircraft, and further increasing the Butterworth controller frequency would reduce the efficiency of the Band-pass controller. To achieve tracking of the elevator movements, the gain and control variable constant for the Butterworth controller were set to 1.0. The control variable is the elevator rotation sensed also in the center of the elevator.

The flutter velocities of the closed-loop model with given controllers according to the number of nodes used for ACS are presented in Fig. 8. The modes involved in the Flutter Case No. 1–3 are the same as mentioned in Chapter 3.1 for the zero gain closed-loop model. The filled symbols also have the same meaning.

Fig. 8
figure 8

Flutter velocity for different ACS configurations analysed with a closed-loop model (solid lines) and open-loop model (dotted line–only the lowest flutter velocity is presented here)

Full size image

There is not enough energy extracted from the airflow to suppress the Flutter Case No.1 for the 2-node and 4-node configurations of the ACS, according to the calculations. In this case, the flutter velocity is slightly above that of the open-loop one. The Flutter Case No.1 can be suppressed for configurations with 6-nodes and more. The flutter velocity of Flutter Case No. 2 is the same as for the zero gain controller. In addition, Flutter Case No. 3 differs from the zero gain controller by 3%. There are two new flutter occurrences. The first is Flutter Case No. 4 appearing in 2-node and 4-node configurations. It is a rudder flutter at a frequency of 16.5 Hz involving the interaction of modes of Rudder rotation and Fin torsion. The second one, labelled as Flutter Case No. 0, arises for low velocities up to 36 m/s. It occurs only for the 2-/4-/6-nodes configuration of ACS. It is caused by the interaction of the 1st vertical fuselage bending mode with the pole of the Band-pass controller and occurs at a frequency of 8.7 Hz. The vertical oscillations of the stabilizer are enhanced by the ACS rather than suppressed in this case. Above the velocity of 36 m/s, the oscillations are damped. There is a trade-off between the flutter velocity for the upper boundary of the unstable area and the flutter velocity of Flutter Case No.1. The reference variable is the Band-pass controller frequency. By reducing the controller frequency, the Flutter Case No.1 velocity will drop simultaneously with the upper boundary velocity of the unstable area. The trade-off goal was to keep the upper boundary of the unstable area at a value of no more than 36 m/s. The problem with the unstable area could be solved by activating the Band-pass controller from a certain velocity, e.g. setting the gain of the controller as a hyperbolic tangent function depending on the velocity.

For the choice of the optimal configuration of the ACS span, the maximum damping of mode 1st vertical fuselage bending over the analysed velocity range was taken into account. This mode from the Flutter Case No.1 is subject to active suppression of flutter. In addition, it is going to be unstable if the flutter case No.1 occurs, otherwise, it is just approaching the border of stability given by the zero damping axis, see Fig. 9. The maximum damping values for all ACS configurations are listed in Table 6. From this perspective, the 8-node configuration is chosen as the most suitable because it has a reasonable margin of stability to cover the uncertainty of the model or the calculation. The new flutter velocity is then 135.8 m/s given by the Flutter Case No. 2 with a frequency of 29.8 Hz. The larger number of ACS nodes leads to a better stability margin, but in the case of an ACS malfunction below the open-loop flutter velocity, e.g. during take-off, a too small elevator span can cause a problem with the aircraft controllability. This study is the subject of Chapter 6.

Fig. 9
figure 9

Damping and frequency plot of the closed-loop model in the 8-nodes configuration

Full size image
Table 6 1st vertical fuselage bending mode parameters
Full size table

4 Dynamic response

The purpose of this chapter is to verify the dynamic response of the ACS, especially at low frequencies used by pilots for aircraft control. The output of both controllers is merged together, thus the dynamic response analysis will focus on the investigation of whether the Band-pass controller does not suppress the Butterworth command and vice versa. The dynamic response is calculated only for the 8-segment configuration of the ACS. A Bode plot for each of the controllers is shown in Fig. 10. According to the Bode plot the frequency span required for the investigation is from 1 Hz up to 5.6 Hz. The gain of the Band-pass controller increases, whereas the gain of the Butterworth controller decreases in this frequency span.

Fig. 10
figure 10

Bode-magnitude plot of both controllers in the 8-node configuration of ACS

Full size image

4.1 Pilot impulse to control

The pilot impulse to elevator control is simulated by adding aerodynamic lift, moment, and hinge moment generated by the elevator rotation. Forces are applied as input to the closed-loop model. The aerodynamic forces are added to strips of the vertical tailplane where the elevator is situated, e.g. nodes 5 ÷ 13. The aerodynamic forces are calculated as follows:

$$\Delta Y = \frac{1}{2}\rho v^{2} bc_{y}^{\delta } \Delta L\hat{\delta }u_{\left( t \right)}^{Pilot} ,$$
(26)
$$\Delta M = \frac{1}{2}\rho v^{2} b^{2} c_{m}^{\delta } \Delta L\hat{\delta }u_{\left( t \right)}^{Pilot} ,$$
(27)
$$\Delta M_{\delta } = \frac{1}{2}\rho v^{2} \frac{{b_{k} }}{b}c_{y}^{\delta } \left( {x_{k} - x_{E} } \right)c\Delta L\hat{\delta }u_{\left( t \right)}^{Pilot} .$$
(28)

with \(\rho\) as the density, \(b\) as the chord, \(c_{y}^{\delta }\) as the elevator lift curve slope ( lift against elevator rotation),\(\Delta L\) as the strip span, \(\hat{\delta }\) as the elevator rotation amplitude set to a value of 10°. \(u_{\left( t \right)}^{Pilot}\) is the unit input signal from pilot, \(c_{m}^{\delta }\) stands for the elevator moment curve slope (moment against elevator rotation), \(b_{k}\) is the elevator chord and \(x_{k}\) is the position of the hinge axis.

Two types of unit input signals were used. The first one represents a deflection of the elevator and holds the position for an aircraft manoeuver along a pitch axis, see Fig. 11a. Six variants of this signal are used with a duration of elevator deflection from 0.7 to 0.2 s. The second type of pilot impulse is an elevator oscillation. It is formed by a sine function with a duration of three periods. The analysed frequency of sine oscillation is from 1 Hz up to 5.6 Hz. The example of the signal for a frequency of 2 Hz is presented in Fig. 11b. Both input signals were analysed for the velocities of 35, 70, 94, and 115 m/s. The plots of dynamic response to elevator deflection presented here are for the velocity with the lowest stability margin, i.e. 94 m/s. The other velocities give a very similar waveform.

Fig. 11
figure 11

Unit input signal to closed-loop model from pilot to elevator control. a Elevator deflection. b Elevator oscillation 2 Hz

Full size image

For the slow elevator deflection with Δt = 0.7 s, the ACS is following the elevator well with a time delay of 110 ms, see Fig. 12a. The faster the impulse, the bigger the amplitude of the negative peak that occurs for the ACS immediately after the start of the impulse, see Fig. 12b and Fig. 12c. The negative peak is caused by the contribution of the Band-pass controller. A percentage expression of the negative peak amplitude against the steady state elevator amplitude is listed in Table 7. All of the time durations except 0.2 s give an acceptable value for the negative peak. In addition, there is a notable oscillation following the ACS transient response for Δt = 0.2 s (Fig. 12c). Thus, the duration of 0.2 s of pilot impulse is not suitable for this design of control law. The maximum actuator time delay is 119 ms for all analysed velocities and time periods.

Fig. 12
figure 12

Dynamic response of the elevator and left ACS to a deflection input to the elevator control for a velocity of 94 m/s. a Input duration Δt = 0.7 s. b Input duration Δt = 0.4 s. c Input duration Δt = 0.2 s

Full size image
Table 7 Percentage expression of the ratio of the negative peak amplitude to steady state amplitude
Full size table

A list of monitored parameters for the sine input to the elevator is presented in Tables 8 and 9. The ACS is following the elevator rotation well up to 2.0 Hz input (Fig. 13a). The 2.5 Hz frequency is borderline due to a 15% value of the ratio of the negative peak to sine amplitude. The frequency of 3 Hz (Fig. 13b) is not suitable due to a 20% negative peak ratio value. Furthermore, the phase delay of the ACS is 90°. This can significantly reduce the controllability of the aircraft. The inputs of 5 Hz (Fig. 13c) and 5.6 Hz produce a rotation of the ACS with a phase delay which is very close to being in antiphase movement and damps the pilot impulse.

Table 8 Percentage expression of the ratio of the negative peak amplitude to the sine amplitude
Full size table
Table 9 Phase delay of the ACS behind the elevator
Full size table
Fig. 13
figure 13

Dynamic response of the elevator and the left ACS to the oscillation input to the elevator control for a velocity of 94 m/s. a Oscillation frequency 1 Hz. b Oscillation frequency 3 Hz. c Oscillation frequency 5 Hz

Full size image

4.2 Excitation of the flutter mode

The flutter mode excitation is simulated by the explosion force produced by pyrotechnic devices. The location of the device is in a single node. Specifically in the bottom part of the vertical tailplane. The orientation of the excitation force is in the vertical direction only, with an amplitude of 500 N. The time progression of the explosion force is shown in Fig. 14.

Fig. 14
figure 14

Time progression of the explosion force

Full size image

The calculation for a velocity of 94 m/s shows that the explosion excites the vertical fuselage bending oscillation at a frequency of 10.74 Hz, which is the same as the frequency listed in Table 6 for 8-node configurations. The ACS actively damps the oscillation by rotating exactly in antiphase to the elevator, with the same amplitude, see Fig. 15. An acceleration of the stabilizer in the centre of the vertical tailplane, for vertical translation, torsion and elevator rotation, is present in Fig. 16. It can be seen that a maximum acceleration of 26.6 rad/s2 is reached for the control surface within three periods. The flutter mode is actively damped in 3 s at the velocity with the lowest stability margin.

Fig. 15
figure 15

Dynamic response of the elevator and the left ACS rotation to the explosion force at a velocity of 94 m/s

Full size image
Fig. 16
figure 16

Dynamic response of the stabilizer centre acceleration to the explosion force at a velocity of 94 m/s

Full size image

5 Control law robustness

The robustness of the control law was examined for the 8-node configuration of the ACS. The goal is to assess whether the control law is sensitive to inaccuracies in the model definition or the manufacturing tolerances. The sensitivity analysis is focused on variations of the model mass and stiffness characteristic, which can vary due to material uncertainty or due to the wet hand lay-up manufacturing process of composite parts, typical for this category of aircraft. The geometric characteristics are fixed by mould and thus they are not a subject of sensitivity analysis. The variation of the model parameter is + 10% or -10%. The results are presented in Fig. 17. In the cases ID 1 ÷ 10 the stiffness characteristics were variable, while in the cases ID 11 ÷ 17 the mass characteristics were variable.

Fig. 17
figure 17

Summary of the results from the control law robustness analysis

Full size image

ID 5—stabilizer torsion stiffness-has the greatest influence on the change in flutter velocity, where reducing stiffness by −10% causes a drop in the flutter velocity of Flutter Case No. 2 by −5%. Case ID 2—stabilizer bending stiffness-also has a certain influence of ± 2% on the flutter velocity, but only for the Flutter Case No. 3. The other cases cause a change in flutter velocity of no more than ± 1%.

The flutter case being actively suppressed—Flutter Case No.1—remains stable for all of the investigated cases. Thus the robustness is evaluated according to the value of maximum damping for the mode 1st vertical fuselage bending, which is the subject of active flutter suppression, see Fig. 17. Case ID 1-vertical bending stiffness of the fuselage—has the greatest influence on the change in maximum damping, where increasing the stiffness by 10% will cause an increase in the negative value of maximum damping, respectively reducing the stability margin by −53%. Also, decreasing the fuselage stiffness will cause a reduction of the stability margin, but by −10% only. Another significant is that of Case ID 13—vertical tailplane mass characteristic—where a 10% decrease in mass, static moment, and moment of inertia cause the stability margin to be reduced by −48%. Cases ID 5-stabilizer torsion stiffness, ID 12—horizontal tailplane mass characteristic, ID 14—elevator and ACS mass characteristics and ID 16—inertia of elevator control—also have a certain influence. However, their influence in comparison with the former is roughly half.

Thus, there is a certain sensitivity of the control law to inaccuracies, or uncertainties in the model. The stability margin of the actively damped mode drops by no more than −53% due to uncertainties of ± 10%, but the observed flutter is still suppressed. The flutter velocity of 135.8 m/s drops by no more than −5% for the same uncertainties. However, the control law has no direct influence on this flutter velocity, mainly because it was designed to suppress the oscillation of about 9 Hz.

The robustness of the control law was also assessed using the Gain Margin (GM) and Phase Margin (PM). Margins were determined from MIMO Bode plots (Fig. 18) of a closed-loop model disconnected at input to the open-loop model. The GM value indicates the number of times the gain of the control law needs to be multiplied until the closed-loop model becomes unstable. The PM value indicates the required increment to phase lag of the controller and/or actuator until the closed-loop model becomes unstable. The GM and PM results for several velocities are summarized in Table 10. The highest analysed velocity of 113 m/s is 20% below the closed-loop flutter velocity.

Fig. 18
figure 18

MIMO Bode plot of the disconnected closed-loop model for a velocity of 94 m/s

Full size image
Table 10 Summary of Gain and Phase Margin for given velocities determined from MIMO Bode plot of the disconnected closed-loop model
Full size table

The lowest GM is for the velocity of 20 m/s, the value of GM = 1.19[–] gives a 19% reserve on the gain of the control law, which is close to the usual safety coefficient of 1.20 used during the flutter certification process. The lowest PM for the same velocity, PM = 10°, indicates that the additional ACS lag cannot be greater than 0.0033 s for a given frequency, otherwise, the closed-loop becomes unstable.

6 Controllability of the aircraft

The aim of this chapter is to evaluate the longitudinal controllability of the aircraft in the case of the ACS malfunction. The analysed malfunction is that both of the ACS get blocked in the neutral position, and longitudinal control is ensured by the elevator only. Calculations are performed for the open-loop model and closed-loop model with a zero-gain control law in all ACS configurations. Controllability is described by the required angular rotation of the control surface to achieve a unit load factor change. This parameter gives a basic insight into the longitudinal controllability of the aircraft. We consider a quasi-stable aircraft manoeuvre on a circular trajectory, which means that the angular velocity about the transverse axis is constant. The focus is on a non-aerobatic flight with small trajectory changes and small deflections of control surfaces. The required rotation of the elevator to change the unit load factor is given by:

$$\frac{\Delta \delta }{{\Delta n}} = - \frac{{c_{y} }}{{c_{m}^{ * \delta } }}\cdot\left( {\overline{x}_{CG} - \overline{x}_{n} + \frac{{c_{m}^{{**\dot{\psi }}} }}{\mu }} \right),$$
(29)

where \(\Delta \delta\) the required rotation of the elevator, \(\Delta n\) is the load factor change, \(c_{y}\) denotes the lift coefficient of the aircraft for a load factor equal to one and for a given flight speed. \(\overline{x}_{CG}\) is the aircraft's centre of gravity position relative to the mean aerodynamic chord, \(\overline{x}_{n}\) denotes the position of the aerodynamic centre of the aircraft relative to the mean aerodynamic chord, \(\mu\) is the dimensionless mass of the aircraft, \(c_{m}^{*\delta }\) is the slope of the curve relating the aircraft pitching moment coefficient to the elevator rotation at\(\overline{x}_{CG} = \overline{x}_{n}\), \(c_{m}^{{**\dot{\psi }}}\) is the slope of the curve relating the wing with fuselage pitching moment coefficient to the angular velocity about the transverse axis at\(\overline{x}_{CG} = \overline{x}_{n}\).

Due to the assumption of a non-aerobatic flight, the aerodynamic coefficient curves are linear, and thus the slopes of the coefficient curve are constant. The aerodynamic characteristics of the wing airfoil and the horizontal tailplane airfoil are calculated by the Xfoil software. The aerodynamic characteristics of the aircraft are obtained using empirical methods from the literature [25] and [26].

The results of the calculation are presented in Fig. 19. With the used presumption of a load factor change \({\Delta }n\) equal to one, the vertical axis of the plot denotes the required angular rotation of the elevator. As expected, the required rotation increases with the number of ACS nodes. Especially for low velocities, the required elevator rotation is higher than the maximum possible. Thus, take-off, landing, and approach for landing are the critical phases of flight with such a malfunction. According to the maximum elevator deflection and approach velocity for landing marked in Fig. 18, the 10- and 12-node configurations of the ACS are unacceptable. Configurations compliant with these limits are 2-, 4- and 6-nodes configurations. The chosen configuration for active flutter suppression with 8-node of the ACS falls short of the limits. To satisfy the limits, the approach velocity for landing should increase from the current 27.8 m/s to at least 28.8 m/s. The actual landing will have to be done without a hold-off period and with forced touchdown at a higher velocity than usual, in the case of such a malfunction.

Fig. 19
figure 19

Required elevator rotation to change the load factor by unity for a given number of ACS nodes blocked in the neutral position

Full size image

It is clear from the preceding that for a malfunction with the ACS blocked in the maximum deflected position, the longitudinal controllability of the aircraft deteriorates and a safe landing will not be possible. The deployment of a whole-aircraft parachute is the only solution in this case. The same applies to any malfunction of the ACS above the open-loop flutter velocity.

7 Results and discussion

The results show that the flutter can be actively suppressed by using just a part of the control surface. The subjected Flutter Case No.1, given by interaction of modes 1st vertical fuselage bending and elevator rotation at a velocity of 53.2 m/s, can be suppressed by the presented method with a 6-node configuration of the ACS, i.e. 38% ACS span of the original elevator span or higher. Nevertheless, this configuration has a very small stability margin. The maximum value of damping over the entire velocity range for the mode being actively damped, i.e. 1st vertical fuselage bending, is just −0.002[–]. The preferable configuration is 8-node with 50% ACS span, where the stability margin with the maximum damping value of −0.018[–] is sufficient. The Flutter Case No. 2 then restricts the aircraft by the flutter velocity of 135.8 m/s.

Figure 20 summarises the maximum damping of the actively damped mode as a function of the ACS span in the percentage of the original elevator. Thus, the remainder up to 100% is for the pilot-controlled elevator. The plot is constructed based on the data shown in Tables 3 and 6 and indicates the quantity of reserve or deficit from the limit of stability. On the basis of linear interpolation of maximum damping between 4- and 6-node configurations, ACS span smaller than 37.4% of the original elevator cannot extract enough energy from the airflow to suppress the flutter. Unfortunately, there is occurrence of Flutter Case No. 0 for the 6-node configuration, with an unstable region from 2 m/s up to 36 m/s, which brings an unnecessary complication of the controller gain as a function of hyperbolic tangent depending on velocity. In addition, on the basis of robustness analysis for the 8-node configuration, there exists a certain tolerance zone for the maximum damping, which is also present in Fig. 20. The upper and lower limits marked in the grey form an envelope overall examined cases of the Flutter Case No.1 in Fig. 17. There is a possibility to use just 44.0% of span for the ACS, if the level of accepted maximum damping is reduced to a value of −0.010. Then, if we assume that the tolerance zone will be same as for 8-nodes, it completely remains in the stable area as marked in Fig. 20 by the grey dashed line.

Fig. 20
figure 20

Maximum damping achieved across the calculation velocity range for the actively suppressed mode of Flutter Case No.1, i.e. 1st vertical fuselage bending, for each configuration of the ACS span

Full size image

The request for the ACS span as small as possible arises from the possible malfunction of the ACS. The controllability analysis shows that an 8-node configuration, i.e. ACS with 50% span of the original elevator, is the maximum for securing the longitudinal controllability of the aircraft at low flight speeds when the ACS gets blocked in the neutral position. Also, a smaller ACS span results in the use of a less powerful and lighter servo-actuator. On the other hand, the shorter the ACS span used, the worse are the values of maximum damping achieved. This means that the stabilization of a disturbance will take longer. It is convenient to take into account the maximum damping also with respect to the related velocity (Tab. 6) and aircraft design speed for practical application. The use of 44% of the ACS span in this case seems to be justified.

It can also be seen from Fig. 20 that the capability of actively suppressing the flutter depends on the span of the ACS, as can be expected from the logic of the matter. However, for the region of interest from which we determine the minimum possible span of the ACS, e.g. between 25 and 50%, the slope of the maximum damping curve is significantly steeper than in the remaining regions. Moreover, the linear interpolation between those points does not have to be accurate. Thus, a FEM mesh at least two times finer would be beneficial for future analysis.

It can be seen that for 12-nodes of ACS, the gradient of the curve on Fig. 20 is in the opposite direction than the rest. It is questionable if the full-span ACS is more efficient than the 10-node configuration.

The dynamic response analysis for the 8-node configuration shows that the control law follows the smooth pilot movements of the control stick with very low-frequency movement. The maximum delay of the ACS behind the pilot impulse is 119 ms. The ACS delay is caused by the actuator's inherent dynamics. The pilot-induced elevator oscillation of 2.5 Hz and higher or a quick movement of the control stick faster than 0.3 s will generate a significant opposite rotation of the ACS, but at the beginning of the impulse only. This is caused by the participation of the Band-pass controller in the output of the control signal, which becomes more significant as the frequency of the controller input signal increases. A negative ACS rotation can cause a slight drop in the aircraft's controllability above/below those limits. Nevertheless, the above-mentioned limits are so high that the pilot will not reach them during a flight in any case. The aircraft oscillation at the flutter frequency, i.e., 10 Hz, is successfully suppressed by the rotation of the ACS exactly in the antiphase to the elevator.

8 Conclusions

The new method of active flutter suppression by control surface split is presented in the paper. The method aims to the Light Sport Aircraft category, where it has never been used. The present solution focuses on as simple as possible solutions of the controller design. The flutter actively suppressed here is the typical flutter case for this category, caused by the interaction of modes 1st vertical fuselage bending and elevator rotation mode. The continuous elevator of the aircraft considered in the paper is split into three parts. The two side parts are driven by actuators with the control law. Meanwhile, the middle part remains under the direct control of the pilot by mechanical linkage. The actuator dynamics representation is included in the closed-loop model. The control law is formed by the two controllers in a feedback loop. The first controller is the Band-pass filter and is designed to actively suppress the unstable oscillation. Meanwhile, the second controller is the Butterworth Low-Pass 4-th order filter designed to track the movement of the elevator. Both of the controller outputs are merged together.

The controller designs are made for several configurations of the ACS span. The 8-node configuration, i.e. 50% ACS span of the original elevator, was chosen as the most suitable and an investigation of dynamic response, robustness, and controllability was carried out for this configuration. The investigated flutter at a velocity of 53.2 m/s was fully suppressed. The aircraft is limited by a second type of flutter at a velocity of 135.8 m/s. In terms of linear interpolation between the analysed configurations, the ACS span of less than 37% of the original elevator cannot extract enough energy from the airflow to suppress the flutter. However, with regard to the robustness analysis and the calculated tolerance zone for maximum damping, the minimum ACS span for suppressing the flutter is 44% of the original elevator.

The dynamic response of the ACS to the pilot impulse in the form of a deflection and to an oscillation input to the control is verified. The calculation shows that the designed control law perfectly follows the pilot’s command up to a frequency of 2.5 Hz or for the quick impulse not shorter than 0.3 s. Above this frequency or below the specified time duration, a significant opposite rotation of the ACS occurs at the beginning of the impulse as a result of the Band-pass filter contribution. However, these limits are too far away from an impulse that is commonly present during a flight. The dynamic response to the excitation of the actively suppressed flutter mode by a pyrotechnical device shows that the ACS suppresses the oscillation within 3 sec for the velocity with the lowest stability margin, i.e. for the velocity of 94 m/s. The excited frequency of the oscillation is 10.7 Hz.

The robustness analysis shows that a change in mass or stiffness characteristics by ± 10% will not cause the flutter, supposed to be actively suppressed, to occur. In the worst case, the stability margin, in the sense of maximum damping, drops by −53%. The flutter velocity limiting the aircraft, 135.8 m/s, drops by no more than −5%.

The longitudinal controllability of the aircraft with an ACS malfunction in the sense of blockage in the neutral position was analysed. The calculation shows that controllability is not achieved in terms of the chosen limits given by the maximum possible elevator deflection and the approach velocity for landing. When the approach velocity is increased by 1 m/s, the limits are satisfied.

The present model is limited by including only the fuselage and tailplane section. Thus, including the full aircraft model with rigid body motion modes and the flight mechanics model would be beneficial. The calculations also show that the ACS with 75% span of the original elevator is not as effective as the 62% span. Future work can investigate whether this trend is continuous and whether ACS with a 100% span is really less effective than 62% or not. Analysis of the minimum possible ACS span for flutter suppression shows that there is a sharp transition in the area of interest. Therefore, a finer mesh would be suitable for any future analyses.