Effects on the design of aeronautical fuel cell systems by inclusion of reliability requirements

Abstract

The change towards carbon neutrality in air traffic involves a huge reduction of greenhouse gas emissions. This goal is beyond reach by the step wise improvement of conventional technologies. Hence, at present a solution which gains much of attraction are electric motors and electric aircraft systems in combination with fuel cells which can be run by green hydrogen. For a holistic comparison of various concepts the consideration of reliability aspects is required even at an early stage of design. In the scope of this work methods from reliability and safety engineering will be introduced and set in context of aeronautical fuel cell systems. On that basis the consequences arising by the requirement of redundancy are investigated on a system level approach. For this purpose, a model of an aeronautical fuel cell system will be set up in order to simulate a generic flight envelope at stationary points. The fuel cell system is chosen to be central-monolithic and its components are sized for the propulsion of a regional aircraft. With the aid of the system simulation, various failure scenarios are investigated from which mitigation strategies can be derived. Finally, the baseline design will be improved in terms of redundancy in order to last in a generic failure scenario. A comparison between the baseline and improved design shows that the additional redundancy comes with the cost of 4.6% weight increase and a 2.5% drop in cruise efficiency.

1 Introduction

It is an indispensable step to reduce the emission of greenhouse gases in the transport sector in order to mitigate and stem the consequences of climate change [1]. The commercial aviation industry causes roughly three percent of the world-wide climate-relevant emissions [3]. For that reason, the Commission of the European Union (EU) seeks with the FlightPath 2050 goals to reduce $\hbox {CO}_{2}$- and NO_X-emissions by 95% and 90%, respectively, compared to a typical new airplane produced in 2000 [2]. This transformation can only be achieved by an technology innovation. A promising solution is the usage of fuel cells because of their ability to supply energy to avionics and electric propulsion by emission-free conversion of green hydrogen [3,4,5].

The combination of fuel cells and electric motors is already used in the automotive industry as can be seen by the example of the Toyota Mirai [6]. However, in airborne applications solely a few demonstrators yet exist, for example the Antares DLR-H2, Hy4 from H2FLY GmbH or a Piper M modified by ZeroAvia with an electric, fuel cell based propulsion [7,8,9]. There are various challenges with regard to integration of fuel cells into aviation, such as the need of low weight, high power density, life time enlargement and heat dissipation on a low temperature level [5]. Still, fuel cell systems and polymer electrolyte membrane fuel cells (PEMFC) in particular are seen as key technology because of their high energy and power densities [5, 10]. In order to operate fuel cell stacks, several Balance of Plant (BoP) components are necessary. Besides the development and optimization of single components, the performance of the overall system is also affected by its design. Because of the implicit dependencies and conflicting goals, it is a challenging task to find an optimized design of a fuel cell system [10, 11].

Additionally, special requirements towards reliability of critical systems exist in the aeronautical sector. Every component and subsystem must achieve a low failure rate. In cases where this is not possible, the build-up of redundancies is mandatory [12]. Nonetheless, aircraft systems shall be lightweight and efficient in order to enable low fuel consumption. The requirements for reliability can be considered at different design stages and levels starting from a single component up to the whole system. The sooner aspects of reliability and their implications are considered in conceptional drafts the better are comparative analysis of aircraft systems.

As known by the authors, by now there exists only a very few studies dealing with reliability of aeronautical fuel cell systems or invoke these aspects into the design process, respectively. Gerbec et al. [13] conducted a hazard and operability study (HAZOP) as well as an Fault Tree Analysis (FTA) for a mobile 7kW fuel cell system. For that purpose, they gathered failure rates for individual components from different literature references. Within the MAHEPA project, Gaspari et al. [14] determined the failure rate of the whole fuel cell system designated for aircraft integration as $8.43\times 10^{-6}\,\hbox {h}^{-1}$. However, they claimed that the figure is highly uncertain because in some cases failure rates of components could only be estimated based on numbers of comparable parts. In [15], Kösters et al. investigated the influence of certification specifications on specific system power. They propose a new operational strategy based on Extended Operation (ETOPS) certification in order to avoid the usage of additional redundancy.

The scope of this research is to investigate which effect reliability aspects have on the design process of an aeronautical fuel cell system. First, the available methods are outlined and related to fuel cell systems for aircraft application. Subsequently, the effects from redundant design towards the system performance is analyzed by means of the usage of a component sizing process and quasi-stationary system simulation. Finally, it will be evaluated which strategies are advantageous in the sense of weight and efficiency of the fuel cell system. The study will be exemplarily performed on a regional aircraft and focuses exclusively on the top system level of the fuel cell system.

2 Safety and reliability engineering in aviation

A commercial aircraft build and certified in Europe needs to fulfill the Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes (CS-25) released by the European Aviation Safety Agency (EASA) [16]. The EASA was founded 2002 as a executive organ of the European Parliament and is responsible for certification as well as monitoring of large aircraft in the EU. The CS-25 sets all minimum requirements which a newly constructed but not yet certified aircraft must meet in order to obtain a type approval.

The requirements towards the safety and reliability level of all aircraft systems has been determined in paragraph CS$-$25.1309 and the related guideline AMC$-$25.1309. They illustrate the various safety concepts (e.g. Fail-safe method, Safe-life method, redundancy method) and provide references for verification methods.

Concerning the fuel cell system which will be analyzed, the required BoP components have been defined ahead. Thus, the different failure modes of the components can be identified by the Failure mode and effects analysis (FMEA). The FMEA is a systematic, inductive bottom-up method which assesses the consequences of every possible failure on the next higher system level [17, 18]. Generally, FMEAs contain the following information:

• Identification of the component, signal or function

• Determination of the various failure modes

• Determination of consequences arising from failures

• Ascertain compensation measures where applicable

• Consideration of the failure at different flight phases

• Severity of the consequences [18]

The consequences of the determined failure modes can have distinct severity with respect to the aircraft, passengers and the crew. Under consideration of the present flight phase, adverse operating conditions or environmental conditions and external events as bird strike for instance the following classifications apply:

• 1. No safety effect:

  The failure mode under consideration has no consequences regarding the safety of the aircraft and the executed mission. The workload of the crew will not be raised by this failure mode.

• 2. Minor:

  The failure mode minimally compromises the safety of the aircraft. This means the crew needs to initiate additional actions of which they are capable.

• 3. Major:

  Within such a failure mode the ability of the aircraft and the crew, respectively to overcome adverse operating conditions is limited in a way that the following consequences may arise:

  • i) A significant reduction of safety margin or the functional abilities.

  • ii) A significant increase of the workload done by the crew.

  • iii) Discomfort up to medical conditions (including injuries) of crew members or passengers.

• 4. Hazardous:

  Such a failure mode compromises the ability of the crew or the aircraft to operate safely such that the following consequences may arise:

  • i) A major reduction in safety margins or the functional abilities of the aircraft.

  • ii) Too high workload of the crew leads to the case that not all accruing tasks can be done accurately or completed entirely.

  • iii) Serious or deadly injuries of passengers

• 5. Catastrophic:

  The occurrence of this failure mode inhibits the safe continuation of the flight as well as a safe landing and leads to several fatalities or loss of the aircraft.

The CS-25 classifies the occurrence probability of the various failure modes of commercial airplanes in four ranges of probability:

• 1. A probable failure occurring with an acceptable failure rate of maximum $1\times 10^{-3}$ per flight hour.

• 2. A remote failure occurring with an acceptable failure rate of less than $1\times 10^{-5}$ per flight hour.

• 3. An extremely remote failure occurring with an acceptable failure rate of less than $1\times 10^{-7}$ per flight hour.

• 4. An extremely improbable failure occurring with an acceptable failure rate of less than $1\times 10^{-9}$ per flight hour.

The paragraph CS$-$25.1309 also specifies which hazard is handled as acceptable. The hazard is a product of occurrence probability and the severity of consequences. The acceptable probability of a failure in dependence of the consequences can be extracted from Fig. 1. The severity and occurrence probability are inversely proportional to each other [19].

Fig. 1

Acceptable probability of a failure according to CS$-$25.1309 [20]

In order to lower the occurrence probability and subsequently minimize the hazard of a failure according to the specification methods like failure detection and monitoring, failure isolation, reconfiguration of system architecture, limited permissions and intervention of the crew can be used. Beyond that the reliability of a system can be further increased by applying redundancy concepts. Within this method individual components which cannot be further improved in terms of reliability will be implemented redundantly. Thus, the loss of functionality of the system caused by the failure of a single component is prevented. One needs to take into consideration that with rising complexity of the system, the required installation space, the system weight and the operational costs may rise [21]. Typically, only components whose loss of function is classified as hazardous or catastrophic will be implemented redundantly. This can be realized in three different ways:

• 1. Active redundancy: With start of operation all elements will be in use. Load sharing is possible. The probability of failure of all elements increases with service life.

• 2. Warm redundancy: Redundant elements will be run in idle until a failed element needs to be compensated. Through this procedure wearout on the idling elements will be reduced compared to active redundancy.

• 3. Standby redundancy: Redundant elements are be turned off until a failure of the operating elements occurs. In this setup start-up or transition effects and latent failures may occur. Load sharing is not possible [22].

3 Modeling and system simulation

In order to conduct the subsequent study, a model of the fuel cell system is needed. The model should enable to determine the performance capabilities in an arbitrary flight phase and degraded state of the system. Since the dynamic state transitions are less relevant in the present case, a quasi-stationary simulation is used. The simulation is based on a component-composite approach programmed in Python in which the stand-alone models of the single components are interconnected according to the architecture of the fuel cell system. In a single simulation run, the dependent variables of the system will be calculated by numerical methods based on the boundary conditions e.g. atmospheric pressure and the free operating variables e.g. stack temperature, respectively.

3.1 Modeling of the components

The simulation includes dimensionless and dimensional determinate models. The latter are characterized by a load-dependent behavior which is additionally limited by operational boundaries. That kind of models are of particular interest when evaluating the performance of components in a redundant setup. In contrast, dimensionless models are freely scaleable and often defined by a single constant parameter. This approach follows the method of behavior models proposed by Lüdders et al. [11], which enables a simplified modeling of the fuel cell system. In the scope of this study, an example of a dimensional determinate model is that of the centrifugal compressor needed to raise the environmental air pressure. Basically, the device can be computed by isentropic compression under adiabatic conditions together with the overall efficiency $\eta _\textrm{cm}$

$$\begin{aligned} P_\textrm{cm} = \dot{m}\frac{c_{\textrm{p}}T_{in}}{\eta _\textrm{cm}} \left[ \left( \frac{p_\textrm{out}}{p_\textrm{in}}\right) ^{\frac{\kappa -1}{\kappa }}-1\right] \text {,} \end{aligned}$$

(1)

whereby the overall efficiency is divided into mechanical $\eta _\textrm{mech}$ and electrical efficiency $\eta _\textrm{el}$ which are assumed to be constant as well as load-dependent isentropic efficiency $\eta _\textrm{is}$. The operational behavior of the compressor is determined by the compressor map and the efficiency map, respectively. Those maps are obtained through regression analysis of performance data and can be analytically computed by the functions $f_\textrm{1}$ and $f_\textrm{2}$, respectively [23].

$$\begin{aligned} \pi&= \frac{p_\textrm{out}}{p_\textrm{in}} = f_1(\dot{m},n) \end{aligned}$$

(2)

$$\begin{aligned} \eta _{\textrm{is}}&= f_2(\dot{m},n) \end{aligned}$$

(3)

Concerning the redundancy analysis, the operative limits represented by minimal and maximal speed of rotation as well as surge and choke line are needed. These are also determined using regression analysis.

When operating the compressor under varying environmental conditions, the corrected characteristic figures are applied with due regard to similarity law on the basis of Mach numbers [24]. These figures are the corrected mass flow and corrected rotational speed.

$$\begin{aligned} \dot{m}_\textrm{red}&= \dot{m}\frac{p_\textrm{ref}}{p}\sqrt{\frac{T}{T_\textrm{ref}}} \end{aligned}$$

(4)

$$\begin{aligned} n_\textrm{red}&= n\sqrt{\frac{T_\textrm{ref}}{T}} \end{aligned}$$

(5)

An instance of a dimensionless model can be taken from the heat exchanger, which can be calculated by means of the $\epsilon$-NTU method with effectiveness $\epsilon$ as the only model parameter [11]. This parameter describes the ratio between maximal and actual heat exchange

$$\begin{aligned} \epsilon = \frac{\dot{Q}}{\dot{Q}_\textrm{max}}\text {,} \end{aligned}$$

(6)

whereas the transferred heat flow is calculated based on the temperature difference at inlet and outlet.

$$\begin{aligned} \dot{Q} = \dot{m}_{\textrm{i}}\cdot c_\textrm{p,i}\cdot (T_\textrm{i,out} - T_\textrm{i,in})\text {,}\quad i=\text {hot, cold} \end{aligned}$$

(7)

The theoretically achievable heat transfer is determined by both inlet temperatures

$$\begin{aligned} \dot{Q}_\textrm{max} = \dot{C}_\textrm{min}\cdot |(T_\textrm{2,in}-T_\textrm{1,in}) |\end{aligned}$$

(8)

and limited by the flow with the lower heat capacity rate.

$$\begin{aligned} \dot{C}_\textrm{min} = \text {min}(c_\textrm{p,1}\cdot \dot{m}_1,c_\textrm{p,2}\cdot \dot{m}_2) \end{aligned}$$

(9)

Within this model an arbitrary quantity of heat can be transferred with a constant effectiveness.

3.2 Dimensioning

In order to dimension the fuel cell system and the single components, respectively, an iterative algorithm is applied, which sets the system parameters by variation of preferably few variables. The priority is a fast and deterministic dimensioning rather than an optimal efficient or lightweight system.

For the purpose of dimensioning, the operating point with the highest required power is used. As can be seen in the flight envelope in Fig. 6, in the scope of this study, this is the top of climb (ToC). On the other hand, a main operating point is chosen, in which the efficiency is to be maximized. Typically, this is a point at cruise flight. At the beginning of the dimensioning procedure, all components except the fuel cell stack are represented by dimensionless models parameterized with estimated values of efficiency $\eta _\textrm{guess}$. This step enables the computation of the overall system state during the process. After the sizing of each component of interest they are replaced by dimensional models.

Fig. 2

Schematic of the dimensioning sequence for the subsequent redundancy analysis

The graphic in Fig. 2 shows the overall dimensioning procedure which was used in the subsequent redundancy analysis including the sizing of fuel cell stacks, boost converters and compressors. More details about the component specific sizing can be found in the Appendix. At the end of dimensioning, it should be checked that the estimated efficiencies of the sized components is in the narrow range of the actual values. Otherwise the installed stack power is either undersized or oversized.

3.3 System simulation

During the quasi-stationary simulation phase, discrete and sequential operating points are computed in a successive manner, based on the according input values as shown in Fig. 3.

Fig. 3

Schematic of the simulation sequence for a flight mission

At each mission point, the power output from the fuel cell system $P_\textrm{avl}$ must match the propulsive energy requirements $P_\textrm{req}$ at each mission point. The available power is calculated by subtracting the power consumed by the BoP components from the power fed into the high-voltage direct current (HVDC) bus.

$$\begin{aligned} P_\textrm{avl} = P_\textrm{HVDC} - P_\textrm{BoP} \end{aligned}$$

(10)

In the present system model, the available power is chosen to be dependent solely on the cell voltage. The cell voltage is assumed to be uniform over all fuel cell stacks. All other variables are predetermined implicitly or explicitly. Thus, a numerical root-finding algorithm is used in order to calculate the operating point according to the respective power demand. The computation of the system state is further described in the Appendix.

In the case of a component failure, the remaining power that the degraded fuel cell system can deliver needs to be determined. This task is accomplished through a numerical optimization, where the operational limits of the components constrain the available power, thereby forming the constraints of the optimization.

$$\begin{aligned} P_\textrm{max} = \max _{u_\textrm{cell}} P_\textrm{avl}(u_\textrm{cell}) \end{aligned}$$

(11)

4 Redundancy analysis

In the subsequent section, with the aid of the system simulation the methods of safety and reliability analysis will be applied to the design of an aeronautical fuel cell system. For that purpose, the conceptual draft of a regional aircraft in the magnitude of a 70-seater with an operating range of 1000 NM and a speed of Mach 0.55 is used by the way of example. Aircraft and mission data has been generated by DLR Institute of System Architectures in Aeronautics in context of the project EXACT. As can be seen in Fig. 4 there are five electric propulsion units per wing.

Fig. 4

Conceptual draft of the regional aircraft with distributed propulsion. ©DLR Institute of System Architectures in Aeronautics, reproduced with permission

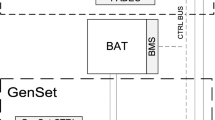
The fuel cells are arranged in a central-monolithic setup and deliver the primary electric energy for the powertrains. The architecture of the fuel cell system, including the BoP components, is depicted in Fig. 5. For the conducted analysis, the system model has been reduced to the components shown in this figure. Three fuel cell stacks together with one boost converter form a thread. Multiple threads are connected in parallel to the HVDC bus in order to cover the power demand. Additionally, a booster battery supplies the electric motors with energy during the take-off. The air supply for the fuel cells is provided by centrifugal compressors, intercoolers and membrane humidifiers. The thermal management of the stacks is done via a cooling circuit consisting of coolant pumps and heat exchangers inside a ram air channel. The hydrogen storage and supply is not considered here. For the sake of simplicity, the redundancy analysis is restricted to the fuel cell stacks, compressors and boost converters. These components are represented by dimensional determinate models. Dimensionless models based on fundamental thermodynamic equations are used elsewhere. More details of the component models used in the redundancy analysis can be found in the Appendix.

Fig. 5

Architecture of the fuel cell system including electric, thermal and air supply subsystems. Dots and dotted lines represent an arbitrary number of parallel components

Comprehensive tools and analyses are necessary in order to identify the required measures that lead to a system with an acceptable risk of hazard. It is mandatory to have information available on the lowest component level and to be able to extend the consequences of a single failure to the whole airplane and its airworthiness, respectively. Thus, in the scope of this study, the analysis is confined to the aspects of fault tolerance through buildup of redundancies. The failure rates of components remain disregarded and all components are subjected to generic redundancy requirements in order to make the system fault tolerant. Redundancy is only taken into consideration at a system level approach. The redundancy of individual parts of a single component is not an aspect of the analysis. Provision is made only for active redundancy since it is assumed that this configuration is preferable in regard of the total system weight. In order to perform the analysis, a generic flight envelope with the power demand as depicted in Fig. 6 is used. The data has been obtained by simulation of the conceptual aircraft and covers standard flight phases, as well as go-around, diversion and loiter. A failure of the overall fuel cell system is defined by the inability of the system to provide the required power at any arbitrary point of the mission. This conservative approach offers a convenient way to define a failure criterion and can be replaced by more specific criteria as the circumstances require.

Fig. 6

Power requirement for the batteries and the fuel cell system during the flight envelope. Blue line marks the altitude of aircraft. Flight phases are Take-off and climb from 10 min, cruise at 27 000 ft from 40 min, descent and go-around from 90 min, diverting and descent from 125 min, loiter and landing from 150  min

The first step of the analysis is to figure out which consequences emerge from a failure of a particular component towards the power supply from the fuel cell system. In doing so, only the complete failure of a component is considered. For that purpose a simulation of the system in a degraded mode is performed. Subsequently, it will be evaluated which measures are preferable for an enhancement of the fault tolerance. For aircraft fuel cell systems there is a Pareto-optimal distribution between system weight and overall efficiency [11]. In order to determine the most favorable configuration in terms of fuel consumption, a simulation of the complete aircraft is necessary. Because this kind of simulation is beyond the scope of the present work, it is only possible to estimate the location of an optimal draft.

When building up redundancies for a specific functionality, there are two options available: (1) Redundancy is gained by adding an additional component with the same size. (2) Under the precondition that initially the load is covered by at least two equal components, they can be oversized in order to compensate a failure. Either way, it needs to be ensured that in the case of a failed component the required functionality or load requirement is still fulfilled. Because active redundancy is used, depending on the number of components and subsequently the load sharing among them, the system will exhibit varying overall efficiency and total weight. In this work only a 1-out-of-n:F redundancy is applied, which means that one of the total number of elements can fail without an effect on the system functionality [22]. Figure 7 illustrates how this kind of redundancy behaves in regard of load sharing, when using different numbers of uniform elements. It is obvious that using a higher number of elements reduces the necessary over-sizing of the one redundant component. Following this observation, the dimensioning process is repeated in order to obtain a set of 1-out-of-n:F designs with different n (total number of components).

Fig. 7

Setup of 1-out-of-n:F redundancies with increasing number of components leads to smaller oversizing. Dotted yellow line represents an arbitrary performance demand for normal operation e.g. required air mass flow, hatched blue area represents partial load of a single component in faultless mode

At the end of the redundancy analysis, based on the gained knowledge an improved redesign of the aircraft fuel cell system is done. To ensure the airworthiness, the propulsion needs to be able to provide sufficient thrust. The respective threshold value differs, depending on aircraft type and flight phase. Hence, the main criterion for a failure of the fuel cell system is the provision of sufficient electric energy according to the propulsion demand. Together with the overall failure rate of the fuel cell system the required redundancy in order to bring the system inside the acceptable area in Fig. 1 can be figured out. The determination of both numbers, threshold of minimum propulsion power and failure rate, is beyond the scope of this work. Thus, a generic failure scenario is assumed. By implementation of redundancy, the fuel cell system must be enabled to deliver the required power in any point of the mission even if the chosen failure scenario arises. Based on the results of a simplified FMEA, this scenario is chosen to the simultaneous failure of a single compressor, four fuel cell stacks and two boost converters.

5 Results and discussion

The baseline design consists of 21 threads with fuel cell stacks having a nominal power of 61.4kW at a current density of $0.7\hbox {Acm}^{-2}$. The boost converters are able to transform a maximum electric power of 235kW to the HVDC bus with 1500 V. Two compressors with a design point air mass flow of $1.66\,\hbox {kg}\,\hbox {s}^{-1}$ each are driven in parallel. The key figures of the system are summarized in Table 3.

Fig. 8

Required power and maximum system power in normal mode and with one failed compressor in the baseline design

Figure 8 shows the available maximum power provided by the fuel cell system. As can be seen, the power declines with increasing flight level from minute ten to minute 30, because more compressor work is needed in the low pressure environment. The smallest distance between maximum and required power is at ToC. The system sizing was run such, that the performance requirements are met with almost negligible margins. The effects of a compressor failure can also be seen at Fig. 8. The maximum power is reduced by 9.7% at ground level and by 44.6% at cruise level in contrast to normal mode. Subsequently, the required power can not be delivered. Especially as the flight level rises the situation worsens because of the increasing compression ratio.

Table 1 Design mass flow of the compressor, weight difference to the baseline design and total hydrogen consumption of the fuel cell system equipped with different numbers of redundant compressors

To mitigate these effects, redundancy is implemented based on a different number of compressors. Table  1 shows the results of the sizing with two to six parallel compressors. As an outcome, the configuration with two compressors exhibits the lowest additional weight compared to the baseline system, whereas six compressors leads to best overall efficiency and hydrogen consumption, respectively. Figure 9 shows the maximum power of the different 1-out-of-n:F configurations in the case of two failed compressors. As expected the remaining power capacity is higher with an increasing number of compressors. With more than five units, the power trajectories are almost the same.

Fig. 9

Maximum system power with two failed compressors in the redundant setup with three up to six parallel compressors

The boost converters and fuel cell stacks are analyzed with the same procedure. In the baseline design the failure of a boost converter is equatable to a failure of a whole thread as can be deduced from Fig. 5. The power loss amounts 3.7% at cruise. In order to mitigate the power loss from a converter failure, besides the approach used for the compressors, there is also the possibility to make advantage of the power margins of the fuel cell stacks. Generally, the stacks are dimensioned to be operated below their maximum possible electric power to gain a better efficiency and life cycle [25, 26]. These power margins offer an interesting approach to compensate for failures without adding additional converters. In order to do so, the boost converters need to be sized such, that they are able to feed in the additional electric power into the HVDC bus. Table 2 shows the key figures of this approach, as well as a redundant setup with two and three parallel converters per thread, respectively. It can be observed that the single converter setup is more lightweight. Adversely, only a limited number of simultaneous converter failures can be compensated, which has been chosen to be three in the present case.

Table 2 Key figures of the fuel cell system with a redundant implementation of the boost converters using either oversizing or two and three parallel converters, respectively

To draw on power reserves of the fuel cell stacks is also an option if a failure of a stack itself occurs. Under the precondition that stacks can be bypassed electronically, the available power is reduced by about 1.5% per failed stack. With more than four stack failures, the system is falling below the required power at ToC. If redundancy is build up by the implementation of additional threads, each of them adds a weight of 107.1 kg. On the other hand, the hydrogen consumption of the flight mission is reduced by 2 kg because of the improved operating point of the fuel cell stacks.

Table 3 Key figures of the baseline design and the improved fault tolerant design

Following the analysis of the individual components, the baseline design is improved in terms of reliability in order to compensate the generic failure scenario described in the previous section. Table 3 summarizes the results. A configuration was chosen which represents a balance between the loss of efficiency and additional system weight. Notably, the failure of fuel cell stacks and boost converts is compensated solely by the power margins of the stacks. The power trajectories in Fig. 10 visualize the increase of maximum power within the improved design and consequently that the required power still can be provided in the failure scenario. The power margin at ToC numbers 772 kW. Whereas it becomes clear that the parasitic consumption of the BoP components increases. Hence, the additional hydrogen consumption during the mission is 21.4 kg (5.5%), the increase in weight is moderate, with an increment of 110 kg.

Fig. 10

Comparison of the baseline design and the improved fault tolerant design based on the power trajectories in normal mode and failure mode. Blue and black color indicates baseline and improved design, respectively

6 Conclusion

Within the present study, reliability methods have been applied to the design process of fuel cell systems for aircraft integration. The focus has been set on the analysis of strategies for the build up of redundancy and the evaluation of the effects on the system performance with the aid of quasi-stationary simulations of a reduced system model. The results show that

• the need for redundancy can have noticeable influence on system weight and overall efficiency. In the examined case of a 70-seater regional aircraft, a change in weight of 4.6% and in cruise efficiency of $-2.5\%$ was observed, while gaining a power margin of 600 kW.

• the consideration of reliability aspects at an preliminary design stage is a challenging but necessary procedure in order to enable a meaningful comparison between different propulsion and energy concepts.

• fuel cell systems offer a certain degree of freedom in the build up of redundancies and by choosing an appropriate strategy, the negative effects of the redundancy demand can be reduced.

• through the employment of novel electric propulsion technology in combination with fuel cells, the safety and reliability process needs to be revised.

Regarding further studies on this subject, a proper and more application-related definition of failure criteria and the knowledge of failure rates is essential in order to determine the actual need of redundancy. Moreover, it has become clear that designing and analyzing redundancy of fuel cell systems by hand is a complex task, especially with an increasing number of considered components. Preferably, a coupled physical and stochastic model is available which describes the system state in terms of functionality together with the failure probability of the particular setup, in order to enable an automatic generation of suitable system designs.

Appendix

1.1 System state determination

The state determination is an crucial part of the system simulation. Within this step, all unknown values of the system components are calculated based on the given inputs. Once the system state is completely known, all important key figures, as for example available electric power, can be extracted. As illustrated in Fig. 11, the process commences with the computation of the fuel cell stacks, succeeded by the boost converters.

Fig. 11

Sequence of the state determination process of the fuel cell system

The second step entails the calculation of the air supply components. Given the interdependencies among the variables of distinct components, not all equations can be analytically resolved. Consequently, a root-finding algorithm is employed to determine the values of these component equations. The same procedure applies to the subsequently cooling circuit computation.

1.2 Fuel cell stack model

The characteristic of a single cell of the PEMFC stack is represented by the polarization curve, which describes the dependency of the current density $i_\textrm{cell}$ by the cell voltage $u_\textrm{cell}$ or vice versa. The course of the polarization curve is influenced by the parameters ${\upalpha }_\textrm{FCS}$ which are stack temperature, pressure and relative humidity of air and fuel gas.

$$\begin{aligned} i_\textrm{cell} = f_\textrm{polcurve}(u_\textrm{cell}, {\upalpha }_\textrm{FCS}) \end{aligned}$$

(12)

The polarization curve of the present model is a multidimensional interpolation. The data source is an one-dimensional two-phase membrane electrode assembly (MEA) model, that has been published by Vetter et al. [27]. With the aim of the MEA model, polarization curves under the conditions listed in Table 4 has been computed.

Table 4 Parameter points at which cell current has been calculated with the help of the one-dimensional MEA model. Points were linearly distributed between minimal and maximal value

The overall fuel cell stack is modeled by a common lumped-parameter approach described in Lüdders et al. [11]. The total electric power is calculated by the active surface area $A_\textrm{cell}$ and cell number $n_\textrm{cell}$ of the stack.

$$\begin{aligned} I_\textrm{FCS}&= i_\textrm{cell}\cdot A_\textrm{cell} \end{aligned}$$

(13)

$$\begin{aligned} P_\textrm{FCS}&= I_\textrm{FCS}\cdot u_\textrm{cell}\cdot n_\textrm{cell} \end{aligned}$$

(14)

Based on the stack current, the required air and hydrogen mass flows can be obtained by using the molar masses M, Faraday constant F, oxygen excess ratio $\lambda$ and oxygen mass fraction $w_\textrm{O2}$ of air.

$$\begin{aligned} \dot{m}_\textrm{H2,req}&= \frac{I_\textrm{FCS}\cdot M_\textrm{H2}\cdot n_\textrm{cell}}{2\cdot F} \end{aligned}$$

(15)

$$\begin{aligned} \dot{m}_\textrm{air,req}&= \frac{I_\textrm{FCS}\cdot M_\textrm{O2}\cdot n_\textrm{cell}}{4\cdot F}\cdot \frac{\lambda }{w_\textrm{O2}} \end{aligned}$$

(16)

To determine the fuel usage over the entire flight mission, the fuel mass flow of a single operating point is multiplied by the duration of a time step. At the simulation end, the sum for all mission points is calculated.

$$\begin{aligned} m_\textrm{H2,mission} = \sum _{\begin{array}{c} i \end{array}}(\dot{m}_\textrm{H2,req,i}\cdot \Delta t) \end{aligned}$$

(17)

The produced waste heat $\dot{Q}_\textrm{FCS}$ and the stack efficiency $\epsilon _\textrm{FCS}$ are related to the lower heating value of hydrogen $H_{l,H2}$.

$$\begin{aligned} \dot{Q}_\textrm{FCS}&= H_\textrm{l,H2}\cdot \dot{m}_\textrm{H2,req}-P_\textrm{FCS} \end{aligned}$$

(18)

$$\begin{aligned} \epsilon _\textrm{FCS}&= \frac{P_\textrm{FCS}}{\dot{m}_\textrm{H2,req}\cdot H_\textrm{l,H2}} \end{aligned}$$

(19)

The pressure loss $\Delta p$ on the cathode side is represented via a quadratic volume flow dependency. The coefficients $k_{\textrm{i}}$ have been fitted to stack measurement data.

$$\begin{aligned} \Delta p_\textrm{ca}&= k_0\dot{V}^2 + k_1\dot{V} \end{aligned}$$

(20)

$$\begin{aligned} p_\textrm{ca,out}&= p_\textrm{ca,in} - \Delta p_\textrm{ca} \end{aligned}$$

(21)

Since the fuel supply system is not further considered, anode pressure loss is not represented. The mass of a single stack is calculated based on weight per area of a single cell and cell count. Additionally, a term representing fixed auxiliary weigh such as end plates, connectors is taken into account. Those values are taken from manufacturer data sheets.

Sizing procedure

Rather than sizing a single stack, the parameters like active cell area and cell count were fixed beforehand to match current state of the art PEMFC stacks. Only the total number of stacks is to be changed during sizing in order to deliver the required maximum power at ToC. As fuel cell stacks are commonly oversized to gain a higher efficiency, there is an additional check for current density at nominal power. If the current density is higher than the threshold value, the number of stacks is raised. Optimal current density is an ongoing research and recommended values can be found in literature [25].

1.3 Boost converter model

The non-isolated boost converter is modeled by a basic circuit consisting of a inductor, diode, power switch and input and output capacitor as depicted in Fig. 12. To handle the high voltage and current, several power switches and diodes are actually put in series and parallel, forming a simplified multi-level converter. In the context of the computation, the ripple current is disregarded, and the respective values are averaged over a single switching period.

Fig. 12

Schematic of simple boost converter consisting of a inductor, diode, power switch and capacitors

The input values of the converter model are low side current and voltage as well as high side voltage. The high side current or outlet current $I_\textrm{out}$, respectively, is calculated by voltage ratio and sum of losses from the electronic components. Since the losses themselves depend on the outlet current, an iterative procedure is necessary, which is described by the pseudo code in Alg. 1.

Algorithm 1

Converter outlet current

The power loss of the inductor is calculated based on direct current resistance (DCR), the power loss of the capacitor by equivalent series resistance (ESR). At the diode and the power switch conduction as well as switching losses occur.

Sizing procedure

The process of determining the size of a converter involves calculating the weight of its components and establishing their electrical parameters to facilitate the computation of associated losses. The semiconductors have a fixed design and are fitted to the electric load by the number of elements in series and parallel. All electric components are sized based on voltage ration, minimal input voltage $U_{in,min}$ and maximal input current $I_{in,max}$. During the overall dimensioning procedure, those values are found by limiting the usable stack power with $0<k_\textrm{P,max}\le 1$. This step takes into consideration that fuel cell stacks are usually oversized in order to achieve a reasonable efficiency and thus, converters do not need to be designed for the entire range of electric power.

$$\begin{aligned} P_\textrm{DCDC,max}&= k_\textrm{P,max} \cdot P_\textrm{fcs,max} \end{aligned}$$

(22)

$$\begin{aligned} U_\textrm{thread,min}&= U_{fcs}(P_\textrm{DCDC,max})\cdot n_\textrm{fcs} \end{aligned}$$

(23)

$$\begin{aligned} I_\textrm{thread,max}&= I_{fcs}(P_\textrm{DCDC,max}) \end{aligned}$$

(24)

The mass of semiconductors is derived from the number of elements used, whereas the mass of a single element is known beforehand. Inductor and capacitor mass is deduced from the stored electric energy and typical gravimetric energy density of the respective components. The total mass of the electric elements is multiplied by a factor representing the additional mass of housing, cooling and cables. A detailed description of loss computation, sizing and mass calculation can be found in [28].

1.4 Air inlet model

A simple air inlet model is used in order to capture the temperature and pressure rise of the ram air. It is assumed, that the relative air velocity is reduced to almost zero. Thus, the inlet temperature approximately equals the stagnation temperature which is composed of environmental $T_\textrm{env}$ and dynamic temperature $T_\textrm{dyn}$, respectively. The dynamic temperature is calculated with Mach number M based on aircraft speed and heat capacity ratio $\kappa$ of air.

$$\begin{aligned} T_\textrm{inlet}&= T_\textrm{env} + T_\textrm{dyn}\nonumber \\&= T_\textrm{env}\left( 1 + \frac{\kappa - 1}{2}M^2\right) \end{aligned}$$

(25)

The inlet pressure is calculated accordingly, but a recovery ratio $0<\xi _\textrm{recov}\le 1$ is introduced to reflect the losses in recovery of dynamic pressure.

$$\begin{aligned} p_\textrm{inlet}&= p_\textrm{env} + \xi _\textrm{recov} p_\textrm{dyn}\nonumber \\&= p_\textrm{env}\left( 1+\xi _\textrm{recov}\frac{\kappa -1}{2}M^2\right) ^\frac{\kappa }{\kappa -1} \end{aligned}$$

(26)

1.5 Compressor model

The compressor model has already been described at Sect.  3.1. The function f1 and f2 of Eqs. 2 and 3, respectively, are realized by the interpolation function griddata of the SciPy-Package in Python. In order to construct the interpolation function, compressor map data is needed. This data is generated following the approach of Li et al. [29]. In the described method, the authors take advantage of similarity laws between well designed compressors, in order to compute the compressor maps based on a specified design point. Figure 13 shows that the data of a real compressor can be well represented by this method.

Fig. 13

Simulated compressor map in comparison with manufacturer data

Sizing procedure

In the scope of this work, sizing of the compressor means to determine the most appropriate map out of an available set of different compressor sizes. For that purpose, 20 compressor maps with different design points have been constructed by the method of Li et al. As can be seen in the sizing algorithm depicted in Fig. 14, the map which can handle the maximum airflow and pressure ratio while having the highest efficiency in the cruise state is chosen.

Fig. 14

The sizing procedure of the compressor chooses the map with maximum efficiency also including the required maximum airflow

The weight of the compressor is linearly interpolated from a set of manufacturer data, based on the nominal mass flow rate. As Fig. 15 reveals, limited number of mass data could be found and the mass estimate, especially in the higher mass flow area, has a high uncertainty.

Fig. 15

Linear regression of compressor mass data provided by various manufacturers based on the maximum mass flow rate

1.6 Humidifier model

For further simplification, the water and heat transfer of the humidifier is not represented. It is assumed that the humidifier can provide a sufficient amount of humid air at the necessary moisture level for the operating conditions of the fuel cell stack. Since the device is downstream of the compressor, its pressure loss needs to be taken into account. This is reflected by using an average static pressure drop based on measurement data.

1.7 Pump model

The pump is considered by a efficiency based model. The specific work results from the pressure rise of the fluid and a constant hydraulic efficiency $\eta _\textrm{hydr}$.

$$\begin{aligned} \Delta h = \frac{p_\textrm{out}-p_\textrm{in}}{\rho \cdot \eta _\textrm{hydr}} \end{aligned}$$

(27)

Electric power consumption is calculated with mechanical and electric efficiency which are also taken as constant.

$$\begin{aligned} P_\textrm{el} = \dot{m}\frac{\Delta h}{\eta _\textrm{mech}\cdot \eta _\textrm{el}} \end{aligned}$$

(28)