1 Introduction

Unmanned aerial vehicles, like quadrocopters, have gained popularity due to their vertical take-off and landing (VTOL) and hover capabilities allowing operation in urban areas. Nevertheless, depending on the mission profile, the operation time of small UAVs may be mostly spent on forward flight [1, 2]. Therefore, optimisation of aerodynamic rotor design in regard to flight in edgewise flow could help to meet an ongoing challenge of increasing flight duration for electric UAVs. On the other hand, the developing UAV market is severely constrained by the public acceptance of the generated noise. Whilst nowadays most multicopters are powered by electrical motors, it is the rotor that represents UAV’s main noise source [3]. Although extensive studies have been done considering propellers operating under axial-flow conditions [4,5,6,7,8], their results are not applicable for forward flight with higher advance ratios. At the same time, the mechanisms acting on a small propeller in such conditions are not yet fully understood and cannot be directly derived from the full-size helicopter rotor. The main difference comes from the blade planform shape, as multicopters are typically driven by rigid blades with nonlinear twist distribution and strong chord variation along the span [6]. As advancing and retreating side effects are not compensated, like in the case of hinged helicopter rotors, a fixed-pitch propeller in forward flight experiences high thrust fluctuations throughout the rotation, which also results in an asymmetry of the produced wake [9]. Additional complexity arises when rotors operate at low Reynolds numbers, which has impact on both performance [10,11,12] and noise generation [13]. Though the main noise sources remain the same as those for helicopter rotors, UAVs typically fly in a laminar-transitional flow regime, which affects the balance between tonal and broadband noise contributions in the pressure signature. Flow effects characteristic for these conditions like separation bubbles or boundary layer transitions, together with intensified wake interactions, increase unsteadiness at blade edges and thereby amplify higher frequency noise components. As a result, noise prediction for small-scale rotors poses a challenge for traditional methods developed for fully turbulent flows [14].

Considering all the facts, separate studies dedicated for small rotors aerodynamics and aeroacoustics are necessary, which implies the demand for accurate calculation methods, capable of handling specifics of the forward flight operation. From aerodynamic tools described in the literature, the ones based on the blade element theory (BET) are the most simplified and time efficient, yet for moderate flight conditions, they show accuracy comparable with higher-fidelity solvers. Gur et al. [8] proved that for the simulation of axial flight, a simple blade element/momentum model offers good agreement with the measurements regarding performance prediction. The quality of BET calculations, however, depends on the quality of the airfoil polar data, which represents a particular challenge for low advance ratios [15]. Forward flight calculations, for which a simple momentum theory is no longer applicable, require corrections to the assumed inflow distribution [1] or involve coupling the BET method with more complicated inflow models [16]. Nevertheless, the reduction of computational cost remains significant compared to the higher-fidelity tools.

Even though URANS simulations offer the highest reliability for a wide range of conditions, the general experimental trends can be often successfully captured by low-fidelity methods, as shown by Cerny et al. [17]. For this reason, BET tools are commonly used as an initial loading estimation during the design process. Gur et al. [3] presented an optimization method based on the BET for a design of a quiet and efficient mini UAV rotor. Weitsman et al. [7] showed using BEMT how the change in blade parameters affects the aerodynamic performance and aeroacoustics of a rotor in hover.

Methods based on potential flow represent a complexity level between BET models and RANS solvers. Their great advantage is the ability to simulate unsteady conditions, whilst ensuring time efficiency [9]. Potential methods are usually coupled with a free-wake method, as described in [18] but can also include extensions for viscous particle wake [19] or post-processing viscous and compressible corrections.

In recent years, a few studies have been dedicated to the experimental research of small rotors operating in sidewise flow conditions. Theys et al. [20] showed the influence of edgewise flow on forces and moments acting a micro-UAV rotor transitioning between axial and forward flight. In a similar study, Kolaei et al. [21] indicated nonlinear variations in thrust, power and rolling moment with regard to inflow angles. Load changes in the forward flight are also reflected in rotor noise emission. Yang et al. [2] expanded the performance measurements with an aeroacoustic investigation of a UAV rotor operating at various rotation speeds and freestream velocities in forward flight. Lößle et al. [22] analysed changes in noise spectra depending on the rotor tilt angle and advance ratio. The computational study described in [9] showed the application of a potential flow method for the analysis of transient thrust during forward flight. Other investigations [1, 17] juxtaposed results from various aerodynamic tools together with experimental data. This study, prepared within the GARTEUR Action Group 25, compares solvers with different fidelity levels including BET, potential flow methods (UPM, RAMSYS), lifting-line method (PUMA) and Navier–Stokes solver (FLOWer) regarding load-prediction, but also examines their applicability as a base for noise estimation.

2 Experimental setup

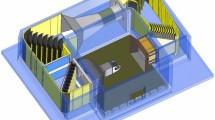
The experiment involved aerodynamic and aeroacoustic measurements and was conducted in the Rotor Test Facility Göttingen (RTG) of the German Aerospace Center (DLR). The aeroacoustic array consisted of 512 MEMS (micro-electrical–mechanical systems) microphones (Fig. 1) and was positioned 1.35 m below the rotor plane, as shown in the sketch of the experimental setup in Fig. 2. Presented noise levels were corrected based on the measurements with loudspeaker emitting white noise to compensate for the effects connected with room acoustics. The analysis was focused on the tonal noise of the blade passing frequency as it was dominant in the measured spectra. Additionally, for most of the studied test cases, the higher frequency components did not exceed the wind tunnel noise.

Fig. 1
figure 1

Microphone positions relative to rotor plane

Full size image
Fig. 2
figure 2

Experimental setup

Full size image

Thrust and torque were measured with a strain-gauge and piezoelectric balance, respectively. The measurements included variations in flight velocity, rotor RPM and tilt angle. The aeroacoustic study was limited to cases presenting the effect of a change in rotor inclination between – 30\(^\circ\) and 30\(^\circ\) (Fig. 3) with fixed flight velocity and rotational speed (advance ratio 0.146). Vortex trajectories were detected by the background-oriented schlieren (BOS) method using a high-speed camera, reflecting mirror and dotted background mounted above the propeller. A detailed description of the experimental setup can be found in [23].

Fig. 3
figure 3

Tilt angle sign convention

Full size image

3 Geometry

A two-bladed, fixed-pitch KDE 12.5x4.3" rotor with 0.318 m diameter and solidity 0.075 was used. Computational models were prepared based on a 3D-scanned blade, divided into series of spanwise cuts (Fig. 4). Figure 5 presents the obtained twist and chord distributions. Due to inaccuracies of a scanned surface, four-digit NACA profiles were identified to approximate a hydraulically smooth airfoil shape at the measured cross-sections [24]. The shape of the trailing edge could be adjusted depending on the computational method applied (Fig. 6).

Fig. 4
figure 4

Scanned blade with cross-sections

Full size image
Fig. 5
figure 5

Twist and chord distributions

Full size image
Fig. 6
figure 6

Example-trailing edge shapes of recreated profiles

Full size image

4 Computational methods

4.1 BET and FW-H code

The blade element theory (BET) represents the most simplified and the least computationally expensive of the applied methods. In the BET, steady lift and drag values are calculated for spanwise blade sections at different azimuthal positions and then integrated for the whole blade and one full rotation. A value of the inflow angle and the corresponding angle of attack can be determined iteratively from a loop with an inflow model. A dedicated Python code used in this study included a linear inflow model developed by Pitt and Peters [25, 26] (Fig. 7). Aerodynamic characteristics for airfoils identified for each spanwise cut were prepared using XFOIL and considered variation of Reynolds and Mach numbers. Lift and drag coefficients were then extrapolated for high angles of attack with the post-stall Viterna model [27] (Fig. 8). The BET code did not include a wake model. Calculations were performed for 15 spanwise and 360 azimuthal elements.

Two ways of including tip-loss effects were investigated, either by adding Prandtl’s function to the solution [28] or by estimating a tip-loss factor B as a constant value (as described in [18] typically between 0.95 and 0.98). The Prandtl’s function approach lead to strong underestimation of thrust values for a rotor operating in a strong upwash (positive tilt angles); therefore, in the presented results, a B factor was simply approximated as 0.97 and mean thrust values were reduced by a factor \(B^{\textrm{3}}\) for forward flight cases [29].

As the final step, the resulting loading distribution served as an input for a coupled aeroacoustic prediction code based on the Ffowcs Williams–Hawkings (FW-H) equation with the formulation described in [3]. Only loading noise was considered in the acoustic calculation due to the analysed observer positions below the rotor plane where no significant thickness noise contribution is present.

Fig. 7
figure 7

Induced velocity distribution with Pitt and Peters model for 5400 RPM, 12.9 m/s, tilt – 10\(^\circ\)

Full size image
Fig. 8
figure 8

Viterna extrapolation of lift coefficient for higher angles of attack used in the BET code

Full size image

4.2 UPM and APSIM

UPM is an unsteady free-wake panel method developed at DLR allowing the simulation of flows with arbitrary body shape and motion [30, 31]. The code solves potential flow, although viscosity and compressibility effects can be included in post-processing. A viscous correction, applied to improve the estimation of torque values, estimates the contribution of profile torque using Eq. (1) [29], where section zero-lift drag coefficient \(C_{d_0}\) has a default value of 0.0075, \(\sigma\) and \(\mu\) stand for rotor solidity and advance ratio, respectively.

$$\begin{aligned} C_{Q_0}=\frac{\sigma C_{d_0}}{8}(1 +1.5\mu ^2-0.37\mu ^{3.7}) \end{aligned}$$
(1)

Lifting bodies in UPM are modelled as a distribution of sources and sinks on the blade surface accounting for the displacement effect and doublet distribution along the chord simulating the lift. The weighting function of doublet strength is prescribed and depends on the profile thickness. An iterative scheme to ensure pressure equality at the trailing edge and satisfy the Kutta condition was applied in the calculations. The panel generation code PANGEN served in this study as a tool to prepare a computational blade model with finite thickness and sharp trailing edge. The model consisted of 15 spanwise and 95 chordwise panels (Fig. 9). The full span free wake of the blades mostly used a vortex lattice, yet additional calculations were carried out using particle wake method, in which the vortex filaments are replaced by point vortices (Fig. 10). The particle model solves the vorticity transport equation derived from the incompressible Navier–Stokes equations [32]. As there are no connections between the neighbouring particles, this approach enables an improved solution for cases where the wake interferes with solid bodies. Calculations were carried out for approximately eight rotations with step size reduced from 5\(^\circ\) to 2\(^\circ\) after five rotations.

A coupled code APSIM (aeroacoustic prediction system based on integral methods) [33] takes into account linear sound propagation and includes two integral formulations of FW-H equation for a permeable and impermeable surface. The latter approach was used in this study based on pressure distribution on the blade surface from the last rotation calculated in UPM.

Fig. 9
figure 9

Distribution of panels on a blade surface from UPM

Full size image
Fig. 10
figure 10

Wake represented in UPM with vortex lattice (left) and vortex particles (right)

Full size image

4.3 PUMA and KIM

PUMA (potential unsteady methods for aerodynamics) is an unsteady lifting-line/free-wake solver developed at ONERA since 2013. It includes a coupling between an aerodynamic module and a kinematic module. The aerodynamic module uses the lifting-line method with a free-wake model based on Mudry theory [34], which describes the unsteady evolution of a wake modelled by a potential discontinuity surface. It can handle some 3D corrections for blade sweep through local Mach number and angle of attack corrections, and 2D unsteady nonlinear aerodynamics effects through dynamic stall models [35, 36]. Moreover, different time discretizations are available to balance between accuracy, numerical stability and computational time. The kinematic module employs a rigid multi-body system approach using a tree-like structure with links and articulations. It enables any arbitrary motion between the different elements. PUMA is usually used for any aerodynamic study of fixed wings and rotating wings configurations which require low computational cost or a large amount of parametric investigations like pre-design studies. It has also been successfully applied for helicopter rotors wake in interactions with obstacles [37, 38] and for rotor / rotor interactions [39].

In this study, the 2D airfoil characteristics, the same as the ones used in the BET method, were included to account for viscosity and compressibility effects. The lifting line was divided into 45 radial stations for wake emission using a square root distribution. A time step of 5\(^\circ\) was used for the unsteady computation over eight rotor revolutions.

The KIM code [40, 41] is used to determine the noise emission by solving the Ffowcs Williams and Hawkings integral with an advanced time formulation. The noise source considered is the surface pressures on the blades but since the PUMA code only provides the spanwise distribution of loads, those quantities need to be reconstructed. An empirical pressure distribution, typical of a propeller blade section, is set on the suction side. The pressure level is then set so that once integrated, the loading in terms of local thrust and torque prescribed by the PUMA code is recovered.

4.4 FLOWer and ACCO

For high fidelity simulation, the numerical process chain used at the IAG was applied. CFD results are generated with the structured code FLOWer, originally developed by DLR [42] and further developed at the Institute of Aerodynamics and Gas Dynamics at the University of Stuttgart [43]. Acoustic coupling was provided by IAG’s FW-H solver ACCO [44] with usage of the data output of FLOWer. A second-order dual time stepping for temporal evolution was used with a time step of 1\(^\circ\) to resolve the acoustic waves. Furthermore, the Menter-SST turbulence model was applied to close the URANS equations. For spatial discretization, the surface of the propeller was meshed with 0.1% of the chord length in streamwise direction. To recognise tip effects, mesh refinement up to 1% of the radius in spanwise direction was set. Using the Chimera technique, a separate background mesh was created utilising hanging grid nodes to reduce the numerical expense. Furthermore, in all background volume cells, the WENO scheme of \(6^{\textrm{th}}\) order is carried out for numerical stability and reduced dissipation. In the surface region, the dimensionless wall distance is kept low at \(y^{+} < 1\). The \(\lambda _{2}\)-criterion for vortex visualisation and numerical setup is shown in Fig. 11 and 12, respectively.

Fig. 11
figure 11

Wake visualised in FLOWer using \(\lambda _{2}\)-criterion

Full size image
Fig. 12
figure 12

Numerical setup in FLOWer—background and propeller mesh with chimera interpolation

Full size image
Fig. 13
figure 13

Integration surface for acoustic coupling as input for ACCO and physical surface of the rotor blade

Full size image

The acoustic code ACCO uses an acoustic integration surface, within which sound is generated by the fluid. The integration is accomplished on a cylindrical permeable surface (red in Fig. 13) to enclose all sound sources. The selection of the spatial discretization in the background mesh was based on the resolution of the first harmonic wave length, with 20 cells discretizing the wave length of the blade passing frequency (BPF). To avoid excessive dissipation, the integration surface is placed in the finest grid area without cell size changes.

The scattering effects described in Sect. 6.1 were computed using the boundary element method (BEM) tool ScatMan [45] developed at the Institute of Aerodynamics and Gasdynamics [46]. Within the ScatMan tool, the sound propagation in the frequency domain is described by the Helmholtz equation, expanded with Green’s second theorem resulting in the Helmholtz–Kirchoff equation [46]. To include ScatMan in the numeric tool chain consisting of FLOWer and ACCO, the shielding had to be discretised in triangle elements. ACCO in the first step calculates the incident sound pressure at the discrete points on the surface of the shielding as well as in a small distance above each surface point. Afterwards, the ambient conditions are added resulting in the complete solution consisting of acoustic and scattering field.

4.5 RAMSYS and ACO suite

The CIRA aerodynamic simulations were carried out using the medium-fidelity code RAMSYS [47], which is an unsteady, inviscid and incompressible free-wake vortex lattice boundary element methodology (BEM) solver for multi-rotor, multi-body configurations developed at CIRA. It is based on Morino’s boundary integral formulation [48] for the solution of Laplace’s equation for the velocity potential \(\varphi\), whilst the wake is modelled according to the novel formulation proposed by Gennaretti and Bernardini [49]. The surface pressure distributions are evaluated by applying the unsteady version of Bernoulli equation, which is then integrated to provide the forces and moments on the configuration and the surrounding obstacles. A computational acceleration is obtained by applying the module for symmetrical flows and geometries implemented in the solver and the parallel execution via the OpenMP API. The applied blade model consisted of 15 spanwise and 50 chordwise elements. The simulations were performed for six rotor revolutions with time step of 2\(^\circ\).

The aeroacoustic simulations were carried out using the acoustic suite developed at CIRA and consisting of several tools for the evaluation of noise generation and propagation. The ACO-FWH solver is used for computing the acoustic free-field generated by the rotor blades. It is based on the FW-H formulation [50] described in [51, 52]. The advanced time formulation of Farassat 1A is employed, and the linear terms (the so-called thickness and loading noise contributions) are computed through integrals on the surrounding surface or moving blades (impermeable/rigid surface formulation). Moreover, the space derivatives of the linear terms are also evaluated through a numerical differentiation for coupling the free-field solution computed with FW-H with scattering solvers [53]. In particular, the coupling of the FW-H code with the boundary element method is enabled through a boundary surface defined in terms of pressure and normal derivative of the pressure. The FW-H code automatically extrapolates a secondary boundary surface along the normal direction to each panel of the primary boundary surface where the acoustic pressure is computed and the corresponding derivative is computed by finite difference techniques amongst the two surfaces. The quadrupole contribution due to the nonlinear terms distributed in the perturbed field around the blade is neglected. The computational acceleration is obtained by a parallel execution via the MPI API. The simulation of the aeroacoustic free-field was carried out using the aerodynamic database evaluated by RAMSYS, and consisting of the rotor blade pressure distributions. The ACO-FAM solver was used for the simulation of the acoustic scattering field. It is based on the numerical solution of the convected Helmholtz equation which can be handled with an integral boundary element method [54]. In particular, ACO-FAM implements a combined Helmholtz integral equation formulation (CHIEF) which is solved with a collocation boundary element method. The ACO-ENV solver implements the acoustic propagation of a generic noise source through a ray approximation as described in [55]. This solver allows for the computation of several noise metrics starting from the definition of the flight trajectory and the noise source database encompassing the flight envelope. Moreover, it is also able to account for single reflections and attenuation by barriers or buildings. Single reflections are managed through an analytical mirroring of the source whereas the attenuation is managed through semi-analytical formulations [56, 57].

5 Results

5.1 Aerodynamic loading prediction

Figures 14, 15 and 16 present, respectively, the effect of change in the rotor RPM, flight velocity and tilt on the time-averaged thrust and torque. The comparison indicates that general tendencies captured in the measurements are reproducible using all computational tools; however, some differences can be noticed in terms of accuracy. It is worth mentioning that for moderate flight velocities, BET solution offers good loading estimation, even with simplified assumptions considering tip-loss factor. As the same 2D airfoil characteristics were used as an input for BET and PUMA, the loading calculated with these both methods is similar in Figs. 14, 15 and for low tilt angles in Fig. 16. The accuracy of these solvers becomes worse for low advance ratios (Fig. 15), which can be explained by the limitations of XFOIL for calculating cases with very small Reynolds numbers and omission of rotational effects in the airfoil data. For most of the analysed points, underprediction of torque values is expected from potential flow solvers, like UPM or RAMSYS caused by neglection of viscosity effects. A post-processing correction in UPM estimating the contribution of profile drag considerably improved the agreement between calculated and measured torque values. The assumption of inviscid flow leads to the underestimation of torque by at least 10% for most of presented cases.

With the rotor tilted backwards, the interaction with vortices becomes dominant and the lines from BET and PUMA diverge, as the BET code did not include a wake model in the solution (Fig. 16b). Nevertheless, the BET outcome lies closer to the experimental data at higher angles of attack. This counter-intuitive result may arise from the sensitivity of PUMA solver to airfoil data imperfections for the cases with intensified blade-wake interactions, which do not affect basic BET calculations.

The increase in interactional effects between positive and negative rotor inclinations can be observed in Fig. 18 presenting wake visualisations and from unsteady loads depicted in Fig. 17. For negative tilt angles, like in Fig. 18a, the horizontal component of the velocity induced by the propeller is in the direction of the free stream velocity and the vertical component pushes the wake downward away from the propeller. This combination of velocities causes a rapid convection of the wake downstream. As a consequence, there is little interaction between the wake and the propeller, the unsteadiness is moderate and so are the effects on the loads acting on the propeller disk (Fig. 17a). Figure 18b shows the wake developed at a positive tilt angle. In this case, the horizontal component of the velocity induced by the propeller is opposite to the free stream velocity. This not only reduces the convection process downstream but also causes the wake to be fully ingested by the propeller disk with the resulting generation of high interactional effects giving rise to unsteady loads (Fig. 17b). The flight regime of a rotor operating in strong upwash transitions towards windmill state, where the blades are driven by the flow, explains the rapid decrease in torque values in Fig. 16b.

Additionally, Fig. 17 presents a comparison of unsteady loading for chosen tilt angles calculated in UPM with vortex lattice and vortex particles. Although the discrepancy between time-averaged thrust values calculated with these both methods was negligible, an apparent difference can be noticed in thrust fluctuations for positive angles of attack (here 20\(^\circ\)), for which the particle method offers a more stable solution. This can be explained by the lower sensitivity of the point vortices in the particle method to interactions with solid bodies due to the lower order modelling of the vortical flow compared to the vortex lines in the lattice representation.

The increase in loading fluctuations due to wake interactions cannot be captured by the BET method, as shown in Fig. 19 compared to the FLOWer result. Moreover, the loading calculated using BET differs in phase compared with results from other methods, whereby the observable shift depends on the assumptions of the inflow model. Whilst for a trimmed helicopter rotor, it is justified to neglect the influence of the rolling moments in the applied model by Pitt and Peters (result PP1 in Fig. 19), the forces produced by a fixed-pitch UAV rotors in the forward flight are always unbalanced between the retreating and advancing side. It means that for the latter, a simplified linear model with a longitudinal gradient of the induced velocity should be replaced by a Pitt and Peters model including both longitudinal and lateral components based on the aerodynamic rolling and pitching moments as shown in Fig. 7 (result PP2). For the assumption PP1, according to the BET, the maximum thrust is reached around azimuth 90\(^\circ\), which is where the calculated relative velocity coming from the rotational motion of the blade and flight velocity reaches the highest value. In case of PP2, including the lateral inflow gradient, the maximum peak appears around 20\(^\circ\) later, more to the front of the rotor, which agrees better with the results from other methods. The remaining phase offset can be due to unsteady effects, which are not covered by a simplified linear inflow model. The phase delay can be partially corrected by means of Theodorsen’s theory, that accounts for unsteady development of lift, as described in [18]. In Fig. 19, phase shift resulted from Theodorsen’s function was averaged throughout the disc for each blade section and used to correct the initial result. The applied correction helped to include a case-dependent time delay in the BET solution; however, it did not ensure complete compatibility with other solvers. In this study, Theodorsen’s function served only as a quick estimation, as the main objective was to investigate the possible applications of basic BET assumptions.

Fig. 14
figure 14

Results for varying rotor RPM with fixed flight velocity of 12.9 m/s and tilt angle – 10\(^\circ\)

Full size image
Fig. 15
figure 15

Results for varying rotor velocity with fixed 5900 RPM and tilt angle – 10\(^\circ\)

Full size image
Fig. 16
figure 16

Results for varying rotor tilt angle with fixed 5400 RPM and flight velocity 12.9 m/s

Full size image
Fig. 17
figure 17

Thrust fluctuations during one rotation for 5400 RPM and flight velocity 12.9 m/s

Full size image
Fig. 18
figure 18

Propeller wake system development for different tilt angles simulated in RAMSYS

Full size image
Fig. 19
figure 19

Time signal of thrust for tilt 20\(^\circ\) during one rotation with 5400 RPM and flight velocity 12.9 m/s

Full size image

5.2 Noise prediction

Aerodynamic results indicate that the effect of tilt change with the other parameters kept fixed had the largest effect on the rotor loading (compare Fig. 14, 15 and 16). For this reason, the aeroacoustic study was focussed on cases with constant velocity of 12.9 m/s and rotational speed of 5400 RPM with a range of rotor inclinations, as analysed in Fig. 16. Noise carpets were prepared based on the calculated loadings using several acoustic solvers described in Sect. 4. The focus of the analysis was put on the blade passing frequency as it had a dominant influence on noise levels.

Fig. 20
figure 20

Noise carpets of the BPF, 5400 RPM, flight velocity 12.9 m/s, tilt angle − 10\(^\circ\). a Experiment, b UPM+APSIM, c BET+FW-H, d FLOWer+ACCO, e PUMA+KIM, f RAMSYS+ACO

Full size image

The noise directivity pattern for cases with forward tilt of the rotor (see Fig. 20) is similar for all of the computational methods. However, the accuracy of results depended on fidelity levels of applied tools with the ACCO solution closest to the experimental data. The noise carpet calculated with BET+FW-H shows qualitative agreement with other methods with regard to the noise directivity profile and the position of the maximum noise level. It indicates that the wake had no great influence in these range of tilt angles, and the phase discrepancy observed for unsteady loading calculated with BET did not considerably affect the quality of the result.

As expected, for higher tilt angles, the loading increases and so do noise levels on all calculated carpets. However, the difference in directivity between the outcome of BET and other methods can be noticed (Fig. 21). This tendency no longer occurred for the highest backward inclination of the rotor as presented in Fig. 22. An explanation of this phenomenon can be found in vortex trajectories detected in (BOS) pictures and also visible in UPM visualisations (Fig. 24). The marked positions of tip vortices for moderate positive tilt angles were always located in the proximity of the blades, strongly affecting rotor loading (Fig. 24a,  b). For 30\(^\circ\), the vortices tend to move away from the rotor plane; therefore, the result of BET neglecting wake influence again agreed with the measurement. This observation could also explain why the highest noise levels were measured for a tilt angle of 20\(^\circ\) even though the highest loading can be observed for 30\(^\circ\) inclination.

With the propeller tilted backwards, more differences in calculated noise levels between analysed methods can be observed, which is connected to increased unsteadiness in the flow and decrease of stability of numerical solutions. For these cases also, a discrepancy between the aeroacoustic results based on loading prepared with vortex lattice and vortex particles in UPM can be observed (compare Figs. 21b and 22b with 23), as high time derivatives of thrust did not appear in the latter (Fig. 17).

Fig. 21
figure 21

Noise carpets of the BPF, 5400 RPM, flight velocity 12.9 m/s, tilt angle 20\(^\circ\). a Experiment, b UPM+APSIM, c BET+FW-H, d FLOWer+ACCO, e PUMA+KIM, f RAMSYS+ACO

Full size image
Fig. 22
figure 22

Noise carpets of the BPF, 5400 RPM, flight velocity 12.9 m/s, tilt angle 30\(^\circ\). a Experiment, b UPM+APSIM, c BET+FW-H, d FLOWer+ACCO, e PUMA+KIM, f RAMSYS+ACO

Full size image
Fig. 23
figure 23

Noise carpets from UPM with particle wake + APSIM (colorbar like in Fig. 22)

Full size image
Fig. 24
figure 24

Vortex trajectories detected in BOS pictures and UPM wake visualisations

Full size image

6 Scattering effects

Although the calculated noise carpets showed satisfactory agreement with experimental data in the vicinity of the rotor, none of completely captured measurement results with the highest deviations observed further behind the rotor. Reasons for this can be found by evaluating the influence of scattering effects at the aerodynamic shielding, rotatable rotor base and ground.

6.1 Influence of the shielding

An acoustic study was carried out to observe the influence of the scattered field caused by the aerodynamic shielding placed beneath the rotor during the measurements (Fig. 25). For 5400 RPM and velocity 12.9 m/s, a case with tilt angle of - 10\(^\circ\) was chosen for the investigation as in these conditions, propeller wake is expected to interfere the most with the shielding. Calculations were conducted using ScatMan tool described in Sect. 4.4 with an assumption of a hard shielding surface (\(v_{n} = 0\)).

Figure. 26 shows that acoustic wave reflection caused an increase of up to 2 dB for the BPF on the upstream side of the shielding surface, as well as decrease of around the same value on the downstream side. However, as the dimensions of the shielding are much smaller than the wavelength of the blade passing frequency (3.8 m), sound waves reflected by the shielding caused a negligible deviation in the noise field, which can be observed comparing Fig. 27 with the baseline numerical approach in Fig. 20d. Additionally, as the presence of the shielding did not cause a change of more than 3% in the thrust values computed for chosen cases in UPM, the baseline approach to neglect its aerodynamic and aeroacoustic influence in the calculations is justifiable.

Fig. 25
figure 25

Propeller included in CFD simulation and shielding element implemented in the Scatman tool

Full size image
Fig. 26
figure 26

Acoustic field for the BPF on the shielding surface including incident noise (a), (b) and the sum of incident and scattered noise (c), (d) for 5400 RPM, flight velocity 12.9 m/s, tilt angle - 10\(^\circ\)

Full size image
Fig. 27
figure 27

Noise carpet including total (incoming and scattered by the shielding) sound pressure level of the blade passing frequency - FW-H + ScatMan for 5400 RPM, flight velocity 12.9 m/s, tilt angle − 10\(^\circ\)

Full size image
Fig. 28
figure 28

Acoustic mesh for BEM calculation

Full size image
Fig. 29
figure 29

Integration surface for FW-H and BEM

Full size image
Fig. 30
figure 30

Noise carpets including scattering effects for 5400 RPM and flight velocity of 12.9 m/s

Full size image
Fig. 31
figure 31

Noise carpets showing the difference between SPL calculated with RAMSYS+ACO and measured; 5400 RPM and flight velocity 12.9 m/s

Full size image

6.2 Installation and ground proximity effects

Further scattering effects were evaluated using ACO-FAM solver as described in Sect. 4.5. The computational setup included the part of ground and the platform on which the propeller was mounted and Fig. 28 depicts the mesh surfaces involved in the BEM calculation. More specifically, the blue surface represents the platform, the bottom black surface is the ground, and the green surface is the microphone carpet. Moreover, the elliptic FW-H boundary surface surrounding the propeller, in black, is more detailed in Fig. 29 showing the discretization of the elliptic surface and the contour plot of the real part of the first BPF. All surfaces have been discretised to guarantee at least six points per wavelength at the maximum frequency of interest.

First, the aerodynamic pressure solution on the isolated rotor blades was computed by RAMSYS and used by the solid formulation of ACO-FWH to calculate the acoustic pressure and its normal derivative on the elliptic surface surrounding the propeller (Fig. 29), the latter achieved with the automatic numerical differentiation explained in the methodology section. Then the FW-H surface was used by the BEM code to compute the incident field and the scattering surfaces (ground and the platform) were treated as rigid walls. Calculations were conducted for tilt angles − 10\(^\circ\) and 20\(^\circ\), 5400 RPM and flight velocity 12.9 m/s. As the dimensions of the analysed objects are in the order of the acoustic wavelength, their influence can be observed in the noise carpets of the blade passing frequency. The acoustic fields including scattering effects (Fig. 30) show a visible difference in both noise directivity and noise levels in comparison with base results from Figs. 20f and 21f. Nevertheless, the differential maps in Fig. 31 indicate no significant improvement in the agreement with the measurements. The slight improvement in results due to consideration of reflections is limited to the area on the advancing side of the rotor for both tilt angles.

7 Conclusions and outlook

Aeroacoustic and aerodynamic calculations were performed, indicating that measurement results for most cases were reproducible with satisfactory agreement by all computational methods, regardless of their fidelity level. The most basic and time-efficient BET shows compatibility with other tools for moderate flight velocities and propeller tilt angles, when it comes to time-averaged results, yet the code is not a reliable tool for reproducing transient loading. The BET approach loses credibility for cases where a three-dimensional wake influence becomes dominant, like flow with backward inclination of the propeller. An accurate result for such conditions can be achieved with methods including wake in the solution, from which codes incorporating viscous effects (like FLOWer, UPM with particle wake) offer more stability. The BET solution regained applicability for the highest analysed tilt angle of 30\(^\circ\), when wake vortices move further downstream from the blades.

Airfoil characteristics used in BET and PUMA allow for including the influence of compressibility and viscosity in the solution. However, one needs to be aware of XFOIL limitations when it comes to accuracy for low Reynolds numbers and lack of consideration of rotational effects in this approach.

Mid-fidelity solvers based on potential flow (UPM, RAMSYS) ensured high accuracy of thrust values for cases, where blades do not operate at stall conditions. However, the assumption of inviscid flow leads to strong underprediction of torque. A simple post-processing correction accounting for profile drag significantly improved the quality of results.

Except for the BET+FW-H solution for tilt angle 20\(^\circ\), calculated noise carpets of the blade passing frequency agreed with the measurement when it comes to the location of the highest noise level. Deviations in the results were more apparent for positive tilt angles and appeared for the area further downwash behind the rotor hub. Objects like rotor base or ground with dimensions comparable with the wavelength caused reflections affecting acoustic results. Although the noise carpets including analysed scattering effects still do not explain all deviations in the acoustic measurements, they clearly indicate the importance of reflections analysis, even for low frequencies.

In practice, the UAV’s aerodynamic performance and noise signature in the forward flight are strongly affected by the interactions between the rotors. For this reason, the future work will be dedicated to the assessment of the solvers’ capabilities to model flow conditions for the full quadrocopter configuration.