1 Introduction

To achieve high maneuverability at high speeds, modern combat aircraft rely on highly swept wings, so-called delta wings. To enhance the aerodynamic characteristics, most current combat aircraft designs are based on multi-swept delta wing configurations. For these configurations, multiple longitudinal vortices can develop at the highly swept leading edges. These vortices typically interact with each other and with shocks that are formed above the wings at high Mach numbers [1]. The specifics of these interactions strongly depend on the wing geometry and flow characteristics. While vortex/vortex interactions can have a stabilizing effect on the vortices involved, vortex/shock interactions have a destabilizing effect and can therefore cause vortex breakdown, i.e., an abrupt change in the flow structure of a vortex [2]. As vortex breakdown leads to a loss of lift and to changes in the lift distribution, it induces high pitching and rolling moments [3].

Early experimental investigations of the flow around multi-swept delta wings mostly focused on subsonic flow conditions [4,5,6]. Depending on the flow conditions and the delta wing geometry, the interaction of the primary vortices either leads to an intertwining or a merging of the vortices [3]. For a fixed geometry, the streamwise location of the intertwining or merging is shifted downstream with increasing angle of attack [7] or increasing Mach number [8]. At transonic flow velocities, vortex/shock interactions may occur above the wing, which can also lead to shock-induced vortex breakdown [1, 9].

In recent years, computational fluid dynamics (CFD) has become increasingly important in the design process of new combat aircraft. To evaluate and improve the capabilities of modern CFD codes used to predict vortex dominated flows, projects such as the "vortical flow experiment for code validation" (VFE) and its successor VFE-2 [10] and the "cranked arrow wing aerodynamics project international" (CAWAPI) [11] were initiated. While these projects showed major improvements in the prediction capabilities of modern CFD codes, they also identified a number of flow conditions that remain difficult to predict accurately, especially subsonic flows at high angles of attack and transonic flows at low to medium angles of attack [12]. In the scope of the NATO Science and Technology Organization (STO) working group AVT-316, these conditions were further studied. An overview of subsonic work is given by Sedlacek et al. [13], the complimentary overview of transonic flows is given by Russel et al. [14].

Due to the importance of the vortical flow structures for the stability-and-control characteristics of delta wing aircraft, it is necessary to understand the physics behind the vortex/vortex and vortex/shock interactions and influence of the interactions on vortex breakdown. Therefore, within the scope of the DLR project Diabolo, the flow around a generic multi-swept delta wing is investigated experimentally and numerically. The objective of this study is to improve the understanding of vortex/vortex and vortex/shock interactions and to assess the capabilities of the DLR flow solver TAU to correctly predict relevant flow features.

2 Description of the test case

In this section, an overview of the setup of the current study is given. In Sect. 2.1, the investigated geometry and flow conditions are presented. Information about the experimental and numerical setup can be found in Sects. 2.2 and 2.3, respectively.

2.1 Geometry and flow conditions

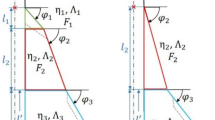
The model geometry investigated, the so-called DLR-F22-LS1 configuration, is shown in Fig. 1. It is a generic triple-delta wing with a flat-plate wing. The leading edges of all parts, i.e., forebody, levcon, strake, and main wing, are sharp. Therefore, flow separation is fixed and no boundary layer tripping was applied in the wind tunnel tests. Flow conditions are expected to be turbulent. This was checked retrospectively by comparison of experiment and CFD. The leading-edge sweep angles are \(\varphi _1 = 45^\circ\), \(\varphi _2 = 75^\circ\), and \(\varphi _3 = 45^\circ\) for levcon, strake, and main wing, respectively. The wind-tunnel model has a total length of \({0.5639}\,{\hbox {m}}\) and a wing half span of \(s = {0.25}\,{\hbox {m}}\). The origin of the coordinate system is located \({0.23416}\,{\hbox {m}}\) downstream of the apex. For the definition of the reference length and reference area, a simplified reference geometry is used, which is highlighted in gray in Fig 1. The resulting reference area is \(A_\textrm{ref} = {0.094520}\,{\hbox {m}^{2}}\), while the reference length is \(l_{\mu } = {0.227}\,{\hbox {m}}\). Finally, the moment reference point (MRP) is located \({0.14938}\,{\hbox {m}}\) downstream of the origin at \(y = z = {0}\,{\hbox {m}}\).

Fig. 1
figure 1

Geometry of the DLR-F22 model, reference area is highlighted in gray and location of pressure port sections is highlighted in red

Full size image

During the study, the Mach number was varied between \(\textrm{Ma} = {0.50}\) and \(\textrm{Ma} = {1.41}\) and the angle of attack between \(\alpha = 8^\circ\) and \(\alpha = 28^\circ\). The numerical study was performed as a blind test, before the wind tunnel measurements were carried out. In all numerical simulations, a total temperature of \(T_t = {310}\,{\hbox {K}}\) was used. The total pressure was set to \(p_t = {95}\,{\hbox {kPa}}\) and \(p_t = {90}\,{\hbox {kPa}}\) for subsonic and supersonic cases, respectively. The Reynolds number with respect to the reference length \(l_{\mu }\) varied between \({2.0}\times 10^{6} \le \textrm{Re}_{l_{\mu }} \le {3.0}\times 10^{6}\). An overview over the resulting farfield conditions of the numerical simulations is given in Table 1. In the experimental measurements, however, a lower total pressure of \(p_t = {70}\,{\hbox {kPa}}\) or \({80}\,{\hbox {kPa}}\) was used to reduce loads on the model. As a result, the Reynolds numbers of the experimental measurements were slightly lower than those of the numerical simulations. However, in the current study, it could be shown experimentally that the Reynolds number influence on the flow field in the investigated Reynolds number range is negligible.

Table 1 Farfield conditions of the numerical simulations
Full size table

2.2 Wind tunnel campaign

The measurements were carried out in the Transonic Wind Tunnel of the German-Dutch Wind Tunnel Association (DNW-TWG) in Göttingen. The DNW-TWG is a Göttingen-type wind tunnel for Mach numbers between \({0.3} \le \textrm{Ma} \le {2.2}\) and total pressures between \({30}\,{\hbox {kPa}} \le p_t \le {150}\,{\hbox {kPa}}\). The test section is \({1.0}\,{\hbox {m}}\times {1.0}\,{\hbox {m}}\). During this study, a test section with perforated walls was used for \(\textrm{Ma} \le {1.1}\), whereas a test section with a Laval nozzle was used for \(\textrm{Ma} > {1.1}\). Both test sections have been calibrated by DNW-TWG so that the Mach number remains constant on their axes. Other flow conditions depend on the particular combination of Mach and Reynolds number as well as on the total pressure and also on the presence of a model. A detailed study of these influences is currently underway in the frame of the NATO STO AVT-387 [15].

The model that was mounted on a rear sting with integrated roll control, see Fig. 2, was equipped with a total of 122 surface static pressure ports, distributed across 8 different pressure port sections. The locations of the pressure port sections are indicated in red in Fig. 1. Additionally, it featured eight dynamic pressure transducers and two temperature sensors. Due to the large number of pressure lines, which were routed through the hollow mounting sting, it was not possible to integrate a standard six component balance. Instead, the normal force as well as the pitching moment were determined using strain gauges attached to the mounting sting, an approach previously used by Chu and Luckring [16]. This approach, that was mainly chosen for safety reason to provide information on loads acting on the model and its support system in the wind tunnel, was calibrated by DNW-TWG prior to the wind tunnel tests. During calibration, errors in the normal force and pitching moment stayed below 25N and 6.5 Nm, respectively. However, during the tests, the pitching moment turned out to be less reliable. A more detailed overview over the experimental measurements is given by Rein [17].

In addition to surface pressure data and forces and moments, velocity field data were gathered using particle image velocimetry (PIV). As tracer particles, small droplets of Di-2-ethylhexyl-sebacat (DEHS) with a diameter of approximately \({1}\,{\hbox {mm}}\) were used. The PIV measurements were performed using two PCO.2000 cameras with a resolution of \(2048\times 2048\) pixels. They were placed symmetrically upstream and downstream of the measurement plane, enclosing an angle of \(100^\circ\) between them. The field of view of the cameras was \({0.2}\,{\hbox {m}}\times \, {0.11}\,{\hbox {m}}\), with a spatial resolution of \({3.1}\,\times \,10^{-3}\,{\hbox {m}}\times {1.7}\,\times \,10^{-3}\,{\hbox {m}}\). To allow for flexible adjustment of the measurement plane, both the cameras and the laser sheet optic were mounted on a movable traversing system. A stereo PIV approach was used to allow for the determination of all three velocity components. For each measurement point, 300 images were recorded with a frequency of \({10}\,{\hbox {Hz}}\) at 12 streamwise positions. The commercial software package DaVis 8.3 by LaVision was used for the recording and post-processing of the data. The displacement of the tracer particles was determined based on a cross-correlation algorithm with a final interrogation window size of \(32\times 32\) pixels and an overlap of 50%. In the area of interest above the main wing, the uncertainty of the mean velocities was \(|\vec {v}_\textrm{err}/U_{\infty }| < 0.05\) [18]. However, due to reflections from the fuselage, the uncertainty close to the fuselage was \(|\vec {v}_\textrm{err}/U_{\infty }| < 0.2\). Therefore, cases where the vortices were located close to the fuselage were not taken into account for the final evaluation.

Fig. 2
figure 2

DLR-F22 mounted in the perforated test section of the DNW-TWG [17]

Full size image

2.3 Numerical setup

The numerical simulations were performed using the DLR flow solver TAU, a three-dimensional finite-volume flow solver for hybrid meshes. A second-order central scheme with artificial matrix dissipation is used for the spatial discretization of the main flow variables, whereas a second-order Roe scheme is used for the discretization of the turbulence terms to increase stability. The temporal discretization is achieved with an implicit backward Euler scheme. All numerical results presented in this paper are based on time-accurate simulations, using either a conventional unsteady Reynolds-averaged Navier–Stokes (URANS) or a scale-resolving improved delayed detached eddy simulations (IDDES) approach. The time stepping is performed using a second-order dual-time technique, together with a lower-upper symmetric Gauss–Seidel method for the solution of the sub-iterations. In the unsteady simulations, a time step of \(\Delta t = {2.5}\,\times \,10^{-4}\,{\hbox {s}}\) and \(\Delta t = {1.0}\,\times \,10^{-6}\,{\hbox {s}}\) is used for the URANS simulations and the IDDES, respectively. Both, URANS simulations and IDDES, use the two-equation Menter shear stress transport model (Menter SST) to model turbulence. The majority of the work presented in this paper is based on URANS simulations, unless explicitly stated otherwise.

The numerical simulations are performed on a symmetric half-model of the DLR-F22-LS1 configuration. The computational grid used during this study is a hybrid grid generated with the commercial mesh generation software CENTAUR [19]. The majority of the model surface is discretized using a quasi-structured surface mesh, compare Fig. 3a. The volume mesh consists of quasi-structured zones close to the wing surface to better resolve the boundary layer flow and in the region above the strake and main wing to correctly capture the vortices above the wing. The rest of the volume mesh is discretized using tetrahedral cells, see Fig. 3b.

Fig. 3
figure 3

Visualization of the computational grid of the DLR-F22 model

Full size image

To assure a dimensionless height of the first cell of \(y^+ < 1\) on the whole wing, the height of the first cell is set to \({1.5}\,\times \,10^{-6}\,{\hbox {m}}\). A mesh convergence study with three different meshes was carried out to determine the necessary mesh resolution for the URANS simulations. The final mesh contains \({31.6}\times 10^{6}\) points for the half-wing configuration, with a minimum cell size of \({5}\,\times \,10^{-4}\,{\hbox {m}}\) in the area above the wing.

3 Results

In this section, the results of the experimental and numerical investigations are presented. First, in Sect. 3.1, an overview of the general flow characteristics of the flow over the DLR-F22 model is given. Afterwards, in Sects. 3.2 and 3.3, the influences of angle of attack and Mach number are discussed. Finally, in Sect. 3.4, a comparison between conventional URANS simulations and scale-resolving IDDES is presented.

3.1 Basic flow structure

The basic flow field that develops around the DLR-F22 model remains qualitatively similar across a large range of Mach numbers and angles of attack. For one case, \(\textrm{Ma} = {0.85}, \alpha = 16^\circ\), the flow structure is shown in Fig. 4. Here, streamlines originating from different parts of the leading edge are highlighted in different colors. The flow field is dominated by three primary vortices that develop along the leading edges of the forebody, the strake, and the main wing. They are labeled as inboard vortex (IBV), midboard vortex (MBV) and outboard vortex (OBV), respectively.

Fig. 4
figure 4

Visualization of the flow structure above the DLR-F22 model, \(\mathrm{{Ma} = 0.85, \alpha = 16^\circ }\)

Full size image

At the leading edge of the levcon, no separate vortex develops. Instead, the separated shear layers from levcon and strake immediately interact, forming a combined vortex, the midboard vortex. Further downstream, the IBV and the MBV interact and finally merge with each other. Additionally, at transonic speeds, shocks form above the strake and main wing, and interact with the vortices, which can lead to shock-induced vortex breakdown, compare Sect. 3.2. For the case of \(\textrm{Ma} = {0.85}, \alpha = 16^\circ\), a visualization of the shock based on Schlieren images is shown in Fig. 5.

Fig. 5
figure 5

Schlieren image showing the formation of shocks above the DLR-F22 model, \(\mathrm{{Ma} = 0.85, \alpha = 16^\circ }\)

Full size image

3.2 Influence of the angle of attack

For delta wings, the circulation and hence the strength of the primary vortices generally increase with increasing angle of attack. However, with increasing circulation, the stability of the vortices declines, resulting in vortex breakdown once a critical angle of attack is reached. Considering \(\textrm{Ma} = {0.85}\), a comparison between CFD and experiment of the development of the normal force coefficient \(C_{Fz}\) and the pitching moment coefficient \(C_{My}\) is shown in Fig. 6. The experimental results show an almost linear increase in the normal force up to \(\alpha = 15^\circ\). At higher angles of attack, the normal force still increases, but at a reduced rate. The cause of the reduced slope is the onset of vortex breakdown of the MBV at the trailing edge. With increasing angle of attack, the location of vortex breakdown moves upstream, leading to a reduction of the normal force coefficient and at the same time an increase of the pitching moment coefficient.

Fig. 6
figure 6

Development of \({C_{Fz}}\) and \({C_{My}}\) with increasing angle of attack, \(\mathrm{{Ma} = 0.85}\)

Full size image
Fig. 7
figure 7

Influence of the angle of attack on the surface pressure distribution, comparison between CFD and experiment at pressure port sections \({S_1 - S_5}\), \(\mathrm{{Ma} = {{0.85}}}\)

Full size image

While the development of the normal force coefficient shows an acceptable agreement between both numerical data sets and the experimental data, large discrepancies can be observed in the pitching moment coefficient of the URANS results. These differences are caused by the fact that in the URANS simulations, the vortex breakdown of the OBV occurs too early, which leads to an additional increase in the pitching moment coefficient as compared to the experiment. Figure 7 compares the pressure coefficient \(c_p\) between URANS simulations and experiment at five different pressure port sections for different angles of attack. Here, the location of vortices is indicated by low values of \(c_p\). Above the forebody, levcon, and strake, shown in Fig. 7a–c, the agreement between URANS and experiment is quite good. Only further downstream above the main wing, larger differences occur. Figure 7e clearly shows the early vortex breakdown of the OBV in the numerical results. The IDDES results do not show this behavior, as will be discussed in Sect. 3.4, and therefore show a much better agreement with the experimental pitching moment coefficient.

As was already exemplified in Fig. 4, the IBV and the MBV strongly interact with each other, eventually merging with each other. To allow for a more detailed comparison between the different cases, the vortex axes were identified using a predictor-corrector approach [20]. After the vortex axes have been identified, additional flow field data can be extracted along the vortex axes. Additionally, it is possible to evaluate the flow field in volume slices normal to the local vortex axis to investigate the velocity or pressure profile within the vortex core.

The trajectories of the three different primary vortices are shown in Fig. 8, where the positions of the axes of the three primary vortices in the xy-plane are plotted for different angles of attack. With increasing angle of attack, the location of vortex merging moves downstream, and no longer occurs over the wing at \(\alpha = 24^\circ\). A similar effect was previously observed, for example, by Verhaagen et al. [7] for a double delta wing at subsonic conditions. The reason for the downstream shift of vortex merging is the increasing vertical distance between the IBV and the MBV with increasing angle of attack, which in turn leads to a reduced interaction between the two vortices.

By extracting the axial velocity in the vortex core, \(v_{x,A}\), it is possible to calculate the axial velocity deficit \(\delta = 1 - (v_{x,A}/U_{\infty })\) of the vortex. If \(\delta > 0\), the vortex has a wake-type velocity profile, whereas for \(\delta < 0\), it has a jet-type velocity profile. For values of \(\delta \ge 1\), an area of recirculating flow exists in the vortex core, which indicates vortex breakdown. The development of the axial velocity deficit within the vortex cores of the IBV and the MBV is shown in Fig. 9a, b, respectively. The location of vortex breakdown is marked by the strong increase in \(\delta\). As was already mentioned above, the location of vortex breakdown of the MBV moves upstream with increasing angle of attack, from \(x/l_{\mu } \approx {1.1}\) for \(\alpha =16^\circ\) to \(x/l_{\mu } \approx {0.25}\) for \(\alpha =24^\circ\). At \(\alpha = 12^\circ\), no vortex breakdown occurs.

Fig. 8
figure 8

Influence of the angle of attack on the trajectory of the vortex cores, \(\mathrm{{Ma} = {{0.85}}}\)

Full size image
Fig. 9
figure 9

Influence of the angle of attack on the streamwise development of the axial velocity deficit of the inboard and midboard vortex, \(\mathrm{{Ma} = {{0.85}}}\)

Full size image

The swirl rate \(S = v_{\varphi ,\textrm{max}}/v_{x,A}\), formed with the maximum azimuthal velocity \(v_{\varphi ,\textrm{max}}\) and the axial velocity \(v_{x,A}\) on the vortex axis, is a commonly used measure for the stability of a vortex. For low-speed flows, vortex breakdown occurs when a critical value \(S_\textrm{crit}\) of the swirl rate is reached, with \({1.12} \le S_\textrm{crit} \le {1.41}\) [21]. The development of S along the vortex axis of the IBV and the MBV is plotted in Fig. 10 for different angles of attack. Additionally, shock positions are indicated by dashed lines and the range of \(S_\textrm{crit}\) is marked by a gray line. Here, vortex breakdown is marked by an abrupt reduction of S.

Furthermore, it can be seen that vortex breakdown of the MBV always occurs slightly downstream of a shock. To decide whether the vortex/shock interaction is the cause of the vortex breakdown, or whether the shock forms due to the presence of a recirculation bubble in the vortex core, the development of S is further analyzed. Two cases are identified. At \(\alpha = 16^\circ\), a strong increase in S only occurs after the interaction with the shock. At \(\alpha = 20^\circ\) and \(\alpha = 24^\circ\), however, the vortex/shock interaction occurs after the increase of S, when \(S > S_\textrm{crit}\). This suggests that for the case \(\alpha = 16^\circ\), the vortex breakdown is shock induced, whereas for \(\alpha = 20^\circ\) and \(\alpha = 24^\circ\), it is not.

Fig. 10
figure 10

Influence of the angle of attack on the streamwise development of the swirl number of the inboard and midboard vortex, \({\textrm{Ma} = {{0.85}}}\)

Full size image

3.3 Influence of the Mach number

The second part of the study deals with the influence of the Mach number on the resulting vortex interactions. Experimental and numerical surface pressure distributions are compared with each other at different Mach numbers in Fig. 11.

Fig. 11
figure 11

Influence of the Mach number on the surface pressure distribution, comparison between CFD and experiment at pressure port sections \({S_1 - S_5}\), \({\alpha = 16^\circ }\)

Full size image

With increasing Mach number, the strength of the three primary vortices is reduced. This is indicated by higher minimal pressure coefficients, i.e., by a reduced suction. A comparison between numerical and experimental results shows good agreement at all Mach numbers except at \(\textrm{Ma} = {0.85}\). The differences are probably caused by the fact that at \(\textrm{Ma} = {0.85}\) vortex breakdown of the OBV is predicted further upstream than in the experimental tests. This was already discussed in Sect. 3.2. For the remaining Mach numbers, no similar disagreements were observed within the investigated parameter range. This may indicate that differences are caused by a failure to correctly predict vortex/shock interaction, because the test case \(\textrm{Ma} = {0.85}\) is the only one with vortex/shock interaction above the wing.

In Fig. 12, the position in the xy-plane of the vortex axes of the different primary vortices is shown for different Mach numbers at \(\alpha = 16^\circ\). Qualitatively, the vortex/vortex interactions are similar for all Mach numbers investigated. However, with increasing Mach number, the location of the vortex merging of the IBV and the MBV moves downstream, from \(x/l_{\mu } \approx {0.35}\) at \(\textrm{Ma} = {0.50}\) to \(x/l_{\mu } \approx {1.25}\) at \(\textrm{Ma} = {1.10}\). At \(\textrm{Ma} = {1.41}\), no vortex merging was observed above the wing; however, the trajectories of the IBV and the MBV suggest that they will merge downstream of the trailing edge. This is consistent with observations of Erickson et al. [8], who observed delayed vortex merging with increasing Mach number for the case of a strake–wing configuration.

Fig. 12
figure 12

Influence of the Mach number on the trajectory of the vortex cores, \({\alpha = 16^\circ }\)

Full size image

In Sect. 3.2, the downstream movement of the vortex-merging location with increasing angle of attack was caused by the increasing distance between the IBV and the MBV. However, this is not the case here, as the distance between the IBV and the MBV remains almost constant in the investigated Mach number range. Instead, vortex merging is delayed due to a reduction in vortex strength with increasing Mach number. This can be seen in Fig. 13, where the development of the non-dimensional vorticity magnitude, \(|\vec {\omega }^*| = |\vec {\omega }|l_{\mu }/U_{\infty }\), is shown along the vortex axes of the IBV and the MBV for different Mach numbers. Due to the reduced strength of the vortices, their interaction with each other decreases, which leads to lower induced velocities and therefore a delayed vortex merging.

Fig. 13
figure 13

Influence of the Mach number on the streamwise development of the vorticity magnitude of the inboard and midboard vortex, \({\alpha = 16^\circ }\)

Full size image

3.4 Scale-resolving simulations

While the results of the URANS simulations generally showed acceptable agreement with the experimental measurements, at \(\textrm{Ma} = {0.85}\) greater differences were observed above the main wing. Therefore, for three different angles of attack, \(\alpha = 12^\circ\), \(\alpha = 16^\circ\), and \(\alpha = 20^\circ\), scale-resolving simulations based on an IDDES approach were performed for this Mach number as well. They were carried out on the same mesh as the URANS simulations; however, for the IDDES, a smaller time step of \(\Delta t = {1.0}\,\times \,10^{-6}\,{\hbox {s}}\) was used, compared with a time step of \(\Delta t = {2.5}\,\times \,10^{-4}\,{\hbox {s}}\) for the URANS simulations.

A comparison of surface pressures at two different pressure port sections above the wing, \(S_4\) and \(S_5\), between URANS, IDDES, and experiment is shown in Fig. 14. The IDDES achieves much better agreement with the experiment than the URANS simulation. The greatest differences occur close to the leading edge of the main wing, see Fig. 14b. While both, the IDDES results and the experimental measurements, still show a pronounced OBV, the URANS simulation instead predicts completely separated flow. This can also be seen in Fig. 15 that compares the x-velocity component in the flow field above the main wing at \(x/l_{\mu } = {1}\) for all three data sets. The position of vortex cores is clearly evident due to the reduced velocity in the vortex cores. Results from PIV and IDDES, shown in Fig. 15a, b, respectively, are in good agreement with each other, both with respect to the position of the vortex cores and the velocity distribution within the vortices. In contrast, the URANS shows a large separation bubble at the leading edge of the main wing. Based on the current results, it is not possible to give a clear explanation for this behavior. However, a possible explanation for the difference between URANS and IDDES results could well be the reduced numerical dissipation of the IDDES compared with that of the URANS. For the IDDES, a low-dissipation, low-dispersion spatial discretization scheme was used, whereas for the URANS simulation, a conventional second-order central scheme was used. The increased numerical dissipation of the URANS simulations could lead to a premature dissolution of the OBV.

Fig. 14
figure 14

Comparison of surface pressure distributions between experiment, URANS simulation and IDDES, \(\mathrm{{Ma} = {{0.85}}, \alpha = 16^\circ }\)

Full size image

To allow for a more detailed comparison of URANS and IDDES, in Fig. 16, the development of the axial velocity deficit \(\delta = 1 - (v_{z,a}/U_{\infty })\) is shown for three different angles of attack along the axis of the MBV. Also, where available, data from PIV measurements are included. For \(x/l_{\mu } \le {0.25}\), the IDDES results show much higher axial velocities in the vortex core than the URANS simulations. Further downstream, the results become more similar. An exception is the case of \(\alpha = 12^\circ\), where the IDDES results show a much stronger shock/vortex interaction than the URANS results at \(x/l_{\mu } \approx {0.85}\).

Fig. 15
figure 15

Comparison of the distribution of the x-velocity component between URANS, IDDES, and PIV in the plane \({x/l_{\mu } = 1}\), \(\mathrm{{Ma} = {{0.85}}, \alpha = 16^\circ }\)

Full size image
Fig. 16
figure 16

Influence of the angle of attack on the axial velocity deficit in the vortex core, comparison between URANS, IDDES, and PIV, \(\mathrm{{Ma} = {{0.85}}}\)

Full size image

Due to strong reflections from the leading edge, only the rearmost PIV measurement locations could be analyzed. However, where available, the velocity data from PIV are in good agreement with the numerical results.

4 Summary and conclusion

A combined numerical and experimental investigation of the structure of the flow around a generic multi-swept delta wing was presented. A special focus was on the analysis of the developing vortex/vortex and vortex/shock interactions above the wing. The Mach number was varied between \({0.5} \le \textrm{Ma} \le {1.41}\) and the angle of attack between \(8^\circ \le \alpha \le 28^\circ\). Vortex/vortex interactions, including vortex merging of the two innermost vortices, was observed over a large range of Mach numbers and angles of attack. The location of vortex merging moved downstream with increasing angle of attack or increasing Mach number. In the case of increasing angles of attack, this was caused by the increasing vertical distance between the vortices, whereas in the case of an increase in Mach number, a reduction of the vortex strength of the involved vortices was identified as the cause. In both cases, the change in vortex interaction observed was gradual. Additionally, at \(\textrm{Ma} = {0.85}\), vortex/shock interaction occurred above the wing. By analyzing the development of the swirl number along the vortex axis, it was possible to identify one case, \(\alpha = 16^\circ\), where the vortex/shock interaction leads to shock-induced vortex breakdown.

The comparison between experimental and numerical data generally showed acceptable agreement between both data sets for the majority of the investigated flow conditions. One noticeable exception is the transonic case, \(\textrm{Ma} = {0.85}\), where large discrepancies were observed when vortex/shock interactions occured above the wing. The biggest differences occurred at the leading edge of the main wing, where conventional URANS simulations failed to correctly predict the formation of a stable primary vortex. Instead, the URANS simulations predicted a large area of reversed flow at the main wing which negatively impacted the prediction of the surface pressures and the pitching moment coefficient. Using a scale-resolving IDDES approach, it was possible to remedy these deficiencies and achieve much better agreement with the experimental results.