1 Motivation

Increasing the application of high-fidelity numerical simulation tools in the early stages of product design is considered to be one of the key drivers for shortening design cycles and reducing risks and costs in the aerospace industry [1]. Employing Multidisciplinary Optimization (MDO) has been identified as one of the most promising tasks in this context. However, there is still a long way to go to fulfill the industrial requirements concerning efficiency, accuracy and comprehensiveness. This work describes a gradient-based trimmed aeroelastic optimization process which is used as an MDO sub-process within DLR’s project VicToria (Virtual Aircraft Technology Integration Platform), a follow-up project of Digital-X [2]. The MDO activities in VicToria target at overcoming the current shortcomings of MDO by combining and further enhancing state-of-the-art Computer Aided Engineering techniques.

An additional focus of this work is an efficient integration of a parametric Computer Aided Design (CAD) model into the optimization process. The challenge is to support adjoint-based optimization processes. The adjoint method computes exact gradients at a computational cost which is independent on the number of design parameters. To get the total derivative of a cost functional, each workflow module is either required to be analytically differentiated or to employ finite differences to compute its partial gradients. Consequently, a shape parameterization module needs to provide derivatives of the surface shape with respect to design variables. Differentiated CAD Kernels like OpenCASCADE [3] or PADGE [4] offer this possibility, but in an industrial context, these special solutions are not likely to replace the established commercial CAD systems. The so-called design velocity method [5] employs finite differences on tessellated CAD-surfaces to compute the gradients. This approach is independent on the CAD software, but the surface gradient accuracy is sensitive to the perturbation step size.

This work follows the approach of Bobrowski et al. [6]. The basic idea is to create a surrogate model for discrete surface displacement fields with respect to aircraft shape parameters a-priori defined by a design engineer. This requires a parameterized CAD model which can be evaluated several times to generate a sampling data set. With the training data, a Proper Orthogonal Decomposition (POD) based Reduced Order Model (ROM) can be built and used for fast and robust displacement and sensitivity predictions. This approach offers the main advantage of having analytic geometric sensitivities which are required for an efficient adjoint-based optimization. At the same time, the approach enables a parameterization setup using the designer’s CAD system of choice and allowing for sophisticated geometrical features. Finally, an optimization workflow which solely relies on Unix-based High Performance Computing (HPC) systems can be achieved.

So far, CAD-ROM parameterizations have been investigated for up to 14 design variables by Bobrowski et al. [6] showing a low geometric prediction error. Stannard [7] employed a 74-dimensional CAD-ROM parameterization for an adjoint-based optimization, but did not evaluate the CAD-ROM method itself. In a typical gradient-based shape optimization problem the design space usually spans over several hundreds of design variables This work evaluates the feasibility of the CAD-ROM method for a high-dimensional parameterization with 126 degrees of freedom and a representative optimization setup including trimming, thrust scaling and static aeroelastic coupling. Such optimization setups for full aircraft configurations have been treated before by the aerodynamic optimization community [7,8,9] and high-dimensional CAD-ROM parameterizations have already been successfully applied by the authors for even more complex aerodynamic [10] and multidisciplinary [11] optimization cases. However, this work focuses on the parameterization aspect itself and highlights potentials and shortcomings of the CAD-ROM method.

First, the optimization process with its components and in particular the CAD-ROM is introduced in Sect. 2. The description of the test case, a long-range transport aircraft configuration, and the problem setup is given in Sect. 3. In Sect. 4, optimization results are presented to evaluate the potentials of applied methods with a special focus on the high-dimensional CAD-ROM performance. Outcomes are reviewed in Sect. 5, which also includes a brief introduction to future work.

2 Methods and tools

The section gives an overview of the trimmed aeroelastic optimization process and explains the tools involved in the underlined subsections.

The primal optimization process is drafted in Fig. 1. The process is driven by a gradient-based optimization algorithm which reduces the aerodynamic drag of an aircraft with respect to a set of shape design parameters.

Fig. 1
figure 1

Schematic description of the trimmed aeroelastic optimization process with potential extensions a, b to MDO

Full size image

The only constraints applied in the process are a balance of all forces and moments acting on the aircraft. This balance is enforced by a trim algorithm (Sect. 2.1) for each new design proposed by the optimization algorithm. Basically, the optimization algorithm treats an unconstrained problem and the trim algorithm ensures that each design is feasible by adapting the trim parameters. This requirement comes from the VicToria MDO architectures [11] which are using this process. For each trim iteration, at least one aeroelastic coupling iteration between the Computational Fluid Dynamics (CFD) and the Computational Structural Mechanics (CSM) domains is performed. The aeroelastic coupling starts with the deformation of the CFD mesh. Therefore, surface displacements coming from the shape parameterization (Sect. 2.2) and from the structural analysis are summed up on the boundaries of the CFD mesh. The boundary displacements are then propagated into the volume mesh (Sect.2.3). The following aerodynamic analysis is performed by a high-fidelity CFD solver (Sect. 2.4). The aerodynamic loads are interpolated from the CFD to the CSM domain (Sect. 2.5) and act as boundary conditions for the structural analysis (Sect. 2.6). The obtained structural displacements are interpolated to the CFD domain and the next aeroelastic coupling iteration starts. The gradients are efficiently computed by the discrete adjoint approach [12, 13] using the differentiated parameterization and mesh deformation methods as well as the linearized CFD solver. Since the coupled aerostructural adjoint method introduced by Martins et al. [14] has not yet been integrated into this process, the gradients handed over to the optimization algorithm do not account for secondary effects representing the inherently coupled aeroelastic displacement response resulting from a design parameter change.

Both the primal and the adjoint workflows are embedded within FlowSimulator [15, 16], an environment for massively parallel multiphysics simulations. Its backbone is the FlowSimulator Data Manager, which allows for an efficient in-memory data exchange between DLR’s in-house plug-ins, i.e. all tools except the structural solver.

The afore-mentioned connection to the VicToria MDO chains is indicated by the dotted lines in Fig. 1. The presented trimmed aeroelastic optimization process requires as input a pre-sized structural model, which is constant in this exercise, but is regularly updated in an actual MDO workflow [17].

2.1 Trim algorithm

The trim algorithm employs Newton’s method for finding the roots of the force and moment balances accounting for aerodynamic loads, gravity forces and the engine thrust. The parameters are the angle of attack, the deflection angle of the Horizontal Tail Plane (HTP) and the thrust. The required Jacobian is updated by Broyden’s Bad Method and the convergence is improved using the Aitken method for accelerating vector sequences. A fast convergence of the trim algorithm is crucial for the optimization runtime, since each trim iteration involves several aeroelastic coupling iterations.

Since the optimization algorithm does not directly consider the trim constraints and parameters, the objective functional gradient is corrected as suggested by Merle et al. [18] to take into account the actions of the trim process.

2.2 Shape parameterization

The shape parameterization is based on an underlying CAD model, which is replaced during the optimization by a ROM. First, the preprocessing steps (Sects. 2.2.1, 2.2.2) which have to be carried out before the optimization is started are presented. Second, the online phase which generates displacement and geometric sensitivities (Sect. 2.2.3) and interpolates them onto the CFD domain (Sect. 2.2.4) is described.

2.2.1 CAD model and surface discretization

The shape parameterization starts with the creation of a fully parametric CAD model, as described by Ronzheimer [19]. The work was done with the commercial software package CATIA V5, but any other parametric CAD system could be used instead. The advantage of employing CATIA V5 is not only its powerful features, but also its popularity and acceptance in the aerospace industry which is supposed to make the CAD-ROM approach more attractive to industrial designers. The CAD model was constructed by combining several CAD parts corresponding to main aircraft parts like wing, fuselage, empennage, etc. Each part is parameterized by a set of construction parameters. Large shape changes are defined by classic conceptual design parameters like aspect ratio, sweep, twist etc. Small shape changes are introduced by variations of Bspline control points defining for example airfoil and belly fairing sections. The designer is essentially free to define his parameterization of choice. All parameters are linked to so-called construction tables which can be externally provided. Besides displacement and sensitivity predictions, the CAD-ROM should later on also be capable of providing geometric functionals such as fuel tank volume and roll and taxi clearances which are required in an MDO process. Therefore, the respective measurements are also defined within the CAD model.

The continuous CAD surfaces need to be discretized to extract later displacement fields as input for the CAD-ROM generation. In contrast to the approach described by Bobrowski et al. where discretization points are distributed on surface intersections or additional section cuts directly within the CAD model, the present approach uses an additional meshing tool which produces a block-structured surface mesh. A sufficiently dense surface mesh enables the resolution of even small geometric features, as demonstrated in the wing-pylon-junction area in Fig. 2. The surface mesh is computed with the tool Ansys ICEM CFD Hexa, which requires the definition of a blocking strategy compatible with the underlying CAD model. The block-structured method ensures a constant surface mesh topology which allows the tracking of displacements with respect to a design parameter change.

Fig. 2
figure 2

Block-structured surface mesh for displacement field computations at the wing-pylon intersection

Full size image

2.2.2 Reduced order model generation

During this phase the ROM is constructed by iteratively evaluating the CAD model following a Design of Experiment (DOE), assembling the snapshot matrix and then applying POD to this matrix based on all surface displacement fields. The necessary steps are:

  1. 1.

    Generation of a DOE plan

  2. 2.

    Sampling Data generation

  3. 3.

    Extraction of displacement fields

  4. 4.

    Generation of the POD-based ROM

The DOE plan is generated using DLR’s in-house Surrogate Modeling for AeRo data Toolbox SMARTy [20] which supports different DOE algorithms such as Full Factorial Design, Latin Hypercube Sampling (LHS), Sobol and Halton sequences. The bounds should cover the design space intended to be used during the optimization, since extrapolation may decrease the prediction accuracy of the obtained ROM. The DOE is executed by sweeping through the design tables and updating the CAD surfaces and the structured surface mesh according to each sample. After the sampling data generation, the CAD model is no longer needed, except when more samples are required, or when a new CAD-ROM with different parameters or larger bounds is generated.

Next, a so-called snapshot matrix is constructed by concatenating all computed surface displacement fields. A POD basis is obtained by applying singular value decomposition to this snapshot matrix. Afterwards, displacement fields \(\Delta {\tilde{\user2{X}}}_S\) can be reconstructed according to

$$\Delta {\varvec{\tilde{X}}}_S \left( {{\varvec{D}}^j } \right) = \mathop \sum \limits_{i = 1}^n a_i \left( {{\varvec{D}}^j } \right)\phi ^i$$
(1)

with \(\phi\) as the left-singular vectors, n the number of valid DOE samples, Dj a design vector from the DOE plan and a(Dj) as POD coefficients corresponding to Dj. The influence of each POD mode onto the system behaviour is governed by the corresponding eigenvalue, also referred to as relative information content. Consequently, the POD subspace can be truncated to \(m < n\) modes by applying a pre-defined cut-off criterion. To represent the entire design space with the POD model, it is important that geometrical features, which may be non-linear with respect to a variation of D, are covered by the DOE. An adequate resolution in each dimension and a uniform distribution of samples is therefore crucial.

2.2.3 Reduced order model evaluation

During the online phase, the CAD-ROM is evaluated to provide surface displacements for a design vector which differs from the initial sampling points. Thus, displacement fields for arbitrary design parameters can be computed by interpolating the POD coefficients and multiplying them with the POD modes. Among the most common interpolation methods are Radial Basis Functions (RBF) with a Thin Plate Spline (TPS) kernel

$$\tilde{a}_i \left( {\varvec{D}} \right) = \mathop \sum \limits_{j = 1}^m \gamma _j^i \varphi \left(\left\| {{\varvec{D}} - {\varvec{D}}^j } \right\|\right)$$
(2)

The coefficients \(\gamma_j^i\) are chosen to match exactly the training data with the TPS function \(\varphi\). For the prediction of geometric sensitivities, i.e. the derivative of the surface displacements with respect to the design parameters, (1) and (2) are differentiated with respect to D.

An alternative to the interpolation of POD coefficients would be to use them directly as optimization parameters as successfully applied by Volpi et al. [21]. Since the handling of actual aircraft design parameters rather than abstract POD coefficients and their communication with other disciplines in an MDO context seems more intuitive, the interpolation-based approach has been followed in this work.

Note that more advanced interpolation techniques such as Kriging have shown superior results in various other ROM applications and might yield even more accurate results than the herein pursued RBF-based technique.

2.2.4 Process integration

The CAD software can be fully replaced by the steps described in the previous subsection and is out of the loop during the optimization phase. The final integration of the CAD-ROM into the optimization process requires an interpolation of the displacement or geometric sensitivity predictions given on the structured surface mesh onto the boundaries of the mesh representing the CFD domain. Therefore, the same interpolation method is used as for aeroelastic coupling. The additional error related to this mesh interpolation has not been evaluated in detail in this work, since it showed to be at least 1–2 orders of magnitude smaller than the error introduced by the CAD-ROM prediction. By integrating the mesh interpolation into the online phase, remeshing could be done during the optimization without the need to regenerate the CAD-ROM.

A few features have been included in the CAD-ROM implementation to make its application more convenient for optimization. Thus, it is possible to load several ROMs built using the same block-structured surface mesh and to return a linear superposition of displacements or sensitivities according to a list of input design vectors. This feature is based on the underlying assumption that the CAD software acts approximately linear with respect to changes of design parameters. The option was introduced to merge design spaces in case CAD-ROMs were built for different sets of design parameters in the preprocessing phase. Furthermore, it is also possible to get predictions from input values relative to the baseline and for design vectors which are defined only on a subspace of the design space spanned by the CAD-ROM. Values on missing dimensions are automatically replaced by values from the baseline geometry. To support these additional features, it is necessary that the CAD-ROM parameterization interface is initialized with the baseline vectors.

2.3 Mesh deformation

The employed mesh deformation tool is based on the theory of linear Elasticity Analogy (EA) as described by Stein et al. [22]. The mesh is modeled as an elastic solid with a variable Young’s modulus which is reciprocal to the volume of the local mesh element in the baseline mesh. Small elements are artificially stiffened and basically perform a rigid body motion, whereas large elements absorb the deformation. As the applied displacements are relatively small, it is sufficient to linearly approximate the model. The resulting linear elasticity equations are discretized by an Finite-Element Method (FEM) and solved on the baseline mesh for each optimization, trim or aeroelastic iteration.

Since the problem is self-adjoint, the implementation of the EA method for computing the final shape sensitivities is straight-forward, as proposed by Nielsen and Park [23].

2.4 Aerodynamic analysis

The Flow is computed by means of the finite-volume RANS method TAU [24] developed at DLR. The negative extension of the Spalart–Allmaras (SA-neg) turbulence model is used for this process. The compressible steady-state flow is computed in fully turbulent conditions on unstructured median-dual grids. The second-order accurate discretization is based on a matrix-dissipative central convection scheme and Green-Gauss gradients for the viscous flux. The discretized set of equations governing the transport of mass, momentum, energy and the SA-neg transport variable are solved by virtue of an agglomeration multigrid method based on the full approximation scheme (FAS). Several implicit-Euler relaxation steps are applied on every grid level. The corresponding linear problems are treated by a symmetric forward–backward Gauss–Seidel (LUSGS) iteration.

For employing the discrete adjoint method in in TAU, the residual of the second-order accurate flow discretization is fully linearized with respect to the conservative flow variables including the turbulence model. The adjoint-residual terms corresponding to the remote-stencil terms of the second-order discretization are reconstructed in two passes, so that the memory requirements of the discrete-adjoint method are similar to the non-linear flow solver. The discrete adjoint RANS problem is solved with a GMRES method, preconditioned by the linear counterpart to the FAS multigrid method. Multigrid smoothing, in turn, was performed by the implicit-Euler method, wherein the transpose of the primal LUSGS operator is applied. More details are provided by the work of Stück [25].

2.5 Load and displacement transfer

The load and displacement transfer are based on a Moving Least Squares (MLS) interpolation method, originally proposed by Lancaster and Salkauskas [26]. It is a mesh-free approach which first constructs local polynomial fits and then assembles them continuously over the whole domain by generating a global MLS interpolation matrix. Data on given target points is forced to be interpolated. The method is by built conservative and since the MLS matrix is used for displacement and its transpose for loads transfer also consistent in the context of aeroelastic coupling.

2.6 Structural analysis

The structural analysis is performed by the commercial software package MLS Nastran. The tool performs a linear static analysis by solving a linear system assembled from an FEM-based discretization of the structural model. Besides the structural displacements, the tool also computes the aircraft’s total mass and centre of gravity, both required to set up the balance of forces and moments for trimming.

3 Test case description

The section describes the aircraft to be optimized and details relevant settings and criteria applied for the optimization. The chosen wing section parameterization is presented and an evaluation of the CAD-ROM prediction error for this specific parameterization is carried out.

3.1 Aerodynamic and structural models

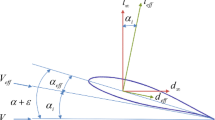
The test object used in this study is a generic multi-disciplinary research test case representing a typical configuration for a modern long range wide body aircraft. The aerodynamic analysis is performed with flow-through nacelles and the thrust is modeled by scalable force vectors aligned with the engine axis, see Fig. 3.

Fig. 3
figure 3

A generic long-range transport aircraft with scalable thrust vectors as optimization test case

Full size image

Mesh convergence studies as a verification method for high-fidelity aerodynamic analysis is often neglected in aerodynamic or aeroelastic shape optimization. Nevertheless, it is a crucial part of the work to increase trust in the applied methods and finally in the optimization result. Therefore, trimmed aeroelastic analysis has been performed on a family of five continuously refined CFD meshes. Since the geometry and the considered maneuvers are symmetric, only one half of the CFD domain has been meshed. The number of mesh points and of assigned computational cores per mesh level are listed in Table 1. The convergence criteria for trimming, aeroelastic coupling and for the flow solver were set as described in Sect. 3.3. Figure 4 shows a continuous reduction of the cruise drag over the refinement levels relative to the L1 value. The computational effort for the L4 and L5 meshes was found to be already high for optimization purposes and the difference in drag with respect to the coarser L3 level is not significant. Therefore, it was decided to perform the optimization only on the L1–3 mesh levels.

Table 1 CFD mesh refinement levels with associated computational resources used for analysis and optimization
Full size table
Fig. 4
figure 4

Mesh convergence study with computational effort for a trimmed aeroelastic analysis

Full size image

The runtimes in Fig. 4 are substantially improved in the optimization using restart solutions for the aerodynamic analysis on equal mesh levels and better initial guesses for the trim parameters and structural displacements.

The structural model represents the load-bearing components of the entire aircraft by FEM shell elements which are internally connected by Rigid Body Elements (RBE), see Fig. 5. Since only wing and empennage boxes are modeled, additional RBEs are placed at the wing and at the horizontal and vertical tail plane leading and trailing edges to improve the load and displacement transfer. Aluminum was chosen as structural material. Furthermore, the structural model also includes distributed payload, secondary masses and fuel masses. The model was pre-sized for the baseline outer shape by accounting for several hundreds of load cases.

Fig. 5
figure 5

Structural model for aeroelastic coupling

Full size image

3.2 Wing section parameterization

The parameterization for this test case is defined by 9 upper and 9 lower Bspline control points on 7 wing sections along the wing span, as shown in Fig. 6. The control points are free to move in vertical direction which results in 126 degrees of freedom. The bounds are set to ± 1% local chord length allowing for maximal displacements of about ± 11 cm. Parameter bounds of control points close to the trailing edge are more restrictive to avoid surface intersections. Bspline control points directly at the leading and trailing edges are fully fixed. Hence, the twist distribution is constant.

Fig. 6
figure 6

Wing CAD part with sections chosen for Bspline-based parameterization

Full size image

To train the CAD-ROM, a Sobol sequence with 3000 samples was defined for the introduced 126-dimensional design space. The run times per sample for CATIA V5 and Ansys ICEM CFD Hexa were about 1.2 min and 0.2 min, respectively. This enabled the computation of around 1000 samples per day. The displacement fields were extracted from a 30,000-nodes structural surface mesh and a cut-off of 99.999999% of the relative energy was used to reduce the number of POD modes from 3.000 to 1.704, since retaining more modes did not enhance the prediction accuracy for this particular case. Only the TPS method turned out to be feasible for interpolating the POD coefficients with a turnaround time of around 8 min on a 16 core compute node of DLR’s HPC system CASE. As mentioned in Sect. 2.2.3, Kriging interpolation is assumed to show more accurate results. However, interpolating the given number of reduced POD coefficients would have taken several weeks. The tested implementation of the Kriging interpolation is only partly shared memory parallelized and treats each output variable separately. The associated hyperparameter optimization and the necessity to invert the correlation matrix for each POD coefficient were detected as show stoppers. In consequence, this approach revealed to be inapplicable due to extremely high runtimes, even if using more computational resources.

As afore-mentioned, the CAD-ROM prediction error is related to the number of samples used for training. To measure this relation, two additional CAD-ROMs were built using only the first 1000 and 2000 samples of the Sobol sequence. The maximal error for parameterization displacements was computed by predicting additional 100 validation samples which have been generated using an LHS strategy. Figure 7 shows that the POD-based prediction improves quickly with the number of samples used for training, whereas the additional POD coefficient interpolation by TPS dominates the final error.

Fig. 7
figure 7

Relation between CAD-ROM displacement prediction error and number of training samples based on 100 validation samples

Full size image

Note that for the POD predictions, the globally optimal POD coefficients are computed by projecting the given displacements of the validation samples onto the POD basis rather than using an interpolation algorithm. For the CAD-ROM built with 3000 training samples, the maximal displacement prediction error (including POD and TPS inaccuracies) is about 34.2% of the maximal allowed bound variation and does not seem to decrease by adding more training samples. These relatively high values are only problematic when it comes to rebuild the optimal design in the CAD system by feeding it with the optimization result. Since the displacement fields are smooth and the corresponding geometric sensitivities are consistent, the CAD-ROM method is well suited for optimization, as demonstrated in Sect. 4.

To enable HTP rotation for trimming, a second CAD-ROM containing only HTP deflection as design parameter was built. Since the same structural surface mesh was used as for the wing section parameterization CAD-ROM, superposition of displacement predictions as described in Sect. 2.2.4 is applied.

3.3 Problem setup

The aircraft drag is optimized for the cruise mission at Mach 0.83 and 38,000 ft. Full payload and a fuel mass of 15% maximal take-off weight are assumed.

A sequential quadratic programming method which reduces to a Newton’s method for an unconstraint problem is used to drive the optimization process. The L2 norm of TAU’s density residual is converged by 6 orders of magnitude. A fixed number of 3 aeroelastic coupling iterations is performed per trim iteration and a constant relaxation factor of 0.7 is applied to each aeroelastic displacement update. The trim tolerances are set to 0.1 force or moment counts for the full equilibrium state. By that, the aerodynamic drag can be evaluated with an accuracy of approximately ± 0.1 drag counts.

To investigate the effect of refined meshes on the optimization result, it was decided to perform a consecutive optimization on the three mesh levels.

4 Optimization results

The optimization history is plotted in Fig. 8. It shows that a significant drag reduction of around 6% (relative to the L3 baseline value) is achieved already on the coarsest mesh level and that the transfers to finer levels come with only little losses on the aerodynamic improvement. The three optimizations took around 5, 7 and 6 days respectively. All optimization iterations are feasible regarding the trim constraints and the process proved to be extremely robust with no crashes occurring.

Fig. 8
figure 8

Cruise drag optimization history relative to the respective baseline value on each mesh level. Only optimization iterations obtaining better drag values are plotted

Full size image

Figure 9 shows the primary source of the drag reduction. For the transonic cruise flow conditions, the baseline geometry produces a strong shock wave on the upper wing surface. The shock region starts around the kink section and propagates down to the tip. This causes a relatively high wave drag. By locally adapting the wing sections, the sharp shock is softened and as a consequence, the wave drag reduces. The thrust scaling is reduced which is in a good agreement with the decrease in drag. The negative HTP deflection angle indicates that the center of gravity has not been defined in an ideal position already for the baseline design. This should not be considered as a deficit of the process, but rather as boundary condition for the present optimization. Results are expected to be more realistic with the VicToria MDO architectures, since these also include preliminary design tools accounting for proper mass distributions.

Fig. 9
figure 9

Comparison of pressure distribution for baseline and optimized shapes on the L3 mesh

Full size image

A secondary source for the efficiency improvement can be associated to small changes in the aerodynamic wing loading, as can be seen in Fig. 10. The lift distribution on the wing tip region gets closer to the ideal elliptic case which causes the lowest amount of induced drag. By setting the wing section twist angles as additional optimization parameters, this effect is expected to be further exploited. The loading on the inner wing is decreased to reduce the engine installation drag. In total, the wing produces less lift, but this is mainly compensated by the fuselage due to the increased angle of attack.

Fig. 10
figure 10

Comparison of span-wise lift distribution for baseline and optimized shapes on the L3 mesh

Full size image

Figure 11 shows how the optimization algorithm adapted the wing to reduce the drag. First, it can be seen that the defined parameter bounds were chosen to be sufficiently large, since the maximal obtained displacements are for the most sections approximately half as big as the allowed values. One of the main geometrical changes is the reduction of the wing leading edge radius over the entire wing span and a thickening of the rear inboard wing region.

Fig. 11
figure 11

Visualization of shape changes with respect to the baseline for the L3 optimization result

Full size image

The maximal CAD-ROM displacement prediction error for the optimal L3 shape was found to be around 7 mm. It is located on the lower wing side in the center of the root wing section. This is the section which has the lowest sampling resolution relative to the maximal allowed displacements. To evaluate the impact of this geometric error on the aerodynamic performance, the design parameters corresponding to the L3 optimum have been exported to the CAD system. The CAD model was updated, remeshed and a trimmed aeroelastic analysis was performed which showed that the drag improvement reduced from 6.0 to 3.9%. This indicates that at least for a retransfer of the optimal shape to the CAD system, the POD coefficient interpolation error still needs to be improved.

5 Conclusions

We have presented an adjoint-based aeroelastic shape optimization process for a trimmed aircraft configuration using a CAD-ROM parametrization, a mesh deformation method based on the linear EA method, the high-fidelity RANS solver TAU, the FEM solver Nastran and an MLS interpolation scheme for consistent and conservative load and displacement transfer. The process was integrated within the efficient HPC environment FlowSimulator.

We found that the process successfully reduced the cruise drag of a modern transport aircraft by about 6% by adapting 126 Bspline control points defining span-wise distributed wing sections. The significant aerodynamic efficiency gain was tracked back to reasonable effects and could be verified on a series of three continuously refined meshes.

A focus of this work was on the applied CAD-ROM method which substituted a high-dimensional parametric CAD model by a POD-based ROM during the optimization process. Detailed analysis of the CAD-ROM revealed that the displacement prediction error was mainly due to the applied POD coefficient interpolation technique which is currently TPS-based and not due to the subspace approximation inherently linked to the truncated POD. It was also observed that the POD accuracy increased with the number of samples used for training, whereas the overall prediction accuracy including the TPS interpolation remained approximately constant. A re-analysis of the true CAD representation of the optimal design vector showed that the drag improvement achieved in the optimization is smaller by 2.1 percentage points.

In future studies, we intend to enhance the process by enabling the aeroelastic shape optimization of a powered engine configuration and to extend the current aerodynamic adjoint method to a coupled aerostructural adjoint approach to account for fully consistent gradients. Furthermore, we plan to conduct further testing on the CAD-ROM approach to evaluate the method in detail for different parameter types, numbers and bounds. Also, our implementation of the hyperparameter-optimized Kriging interpolation of POD coefficients is currently improved to deal with the problem complexity within a feasible time frame and to further reduce the overall prediction error.