1 Introduction

A gyroplane is a rotary wing aircraft with an auto-rotating rotor system. In contrast to a helicopter, the engine does not drive the rotor but relies on a propeller to provide the required thrust [1]. The gyroplane has a long history and was invented by Juan de la Cierva back in 1923 [2]. After significant improvements in helicopters, the gyroplane technology was somehow neglected [3]. However, since the beginning of this millennium, the number of gyroplanes with a maximum takeoff mass of up to 600 kg continuously increased and today several thousand gyroplanes are operated all over the world [4]. Figure 1 shows DLR’s MTOsport gyroplane which has been used for different research tasks.

Fig. 1
figure 1

DLR’s MTOsport gyroplane

Full size image

A gyroplane requires a short takeoff roll of about one-hundred meters depending on the aircraft weight and the current wind situation. Once airborne, a gyroplane is very agile and flying at extremely low velocities is possible without fearing to stall the aircraft. The landing technique is similar to fixed-wing aircraft, but with much lower landing distances. The procedure has to be strictly followed according to the manufacturer’s Pilot Operating Handbook [5].

The most important safety feature of a gyroplane is the fact that the rotor is in autorotation independently of the engine status. Hence, an engine failure is easy to handle for the pilot compared to a helicopter [6].

A gyroplane is very stable during flight and can be controlled with minimal workload and without exceptional pilot skills [7]. Safe operations are possible including the take-off and landing flight phases presupposed the trained procedures are strictly followed. Otherwise a gyroplane is prone to rollover when landing and taxiing with the rotor still rotating. In a rollover accident, a vehicle tips over onto its side caused by lateral forces acting at its undercarriage [8].

A safety analysis has been performed in [8] based on gyroplanes using the European Central Repository of civil aviation occurrences and the EASA occurrence database (2009–2018). For the landing phase, two main accident causes were identified:

  1. I.

    Rolling over during excessive sideways drift, usually in a crosswind.

  2. II.

    Rolling over immediately after landing (initiating the taxi before slowing down).

The following list contains a summary of three exemplary rollover accidents from the UK Air Accident Investigation Branch falling into the category II:

  • EW/G2011/08/19 [9]: “The approach and initial touchdown on the mainwheels appeared normal but, as the nose wheel came into contact with the runway surface, the student reported that he felt a slight shimmy through the combined rudder and nose wheel steering pedals before the aircraft then yawed slightly to the left. The student recalled trying to apply corrective right pedal but aircraft veered further to the left before it rolled onto its right side and came to a stop.”

  • EW/G2011/04/18 [10]: “During the landing ground roll, the pilot moved the cyclic control forward and leant forward to apply the rotor brake. The gyroplane rolled onto its right side, skidded forward while rotating to the right, and came to rest after turning through 180°.”

  • EW/G2006/04/39 [11]: “During landing, as the nose wheel touched down, the autogyro turned left and rolled over. The pilot attributed the cause of the accident to a combination of his failure to prevent nose wheel contact before it could be centered, and a high turn speed. He considered that the calm wind conditions, high aircraft centre of gravity and fixed nose wheel to rudder pedal relationship made control of the landing overly sensitive.”

The dynamic rollover phenomenon is also known from helicopters [12]. If the skid or wheels contact a fixed object on the ground while hovering sideward, a rolling moment due to the rotor force may occur. Most effective way to stop the helicopter rollover is to apply down collective to remove the rotor lifting force.

This paper delivers insight into the physics of gyroplanes rolling over immediately after landing. For this purpose, the flight physics of gyroplanes and the nominal landing procedure are depicted. Analytical equations are derived which can be used to examine the rollover susceptibility of gyroplanes while taxiing with the rotor rotating. The single-track model known from road vehicle dynamics is applied to analyze a gyroplane taxiing with the rotor rotating. Additionally, nonlinear simulations for a reference gyroplane in tandem configuration are conducted to verify the results obtained analytically. Finally, a design parameter study is presented.

2 Gyroplane technology

As the rotor of a gyroplane is driven by the aerodynamic forces acting on its blades, this state is called autorotation. A gyroplane is not able to take off vertically, but it requires a short takeoff distance. A triangular landing gear is usually installed for this purpose.

The flight physics of gyroplanes with emphasis on the auto-rotating rotor is described in detail in [13]. Fig. 2 illustrates the forces acting on the gyroplane during flight. The rotor is tilted back slightly such that the rotor angle of attack \(\alpha_{R}\) is positive. When the gyroplane flies forward with an air speed \(V\), the air flows bottom-up through the rotor plane and keeps the rotor spinning at sufficient rotational speed. The rotor force \(F_{R}\) is acting perpendicular to the rotor plane and acting roughly against the weight force \(m \cdot g\). The propeller thrust force \(F_{{{\text{Prop}}}}\) is acting against the parasitic drag force \(D_{P}\) and the rotor drag force \(D_{R} \approx F_{R} \cdot sin\alpha_{R}\).

Fig. 2
figure 2

Forces acting on the gyroplane during horizontal flight [13]

Full size image

A gyroplane is controlled by tilting the rotor plane as illustrated in Fig. 3. The rotor plane can be tilted laterally around the roll pivot bolt (RPB) and longitudinally around the pitch pivot bolt (PPB) by moving the control stick, which is mechanically connected to the rotor head system. Hence, the direction of the rotor force and in consequence the roll and pitch moments can be controlled. Yaw control is performed via a rudder which is connected mechanically to the steerable nose wheel controlled by pedals.

Fig. 3
figure 3

A gyroplane is controlled by tilting the rotor around the roll and pitch axes. The yaw axis is controlled by a rudder and a nose wheel

Full size image

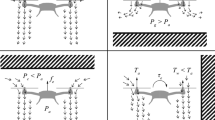
One of the most important features of a gyroplane is its ability to perform extremely short landings. Before touching down, an approach similar to a fixed-wing aircraft must be performed. During the approach, an airspeed of about 90–100 km/h is sufficient while the engine power is low or in idle. At about 10 m above the ground, a flare manoeuvre is initiated. The nominal sequence of a typical gyroplane touching down is shown in Fig. 4:

  1. 1.

    Touching down on the main wheels at an airspeed of about 50 km/h. The control stick is slowly pulled backward while rolling out on the main wheels. By this, the rotor plane is tilted back further producing significant rotor drag which slows down the gyroplane most effectively without using the wheel brakes.

  2. 2.

    Once the nose wheel touches the ground, the rotor head remains tilted back continuing the rollout until the velocity falls below a value of about 10 km/h. Some training organisations recommend a full stop before initiating the taxiing.

  3. 3.

    Pushing the control stick fully forward to leave the runway at a low taxiing velocity of 10–20 km/h.

Fig. 4
figure 4

Nominal touchdown and rollout procedure of a gyroplane

Full size image

It has to be noted that the values quoted above are typical for a category of gyroplanes with a weight of 450 to 600 kg.

Pulling the control stick and the rotor plane backward is of highest importance within this procedure. By this, the rotor force primarily unloads the nose wheel which is beneficial for the yaw stability during taxiing. By this, the gyroplane decelerates and the use of the wheel brakes is not required. By applying this landing technique, a rollover with a gyroplane is most unlikely as will be shown by the analyses and simulations presented below.

3 Gyroplane rollover analysis

The objective of this analysis is to investigated the physical principles for the rollover of a gyroplane taxiing on the runway. A gyroplane begins to roll over when the lateral acceleration exceeds its critical value \(a_{y,crit}\). The lateral acceleration directly corresponds to the lateral forces acting on the gyroplane. During taxiing, the lateral forces are predominantly acting on the rotor and, on the wheels, generating rolling moments which may lead to rollover. The lateral forces acting at the wheels of a gyroplane are caused by the slip angles of the tires due to nose wheel steering inputs as well as by aerodynamic forces acting on the rotor, which can be tilted to the side.

In the following sections, analytical equations are derived to illustrate the physical effects leading to rollover. Note that no atmospheric disturbances are considered within this study.

3.1 Forces acting on the gyroplane during taxi

In Figure 5, the lateral and vertical forces acting on the gyroplane during taxi are shown. Propeller forces and moments, the wheel brake and aerodynamic forces of the gyroplane body are not shown. These do only play a minor role during rollover and are therefore not considered in this study.

Fig. 5
figure 5

Lateral and vertical forces acting on the gyroplane during taxiing and definitions of rotor head roll and pitch control angles

Full size image

For the determination of the rotor force \(F_{R}\) during taxi, the analytical equations from [13] are applied. The rotor force \(F_{R} { }\) is depending on the rotor angular velocity \(\Omega_{R}\), the rotor angle of attack \(\alpha_{R}\), the induced downwash velocity \(w_{Ri}\) and the taxiing velocity \(V\) as well as on the air density \(\rho\), the size of the rotor (\(t_{Bl} ,{ }r_{R}\)), the blade incidence angle \(\varepsilon_{Bl}\) and the lift coefficient at zero angle of attack \(C_{LBl0}\). There is no ground effect on aerodynamics considered in this equation.

$$F_{R} \approx \rho \cdot t_{Bl} \cdot r_{R}^{3} \cdot \Omega_{R}^{2} \cdot \left[ {\pi \cdot \frac{{V \cdot sin\alpha_{R} - w_{Ri} }}{{\Omega_{R} \cdot r_{R} }} + \frac{1}{3} \cdot \left( {2 \cdot \pi \cdot \varepsilon_{Bl} + C_{LBl0} } \right)} \right]$$
(1)

Without inclination, the fuselage pitch angle is almost zero during taxiing. Therefore, it can be assumed that the rotor angle of attack is approximately equal to the rotor head pitch control angle \(\alpha_{R} \approx \eta_{RH}\).

The rotor induced downwash velocity \(w_{Ri}\) can be determined by Glauert’s “high speed” approximation considering the rotor as an elliptical loaded fixed-wing [6]. Within this approximation, the downwash velocity \(w_{Ri}\) is depending on the rotor force \(F_{R} ,\) the velocity \(V\) and the rotor radius \(r_{{\text{R}}}\).

$$w_{Ri} \approx 0.86 \cdot \frac{{F_{R} }}{{\rho \cdot \pi \cdot r_{R}^{2} }} \cdot \frac{1}{V}$$
(2)

The factor \(0.86\) is based on flight test data of DLR’s MTOsport Gyroplane [13].

Combining Eqs. (1), (2) leads to a new equation allowing to determine the rotor force directly based on a given rotor angular velocity and the rotor head pitch control angles.

$$F_{R} \approx \frac{{V \cdot \Omega_{R} \cdot t_{Bl} \cdot \rho \cdot \pi \cdot r_{R}^{2} }}{{V + \Omega_{R} \cdot t_{Bl} \cdot 0.86}} \cdot \left[ {V \cdot \sin \eta_{RH} + \frac{{\Omega_{R} \cdot r_{R} }}{3 \cdot \pi } \cdot \left( {2 \cdot \pi \cdot \varepsilon_{Bl} + C_{LBl0} } \right)} \right]$$
(3)

Equations (1), (3) assume zero lateral flow velocity.

The total lateral forces acting on the wheels of the landing gear are depending on the lateral acceleration \(a_{y}\) as well as the rotor force and the rotor head roll and pitch control angles \(\xi_{RH} ,{ }\eta_{RH}\).

$$Y_{LG} = Y_{NW} + Y_{MW,l} + Y_{MW,r} = m \cdot a_{y} - F_{R} \cdot \sin \xi_{RH} \cdot \cos \eta_{RH}$$
(4)

The total vertical force acting on the landing gear is dependent on the aircraft weight force \(m \cdot {\text{g}}\) as well as the rotor force \(F_{R}\) and the rotor head roll \(\xi_{RH} { }\) and pitch control angle \(\eta_{RH}\).

$$Z_{LG} = Z_{NW} + Z_{MW} = F_{R} \cdot \cos \xi_{RH} \cdot \cos \eta_{RH} - m \cdot g$$
(5)

The total roll and pitch moments around the CG are zero during steady-state taxiing.

$$L = - Y_{LG} \cdot h_{CG} + \left[ {Z_{MW,r} - Z_{MW,l} } \right] \cdot \frac{{s_{LG} }}{2} + F_{R} \cdot \sin \xi_{RH} \cdot \cos \eta_{RH} \cdot h_{R} = 0$$
(6)
$$M = - Z_{NW} \cdot \left[ {l_{LG} - l_{MW} } \right] + Z_{MW} \cdot l_{MW} + F_{R} \cdot \cos \xi_{RH} \cdot \left[ {\sin \eta _{RH} \cdot h_{R} - \cos \eta _{RH} \cdot l_{R} } \right] = 0$$
(7)

The vertical force acting on both main wheels is derived from Eq. (5).

$$Z_{MW} = - m \cdot g + F_{R} \cdot \cos \xi_{RH} \cdot \cos \eta_{RH} - Z_{NW}$$
(8)

The vertical force acting on the nose wheel is derived by reformulating the pitch moment Eq. (7).

$$Z_{NW} = - \frac{{\left[ {m \cdot g - F_{R} \cdot \cos \xi_{RH} \cdot \cos \eta_{RH} } \right] \cdot l_{MW} - F_{R} \cdot \cos \xi_{RH} \cdot \left[ {\sin \eta_{RH} \cdot h_{R} - \cos \eta_{RH} \cdot l_{R} } \right]}}{{l_{LG} }}$$
(9)

The critical lateral acceleration \({ }a_{y,crit}\) is reached when one of the two main wheels is completely unloaded. A rollover to the left side (during a right turn) begins when the vertical force acting on the right main wheel disappears (\(Z_{MW,r} = 0\)). The vertical force acting on the right main wheel is derived from Eq. (6) with \(Z_{MW,l} = Z_{MW} - Z_{MW,r}\).

$$Z_{MW,r} = \frac{1}{{s_{LG} }} \cdot \left( {\left[ {m \cdot a_{y} - F_{R} \cdot \sin \xi_{RH} \cdot \cos \eta_{RH} } \right] \cdot h_{CG} - F_{R} \cdot \sin \xi_{RH} \cdot \cos \eta_{RH} \cdot h_{R} } \right) + \frac{1}{2} \cdot Z_{MW} = 0$$
(10)

Hence, the critical lateral acceleration can be derived from Eq. (10).

$$a_{y,crit} = \frac{1}{m} \cdot \left( { - Z_{MW} \cdot \frac{{s_{LG} }}{{2 \cdot h_{CG} }} + F_{R} \cdot \sin \xi_{RH} \cdot \cos \eta_{RH} \cdot \left[ {\frac{{h_{R} }}{{h_{CG} }} + 1} \right]} \right)$$
(11)

It can be seen from Eq. (11) that the critical lateral acceleration \(a_{y,crit}\) is dependent on the aircraft mass \(m\), the vertical force acting on both main wheels \(Z_{MW}\), the rotor force \(F_{R}\) and the rotor head roll \(\xi_{RH}\) and pitch control angle \(\eta_{RH}\). Furthermore, the gyroplane’s geometry, i.e. landing gear track width \(s_{LG}\) vertical distance between CG and ground \(h_{CG}\) and vertical distance between rotor head PPB and CG \(h_{R}\), do directly influence the critical lateral acceleration.

The relationship between \(s_{LG} /h_{CG}\) is obviously an important parameter. A larger track width with respect to CG height causes a higher critical lateral acceleration \(a_{y,crit}\). The same is true for the amount of the vertical force acting on the main wheels \(Z_{MW}\), which can be determined by Eq. (8). The critical lateral acceleration \(a_{y,crit}\) increases further if the pilot moves the rotor to the right-hand side which is per definition a positive rotor head roll control angle \(\xi_{RH} > 0\).

3.2 Gyroplane steering dynamics

The correlation between the nose wheel steering angle \(\delta_{NW}\) and the lateral acceleration \(a_{y} { }\) can be evaluated using a single-track model. The single-track model allows a physically plausible description of the driving behavior of vehicles without major modeling and parameterization effort [14]. Hence, this simple model is used to explain and analyze the steering characteristics of a gyroplane taxiing on the runway. Within the single-track model the front and rear tires of the vehicle are represented as one single tire, see Fig. 6.

Fig. 6
figure 6

Single-track model: the front and rear tires (blue) of the landing gear are represented as one single tire (gray), respectively

Full size image

The lateral acceleration amplification factor is defined as the steady-state relationship of the lateral acceleration \(a_{y}\) and the nose wheel steering angle \(\delta_{NW}\). It is depending on the landing gear wheel base \(l_{LG}\), the velocity \(V\) and the self-steering gradient \(EG\) [14]:

$$K_{a} \left( V \right) = \frac{{a_{y} }}{{\delta_{NW} }} = \frac{{V^{2} }}{{l_{LG} + EG \cdot V^{2} }}$$
(12)

The self-steering gradient describes the steering characteristics of the vehicle. For vehicles with understeering characteristics, the self-steering gradient is positive (\(EG > 0\)). In this case, the steering angle must be increased by the driver/pilot with rising velocity during a turn with a constant radius. The reverse is true for vehicles with oversteering characteristics (\(EG < 0).\)

The self-steering gradient is depending on the mass \(m\), the landing gear wheel base \(l_{LG}\), the horizontal distances of the nose and main wheels and the CG (\(l_{NW}\),\({ }l_{MW}\)) as well as on the cornering stiffnesses of the nose and main wheels (\(c_{\alpha ,NW}\),\({ }c_{\alpha ,MW}\)) [14].

$$EG = { }\frac{m}{{l_{LG} }} \cdot \left[ {\frac{{c_{\alpha ,MW} \cdot l_{MW} - c_{\alpha ,NW} \cdot l_{NW} }}{{c_{\alpha ,NW} \cdot c_{\alpha ,MW} }}} \right] _{{}}$$
(13)

The cornering stiffnesses are defined as the gradients of the lateral forces acting on the nose and main wheels (\(Y_{NW} ,{ }Y_{MW} ){ }\) and the slip angles \((\alpha_{NW} ,{ }\alpha_{MW} )\), see Fig. 6.

$$c_{\alpha ,NW} { } = \frac{{Y_{NW} }}{{\alpha_{NW} }},{ }c_{\alpha ,MW} { } = \frac{{Y_{MW} }}{{\alpha_{MW} }}$$
(14)

It is a linear representation of the complex tire characteristics, which are depending on several parameters, such as tire width, rubber, friction coefficient or load. For the present analysis, the cornering stiffnesses are dependent on the landing gear vertical forces.

$$c_{\alpha ,NW} { } = \frac{{Z_{NW} }}{{Z_{NW0} }} \cdot c_{\alpha ,NW0} ,\,c_{\alpha ,MW} { } = \frac{{Z_{MW} }}{{Z_{MW0} }} \cdot c_{\alpha ,MW0}$$
(15)

The cornering stiffnesses \(c_{\alpha ,NW0} { }\) and \(c_{\alpha ,MW0}\) represent the values for the case of gyroplane taxi without a rotor force (\(F_{R} = 0\), non-rotating rotor). In this case, the vertical forces acting on the nose and main wheels are only depending on the longitudinal distances between nose and main wheels and CG.

$$Z_{NW0} = - m \cdot g \cdot \frac{{l_{MW} }}{{l_{LG} }},\,Z_{MW0} = - m \cdot g \cdot \frac{{l_{NW} }}{{l_{LG} }}$$
(16)

In the final step, the lateral acceleration amplification factor \(K_{a} { }\) and the critical lateral acceleration \(a_{y,crit}\) are used to determine the critical nose wheel steering angle \(\delta_{NW,crit}\). The latter is defined as the steering angle at which the gyroplane begins to roll over. It is derived from Eqs. (12), (11).

$$\delta_{NW,crit} = \frac{{a_{y,crit} }}{{K_{a} }}$$
(17)

3.3 Evaluation with reference gyroplane data

In this section, the analytic equations are evaluated. The relevant data of a reference gyroplane based on AutoGyro’s MTOsport from [13] are applied to perform a rollover analysis. Table 1 shows the data required for the evaluation of the analytical equations. The cornering stiffnesses \(c_{\alpha ,NW0}\) and \(c_{\alpha ,MW0}\) were determined the by taxi tests with the rotor not rotating [15, 16]. It has to be noted that these values are only valid for the specific CG position in these tests represented by the parameters \(l_{MW}\) and \(l_{MW}\).

Table 1 Reference gyroplane data from different sources ([13, 15, 16])
Full size table

Three different cases are considered in windless conditions.

  • Case 0: rotor standing still (\(n_{R} = 0 rpm);\)

  • Case 1: rotor rotating (\(n_{R} = 300 rpm\)), stick pushed forward \(\eta_{RH} = - 1 deg\);

  • Case 2: rotor rotating (\(n_{R} = 300 rpm\)), stick pulled backward \(\eta_{RH} = 10 deg\).

The three cases were chosen with respect to the touchdown and rollout procedure of a gyroplane, see Fig. 4. Case 2 represents the situation when the nose wheel touches the ground. Case 1 represents the pushing of the stick after the nose wheel touching the ground and case 0 the rollout phase.

The evaluation of the analytical equations using the reference gyroplane data (Table 1) and an air density of ρ=1.225 kg/m³ (ISA on ground) is presented in Table 2. The chosen taxiing velocity of \({\text{V}} = 45{\text{ km}}/{\text{h}}\) represents the value immediately after touchdown.

Table 2 Evaluation for different cases: numerical values of different parameters revealing the gyroplanes rollover tendency based on the derived analytical equations (\({\text{V = 45 km/h}}\))
Full size table

For case 0 (rotor not rotating), the critical lateral acceleration is \(a_{y,crit} \, \approx \,7.4m/s^{2}\), which is rather high. For cases 1 and 2 (rotor rotating at 300 rpm), the critical lateral acceleration decreases to \(a_{y,crit} \, \approx \,2.5 - \,2.9\,m/s^{2}\) due to the rotor force unloading the main landing gear. This is a fairly low value compared to a passenger car. However, it should be noted that an attentive pilot would be able to move the roll control stick in the opposite direction to mitigate the tendency to rollover when the rotor is rotating.

When the rotor is not rotating (case 0), the gyroplane has understeering characteristics (\(EG > 0\)) leading a critical nose wheel steering angle of \(\delta_{NW,crit} \left( {45{\text{ km}}/{\text{h}}} \right) \approx 6.2{ }deg\). This result represents a medium rollover susceptibility of the gyroplane while taxiing with 45 km/h, which is not recommended. Typical taxiing velocities are below 25 km/h.

With the rotor rotating and the control stick pushed forward (case 1), the gyroplane becomes oversteering (\(EG < 0\)). The critical nose wheel steering angle reduces to \(\delta_{NW,crit} \left( {45{\text{ km}}/{\text{h}}} \right) \approx 0.9{ }deg\). This is a very low value indicating a high rollover susceptibility of the gyroplane. It is most likely that the pilot, unintended, applies this very low nose wheel steering angle the by slightly moving the pedals.

With the rotor rotating and the control stick pulled backward (case 2), the critical nose wheel steering angle is much higher \(\delta_{NW,crit} \left( {45{\text{ km}}/{\text{h}}} \right) \approx 17.9{ }deg\). In this case, it is most unlikely to provoke a rollover by means of nose wheel steering inputs. The main reason for this rollover insensitivity is the unloaded nose wheel.

Figure 7 shows the lateral acceleration amplification factor \(K_{a}\) and the critical nose wheel steering angle \(\delta_{NW,crit}\) for different taxiing velocities \(V\). It appears that the steering oversensitivity of case1 (rotor pushed forward) worsens with rising velocity. Increasing the taxing velocity from \(45{\text{ km}}/{\text{h}}\) to \(50{\text{ km}}/{\text{h}}\) more than doubles the lateral acceleration amplification factor \({ }K_{a}\) in this case. This extremely critical behaviour is caused by the oversteering characteristics for case 1.

Fig. 7
figure 7

Lateral acceleration amplification factor and critical nose wheel steering angle as a function of the taxiing velocity for the three cases (0: \(n_{R} = 0 rpm\), 1: \(n_{R} = 300 rpm\), \(\eta_{RH} = - 1 deg\), 2: \(n_{R} = 300 rpm\), \(\eta_{RH} = 10 deg\))

Full size image

For the case 1 (rotor pushed forward), the critical nose wheel angle \(\delta_{NW,crit}\) is falling dramatically with rising taxiing velocity. At 50 km/h, it is almost zero such that a rollover is almost inevitable.

For the cases 0 (rotor standing still) and 2 (rotor pulled backward), the tendency to roll over is much lower. In these cases, a rollover is unlikely below a taxiing velocity of 20 km/h even with a nose wheel deflection \(\delta_{NW} = 25 deg\), which represents a typical maximum value for the gyroplane nose wheel steering range.

The final analysis addresses the possibilities to counteract with the rotor roll control. Fig. 8 shows the critical nose wheel steering angle at a taxiing velocity of \({\text{V}} = 45{\text{ km}}/{\text{h}}\) for different rotor head roll control angles \(\xi_{RH}\).

Fig. 8
figure 8

Critical nose wheel steering angle at a taxiing velocity of 45 km/h for different rotor head roll control angles (0: \(n_{R} = 0 rpm\), 1: \(n_{R} = 300 rpm\), \(\eta_{RH} = - 1 deg\), 2: \(n_{R} = 300 rpm\), \(\eta_{RH} = 10 deg\))

Full size image

Obviously, for case 0 (rotor standing still), the rotor head roll control angle \(\xi_{RH}\) does not have an influence on the critical nose wheel steering angle \(\delta_{NW,crit}\). But for the cases with rotating rotor (case 1: rotor pushed forward, case 2: rotor pulled backward), the critical nose wheel steering angle \(\delta_{NW,crit}\) is increased by moving the rotor plane to the right (towards positive \(\xi_{RH}\)) during a right turn. However, for case 1, the overall values of \(\delta_{NW,crit}\) are still very small (\(\delta_{NW,crit} < 2 deg\)) indicating a very high likelihood to rollover although the pilot would be able to counteract with roll control input.

In contrast, by moving the rotor head to the left-hand side during a right turn, the critical nose wheel steering angle is lowered significantly. For case 2, it even can become negative (\(\delta_{NW,crit} < 0 deg\)) which means the gyroplane can roll over while taxiing straight in forward direction if the pilot moves the rotor head intensively to the left (\(\xi_{RH} < - 7 deg\)).

This analysis was conducted at a taxiing velocity of 45 km/h. At a different velocity, the limits rollover limits change.

4 Gyroplane rollover simulation

The gyroplane simulation model was developed at DLR and validated with flight test data [15, 16]. It is implemented in a training simulator and contains the characteristics of the gyroplane body, the rotor, the engine, and the landing gear. A derivative model for the aerodynamics of the gyroplane body is utilized feeding the equations of motion with six degrees of freedom. For the rotor aerodynamics, the blade element method with ten elements per blade is applied. The rotor rotational speed is derived by a first order differential equation while the flapping angle motion is implemented by a second order differential equation. The propeller of the Rotax 912 engine of the gyroplane is modelled by the blade element method containing dynamic and gyroscopic effects as well as the interaction of the propeller stream with the gyroplane horizontal and vertical tails. Each wheel of the landing gear is modeled as a spring-damper system considering the specific tire characteristics.

No atmospheric disturbances are considered during this simulation study. Two landing scenarios are simulated: one with the correct procedure and one with incorrect procedure pushing the stick forward immediately after touching down.

Figure 9 shows the results from a simulation of the correct landing procedure. The gyroplane touches down at an airspeed of about \(V \approx 50{\text{ km}}/{\text{h}}\) and rolls out on the main wheels for a few seconds. Once the nose wheel touches the ground, the rotor head pitch control angle is slowly increased to its maximum (representing case 2 with pitch control stick pulled backward). By this, the gyroplane decelerates and the taxiing velocity falls below 10 km/h.

Fig. 9
figure 9

Gyroplane landing simulation with correct procedure (o: touchdown, x: nose wheel drop, +: taxiing)

Full size image

For testing purpose, a tiny nose wheel steering angle of \(\delta_{NW} = 1.2 deg\) was applied leading to a small lateral acceleration (\(a_{y} < 0.2 m/s^{2} )\) far away from the critical value (\(a_{y,crit} \, \approx 2.5\,m/s^{2}\), see case 2 in Table 2). Hence, the rollover susceptibility is almost zero in this case. It has to be noted that neither crosswind nor any roll control is applied.

Figure 10 shows the simulation results for the case of an incorrect landing procedure. The rotor head pitch control angle was reduced to \(\eta_{RH} = - 1 deg\) immediately after touching down. This represents case 1 with pitch control stick pushed forward. An unintendedly applied nose wheel steering angle (\(\delta_{NW} = 1.2 \deg\)) leads to a lateral acceleration of \(a_{y} > 2.5 m/s^{2}\) which almost reaches the critical value (\(a_{y,crit} \approx 2.8\,m/s^{2}\), see case 1 in Table 2). Once the gyroplane begins to roll over, the lateral acceleration increases and the roll angle exceeds 20 degrees about 3 s after the rollover onset. It is assumed that no roll control is applied for compensation representing an inattentive pilot.

Fig. 10
figure 10

Gyroplane landing simulation with incorrect procedure (o: touchdown, x: nose wheel drop, +: taxiing)

Full size image

The results obtained from non-linear simulations verify the analyses presented above. The rollover susceptibility caused by the steering oversensitivity with the rotating rotor pushed forward (case 1) was proved as well as the large margin when the rotor is pulled backward (case 2).

5 Design parameter study

The analytical equations can be applied for new gyroplane types—already during their design phase—to estimate their susceptibility to roll over after landing. Therefore, a parametric study is performed limited to three design parameters:

  1. 1.

    Landing gear track width,

  2. 2.

    Nose wheel size,

  3. 3.

    Longitudinal CG position.

5.1 Landing gear track width

Increasing the landing gear track width \(s_{LG}\) will obviously reduce the rollover susceptibility of the gyroplane. The critical lateral acceleration \({ }a_{y,crit}\) is increased by this as well as the critical nose wheel steering angle \(\delta_{NW,crit}\), see Table 3. Increasing the landing gear track width \(s_{LG}\) by 20% leads to an increase of the critical nose wheel steering angle \(\delta_{NW,crit}\) of about 10% for the case 1 (rotor pushed forward). However, the value is still very small (\(\delta_{NW,crit} = 1.0 deg\)).

Table 3 Effects of landing gear track width (\({\text{V = 45 km/h}}\))
Full size table

It appears that a wider landing gear is beneficial with respect to rollover, but, on the other hand, it may increase the weight of the vehicle and worsen the ground handling of the gyroplane, such as transporting it with a trailer or moving it into the hangar.

5.2 Nose wheel size

The nose wheel size especially the tire width is influencing the cornering stiffness \(c_{\alpha ,NW}\). A narrow tire is creating smaller lateral forces due to slip angles. This means the cornering stiffness of the nose wheel \(c_{\alpha ,NW}\) and in consequence the steering sensitivity are reduced. The lateral acceleration amplification factor \(K_{a} \left( V \right)\) is decreased and the critical nose wheel steering angle \(\delta_{NW,crit}\) is increased, see Table 4. A reduction of \(c_{\alpha ,NW0}\) by 20% would increase the critical nose wheel angle by 78% for case 1 (rotor pushed forward), which is favorable for the roll stability. However, its absolute value is still very small: \(\delta_{NW.crit} = 1.6 deg\).

Table 4 Effects of nose wheel cornering stiffness (\({\text{V = 45 km/h}}\))
Full size table

5.3 Longitudinal CG position

The longitudinal CG position may vary due to different loading of the gyroplane. It is defined by the quotient of the longitudinal distance between main wheels-CG and the landing gear wheel base \(l_{MW} /l_{LG}\). For the reference gyroplane, the value is \(l_{MW} /l_{LG} = 0.23\). This means that 23% of the aircraft weight is carried by the nose wheel and 77% by the main wheels when the rotor is standing still. By moving the CG 3% backwards (about 6 cm), the critical lateral acceleration \({ }a_{y,crit}\) is increased by about 3%, see Table 5. This increase is caused by the higher amount of the vertical force acting on both main wheels. On the other hand, the lateral acceleration amplification factor \(K_{a} \left( V \right)\) is increased by about 18% for case 1 (rotor pushed forward) making the gyroplane more prone to rollover. This results in a further reduction of the critical nose wheel steering angle to a value of \(\delta_{NW,crit} = 0.75 deg\).

Table 5 Effect of longitudinal CG position (\({\text{V = 45 km/h}}\))
Full size table

The main result from this parameter study can be summarized as follows: practically, it is not possible to design the gyroplane completely robust with respect to rollover. Hence, applying the correct procedure pulling the control stick back properly after touching down is most important.

6 Conclusion

This paper explains the physics behind the known problem of gyroplanes rolling over immediately after touch down. Analytical equations were derived and evaluated with data of a reference gyroplane which provide an insight into the mechanisms provoking such a rollover. It was shown that a rollover is most likely when a pilot pushes the control stick into the forward position immediately after touchdown in combination with a high rotor rotational speed, which is an incorrect procedure.

Two main factors contribute to this problem:

  1. 1.

    Low critical lateral acceleration

    The high rotor rotational speed leads to a significant rotor force and hence the main landing gear is unloaded. The unloading of the main landing gear reduces the critical lateral acceleration. The result is that the gyroplane rolls over at a lower lateral acceleration caused by an unintended nose wheel steering input in comparison to the case with the rotor not rotating.

  2. 2.

    Nose wheel steering oversensitivity

The cornering stiffness of the main landing gear is reduced due to the unloaded main landing gear. This leads to oversteering characteristics of the gyroplane while taxiing out. For example, the reference gyroplane analysed in this study may roll over at taxi velocities above 45 km/h if the pilot unintentionally applies a tiny nose wheel steering angle of only 1 or 2 degrees.

Finally, this study confirmed that the current landing procedure is safe with respect to rollover, which means pulling the control stick back properly after touching down. By doing so, a rollover of a gyroplane during landing is most unlikely.