Conceptual design of sonic boom stealth supersonic transports

Abstract

This paper introduces a supersonic transport aircraft design model developed in the GENUS aircraft conceptual design environment. A conceptual design model appropriate to supersonic transports with low-to-medium-fidelity methods are developed in GENUS. With this model, the authors reveal the relationship between the sonic boom signature and the lift and volume distributions and the possibility to optimise the lift distribution and volume distribution together so that they can cancel each other at some region. A new inspiring design concept—sonic boom stealth is proposed by the authors. The sonic boom stealth concept is expected to inspire the supersonic aircraft designers to design low-boom concepts through aircraft shaping and to achieve low ground impacts. A family of different classes of supersonic aircraft, including a single-seat supersonic demonstrator (0.47 psf), a 10-passenger supersonic business jet (0.90 psf) and a 50-seat supersonic airliner (1.02 psf), are designed to demonstrate the sonic boom stealth design principles. Although, there are challenges to balance the volume with packaging and control requirements, these concepts prove the feasibility of low-boom low-drag design for supersonic transports from a multidisciplinary perspective.

Introduction

There has been a renewed interest to design an environmentally friendly, economically viable and technologically feasible civil supersonic transport. It is desirable for the next-generation supersonic transport to have not only low sonic boom level but also high fuel efficiency. There has been a progress in low-boom technology by tailoring the lift and volume distribution [1]. However, the future supersonic civil transport can be viable only if overland supersonic restrictions are relaxed or entirely lifted [2].

NASA is working on a single-seat quiet supersonic demonstrator X-59 [3] to prove the low-boom design technology and support the potential changes in FAA regulations. BOOM Technology is building a demonstrator XB-1 [4] to test the supersonic technologies. The supersonic business jet (SSBJ) is regarded as the pioneer for the next-generation supersonic transport [5, 6]. Aerion Supersonic [7] has been updating its supersonic concept to get a higher cruise aerodynamic efficiency. Spike Aerospace [8] is developing a low-boom SSBJ concept with innovative digital cabin. There have been many studies focusing on the business class supersonic transport concepts [9,10,11,12]. The supersonic airliner will be a next-step after the civil supersonic market is reopen. BOOM Technology [13] is developing a 55–75 passenger supersonic aeroplane with business-class fares. JAXA has been conducting research and experiments on next-generation supersonic transports, including 36–50 passenger supersonic aircraft [14]. To stress these design concerns, this research studies three different designs: a single-seat supersonic demonstrator, a 10-seat SSBJ concept and a 50-seat supersonic airliner concept.

For the study of the sonic boom minimization, the F-function method and the equivalent area developed by Whitham [15] and Walkden [16] are widely used. Seebass [17], George [18], and Darden [19, 20] developed the popular SGD sonic boom minimization theory through aircraft shaping. The recent studies on sonic boom minimization focus more on the numerical optimisation techniques [21,22,23]. The theoretical analysis is effective in the conceptual design stage, while the numerical optimisations are useful for practical solutions. This paper studies the low-boom design through numerical techniques and try to conclude the design principles in a versatile approach.

Through the previous studies, the authors have established a multidisciplinary methodologies for supersonic transport [24], validated the design model against different designs [25], demonstrated the sonic boom can be shaped by tailoring the lift and volume distribution [1], and proven the feasibility of low-boom and low-drag design optimisation [26]. This paper is a further study based on the previous research. In this paper, we propose the sonic boom stealth concept to converge the design ideas on low-boom low-drag supersonic aircraft design and demonstrate the low-boom optimum design concepts at three different classes.

The GENUS aircraft conceptual design environment

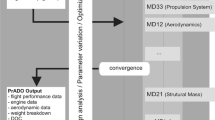
Multidisciplinary design analysis and optimisation plays a key role in the conceptual design studies of novel aircraft configurations. Presently, there is a need to compare different classes of aircraft through equivalent methodologies to quantify the real differences and advantages, if any, that each configuration can offer. The GENUS aircraft design environment [27] aims to address this need through a common central architecture, as shown in Fig. 1. In GENUS, the former modules provide control variables for the later modules and constraints can be built to provide feedback connections. In this approach, GENUS becomes an effective synthesis, analysis and optimisation platform for aircraft conceptual design.

Fig. 1

Framework and data link of GENUS

Geometry

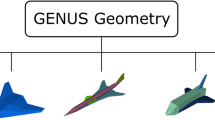
The geometry module provides enough flexibility for the designers to model different configurations and controllability for design optimisations. The model is fully parametric, consisting of body components and/or lifting surfaces. A body component is a combination of linearly interpolated cross-sectional shapes defined by class shape transformation (CST) method [28], while lifting surfaces have NACA 4 series, NACA 5 series, NACA 6 series, wedge, double wedge, biconvex aerofoils, and the CST method as available input options. Different geometry formats are built in for the visualization and aerodynamic analysis.

Mission

The mission module defines the design specifications derived from the market or customer requirements, such as estimated maximum take-off mass, target range, cruise Mach number, payload, etc. This module provides the basic design variables for most of the modules. The F-design conditions’ performance can be analysed by changing variables in this module.

Mass breakdown

The mass breakdown module defines the estimated the mass, shape, dimensions of various components. At this stage, the structure and system mass build-up of novel configurations still rely on empirical methods derived from textbooks, such as Howe’s method [29], Raymer’s method [30], Cranfield lecture method, etc. Physical-based mass prediction methods are being developed to provide higher fidelity results.

Aerodynamics

There are multi-fidelity analysis methods available in the GENUS aerodynamic module. The main aerodynamic analysis tool for supersonic transport design is PANAIR [31]. PANAIR is a higher order subsonic and supersonic potential flow solver for arbitrary configurations. For aerodynamic analysis, PANAIR can provide lift coefficients and induced drag coefficients. The drag components for supersonic flight are denoted by Eq. (1):

$$C_{{\text{D}}} = C_{{{\text{D}}_{f} }} + C_{{{\text{D}}_{{{\text{wave}}}} }} + C_{{{\text{D}}_{i} }} ,$$

(1)

where $C_{{\text{D}}}$ is the total drag coefficient, $C_{{{\text{D}}_{f} }}$ is the friction drag coefficient,${ }C_{{{\text{D}}_{{{\text{wave}}}} }}$. is the supersonic wave drag coefficient, $C_{{{\text{D}}_{{\text{i}}} }}$ is the lift induced vortex drag coefficient.

The form factor method [32] is integrated to correct the zero-lift skin friction and form drag. The result comes from the contribution of each component, as shown in Eq. (2):

$$C_{{{\text{D}}_{f} }} = \mathop \sum \limits_{j = 1}^{N} \frac{{{\text{FF}}_{j} C_{{{\text{F}}_{j} }} S_{{{\text{wet}}_{j} }} }}{{S_{{{\text{ref}}}} }},$$

(2)

where N is the number of components used to model the configuration, ${\text{FF}}_{j}$ is the form factor of component $j$, $C_{{F_{j} }}$ is the skin friction coefficient of component $j$, $S_{{{\text{wet}}_{j} }}$. is the wet area of component $j$, $S_{{{\text{ref}}}}$ is the reference area of the total aircraft.

The supersonic area rule [33] is applied to calculate wave drag due to volume, as indicated in Eqs. (3) and (4). For accurate wave drag calculation, the Mach plane cross sectional area intersecting with the geometry is required:

$$C_{{{\text{D}}_{{{\text{wave}}}} }} \left( \theta \right) = - \frac{1}{2\pi }\mathop \smallint \limits_{0}^{l} \mathop \smallint \limits_{0}^{l} A^{\prime\prime}(x_{1} )A^{\prime\prime}\left( {x_{2} } \right)\ln \left| {x_{1} - x_{2} } \right|{\text{d}}x_{1} {\text{d}}x_{2}$$

(3)

$$C_{{{\text{D}}_{{{\text{wave}}}} }} = \frac{1}{2\pi }\mathop \smallint \limits_{0}^{2\pi } C_{{{\text{D}}_{{{\text{wave}}}} }} \left( \theta \right){\text{d}}\theta ,$$

(4)

where $\theta$ is the angle between the Y-axis and a projection onto the Y–Z plane of a normal to the Mach plane, ${ }l$. is the overall aircraft length, $A\left( x \right)$. is the Mach plane cross-sectional area at longitudinal coordinate $x$, as illustrated in Fig. 2.

Fig. 2

Illustration of wave drag computing procedure

Propulsion

The propulsion module calculates the performance of a combination of available powerplants at different flight conditions (Mach, altitude, and throttle). The NASA EngineSim applet [34] has been adapted to simulate the thermodynamic analysis of turbojet, turbofan, and ramjet engines based on the component settings, as shown in Fig. 3.

Fig. 3

Engine model component settings

Where A2 is the fan area, A8 is the nozzle area, BPR is the engine bypass ratio, T_max is the maximum temperature, T_limit is the temperature limit of the material, $\rho$ is the density of the material.

Packaging and C.G.

Packaging is a novel and essential module in the GENUS environment. This module checks the accommodation of cabin, payload, fuel tanks, etc. Another function is to adjust the positions of inner components to achieve required static margin. In the case of supersonic transports, the wing volume is usually not enough for the mission fuel. Therefore, fuselage fuel tanks are introduced to the design. For the distributed fuel tanks, fuel consumption is scheduled to adjust the overall C.G. position and obtain better longitudinal stability. Landing gear loads, sizes and positions are also calculated in this module.

Performance

The performance module is designed to flexibly combine different segments, as shown in Fig. 4. Each segment consists of a set of control points. This module takes information from aerodynamic coefficients and propulsion performance maps. The next segment gets mass and C.G. updates from the previous segment. Each point is iterated by the kinetic and kinematic equations. In this way, the point and field performance can be predicted.

Fig. 4

Performance segments combination

Stability and control

USAF Digital DATCOM [35] has been integrated into the GENUS environment through a legacy code linking process (Fig. 5). The stability characteristics and trim abilities at various flight conditions can be calculated and checked in this module.

Fig. 5

GENUS and DATCOM data sharing and processing

Sonic boom prediction

Sonic boom constraints are crucial to the design of next-generation supersonic transport. In this research, there are two steps to predict the sonic boom intensity. The first step is to get the near-field pressure distribution. The second step is to propagate the near-field pressure to the ground through considering the nonlinear characteristics of the atmosphere.

The F-function theory developed by Whitham [15] and Walkden [16] is used for the near-field pressure calculation. The equivalent area due to volume and equivalent area due to lift are required for the near-field pressure calculation. The equation for the total effective area calculation is indicated in Eq. (5):

$$A_{{\text{e}}} \left( {x,\theta } \right) = A_{{\text{v}}} \left( {x,\theta } \right) + \frac{\beta }{{2q_{\infty } }}\mathop \smallint \limits_{0}^{x} L\left( {x,\theta } \right){\text{d}}x,$$

(5)

where ${A}_{\mathrm{e}}\left(x,\theta \right)$ is the equivalent area at coordinate $x$ and angle $\theta$, ${A}_{\mathrm{v}}\left(x,\theta \right)$ is the Mach plane cross sectional area at coordinate $x$ and angle $\theta$, $\beta =\sqrt{{M}^{2}-1}$, ${q}_{\infty }$ is the ambient dynamic pressure, $L(x,\theta )$ is the lift on a spanwise strip per unit chordwise length.

The F-function derives from the equivalent area, as shown in Eq. (6):

$$F\left( x \right) = \frac{1}{2\pi }\mathop \smallint \limits_{0}^{x} \frac{{A_{{\text{e}}}^{^{\prime\prime}} \left( {\overline{x},\theta } \right)}}{{\sqrt {x - \overline{x}} }}{\text{d}}\overline{x}.$$

(6)

The near-field pressure is then calculated based on the Whitham theory, as shown in Eq. (7):

$$\Delta p\left( x \right) = p_{0} \frac{{\gamma M^{2} F\left( \chi \right)}}{{\left( {2\beta r} \right)^{1/2} }},$$

(7)

where $\Delta p=p-{p}_{0}$, ${p}_{0}$ is the ambient pressure, $\gamma$ is the ratio of specific heat, $M$ is the flight Mach number, $r$ is the radius in polar coordinate.

The sonic boom propagates method is the waveform parameter method [36]. This method is based on geometrical acoustics and calculates the sonic boom signature directly with distance steps along a ray, which is more suitable for automatic computation. It is reprogrammed in JAVA and implemented as a special module method. A weakness of the method is that the code expects one shock formation or coalescence at a time. For a complex signature with large numbers of points specified, there is a big chance of failure. This becomes a problem when using CFD data as F-function inputs. Another problem with the propagation code is that it cannot predict the rise time of the ground signature. As a result, this method is not suitable for the perceived loudness level calculation. The validation of the sonic boom prediction methods can be found in Fig. 6.

Fig. 6

Sonic boom intensity validation (data source: [5, 37])

Low-boom and low-drag solutions

Sonic boom stealth solution

From the previous studies [1, 26], the authors have noticed the ground signature intensity is proportional to the near-field overpressure, which results from the combining effect of the volume distribution and the lift distribution. Insert Eq. (5) into Eq. (6) to get Eq. (8), which is a sum of two parts. We name the first part as F-function due to volume, as shown in Eq. (9), and the second part as F-function due to lift, as shown in Eq. (10). In this research, we decompose the F-function to F-function due to volume and F-function due to lift to study the individual effects on sonic boom intensity. Therefore, the sonic boom signature can be modified by altering the volume distribution and lift distribution, respectively or collectively:

$$F\left( {x,\theta } \right) = \frac{1}{2\pi }\mathop \smallint \limits_{0}^{x} \frac{{A_{v}^{^{\prime\prime}} \left( {\overline{x},\theta } \right)}}{{\sqrt {x - \overline{x}} }}{\text{d}}\overline{x} + \frac{\beta }{{4\pi q_{\infty } }}\mathop \smallint \limits_{0}^{x} \frac{{L^{\prime}\left( {\overline{x},\theta } \right)}}{{\sqrt {x - \overline{x}} }}{\text{d}}\overline{x}.$$

(8)

$$F_{{{\text{volume}}}} \left( {x,\theta } \right) = \frac{1}{2\pi }\mathop \smallint \limits_{0}^{x} \frac{{A_{v}^{^{\prime\prime}} \left( {\overline{x},\theta } \right)}}{{\sqrt {x - \overline{x}} }}{\text{d}}\overline{x}.$$

(9)

$$F_{{{\text{lift}}}} \left( {x,\theta } \right) = \frac{\beta }{{4\pi q_{\infty } }}\mathop \smallint \limits_{0}^{x} \frac{{L^{\prime}\left( {\overline{x},\theta } \right)}}{{\sqrt {x - \overline{x}} }}{\text{d}}\overline{x},$$

(10)

where ${F}_{\mathrm{volume}}$ is the F-function due to volume, ${F}_{\mathrm{lift}}$ is the F-function due to lift.

Through the study, we have noticed that the sonic boom signature is sensitive to the geometry. Improper geometry design can cause a big sonic boom overpressure. On the other hand, the signature can be mitigated through proper design of the volume distribution and lift distribution, however, can never be eliminated. This makes the low-boom design similar to the radar cross section (RCS) stealth design. There have been design principles for the low RCS configurations, resulting in RCS stealth featured aircraft, such as the F-117, B-2, F-22, F-35, etc. Sonic boom stealth design is a new terminology come up by the authors. Sonic boom stealth means to use geometry shaping and lift shaping techniques to optimise the near-field pressure, changing strong N shape signatures to flat-top or multiple-peak signatures for lower ground impacts. The sonic boom stealth concept, compared with sonic boom shaping or sonic boom mitigation, is twofold: it indicates the approach to mitigate the sonic boom intensity—aircraft geometry shaping; and it also indicates the results of low ground impacts—low intensity or low loudness level. This paper tries to conclude some sonic boom stealth design principles to inspire other designers for the low-boom supersonic transports. From a comparison in Fig. 7, some design principles for sonic boom stealth configuration can be concluded:

• (1) A slender body to mitigate the rate of change in volume, especially at the front body.

• (2) The lifting surfaces design should make the longitudinal lift distribution more uniform.

• (3) Adjust the lift distribution and volume distribution so that they can cancel each other at key areas, especially the surface-body connection areas.

Fig. 7

Comparison of the original design (up) and sonic boom stealth design (down)

These design principles are very general. For a specific design, an integrated design optimisation environment would be essential for low-boom configuration optimisation. Work remains to be done on the theoretical part of the sonic boom stealth concept.

Low supersonic drag solution

The supersonic drag mainly consists of the friction drag, induced drag and wave drag. The friction drag can be reduced significantly by the supersonic laminar flow technology. The induced drag is affected by the wing design. The wave drag is related to the first derivative of the volume distribution (as F-volume illustrated in Fig. 7). Here are some design principles for low supersonic drag designs:

• (1) Hybrid or natural laminar flow control technology to reduce friction drag.

• (2) Properly wing design to reduce induced drag.

• (3) A long nose to mitigate the volume change at the front.

• (4) Wing and fuselage together shaping to minimize the rate of change in the middle.

• (5) Aft fuselage shaping together with the empennage size and position to avoid a sharp change in the aft part.

Design and optimisation of a family of supersonic transports

This part presents the conceptual design results of a supersonic demonstrator, a supersonic business jet and a supersonic airliner. These three-class designs cover most of the current supersonic transport research in academia and industry. Therefore, they are design and optimised in this paper. The results are arranged in a comparison pattern so that the readers can get intuitions among different concepts.

Optimisation settings

The baseline wing design is modified based on the NASA X-59, which has been proved to be a low-boom design through previous study [1]. The optimiser settings (see Table 1) are more or less like a previous case study [26]. The objective is to minimize the sonic boom intensity on the ground. The fuselage geometrical variables control mainly the volume distribution. The wing planform and cross-sectional variables mainly change the lift distribution but can also affect the volume distribution. The wing and tailplane apex positions mainly influence the interaction of the lift and volume distributions. The optimiser is a genetic algorithm.

Table 1 Low-boom optimisation settings

Design mission

The design mission specifies the flight requirements for designs. These requirements are derived from the market or customer specifications. The mission requirements, shown in Table 2, for supersonic transport have been analysed by the authors in a review paper [6], considering the environmental impacts, technological challenges, and market analysis.

Table 2 Mission requirements for the designs

General geometry

The authors have analysed several different wing and fuselage combinations in a previous study [1] and find that a low-boom low-drag design should have more uniform longitudinal volume and lift distributions. The fuselage is expected to be slenderer and a highly swept wing is expected to flat the lift distribution. Horizontal tail is preferred rather than the canard, because horizontal tail can help to reduce sonic boom signature in the aft part. The design of the supersonic demonstrator (Fig. 8) is based on the NASA X-59 design. The SSBJ (Fig. 9) and supersonic airliner (Fig. 10) share almost the same wing shape as the demonstrator. The fuselage is optimised to not only meet the requirements of passenger comfortability and packaging requirements, but also for low-boom and low-drag objectives.

Fig. 8

General geometry of the supersonic demonstrator design

Fig. 9

General geometry of the SSBJ design

Fig. 10

General geometry of the supersonic airliner design

Mass prediction

The reference MTOM of the supersonic demonstrator is the NASA X-59. The MTOMs of the SSBJ and supersonic airliner are in line with statistics of supersonic designs, as illustrated in Fig. 11.

Fig. 11

MTOM prediction

Packaging

Unlike the subsonic aircraft, the supersonic aircraft have very thin wings. The wing tank volume is usually not enough for mission fuel. Fuselage fuel tanks are required. Packaging is an important aspect of supersonic aircraft fuselage volume allocation. On the one hand, the supersonic wave drag reduction tends to an area-ruled fuselage. On the other hand, the passenger cabin and the fuselage fuel tanks require large blocks of volume. One of the most important function of the packaging is to check the available wing tank volume and arrange the fuselage fuel tanks to avoid interface with other inner components. The trim fuel tanks are also designed to control the centre of gravity directly. As can be found from Fig. 12, the packaging challenge for the supersonic demonstrator is relatively weak without a passenger cabin (see Fig. 13). On the other hand, it is very challenging for the supersonic airliner to achieve an area-ruled fuselage, as shown in Fig. 14.

Fig. 12

Packaging of the supersonic demonstrator design

Fig. 13

Packaging of the SSBJ design

Fig. 14

Packaging of the supersonic airliner design

Aerodynamics

The aerodynamic coefficients are important for the performance estimation in the conceptual phase. For the supersonic aircraft, the low-drag optimisations mainly focus on decreasing the supersonic wave drag through geometry variation. Therefore, the supersonic cruise efficiencies (demonstrator L/D = 12.17, SSBJ L/D = 10.77, airliner L/D = 11.89) of these concepts (with nacelles) are higher than the last-generation supersonic transport (e.g., Concorde L/D = 7) (see Figs. 15, 16, 17).

Fig. 15

Supersonic demonstrator drag components and drag polar

Fig. 16

SSBJ drag components and drag polar

Fig. 17

Supersonic airliner drag components and drag polar

Sonic boom intensity

The idea of low-boom optimisation is to tailor the lift and volume distribution to achieve a low near-field pressure, thus a low ground signature. The sonic boom intensity is calculated for the initial cruise condition. The design concepts have been optimised for the lowest sonic boom intensity. As can be found in Figs. 18 and 19, the near-field signatures are optimised to have no single highest peak, especially the overpressure. Even lower boom intensity will require modifications to all the peaks. The optimum sonic boom intensity for the three concepts (without nacelles) are 0.47 psf, 0.90 psf and 1.08 psf, respectively.

Fig. 18

Sonic boom near-field pressure generation

Fig. 19

Sonic boom propagation

Conclusion

This paper has introduced the development of supersonic transports and the progress made in low-boom research. An integrated multidisciplinary design model, with low-to-medium-fidelity methods, has been developed in the GENUS environment. With this model, the authors reveal the link between the sonic boom signature and the lift and volume distributions, especially the cancelling effect between the two distributions. This makes it possible to design low-boom supersonic transport. Sonic boom stealth as a new terminology is presented with design principles for low-boom supersonic transport aircraft. Similarly, low-drag design principles are concluded as a result.

A single-seat supersonic demonstrator is designed and ends up with a sonic boom intensity of 0.47 psf supersonic cruise lift to drag ratio of 12.17. A 10-passenger SSBJ concept is designed and optimised following the same procedure. The sonic boom intensity of this design is optimised to be 0.90 psf. The supersonic cruise lift to drag ratio is 10.77. For the 50-passenger supersonic airliner, the sonic boom intensity is 1.08 psf and the supersonic cruise lift to drag ratio is 11.89.

However, the low-boom optimisation for supersonic aircraft with nacelles is still very challenging. The relatively bulky volume of the nacelles has a huge impact on the volume distribution, thus the sonic boom intensity. More efforts are required to converge the design ideas on low-boom aircraft, to study the low-boom design with nacelles or distributed propulsion system.