1 Introduction

The recent developments in the field of electric motors for air vehicles bring a growing use of propellers with them. Many new concepts e.g. for Urban-Air-Mobility use propeller powered by electric motors. Due to the unique characteristics of electric motors and the resulting configurational aspects, these configurations can appear very different from the conventional propeller powered aircrafts [10]. Some of these aspects are:

  1. 1.

    The motors themselves are lighter and allow for more freedom in the placement of the propellers (e.g. at the wing tips).

  2. 2.

    Some configurations feature V/STOL capability, leading to more powerful/larger propellers.

  3. 3.

    Electric engines are more compact, resulting in less distance between the propeller and its support structure.

Some of these can have a detrimental effect on the aeroelastic stability and especially on a phenomenon called propeller whirl flutter, which involves the gyroscopic whirl modes of a rotating engine on a flexible support structure. These whirl modes can become unstable. Exceeding the critical flight speed (or shaft speed) leads to growing amplitudes of the propellers whirling motion and can result in rapid in-flight destruction of its support structure [9]. Because of this, whirl flutter assessment is also part of the certification based on CS23/CS25 [5]. To prevent a later reduction of the flight envelope due to aeroelastic limitations, it is advisable to assess the whirl flutter stability in the design process.

The method used in this paper to do this assessment were originally developed by Houbolt and Reed [12] to investigate the stability of turboprop aircraft with a simple pylon model. Rodden [21] refined them for the use in conjunction with the simulation code NASTRAN and therefore with arbitrary structural models. Cecrdle later applied them [3] to the analysis of full aircraft models and demonstrated their application to aircraft certification [2]. He uses an optimisation procedure [1] to find the stability boundary with respect to propeller pitch and yaw frequencies and highlights the importance of such modes for the whirl flutter stability of turboprop aircraft.

Not only turboprop aircraft are affected by whirl flutter, but for example tilt rotor aircraft in forward flight, too. The main difference to turboprop propeller whirl flutter is the inclusion of the dynamics of the large rotor blades, as for example Johnson [14] demonstrates in his analytical model. [17] gives a brief overview about some basic phenomena in such a system, also using a simple analytical modal. Modern tilt rotor configurations are being analysed with more complex numerical simulations using rotorcraft comprehensive codes [8, 22, 23]. [16] used multibody simulation to study the effect of nonlinear spring stiffness on a whirl flutter wind tunnel model using linearisation and nonlinear time simulation. Mair et al. used nonlinear analysis techniques like bifurcation and eigenvalue analysis to demonstrate the effect of nonlinearities for tilt rotor gimbal stiffness [18] and propeller pylon stiffness [19] using analytical models. They concluded that in some cases there can be areas for pylon (or gimbal) stiffness which are unstable in the non-linear case but predicted as stable by the linear methods.

Many of the references above either use a simple analytical pylon model with a pitch and yaw degree of freedom to study certain aspects of the whirl flutter phenomenon or complex aircraft models to analyse specific configurations. This paper aims at comparing these approaches in a numerical parameter study by refining the modelling step by step from the classical two-DOF model to a more complex one with wing dynamics and aerodynamics. It will therefore highlight the differences in the stability results obtained with the different modelling approaches.

A generic model of a propeller at the tip of a lifting surface will be used for this study. Its effect on the stability of the local pylon support structure as well as the influence of the global dynamic / aeroelastic system will be discussed. After describing the methods and models used and presenting the results of an extensive parameter study, conclusions and recommendations regarding whirl flutter stability assessment practices will be drawn.

2 Methods

Before introducing the generic whirl flutter model and its stability characteristics, the methods for their assessment are presented. This involves a brief introduction to the inclusion of unsteady propeller aerodynamics into a flutter calculation. As the goal is to do extensive parameter studies, the in-house tool used for doing such parametric flutter analyses, PySTAB, is also described.

2.1 Theory of (whirl-) flutter analysis

A rotating propeller in a flexible engine bed is subjected to gyroscopic whirl modes. Due to the aerodynamic forces these whirl modes can become unstable [4]. This phenomenon is called whirl flutter. A simple model to describe this behaviour is shown in Fig. 3. This system consists of a rigid propeller on a shaft with a yaw and pitch degree of freedom. The yaw and pitch modes merge to a forward and backward whirl mode when rotating. Considering the aerodynamic forces caused by this whirling motion the backward whirl mode eventually becomes unstable [4].

Considering a linear strip theory one can describe the propeller aerodynamics by stiffness and damping terms for the propeller hub point [21]. In Eq. (1) these terms are expressed as non dimensional derivatives. \(C_{m\psi }\) for example is the non-dimensional pitching moment m caused by a steady yaw angle \(\psi\). In general, these coefficients are dependant on the forward and rotational speed. To obtain Eq. (1) equations (1)–(4) in [21] are reformulated into matrix notation, yielding the side forces (\(F_y\) and \(F_z\)) and torques (\(M_y\) and \(M_z\)) at the propeller hub point.

$$\begin{aligned} \begin{aligned} \dfrac{1}{q_\infty 2\pi R^3} \begin{pmatrix} F_y \\ F_z \\ M_y \\ M_z \\ \end{pmatrix} ~&=~ \underbrace{\begin{bmatrix} 0 &{} 0 &{} \frac{C_{y\theta }}{2R} &{} \frac{C_{y\psi }}{2R} \\ 0 &{} 0 &{} \frac{C_{z\theta }}{2R} &{} \frac{C_{z\psi }}{2R} \\ 0 &{} 0 &{} C_{m\theta } &{} C_{m\psi } \\ 0 &{} 0 &{} C_{n\theta } &{} C_{n\psi } \\ \end{bmatrix}}_{\underline{K}_p} \begin{pmatrix} y \\ z \\ \theta \\ \psi \\ \end{pmatrix}\\&+~ \underbrace{\begin{bmatrix} -\frac{C_{y\psi }}{2RV} &{} \frac{C_{y\theta }}{2RV} &{} \frac{C_{yq}}{2V} &{} \frac{C_{yr}}{2V} \\ -\frac{C_{z\psi }}{2RV} &{} \frac{C_{z\theta }}{2RV} &{} \frac{C_{zq}}{2V} &{} \frac{C_{zr}}{2V} \\ -\frac{C_{m\psi }}{V} &{} \frac{C_{m\theta }}{V} &{} \frac{C_{mq}R}{V} &{} \frac{C_{mr}R}{V} \\ -\frac{C_{n\psi }}{V} &{} \frac{C_{n\theta }}{V} &{} \frac{C_{nq}R}{V} &{} \frac{C_{nr}R}{V} \\ \end{bmatrix}}_{\underline{D}_p} \begin{pmatrix} \dot{y} \\ \dot{z} \\ \dot{\theta } \\ \dot{\psi } \\ \end{pmatrix}. \end{aligned} \end{aligned}$$
(1)

To analyse an aeroelastic system with this method the propeller aerodynamics have to be coupled with a dynamic model of the structure. This is done by adding the stiffness and damping terms of the propeller to the structural model in physical coordinates [21]. To reduce the number of degrees of freedom for the stability analysis, the complete model is transformed into modal coordinates. This results in:

$$\begin{aligned} \begin{aligned} \underline{M}_{gen} \ddot{q} + \underline{K}_{gen}q ~=&~ \underline{\phi }^T \underline{K}_P \underline{\phi } q + \underline{\phi }^T (\underline{D}_P~+~\underline{G}) \underline{\phi } \dot{q} \\&+~ \frac{1}{2} \rho _\infty V^2 \underline{Q}_{hh}(k), \end{aligned} \end{aligned}$$
(2)

\(\underline{M}_{\text {gen}}\) and \(\underline{K}_{\text {gen}}\) represent the modal mass and stiffness matrix of the base structure, \(\underline{\phi }\) is the modal matrix transforming physical into modal coordinates q. \(\underline{K}_P\) and \(\underline{D}_P\) represent the propeller terms from Eq. (1) and \(\underline{G}\) the skew symmetric gyroscopic matrix. The last part of Eq. (2) allows for the inclusion of frequency-domain aerodynamics for the remaining part of the aircraft such as wings and other lifting surfaces. \(\underline{Q}_{hh}(k)\) are the generalized aerodynamic forces, for example on the wing or tailplane lifting surface, that depend on the reduced frequency k. In the model given later, an unsteady acceleration potential method [7] is used to form the \(Q_{hh}\)-matrices. If these are included into the stability analysis, the problem changes from a set of explicit eigenvalue problems (first terms in Eq. (2) are only velocity-dependant) to an implicit flutter problem, because the \(Q_{hh}\)-term is frequency dependent. These implicit eigenvalue problems can be solved, for example, using the g-method for flutter solutions [6] or other common flutter solvers. The solution of Eq. (2) in different varieties is a very common problem for aircraft flutter application and is therefore automated in the in-house tool PySTAB.

2.2 Linear frequency domain flutter process: PySTAB

To analyse aircraft configurations on their flutter stability in the linear frequency domain, a python environment is used to automate the flutter analysis process. This environment uses the commercial software ZAERO [13] as a core. ZAERO is used to compute the unsteady aerodynamic forces using an unsteady acceleration potential method [7] and to solve the coupled aeroelastic equation of motion using the g-method [6]. Additionally PySTAB allows for the consideration of different aspects like engine gyroscopic loads, in-plane aerodynamic forces, propeller forces or even the generalized aerodynamic forces from the CFD Solver TAU (cf. Fig. 1). By switching to a state-space formulation, aeroservoelastic calculations can be carried out. Depending on the needs of the configuration to be analysed, the user can decide which effects to consider.

Fig. 1
figure 1

PySTAB: Linear frequency domain stability process

Full size image

As the flutter assessment of an aircraft usually needs a lot of parameter studies (Mach number, density, mass cases, control system, structural parameters, etc.), PySTAB uses a three-layer architecture (cf. Fig. 2). An underlying database stores all data for the different configurations and analysis steps, while a functional layer manages all the tasks during the analysis. Finally, control scripts and a GUI provide easy access and control over the simulations and results.

Fig. 2
figure 2

PySTAB program architecture

Full size image

3 Models

Before introducing the generic model which will be used for most of the parameter studies in Sect. 5, the classical whirl flutter model [12] will be described, as it is still useful to study the effect of basic system parameters on the stability.

3.1 Classical model

Early whirl flutter studies used a simple model of a propeller attached to a rigid pylon with a pivot joint at the other end (cf. Fig. 3). As this is the most simple structural model showing whirl flutter, it will be used later as an introduction into the parameter studies.

Fig. 3
figure 3

Classical 2-DOF whirl flutter model

Full size image

The system can be described with the help of Eq. (2), neglecting any unsteady aerodynamics \(Q_{hh}\) from other sources and using the following modal coordinate transformation between the propeller hub coordinates x in Eq. 1 and the generalized pivot angles q in Eq. (2)

$$\begin{aligned} x ~=~ \begin{pmatrix} y \\ z\\ \theta \\ \psi \end{pmatrix} ~=~ \underline{\phi } q ~=~ \begin{bmatrix} 0 &{} a \\ -a &{} 0 \\ 1 &{} 0 \\ 0 &{} 1 \\ \end{bmatrix} \begin{pmatrix} \theta \\ \psi \end{pmatrix}_{\text {pivot}}, \end{aligned}$$
(3)

using the distance a between the propeller hub and the pivot joint. The resulting equations of motion for the aeroelastic system can then be evaluated for its eigenvalues and therefore its stability characteristics. Having the equations of motion in analytical form helps with varying parameters and demonstrating their effect on the system stability. While this model is useful for demonstrating trends it is of limited use for the assessment of a real aircraft structure. Table 1 shows the parameters for the classical model that are used in this study.

Table 1 Parameters for the classical model
Full size table

3.2 Generic model

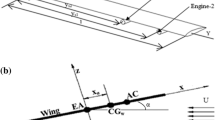
Since the classical model is not suitable for demonstrating the effects appearing in a real aircraft structure, a more complex model will be used for the rest of the parameter studies (Sect. 5). It consists of a three-bladed propeller at the tip of a lifting surface (c.f. Fig. 4) with a flexible MSC.Nastran beam model as base structure. The model is derived from the design of a V-tail structure of the hybrid-electric motor glider FVA 30, which has electric motors at the tip of its V-Tail, and therefore shows dihedral (see [15, 20] for more detail about the configuration). Nevertheless, the effects studied are applicable to other configurations and the structural parameters are more or less generic.

Fig. 4
figure 4

Generic whirl flutter model

Full size image

The model consists of different components that can be modified independently (cf. Fig. 4). Beginning with the propeller and the electric motor (represented by a point mass) the first flexible element is a rotational spring representing the engine shock mounts. The pylon is modelled with flexible beam elements and is the main focus of the parameter studies. The pylon is attached to the tip of the actual base structure, which also consists of beam elements and is clamped at the bottom. Figure 4 also shows the aerodynamic grid used for calculating the unsteady aerodynamics of the lifting surface with an unsteady acceleration potential method [7]. Table 2 in App. A gives more details about the model geometry and properties.

For the parameter study, the stiffnesses of the components are varied and expressed in uncoupled component natural frequencies (all other components set rigid). The resulting eigenfrequencies of the complete model will differ from these uncoupled values due to dynamic coupling. Nevertheless, the uncoupled eigenfrequencies are used as a measure of component stiffness.

4 Results using classical model

In this section the influence of some basic parameters on the stability of a whirl-flutter system will be shown. These results can be applied for the design of propeller driven aircrafts regarding whirl flutter safety. As Sect. 5 will show later, this model also has its restrictions, making an evaluation of whirl-flutter on aircraft-level mandatory.

Most results in this paper will be shown in plots like Fig. 5. In these diagrams the stability of the system is plotted for a variation of the pivot stiffnesses (or uncoupled pitch/yaw frequencies \(\frac{1}{2\pi }\sqrt{K_{\theta }/I_{\theta }}\)), as these are the most important parameters for the whirl flutter stability. The characteristic bell curves forming at the bottom left indicate the boundary towards dynamic whirl flutter. Regions of higher pivot stiffness are stable, lower stiffness results in an unstable whirl motion. The areas near the axes, beyond the horizontal or vertical line, represent the special case of one stiffness being low and resulting in a static divergence instability. This leads to the first and most important rule for preventing whirl flutter: Higher support stiffness can prevent whirl flutter. This includes failure cases [5], which account for possible failures in the engine support structure. A structural failure in a supporting element can significantly reduce the stiffness of the support and therefore make the system more prone to whirl flutter. The following plots (Figs. 6, 7, 8, 9 and 10) will compare this boundary for a 20% variation of one of the model parameter in Table 1 while keeping the others fixed. First the effect of airspeed and shaft speed will be demonstrated in Figs. 6 and 7, then the model geometry (radius and hub distance) will be varied in Figs. 8 and 9 and last the system will be changed from a tractor into a pusher configuration in Fig. 10.

Fig. 5
figure 5

Typical whirl flutter boundaries with respect to pivot stiffnesses

Full size image
Fig. 6
figure 6

Whirl flutter boundaries for \(\pm 20\%\) variation in flight speed

Full size image
Fig. 7
figure 7

Whirl flutter boundaries for \(\pm 20\%\) variation in shaft speed

Full size image
Fig. 8
figure 8

Whirl flutter boundaries for \(\pm 20\%\) variation in propeller radius

Full size image
Fig. 9
figure 9

Whirl flutter boundaries for \(\pm 20\%\) variation in distance propeller to hub

Full size image
Fig. 10
figure 10

Whirl flutter boundaries for a system in pusher and tractor configuration

Full size image

4.1 Operational parameter

Figures 6 and 7 show the influence of the operational parameters on the stability. As the larger areas of instability indicate, an increase in airspeed (c.f. Fig. 6) is more critical than an increase in shaft speed (c.f. 7). Whirl flutter is therefore a high-speed phenomenon, making the high speed end of the envelope as well as failure cases like propeller overspeed most critical. Often, boundaries like Fig. 5 are plotted for certification speed of 1.2 time the dive speed \(V_D\) [2].

4.2 Geometric parameter

The geometry of the system also has an impact on its stability characteristics. Figure 8 shows the influence of the propeller radius. Larger propeller are more prone to whirl flutter, because they produce larger aerodynamic forces. Even more important for the whirl flutter stability is the distance between propeller hub and pivot as shown in Fig. 9. As the hub distance a decreases, the destabilising aerodynamic moments gain influence over the stabilising forces, as the latter are scaled by a (see Eq. (3)). This is important especially for systems powered directly by an electric motor. As already pointed out in the introduction, most electric motors are more compact than their conventional turboprop equivalent, resulting in less distance between the propeller and the first elements of the support structure. This has to be kept in mind when designing the support structure and eventual engine shock mounts, as they tend to be the first element providing relevant amounts of flexibility. At this point it shall be mentioned that these elements may also provide damping, which positively affects the whirl flutter stability.

4.3 Configurational parameter

The last part of this section will briefly cover the difference between a pusher and tractor configuration. By modifying the system kinematics in Eq. (3) (a change of sign for the “a”-terms in the matrix \(\underline{\phi }\)), the classical whirl flutter model can easily be adapted to this configuration. Figure 10 shows the stability characteristics for the system in both arrangements. The pusher configuration shows a higher susceptibility to dynamic whirl flutter, indicated by the larger extension of the bell curve in the bottom left. However, unlike the tractor configuration, the pusher propeller does not show any static divergence, as the forces driving this phenomenon change sign due to kinematics and are stabilising in this case.

5 Results using the generic model

After showing the influence of some basic parameters using the classical two-DOF model, the following section will demonstrate the effect of a more complex modelling approach on the results of the stability assessment while keeping the operating point and propeller from Table 1. Step by step more substructures of the generic model in Fig. 4 are taken into account, starting with the shock mounts and adding the pylon, the base structure and the lifting surface unsteady aerodynamics to the model. After evaluating the stability in terms of shock mount stiffness, mostly pylon stiffness charts as seen before will be used to display the results.

5.1 Shock mounts

Figure 11 shows the shock mount pitch and yaw frequencies necessary for providing a stable subsystem. All the other components are set to rigid for this assessment, so that the system resembles the classical two-DOF model (the only two DOF are the two rotations about the mounting point of the shock mounts). Due to the compactness of the motor, the distance between the propeller and its shock mounts is small, leading to a high amount of stiffness needed for stabilising the system and a more extensive whirl flutter region (c.f. Fig. 9). The dashed line highlights the critical region of equal pitch and yaw stiffness. For convenience, the stiffness of the shock mounts for the following analysis are picked from this line: One on the stable region at 100 Hz, one at the border at 45 Hz and one in the unstable region at 40 Hz.

Fig. 11
figure 11

Whirl flutter boundary for the shock mount subsystem of Fig. 4. The marked points (1: 40 Hz, 2: 45 Hz, 3: 100 Hz) will be used in Sect. 5.2ff as example shock mount stiffnesses

Full size image

5.2 Pylon and shock mounts

Next the pylon is added as a flexible beam to the model. With stiff shock mounts one would again see a behaviour as displayed in Fig. 5. Figure 12 resembles this case in dark grey for the stiff shock mounts (100 Hz). Plotted are the uncoupled pylon frequencies (the pitch and yaw frequencies of the isolated pylon substructure) as a measure of pylon stiffness. As the system is still symmetric in pitch and yaw the area of equal stiffness is the most critical.

Fig. 12
figure 12

Stability of the coupled system for two levels of shock mount stiffness

Full size image

This still applies for the second case in Fig. 12, showing the stability of the coupled system with shock mounts at the border of their subsystems stability ((2) in Fig. 11 at 45 Hz, displayed in light grey). But as the larger extension of the area of instability shows, the coupled system is now much more sensitive in terms of pylon stiffness. Compared to the case of stiffer shock mounts, the system needs a factor of 2.5 more pylon stiffness to stabilise. This is because with lower shock mount stiffness, the low frequency coupled modes of the system show more portions of shock mount displacement together with pylon motion, moving the effective hub distance (distance between the node of the mode and the propeller) closer to the propeller. This already gives a hint on how adding subsystems to the assessment complicates the interpretation. However, it is still valid that higher pylon stiffnesses are stabilising and equal pitch and yaw frequencies are critical as the largest extension of the whirl flutter region is on the bisecting line.

When coupling the pylon subsystem with a shock mounts that yield an unstable shock mount subsystem (c.f. Sect. 5.1, Fig. 11, point (1) at 40 Hz pitch/yaw frequency), one would expect instability due to shock mount whirl flutter regardless of the pylon stiffness. Figure 13 shows this case, and again, the coupled system behaves different than the two separate subsystems, this time by stabilising the system in certain areas (marked white in Fig. 13). Again, this is due to the mixed content of the first coupled mode, which moves the effective hub distance away from the propeller compared to the pure shock mount whirl. For higher pylon frequencies the system again shows a pure shock mount whirl flutter as expected for a quasi-rigid pylon.

Fig. 13
figure 13

Stability of the coupled system with an unstable shock mount subsystem

Full size image

Figure 14 is evaluated at a slightly lower airspeed (93 instead of 100 m/s) and shows more clearly, how the large instability area in Fig. 13 is formed. Figure 13 actually consists of four fused instability regions, all representing different flutter mechanisms:

  1. 1.

    For high pylon stiffnesses, the pylon acts quasi-rigid and the system shows pure shock mount whirl flutter

  2. 2.

    For both pylon stiffnesses being low the system shows a pylon whirl similar to Fig. 12

  3. 3.

    In regions where only one pylon stiffness is high and the other matches a shock mount mode, a coupled whirl flutter mechanism arises, which consists of pylon displacement in one (e.g. yaw) and shock mount motion in the other (e.g. pitch) direction. The associated complex mode shape is displayed in Fig. 15 with two steps with 90 deg phase in between, showing the different participations of pylon yaw and shock mount pitch.

Fig. 14
figure 14

Different regions making up Fig. 13 (airspeed reduced to 93 m/s)

Full size image
Fig. 15
figure 15

Flutter Mode shape associated to point 3 in Fig. 14

Full size image

Region 3 has a mirror about the bisecting line, basically rotating the mode shape by 90 deg. Figure 14 demonstrates that a whirl flutter mode can arise from portions of different substructures. Basically any mode leading to a tilting of the propeller plane can take part in a coupled whirl flutter mode, as long as there is a counterpart with tilting in the other direction to form the whirling motion. Due to the dynamic coupling and the difference in mode shape (and therefore different activation of the propeller aerodynamics) the frequencies of the uncoupled systems don’t necessarily have to match. Figure 14 shows this for region 3 (pylon frequencies of 25 Hz are critical, while the uncoupled shock mount is at 40 Hz). This makes an evaluation of the coupled system with the help of Eq. (2) essential to cover all dynamic couplings, instead on relying on the classical two-DOF model. The next section will highlight this even more, as now the full generic model is considered, which is not symmetric any more.

5.3 Full model

From now on, the full dynamic model of Fig. 4 is taken into account. The base structure (with rigid pylon and shock mounts) has three modes in the frequency range of interest: first out-of-plane bending at 4.3 Hz, first in-plane bending at 15 Hz and first torsion at 20 Hz. Due to the mass coupling by the large motor mass the first mode also shows portions of torsion motion.

As other publications [4] already pointed out by expanding the classical pylon model with a simple wing model, wing torsion motion can also serve as part of a whirl flutter mode due to its rotational contribution. In this case, all three modes provide rotation of the propeller plane (though in different directions and quantities). Therefore, one expects an influence on the whirl flutter behaviour.

Figure 16 shows this for the stiff shock mounts (100 Hz uncoupled subsystem frequency). Due to the asymmetry introduced by the base structure Fig. 16 shows different behaviour with regards to pitch and yaw. Yaw refers to a motion perpendicular and pitch therefore to a pylon motion in the plane of the lifting surface. Figure 16 shows these three couplings (or flutter mechanisms) as unstable areas:

  1. 1.

    Low pylon pitch frequencies couple with the first out-of-plane bending mode, which serves as propeller plane yaw.

  2. 2.

    For higher pylon pitch frequencies the coupling changes to the torsion mode.

  3. 3.

    Perpendicular to this, in-plane bending couples with pylon yaw.

Interestingly the regions of equal pylon stiffness is the most stable, emphasizing how important a consideration of the full dynamic model is for assessing the system stability. The usage of a simplified model (c.f. Fig. 13ff) only taking the pylon into account would have lead to the wrong conclusion that equal pylon stiffness is most critical, as the preceding section suggested.

Fig. 16
figure 16

Whirl flutter boundaries for the full dynamic system with stiff shock mounts

Full size image

5.4 Full model with aerodynamics

The motion of the base structure also activates a considerable amount of unsteady aerodynamics of the lifting surface, which have been neglected so far. These have to be considered to provide the most comprehensive stability assessment of the generic model. Due to the large motor mass in front of the elastic axis, no classical bending torsion flutter (without the rotating propeller) is found. As other authors already stated (e.g. [11]), the lifting surface aerodynamics have great influence on the stability characteristics of the system and are stabilising in this case, as the out-of-plane bending provides large amounts of aerodynamic damping. Figure 17 shows this for the most critical dynamic system with low stiffness shock mounts. Almost all unstable areas stabilise and only a small coupling of pylon motion with the first bending mode can be observed for small pylon stiffnesses (c.f. the dent in the enlarged area in Fig. 17) This further emphasises the importance of evaluating the whirl flutter stability of a system using a full aeroelastic model considering all relevant dynamic aspects as well as unsteady aerodynamics.

Fig. 17
figure 17

Whirl flutter boundaries for the full system with low stiffness shock mounts and considering unsteady lifting surface aerodynamics

Full size image

6 Conclusion and outlook

Using the classical two-DOF pylon whirl flutter model as well as a generic model of a propeller mounted at the tip of a lifting surface, several parameter studies with regards to whirl flutter have been conducted. The simple model was used to explore the influence of some basic parameters, showing that higher speeds as well as larger propeller and shorter distances between propeller and pivot are critical. However, the results from the generic model demonstrated, that due to dynamic coupling between different substructures the simplified model can give misleading results and a full dynamic or even aeroelastic model (also considering unsteady lifting surface aerodynamics) should be used to assess the system stability. In contrast to classical flutter whirl flutter does not require a frequency neighbourhood, and depending on the mode shapes it is difficult to predict the possible couplings, as Sects. 5.2 and 5.3 demonstrated. Basically, any mode that leads to a tilting of the propeller plane can be part of a whirl flutter mechanism. Using only a reduced dynamic model (for example only a local model of the engine support as in Sect. 5.2) can still lead to a wrong estimation of the stability behaviour, because frequencies and mode shapes change when considering a more detailed structural model. Especially the motion of a lifting surface (for example the wing the engine is attached to) can drastically change to stability due to the activation of unsteady aerodynamics. In the case considered here the lifting surface aerodynamics have a strong stabilising effect due to aerodynamic damping. The studies presented here stress therefore the importance of including whirl flutter assessments on aircraft level into the aeroelastic stability evaluation and demonstrates a simple method for this purpose.

Uncovered cases comprise an unstable aeroelastic system without propeller and which effect the propeller has on these systems. This is left for future work, as well as a more thorough exploration of the whirl flutter of pusher configurations, which seem to be more susceptible to whirl flutter.