Abstract
Composite structures have shown a prominent impact in the aircraft structural design. With an increasing shift towards incorporating more composite materials in the primary aircraft structure it is imperative to have corresponding design tools to simplify the design process. In the present work, a simplified implementation for composite optimization has been developed within the DLR-AE (German Aerospace Centre, Institute of Aeroelasticity) automated aeroelastic structural design framework cpacs-MONA. This paper presents the results of structural optimization of a high aspect ratio composite wing aircraft model developed in the DLR project ATLAs. The generation of almost all involved simulation models for this study is done using the in-house DLR tool ModGen. An aeroelastic trim analysis is conducted for various manoeuvre and gust conditions. A load selection process is used to determine the most relevant sizing load cases. A comparison is made between the optimization results of a composite wing and an aluminium wing to demonstrate the more favourable strength to weight ratio of the composite wing. A manoeuvre load alleviation procedure has been introduced in the load calculation process. The results show further weight savings in the design process when load alleviation is utilized due to reduction in the span wise bending moment.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Enhancement of aircraft performance characteristics is one of the focal points in modern day aircraft design procedures. Technological progress in the field of aeronautics has made it possible to experiment more with conceptual ideas and designs. One of the more prominent introductions into the aircraft industry has been the utilization of composite materials for structural components. The benefits of composite materials lie in their high strength-to-weight ratio in comparison to the conventionally used metals. A direct impact of this is seen in structural mass reduction and, therefore, improved fuel efficiency. Furthermore, composite materials offer better fatigue life and higher corrosion resistance. Overtime, this has led to increased utilization of composites in aircraft primary structures with the Airbus A350 and Boeing B787 leading the pack with more than 50% of the structure made of composite materials [1]. This necessitates adaptations of aeroelastic design procedures to satisfy the design constraints of fibre reinforced materials. Early studies have shown that use of composite materials allows more flexibility in satisfying design constraints as compared to aluminium, because it allows for the changes in fibre orientations in different layers besides the overall laminate thickness [2, 3]. This has been further demonstrated in [4] by conducting aeroelastic tailoring for divergence, control surface effectiveness and shift of centre of pressure on the forward swept wing. In the DLR-AE, there has been a significant amount of research on aeroelastic tailoring and structural optimization of composite wings. In [5], stiffness optimization of lower and upper skins of the wing box has been demonstrated by considerations of mass, strength, buckling, aerodynamic twist and aileron effectiveness. The design, manufacturing and testing of an aeroelastically tailored composite forward swept wing is presented in [6]. A detailed optimization procedure, based on the use of lamination parameters, is demonstrated in [7] for a long-range transport aircraft with considerations of manufacturability of the composite structure in early design stage.
Another factor affecting the efficiency is the lift induced drag. From an aerodynamics point of view, a high aspect ratio wing is advantageous in reduction of the induced drag. However, depending on the flexibility of the structure, it could potentially introduce geometrically nonlinear effects. Thin walled structures and beams are known to show a stiffening effect under large deformation which has a direct impact on the static and dynamic response of the structure, thus affecting the vibration and aeroelastic characteristics of the structure.
This paper presents a study of the aeroelastic response and structural optimization of a mid-range passenger aircraft designed in the DLR project ATLAs which incorporates a fully composite wing design and a higher than usual wing aspect ratio. The focus of the paper is on the in-house parametric load computation and structural optimization process chain cpacs-MONA [8, 9], developed in the DLR-AE, and its application to the aforementioned aircraft called ARB2028. Further details of the aircraft design have been presented in [10]. The design process chain is compatible with design data set defined in the Common Parametric Aircraft Configuration Schema (CPACS) format. CPACS is a data exchange format for air transportation systems [11]. So far, the automated process in cpacs-MONA has been used for the aeroelastic design of traditional metallic wing aircraft using linear aeroelastic analysis. The analysis of composite aircraft previously required intermediate pre-processing steps. In the present work, the automated design framework is extended to composite wing aircraft with a first implementation of a composite thickness optimization procedure. A comparison is made between the results of structural sizing when a composite material is used and when aluminium is used. Furthermore, a manoeuvre load alleviation (MLA) procedure is implemented to demonstrate its effect on structural mass reduction in the sizing process. Additionally, an overview of the conceptual load computation tool LOADzero [12] and its application are also presented.
2 Model description
The aircraft model, in the MSC Nastran format, is generated with the DLR–AE in-house modelling tool ModGen [13] which is integrated within the cpacs MONA framework for automation of the process. In the present analysis, a detailed wing box model is generated for the main wing, horizontal tail plane (HTP) and vertical tail plane (VTP). An example of the wing box topology can be seen in Fig. 1. The overall wing box structural model consists of primary structural elements- skin, spars, ribs and stiffeners. The secondary structural elements are simply integrated as concentrated masses at appropriate locations. A beam structural model is deemed sufficient for the fuselage, since the primary focus is on the wing box thickness optimization.
A loads reference axis (LRA) defined along the wing span is used to condense the aerodynamic loads onto the structure. The LRA is connected to the Finite element (FE) structural elements with the use of rigid body elements as depicted in Fig. 2. Furthermore, a condensed mass model is generated, where the masses are distributed over the LRA and fuselage central axis. The mass distribution is defined in a manner that the centre of gravity of the aircraft lies between 10 and 40% of the mean aerodynamic chord (MAC) to satisfy flight stability and controllability conditions. Modelling of several mass configurations and centre of gravity (CG) locations are considered in the design to ensure determination of an extensive set of load cases.
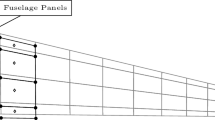
The aerodynamic loads are calculated using the Vortex Lattice Method (VLM) integrated within the aeroelastic module of MSC Nastran [14]. The modelling of the lifting surfaces is done in the form of panels as depicted in Fig. 3, where the fuselage mesh is omitted for better visualization. The fuselage aerodynamic panels are modelled as two mutually perpendicular two-dimensional planes to account for the vertical and lateral forces. Control surfaces are distinguished by associating the relevant panels to specific hinge lines that are defined by local coordinate systems.
Some basic geometrical and mass configuration details of the aircraft can be found in Table 1. The interesting feature of the ARB2028 model is the relatively higher aspect ratio of 12.3 in comparison to conventional commercial aircraft. This leads to a slender wing box design as depicted in the global finite element model (GFEM) in Fig. 4.
The composite material used in the design is a carbon fibre reinforced plastic. Different ply layups are chosen for the wing skins which are more longitudinally loaded as compared to the more shear loaded structural components such as ribs and spars. A layup of (60% 0°, 20% ± 45°, 20% 90°) is used for the wing box skin panels and a layup of (10% 0°, 80% ± 45°, 10% 90°) is used for the ribs and spars. The analysis of the metallic wing aircraft is conducted using the material properties of Aluminium 2024.
3 Loads computation
3.1 Conceptual loads
The conceptual design phase of the aircraft involves preliminary sizing based on simplified loads calculation methods. This is essential in the early design phase to obtain an initial weight estimate. At DLR-AE the conceptual design loads are computed using the in-house tool LOADzero [12] which is based on analytical handbook methods. The tool has been designed for quick loads estimation for a rigid aircraft with the availability of minimal geometrical inputs and flight conditions data. For the computation process, an elliptical lift distribution is assumed, therefore, eliminating requirement of detailed wing geometry inputs. The approximation of the geometrical definition is shown in Fig. 5. A simple elliptical planform is used for the wing load calculations. The implemented load cases are in accordance with the requirements defined in the certification specification documentation for large aircraft CS25 [15]. Overall, the tool capabilities include simulation of quasi-static manoeuvre and gust load cases. The total gust load is introduced as the additional lift generated due to the gust impact, superimposed on the aerodynamic loads in 1 g cruise flight conditions. Furthermore, inertial loads are calculated based on an effective load factor which is dependent on the pitch acceleration at the centre of gravity of the aircraft and distance of the geometrical point from the CG. The effective load acting is computed as the sum of inertial forces and moments and aerodynamic forces and moments. These loads are distributed as nodal loads across the loads reference axis defined along the wing span, tail and the fuselage centre line. The conceptual loads are used for a pre-sizing process, where the simplified cross-sections of the primary structural elements such as skin, spars, ribs etc. are estimated based on stress allowable and analytical buckling constraints. The pre-sizing process based on the analytical load computations gives a good initial estimate for the structural dimensions to be used as an input for the detailed structural optimization process.
3.2 Finite element loads
The detailed design is done using loads computed from the Vortex Lattice Method implementation in SOL144 solver of MSC Nastran [14]. For this, the aerodynamic model described in Sect. 2 is utilized. The structural dependencies of the model are integrated in the analysis through the use of pre–extracted stiffness properties and a condensed mass model. cpacs-MONA is able to set-up an extensive set of load cases based on the CS25 requirements including manoeuvre and gust load cases. The gust loads in this analysis are considered as quasi-steady cases in the form of Pratt gust formulation. Furthermore, several mass configurations and flight conditions are considered for each of these load cases to determine the most relevant sizing load cases. The mass configurations are—maximum take-off (MTOM), maximum zero-fuel (MZFM) and operating empty (OEM) with variations in forward and aft CG positions. The variations in the CG positions are achieved by appropriate distribution of the payload and fuel masses. The description of the mass cases is shown in Table 2. For considerations of various flight conditions, design speeds as specified in CS25.335 are considered along with different flight altitudes ranging from sea level to ~ 11 km and by extension, various Mach numbers and dynamic pressures. In combination with the multiple mass configurations, this results in a large number of load cases. In the present study, ~ 450 load cases are considered. Utilizing each of these load cases for the aircraft sizing would result in a large computation time. To select the most relevant load cases, a load extraction procedure is used within cpacs-MONA.
For each trim analysis, monitoring points for force and moments are defined along the wing span, HTP span, the VTP and the fuselage. A total of 95 monitoring points is defined at different structural locations along the whole aircraft body of the ARB2028. Investigation of 2-d loads envelope (e.g., My vs Mx) is conducted at these monitoring points. The load cases on the estimated envelope are taken as design loads for the dimensioning. The 2-d loads plots generated are a visualization of this approach. An example of the loads envelope is depicted in Figs. 6 and 7. This approach minimizes the number of load cases considered in the sizing, therefore, reducing the optimization effort.
3.3 Manoeuvre load alleviation
The peak loads due to aircraft manoeuvres usually tend to have a significant impact on the sizing process in aircraft design. It can directly be concurred that to uphold structural integrity during high loads, thicker structural elements (for, e.g., skins, spars, ribs etc.) are required, which increases the structural mass. Load alleviation systems are very effective in decreasing operational loads and, therefore, the designed structural mass. The basic idea behind manoeuvre load alleviation (MLA) systems is to deflect the control surfaces (ailerons or sometimes spoilers) to an appropriate extent such that the lift distribution on the wings is shifted in-board, i.e., more towards the wing root. This reduces the overall bending moment across the span and, therefore, requires lower stiffness in structures to withstand the load.
Figure 8 is representative of the shift in lift distribution due to aileron deflection. In operational conditions, MLA is applied by symmetric deflection of control surfaces. Several studies of load alleviation effect on transport aircraft and its effect on the structural mass have already been published. Handojo et al. [16] presented the effect of passive and active load alleviation on a generic mid-range transport aircraft. Bramsiepe et al. [7] presented a comparison of stiffness and thickness distribution of structural elements obtained when the design is done with and without MLA while considering different types of design constraints in the optimization procedure. In the present work an MLA procedure is implemented within the cpacs-MONA process and a parametric study is performed on the aircraft model to determine an appropriate aileron deflection angle to obtain an optimal load alleviation effect.
4 Optimization process
A composite optimization procedure is implemented in cpacs-MONA to expand the tool capabilities to handle aeroelastic structural design of composite wing aircraft. Figure 9 depicts the basic automated process flow of cpacs-MONA for obtaining an optimized structural model based on aeroelastic loads.
The highlighted section of the flowchart is the work that has been conducted as a part of the present study. The loads computation and selection processes have been defined in the previous Sect. 3. In this section, the structural optimization process for a composite structure is defined. The structural optimization is performed using the MSC Nastran SOL200 solver [17] which solves a minimization problem for the objective function based on the specified constraints and design variables. The minimization of the primary structural mass is chosen as the objective function for the design problem of the presented study. In the first simplified implementation a thickness optimization procedure is incorporated, i.e., only the thicknesses of the structural elements (skin panels, ribs and spars) are chosen as design variables. The design responses are chosen to be the principal strains and shear strain. These design responses are constrained by user-defined strain allowable. The maximum strain criterion is a relatively more conservative procedure for composite optimization as shown by Bramsiepe et al. [7]; however, it is deemed sufficient for a first implementation in the automated framework.
The main steps involved in the setup for composite optimization can be described as following:
-
1.
Reading the material properties data which is defined in the input CPACS file. The available data is in the form of ply layup distribution and material properties of the 0° plies.
-
2.
Transformation of the ply material properties to compounded laminate properties. This is done using the generically known classical laminated plate theory to formulate ABD matrices [1, 18].
-
3.
Definition of the design fields, design variables and design constraints and property relations as an input for the MSC Nastran SOL200 solver.
The ply level material properties and design constraints are defined with reference to IJsselmuiden [19]. All shell elements forming the skin between two consecutive ribs are collectively defined within a single design field. Similarly, all spar elements between two consecutive ribs are defined in one design field. Each rib element is defined within one design field. This results in a total of 141 design variables for the main wing structure. The design responses constrained are major principal strain, minor principal strain, and shear strain. These responses are computed within the optimization cycles through a linear static analysis. The starting value of the design variable is set based on the estimated structural thicknesses in the pre-sizing process. A minimum allowable thickness of 2–3 mm is set for different locations on the structure to ensure that the thickness is not reduced below a practical limit as a result of sizing.
Subsequently, an iterative procedure involving aeroelastic loads calculation, structural optimization and update of the structural mass model is followed until convergence in the masses and loads of the wing structures is obtained. In the analysis presented here, a symmetric laminate is chosen such that there are no membrane-bending coupling effects. The layup is assumed to be fixed throughout the optimization procedure and micromechanical effects of the composite material are ignored.
5 Results
5.1 Structural optimization
The results of the optimized composite wing aircraft model (with no implementation of MLA) are presented in this section. The laminate thickness variation obtained in the upper skin panel of the right wing is depicted in Fig. 10.
The distribution indicates the lowest skin thickness is near the out-board region of the wing, while the thicknesses are higher towards the wing root. The maximum skin thickness can be observed near the engine-pylon-wing attachment region. This is expected due to the kink at the trailing edge, change of the planform and the high localized mass in the region which requires greater structural strength to sustain the additional loads. A comparison is made with the optimized aluminium wing model in terms of component masses. The comparison is tabulated in Table 3. The complete process requires 5–6 cycles of aeroelastic loads computation, structural sizing and mass update to achieve convergence. Figure 11 shows the variation of normalized operating empty mass (OEM) in different cycles of the loads and optimization process. The masses have been normalized with respect to the initial structural mass prior to the first optimization cycle.
A significant amount of weight reduction is observable when using composite materials for the primary structure. It is notable that the optimization results could further vary depending on the choice of design variables, design constraints and the optimization approach. For example, the choice of a higher strain allowable in design constraints has a tendency of reducing thicknesses in the optimization cycles and, therefore, the weight of the structural elements.
Furthermore, using a variable stacking sequence and using the fibre orientation of the individual plies as design variables, offers more flexibility in the optimization process and would lead to a different optimized design. The availability of ply orientations as design variables makes it possible to vary the laminate stiffness properties within the optimization process. This consequently results in potentially lower strains/ stresses and, therefore, relatively light weight designs. The integration of lamination parameters and stacking sequence optimization is a consideration for the future developments of the automated framework.
5.2 Effect of MLA
The choice of aileron deflection is undetermined in the initial study, since no generic formulation has been used to compute the appropriate aileron deflection. However, it is known that a higher aileron deflection would have a greater impact on reducing the wing root bending moment. The choice of magnitude of aileron deflections during a pull up or push down manoeuvre is primarily limited by the designed maximum allowable limit and local aerodynamic effects. The designed MLA deflection, in principle, could be chosen such that the gust loads become the dominant sizing case, while a gust load alleviation system is not used. A parametric study is conducted on the effect of the different aileron deflection angles chosen for the load alleviation cases. Sized structural models have been generated for five cases of aileron deflections during MLA: 7.5, 10, 12.5, 15 and 17.5 degrees. The results of the study are presented in this section. The effect of introducing MLA on the primary structural mass of the wing is presented in Table 4.
The results show that the wing mass reduces with increasing aileron deflections. This is, as expected, a consequence of the shift in the lift distribution towards the wing root. It can be observed that the relevant sizing loads gradually shift from the initially dominant manoeuvre cases to a few gust load cases on the outer region of the wing. In Fig. 12, the relevant sizing load case distribution based on bending moment across the half wing span is depicted when the sizing is done without MLA. The dominant sizing cases are found to be primarily pull-up and push down manoeuvres for different flight conditions.
In Fig. 13, a similar distribution of bending moment across the half wing span is generated when an aileron angle of 17.5 degrees is used for MLA in the sizing load cases. It is observed that gust load cases become more relevant for sizing in the outer region of the wing (highlighted in red in Fig. 12). The gust loads become more dominant as the lift distribution for manoeuvre loads is shifted towards the wing root due to the application of MLA. However, the sizing cases are not completely dominated by gust loads which indicate that more advantage in mass reduction can be obtained by further increasing the aileron deflections during manoeuvre cases. For the purpose of this study, the maximum aileron deflection is limited to 17.5 degrees.
The wing root bending moment is compared for one of the dominant sizing load cases for the upper skin which is a pull-up manoeuvre in the maximum take-off weight configuration. The aileron deflections considered for this comparison vary from 0 to 17.5 degrees. Overall, a 5.12% reduction in the wing root bending moment is observed. The direct consequence of this can also be seen in the reduction of the primary wing structural mass. This has been depicted in Fig. 14.
5.3 Static response
A static deformation check is conducted for the optimized wing model using a linear static analysis (SOL 101 in MSC Nastran) under a 2.5 g manoeuvre load case found to be dominant in the sizing process. The tip deflection is computed to be 4.58 m (depicted in Fig. 15) which is approximately 17.5% of the half wing span. Such high deformations tend to introduce local buckling effects if the design is not pre-constrained by buckling limitations. Large structural deflections also have the potential to introduce geometric nonlinearities in the structural response, i.e., the stiffness becomes dependent on the extent of the structural deformation due to a coupled bending-stretching response of structural elements. This has been demonstrated in [20], where a wing tip deformation of approximately 10% with respect to the semi-span is seen to be a threshold for activation of geometric nonlinearities, albeit for HALE aircraft.
The activation of geometric nonlinearities leads to either a stiffening or a softening effect resulting in deviations from the linear response. In Fig. 16, a stiffening effect in the wing deformation has been demonstrated, where the wing stiffness increases with increasing deflection. The figure has been obtained by comparison of the static displacement responses obtained from MSC Nastran modules SOL 101 (linear static) and SOL 106 (nonlinear static). It has been validated that a global buckling does not occur in the wing structure so that the nonlinear stiffness has no contributions from post-buckling effects. The figure depicts the reduction in the wing tip deflection when nonlinearity is considered (in red).
It can be inferred that the presence of deflection dependent stiffness properties would also have an impact on the aeroelastic characteristics of the aircraft. The use of conventional linear aeroelastic design methodologies, in such cases, might prove to be a conservative approach. Moreover, the structural optimization procedure in MSC Nastran follows an optimization scheme coupled with a linear static analysis which becomes redundant for a nonlinear structure.
Therefore, it is imperative that, in the future, a more detailed study be conducted with considerations of the nonlinear effects for validation of the preliminary results obtained through the linear aeroelastic design framework.
6 Conclusion and outlook
Aeroelastic structural design of a high aspect ratio composite wing aircraft has been conducted. The model generation, loads computation and structural optimization process is incorporated in an automated process chain of DLR-AE called cpacs-MONA. The structural and aerodynamic models are generated using the in-house model generation tool ModGen. An initial cross-section sizing of the structure is performed using the loads computed from the conceptual design tool LOADzero. Subsequently, a more detailed loads calculation process is used based on the VLM implementation in MSC Nastran. These loads are used as an initial input for the iterative structural optimization process. To adapt to the requirements of the aircraft designed in the project ATLAs, a composite optimization scheme based on the maximum strain criteria and laminate thickness optimization is implemented in cpacs-MONA. The optimized composite structural model is compared with an aluminium aircraft. A reduction of about 3.6% is obtained in the operating empty weight of the aircraft while using the composite structural model. Furthermore, a manoeuvre load alleviation method is implemented in cpacs-MONA. A fixed aileron deflection is enforced for 2.5 g and − 1.0 g manoeuvre load cases. Comparisons are made between the wing structural masses for different values of enforced aileron deflections. Furthermore, the cut loads for different cases of aileron deflections are considered. A reduction of 8.6% of the wing structural mass is computed on enforcing the MLA system, while a 5.1% reduction in the wing root bending moment is seen. The gust loads become more dominant for sizing as the influence of manoeuvre loads is reduced with increasing utilization of the MLA system. Lastly, a design check is done by conducting a linear static analysis with the peak loads obtained from a 2.5 g manoeuvre sizing case. A wing tip deformation of 4.55 m is computed which is approximately 17.5% of the half wing span. A comparison with nonlinear static analysis is conducted. It has been demonstrated that the wing tends to show a stiffening effect under large deformations which demands more detailed studies.
It has been shown in [7] that optimization of a composite structure purely based on maximum strain criteria can be over-conservative. The use of lamination parameters for structural optimization offers more flexibility in satisfying various constraints and would be considered in future studies involving the automated aeroelastic design framework cpacs-MONA. Furthermore, it has been shown that the wing tip deformation is significantly high to potentially be able to introduce effects such as buckling and geometrically nonlinear effects. These considerations will be considered for the more detailed future analysis of the presented aircraft configuration.
References
Kassapoglou, C.: Design and analysis of composite structures: with applications to aerospace structures. Wiley, Oxford (2013)
Starnes, J.H., Jr., Haftka, R.T.: Preliminary design of composite wings for buckling, strength, and displacement constraints. J. Aircraft 16(8), 564–570 (1979)
Haftka, R.T.: Optimization of flexible wing structures subject to strength and induced drag constraints. AIAA J. 15(8), 1101–1106 (1977)
Weisshaar, T.A.: Aeroelastic tailoring of forward swept composite wings. J. Aircraft 18(8), 669–676 (1981)
Dillinger, J.K.S., Klimmek, T., Abdalla, M.M., Gürdal, Z.: Stiffness optimization of composite wings with aeroelastic constraints. J. Aircraft 50(4), 1159–1168 (2013)
Meddaikar, Y.M., Dillinger, J.K., Sodja, J., Mai, H. and De Breuker, R.: Optimization, manufacturing and testing of a composite wing with maximized tip deflection. In: 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, p. 0489 (2016).
Bramsiepe, K.R., Handojo, V., Meddaikar, Y.M., Schulze, M. and Klimmek, T.: Loads and structural optimization process for composite long range transport aircraft configuration. In: Multidisciplinary Analysis and Optimization Conference, p. 3572 (2018).
Klimmek, T., Schulze, M., Abu-Zurayk, M., Ilic, C. and Merle, A.: cpacs-MONA–An independent and in high-fidelity based MDO tasks integrated process for the structural and aeroelastic design of aircraft configurations. In: Proceedings of International Forum on Aeroelasticity and Structural Dynamics (IFASD, 2019).
Leitner, M., Liepelt, R., Kier, T.M., Klimmek, T., Müller, R. and Schulze, M.: A fully automatic structural optimization framework to determine critical design loads. In: Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal Oberth eV(2016).
Woehler, S., Hartmann, J., Prenzel, E., & Kwik, H: Preliminary aircraft design for a midrange reference aircraft taking advanced technologies into account as part of the AVACON project for an entry into service in 2028. Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV (2018).
Nagel, B., Böhnke, D., Gollnick, V., Schmollgruber, P., Rizzi, A., La Rocca, G. and Alonso, J.J.: Communication in aircraft design: Can we establish a common language. In: 28th International Congress of the Aeronautical Sciences, pp. 1–13 (2012).
Chiozzotto, G.P.: CDloads: Conceptual design loads estimation. Internal report at DLR, Göttingen: unpublished (2013).
Klimmek, T.: Parametric set-up of a structural model for FERMAT configuration aeroelastic and loads analysis. J. Aeroelast. Struct. Dyn. 3(2) (2014).
MSC Software: MSC Nastran Aeroelastic analysis user’s guide, USA (2018).
EASA, C.S.: Acceptable means of compliance for large aeroplanes cs-25. Tech. Rep. Amendment 20, European Aviation Safety Agency (2013).
Handojo, V., Lancelot, P. and De Breuker, R.: Implementation of active and passive load alleviation methods on a generic mid-range aircraft configuration. In: Multidisciplinary Analysis and Optimization Conference, p. 3573 (2018).
MSC Software, 2018. MSC Nastran 2018 design sensitivity and optimization user’s guide, USA (2018).
Kaw, A.K.: Mechanics of composite materials. CRC Press, Boca Raton (2005)
IJsselmuiden, S. T.: Optimal design of variable stiffness composite structures using lamination parameters, doctoral dissertation, TU Delft (2011).
Ritter, M.R.: An extended modal approach for nonlinear aeroelastic simulations of highly flexible aircraft structures, Ph.D. Thesis, Technical University of Berlin (2019).
Acknowledgements
The authors would like to thank DLR, Institute of System Architecture in Aeronautics, Hamburg, Germany for providing the initial design parameters of the aircraft.
Funding
Open Access funding enabled and organized by Projekt DEAL. The work was conducted within the framework of DLR internal project ATLAs. No specific funding was obtained for the work conducted.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sinha, K., Klimmek, T., Schulze, M. et al. Loads analysis and structural optimization of a high aspect ratio, composite wing aircraft. CEAS Aeronaut J 12, 233–243 (2021). https://doi.org/10.1007/s13272-021-00494-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13272-021-00494-x