Abstract
The aeroelastic behaviour of a wing with an over-the-wing pylon-mounted ultra-high bypass ratio engine and high-lift devices is studied with a reduced-order model. Wing, pylon and engine structures are reduced separately using the modal approach and described by their natural frequencies and modes. The characteristic aerodynamic loads are investigated with steady and unsteady flow simulations of a two-dimensional profile section. These results indicate possible heave instabilities at strongly negative angles of attack. Three-dimensional effects are taken into account using an adapted lifting line theory according to Prandtl. Due to high circulations resulting from the high-lift systems, the effective angles of attack are in the range of the potential instabilities. The substructures and aerodynamic loads are coupled in modal space. For the wing without three-dimensional effects, the bending instability occurs at the corresponding negative angles of attack. Even though there is potential for improvement, including the three-dimensional effects shifts the endagered area to possible operation points.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The number of flights is continuously increasing. To shorten the journey and ease the traffic at large airports, small existing airports are taken into consideration. Since these airports are often close to populated areas, fuel and noise emissions must be reduced. Due to short runways, the aircraft must also be designed for short take off and landing. The reference aircraft shown in Fig. 1 was designed by the Coordinated Research Centre (CRC) 880 [18, 19]. The wing has a halfspan of 14.37 m, a leading-edge sweep angle of \(26^\circ\), a taper ratio of 0.32, and a dihedral angle of \(3^\circ\). Noise reduction is realised by an over-the-wing mounted ultra-high bypass ratio (UHBR) engine [3]. High-lift is achieved with both passive and active systems. The active system, the Coandă flap, is a combination of a trailing edge flap and a thin jet, described by its momentum coefficient
It describes the ratio of introduced jet momentum per time at the jet exit section \({\dot{m}}_{\text {jet}}v_{\text {jet}}\) to the freestream dynamic pressure \(q_\infty\) and the wing reference area \(A_{\text {ref}}\). According to the Coandă effect [24] the thin jet is blown out upstream of the flap to deflect the flow to follow the curved surface. This leads to an increase in lift, which has been investigated extensively [5,6,7, 9, 11, 16, 23]. As a side effect, a suction peak can be observed at the leading edge, which is decisive for the stall behaviour [1]. To reduce the suction peak at the so called clean nose a different nose shape, called droop nose, is designed to counteract the weaknesses of the active system [2]. As a result, the stall angle of attack is increased and the power needed for an efficient flow control is reduced. However, based on two-dimensional (2D) calculations and strip theory, the heave flutter phenomenon of circulation-controlled wings, detected by Haas and Chopra [8], can be observed for both leading edge shapes—clean nose and droop nose [4, 15]. Yet, three-dimensional (3D) effects have not been taken into account so far.
Reference aircraft with over-the-wing mounted UHBR engine [19]
The existing reduced-order model (ROM) [10] is updated to the new configuration. A substructure technique is added to consider the dynamic behaviour of the wing and the UHBR engine [14], both derived from full scale 3D finite element models. Additionally, a 3D-correction based on Prandtl’s lifting line theory [17] is presented and embedded in the ROM. All results of numerical flow simulations presented are computed with the DLR TAU code of the German Aerospace Center [20], an unstructured finite volume code solving the Reynolds-averaged Navier–Stoke equations. The original Spalart–Allmaras model is used for turbulence modelling [22]. The mesh used was adopted from previous detailed investigations in the CRC [1, 2].
2 Reduced-order model
The presented ROM is based on [10] and has been continuously updated [4, 15, 21]. It is now transferred to the new reference aircraft with an over-the-wing mounted UHBR engine. Wing and UHBR engine are adapted from 3D finite element models and reduced independently. Generally the dynamics of structures are described by their equation of motion
with \({\mathbf {M}}_{\text {S}}\) being the mass and \({\mathbf {K}}_{\text {S}}\) the stiffness matrix. \(\varvec{x}_{\text {S}}\) describes the displacement degrees of freedom and \({\varvec {g}}_{\text {S}}\) is the net weight of the structure. The modal approach
with \(\varvec{q}\) being the vector of generalised coordinates and \({\mathbf {X}}\) the modal matrix, leads to the decoupled system of equations
In modal space, the structure may be approximately described by selected eigenfrequencies \(\omega _{0j}\), natural modes \(\varvec{{\hat{x}}}_j\) and associated participation factors \(\gamma _j\). The eigenfrequencies and mode shapes of the UHBR engine depend on the rotational speed of the shafts [14]. The wing, however, is strongly influenced by the aerodynamic forces.
The ROM considers lift and pitching moment, described by their dimensionless coefficients
with the mass inertia being ignored. The pitching moment is related to the quarter chord and the terms are made dimensionless by chord length l and freestream velocity \(v_\infty\). The aerodynamic loads can be calculated along the span using strip theory, leading to
with a constant load vector \(\varvec{L_0}\), the aerodynamic stiffness matrix \({\mathbf {A}}_{\mathbf{0}}\) and aerodynamic damping matrix \({\mathbf {A}}_{\mathbf{1}}\).
The aerodynamic degrees of freedom according to Eq. 5, vertical displacement h and torsional rotation \(\alpha\), differ from the discretisation of the finite element model. The structural modes are transformed to aerodynamic discretisation \(\varvec{{\hat{x}}}_{Aj}\) whereby using the modal approach in Eq. (3) leads to a decoupled and reduced system of equations
The ROM is enhanced by a 3D-correction based on the lifting-line theory with the approach being described in [21]. Accordingly, downwash angles \(\alpha _i\) are added as additional degrees of freedom, leading to the schematically system of equation
Here, \(\varvec{L_{0q}}\), \({\mathbf {A}}_{{\mathbf{0q}}}\) and \({\mathbf {A}}_{\mathbf{1q}}\) are the aerodynamic matrices according to Eq. 6 transformed to the generalised coordinates. \({\mathbf {I}}\) is the unit matrix, equivalent to the reduced mass matrix, \(\varvec{\omega _0}^2\) is the reduced stiffness matrix and \(\varvec{g_q}\) is the generalised net weight of the structure. The first line of Eq. 8 equals Eq. 7 plus the additional matrices \({\mathbf {D}}_{\mathbf{q}\varvec{\alpha _i}}\) and \({\mathbf {K}}_{{\mathbf{q}}\varvec{\alpha _i}}\) referring to the downwash angle \(\alpha _i\). The second line contains the 3D-correction terms from lifting-line theory.
3 Substructure technique
To enable a high degree of adaptability of individual components, the structure is divided into substructures (s. Fig. 2). All substructures are reduced independently and need to be merged into one in modal space. Next to the flexible wing and UHBR engine structures, pylon and nacelle are considered as rigid bodies.
The coupling is realised using Lagrange multipliers \(\varvec{\sigma }\). Introducing coupling matrices \({\mathbf {C}}\), the physical degrees of freedom of the coupling points of two structures n and m are equalized
using their reduced modal matrices \({\mathbf {X}}_{\mathbf{r}}\). The first six mode shapes of the coupled reduced models with droop nose, rigid body pylon and nacelle and UHBR engine with 1000 rotations per minute are displayed in Fig. 3. Mode 1 and 2 are the first two bending modes. Mode 3–6 are coupled bending-torsion modes. While mode 3 is primarily a bending mode, Mode 4 shows a greater amount of torsion.
4 Aerodynamics
Previous studies [4, 15] were based on 2D aerodynamics and strip theory. Especially the area around the maximum angle of attack was of great interest because the stall behaviour led to the observed heave flutter phenomenon. However, 3D effects were neglected and need to be taken into account. Therefore, Prandtl’s lifting-line theory is applied and extended by empirical correction for fuselage and engine effects to approximate 3D aerodynamics. To emphasize the need for the large examination area in Sect. 4.2, the 3D-correction and its results are described first. The 2D database for clean and droop nose profile shapes is presented and discussed in the following.
4.1 3D-correction
While 2D aerodynamics theoretically refer to an infinite wing, 3D aerodynamics consider the finite ending of a wing. Due to the circulation
a downwash velocity \(v_w\) and a vortex is induced at each point. Depending on the wingspan b along the spanwise coordinate \(y_0\) the downwash velocity results to
inducing the downwash angle
and, therefore, influencing the effective angle of attack
Since the circulation in Eq. 10 is directly related to lift and angle of attack, an iterative solution is required. At each point along the wing span, the vortices at the right-hand side and left-hand side cancel each other out. At the wing tip \(y = l_{\text {S}}\) however, the circulation results in a free vortex of strength
The same happens at discontinuities such as the fuselage, engine or variations in the flap angle. To establish an equilibrium in the system of equations at these discontinuities, corresponding vortices are placed along the wingspan. The strength of the vortices is chosen empirically depending on 3D computational fluid dynamic (CFD) simulations. Figure 4 shows the comparison of lift coefficient distributions calculated with 3D CFD simulations, strip theory and the Prandtl-based 3D-correction along the dimensionless wingspan \(\eta\). An aircraft angle of attack \(\alpha _{AC}\) of \(6^\circ\) and a thrust coefficient \(c_t\) of 0.228 are given. The installation angle of the wing is \(0^\circ\) from the wing root to the engine and then changes linearly to \(-\,6.94^\circ\) at the wing tip. Therefore, at an aircraft angle of \(6^\circ\) the local angles of attack vary between 6\(^\circ\) and \(-\,0.94^\circ\). The landing configuration with droop nose, flap deflection angles of \(65^\circ\) along the wing and \(45^\circ\) at the aileron, a momentum coefficient of 0.029 and a velocity of 57.17 m/s is displayed. The 2D lift coefficients used are presented in Sect. 4.2. They are approximated with spline functions, depending on the angle of attack, flap deflection angle and momentum coefficient for the clean nose and the droop nose profile shape. It becomes apparent that coefficients based on strip theory are overestimated along the whole wing span. Wherever the coefficients decrease there are discontinuities in the structure. The wing root connects to the fuselage at a dimensionless wingspan of 0.1. At approximately 0.3 and 0.35 vortices left and right of the engine pylon justify the break-in. At a dimensionless wingspan of 0.82 the flap deflection angle changes from \(65^\circ\) to \(45^\circ\) and the wing tip is reached at 1. Figure 5 schematically shows the wake-evolution. Prandtl’s lifting line theory with vortices placed accordingly in the ROM leads to the third distribution. Here, lift coefficients in between a dimensionless wingspan of 0.4 and 0.8 are underestimated due to the neglection of sweep.
The effective angles of attack \(\alpha _{\text {e}}\) resulting in the lift distribution approximated by the 3D-correction are pictured in Fig. 6. Whereas the aircraft angle of attack is \(6^\circ\), 2D aerodynamics in between \(-\,32^\circ\) and \(-\,7^\circ\) are used for the approximation. The strongly negative angles of attack result from the large circulation induced by the Coandă jet. It is shown in Sect. 4.2, that even at an angle of attack of \(-\,30^\circ\) a lift coefficient of 2 is reached.
Prandtl’s lifting line theory applies only to lift, but not to pitching moment coefficients. However the pitching moment coefficient is directly dependent on the lift coefficient and the chordwise position of the neutral point:
Based on this, the 3D pitching moment distribution is derived from 2D pitching moment coefficients \(c_{M,{\text {2D}}}\) and an induced pitching moment coefficient \(c_{Mi}\), which is equally composed
with
Again, the unknown 3D base pitching moment coefficient \(c_{M0,{\text {3D}}}\) and the 3D chordwise position of the neutral point \(x_{n,{\text {3D}}}\) are empirically determined to fit the 3D-CFD results. Figure 7 shows the 3D-CFD results compared to results in the ROM calculated by strip theory and the presented Prandtl-based 3D correction. While the strip theory coefficients are either too high or too low, the coefficients with applied 3D-correction are a good approximation with weaknesses at the wing root and the wing tip.
4.2 Steady aerodynamics
2D-calculations are carried out for the profile with both nose shapes pictured in Fig. 12 at the approach velocity of 51 m/s. The flap deflection angle \(\delta _{\text {fl}}\) is set to \(65^\circ\). Angles of attack \(\alpha\) are varied between \(-\,30^\circ\) and \(6^\circ\) for the clean, and up to \(16^\circ\) for the droop nose shape. Three momentum coefficients \(c_\mu\) are investigated. Additionally the degrees of freedom, h and \(\alpha\), are defined in Fig. 12. Pitching moment M and lift L are calculated at the quarter chord and made dimensionless.
The resulting lift and pitching moment coefficients are shown in Figs. 8 and 9. Discrete results are marked and approximated by a parameterised spline function depending on the angle of attack, flap deflection angle and momentum coefficient. The coefficients and the related mechanisms of both profile shapes have already been discussed in detail for angles of attack above \(-\,10^\circ\) [1, 2, 4, 15]. According to Fig. 6 the effective angle of attack is reduced significantly by applying the 3D-correction. Therefore, this paper focuses on the coefficients and related mechanisms below \(-\,10^\circ\). Due to the large circulations induced by the Coandă flap, lift coefficients are already at 2 at an angle of attack of \(-\,30^\circ\) (s. Fig. 8). The lift coefficients of the clean nose profile increase almost linearly from \(-\,30^\circ\) to \(-\,10^\circ\). In comparison, the lift coefficients of the droop nose profile show a significant change in gradient. While there is only a small increase in lift coefficients from \(-\,30^\circ\) to \(-\,20^\circ\), the lift coefficient increases rapidly in between \(-\,20^\circ\) and \(-10^\circ\). The change in gradient can be seen evidently in Fig. 10, which shows the partial derivatives of the lift coefficients for both profile shapes approximated with parameterised spline functions. For both profile shapes, the lift coefficients increase with increasing momentum coefficient.
The pitching moment coefficients are negative in the investigated range for both profile shapes. This results from a suction peak at the Coandă flap caused by the blown-out jet (s. Fig. 14). For the clean nose profile, the pitching moment decreases quadratically reaching a minimum at \(-\,12^\circ\) for a momentum coefficient of 0.033 and at \(-\,10^\circ\) for momentum coefficients of 0.039 and 0.048. Again, the pitching moment coefficients of the droop nose profile show a change in gradient in between \(-\,20^\circ\) and \(-\,10^\circ\). The minimum is reached at approximately \(-\,8^\circ\). With increasing momentum coefficient the suction peak at the Coandă flap increases, wherefore the pitching moment coefficient decreases. Figure 11 shows the resulting partial derivatives. As formulated in Eq. 5, the derivatives form the aerodynamic stiffness matrix.
According to Eq. 8 positive derivatives decrease the overall stiffness and negative derivatives lead to an increase. In addition to the rapid change in gradients for the coefficients of the droop nose profile, it is, therefore, also important to understand what causes the change in sign of the pitching moment derivatives for both profile shapes (Fig. 12).
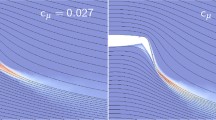
Looking into this, Fig. 13 shows the streamlines with underlying eddy viscosity for the clean nose and the droop nose profile at an angle of attack of \(-\,15^\circ\) and a momentum coefficient of 0.039. In both cases a detachment of the streamlines on the lower side becomes apparent. While for the clean nose the separation is limited to the area at the rear edge flap, the droop nose causes a large recirculation area. The formation of this recirculation area leads to a pressure loss on the lower side of the profile, resulting in the observed high gradient of lift coefficient. Below the inflection point, the recirculation area grows at a slower rate, which explains the flattening of the curve.
The change in sign of the pitching moment derivatives becomes intelligible by looking at Figs. 14 and 15. Figure 14 shows the pressure coefficient distribution along the chord for the droop nose shape at three angles of attack derived from time-dependent unsteady CFD simulations. The suction areas at the nose and at the Coandă flap are visible, which cause the negative pitching moment coefficients. It is noticeable that the suction area at the nose decreases with decreasing angle of attack. This alone would lead to continuously more negative pitching moment coefficients with decreasing angle of attack. Yet Fig. 9 shows, that the pitching moment coefficient increases for strongly negative angles of attack.
The decisive reason becomes apparent in Fig. 15. Here, the difference in pressure distributions for the respective angles of attack is displayed. The black line shows the difference of \(2^\circ\) and \(-\,6^\circ\) and in comparison the grey line shows the difference of \(-\,6^\circ\) and \(-\,15^\circ\). In both cases the loss of negative pressure at the nose is comparable. But while the suction peak at the Coandă flap increases from \(2^\circ\) to \(-\,6^\circ\), it is reduced from \(-\,6^\circ\) to \(-\,15^\circ\). Therefore, the change of the suction peak at the Coandă flap causes the change of sign for the pitching moment derivative. For the droop nose, this process happens fairly rapidly, while it is more continuous for the clean nose shape. These circumstances explain the large gradient of the pitching moment coefficient.
4.3 Unsteady aerodynamics
For the investigation of the unsteady aerodynamics an impulse motion according to [12, 13] is used. A pulse movement is impressed on the profile in the time domain and the resulting coefficients are recorded. Applying a Fourier transform, the time-dependent system response is converted into the frequency range. According to Eq. 8 positive damping derivatives favour an instability whereas negative damping derivatives support damped behaviour. The terms on the main diagonal are most relevant in this respect. The unsteadiness of the flow is best described in terms of reduced frequency
With a profile depth of 5.3 m at the wing root and 1.7 m at the wing tip the reduced frequencies for the first bending mode at \(\omega \approx 30\) are in between \(k_r= 1.56\) and \(k_t=0.5\). Figures 16 and 17 show the lift derivatives resulting from a heave motion at a reduced frequency of 0.5 and 1.5 for the clean nose and the droop nose profile shapes. Again, discrete results are marked and approximated with a parameterised spline function. Here, the reduced frequency is added as a parameter. The results for the clean nose profile are negative for all investigated angles of attack and both reduced frequencies. This indicates a damped behaviour. The results for the droop nose profile at a reduced frequency of 0.5 show positive lift derivatives in between \(-\,10^\circ\) and \(-\,18^\circ\) for all momentum coefficients. At a reduced frequency of 1.5 only the momentum coefficient of 0.033 shows positive derivatives at \(-\,12^\circ\), however below \(-\,20^\circ\) all momentum coefficients result in positive derivatives. Since the reduced frequencies concern the first bending mode, bending instabilities seem possible in these areas. To at least show both main diagonal entries, Figs. 18 and 19 show the corresponding pitching moment derivatives due to a pitching motion. At a reduced frequency of 0.5 both profile shapes show positive derivatives. For the clean nose shape, these concerns angles of attack below \(-\,20^\circ\). The droop nose shape shows positive derivatives in between \(-\,12^\circ\) and \(-\,23^\circ\). However, at a reduced frequency of 1.5 both profile shapes result in negative damping terms. If the corresponding mode shape under load changes from a bending to a bending-torsion mode, torsion would be enhanced at the wing tip for the droop nose profile.
The first mode shape with significant torsion has an eigenfrequency of approximately 85 (s. Fig. 3). Accordingly the reduced frequencies for this motion are in between \(k_r = 4.4\) and \(k_t = 1.4\). With higher reduced frequencies, the derivatives become more negative. Therefore, no instabilities are to be expected here.
To understand the mechanism behind the positive lift derivatives in Figs. 16 and 20 shows flow conditions over one period. For comparison, the flow field under steady condition and no movement is pictured in the lower right. A steady movement downwards would lead to better flow conditions and, therefore, more lift. A steady movement upwards would lead to worse flow conditions and accordingly less lift. However the movement \({\dot{h}}\) changes during the period and is displayed with grey arrows. The change in lift with respect to the steady condition \(\varDelta L\) is displayed with black arrows. A phase shift of the expected lift becomes obvious. The pictured flow field shows, that this is directly related to the propagation of the vortices. Therefore, the work
is positive over one period. Accordingly, the excitation of the heave motion results from the time-dependent propagation of the vortices.
5 Dynamic behaviour
For the investigation of aeroelastic stability, Eqs. 8 and 9 are combined, leading to the general eigenvalue problem
of the coupled system. With
the damping coefficients \(\delta _j\) and eigenfrequencies \(\omega _j\) of the coupled system are determined. Since aerodynamic damping strongly depends on the frequency, the aerodynamic loads are updated in case the coupled eigenfrequency \(\omega _{j,i}\) differs from the previously used eigenfrequency \(\omega _{j,i-1}\). If the difference in eigenfrequencies is less than \(\varepsilon\), the corresponding damping coefficient \(\delta _j\) defines whether the corresponding eigenmode is excited or damped. If \(\delta _j\) is negative, the eigenmode is damped. If \(\delta _j\) is positive, the eigenmode is initially excited.
This process, illustrated in Fig. 21, is carried out for various aircraft angles of attack and momentum coefficients. Also each eigenmode j is investigated individually.
The investigations concern the presented configuration with a droop nose profile shape and a thrust coefficient of 0.228. Combinations of aircraft angles of attack \(\alpha _{AC}\) and momentum coefficients are each evaluated independently. To link the results to the 2D database presented in Sect. 4.2, Fig. 22 shows the stability map with applied loads according to strip theory. Looking at the stability map, one needs to keep in mind that the installation angle of the wing varies between \(0^\circ\) at the wing root and \(-\,6.94^\circ\) at the wing tip.
The red to purple colouring shows initially exciting combinations. Green to yellow areas are stable. Figure 22 shows an unstable area stretched over all investigated momentum coefficients. At a momentum coefficient of 0.03 aircraft angles of attack in between \(-\,5^\circ\) and \(-\,8^\circ\) are affected. With higher momentum coefficients the concerned aircraft angles of attack lower to \(-\,7^\circ\) to \(-\,12^\circ\). This is in accordance with the lift derivatives shown in Fig. 16. The local angle of attack at the wing tip is \(6.49^\circ\) lower than the aircraft angle of attack and, therefore, in the range of positive lift derivatives. With higher momentum coefficients the area of positive lift derivatives is shifted towards lower angles of attack, just like the unstable area displayed in Fig. 22. Therefore, applying the loads according to strip theory lead to a bending instability of the wing structure.
However, Fig. 4 shows that applying strip theory is insufficient. Applying the loads according to the 3D-correction leads to the stability map displayed in Fig. 23. This shows the current weakness of the 3D-correction, as a range of parameter combinations does not converge due to the strongly negative effective angles of attack. However, an unstable area is visible for momentum coefficients up to 0.38. It can be seen from Fig. 6, that an aircraft angle of attack of \(6^\circ\) leads to effective local angles of attack below \(-\,10^\circ\). Especially at the wing tip, the effective angle of attack lies in the endagered area. Therefore, the bending instability also occurs at the wing with applied 3D loads.
Since the ROM used to create the stability maps is quasi-steady, full unsteady 3D simulations are necessary to validate the behaviour. The method presented here serves as an initial assessment to quickly identify endangered parameter combinations.
6 Conclusion
This paper describes the investigation of aeroelastic effects of a circulation controlled wing with an over-the-wing mounted UHBR engine. A ROM is adapted to the new configuration, using a full scale three-dimensional finite element wing and engine model, which are coupled using reduced modal systems. Aerodynamic loads are mapped onto the wing structure by strip theory, based on 2D CFD calculations for two different profile shapes. To consider the effects of 3D flow, the model is extended by a 3D-correction according to Prandtl’s lifting line theory. Results from steady 3D CFD calculations are used for comparison. It is shown, that effective angles of attack down to \(-\,30^\circ\) are needed to provide consistent results. This is due to the large circulations induced by the active high-lift device. Therefore, the 2D calculations are extended to strongly negative angles of attack and the characteristics are elaborated. An impulse method is used to calculate the aerodynamic damping derivatives for a whole frequency spectrum. Results of the steady and unsteady simulations of the droop nose profile show unusual behaviour in between \(-\,20^\circ\) and \(-\,10^\circ\). This behaviour is directly linked to the formation of a recirculation area on the lower side of the profile. As a result, a phase shift in lift coefficients at low reduced frequencies leads to positive lift derivatives and, therefore, an excited heave motion.
Applying the loads to the wing according to strip theory shows a bending instability in the corresponding area of the positive lift derivatives. Taking the 3D-correction into account shifts the unstable areas to higher angles of attack. However, the 3D-correction does not converge for a range of parameter combinations and needs improvement.
It is shown, that the applied active and passive high-lift devices strongly affect the aerodynamics. As a result, a bending instability for the wing with a droop nose becomes apparent. Further investigations must examine whether this excitation leads to flutter. In addition, it must be verified whether the 3D-correction carried out on the basis of steady results can be applied to the unsteady values.
References
Burnazzi, M.: Design of efficient high-lift configurations with Coanda flaps. TU Braunschweig-Niedersächsisches Forschungszentrum für Luftfahrt (2016)
Burnazzi, M., Radespiel, R.: Design of a droopnose configuration for a Coanda active flap application. In: 51th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Dallas (TX), AIAA 2013-0487 (2013)
Delfs, J., Appel, C., Bernicke, P., Blech, C., Blinstrub, J., Heykena, C., Kumar, P., Kutscher, K., Lippitz, N., Rossian, L., Savoni, L., Lummer, M.: Aircraft and technology for low noise short take-off and landing. In: 35th AIAA Applied Aerodynamics Conference. https://doi.org/10.2514/6.2017-3558. (2017)
Dinkler, D., Krukow, I.: Flutter of circulation-controlled wings. CEAS Aeronaut. J. 6(4), 589–598 (2015). https://doi.org/10.1007/s13272-015-0166-z
Englar, R., Smith, M., Kelley, S., Rover, R.: Application of circulation control to advanced subsonic transport aircraft, part I—airfoil development. J. Aircr. 31(5), 1160–1168 (1994). https://doi.org/10.2514/3.56907
Englar, R., Smith, M., Kelley, S., Rover, R.: Application of circulation control to advanced subsonic transport aircraft, part I—airfoil development. J. Aircr. 31(5), 1169–1177 (1994). https://doi.org/10.2514/3.46627
Englar, R.J., Huson, G.: Development of advanced circulation control wing high-lift airfoils. J. Aircr. 21(7), 476–483 (1984). https://doi.org/10.2514/3.44996
Haas, D., Chopra, I.: Flutter of circulation control wings. J. Aircr. 26(4), 373–381 (1989)
Korbacher, G.: Aerodynamics of powered high-lift systems. Annu. Rev. Fluid Mech. 6(1), 319–358 (1974)
Krukow, I., Dinkler, D.: A reduced-order model for the investigation of the aeroelasticity of circulation-controlled wings. CEAS Aeronaut. J. 5(2), 145–156 (2014)
Lighthill, M.: Notes on the deflection of jets by insertion of curved surfaces, and on the design of bends in wind tunnels. Reports and memoranda 2105, Aeronautics Research Council (1945)
Lisandrin, P., Carpentieri, G., Van Tooren, M.: An investigation over cfd-based models for the identification of nonlinear unsteady aerodynamics responses. AIAA J. 44(9), 2043–2050 (2006)
Marques, A., Simões, C., Azevedo, J.: Unsteady aerodynamic forces for aeroelastic analysis of two-dimensional lifting surfaces. J. Braz. Soc. Mech. Sci. Eng. 28(4), 474–484 (2006)
Müller, T., Hennings, H.: Structural dynamic influence of an uhbr engine on a coanda-wing. In: IFASD (2017)
Neuert, N., Dinkler, D.: Aeroelastic behaviour of a parameterised circulation-controlled wing. CEAS Aeronaut. J. 10(3), 955–964 (2019). https://doi.org/10.1007/s13272-018-0348-6
Pfingsten, K., Radespiel, R.: Experimental and numerical investigation of a circulation control airfoil. In: 47th AIAA Aerospace Sciences Meeting, Orlando, FL, AIAA 2009-533 (2009)
Prandtl, L.: Tragflügeltheorie. I. Mitteilung. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, pp. 451–477 (1918)
Radespiel, R., Heinze, W.: SFB 880: fundamentals of high lift for future commercial aircraft. CEAS Aeronaut. J. 5(3), 239–251 (2014). https://doi.org/10.1007/s13272-014-0103-6
Radespiel, R., Heinze, W., Bertsch, L.: High-lift research for future transport aircraft. In: DLRK (2017)
Schwamborn, D., Gardner, A., von Geyr, H., Krumbein, A., Lüdecke, H.: Development of the DLR TAU-code for aerospace applications. In: Proceedings of the International Conference on Aerospace Science and Technology, Bangalore, India, pp. 26–28 (2008)
Sommerwerk, K., Krukow, I., Haupt, M., Dinkler, D.: Investigation of aeroelastic effects of a circulation controlled wing. J. Aircr. 53(6), 1746–1756 (2016)
Spalart, P., Allmaras, S.: A one-equation turbulence model for aerodynamic flows. AIAA Paper 92-0439, (1992)
Wood, N.: Circulation control airfoils—past, present, future. Technical report 85-0204, AIAA (1985)
Young, T.: Outlines of experiments and inquiries respecting sound and light. Philos. Trans. R. Soc. Lond. 90, 106–150 (1800)
Acknowledgements
Financial support has been provided by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) in the framework of the Coordinated Research Centre SFB 880.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neuert, N., Dinkler, D. Aeroelastic behaviour of a wing with over-the-wing mounted UHBR engine. CEAS Aeronaut J 11, 1045–1055 (2020). https://doi.org/10.1007/s13272-020-00467-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13272-020-00467-6