1 Introduction

Building and optimizing space vehicles are a complex problem, as, depending on the flight trajectory, temperatures of over to 2000 K may occur. Damage to the thermal protection system of a space vehicle during atmospheric re-entry is a serious safety issue, especially when considering re-usability of space transportation systems. The need for structural health monitoring systems and non-destructive inspection methods is obvious; since then, minor or major defects can be detected which makes an intervention possible, potentially saving a spacecraft and also human lives. Damages occur often undetected or not correctly detected already as early as during launch of the spacecraft [1, 2].

It is a crucial challenge for scientists to develop materials and sensors which can withstand the extreme conditions of re-entry. For gaining better knowledge of the re-entry phase and for subsequently optimizing structural safety margins, sensors are needed which can collect data and monitor the heat shield before and during an actual re-entry flight. This is not only important for developing better thermal protection systems, but also for detecting defects which occurred any time between launch and re-entry.

There are different concepts of electrical monitoring of defects in ceramic matrix composites. Todoroki et al. [3,4,5] use contacts in regular distances on a sample surface to monitor delamination in the sample. They measure the voltage drop between two neighbouring contacts. With this, they determine the depth and the distance of a delamination in relation to a contact. Baltopoulus et al. [6] measure quadratic thin samples of CFRP material. They have 20 contacts on all four edges of a sample and set a current into two opposing contacts. After the system settles, they measure the voltage drop of each of the 20 contacts except the two contacts which are used for current injection against ground. The solution is an electric potential field and they solve the ill posed backwards problem with an deterministic approach of the smallest squares method with the Tikhonov regulation [7]. For good solutions, they measure every contact 100 times. They can determine the location of a defect with a deviation of 10% from the real location. This method cannot be used for time resolved measurements as one measurement cycle takes approx. 20 min. Spacecraft re-entry is a time-critical manoeuvre which only lasts a few minutes, which means that this method is not suitable. Also time-critical changes as fluctuations in temperature are too influential in this method. Therefore, it is not suitable for transient measurements.

A method was developed by the authors which can be used time and spatially resolved for in-situ measurements of critical structures. The development of the localisation algorithm and the test set-up is described in the following.

2 Materials and methods

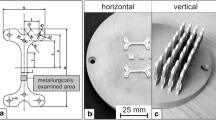
The material C/C-SiC consists of carbon fibres within a silicon carbide matrix. It has a strong resistance against high thermal loads up to 2100 K. It is a \(0^\circ /90^\circ\) twill twin weave with a density of \(1.9\hbox { g}/\hbox {cm}^3\). It has a high resistance against thermal shock and a low mass loss of less than \(0.1\,\hbox {kg}/(\hbox {m}^2\hbox {h}\)) [8,9,10]. A material sample can be seen in Fig. 1. The ceramic matrix composite material is made of 13 plies of the aforementioned 2 \(\times\) 2 twill weave carbon. It is infiltrated with phenolic resin and pyrolysed in an inert atmosphere. Afterwards, a liquid silicon infiltration is conducted leading to the end product of C/C-SiC, and for more information on the production process, it is referred to [11,12,13].

Fig. 1
figure 1

C/C-SiC sample with different virtual current paths, such as horizontal paths (red), diagonals (green), and any other current paths of which three are shown in white

Full size image

A flat sample with approx. 320 mm \(\times\) 120 mm \(\times\) 3 mm is equipped with 12 copper or metal contacts at each of the edges of the 120 mm long sides, as shown in Fig. 1. The numbering of the contacts starts in the lower left corner going right and upwards; with all even numbered contacts on the right side, all odd numbered contacts on the left side. A measurement path is the current path between, e.g., contact MP01 and MP02, shown in red. It will be referred to as MP01-02. Horizontal measurement paths are all paths which correspond to horizontal connections. Some are shown in red in Fig. 1. The diagonal measurement paths correspond to the two connections farthest apart, in this case the paths MP01-24 and MP23-02, which are shown in green. The odd numbered contact in a measurement path is always referred to first. The measurements of these paths are conducted with a four wire electrical resistance measurement method. This method is independent of additional resistances in the system like transition resistances or resistances of connecting cables. Each contact of one side to all contacts on the other side one after another are measured, resulting in 144 single measurements. After each full measurement of all contacts, these values are saved before beginning a new measurement cycle. As the measurement area has to be as big as possible, and due to restrictions when a sample is mounted on a structure, it is not possible to contact the outer edges. Therefore, current injection and measurement are done at the same contact using two wires on each contact. This reduces as well the area which cannot be measured and, therefore, the area where a defect will not be detected. To detect defects, the quotient of the newest measurement of each contact combination with the begin value of this contact combination is calculated. This eliminates also differences which are due to the method of injecting and measuring at the same contact. Changes in electrical resistance can be due to tensile stress, heat, unequally distributed temperatures, or damage. Each of the different influences can be determined. The detailed test set-up is described in the previous works [14, 15].

In earlier work, it was shown that a defect can be located even if damage is only located in a small area [16]. This means that even a reduction of the cross-sectional area in a small area will lead to a change in electrical resistance. As the electric current distributes itself in the material between the current injection points, the electric field near these points is not homogeneous. This can be made more clear by the ANSYS simulation results which are shown in Fig. 2 with two different injections. In part Fig. 2a, the current is injected between the two lower contacts MP01 and MP02. The electric field density is high near the contact points and nearly zero in the upper left and right corners. In the middle of the sample, the electric field density is nearly homogeneous in two-thirds of the sample width direction. Figure 2b shows a current injection at two middle contacts; it can be noted that the area with homogeneous distribution in the middle of the sample is bigger, as the electric field can spread upwards and downwards.

Fig. 2
figure 2

Electric field intensity in samples with different current injection points (ANSYS simulation)

Full size image
Fig. 3
figure 3

Change in electrical resistance due to defects in different horizontal locations (ANSYS simulation)

Full size image

Different behaviour of electrical resistance corresponds to different damage locations. In Fig. 3, ANSYS simulations of different damage locations varying on a horizontal line and the corresponding current change are shown. The damages are named from A to F in the depiction of the sample within Fig. 3. Case A is the nearest damage to the contact points. The single results of all horizontal measurement paths (simulated) are shown. The lines between the different data points in Fig. 3 are only for an easier optical comparison of the simulation results of the different damage areas. MP01-02 in case A has the highest reaction, concerning the damage marked as A. Its resistance changes by 12%. The farther apart a horizontal path is from the damage location, the less it is affected by it. The least affected measurement path is MP23-24 with a change in resistance nearly at zero. In the instance of case F, the damage is in the middle of the sample length as indicated in Fig. 3. Even though MP23-24 is still farthest away from the damage, it has nearly the same change in resistance as MP01-02. In this case, it is again referred to Fig. 2. When the electric field density of a middle path Fig. 2b is compared to an edge path Fig. 2a, it can be seen that the electric field density is differing in both cases only slightly around 1 V/mm. Therefore, damage in this area will influence both paths in approximately the same way. However, as 1.0 V/mm is still a low electric field density compared to areas near current injection with values from 1.6 V/mm up to 4 V/mm, the influence is smaller than in the cases A, B, or C. As only horizontal paths are compared in this example, the current change is identical when the damage is mirrored. Therefore, not only horizontal paths but also all other possible combinations of measurement points are taken into account. With this example, it is shown that a triangulation of a defect location is possible with this method.

3 Localisation algorithm

Fig. 4
figure 4

Schematic of a grid for localisation of defects with the matrices A, B, and C

Full size image
Fig. 5
figure 5

Schematic of a grid for localisation of defects with the matrices C and D

Full size image
Fig. 6
figure 6

Result of localisation algorithm in matrix C of experiment V2022

Full size image
Fig. 7
figure 7

Result of localisation algorithm after a first refinement step in matrix D of experiment V2022

Full size image

The sample is divided into a grid of a user-defined size, it this case with the size of 13 × 12 (column × row), and matrices in the size of the grid are created. Then, five steps are conducted. First, the Liang–Barsky algorithm  [17] is used to determine which measurement path crosses which grid elements on the sample surface, two are shown as examples in Fig. 4. However, unlike as in the algorithm, a measurement path is no longer represented as a line but as an area with at least the height of the distance between two contacts. This is done to make sure that all grid elements have measurement paths crossing even in case of a smaller grid. Therefore, the Liang–Barsky algorithm was adapted to use as boundaries the upper and lower limits of a measurement path area to determine the grid sections which are crossed by a measurement path. The first two matrices are filled with the information how many paths cross a specific element A and to take the sum of all these measurement paths changes’ B in each specific element. Third, each element of B is then divided by A, resulting in an average resistance change in each specific matrix element, the result of which is then put in matrix C. This results in a first resistance change map, as shown in Fig. 6, which shows experimental data from an impact experiment processed with the described algorithm. The real damage location is shown with a red pole and the highest local resistance change values are pointed out. It can already be seen that the localisation is correctly determined in the right area, whereas the real location was not yet met. Fourth, in a next step, the developed algorithm will weigh the results based on the change of each horizontal measurement path value. Therefore, the measurement path with the highest resistance change in horizontal direction is found, and in matrix D, all elements are weighted based on the quotient of the horizontal measurement path which they lie on and the maximum horizontal measurement path. This can be calculated as:

$${\mathbf{D}}_{{i,j}} = {\mathbf{C}}_{{i,j}} \cdot \frac{{{\text{MP}}_{{{\text{horizontal}}}} (j)}}{{{\text{max (MP}}_{{{\text{horizontal}}}} )}}$$
(1)

with the new results being matrix D. Three examples of calculations for matrix D are also shown in Fig. 5. The result already shows the real location of the defect much clearer, as can be seen in Fig. 7. The wrongly detected peak of 0.179% could be eliminated by this method. Finally, a fifth step is conducted with Matrix E which only emphasizes the result. With a boundary filter, all matrix elements of matrix D which are lower than the boundary value GW:

$${\mathrm {GW}} = {\mathbf{D }}_{i,j}({\mathrm {min}})+0,97\cdot \left( {\mathbf{D} }_{i,j}({\mathrm {max}})-{\mathbf{D }}_{i,j}({\mathrm {min}})\right)$$
(2)

are further processed according to:

$${\mathbf{E} }_{i,j} = \frac{{\mathbf{D} }_{i,j}}{\text{max}}({\bf D}) \quad \text{for} \quad {\mathbf{D }}_{i,j}<{\text{GW}},$$
(3)

which is the quotient of each element with respect to the value of the highest element. This leads to the end result shown in Fig. 8. Now, the highest peak which corresponds to the area with the most likely damage is directly next to the real damage location. A correct localisation is defined by the distance between the real damage location and the damage location derived from the algorithm in comparison to the grid size. When the distance between real and derived location is smaller in each direction, than the respecting length of one grid element; the damage was localized correctly. In the case shown here, the damage was localized correctly by this definition.

Fig. 8
figure 8

Weighted resistance quotient of matrix E (end result) after two refinement processes

Full size image

4 Results

The localisation of defects is now shown and discussed with another experiment. The sample was damaged with a superficial defect. In five steps, A–E, the defect is further deepened at the same position until the damage is so deep, that it results in a slit in the sample after step E. The experimental data of all horizontal paths are shown in Fig. 9. These data are already preprocessed, eliminating thermo-electrical effects, temperature gradients, and other factors [18, 19]. The defect location and size can also be taken from Fig. 9. Damage A is a thin scratch with less than 2/10 mm in depth. Even though the damage is small, it can still be detected as shown in the detail graph in Fig. 9. Dependent on the paths distance to the defect, the resistance rises up to 0.25%. As paths near the defect are affected more, the localisation algorithm gives already good results despite the defect affecting only 0.007% of the sample volume. It can pinpoint the defect to the outer edge of the sample, as shown in Fig. 10.

Fig. 9
figure 9

Resistance change during five steps of deepening of a defect after step

Full size image
Fig. 10
figure 10

Result of the localisation algorithm after the surface damage A, shown in red

Full size image

The detected shape of the defect stretches horizontally in the sample’s longitudinal (width) direction. This is even more pronounced when looking at the last defect which removes the material completely in a length of 38 mm at \(t=8000\,\mathrm {s}\). The cross-sectional area of the sample is not only smaller; there is also no possible current flow in the removed area. This means that not only a smaller cross-sectional area is increasing the electrical resistance in the sample, but also the current has to follow a longer path when, for example, the lower measurement points MP01 and MP02 on both sample sides are measured. The prolongation of the current path is in these cases up to 5.5%. The results of the localisation algorithm are shown in Fig. 11. All measurement paths are affected by this damage, as can be seen in Fig. 9. The electrical resistance rises between 1.6% and 12.9%, which equals a weighted change of 0.01% up to 10.9%. This is a higher rise in resistance as the prolongation of the path accounts for. That shows again that both, prolongation of a path and reduction of the cross-sectional area, have a role in the rise of the resistance. The highest resistance change determined by the localisation algorithm is in the element where the damage, marked as a red box, is. Therefore, the damage was located successfully.

Fig. 11
figure 11

Result of the localisation algorithm after infliction of damage E, when the material in the area marked red is completely removed

Full size image
Fig. 12
figure 12

Electrical current density simulated in ANSYS when an electric current of 10 mA is injected at the outer left and right sample edges

Full size image

Nevertheless, the expansion of the damage seems to be different. To understand this, a simulated electric current field of the whole sample is discussed. In Fig. 12, an electric current of 10 mA (same as in the measurements) is injected virtually into the outer left and right sample sides. This equals the combined electric current density when all measurement points are measured. A theoretical current path of MP01-02 is shown in red. In the right and left of the defect, the electric current density is very low nearly equalling zero. As no current can pass through the area with the missing material it has to follow approximately along the red line. Therefore, no current flows right next to the lower part of the defect, whereas the upper part has a higher electric current density. All current paths of the lower contact areas pass there and the cross-sectional area in this region is smaller. Therefore, a lower current density next to the defect needs to be balanced by a higher current density in the remaining area. This is due to the fact that the sum of the current density of any infinitesimal cross section in the sample has to have the same current (10 mA) flowing through it as any section.

The results shown in Fig. 11 in accordance with Fig. 12 demonstrate that the change in resistance measurement only shows as a side effect where a damage is located. Foremost, it shows where the current density changes. As the current density increases the most directly next to the inner part of the defect, this area will have the highest weighted current change. This means the map shown in Fig. 11 equals a change in current density. As a decreasing current density indicates a material change or loss, the area with the biggest decrease in current density is most likely to be damaged. Even though the results of the localisation algorithm present an elongated horizontal area, the defect can still be located, as it is usually directly next to the area with the highest resistance change. The knowledge of the reason behind this effect enables a more precise localisation in future work when the electric current density change is taken into account.

The localisation is successfully demonstrated with a deviation from the real location of 17% in longitudinal direction and a deviation from the real location of 8% in sample width direction. This method shows, therefore, very good results in the localisation of defects with electrical resistance mapping but also a very high potential for much more precise localisation of defects. These results were also simulated in ANSYS and simulation data corresponds very well with experimental data. These results were also obtained in different damage experiments such as experiments with surface damage and impact. They all confirm the results shown in this paper.

5 Conclusion

A localisation algorithm for time and spatially resolved electrical resistance measurements is presented. These measurements can be used to detect a defect and to determine its position. It is shown that the change in electric resistance is due to a change in electric current density. Therefore, the localisation shows the area with the biggest change in current density and technically not the defect. As this location in general corresponds to a damage location, it is shown that a damage can be located with this method. This is shown experimentally and with simulations to confirm these findings. Defects which cover more than 0.006% of the sample volume will be successfully detected. The deviation of the defect from the detected area has a deviation of 17% in longitudinal direction and of 8% in sample width direction relating to the sample size. For future work, the fact that results of the localisation algorithm show a change in electric current density can be used to obtain more precise localisations of defects. Due to high-temperature experiments which are conducted with this method, contacting is only possible on two sample sides. To furthermore improve the localisation, it is also possible to contact a sample in future work on all four sides.