Abstract
The paper addresses the application of a parametric design process for a flying wing configuration. The multi-disciplinary configuration (MULDICON) is a generic unmanned combat air vehicle (UCAV) developed for research purposes, a further development of the DLR-F19 configuration, which was used for research activities in the scope of the DLR project Mephisto and its predecessors FaUSST and UCAV2010. For the MULDICON, the DLR parametric design process MONA is applied. Special emphasis is placed on the structural modeling with composite material where each layer is modeled and analyzed. Various failure criteria are compared to define suitable constraints for the optimization of the load carrying structure. In contrast to optimize the thickness of composites with global allowable strains, such strategy allows for a detailed analysis of every layer. The number of constraints due to the set-up of every ply is substantially increased compared to the strain allowables but the structural optimization is still applicable. The detailed structural and mass models represent the global stiffness and structural dynamic characteristics of the aircraft. For the loads analysis part of the design process, 9 different mass configurations with a total of 306 maneuvering load cases as well as 336 1-cos gust load cases are taken into account. Furthermore, a new simplified landing impact simulation is introduced to consider 12 landing load cases. All load cases are defined according to regulations like CS-25. Such number of load cases is necessary to cover a sufficient number of flight conditions. For the selection of the design loads for the structural optimization, the essential loads are analyzed for a subset of locations. Together with a parametrized optimization model, the structural optimization is conducted. The result is a weight-optimized structural model for the MULDICON. This entire model allows for the investigation of physics-based effects already at an early stage of the design process.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A flying wing is still a promising aircraft configuration especially regarding its aerodynamic characteristics. The aircraft, described in this paper, is such a configuration.
The MULDICON is an unmanned combat air vehicle (UCAV). The configuration is applied to a parametric design process that includes the parametric set-up of all simulation models, a comprehensible loads analysis, and finally a structural optimization using composite material. The MULDICON is the result of further developments and improvements of the DLR-F19. The DLR-F19 configuration was applied to a similar design process as the MULDICON (see [2]). Due to various disadvantages of the DLR-F19 configurations, like an insufficient roll performance and a nonlinear pitch moment at high angles of attack, a new design was considered [1, 3]. The investigations on control and stability are part of the DLR project Mephisto. Previous DLR projects dealing with UCAV configurations were FaUSST and UVAV2010. As the MULDICON is an evolution of the DLR-F19, the modelling process is similar. The focus of this paper is on the new lamina-by-lamina optimization and on the new integration of landing loads.
Similar flying wing configurations have been developed, e.g. the X47-B (NorthropGrumman) [4] and the RQ-170 (LockheedMartin) [5], but data are rarely available. Furthermore, there are also testing configurations for civil aircraft like X-48C [6].
The MULDICON is a lambda wing configuration. Its wingspan is equal to the DLR-F19 wingspan of 15.375 m. The wing area is still 77.8 m2. Parallel edges are mandatory for the required stealth characteristics of the MULDICON [1]. The new design is characterized by moving the trailing edge in rearward direction (see Fig. 1). This was also done to increase the effectiveness of the control surfaces [1]. Moreover, new airfoils are selected to improve flight characteristics [7]. Such big modification led to the necessity to set-up of a new structural model for the MULDICON to be used for the parametric design process.
Change from DLR-F19 to MULDICON [1]
The design process starts with the set-up of all involved simulation and optimization models. For the loads analysis, a structural model representing the stiffness and separate mass models are prepared. After the loads analysis, the design loads are selected to be used for the structural optimization task. The design process is repeated until sufficient convergence, e.g. regarding the mass, is achieved.
In Sect. 2, the parametric modeling process is explained. In Sect. 3, the selected simulation models are described: structural model, mass model, aerodynamic model, and optimization model as well as their coupling strategy. A special emphasis of this paper is on the structural model using composite material, where each layer is modeled and analyzed. Section 4 explains the methods to simulate maneuver, gust, and landing cases and specifies the selected load cases. In this part, the estimation of landing loads is a new step in the sizing process. In Sect. 5, the results of the structural optimization are shown. A preliminary examination of the loads analysis results is done in Sect. 6. The results are summarized in Sect. 7 and an outlook on further work is given.
2 Parametric modeling, loads, and design process—MONA
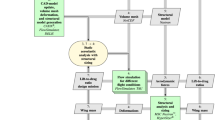
The concept of parametric modeling is chosen, because all involved simulation models are based on one set of parameters. To develop such a parametric aeroelastic model, several steps are considered. In general, there are three main steps: model generation, loads simulation, and structural optimization, as shown in Fig. 2. This design process is called MONA because of the two principal computer programs used, ModGen and MSC Nastran. MONA is embedded in a conceptual design process for multidisciplinary design optimization [8]. Some example of usage are the configurations FERMAT [9], ALLEGRA [10], and DLR-F19 [2].
The MONA process in this work is using three software tools: the two in-house tools ModGen [11] and Loads Kernel [12] as well as the commercial software MSC Nastran [13]. ModGen is used to set up the structural, the aerodynamic, the mass and the optimization model. The loads simulation is done using the LoadsKernel. Finally, the structure is optimized for minimum weight using MSC Nastran SOL200. MONA is an iterative process as the structural optimization has an influence on the structural mass and thus on the loads simulation. The coupling is performed with nodal loads.
For the first step, basic information such as the aircraft’s planform, aerodynamic profiles, and their positions along the wing are required input for ModGen. Furthermore, the positions of ribs and spars have to be defined as load carrying structure. In this way, a geometric model is created. Taking suitable meshing parameters into account, a finite element (FE) model is derived. For most of the structure, shell elements are used. Several mass modeling options like realistic fuel modeling are available. As an extension to the FE-model, an optimization model is created by defining an objective function (mass), design variables (thickness of design fields), and constraints (e.g. failure indices). Apart from the structural and mass models, ModGen is also generating a mesh for aerodynamic panel methods based on the defined planform and taking also into account geometrical parameters like camber and twist.
In a second step, quasi-static and dynamic loads are calculated. The structure needs to be designed to withstand the defined loads, which are composed out of balanced aerodynamic and inertia loads for an elastic structure. The Loads Kernel is using panel methods for aerodynamic forces. Different flight cases can be adjusted and simulated. These cases are divided in three categories: maneuvering cases, gust encounters, and landing cases. Here, a total of 654 load cases are simulated. In a post-processing step, the design loads are determined to use only the decisive loads for the structural sizing. This is done by investigating the resulting loads for the bending moment, the torsion moment, and the shear force at 7 defined monitor stations. The corresponding nodal loads acting on the structure are finally extracted.
As the third step, a structural optimization is done with the resulting design loads. Applying the design loads to the structure, MSC Nastran SOL200 estimates with a static analysis the failure criteria as constraints for each layer of the shell elements and every load case. Furthermore, the sensitivities of the objective function and the constraints with respect to the design variables are calculated. MSC Nastran SOL200 optimizes the structure with a gradient-based optimization algorithm, aiming at a minimum structural weight. This is an iterative process which may be repeated until convergence is achieved. This final structural model is then ready for use in further studies and investigations.
3 Simulation models of the MULDICON
In general, the focus on aeroelastic aspects leads to a number of requirements for the FE model which differ from those for a classical FE model for stress analysis. The structure should be as realistic as necessary because global elastic characteristics such as wing bending and twist are of major interest. Local effects, like stress concentrations at sharp edges or at holes, are neglected. This means that all primary structural components, such as skin, spars, ribs, and stringer, should be modeled. In addition, a mass model with proper distributed mass entities (e.g. structure, systems) and the consideration of various mass configurations (e.g. fuel, payload) are important to conduct proper dynamic calculations. Also the aerodynamic panel model is an approximation and has not the same accuracy as a CFD solution. Hence, the following four models are insufficient e.g. for detailed component stress analysis, but adequate for aeroelastic investigations.
3.1 Structural model
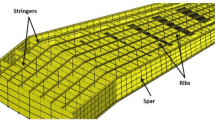
The structure is represented by an FE model. Theories for FEM are summarized, among others, in MSCNastran’s Getting Started Guide [14]. Preliminary design [8] and the latest aerodynamic investigation [7] are providing the basic shape (layout and airfoils). Positions and sizes of system items are defined as well. Hence, three main spars and eight ribs are estimated as primary structure, as shown in Fig. 3. Relative positions of these structural components are dependent on parametric values such as bay lengths and engine diameter. The last rib is placed at 75 % of the third wing segment. As a result, there are 282 structural subsegments. Subsegments are the resulting surfaces of the intersection of skin, spar, and rib surfaces.
This primary structure is meshed with standard finite elements. To be more precise, every subsegment is filled with rectangular CQUAD4 elements with an equidistant partition. At triangular subsegments, CTRIA3 elements are used. Subsegments beyond the last wing rib are neglected to avoid elements with high aspect ratio and taper ratio. The impact of the structure at the tip on global characteristics is assumed to be negligible due to its small mass. In conclusion, this leads to 6294 finite elements in a structured mesh shown in Fig. 4.
The control surfaces are structurally modeled as well and attached to the wing with adaptable hinge stiffness. The hinge modeling concept is shown in Fig. 5. Introducing a torsional spring element, stiffness about the rotation axis can be controlled while all other degrees of freedom are fixed. This adequate modeling ensures a realistic behavior and allows physically meaningful investigations on control surface as well as aeroservoelastic investigation and controller design.
Assembly of the control surfaces [2]
Subsegments are stiffened with reinforcement elements like stringer for the skins. On the one hand, this stabilizes the primary structure against buckling. On the other hand, this avoids local eigenmodes which are undesired in the following modal analysis. For the skin stringers, a hat profile is chosen as a simplification of an omega profile. The dimension of the hat profile are: \(\hbox {H} = 55\,\hbox {mm}\), \(\hbox {t} = 2.5\,\hbox {mm}\), \(\hbox {W}1 = 25\,\hbox {mm}\), and \(\hbox {W}2 = 5.0\,\hbox {mm}\). Due to the limited available space in the third wing segment, the hat profile is scaled down to \(\hbox {H} = 35\,\hbox {mm}\). For rib and spar stiffeners, a rectangular profile is chosen. In some areas, the use of spars is not possible, e.g. in the middle section where an engine is installed as shown in Fig. 6. In such case, flanges are selected to allow for a more integrated structural design. These flanges have the dimensions: \(\hbox {H} = 150\,\hbox {mm}\), \(\hbox {W} = 12.5\,\hbox {mm}\), \(\hbox {t}1 = 2.5\,\hbox {mm}\), and \(\hbox {t}2 = 2.5\,\hbox {mm}\).
3.1.1 Modeling of composite material
For the MULDICON, a composite material is chosen. Carbon fiber-reinforced plastic (CFRP) is composed of thin fibers in a polymer matrix. For aeronautical structures, unidirectional plies are typical. Their long fibers are orientated in one direction in one thin layer. A laminate consisting of several layers can be built to fit the material to its loading.
The classical laminate theory (CLT) is used to calculate the stresses and strains of thin composite material. It is assumed that layers are perfectly glued together and the strain characteristic is linear. The CLT and more details about CFRP are explained in the work of Schürmann [15] and Jones [16]. Also, the VDI (Association of German Engineers) provides a guideline for calculating composite laminates using the CLT [17]. This guideline is used in this work.
An unidirectional ply is described by a stiffness matrix Q. This relates the strains of a thin plate to the stresses by assuming plane stress:
Using transformation matrix T, the stiffness matrix \(Q'\) in a global coordinate system can be calculated for each ply with the angle \(\alpha\).
The mechanical equilibrium condition is used to calculate the stiffness matrices A, B, and D of the laminate which relate the section forces n and moments m to the global strains \(\epsilon\) and \(\kappa\):
where matrix A is the extensional stiffness, B the coupling stiffness, and D the bending stiffness. For symmetric laminates, the B matrix is equal to zero. These submatrices can be calculated by the following equations:
With a given loading and the inverse notation of Eq. 3, the global strains can be calculated. With these global strains, the local stiffness matrix, and the ply boundary dimensions the local stresses and strains can be estimated. Using the CLT, the structural characteristics of composite laminates can be simulated and it allows for the modeling of every layer, resulting in local stresses instead of global strains.
In MSC Nastran, this modeling of composite material by layers can be done with PCOMP and MAT8 cards. Every angle and every property of each ply can be modeled. Therefore, the elasticity values \(E_\parallel\), \(E_\perp\), \(\nu _{\perp \parallel }\), and \(G_{\perp \parallel }\) are necessary. In the FE model of the MULDICON, there are three different stacking sequences for skin, spar, and rib as shown in Table 1. Each ply thickness is \(t_k =0.125\,\hbox {mm}\), resulting in a minimum laminate thickness of \(\hbox {t} = 2.5\,\hbox {mm}\). The used material values in Table 2 are given by the DLR Institute of Composite Structures and Adaptive Systems.
3.1.2 Failure criteria
If global stresses are used for structural optimization as constraint the structure must be analyzed by a global allowable stress for all directions. This could lead to an oversized structure, because e.g. the maximum stress for tension of the matrix is also used for tension in fiber direction. The design with first ply failure is also considering the tension of the matrix but only for the ply which is loaded under that direction. Hence, an analysis of each ply is more detailed. For a strength analysis of a composite ply, the strength values \(R_\parallel ^t\), \(R_\parallel ^c\), \(R_\perp ^t\), \(R_\perp ^c\), and \(R_{\perp \parallel }\) are required. These values are used in MAT8 cards. With these values, four different failure criteria can be considered by MSC Nastran: Hill, Tsai-Wu, Hoffman, and the maximum strain criterion. The first three are second-order tensor polynomials. They are comparable to the Von Mises criterion for isotropic material. In plane stress, they are generating an ellipsoidal fracture body as shown in Fig. 7 for the Hill criterion. The maximum strain criterion relates the maximal strength with the local strain, while considering lateral contraction with the Poisson’s ratio.
There are two failure mechanisms of unidirectional plies: fiber fracture (FF) and interfiber fracture (IFF). All the four criteria determine a fracture body for IFF, while the fracture body of the Hill criterion is in between the fiber fracture. Hence, sizing the structure with the Hill criterion is conservative. Furthermore, the combined loading of tension and compression is considered as most conservative, as shown Fig. 8. So, the Hill criterion is used for structural optimization. This decision also reduces the computational effort, because the Hill criterion needs just one failure index. The calculated failure indices are not equal to the load factor.
3.2 Mass model
An aircraft is subject to different mass distributions. Fuel tank level and payload are varying during flight. According to the regulations like CS25, this has to be considered for the loads analysis. The structural mass is derived from the material density and thickness given in the FE model. Additional masses due to manufacturing need to be added. The mass of systems, payload, and fuel are considered as concentrated point masses shown in Fig. 9. These concentrated point masses are located at the system’s center of gravity. The fuel tanks are discretized over the wing, bounded by spars and ribs. For each fuel bay, a volume element is generated by ModGen to calculate the mass and inertia moments of the fuel tanks (CHEXA, CPENTA). This is done for three different filling levels: full, half, and empty.
All point masses are connected to the structure using interpolation constraint elements (RBE3). The RBE3 element distributes the mass properties defined at a reference point to a set of defined points of the FEM (all corner points of the surrounding primary structure). In this way, its inertia forces are introduced into the structure. As shown in Table 3, nine different mass configurations are selected. Accordingly, many flight states can be considered. The mass configurations with half payload are asymmetric cases (only left payload).
3.3 Aerodynamic model
The vortex lattice method (VLM) [18] is a fast panel method suitable for aerodynamic loads simulation in the aeroelastic sizing process. Due to the underlying theory, its validity is limited to the subsonic regime but transonic effects can be considered using various correction techniques [19,20,21,22] or an enhancement with CFD calculations for selected parameters [23].
The aerodynamic surfaces are discretized with aerodynamic panels. As shown in Eq. 7, the VLM relates the induced downwash \(w_{j}\) on each panel to the pressure coefficient \(\varDelta c_{p}\) between the lower and the upper surface. The downwash is an induced normal velocity by every panel at the 3/4-point of each panel. The aerodynamic influence of a panel on the others can be calculated by geometrical distances and angles due to the theory of horseshoe vortices. These aerodynamic influence coefficients are cast into an AIC matrix. For unsteady aerodynamics, the Doublet Lattice Method (DLM) is selected. That method is described in the work of Albano and Rodden [24], and Blair [25]. It makes use of the same input and also returns an AIC matrix. The difference is the formulation in the frequency domain and the dependency of the AICs on the reduced frequencies. The AIC matrix is dependent on the mach number Ma and the reduced frequency k.
In the present model, 24 panels in flow direction and 52 in spanwise direction lead to a structured mesh of 1248 panels shown in Fig. 10. Recommendations for the minimum chord length of an aerodynamic box are taken into account [26]. This grid is suitable up to a reduced frequency of \(k=2.0\).
To avoid triangular panels at the pointed wing tip and because their influence is negligible, the outer quarter of the wing tip segment has not been modeled. Also, panels with an high aspect ratio are undesired. The quantity of the panels in span direction is adjusted to get a maximal aspect ratio of \(AR _\mathrm{max}=4\).
The four control surfaces, located along the trailing edge of the wing, are discretized with five panels in flow direction. A rotation of a surface around its hinge line causes an additional force \(P_k^\mathrm{aero,cs}\). Therefore, the induced downwash at these panels is enlarged.
Aerodynamic effects are modeled by applying an appropriate downwash vector \(w_j\). The calculation principle of the aerodynamic forces is given by Eq. 8.
with:
- \(q_{\infty }\):
-
Dynamic pressure
- \(S_{kj}\):
-
Aerodynamic integration matrix
- AIC:
-
AIC-matrix
- \(D_{jrbm}\):
-
Differential matrix of rigid body motion
- \(D_\mathrm{jcs}\):
-
Differential matrix control surface deflections
- \(D_{jk}^1\):
-
Differential matrix of deformations
- \(D_{jk}^2\):
-
Differential matrix of velocity
- \(\varPhi _{gf}\):
-
Modal matrix of flexible modes
- \(u_{rbm}\):
-
Rigid body motion
- \(u_{cs}\):
-
Control surface deflections
- \(u_{f}\):
-
Flexible structural deformation
- \(\dot{u}_{f}\):
-
Flexible structural motion
- \(T_{kg}\):
-
Spline matrix for aero-structural coupling
- \(\varPhi _{gf}\):
-
Modal matrix of flexible structural modes
- \(U_{\infty }\):
-
Free stream velocity
Equation 8 contains several sources of aerodynamic forces. Forces due to rigid body motions are given by \(D_{jrbm}\)\(u_{rbm}\) and control surface deflections are considered in \(D_\mathrm{jcs}\)\(u_{cs}\). Flexibility is incorporated in the two terms \(D_{jk}^1\)\(T_{kg}\)\(\varPhi _{gf}\)\(u_f\) and \(D_{jk}^2\)\(T_{kg}\)\(\varPhi _{gf}\)\(\dot{u}_f\) for the structural deformation and motion respectively. Application of the AIC matrix leads to a local pressure distribution which is integrated and translated to the structural grid using the matrices \(S_{kj}\) and \(T_{kg}\). As the AIC matrix is normalized with the dynamic pressure \(q_{\infty }\), the resulting loads need to be denormalized with \(q_{\infty }\) to obtain forces and moments.
The aerodynamic forces due to rigid body motions are usually the most significant contributor to the overall forces. In this implementation, forces from the different sources are calculated independently and superimposed linearly, as shown in Eq. 9.
Unsteady aerodynamics are available in the time simulation using a rational function approximation as suggested by Roger [27] and are added to Eq. 9. The implementation is similar to other publications [28,29,30]. A difference is the approximation on panel level using physical coordinates. This leads to a large number of lag states but the implementation is straight forward.
A rational function approximation allows for a decomposition of the aerodynamic forces into a steady part \(A_0\) depending on the downwash \(w_j\), a damping part \(A_1\) depending on the change of the downwash \(\dot{w}_j\), and a part \(A_2\) depending on the acceleration of the downwash \(\ddot{w}_j\). However, matrix \(A_2\) is omitted during the approximation, as suggested in [30]. The unsteady parts \(A_3\), \(A_4\), ..., \(A_{3+n}\) depend on the lag states \(lag_a\), \(lag_2\), ..., \(lag_n\). As the time simulation usually starts from an initial steady level flight, the lag states are assumed to be zero at the beginning. The lag-state derivatives \(\dot{lag}_i\) are given by Eq. 11.
The poles \(\beta _i\) used during the approximation may be determined by Eq. 12 [27]. A slightly different proposal is given in [26].
The quality of the approximation has to be checked always, because too few poles may cause a bad approximation, leading to nonphysical results. For the MULDICON, the selected number of poles is \(n_{poles}=9\) for a highest reduced frequency \(k_\mathrm{max}=2.0\).
3.4 Coupling strategy
The aerodynamic forces and moments are best calculated in their original frame of reference. The structural grid might be of much higher or lower granularity and in some cases, local coordinate systems might be used. This is one typical example where forces and moments need to be transferred from one grid to another. In addition, structural deflections need to be transferred back onto the aerodynamic grid. This operations can be handled with the help of the transformation matrix \(T_{di}\) which relates displacements of an independent grid \(u_i\) to displacements of a dependent grid \(u_d\).
In addition, as in Eq. 14, the transposed matrix \(T_{di}^T\) transforms forces and moments from a dependent grid \(P_d\) to an independent grid \(P_i\).
The transformation matrix \(T_{di}\) may be defined by various methods. One commonly used approach for loads calculation is the rigid body spline. Each grid point of the dependent grid is mapped to exactly one point on the independent grid. The distance \(\overrightarrow{r}\) between these two grid points is assumed as a rigid body that transfers forces and moments. In addition, forces F create moments M due to their lever arm \(\overrightarrow{r}\) as stated in Eq. 15.
In reverse, translations and rotations are directly transferred and rotations create additional translations. The mapping of the points may be defined manually or automatically, e.g. with a nearest neighbor search. As this concept is quite fast and versatile, it is selected for the aero-structural coupling in this work and depicted in Fig. 11. The small black lines between the blue and red dots visualize the mapping. By this, aerodynamic forces can be attached to the structural model and deformation of the structure change the aerodynamics.
3.5 Equation of motion
The motion of the aircraft is divided into a rigid and a flexible part. For the rigid body motion, the mass model of the complete aircraft is represented by one lumped mass with corresponding inertia matrices \(M_b\) and \(I_b\), positioned at the center of gravity. All external forces and moments \(P_b^{ext}\) are gathered at the same point. Equations 16 and 17 give the translational and rotational accelerations \(\dot{V}_b\) and \({\dot{\varOmega }}_b\) of the aircraft due to these forces and moments. Additional coupling terms derived by Waszak, Schmidt, and Buttrill [31,32,33] may be added at this point.
In addition to the rigid motion of the aircraft, linear structural dynamics are incorporated by Eq. 18. Here, generalized external force \(P_f^{ext}\) interact with linear elastic deflections \(u_f\), velocities \(\dot{u}_f\) and accelerations \(\ddot{u}_f\). The matrices \(M_{ff}\), \(D_{ff}\), and \(K_{ff}\) refer to the generalized mass, damping, and stiffness matrices. However, damping is assumed to be zero.
3.6 Optimazation model
The objective of the structural optimization is to minimize the structural weight while keeping the responses such as failure indicies inside their boundaries. The task is treated as a mathematical optimization problem and is formally defined in Eq. 19. Therein, f is the objective function with vector x containing the design variables and g is the constraint vector.
The ply thicknesses of upper and lower skin, spars, and ribs are defined as optimization variables. Here, the minimal thickness is set to 2.5 mm. The elements are grouped in the 282 subsegments and linked in order to define one variable per subsegment. Therefore, the element with the maximal ply failure index governs the whole subsegment. For the design responses, the failure index of Hill is utilized. The optimization is done by a continuous increase of the laminate thickness because of a straight increase of the layer thickness. The stacking sequence and layer orientation given in Table 1 remains unchanged. The structural model is designed in such a way that left and right side have the same properties, whereby the corresponding design fields are changed simultaneously, too. This is to ensure symmetry, a necessity if unsymmetrical load cases are considered. Summing up, the optimization problem has 282 design variables. The 6294 design responses multiplied by 654 load cases lead to ca. 4.1 Mio constraints.
4 Loads simulation
For the structural optimization, maneuver, gust, and landing loads are considered. The basic equations for each type of simulation are explained in the following paragraphs.
4.1 Quasi-steady maneuver loads
Regarding maneuver loads, the MULDICON is designed for loads resulting from various pitching and rolling conditions. Due to insufficient control about the vertical axis, yaw maneuvers are not considered here. The loads are calculated by a determination of different flight states whose aerodynamics are assumed as quasi-steady. Therefore, the aerodynamics (Sect. 3.3) and the equations of motion (Sect. 3.5) are cast in a first-order system, as shown in Eqs. 20 and 21. For every maneuver, a set of trim condition is defined to get a solvable system of equation. This trim equation is then solved with a generic non-linear solver using the HYBRD algorithm [34].
According to the certification specifications CS 25.331 [35], pitching maneuvers are selected in the range of −1.0 g to 2.5 g. Beside the pitching maneuvers, an 1.0 g horizontal level flight is simulated. Additional rolling conditions were provided by Airbus D&S as part of a cooperation between DLR and Airbus D&S in the frame of the DLR project Mephisto. Such rolling conditions indicate an enlarged maneuver load envelope (v-n diagram) for a typical UCAV configuration. They take into account the range of −1.8 g to 4.5 g. All maneuver load cases are combined with all mass configurations, see Table 3, for design cruise speeds \(V_c\), respectively, \(M_c\) and design dive speeds \(V_d\), respectively, \(M_d\), and at five Flight Levels (FL). The design cruise speed is Mach 0.8 at sea level and increases to Mach 0.9 at FL 75, while the design dive speed is Mach 0.9 at sea level and increases to Mach 0.97 at FL 55. Further flight levels are FL 200, FL 300, and FL 450 at Mach 0.9 for design cruise speed and Mach 0.97 for design dive speed. In total, 306 maneuvering load cases are considered.
4.2 Dynamic, unsteady gust loads
A dynamic gust analysis is performed according to the certification specifications CS 25.341 for large aircraft [35]. The aircraft is exposed to a series of 336 vertical 1-cosine shaped gusts with lengths H of 9, 15, 30, 45, 65, 85, and 107 m. The vertical velocity U is given in Eq. 22 and is defined in dependence of the distance s penetrated into the gust and the design gust velocity \(U_{ds}\).
This leads to an additional downwash \(w_{j,gust}\) due to the gust velocity on each aerodynamic panel. The resulting aerodynamic forces \(P_k^{aero,gust}\) are added to Eq. 9. Typically, gust loads are of very short and sudden nature. Especially for the shorter gusts, unsteady aerodynamics are absolutely necessary for an adequate simulation for the resulting loads.
4.3 Dynamic landing loads
The landing gear of an aircraft has to fulfill several purposes. An overview is given in [36]. In this work, the emphasis lies on the absorption of vertical kinetic energy occurring during the landing impact. The task is to analyze the effect on the aircraft structure and to include the resulting loads in the sizing process.
State of the art aircraft landing simulations are normally carried out using multi-body simulation techniques, e.g. as described in [37, 38] and include a detailed model of the landing gear and tires. However, the aircraft is often assumed as a rigid body, neglecting the dynamic response of the aircraft’s flexible structure. There are several possibilities to address this shortcoming. One approach is to incorporate the aircraft’s structural properties in the multi-body simulation environment. This can be achieved by a modal representation of the aircraft as Lemmens [39] demonstrates for a business jet. Castrichini et al. [40] even includes unsteady aerodynamics for the calculation of both gust and ground loads. An alternative to the modal representation is the discretisation of the elastic structure by means of rigid bodies which are connected by rotational springs to account for wing bending and rotational stiffness [41]. A different approach by Jaques and Garrigues [42] uses a dynamic, transient finite elements analysis. Special nonlinear elements, joints, and hinges are added to the FE code to describe the behavior of the landing gear.
The approach in this work includes the landing gear directly within the transient, dynamic simulation. Therefore, a generic landing gear model is added to the simulation code. For a sizing procedure in a pre-design phase, some simplifications may be made while maintaining the key elements, which are explained in the following.
A typical landing gear of a larger aircraft is shown in Fig. 12. One key feature is a hydropneumatic air and oil shock absorber. The gas spring force \(F_f\) is given in Eq. 23. The force is calculated based on a pre-stress force \(F_0\), a stroke length s, a maximal stroke \(s_m\), and a polytropic coefficient n with \(1 \leqslant n \leqslant \kappa\). The damping force \(F_d\) is given in Eq. 24 with the stroke velocity \(\dot{s}\) and damping coefficient d.
For the tires, a linear behavior is assumed, forces act in z-direction and only when the tire makes contact with ground. Its deflection \(d_z\) is determined by subtracting its rolling radius \(r_r\) from its nominal radius \(r_{nom}\). This leads to Eq. 25 with a tire stiffness c and damping coefficient d. In addition, the tire may have a mass \(m_{tire}\), causing a force \(F_{tire}\).
In a next step, the landing gear model is incorporated into the time simulation of the Loads Kernel software. The positions, velocities, and accelerations of the landing gear attachment point, indicated in Fig. 12, are extracted at every time step and feed into the landing gear module. The landing gear reaction forces are then applied as external forces \(P_g^\mathrm{ext}\) on the aircraft. As the landing gear model is evaluated on-the-fly, the interaction between aircraft and landing gear is captured.
Key feature of a typical nose landing gear, photograph from [43]
In this way, the landing gear forces are counteracted by the aircraft’s inertia, leading to a balanced set of loads.
According to CS 25.473, two different sink rates are chosen. Cases with one, two, and three wheels landing are considered for two mass configurations, leading to 12 landing cases.
5 Results of the structural optimization
The iterative sizing loop of Loads Kernel and MSC Nastran SOL200, as laid out in Sect. 2, starts with an initial loads simulation. Out of the 654 load cases only the dimensioning load cases are determined to size the components. In the initial simulation loop, for example 121 design load cases are identified and used for the structural optimization with MSC Nastran SOL200. In every iteration, all 654 load cases are considered but just the necessary design load cases are used for optimization depending on the load selection process.
The pure structural mass is used as the convergence criterion. It converges rather quickly, as shown in Fig. 13, so only three iterations are necessary. This is due to the stiff configuration which deforms barely, in comparison to configurations with a slender wing. Furthermore, the cross sectional areas are quite huge because of the chosen thick airfoils (ca. 15 %). As a result, the configuration deforms rarely. Finally, the pure structural weight is 1383.1 kg.
As pictured in Figs. 14 and 15, the thickness of the subsegments is mostly the minimal thickness of 2.5 mm. Only at the leading edge, some subsegments are increased to a maximum of 7.5 mm. All rib and spar subsegments are not changed by the optimization process and have the minimum thickness of 2.5 mm. After the optimization, the Hill failure index is less than one, as exemplarily shown for three design load cases in Figs. 16, 17 and 18. The failure indices for the most of the load cases are low, so the optimization does not have to change much. Only at the leading edge, the design loads lead to small changes due to the high \(\varDelta c_p\) coming from DLM aerodynamics.
In contrast to slender wings, the eigenfrequencies are much higher, as listed in Table 4. Generally, for heavier mass configurations, the frequencies become smaller. In comparison to its predecessor, the DLR-F19, the eigenfrequencies are twice as high which also relates to the more compact planform (like a delta wing). However, the characterization of the mode shape is difficult, because the modes interact strongly. For a configuration like the MULDICON pure bending and torsion modes, as known for slender wing configurations, are seldom.
As an example, the heaviest mass configuration is chosen to show typical mode shapes. The 1st eigenmode, an asymmetric bending mode, is shown in Fig. 19. At the 2nd eigenmode, the bending mode interacts with a nose pitching mode. The 3rd eigenmode is an asymmetric twist mode. The mode shapes differ from each other depending on the mass configuration.
6 Loads analysis
For an assessment of the loads analysis and to down select the design loads, the three major internal loads shear force \(F_z\), bending moment \(M_x\), and torsion moment \(M_y\) are plotted against each other for selected combinations. In Figs. 20 and 21 such two-dimensional load envelopes for the load station at the first wing-kink are displayed. The landing loads (pink) at that point are insignificant while the gust loading (blue) has a greater shear force \(F_z\) and bending moment \(M_x\), whereas the torsion moment \(M_y\) is greater in the maneuver load cases (green). The landing loads lead to high local forces which have to be introduced into the aircraft structure. But in an overall view, as shown in Fig. 18, the landing loads with a maximum failure index of 0.32 have only marginal influence for such an configuration. The attachment structure for mounting the landing gear has to be designed adequately, while the primary structure is sized by maneuver and gust loads. Nevertheless, it is necessary to consider landing loads for overall aircraft design.
The pitch maneuver load cases cause a similar failure index contribution as a gust encounter. Looking at the example of a roll maneuver, as in Fig. 17, the failure index is less while the attachment region of the control surfaces is affected mostly. So the maneuvering load cases are also important in overall aircraft design but for this configuration they have less influence on the structural optimization, whereas the gust load cases have strong influence on the leading edge structure.
7 Conclusion and outlook
In this paper, DLR’s parametric modeling process MONA is used successfully to set up an aeroelastic model of the MULDICON. The resulting model is sized with 654 load cases, including maneuver, gust, and landing loads. As a further development of the design process MONA, the landing loads are simulated as a new part in that process with a simplified generic landing gear model. Also, the gust encounters are simulated with a dynamic unsteady time simulation, instead of the Pratt prediction model, in contrast to previous work [2].
The structural model is comparatively detailed for a conceptual design phase and a model condensation typical for loads analysis is avoided. This is a more physical way of introducing the loads to a structure, compared to the use of a so-called load reference axis. Such concept is not useful for a configuration like a deltawing. By setting up the model, special emphasis is placed on the modeling of composite materials by layers. Here, the four different failure criteria implemented in MSC Nastran are studied and as a result the Hill criterion is used for the structural optimization, because of its simplicity and conservatism. Finally, an aeroelastically sized model is given for further analysis of the MULDICON, as an example for flying wing configurations. With this aeroelastic model, a flutter investigation is performed in [44] concerning the body freedom flutter phenomenon like in a previous work regarding the predecessor DLR-F19 [45]. Moreover, the influence of high-fidelity aerodynamics on the sizing process using a CFD correction is investigated in [23]. An uncertainty qualification based on this configuration is assessed in [46] and different modelling strategies are compared in [47].
On the composite modeling side, the optimization process could be enhanced. A stepwise optimization of the laminates is possible to bring the modeling closer to manufacturing. Therefore the command DDVAL of MSC Nastran for discrete design variable values could be used. Also, the influence of delamination failure towards the sizing may be investigated. Therefore, impact load cases have to be considered.
Because of the small change in the thickness of the material, a lower minimum thickness value could be used. Here, the minimum stacking sequence of 20 layers, which is equivalent to a minimum thickness of 2.5 mm, is a strong constraint which is probably to high. A lower minimum value of 1.6 mm, as chosen in [48], could be a better approach.
Otherwise, a variable stiffness of each subsegment could be used as a design variable to fit the structure better to its loading. This procedure is explained in [49], followed by a stacking sequence design with a generic algorithm, as presented in [50].
References
Schütte, A., Huber, K.C., Zimper, D.: Numerische aerodynamische Analyse und Bewertung einer agilen und hoch gepfeilten Flugzeugkonfiguration. In: Deutscher Luft- Und Raumfahrtkongress 2015. Rostock, Germany (2015)
Voß, A., Klimmek, T.: Design and sizing of a parametric structural model for a UCAV configuration for loads and aeroelastic analysis. CEAS Aeronaut. J. 8(1), 67–77 (2017). https://doi.org/10.1007/s13272-016-0223-2
Schwithal, J., Rohlf, D., Looye, G., Liersch, C.M.: An innovative route from wind tunnel experiments to flight dynamics analysis for a highly swept flying wing. CEAS Aeronaut. J. (2016)
X47B UCAS Datasheet. http://www.northropgrumman.com/MediaResources/MediaKits/WEST/Documents/X47B_UCAS_Datasheet.pdf (2015)
Unmanned Systems \(\cdot\) Lockheed Martin. http://www.lockheedmartin.com/us/what-we-do/aerospace-defense/unmanned-systems.html (2017)
NASA Armstrong Fact Sheet: X-48 Hybrid/Blended Wing Body. https://www.nasa.gov/centers/armstrong/news/FactSheets/FS-090-DFRC.html (2014)
Schütte, A.: Numerical investigations of vortical flow on swept wings with round leading edges. J. Aircraft (2016)
Liersch, C.M., Huber, K.C., Schütte, A., Zimper, D., Siggel, M.: Multidisciplinary design and aerodynamic assessment of an agile and highly swept aircraft configuration. CEAS Aeronaut. J. 7(4), 677–694 (2016)
Klimmek, T.: Parametric set-up of a structural model for FERMAT configuration for aeroelastic and loads analysis. J. Aeroelast. Struct. Dyn. 3(2), 31–49 (2014)
Krüger, W.R., Klimmek, T., Liepelt, R., Schmidt, H., Waitz, S., Cumnuantip, S.: Design and aeroelastic assessment of a forward-swept wing aircraft. CEAS Aeronaut. J. 5(4), 419–433 (2014)
Klimmek, T.: Parameterization of topology and geometry for the multidisciplinary optimization of wing structures. In: Proceedings “CEAS 2009”, Manchester, UK (2009)
Voß, A., Klimmek, T.: Maneuver loads calculation with enhanced aerodynamics for a UCAV configuration. In: AIAA modeling and simulation technologies conference, Washington, DC (2016). https://doi.org/10.2514/6.2016-3838
MSC.Nastran: MSC.Nastran 2012 Quick Reference Guide (2011)
MSC.Nastran: MSC.Nastran 2012 Getting Started User’s Guide (2011)
Schürmann, H.: Konstruieren Mit Faser-Kunststoff-Verbunden. Springer, Berlin (2007)
Jones, R.M.: Mechanics of Composite Materials. Taylor & Francis Inc, New York (1999)
VDI 2014 - Blatt 3: Entwicklung von Bauteilen aus Faser-Kunststoff-Verbund—Berechnugen Development of FRP components(fibre-reinforced plastics)—analysis (2006)
Katz, J., Plotkin, A.: LOW-Speed Aerodynamics. McGraw-Hill, Inc., New York (1991)
Giesing, J.P., Kalman, T.P., Rodden, W.P.: Correction Factor Techniques for Improving Aerodynamic Prediction Methods (1976)
Thormann, R.: Extension of the subsonic doublet lattice method in transonic region using successive kernel. In: Deutscher Luft- Und Raumfahrtkongress 2009. Aachen, Deutschland (2009)
Brink-Spalink, J., Bruns, J.: Correction of unsteady aerodynamic influence coefficients using experimental or CFD data. In: AIAA/ASME/ASCE/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit (2000). https://doi.org/10.2514/6.2000-1489
Quero, D., Krüger, W., Jenaro, G.: A Reduced Order Model for Dynamic Loads Prediction including Aerodynamic Nonlinearities. In: International Forum on Aeroelasticity and Structural Dynamics (IFASD-2015). Sankt Petersburg, Russland (2015)
Voß, A.: Comparing VLM and CFD maneuver loads calculations for a flying wing configuration. In: International Forum on Aeroelasticity and Structural Dynamics. Savannah (2019)
Albano, E., Rodden, W.: A doublet lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. New York (1968)
Blair, M.: A Compilation of the Mathematics Leading to the Doublet Lattice Method. Tech. Rep. WL-TR-92-3028, WRIGHT LAB WRIGHT-PATTERSON AFB OH (1992)
ZONA Technology Inc.: ZAERO Theoretical Manual Version 9.0. Scottsdale, Arizona (2014)
Roger, K.L.: Airplane Math Modeling Methods for Active Control Design. AGARD-CP-228, pp. 4.1–4.11 (1977)
Karpel, M., Strul, E.: Minimum-state unsteady aerodynamic approximations with flexible constraints. J. Aircraft. (2012). https://doi.org/10.2514/3.47074
Gupta, K.K., Brenner, M.J., Voelker, L.S.: Development of an integrated aeroservoelastic analysis program and correlation with test data (1991). OCLC: 25535531
Kier, T., Looye, G.: Unifying Manoeuvre and Gust Loads Analysis. In: IFASD 2009. Seattle, USA (2009)
Waszak, M.R., Schmidt, D.K.: Flight dynamics of aeroelastic vehicles. J. Aircraft 25(6), 563–571 (1988)
Buttrill, C., Arbuckle, P., Zeiler, T.: Nonlinear Simulation of a Flexible Aircraft in Maneuvering Flight. In: AIAA Paper 87-2501-CP, AIAA flight simulation technologies conference (1987)
Waszak, M.R., S. Buttrill, C., Schmidt, D.K.: Modeling and model simplification of aeroelastic vehicles: an overview (1997)
Scipy.optimize.fsolve — SciPy v1.0.0 Reference Guide. https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html
CS25 - Certification Specifications and Acceptable Means of Compliance for Large Aeroplanes - Amendment 16 (2015)
Krüger, W., Besselink, I., Cowling, D., DOAN, D., Kortüm, W., Krabacher, W.: Aircraft landing gear dynamics: simulation and control. Vehicle Syst. Dyn. 28, 119–158 (1997). https://doi.org/10.1080/00423119708969352
Krüger, W.: Integrated Design Process for the Development of Semi-Active Landing Gears for Transport Aircraft. Dissertation, Universität Stuttgart, Stuttgart (2000)
Cumnuantip, S.: Landing Gear Positioning and Structural Mass Optimization for a Large Blended Wing Body Aircraft. Dissertation, TU München, Köln (2014)
Lemmens, Y., Verhoogen, J., Naets, F., Olbrechts, T., Vandepitte, D., Desmet, W.: Modelling of aerodynamic loads on flexible bodies for ground loads analysis. In: IFASD 2013 - International Forum on Aeroelasticity and Structural Dynamics (2013)
Castrichini, A., Cooper, J., Benoit, T., Lemmens, Y.: Gust and Ground Loads Integration for Aircraft Landing Loads Prediction. In: 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Grapevine, Texas (2017). https://doi.org/10.2514/6.2017-0636
Krüger, W.R.: Multibody analysis of whirl flutter stability on a tiltrotor wind tunnel model. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. (2015). https://doi.org/10.1177/1464419315582128
Jacques, V., Garrigues, E.: Ground dynamic loads calculations strategies for civilian and military aircrafts. In: International Forum for Aeroelasticity and Structural Dynamics. Bristol (2013)
Bohn, M.: Aviation Photo #1829344 | Airbus A320-233 - LAN Airlines|Airliners.net. http://www.airliners.net/photo/LAN-Airlines/Airbus-A320-233/1829344 (2010)
Schreiber, P., Vidy, C., Voß, A., Arnold, J., Mack, C.: Dynamic aeroelastic stability analyses of parameterized flying wing configurations. In: Deutscher Luft- Und Raumfahrtkongress 2018. Friedrichshafen, Deutschland (2018)
Schäfer, D., Vidy, C., Mack, C., Arnold, J.: Assessment of Body-Freedom Flutter for an Unmanned Aerial Vehicle. Braunschweig, Deutschland (2016)
Ronch, A.D., Drofelnik, J., van Rooij, M.P., Kok, J.C., Panzeri, M., Voß, A.: Aerodynamic and aeroelastic uncertainty quantification of NATO STO AVT-251 unmanned combat aerial vehicle. Aerosp. Sci. Technol. 91, 627–639 (2019). https://doi.org/10.1016/j.ast.2019.04.057
Schweiger, J.M., Cunningham, A., Sakarya, E., Dalenbring, M.J., Voß, A.: Structural design efforts for the MULDICON configuration. In: 2018 Applied Aerodynamics Conference. American Institute of Aeronautics and Astronautics, Atlanta (2018). https://doi.org/10.2514/6.2018-3325
Breuer, U.: Metal and Carbon–the Development of a New Multi-fuctional Material for Primary Structures (2016)
Dillinger, J.: Static Aeroelastic Optimization of Composite Wings with Variable Stiffness Laminates. Thesis, Delft University of Technology (2014)
Meddaikar, Y.M., Irisarri, F.X., Abdalla, M.M.: Blended Composite Optimization combining Stacking Sequence Tables and a Modified Shepard’s Method, Sydney (2015)
Acknowledgements
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bramsiepe, K., Voß, A. & Klimmek, T. Design and sizing of an aeroelastic composite model for a flying wing configuration with maneuver, gust, and landing loads. CEAS Aeronaut J 11, 677–691 (2020). https://doi.org/10.1007/s13272-020-00446-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13272-020-00446-x