LARUS: an unmanned aircraft for the support of maritime rescue missions under heavy weather conditions

Abstract

In maritime emergencies, the time until arrival at the scene of an accident is a decisive factor for a successful rescue operation. In this context, the research project LARUS aims to support the rescue forces at sea with unmanned aerial systems and thus to optimize the rescue process. This refers on the one hand to the localization of potential accident sites and on the other hand to informing the rescuers about the situation on site as well as the provision of an efficient communication infrastructure. For this purpose, the UAS is equipped with various sensors and communication media. To ensure a seamless rescue procedure, the aircraft must be capable of operating even under severe weather conditions. In this regard, the Institute of Flight System Dynamics is currently investigating measures to reduce the gust loads to make the UAS robust against challenging weather conditions. The integration of the LARUS aerial system into airspace using an active collision avoidance system is also an important research aspect. In addition, the adaptation of flight control to the expanded requirements and influencing factors as well as the implementation of international SAR search strategies for flight guidance are also the subject of development work.

1 Research project LARUS

The LARUS project deals with the situation support of maritime emergency operations by unmanned aerial systems (UAS). For a total of 3 years, the research activities within the framework of the programme “Forschung für die zivile Sicherheit”¹ in the field of “Zivile Sicherheit—Innovative Rettungs- und Sicherheitssysteme”² were funded by the German Federal Ministry of Education and Research (BMBF). The consortium consists of six partners: the Communication Networks Institute of the Technical University of Dortmund, which is also responsible for coordination, the Institute of Flight Systems Dynamics of the RWTH Aachen University, the German Maritime Search and Rescue Service—Deutsche Gesellschaft zur Rettung Schiffbrüchiger (DGzRS) as well as the SMEs Hanseatic Aviation Solutions GmbH, Opto Precision GmbH and IMST GmbH. The work was started in October 2016 [1].

2 Scenario

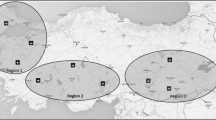
In an emergency at sea, every minute counts. The duration until the arrival of the rescue forces has a significant influence on the probability of rescue or survival. Therefore, it is a primary goal to optimize this time span. DGzRS currently operates a network of 54 stations along the German coastlines and a fleet of 60 rescue boats and cruisers [2], depicted in Fig. 1. However, operations far from the coast often require long approach times. Here, flying systems can help to increase the efficiency of rescue missions, as they can reach the scene much faster in relation to ships and observe from a different perspective due to their elevated position.

Fig. 1

Overview of DGzRS stations in Germany, ©DGzRS

In contrast to multicopter UAS, which are already used close to the shore in France to rescue drowning people by providing buoyancy aids [3], or similar systems, which are currently being tested by the German Red Cross [4], the LARUS aerial system is not intended to intervene directly in the rescue operation. Instead, it is supposed to support the rescue forces with its technical equipment to locate the scene of an accident quickly, to distribute information about the situation on site and to provide them with an efficient communication infrastructure for telemedical first aid. A quick on-site investigation of the situation can also help to identify false alerts, e.g., when missing persons are reported, and reduce the unnecessary commitment of available rescue teams and technical resources.

Accordingly, special attention is foremost paid to the rapid location of the accident site. In many cases, however, the information on the position of a damaged ship is inaccurate, for example, if the technical equipment for direct location is inadequate or if the information when making the emergency call is not sufficiently specific and includes estimates. It should also be noted that the locations of operation are constantly drifting. Particularly in the case of reports from persons, which are not directly involved, such as notifications of missing persons by third parties, the situation is often completely unclear. The initial point for a search and rescue operation is based on information about the last known position as well as weather and current conditions. The more imprecise these inputs are and the longer the period of time since the last concrete location is, the wider the potential search area is. With the help of UAS, it is intended to reach the locations where accidents occur more quickly or to find missing persons or ships in less time than is possible by sea. Depending on weather conditions and swell, the LARUS aerial system moves up to five times faster than a rescue cruiser and thus has a considerable time advantage. In cooperation with the DGzRS, the search strategies used so far at sea are to be incorporated into the automated flight control system of the UAS and to accelerate the location of the accident site. The first rough localization in the area of application is carried out with the aid of on-board communication technology, which locates mobile phones and other transmitters in the vicinity. At the same time, a laser-assisted multi-spectral camera system specially developed by Opto Precision GmbH for this application is used to precisely identify the accident site. The extended viewing angle from the chosen altitude significantly increases the probability of detection compared to the sighting from a ship and creates an important basis for a fast, coordinated rescue operation. The UAS should not only support the search, but also supply airborne information and provide a powerful communication platform.

3 LARUS aerial system

The LARUS aerial system is based on the fixed wing UAS S360 from the project partner Hanseatic Aviation Solutions (see Fig. 2), which is modified and expanded for the special purpose regarding performance, structure, communication systems, sensors and flight control. The fixed wing configuration was already selected in an internal evaluation process during the preparation of the project proposal, because it offers the best performance range in terms of flight speed, operating time, range, payload and robustness for the particular conditions of use instead of, e.g., multirotor systems.

Fig. 2

Fixed wing UAS S360, ©Hanseatic Aviation Solutions

The S360 has a wingspan of 3.6 m. In addition to the ailerons, each wing is equipped with two flaps, which can be controlled independently of each other. Due to the pusher drive configuration, the tail is designed as a box-type tailplane with one elevator and two rudders. A combustion engine is used as the propulsion system, allowing a maximum flight time of up to 4 h at speeds between 80 km/h and 170 km/h. The maximum take-off mass is 25 kg. This includes 5 kg as payload or additional sensors, for which the fuselage has a volume of 15 l available [5]. The technical data are summarized in the following Table 1.

Table 1 Technical data of the LARUS UAS

4 Enhancements/modifications

The greatest challenge from an aeronautical point of view is the high operational availability of the UAS, even in heavy weather conditions up to wind force 10 or up to wind speeds of 100 km/h. This requirement is an important prerequisite for seamless integration into the rescue process. In this context, one of the tasks of the Institute of Flight System Dynamics is to make the flight system more robust against environmental influences. This applies to both structural changes and flight control. However, the integration of the unmanned aerial system into the airspace and risk-free operation over distances of several kilometers also require technical solutions, which are addressed below. In addition, the UAS has to carry out its search for the exact location of the accident autonomously after reaching the suspected area of operation. To achieve this, search strategies are applied which are also used on the sea side or in combination with watercraft and aircraft. In contrast to manned rescue equipment, the UAS is equipped exclusively with sensors that are used fully automatically in the area of application. For this purpose, the flight control system of the LARUS aerial system must receive corresponding search patterns in the form of parameterizable trajectories from a software and process these.

4.1 Flight guidance system

The UAS, which is based near the coast, is coordinated by a control center, but performs its tasks completely automatically. The utilization in heavy weather conditions, especially with strong winds and gusts, requires a powerful flight control system which ensures that the specified trajectories can be flown accurately in turbulent atmosphere without exceeding the performance limits of the aircraft. In this respect, the existing flight control system is adapted to suit the more difficult conditions in terms of control quality and damping as well as the trajectory guidance. The modifications are based on measuring data from the 300 m high Hamburg Weather Mast [6], which is used for research of the processes in the atmospheric boundary layer and is equipped with measuring equipment at various altitudes for this purpose. The recorded long-term weather data are used to estimate the expected interference effects on the LARUS aerial system. In addition to the modifications of the existing flight control, three important components will be added to the flight guidance system. These are a gust load alleviation system, an active collision avoidance and a trajectory generation. In this respect, suitable interfaces are implemented that allow integration into the current flight control system. Commands of the collision avoidance system are given preference by a decision logic and carried out immediately. After a successful avoidance maneuver, the UAS is then returned to the original route in a coordinated manner. Influences, such as a pitching moment due to the active gust load alleviation system, are also compensated by appropriate measures. Figure 3 shows the structure of the flight guidance system including the enhancements.

Fig. 3

Structure of the flight guidance system of the LARUS UAS including enhancements

Three automatic operating modes are available for use in mission scenarios. In transfer mode, the system flies at high speed on the most direct route from the base to the area of operation and back. In the search mode, the UAS activates the camera sensor that was previously switched off for energy-saving reasons and flies the search patterns specified by the control center at an appropriate speed. The search strategy to be implemented depends on the level of knowledge about the location of the accident site and the prevailing external influences. Once the scene of the accident has been found, the flight system switches to the on-site mode and continuously circles around the scene of the accident to provide the rescue forces with information about the situation and, if possible, to establish a direct communication connection with the accident victim.

4.2 Gust load alleviation system

In addition to the control-based requirements for operation in heavy weather conditions, the UAS must also be protected against structural damage due to heavy loads caused by gusts. For this reason, an active gust alleviation system (GLAS) will be developed which uses high-performance actuators. Coordinated deflecting of the flaps significantly reduces structural loads. A flush air data sensing system (FADS) will be integrated into the nose section of the UAS, which is being developed as part of the project at the Institute of Flight System Dynamics, to assess the ambient atmospheric conditions and to predict the gusts hitting the LARUS aerial system. On the basis of a differential pressure measurement, the flow vectors and effective accelerations can be identified, which are used as input variables for the gust alleviation system. The FADS was selected as sensor technology because it has no mass inertia compared to a wind vane, which makes the measurement of high-frequency flow events more comfortable and precise.

The overall system for gust load alleviation consists of sensors, a control system and actuators. In particular, the structural load at the root of the wing should be reduced due to the change of the load factor to avoid damage and, if necessary, to reduce the structural weight. Gusts cause a temporary change of lift ΔL at the flying system compared to the stationary flight, resulting in changes of the load factor, as indicated in Eq. (1) below:

$$\Delta n = \frac{L + \Delta L}{G} - 1$$

(1)

For the design of the gust load alleviation, wind data measured in real time from the Hamburg Weather Mast were again used [6]. The naturally occurring gusts have amplitudes of up to 3.8 m/s (3σ) at wind speeds of 20 m/s and above. For gust load reduction, however, the change behavior of the inflow is of utmost importance as this defines the requirements for the deflection speed of the actuators.

4.2.1 Detection with FADS

The FADS system uses the data from pressure sensors, which take the local total pressures at five positions in the nose of the UAS (see Fig. 4). Based on a calibration data set from wind tunnel tests, which are illustrated in Fig. 5 as an example, a neural network was trained in [7], which maps the measured pressure information on the inflow. This makes it possible to provide the angle of attack and the angle of sideslip as well as the inflow velocity with a sampling rate of 1 kHz during flight operation.

Fig. 4

Positions for pressure measurement in the nose (green circles)

Fig. 5

Calibration procedure of the FADS system in the FSD wind tunnel

The limits and accuracy of the calibration are summarized in the following Table 2. The accuracy is based on the assumption of a normal distribution as double standard deviation 2σ.

Table 2 Calibration parameters of the FADS [7]

4.2.2 Design of the gust load alleviation

Figure 6 shows the process sequence for the gust load reduction as a flowchart. The FADS sensor system measures the incoming air flow at the nose with high frequency. The flap deflections calculated subsequently by the controller are delayed in a timing module and passed on to the PWM generator, which commands the settings to the actuators. The time delay is required to match the temporal course of the flap deflections to the temporal course of the additional incident flow at the wing.

Fig. 6

Flow chart of the gust load alleviation process

The PWM signals are processed by high dynamic actuators that deflect the flaps, as shown in Fig. 7. It is to be expected that aerodynamic effects occur due to the highly dynamic operation of the flaps as well as the turbulent flow at the wing, which can shift the effect of gusts and flaps over time. Therefore, a correction of the time delay in a small range around the expected value is provided, so that a compensation of the named effects can be achieved. This also helps to compensate for deviations in the dead times of the individual components.

Fig. 7

Flaps utilized for the gust load alleviation system

A gust can be broken down into a longitudinal gust, a lateral gust and a vertical gust relative to the direction of flight. The longitudinal gust changes the inflow velocity U_∞. The lateral and vertical components change the angle of sideslip β and the angle of attack α.

The runtimes of the gusts to the wing as well as to the elevator result in the available reaction time for the gust load alleviation system. Figure 8 shows the reaction times for the gust load reduction at an average airspeed of 55 m/s. The available response time for the flap deflection of 16 ms is decisive; within this period of time the deflection must have taken place.

Fig. 8

Reaction times for the gust load alleviation system at an airspeed of V_A = 55 m/s

In [7], a data set of measurements from the Hamburg Weather Mast has been examined with regard to the maximum angles of incidence at LARUS UAS. These explanations are supplemented here for the estimation of the actually occurring loads taking into account the vertical movements of the flying system by a dynamic observation, which was implemented with the help of a mass point simulation. In particular, the question to be answered is which maximum deflection angles are required to achieve an effective reduction of the gust loads. This information can then be used to select suitable actuators.

The data required for the mass point simulation is shown in the following Table 3. The effectiveness of the flaps

$$\frac{{\partial C_{L} }}{\partial \kappa } = 1.48$$

(2)

was estimated according to [8].

Table 3 Parameters of the mass point simulation

The mass point simulation takes into account the changes of V_A and α due to longitudinal and vertical gusts from the wind data [6] with wind speeds of 20 m/s and above. The wind data were measured on a stationary measuring system so that the relative movement between air mass and measuring device corresponds to the measured wind speed. An aircraft which moves through this mass of air at speed V_A will be affected by gusts at a different frequency. For this reason, the sampling rate in the wind data was corrected according to Eq. (3).

$$\Delta t_{\text{new}} = \Delta t_{\text{old}} \cdot \frac{{U_{\infty } }}{{V_{\text{W}} }}$$

(3)

On the basis of the wind data and a given mean speed compared to the air mass $U_{\infty }$, the incident flow conditions are calculated as follows:

$$\alpha = \tan^{ - 1} \left( {\frac{{\dot{z} - w_{\text{w}} }}{{U_{\infty } - u_{\text{w}} }}} \right)$$

(4)

$$V_{\text{A}} = U_{\infty } - u_{\text{W}}$$

(5)

For this purpose, without any limitation of generality, it is assumed that the flight direction is along the x-axis of the wind data’s coordinate system.

The modeling includes lift

$$L = \frac{\rho }{2}V_{\text{A}}^{2} \left( {C_{L0} + C_{L\alpha } \cdot \alpha } \right)S$$

(6)

and the pulse theorem for translatory aircraft motions. To develop a disturbance variable input for the gust load reduction, the dead times of the individual system components as well as the running time of the flow from the measurement at the FADS to the wing and tailplane are also taken into account.

The gust load alleviation system is designed to deflect the flaps in such a way that changes in lift due to gusts are compensated accordingly. For this purpose, the equation for lift as a function of α and V has been linearized around the operating point [α = 0, V_A = V_A,OP]:

$$\frac{\partial L}{\partial V}|_{\alpha = 0} = \rho SC_{L0} V_{{A,{\text{OP}}}}$$

(7)

$$\frac{\partial L}{\partial \alpha } = \frac{\rho }{2}SC_{L\alpha } V_{{A,{\text{OP}}}}^{2}$$

(8)

For the effect of the flaps the correlation

$$L_{\kappa } = \frac{\rho }{2}V_{\text{A}}^{2} C_{L\kappa } \kappa S$$

(9)

is used to keep lift constant:

$$\frac{\partial L}{{\partial V_{A} }}\Delta V_{\text{A}} + \frac{\partial L}{\partial \alpha }\Delta \alpha + \frac{{\partial L_{\kappa } }}{\partial \kappa }\kappa = 0$$

(10)

The flap deflections thus determined for each measured incident flow condition are then provided with a dynamically calculated dead time in a timing module. In addition to the delays of the individual system components, which are assumed to be constant, the current measured flow velocity $U_{\infty }$ is also included in the calculation to determine the current runtime. The obtained value is then adapted to the operating frequency of the gust reduction system of 1 kHz by rounding the dead time to an accuracy of 1 ms.

During the simulated flight through the gust field with and without gust load reduction, changes in the load factor with the spread width of the Gaussian normal distribution shown in Fig. 9 occur.

Fig. 9

Change of load factor during the simulated flight trough the measured wind field

Under the ideal conditions of the simulation, the disturbances due to gusts were reduced by 92% up to 3σ and by 60% up to 6σ. In particular, reducing the gust loads from extreme events by 60% is of great importance for reducing structural loads. The decrease in the gust reduction efficiency for extreme events is due to the current limitation of flap deflections to ± 12°. However, with an extension of the flap angle range this limitation will become obsolete.

Assuming a constant distribution of lift, the reduction of the load factor can be applied directly to a reduction of the bending moments at the wing root. Based on the presented simulation results, a significant reduction of wing root moments by up to 60% is possible. If the GLAS has a sufficiently low probability of failure, this knowledge could be incorporated into the mechanical design of the structure and thus be used to reduce the mass of the flight system.

The required positioning rate for the actuators depends on the required probability with which gusts are to be compensated. Figure 10 shows the positioning rates at the flaps of the LARUS flight system at which required probabilities for compensation are needed. Assuming a normal distribution, 68% (1σ) of all gusts can be compensated with a maximum deflection rate of 9.5°/s. The maximum gusts contained in the wind data could be compensated with a deflection rate of 190°/s. This maximum value can be used to dimension the actuators.

Fig. 10

Required flap deflection rate to compensate gusts

4.3 Collision avoidance

To ensure the safe integration of the LARUS aerial system into the common airspace, it requires technical equipment to prevent collision situations. Such a collision avoidance system must be carried on board the UAS and must be fully automated to ensure that there is no danger to other manned and unmanned aircraft, even in the event of communication disruption or loss to the control center. The system must therefore have the ability to detect and analyse potential collisions with other airspace participants independently and to initiate appropriate avoidance maneuvers if necessary. The collision avoidance system must be able to detect both cooperative and non-cooperative airspace participants and, with regard to the overall take-off mass of the vehicle, with a minimum sensing mass installed. The latter either has no transponder systems or this equipment is activated on.

Due to these boundary conditions, corporative-only surveillance technologies like automatic dependent surveillance broadcast ADS-B transponders are not installed as they only cover a part of the potential threats for the UAS.

The sensor technology required for these described boundary conditions must be robust against the adverse weather conditions prevailing in the area of application, such as snow, rain, fog and darkness. In addition, the aim is to achieve the lowest possible weight and package volume as well as low electrical power consumption to be integrated into the UAS. Taking this into account, optical sensor technologies like classical electro-optical/infrared systems or lidar systems cannot cope with the above-mentioned adverse weather conditions which can occur in maritime rescue missions where the UAS will be operating [9], as they have a strong degradation in a rainy or foggy environment [10]. In addition, they do need a demanding computation power for their operation [9, 10]. Other sensing technologies like radar have been considered in bigger UAS types [9], but mostly as impulse radar systems with larger size and bigger system mass [11]. Preliminary studies have shown that the choice of a miniaturized continuous wave radar system as a possible detection sensor technology offers a promising approach to meet the requirements [12, 13] while using only microcontroller resources to compute detection results. Due to these advantages, a system concept for automated collision avoidance based on the utilization of compact modulated continuous wave radar systems is investigated within the LARUS project.

4.3.1 Characteristics of the continuous wave radar system

The LARUS aerial system is equipped with a three-dimensional modulated continuous wave radar, which is developed by the reproject partner IMST GmbH. The radar system uses four integrated patch antenna structures in monopulse configuration, composed of four smaller rectangular flat aperture antennas. The large number of the smaller aperture antennas results in a superpositioned large effective antenna area [14]. Due to this structure, the radar system is able to determine not only the detection distance of a reflecting object, but also the required directional angle in azimuth and elevation. The modular structure of the radar system is shown in Fig. 11.

Fig. 11

Composition of the utilized continuous wave radar system for LARUS

The basic characteristics of the continuous wave radar system are listed in Table 4.

Table 4 Technical data of the continuous wave radar

Regarding classic impulse radar systems like the type used in [11], the utilized sensor has a smaller detection range (2 nautical miles as described in [11] compared to 900 m) but significant lower electrical power consumption and overall sensor system mass (25 kg sensor mass [11] compared to 164 g per continuous wave radar system, which includes the signal processing and hardware interface units).

The advantage of this radar sensor type for the detection of non-cooperative airspace participants compared to other sensor technologies becomes clear when looking at the usable frequency range (framed in red) under consideration of the attenuation by the earth’s atmosphere, see Fig. 12.

Fig. 12

Attenuation of electromagnetic waves due to atmosphere and precipitation, according to [15]

The frequency band of 23.5–24.5 GHz has, in comparison to the frequency range of the visible light, a significantly lower atmospheric attenuation. In particular, the influence of water molecules in the form of different rain intensities and fog has a dampening effect on the radar system that is several orders of magnitude lower than on electro-optical sensors and lidar systems, for example, which operate typically in the frequency range of visible light.

4.3.2 Detection range and distance resolution

The functioning of a modulated continuous wave radar is based on the principle of transmitting and receiving electromagnetic waves in a spatially directed manner. A transmitter generates a pulse, which is sent out in a directed manner. If this impulse hits an object, a certain portion of the energy contained in the transmitting impulse is reflected and detected as scattering field at the receiver antennas, depending on the object properties, for example, the permittivity.

The receiver of the radar system can determine the magnitude, distance, relative angle and velocity of the detected object from the intensity of this scattering field, the propagation time between the transmitted and the received signal, the shift of the phase fronts as well as the temporal change of the phase [15, 16].

A linear ramp modulation with triangular shape is depicted as an example for the operation of a modulated continuous wave radar, see Fig. 13.

Fig. 13

Exemplary linear ramp modulation of the FMCW radar sensor prototype, according to [16]

The frequency response of the transmit signal is described by the parameters specific ramp time T and bandwidth B as a function of the selected carrier frequency f₀. According to [16], the following time-dependent progression equation applies to the ascending ramp:

$$f\left( t \right) = f_{0} - \frac{B}{2} + \frac{B}{T} \cdot t$$

(11)

Depending on the carrier frequency f₀ and a selected bandwidth B, starting at the lower limit of the selected frequency range, the frequency ramp is traversed within a running time t up to a specific ramp time T. At a descending ramp, the algebraic signs of the second and third terms of the Eq. (11) change.

After a transit time difference Δt_p, the continuous wave radar receives a temporally shifted reflection signal of the object (dashed red line in Fig. 13). This echo signal has a frequency difference ∆f₁ to the transmission signal at the time of measurement. The detection distance from the continuous wave radar R_Radar to the detected object results from the multiplication of the half transit time difference by the propagation velocity of electromagnetic waves c₀ in space:

$$R_{\text{Radar}} = \frac{{\Delta t_{p} }}{2} \cdot c_{0}$$

(12)

The transit time difference can be determined in accordance with [16] using the measured frequency difference as well as the ramp time and bandwidth at any point in time by means of Eq. (13):

$$\Delta t_{p} = \Delta f_{1} \cdot \frac{T}{B}$$

(13)

The substitution of Δt_p in Eq. (12) by Eq. (13) results in the characteristic continuous wave radar equation for the detection range R_Radar:

$$R_{\text{Radar}} = \Delta f_{1} \cdot \frac{T}{2B} \cdot c_{0}$$

(14)

Equation (14) shows that the selection of the two setting parameters ramp time and bandwidth have a direct effect on the detection range of the continuous wave radar system. If the ramp time is shorter in combination with a higher bandwidth (faster frequency change per time unit), the frequency difference must increase to detect the same slope distance. At the same time, however, the selection of the parameters influences not only the detection range but also the distance resolution of the continuous wave radar.

The range resolution ΔR indicates the minimum distance between two reflective objects where the radar system can still detect the two objects separately. Since the minimum distance is characterized by the minimum sampled frequency spacing during linear ramp modulation, this relationship can be expressed in Eq. (15), according to [16]:

$$\Delta R = \frac{{c_{0} }}{2B}$$

(15)

By selecting a high bandwidth, a better detection resolution of the environment can be achieved. At the same time, however, this leads to a lower detection range of the continuous wave radar. This diametric relationship is responsible for the fact that a compromise must be found between resolution and detection range [17].

4.3.3 Determination of object angles

In addition to the detection distance, the modulated continuous wave radar system can determine the two object angles of the reflecting object for direction finding. The functional principle is shown as an example for the azimuth object angle Ψ_Radar in the horizontal detection plane. The object angle is determined by measuring the phase shift of the reflected echo signal using two receiver antennas installed in the horizontal detection plane. The necessary geometric relations are illustrated in Fig. 14 on the basis of [18].

Fig. 14

Geometric relations to determine the azimuth object angle ψ_Radar with the utilized FMCW radar sensor [18]

The phase shift of two reflection signals can be determined according to [18] from the signal path difference Δx and the wavelength λ by means of Eq. (16):

$$\Delta \varphi_{\text{Phase}} = \frac{2\pi }{\lambda } \cdot \Delta {\text{x}}$$

(16)

Taking into account the geometric relationship between the signal path difference and the known installation distance d of the receiver antennas, the signal path difference can be expressed as a function of the installation distance.

$$\Delta x = d \cdot \sin \left( {\varPsi_{\text{Radar}} } \right)$$

(17)

Consequently, using both Eqs. (16) and (17), the desired object angle function is obtained:

$$\varPsi_{\text{Radar}} = \arcsin \left( {\frac{{\Delta \varphi_{\text{Phase}} \cdot \lambda }}{2\pi \cdot d}} \right)$$

(18)

For the determination of the elevation object angle Θ_Radar results in an analogous geometry and calculation.

4.3.4 Experimental validation of the continuous wave radar system

Within the scope of an experimental validation of the radar system, a measurement campaign was carried out in December 2016 with a previous, two-dimensional development stage of the radar system in cooperation with the police helicopter squadron of the Bavarian Police. An attempt was made to detect an EC 135 helicopter (see Fig. 15) at different distances [12, 19].

Fig. 15

The EC 135 helicopter used as reflective airspace participant

An exemplary detection is shown in Fig. 16, without any applied filter on the raw radar data. The measurement was performed with a bandwidth of 400 MHz in the frequency range 24–24.4 GHz and a ramp time of 5 ms. The detected flight trajectory of the police is highlighted by a red frame.

Fig. 16

Detection of the EC 135 helicopter with a relative distance of approx. 160 m

At first, the helicopter was facing the radar system. At the beginning of the measurements, the EC135 performed a full rotation around the vertical axis, which resulted in the measurement of the arc-shaped distance over a period of 3–14 s. Due to the helicopter’s drifting movement during this maneuver, the position shifted laterally to the radar system, increasing the distance. After the yawing maneuver, the pilot kept the relative distance to the radar system constant.

This exemplary measurement illustrates the ability of the early development stage of the radar system to detect other airspace participants without the need for filter algorithms. In further tests, a maximum detection range of 713 m has been demonstrated [12, 13].

4.3.5 Collision detection concept

The LARUS aerial system will be equipped with six radar systems, which cover a total of 360° in the horizontal plane, see Fig. 17.

Fig. 17

Horizontal coverage area of the radar systems integrated in the LARUS UAS

The all-round visibility in the plane is required because other airspace participants (e.g., an EC135 rescue helicopter [20]) can move through the airspace much faster and overtake the LARUS aerial system. A vertical coverage range of 60° is considered sufficient, as the high airspeed of the UAS and the detection range of the radar systems prevents collision scenarios in vertical direction.

The values continuously measured by the six radar sensors must be processed and analyzed by an automated detection system. For this purpose, the collision detection system needs to be capable of predicting the flight trajectories of potential collision partners based on the measured data. The calculations required for this must be carried out by efficient algorithms on board the LARUS aerial system to prevent immediate collision hazards even in the event of a communication loss to the control center. Due to the low take-off mass of the UAS, an implementation based on microcontrollers is developed. If necessary, the evaluated data can be used to initiate an evasive manoeuver adapted to the detected collision scenario. The most challenging collision scenario to be detected is where the LARUS aerial system and another aircraft will approach head on to each other. Within this scenario, both aircraft velocities will sum up to a greater relative velocity. As introduced in the scenario chapter, the LARUS UAS will support the rescue forces by locating the scene of the accident quickly, to distribute information about the situation on site, and to provide them with an efficient communication infrastructure for telemedical first aid, all in a shared airspace. Typical airspace users during those missions, which could be encountered are manned general aviation participants as well as legal authorities, for example, police as well as search and rescue helicopters or even other LARUS vehicles. Based on a survey conducted in [12] the most legal authorities in Germany use helicopters, of which the EC 135 rescue helicopter model is mostly common with a maximum cruise velocity of 259 km/h. With respect to the maximum detection range of the FMCW radar system of 900 m, a head on approach of an EC 135 and the LARUS UAS flying with maximum cruise velocity of 170 km/h will lead to an minimum time-to-go of 7.5 s. Due to this minimum reaction time a novel avoidance algorithm has to be developed, to ensure a safe and successful separation maneuver.

4.3.6 Description of the collision avoidance algorithm

The applied collision avoidance algorithm set is based on an amended and extended version of the original proportional navigation law (PN) with combined velocity commands, proposed within [12] for small tiltwing UAS.

PN guidance techniques are originally used for interceptor systems, where the homing system has a significant thrust and maneuverability surplus compared to the locked target [21]. The transfer of these guidance techniques into DAA systems customized for UAS, where the ownship has equal or less thrust but a significant maneuverability surplus compared to the potential collision threat, requires several modifications and adjustments to the original PN guidance law. To determine a collision threat, a set of heuristic safety criteria and threshold values to ensure an unambiguous collision threat warning were defined in [12]. In addition, a microcontroller executable PN-based collision avoidance controller architecture customized for small UAS is introduced in [12], which is described briefly in the following:

The fundamental mode of operation of the PN guidance law for collision avoidance presented in [12] and [13] is the execution of a commanded acceleration normal to the longitudinal velocity vector of the UAS. This acceleration command causes a rotation of the UAS ownship velocity vector and therefore initiates an arc-shaped separation maneuver around a predefined and calculated safety sphere surrounding the collision threat to prevent a collision between both airspace participants. The acceleration command can be divided into a lateral and vertical acceleration command regarding the body-fixed coordinate system of the UAS ownship. For the sake of brevity, the lateral acceleration command calculation is described in more detail, as the vertical acceleration command is acquired in a similar way, as already derived in [12]. The lateral acceleration command is only executed, if the relative velocity vector lies inside the collision cone formed by the safety sphere of the collision threat and its tangents originating from the UAS ownship (|Λxy| < |Δxy|). Figure 18 shows the geometric relationship between the LARUS aerial system and the detected collision threat in the lateral plane.

Fig. 18

Geometric relationships between intruder and the UAS regarding the geodetic and body xy-planes

To perform a sufficient and successful separation maneuver, the relative velocity vector is rotated through the lateral collision avoidance angle Ο to the nearest of the two collision cone borders, formed by the two tangents, in order that the condition (|Λxy| > |Δxy|) is satisfied. This is done through the lateral acceleration command.

$$a_{\text{cmd lateral}} = {\text{Dist}}_{\text{corr}} \cdot N_{\text{var}} \cdot \left| {\vec{v}_{{{\text{rel}} xy}} } \right| \cdot \dot{\rm O}_{\text{NAV}}$$

(19)

Compared to the classical PN navigation law presented in [23], the proposed PN command contains a variable navigation constant N_var, which has to be greater than 2 and is highly dependent on the flight performance and flight mechanical properties of the UAS ownship [12, 13]. Furthermore, a detected distance correction term Dist_corr is included in this mathematical formula to ensure an early initiation of a distinct separation maneuver against large detection distances. Both augmentations have been defined to compensate the previously addressed limited maneuverability and thrust properties of small UAS [12, 13].

The variable v_rel is the relative velocity vector between intruder and UAS ownship, $\dot{O}$ represents the time rate of change of the lateral collision avoidance angle to avoid the intruder. As shown by Fig. 18, the collision avoidance angle Ο can be calculated from the radar bearing angle ψ_Radar, the UAS ownship azimuth Ψ and the half apex angle of the collision cone Δ_xy [12, 13]. The computed lateral acceleration command is used to calculate the needed bank angle command Φ_cmd using the following equation derived from [22], where g represents the gravity constant:

$$\varPhi_{\text{cmd}} = { \arctan }\left( {\frac{{a_{\text{cmd lateral}} }}{g}} \right)$$

(20)

The corresponding heading rate command is derived from the following consideration. The flight path azimuth χ can be stated as trigonomic relation between the commanded longitudinal (u_c) and lateral (v_c) velocity of the UAS ownship [22]:

$$\chi = \arctan \left( {\frac{{v_{c} }}{{u_{c} }}} \right)$$

(21)

By calculating the derivation of Eq. (6), the corresponding heading rate results in

$$\dot{\chi } = \frac{{{\text{d}}\chi }}{{{\text{d}}t}} = \frac{{u_{c} \cdot a_{\text{cmd lateral}} - v_{c} \cdot a_{\text{cmd longitudinal}} }}{{u_{c}^{2} + v_{c}^{2} }}$$

(22)

where a_{cmd longitudinal} is a function of the UAS flight performance and flight mechanical properties of the UAS ownship and need to be empirical resolved through flight tests of the respective prototype [12, 13]. The corresponding velocity commands have to be calculated regarding the specific characteristics of the LARUS aerial system.

The superposition of the described lateral, longitudinal and vertical acceleration and velocity commands, calculated from the radar-based detection and tracking of a potential collision threat while knowing the flight characteristics of the UAS ownship, facilitates the LARUS UAS, the resolution of collision scenarios using a near-real time capable and therefore effective guidance method, which has been successfully tested on a small tiltwing UAS [12]. If a safe separation distance between the LARUS aerial system and the collision threat is obtained, a sufficient collision avoidance termination criterion must be executed for a return of controller authority from the DAA system to the navigation and guidance controller of the UAS. For this, [12, 13] defined the termination condition

$$\left| {\varLambda_{xy} } \right| > \left| {\Delta_{xy} } \right| + \Delta_{{{\text{Threshold}} xy}}$$

(23)

for the collision avoidance system. The threshold has to be derived from the known characteristics of the UAS and the utilized radar system, which is exemplarily done in [12].

4.4 Trajectory generation

The trajectories required for the automated flight are generated by use of a planning software, including the sensor system parameters and current position information, and transmitted to the UAS via a long-range communication link. The datasets are dynamically processed by the on-board flight control system and can also be adapted at a later stage to react to external influences, territorial restrictions and obstacles during flight.

For the transfer mode, a trajectory between the starting point and the application area is either created from several segments or specified as a direct connection. In the on-site mode, the UAS circles with a fixed radius around the point of interest. To find the accident site, larger areas must be searched as completely as possible. The path planning for this operating mode is therefore considerably more complex and requires the implementation of different search strategies or search patterns in flight trajectories including further input variables.

4.4.1 Search strategies

To search the area of application, the flight guidance system of the LARUS UAS must be able to implement various search strategies in the form of parametric trajectories. The International Aeronautical and Maritime Search and Rescue Manuel Vol. III [23] as well as the SAR Manual [24] list various visual search strategies for use in rescue missions with aircraft and/or watercraft, of which the most common procedures for the LARUS system are implemented. It is important to note that it is not possible to define general procedures for all searches, as these are influenced by, for example, incomplete information and changing circumstances. However, the following procedures indicate a high detection probability if used correctly [24].

4.4.1.1 Track search

The track search is an initial action if the last or planned course is known. There are two variants. In the case of the “route search without return”, the first search is carried out directly on this known course or on the opposite course. If there is no sighting, the search is repeated in the opposite direction at a distance of one width of the field of view (S) and, if the search fails again, it is repeated in the original direction on the other side of the course of origin, see Fig. 19 (I). In the “route search with return”, the original course is searched in both directions at intervals of half a field of view (1/2 s) as shown in Fig. 19 (II) [24].

Fig. 19

Schematic illustration of the track search without return (I) and with return (II) [23]

4.4.1.2 Parallel sweep search

The parallel sweep search is used when the search area is larger and the last position is only inaccurate or not known at all. The search begins with a distance of half a field of view from the defined boundary parallel to the longitudinal axis of the search area and is then carried out alternately on parallel paths with a distance of one field of view each, see Fig. 20. To achieve an even higher coverage of the search area, the course turnarounds can alternatively also take place outside the search area.

Fig. 20

Schematic illustration of parallel sweep search [23]

In the presence of a high drift intensity, the search area should be created with the longitudinal axis in the drift direction for compensation and, if necessary, the search sections should be shortened. Alternatively, the search speed can be increased if possible [24].

4.4.1.3 Creeping line search

A creeping line search is performed if the missing persons or vessel is suspected to be close to the initial course in a narrow search field. The search is then carried out in a similar way to the parallel sweep search, but orthogonal to the course at a distance of one field of view width in both directions, as shown in Fig. 21. With this method, a quick coverage of the most likely accident site can be achieved. The procedure can also be supplemented by the use of a rescue cruiser on the original route [24].

Fig. 21

Schematic illustration of creeping line search [23]

4.4.1.4 Expanding square search

The method of square search is often used when the area to be searched is relatively small and indications point to a certain position of the missing persons or vessel. Starting from this position, a quadratic spiral of single sections with the distance of one search field width S is flown. The first search section begins in the direction of the drift movement and has the length S. At the end of each section a 90° change of heading is carried out. After two sections each, the section length is extended by a search field width, so that the spiral shape shown in Fig. 22 is the result.

Fig. 22

Schematic illustration of expanding square search [23]

If the search for the first pass is unsuccessful, the procedure can be continued with a 45° offset [24].

4.4.1.5 Sector search

The sector search is used if a specific position is suspected on the basis of concrete indications. A circle with a defined radius is flown through. The flight on the opposite course is then always offset by a fixed angle, so that the search area is divided into several triangle sectors of equal size, see Fig. 23. A further run of the search area can take place with a different offset [24].

Fig. 23

Schematic illustration of sector search [23]

4.4.2 Implementation of search strategies into trajectories

A suitable search method can be selected in the trajectory planning software and a corresponding trajectory can be generated by specifying parameters. The essential input information is the position of the search area and its dimensions, defined by the indication of length L and width W or a radius R, known or suspected information about the azimuth Ψ, wind and drift directions as well as their strengths $\overrightarrow {{V_{W} }}$, $\overrightarrow {{V_{D} }}$, the flight altitude H and the speed V_A. Another particularly important and at the same time limiting parameter for planning the web distance is the search field width S, which is directly related to the performance of the camera sensors used and the prevailing ambient conditions. In the case of a normal view search, it is up to the observer to decide whether the range of vision is sufficient or whether the width of the search field must be reduced. In an automated system, reliable detection must be ensured in every situation to prevent the non-detection of an overflown accident site. Depending on the degree of the optical influencing factors (e.g., rain, daylight) and the expected size of the search targets, the flight altitude is determined, which results in the size of the sensor scanning area on the water surface. In the LARUS project, the company Opto Precision GmbH is developing a custom-made multi-spectral camera system consisting of a laser-assisted optical camera and a thermal imaging camera. The design width for the sensor search field is fixed at 120 m with a slant distance of 300 m to the object. To achieve the most complete coverage of the search area, the search field width S is selected in the trajectory calculation to be 15% smaller than the width of the sensor scanning range, so that deviations from the flight trajectories are compensated to a certain extent by an overlap of the sensor scanning ranges. The generated flight path data records are transferred directly from the software to the UAS and processed on board.

5 Future work

After completion of the conceptual work, the next steps envisage the integration of extended functional models of the gust load alleviation system and the collision avoidance system into an UAS demonstrator. Furthermore, the implementation of software algorithms for the analysis and control of these systems on microcontrollers is required. In addition, it is planned to validate the flight control algorithms in free flight. The planning software for trajectories will be implemented in the next instance for use on PC and mobile devices.