Abstract
The aim of this research is the identification of a unified bookkeeping and evaluation scheme for the integrated performance analysis of a boundary layer ingesting (BLI) concept in the conceptual design phase. A thorough review and classification of existing performance bookkeeping schemes suits as a basis for the derivation of a bookkeeping scheme suitable for the initial sizing as well as detailed design analysis during the conceptual phase of a BLI concept. Figures of merit for the concept performance assessment are evaluated with regard to the requirements of aircraft multidisciplinary conceptual design. Based on the survey, the most practical integral momentum conservation approach is deduced and its application to integrated conceptual sizing and a subsequent design analysis is evaluated. The proposed scheme is universally applicable to coupled airframe–propulsion aircraft concepts, compatible with standard aircraft and propulsion system sizing tools and, under certain assumptions, deployable for low- and high-fidelity evaluation methods. Finally, several figures of merit are selected to cover a range of design aspects in the BLI evaluation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Targeting the exploitation of thus far unused vehicular efficiency benefits, aircraft concepts with a more closely coupled propulsion–airframe integration have gained much attention in the recent past. In particular, the utilization of the wake-filling or boundary layer ingestion (BLI) principle is a strong lever for overall vehicular efficiency gains. The impact mechanisms of BLI on an aircraft’s aerodynamic performance include a reduction of excess kinetic energy in the aircraft wake and a reduced nacelle (and pylon) wetted area, while inlet distortion has a negative impact on the fan efficiency. At aircraft level, additional effects on aircraft component weights as well as design cascade effects contribute to the fuel burn effects of BLI propulsion integration. Especially concepts featuring a full annular propulsor enjoy popularity. As the fuselage accounts for a big portion of the aircraft’s drag, the wake-filling potential of a fuselage propulsor is promising. Furthermore, the integration of a single fuselage propulsor on a conventional tube and wing aircraft is potentially feasible in the near future.
Exemplary aircraft configurations include the boundary layer ingesting aft fuselage fan concept “Fuse Fan” by NASA [1], the Bauhaus Luftfahrt “Propulsive Fuselage” [2], the propulsive fuselage concepts investigated in the projects “DisPURSAL” [3] and “CENTRELINE” [4], the EADS/AGI “VoltAir” [5], the Boeing “SUGAR Freeze” [6], NASA “STARC-ABL” [7, 8], and the embedded BLI configurations “SAX-40” [9], “Claire Liner” [10], “D8” [11] and the “N3-X” (BWB) [12].
The assessment of the fuel burn reduction potential of such unconventional aircraft configurations and the evaluation of their characteristics compared to conventional integration paradigm requires compliance with common control volumes, standards and definitions. However, BLI concepts feature a more closely integrated propulsion system and, thus, exhibit a high level of coupling between airframe aerodynamics and propulsion system characteristics. In case of aft–fuselage propulsion system integration, a strong mutual coupling between the fuselage flow field and surface pressure distribution and the internal aerodynamic performance of the BLI propulsor exists.
A distinct definition of drag and thrust terms based on well-established practices in aircraft and engine drag/thrust bookkeeping, such as the widely accepted definitions proposed by the MIDAP Study Group in 1979 [13] is thus challenging: due to the strong aerodynamic coupling of airframe and propulsion system aerodynamics in a BLI propulsion arrangement, classic simplifications allowing for a direct relation between the aerodynamic forces acting on the individual component of the airframe and propulsion system and their corresponding individual drag shares do not apply.
Many studies investigate the potential of BLI based on different bookkeeping schemes that are derived for specific configurations and particular objectives. Approaches are developed and adapted, for example, to determine the potential of BLI as a propulsion system [14,15,16] or as an integrated aircraft concept in comparison to conventional aircraft [17, 18]. Most of the existing schemes are applicable only to a small range of configurations and under specific assumptions and simplifications. However, to allow for a fair comparison of different BLI concepts, a unified bookkeeping approach is necessary. Furthermore, especially during the stages of a multidisciplinary conceptual aircraft design, different tools and methods are applied at an increasing level of flow resolution. Therefore, a consistent sizing and performance analysis and a comparison with conventional concepts require the application of a unified bookkeeping scheme, which is applicable to the very first initial integrated sizing studies as well as a more detailed design analysis allowing for the identification of improvement potentials (cf. [13]).
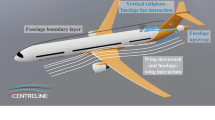
In the following, existing bookkeeping schemes and figures of merit for the performance evaluation of BLI concepts are reviewed and evaluated. In accordance with derived requirements, a unified bookkeeping scheme is developed and discussed with the use case of the multidisciplinary conceptual design analysis of the CENTRELINE propulsive fuselage concept [4] (cf. Fig. 1; Sect. 4.1.2).
2 Review and categorization of performance bookkeeping schemes
The first approach to categorize bookkeeping schemes applied to BLI configurations was pursued by Hendricks in 2018 [19]. Hendricks reviewed modeling approaches and performance metrics for the assessment of different BLI concepts at NASA. Due to the existence of several different approaches even within one institution, he established the need for a unified modeling approach. Hendricks categorized the approaches by the type of model used for the representation of the propulsion system and vehicle aerodynamics and the degree of coupling (interaction) of the two disciplines [19]. As an alternative to Hendrick’s categorization, a categorization of bookkeeping schemes by conserved quantity and control volume approach will be deduced in the following.
In case of the classic separation of airframe and propulsion system, a variety of bookkeeping schemes employ momentum conservation on a body-centered control volume. From Newton’s second law of motion, which states that the impulse of a force \( F \) affects a change of momentum \( {\text{d}}I \) to a specified mass (here: a fixed control volume) during a time interval \( {\text{d}}t \), the momentum conservation equation can be derived in its integral form:
The first term on the left-hand side of the equation identifies the instantaneous change of momentum inside the control volume (zero for steady flow); the second term is the momentum efflux across the control volume boundaries. The right-hand side of the equation equals the sum of pressure and viscous force integrated over the surfaces of the control volume and the body forces acting on the fluid inside the control volume. To determine forces on a closed body, e.g., an aircraft, control surfaces can run over the body’s surface (near field surface) or be situated in the far field of the body (far field surface). In either case, forces are calculated from an integration of flow characteristics over control volume boundaries.
Examples of momentum conservation application for drag calculation include the determination of drag components from wake properties or from the evaluation of body forces (e.g., [20, 21]). As the application of computational fluid dynamics (CFD) increased in popularity, further drag prediction methods were derived from momentum conservation. Paparone and Tognaccini, for example, proposed the application of entropy volume integration to calculate wave and viscous drag contributions of two-dimensional flow CFD results [22].
The traditional drag/thrust bookkeeping scheme, which is widely used for propulsion system performance assessment, today, was introduced by the MIDAP Study Group in 1979 [13]. Making use of a momentum conservation approach, it is based on a decoupled flow assessment of propulsion system and airframe through predefined control volumes. The airflow, which enters the propulsion system, is evaluated independently from the external flow associated with the airframe. BLI configurations, however, feature a strong coupling between propulsion system and airframe, which leads to a more complex definition of thrust, drag and force terms.
Thus, the need for a holistic bookkeeping scheme, which is easily and universally applicable to the evaluation of unconventional aircraft configurations has grown significantly. The introduction of the power balance method by Drela in 2009, a tailor-made method for the evaluation of highly coupled airframe–propulsion configurations, has added a new point of view on bookkeeping. Instead of the traditional force-based calculation of drag and thrust, the benefit of BLI is measured by an integrated propulsion power [17]. Drela’s method is widely applied in BLI concept studies featuring a trailing edge propulsor in the MIT and NASA D8 projects, at the Delft University of Technology and sparsely in similar projects [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41].
In 2014, Arntz introduced an advancement of the power balance method [42]. The exergy balance method is similar to the power balance method, but instead of kinetic energy, it is based on the conservation of kinetic exergy within a defined control volume. It has mostly been applied to BLI concepts at the French Aerospace Lab Onera and at Safran Aircraft Engines [43,44,45,46].
The following classification of aircraft bookkeeping schemes and figures of merit is the result of a comprehensive literature review. In general, all methods are based on the integration of conserved quantities in a control volume. Methods that are based on the integral momentum conservation are differentiated from methods based on the integral kinetic energy or total energy conservation. The methods might either be applied to a control volume in which parts of the control volume boundary run over the model surface (body perspective) or a control volume in which the aircraft is located inside a closed volume surrounding the model. In this case, all control volume boundary surfaces are situated in the aircraft’s far field (fluid flow perspective) [21]. Most approaches apply a body perspective, excluding some integral momentum conservation methodologies [47,48,49,50,51]. It is found that methods based on integral momentum conservation are utilized for either the evaluation of uninstalled propulsion systems without a coupling of aerodynamic and propulsion system effects related to BLI, or, the assessment of propulsion system and airframe as a joint system. In contrast, power balance as well as exergy balance methods based on the volume integration of the kinetic energy equation (dot product of momentum equation and velocity vector) or exergy equation always consider bi-directional aero-propulsive effects (cf. Fig. 2).
2.1 Integral momentum methods
For the application of the integral momentum approach, two main strategies are identified—the assessment of the uninstalled propulsion system and the holistic view, which takes into account the bi-directional impact of BLI on aerodynamics and propulsion system performance. Some of the latter approaches examine the performance from a fluid flow perspective, but most follow an approach from a body perspective. Fluid flow-centered control volume methods mostly use streamtubes surrounding the whole airframe or the propulsion system, with an inlet upstream of the fuselage nose/engine inlet and an outlet far downstream of the fuselage trailing edge/engine exit. The scheme was successfully applied for a detailed drag calculation of conventional aircraft from downstream wake properties, proving to be suitable for the physical breakdown of drag into pressure, viscous, lift-induced and wave drag based on experimental and numerical data and the performance assessment of conventional airframe–propulsion systems [20, 21, 52].
Smith performed the first holistic investigation of a wake ingestion concept in 1993 and identified the benefit of unducted wake ingestion concepts [47]. In the years following Smith, the BLI propulsion system performance was often described by a reduction of the ram drag, i.e., a momentum flux reduction in the engine inlet streamtube. Rodriguez evaluated unducted and ducted propulsor performance, based on ram drag reduction, reduced pressure recovery and total aircraft drag with inner and outer control volumes [48]. Following similar principles, Daggett et al. investigated in the benefit of a BLI propulsion system for a BWB configuration in terms of a reduction of (momentum) ram drag and inlet pressure recovery. The theories are based on the assumption that the total drag of the aircraft is identical for the non-BLI and BLI configurations, however, for a BLI aircraft, the propulsor ram drag is reduced due to the reduced momentum inflow. Thus, the net thrust for the BLI and non-BLI configurations is identical, but the gross thrust of the BLI configuration is reduced [53, 54]. Elmiligui et al. used a control volume with far field boundaries for the calculation of the wake drag coefficient for wind tunnel test and Euler and Navier–Stokes CFD simulation of an airship, a BLI airship, and a propelled and an unpropelled Goldschmied propulsor [55]. The BLI benefit was identified as the power savings of a configuration with net axial force equaling zero compared to reference power required while neglecting the inlet ram drag [49]. Wiart et al. applied a post-processing method based on a far field drag evaluation (corrected by near field drag results) to CFD for a performance analysis of the BLI NOVA configuration [50]. The same configuration was later analyzed by the use of the power saving coefficient [49]. Within the “DisPURSAL” project, the net axial force acting on the fuselage was evaluated considering coupled aero-propulsive effects [56, 57]. Lundbladh et al. focused on the potential penalty of an efficient engine design on aircraft performance due to the nacelle design. Drag and thrust were derived from surface force evaluations [58].
Detailed assessments of BLI concepts first studied the performance of uninstalled propulsion systems. The evaluation of the uninstalled propulsion system is inherently uncoupled, as it does not take the interaction between airframe and propulsion system into account. Smith’s theoretical method was extended and applied by Plas et al. for the “Silent Aircraft” Concept in 2006 [49, 50]. Hardin et al. applied the flow properties of the airframe at engine inlet and exit and took into account the impact of the airframe flow field on the engine performance ignoring the impact of the engine and nacelle on the airframe [16]. A different approach was followed in the investigation of the NASA N3-X BWB. The so-called internal volume method decouples airframe and propulsion system and assesses the propulsion system without accounting for ingested drag. The control volume inlet properties are equal to the boundary layer mass-averaged values. Therefore, the method requires the properties of the propulsion system inlet boundary layer to be known [51, 59, 60]. Goldberg et al. assessed the same concept by means of a net propulsive force (NPF) (cf. Sect. 3.2) [61, 62]. Lee et al. performed the quasi-2D design and optimization of NASA STARC-ABL’s full annular tail cone propulsor through a momentum analysis of the uninstalled propulsor. It was based on the assumption that the decoupling of airframe, inlet and nacelle from the propulsor design resulted in only a minor error [63, 64].
Following a more coupled approach, Gray et al. applied drag and thrust accounting in a multidisciplinary, fully coupled analysis of the same configuration. They evaluated the performance of the installed system. Drag and thrust were calculated as net forces integrated over aircraft and propulsion system surfaces, respectively. The overall net force in axial direction was determined as the sum of the integrated pressure and viscous forces over all body surfaces and the pressure and momentum flux contributions on the fan face and fan exit [65,66,67,68]. In a similar manner, Ordaz et al. carried out an adjoint-based numerical design and optimization of BLI concepts (NASA STARC-ABL and MTA450—business jet with aft fan) with the objective of minimized flow distortion at the propulsor [69, 70].
The application of bookkeeping schemes based on integral momentum conservation, in particular Smith’s advances on the wake-filling effect, is important to understand the fundamental principles of boundary layer ingestion. The direct integration of stresses on a body’s surface might be the most straightforward approach from an engineer’s perspective. For a conventional engine installation, the total force on the aircraft can be easily broken down into pressure and friction drag [46]. This method is often applied when the flow field is resolved by CFD. The calculation of forces on the aircraft allows consistence with the traditional multidisciplinary aircraft design, which is based on a drag and thrust force definition. However, momentum conservation approaches are often limited to a propulsion system perspective due to the underlying assumptions and simplifications. The influence of the propulsion system on the incident flow characteristics is often neglected, thus, the bi-directional influence of airframe aerodynamics and propulsion system performance is uncoupled. A consistent bookkeeping approach based on integral momentum conservation which captures all coupled effects of BLI might be able to close the gap between traditional conceptual aircraft design paradigm and the benefit evaluation of unconventional propulsion–airframe integration.
2.2 Integral energy methods
In contrast to the integral momentum methods, the power balance and exergy balance methods are based on an integral energy conservation approach from a fluid flow perspective.
2.2.1 Power balance method
In 2009, Drela approached the challenge of evaluating aircraft with BLI from a different perspective. He proposed a method, which analyzes the kinetic energy conservation equation inside a defined control volume and incorporates the coupling effect of propulsion system and aerodynamics. The approach relies on the principle that inside the wake system of the propelled aircraft, wake energy is conserved. The wake energy is the sum of the kinetic wake energy, which is deposited in the Trefftz plane and the energy, which is dissipated inside the wake region. Following this approach, the sum of the global kinetic energy satisfies the energy conservation for a finite control volume [30]. The integration of the mechanical (kinetic) energy equation over the control volume boundaries yields the power balance equation:
The terms on the left side of the equation represent the total mechanical power supply, production and inflow in the defined control volume (net propulsor shaft power \( P_{\text{S}} \), net pressure volume \( P_{\text{V}} \) and net propulsor mechanical energy flow rate into the control volume \( P_{\text{K}} \)). The terms on the right equal the total mechanical power consumption and outflow due to physical processes, which are taking place inside the control volume (viscous dissipation rate \( \varPhi \) i.e., rate at which kinetic energy is converted into heat inside of the control volume and the mechanical energy flow rate out of the volume \( \dot{\varepsilon } \)). A detailed explanation of the terms can be found in [17]. The volume integration of the time-averaged mass continuity equation over the control volume (CV) yields the integral mass equation. The analog integration of the time-averaged momentum equation yields the integral momentum equation. Both equations are used in Drela’s method only to simplify the results of the power balance equation [17].
In recent years, the power balance method has been employed multiple times to evaluate the benefit of different BLI configurations. Sato derived an integral mechanical energy defect equation from the power balance method and applied the power balance method to a BLI concept with a propulsor installed behind the trailing edge of the fuselage [36]. Pandya et al. applied the power balance method by integration over a control volume around a propulsor. The boundaries of the control volume are the inflow and outflow planes of the propulsor. They explained the benefit of a BLI configuration by making use of the power balance approach in the following way: from the law of energy conservation, it is derived that the power supplied by the propulsor (i.e., the mechanical flow power) equals the total viscous dissipation in the fluid flow, which in turn equals the entropy generation in the control volume. In case of BLI, a part of entropy generation associated with wake mixing is eliminated, because a part of the wake is ingested by the propulsor. Therefore, the propulsor shaft power can be reduced, compared to a conventional podded engine, while the rest of the configuration stays the same [34]. Lv et al. [32] used the power balance method to experimentally analyze power conversion processes and quantify the different powers of a boundary layer ingesting propulsor placed in the wake behind a body. The control volume incorporates the wake-ingesting propeller, thus, capturing the influence of the propeller on the body through the change in the inlet conditions of the control volume. As a result, they identified two physical mechanisms, which are mainly responsible for the shaft power reduction: the power within the body wake, which is used as a power input for the propeller and the reduction of the power within the downstream wake of the propeller. In addition, the approach was applied to the evaluation of several BLI configurations with fuselage trailing edge propulsors at MIT, Georgia Tech, NASA and TU Delft [23,24,25,26, 29, 35, 37,38,39,40,41, 43].
The power balance method is a useful method for analyzing the potential benefit of a BLI configuration compared to a non-BLI reference aircraft as a whole. An application of the original method as described by Drela requires a detailed knowledge of the flow field characteristics, which can be extracted from CFD simulations or wind tunnel experiments. The optimization of components as part of a conceptual aircraft design, however, proves to be difficult: The derivation of force, drag or thrust terms on which conventional design tools are based, requires the application of a number of simplifications and approximations (cf. Sects. 3.3, 4.3.5–4.3.7). To the knowledge of the authors, until the publication of this review, the method has only been applied to the conceptual design of BLI configurations under the assumption that the propulsor was placed at the trailing edge of the fuselage.
2.2.2 Exergy balance method
Arntz built on an ongoing trend to use exergy-based analyses for aircraft performance assessment. The exergy balance method, which he proposed in 2014, provided a consistent system-level framework for complex aircraft systems [18]. The motivation for the development of the method was to provide a post-processing tool for high-fidelity CFD–RANS simulations, which are conducted in the preliminary aircraft design phase of sub- and transonic, commercial aircraft. It is based on a combination of momentum balance and first and second law of thermodynamics. It describes the exergyFootnote 1 supply by the propulsion system and its partial destruction within the control volume, which is associated with the mechanical equilibrium of the aircraft. The control volume is thermodynamically open, therefore, the exchange of mass, work and heat with surrounding flow across boundaries is possible [43]. Analog to the power balance method, there is no distinction between thrust and drag, but the aircraft’s performance is assessed from an exergy performance point of view. However, in addition to the mechanical energy, the thermal energy is taken into account, allowing for a more global approach to the aero–thermo-propulsive performance assessment, which includes the growing importance of aircraft thermal management. The application of the exergy balance method aims at the identification of a configuration with minimum waste and destruction of energy, which therefore requires the least propulsive energy to compensate for the energy losses [42,43,44, 71].
The method was applied in the framework of Arntz’s dissertation at ONERA and recently at Safran Aircraft Engines. Applications include several unpowered airframe CFD solutions [45], an academic case of a propulsor situated downstream of a fuselage trailing edge, ingesting 100% of the aircraft wake [44], a simplified (2D) BWB with BLI [46] and the heat exchanger integration on an aircraft [18]. Furthermore, the accuracy and robustness of the exergy method was validated against two momentum-based methods and wind tunnel data provided by the AIAA drag prediction workshop of the unpowered NASA Common Research Model [46]. More applications include the thermodynamic CFD investigation of a turbofan exhaust mixer [71], an extension of the method for a numerical blade performance assessment [72] and its application to the BLI “Nautilius” concept [73].
Similar to the power balance method, the exergy balance method requires a detailed resolution of the studied flow field. Hence, the original method by Arntz is only applicable to CFD results or highly resolved wind tunnel results with the aid of customized flow field evaluation tools and therefore not suitable for the conceptual design phase (cf. Sect. 4.3.8).
3 Review of figures of merit for boundary layer and wake ingestion benefit evaluation
All bookkeeping schemes applied to BLI concepts are accompanied by figures of merit. These figures are employed to quantify the performance benefit of the assessed configurations. The figures of merit that are reviewed are selected according to the authors’ best judgement and are not exhaustive. For an easy understanding of their definitions, traditional power and propulsion efficiency terms as well as drag, thrust and force definitions are presented in the following.
The system efficiency terms commonly used in propulsion performance calculation include the core or energy conversion efficiency \( \eta_{\text{ec}} \), transmission efficiency \( \eta_{\text{tr}} \) and the propulsive efficiency \( \eta_{\text{p}} \) with the product of those three constituting the overall efficiency \( \eta_{\text{ov}} \) (cf. e.g., [74]).
The propulsive efficiency relates the useful power output \( P_{\text{thrust}} \) to the propulsive power \( P_{\text{P}} \).
The thrust power needed for an aircraft to maintain steady level flight under given atmospheric conditions is defined as power required:
For conventional aircraft featuring under-wing engines, the drag and thrust definition seems to be clearly defined. However, for BLI conforming with existing conceptual design tools is more difficult. In compliance with the publication by the MIDAP Study Group in 1979 [13], drag is defined as the difference of integrated surface forces in a real (viscous) flow and the potential flow buoyancy for the same body. For a whole body, the potential flow buoyancy equals zero. Thus, the drag of a body equals its sum of integrated skin friction and pressure forces over the whole body surface. However, if only a part of a body is considered, the potential flow buoyancy cannot be neglected. Drag terms can only be calculated if the characteristics of the same body parts in potential flow are known.
3.1 Power saving coefficient and propulsive efficiency
In 1993, Smith introduced a non-dimensional power saving coefficient (PSC) as a figure of merit for the propulsion benefit of unducted, axisymmetric fans with BLI (compared to a reference non-BLI configuration) [47]. The figure of merit is based on a body-centered evaluation of the momentum conservation equation (cf. Fig. 3). It is defined as the ratio of the propulsive power difference for non-BLI and BLI configuration to the propulsive power required to propel the body when the wake is not ingested (non-BLI):
CV adapted from Smith [47] to calculate PSC and \( \eta_{{{\text{P}},{\text{in}}}} \) (propulsor nacelle is not accounted for)
For propellers with wake ingestion it is derived that the PSC is a function of the fluid density \( \rho \), upstream and downstream freestream velocities \( v_{0} \) and \( v_{j} \), the upstream and downstream wake velocities \( v_{w} \) and \( v_{jw} \), the wake momentum area \( \theta \) and the propulsor disk diameter \( \delta_{\text{P}} : \)
To differentiate between airframe drag and propulsion thrust effects of BLI, Smith calculates drag from wake properties by an analysis of a CV boundary in the far field of the airframe:
The thrust for a propulsor with wake ingestion is also a function of fluid, propulsor and wake properties.
Smith derived an additional figure of merit. Under the assumption of incompressibility, the definition of the propulsive efficiency with wake ingestion as a function of disk loading \( \frac{{v_{j} }}{{v_{0} }} \), the pseudoenergy factor \( K \), and the wake recovery \( R \) is the same for cases with and without wake ingestionFootnote 2:
Substituting drag, thrust, recovery and pseudoenergy factor and assuming that \( v_{j}^{'} = v_{0} \) yields:
To investigate the benefits of the embedded, axisymmetric BLI concept study “Silent Aircraft” SAX40, Smith’s PSC was applied as a figure of merit and the propulsive efficiency formula was extended to compressible flow cases under the assumption that the changes in nacelle drag can be neglected [75]. Plas et al. made use of the propulsive efficiency definition of Smith (Eq. 10) in conjunction with the integral momentum equation and the propulsive kinetic energy equation to derive a general definition of the propulsive efficiency, which is valid for compressible flow conditions:
The propulsive efficiency is a function of boundary layer integral properties and the ratio of ingested drag to total aircraft drag. The energy factor \( H^{*} \) is derived from a first estimation of the boundary layer profile. \( \beta \) is the ratio of uningested drag to ingested drag [75]. In an abstract definition, the propulsive efficiency is the ratio of useful power to available mechanical power. However, as the propulsive efficiency can be greater than unity,Footnote 3 this figure of merit does not measure the amount of energy, which is lost. Therefore, Plas rather applies the PSC as a figure of merit to compare BLI and non-BLI propulsion systems [76].
3.2 Thrust benefit and net propulsive force
The integration over the body surfaces offers the possibility for the calculation of axial net forces and, thus, allows for a component-based description and assessment of the aircraft (e.g., [57]).
Kim and Felder used the “internal volume” method, in which the boundary layer properties are mapped to the inlet of a control volume inside the propulsion system. They evaluated the propulsion system benefit using the non-dimensional thrust-specific fuel consumption benefit as well as the thrust benefit, which is the percentage in increased net thrust of a BLI propulsion system compared to a propulsion system in free stream without total pressure loss ahead of the inlet [15]. The thrust benefit is defined as:
Goldberg et al. [61] applied the net propulsive force (NPF) as a figure of merit to evaluate the performance of a BLI propulsion system at the concept design phase. Instead of using the net thrust as a definition for the thrust produced by the propulsion system, the integration aspects of the system are included in the figure of merit. As introduced by the MIDAP Study Group in 1979 [13], the NPF based on force accounting can be defined as the difference of intrinsic net thrust (gross thrust \( F_{{{\text{G}}9}} \) minus the force that acts on the propulsor inlet \( F_{{{\text{G}}1}} \)) and the nacelle force the sum of gross thrust, the force that acts on the propulsor inlet and the nacelle force \( \varPhi_{\text{Nacelle}} \):
In Goldberg et al.’s approach, only a portion of the airframe propulsion drag (the airframe, which lies up to approximately twice the inlet height ahead of the propulsor highlight (i), cf. Fig. 4), is accounted for, to simplify the calculation while taking into account the effect of the BLI system on the airframe drag [61]. This leads to the following definition of the NPF:
\( \tau_{\text{w}} S_{\text{wet}} \) is the skin friction drag from the wetted surface area of the airframe [63]. In addition to the NPF, Goldberg et al. made use of ingested drag as well as propulsive efficiency (performance and efficiency of propulsion system) and PSC (benefit of propulsion system as a whole) to evaluate the BLI benefit from different perspectives [61]. In further research, the method was applied to the N3-X BWB concept [61, 62, 73].
CV adapted from Goldberg et al. [62] to calculate the NPF
3.3 Mechanical flow power, power-based propulsive efficiency and power saving coefficient
The power balance method uses the mechanical flow power (the power, which is required to balance all dissipation sources in the flow field) as the figure of merit to describe the benefit of a particular aircraft configuration. When applied to BLI, the benefit of a configuration can thus be described as a reduction of dissipation in the flow [17]:
Hall et al. [26, 27] applied the power balance method to a ducted BLI configuration in which the whole propulsion system is simplified by a single propulsor installed at the trailing edge of the fuselage. Their approach is based on a formulation of the power balance method applied to a control volume in the manner of Fig. 5:
as well as the following assumptions:
CV for the application of the power balance method adapted from Drela [17]
Volumetric flow power negligible for low-speed flows (assumption valid for compressible flow, cf. [38])
Constant mass flow
Steady (turbulent) flow
Trefftz plane far downstream of the propulsor to ensure that the flow is mixed to freestream conditions
Surface dissipation almost unaffected by the propulsor, because the propulsor is positioned at the trailing edge of the fuselage
Surface dissipation of nacelle surface is neglected, i.e., nacelle drag is neglected
Propulsor has no effect on spanwise lift distribution and mixing of trailing vorticity far downstream
Thin shear layer approximation of constant static pressure across the shear layer
Freestream static pressure just downstream of the propulsor
Subsequently, the following equations for the power balance and mechanical flow power in terms of non-BLI profile and total drag are derived by Hall et al.:
In this case, \( f_{\text{BLI}} \) is a function of kinetic energy defect at the propulsor inlet and the kinetic energy defect at the trailing edge of the fuselage and \( f_{\text{wake}} \) is a function of bare fuselage wake and surface dissipation. \( D^{\prime\prime} \) and \( D^{\prime\prime}_{\text{p}} \) account for total and profile drag of the reference, non-BLI configuration. For cruise conditions (steady-state, level flight), the net streamwise force simplifies to \( F_{x} = 0 \), thus, the decrease of the mechanical flow power \( P_{\text{K}} \) serves as a key figure of merit for the aircraft energy consumption and as a surrogate for the fuel consumption to evaluate the BLI benefit [26].
Additionally, under the assumption of a uniform jet velocity, Hall et al. derived a new definition for the propulsive efficiency for BLI and non-BLI configurations in steady, level flight, based on power terms:
They showed that the reduction of mechanical flow power with BLI depends highly on the amount of ingested boundary layer and the mass flow through the propulsor. Two main fuel consumption benefits for BLI were identified: the reduced wake dissipation (reduced airframe required propulsive power) and the reduced jet dissipation, which results in an increased propulsive efficiency. Thus, the aerodynamic performance is not suitable as a figure of merit on its own.
As traditional aircraft performance and sizing methods, which are used in the early conceptual phase, ground on drag and thrust values as input variables, the application of the power balance method is not straightforward. Thus, Marien et al. adapted the method proposed by Hall et al. [26] to translate the power balance equation into drag and thrust terms (Eq. 18) [33]. When applied to a BLI concept in cruise with the propulsor installed at the trailing edge of the fuselage, all necessary terms for the BLI benefit evaluation can be determined from the total drag and the profile drag of the isolated fuselage, an estimation or calculation from a detailed aerodynamics analysis from, e.g., CFD results and results from a propulsion system design tool [33]. This approach allows to adapt the power balance method to traditional conceptual aircraft sizing tools.
The method described by Hall et al. was applied to the D8 double-bubble concept by Yutko et al. [41]. Additionally, the lift-to-drag ratio as a figure of merit of external aerodynamic performance was defined based on lift, freestream velocity as well as surface, wake, wave and vortex dissipation terms:
Blumenthal [23] and Blumenthal et al. [24] used the power balance method for an investigation of propulsive and aerodynamic benefits of an unducted BLI system installed at the trailing edge of the fuselage of the common research model with CFD. They used the definition of the net propulsor mechanical energy flow rate into the control volume \( P_{\text{K}} \) to define a net propulsor power coefficient
The coefficient was employed to express the aerodynamic benefit in terms of a “power balance saving coefficient”:
A comparison of BLI configuration to non-BLI configuration was achieved by constraining the net axial force coefficient to zero. The net force coefficient is the difference of thrust coefficient and drag coefficient, whereas the drag coefficient is defined as the sum of all force components in streamwise direction on all solid surfaces and the thrust coefficient is the sum of the forces on inlet and exit plane of the propulsor [23]:
3.4 Exergy recovery coefficient
To evaluate the aero-thermal propulsion performance of aircraft, Arntz introduced the exergy recovery coefficient applied to the control volume pictured in Fig. 6 [18]. The exergy recovery coefficient represents the efficiency of the exergy recovery by the application of BLI:
CV for the application of the exergy balance method adapted from Arntz [18]
The figure of merit is based on the following assumptions:
Compressible and viscous fluid
Mean steady flow
Flow with energy supply from propulsion system and via heat transfer at the surface of the aircraft
4 Evaluation of figures of merit in the conceptual design context
In the following, requirements for the application of figures of merit during the conceptual design are established. Based on them, the figures of merit presented in Sect. 3 are assessed.
4.1 Requirements during aircraft conceptual design
Certain requirements for the selection of sensible figures of merit derive from the multidisciplinary evaluation of aircraft configurations during the conceptual design phase. They are presented in the following.
4.1.1 General requirements
Product life cycle costs (LCC) are strongly associated with the impact of design decisions. At early stages of the product development, such as the conceptual design phase, significant shares of the overall program costs are determined. Roskam indicates typical LCC shares at different design stages [77, 78]. Approximately two-thirds (65%) of the aircraft LCC are defined during the feasibility phase, increasing to 85% during the concept phase. Further optimization of conventional systems design and even much more critically, the analysis and optimization of unconventional systems design triggered by novel technologies increases the complexity of design decision making dramatically. As a result, key requirements for modeling and simulation activities in the aircraft conceptual design phase can be identified. Especially for unconventional configurations, it is necessary to rapidly gain knowledge on the system behavior in the early stages of the system design. Therefore, rapid design space explorations are conducted, which rely on fast-responding design and analysis methods and a highly efficient human machine interfacing. An efficient handling of system complexity is required, in particular when novel or highly integrated systems design is involved, such as BLI or wake-filling propulsion integration. This requirement asks for an efficient, task-oriented problem decomposition capability (cf. e.g., 79]) and the integration of detailed component or subsystem design aspects into full parametric multidisciplinary studies for a multidisciplinary design analysis and optimization. As analysis tools and methods change with the progress of the design, flexibility in the incorporation (i.e., problem-oriented interchangeability) of low- and high-fidelity analysis including semi-empirical and physics-based methods is required. Throughout the conceptual design phase, the methods applied must be capable of increasing robustness and improving confidence whenever technical decisions take place. Furthermore, in projects involving multiple partners and stakeholders, it is of importance to ensure a multi-partner inter-disciplinary data exchange and knowledge management.
4.1.2 The CENTRELINE configuration
The physical nature of the BLI concept developed within the CENTRELINE project leads to additional requirements. The concept under study is a full annular propulsor. The fan plane is located upstream of the fuselage trailing edge with a non-negligible aft body present. Following a fuel burn optimum, the BLI propulsion device is not sized to ingest the entire boundary layer momentum deficit. The reference aircraft is based on a commercial wing-and-tube configuration similar to an advanced conventional reference aircraft for EIS 2035 (R2035) featuring 340 PAX at 6500 nm design range and transonic flight conditions at M0.82 (i.e., compressible fluid) [4].
4.2 Detailed assessment of the figures of merit
To evaluate the applicability of the figures of merit presented in Sect. 3 to the conceptual design, they were assessed in a detailed rating. Two main criteria were evaluated: the degree of universality of the figure of merit, and the applicability to the conceptual design phase. The former describes the applicability of the figure of merit to a diverse range of configurations and flight conditions, the latter is a combination of requirements derived from Sect. 4.1. The two main categories are comprised of eight or ten sub-criteria, respectively. The sub-criteria are presented in Table 1.
Each figure of merit was rated for all criteria on a given scale ([0 or1] for degree of universality criteria; [0–3] for application criteria) based on the authors’ judgment. The individual criteria were given intuitive weighting with regard to their individually expected relevance to the assessment. To gauge the robustness of the assessment of these intuitive criteria weightings, synthetic weighting scenarios were defined following the method described by Mistree et al. [80]: criteria weightings were systematically varied with a robustness factor of 5, i.e., the weighting of one sub-criterion is set to 5, while all others are kept at 1. The standard deviation of the robustness analysis was determined, reflecting the dependency of the results on the chosen weighting criteria. The detailed quantitative rating results can be found in “Rating of figures of merit” in “Appendix”, and the consolidated results of the assessment are pictured in Fig. 7. The figures of merit based on energy and exergy conservation show the highest degree of universality, but a low applicability to the concept phase. The figures of merit, which evaluate the uninstalled propulsion system only, show an inherent low degree of universality at a high degree of applicability to the conceptual design phase. The figures of merit proposed by Smith can only be applied to some specific BLI configurations, leading to a medium degree of universality. The general propulsive efficiency, however, is applicable to almost all configurations if detailed information about the boundary layer properties is available.
4.3 Discussion of the figures of merit with respect to aircraft conceptual design
In conjunction with the rating of the figures of merit presented in Sect. 4.2, some aspects of their applicability and limitations with respect to the specific requirements of the aircraft conceptual design phase are highlighted in the following.
4.3.1 Power saving coefficient and propulsive efficiency by Smith
The PSC is suitable as a first indicator for fuel savings when comparing a BLI concept against a non-BLI concept. The calculation of the PSC with the simple power definition can be performed by use of standard propulsion system sizing tools. However, when strictly applied as described by Smith, it is only valid for unducted, axisymmetric BLI concepts and incompressible flow. The effect of the propulsor performance on the non-uniformity of the inlet flow is captured only implicitly. When applying the figure of merit to the conceptual design, it is necessary to make some estimations on the applied boundary layer properties or employ initial CFD results. Drag and thrust terms are calculated individually, assuring compatibility with typical aircraft conceptual design methods.
4.3.2 General propulsive efficiency by Plas et al.
In contrast to Smith’s definition, ducted propulsors and compressible flow can be described with the general propulsive efficiency definition by Plas et al. However, the propulsive efficiency can only capture the effect of BLI on the propulsion system, the impact on the airframe aerodynamic, such as changes in nacelle and fuselage drag, are not considered. The downstream flow is assumed to have uniform velocity (ideal BLI). Again, boundary layer properties at the fan face have to be resolved in detail (e.g., by CFD) to calculate the defined “uningested drag”.
4.3.3 Thrust benefit by Kim and Felder
The internal volume method captures the influence of the boundary layer on the propulsion system performance. Yet, it does not consider the reverse effect of the installed propulsion system on the boundary layer at the fan face. The required net thrust can be derived by the application of a standard propulsion system sizing tool. Similar to other momentum conservation-based methods, wave drag effects and the impact of the propulsor upstream interaction effects with the aircraft surface cannot be captured.
4.3.4 Net propulsive force by Goldberg et al.
The influence of the boundary layer on the performance of the propulsion system is not directly taken into account, as the propulsor intake and fan efficiency losses due to the flow distortion cannot be represented in a direct manner. First estimations of the non-dimensional propulsion system characteristics are the result of a standard propulsion system sizing tool. Skin friction and nacelle drag can be determined by use of a semi-empirical method. Similar to the thrust benefit, the application of the net propulsive force requires little pre-processing time and effort and has a fast response time. Overall, it shows high agreement to the conceptual design requirements.
4.3.5 Propulsor mechanical flow power by Drela
The power balance method in general allows to distinguish the quantities, which influence the power requirements the most. Relevant physical mechanisms can be identified and the dissipation terms capture interference and build-up drag better than force based methods [17]. For its application, it is not necessary to define thrust and drag terms, which is especially useful for complex and coupled configurations such as BLI. However, in a multidisciplinary concept design with standard sizing tools, it is useful to account for drag and thrust. Additionally, even though the problem of drag and thrust bookkeeping is addressed, the power balance method requires the modeling of the propulsion–aerodynamic coupling to a certain degree to ensure the capturing of multidisciplinary interactions [63]. Furthermore, it is difficult to evaluate the propulsion system and airframe design independently, as is the case during a part of the conventional conceptual design phase. During the conceptual design, design values may change frequently. As detailed knowledge of the configuration is needed to apply the power balance method, the multidisciplinary analysis of a number of configurations is time consuming [61, 62]. Until now, the method has only been applied to cases in which the propulsor was placed at the trailing edge of the fuselage. An application of the method to the CENTRELINE concept (propulsor fan face at ~ 93% of the fuselage length) under assumptions stated in literature [17, 25, 26, 35, 38] yields some difficulties when intending to apply the power balance method during the multidisciplinary conceptual phase. To account for the interaction of the jet with the surface aerodynamics, several assumptions have to be made. Unlike Hall et al.’s derivation, when nacelle and aft body drag (fuselage behind propulsor exit) are taken into account, it is in this case not possible to express the power balance formulation in terms of drag and thrust. Furthermore, a detailed resolution of the kinetic energy defect from boundary layer and wake properties would have to be undertaken.
4.3.6 Power balance power saving coefficient by Blumenthal et al.
The aim of Blumenthal et al. is to show that the application of BLI shows a benefit for the configuration performance. Thus, they do not intend to optimize the configuration. The power balance method is here applied to evaluate the benefit of the overall configuration, instead of the different components. Therefore, the power saving coefficient based on the power balance approach is neither very suitable for conceptual sizing (a detailed resolution of the flow field is required) nor design analysis (little information about the component potential can be gained).
4.3.7 Power definition of the propulsive efficiency by Hall et al.
In contrast to the definition of propulsive efficiency by Smith, or Plas et al., this definition does not require the calculation of drag and thrust terms. Furthermore, the propulsive efficiency cannot exceed unity, because the jet dissipation is always positive. The figure of merit is successfully applied to CFD results. The propulsor mechanical flow power is the result of an integration of properties over the propulsor inlet and outlet planes, while the net stream wise force is the sum of integrated pressure and viscous forces on the fuselage surface and the axial momentum flux across propulsor inlet and outlet planes. The non-BLI dissipation is gained from additional CFD results for an isolated fuselage. When applied to wind tunnel experiments, forces are not measured, only the propulsor power is of interest. Either pressure field, velocity magnitudes and flow directions are numerically integrated at propulsor inlet and outlet to determine the mechanical flow power directly or the electrical power supplied to the motor as well as motor and fan efficiencies are measured to calculate the mechanical flow power indirectly.
4.3.8 Exergy recovery coefficient by Arntz
The exergy method was developed to evaluate the aircraft performance in the preliminary design phase. Thus, to apply the exergy evaluation to a configuration, it is necessary to resolve the flow field in detail. Local properties such as local entropy or enthalpy are needed to calculate exergy terms. Until now, the method has been used only through an application of a post-processing tool to RANS CFD simulation results and it has not been traced back to drag and thrust terms. Arntz states that “Additional developments are likely to be required before the approach can be readily adopted by aircraft designers, however, chances are good that it would fit traditional aircraft performance indicators” [42].
5 Recommendation for the aircraft conceptual design of BLI concepts
A bookkeeping scheme deemed to be best suited for the multidisciplinary analysis of a propulsive fuselage aircraft concept is developed and the selected figures of merit are presented.
5.1 Recommended bookkeeping scheme
A practical bookkeeping scheme does not only have to conform with the requirements stated in Sect. 4.1, but also has to align with following general requirements stated by the MIDAP Study Group in 1979 [13]:
- 1.
“It must be free from ambiguity”
- 2.
“It must, so far as possible, provide for the separate study of engine and airframe performance […], both in preliminary paper projects and in any subsequent model and/or flight testing”
- 3.
“It must include clear definition of the interfaces where engine and airframe responsibilities meet, and facilitate a proper understanding of any zones where responsibilities overlap”
- 4.
“It must assist in planning model and flight testing in such a way as to provide the information required for design and performance evaluation at minimum total cost.” (component-wise testing: airframe model, intake, nozzle, engine test bed)
- 5.
“It must recognize practical limitations in experimental and theoretical techniques”
A thorough review of existing bookkeeping methods with respect to the early conceptual phase, in which hundreds or thousands of alternative aircraft designs need to be evaluated in a short period of time to find the best and balanced solution, leads to the following conclusion. A universally applicable bookkeeping method is required, which allows for a rapid response, multidisciplinary initial sizing as well as local design analysis.
Based on an integral momentum approach and taking into account the approach described by Seitz and Gologan [57, 81], a bookkeeping scheme is developed, which meets the requirements stated in Sect. 4.1 as well as the requirements for a practical bookkeeping scheme defined by the MIDAP Study Group. As the forces on wing and empennage are expected to have secondary effects on the potential BLI benefit, the focus is on a 2D axisymmetric fuselage–ropulsor configuration. The control volume definition is pictured in Fig. 8.
Momentum is conserved across a control volume, which includes boundaries along the body’s surface, as it allows for the computation of defined forces on the aircraft in coherence with a number of multidisciplinary aircraft sizing tools. The proposed bookkeeping scheme is based on a force bookkeeping in accordance with the definition by the MIDAP Study Group (cf. Sect. 3). Net thrust is defined as the sum of fan disk force and integrated surface forces occurring within the propulsion system between station 0 and 8.
The overall control volume CV 0 is subdivided into five interfacing control volumes. They are chosen in such a way that all parameters of interest can be calculated with a momentum conservation approach. The inlet flow properties of Cv 1 and 3 equal freestream conditions (index 0). The outlet of CV 5 is located at the trailing edge of the fuselage. The interface of Cv 1 and 3 is the propulsion system streamtube contour. The streamtube contour is assumed to approximately follow the fuselage contour from the propulsor inlet upstream until the leading edge of the fuselage. CV 4 aligns with the surfaces of the propulsor duct. The disk force \( F_{\text{Disk}} \) is the propulsor force calculated from rotor inlet to stator outlet (thermodynamic stages 2 and 13), i.e., already including the polytropic stage efficiency \( \eta_{\text{pol,fan}} \). Aerodynamic forces acting outside of the propulsion streamtube are part of the airframe force bookkeeping. Therefore, the nacelle force term includes all aerodynamic forces acting on the nacelle outside the propulsion system streamtube.
Applying momentum conservation to the proposed bookkeeping scheme yields the following equation for the total momentum efflux from the overall control volume CV 0 (cf. in “Momentum conservation application” in “Appendix”, Eq. (37):
\( F_{\text{p,in,CV1}} + F_{\text{p,in,CV3}} - F_{\text{p,out,CV5}} \) is the sum of axial pressure forces acting on the overall control volume. \( \dot{I}_{\text{in,CV1}} + \dot{I}_{\text{in,CV3}} \) is the inlet momentum flow. \( F_{\text{Disk}} \) is the disk force between station 2 and 13. Each surface force term represents the sum of pressure and skin friction force of a certain component in streamwise direction. \( F_{\text{Duct}} \) is the sum of force components acting on the tip and hub contour within the duct, \( F_{\text{nacelle}} \) is the external nacelle force, \( F_{\text{Fuselage}} \) is the force acting on the fuselage upstream of the propulsor inlet and \( F_{\text{aftbody}} \) is the force on the fuselage contour downstream of the propulsor outlet.
Figure 9 pictures the application of the momentum conservation approach to the exemplary CV 4, which incorporates the propulsion system duct. The inlet properties are the result of an evaluation of the propulsion system streamtube (CV 3) in conformation with the traditional propulsion system bookkeeping approach. All forces acting on the CV are fully resolved, ensuring compatibility with existing sizing tools.
The presented approach can be applied universally to the different phases of the conceptual design. During the initial sizing, approximations and assumptions are implied, to assure a rapid response, multidisciplinary analysis of many configurations. In this stage, the evaluation of the configuration is based on low-fidelity tools and semi-empirical methods. When applied to the design analysis, which aims at the identification of optimization potential of the different components, the low-fidelity methods are replaced partially or fully by high-fidelity CFD or experimental testing results to allow for a component-based force analysis. The degree of coupling of the scheme simply depends on the applied analysis methods/tools.
For the initial sizing in the CENTRELINE project, the following, conservative assumptions are applied. The suction effect of the propulsor on the flow profile shape in front of the inlet is small for different power settings (cf. [26]). Therefore, a representative boundary layer profile (from literature or a singular CFD analysis) near the propulsor inlet is used, which does not change in shape along the fuselage contour. From initial CFD simulations conducted within the CENTRELINE project, it is known that due to the aerodynamic interaction of fuselage and fuselage fan nacelle the total force (sum of viscous pressure and skin friction force) of the fuselage in front of the propulsor inlet can be smaller for a powered fuselage propulsor compared to the bare/isolated fuselage (no propulsor present). Thus, the assumption that the force of the front fuselage is equal for both cases is conservative. For practical reasons, it is assumed that only a certain amount of the boundary layer is ingested by the propulsor, never the whole boundary layer or more. The static pressure is assumed to be constant in radial direction of the boundary layer. The static pressure within the boundary layer is assumed to equal the fuselage surface static pressure. Under the assumption of a slender body, the boundary layer profile is evaluated normal to the x-axis instead of normal to the body surface. In all cases, the body contours (fuselage, duct, nacelle, aft body) are assumed to be streamlined, without any separation occurring. The static pressure over the aft body surface equals the static pressure at the propulsor exit. This assumption was tested by an evaluation of CFD results within the CENTRELINE project. It was found that the difference in pressure force of the aft body under the constant static pressure assumption compared to the CFD pressure distribution is only ~ 3%. Furthermore, the jet is assumed to expand between propulsor outlet and fuselage trailing edge. For simplification, the interaction of the fuselage boundary layer with the external nacelle aerodynamics is neglected. This is deemed as a conservative assumption, since under boundary layer flow conditions, the dynamic pressure of the external nacelle force is reduced. Semi-empirical methods are employed to calculate the viscous and pressure drag on the bare PFC body including its fuselage and nacelle surfaces corrected by potential pressure forces where applicable. A standard propulsion system performance tool (here: BHL in-house code APSS [74, 81]) is used to calculate propulsor and flow properties within the duct such as disk force, jet velocity and static pressure.
When applying semi-empirical methods during the initial sizing, the coupling of airframe forces and propulsion system performance is captured only partially. The influence of the presence of the boundary layer, which builds up along the fuselage contour, on the propulsion performance is captured through the application of a control volume around the propulsion system streamtube. Similar to traditional propulsion system bookkeeping schemes, wake mixing downstream the fuselage trailing edge is neglected. Under realistic design assumptions, the wake dissipation is reduced through the application of BLI. Hall et al. derived that the wake dissipation for BLI configurations is a linear function of the wake dissipation of the reference non-BLI configuration and the ratio of the kinetic energy defect at the propulsor inlet to the total airframe surface dissipation (boundary layer fraction) [35]. The error, which is made due to neglecting the wake dissipation reduction thus, scales linearly with the amount of ingested boundary layer. The more the boundary layer is ingested, the higher the error [26]. Neglecting wake dissipation is therefore a conservative assumption. The effect of the nacelle design on the overall performance is indirectly included through the change of nacelle external surface area. For a reference design point, the boundary layer profile at the propulsor inlet is evaluated through the application of CFD. However, the change in shape for different designs cannot be represented. The effect of the duct design on the performance can be evaluated when its properties are captured by a fully resolved CFD analysis.
For reasons of consistency, it is suggested to use the presented method in all parts of the conceptual design phase. However, at an advanced design stage, when CFD results as well as experimental results are generated to conduct few, but thorough design iterations, it is also possible to apply the power balance method. In this way, a more detailed knowledge about the BLI performance benefit can be gained and the wake dissipation reduction effect of the configuration can be investigated. A tailored approach for the power balance method applied to the CENTRELINE BLI configuration was derived and will be evaluated against the presented method in future work.
5.2 Applied figures of merit
As concluded in Sect. 4.2, there is no universal figure of merit, which is able to describe any configuration and any flow properties, while being easily applicable to the requirements of the conceptual design phase. Therefore, it is suggested to apply different figures of merit, when investigating the various facets of the BLI performance benefit.
Rearranging Eq. (26) yields the following expression for the bare net axial force, which is the resulting force of all forces acting on the bare aircraft surface, i.e., the total effective net force acting on the fuselage propulsor configuration without wing, empennage, etc.:
From the presented definition arises the need to design propulsor and fuselage jointly. The bare BLI efficiency factor relates the product of bare net axial force and flight velocity (i.e., the net useful propulsive power) to the expended propulsor shaft power \( {\text{P}}_{\text{S}} \), which allows an initial inter-comparison of alternative conceptual designs:
A comparative evaluation of the BLI system-level benefit (comparison of BLI to reference non-BLI configuration) from a propulsion system standpoint is convenient for the application of the power saving coefficient in its fundamental formulation:
The figure of merit is applicable to a variety of configurations and for all degrees of flow resolution.
Another important indicator for the wake-filling potential of BLI aircraft configurations is the so-called ingested drag ratio. It relates the sum of forces due to non-ideal freestream total pressure recovery incorporated in the propulsion system streamtube (CV 3) to the aircraft total net thrust requirement in the non-wake-filling reference case, \( F_{\text{N,REF}} \).
Lastly, the results from the simplified, 2D axisymmetric analysis of the BLI propulsion system are incorporated in the integrated, multidisciplinary aircraft sizing. The comparison of different BLI configurations with each other and the evaluation of the BLI benefit compared to a reference, non-BLI configuration, on aircraft level can be achieved through the application of the energy specific air range, introduced by Seitz et al. [74]. The ESAR measures the change of aircraft range, \( R \), per change of energy, \( E \), in the system. It is an aircraft-level figure of merit, which considers sizing effects, such as the effect of the propulsor design on aircraft component masses:
\( \eta_{\text{ov}} \) is defined as the instantaneous overall efficiency of the propulsion system as defined in Eq. (3), \( m_{\text{A/C}} \times g \) is the instantaneous aircraft weight force and \( L /D \) is the lift-to-drag ratio.
For practical purposes, the bare BLI efficiency factor \( f_{{\eta ,{\text{BLI, bare}}}} \) can be applied during the initial sizing to compare different BLI designs with each other. The BLI benefit of each configuration on propulsion system level can be described by the power saving coefficient, while the so-called ingested drag ratio quantifies the wake-filling potential of the configuration. To evaluate the BLI benefit on an integrated aircraft level, the energy-specific air range ESAR can be employed.
6 Conclusion
In this paper, bookkeeping schemes and figures of merit, which are used to evaluate the benefit of BLI and wake-filling aircraft concepts, have been reviewed and assessed with a focus on the conceptual sizing and design analysis. Based on the findings, a unified bookkeeping scheme following a body-centered integral momentum conservation approach was derived. Its application to integrated conceptual sizing and a subsequent design analysis was evaluated and limitations were considered. The application of several figures of merit, which cover a range of design aspects, was suggested. The proposed scheme is universally applicable to coupled airframe–propulsion aircraft concepts, compatible with standard aircraft and propulsion system sizing tools and, under certain assumptions, deployable for low- and high-fidelity evaluation methods, such as semi-empirical methods as well as CFD or physical testing results.
Notes
The part of the energy, which is (theoretically) fully convertible into mechanical work, the “useful” part of the energy.
The propulsive efficiency defined by Smith is denoted as incompressible (in) to distinguish it from the following definition by Plas et al.
Assume that β approaches 0 for full boundary layer ingestion and H* approaches 1 for a specific boundary layer profile shape, then ηp → 2.
Abbreviations
- β (–):
-
Ratio of uningested to ingested drag
- δ (m2):
-
Wake area
- δ* (m2):
-
Wake displacement area
- \( \dot{\varepsilon } \) (W):
-
Mechanical energy outflow rate
- ηov (–):
-
Overall efficiency
- ηP (–):
-
Propulsive efficiency
- ηth (–):
-
Thermal efficiency
- θ (m2):
-
Wake momentum area
- ρ (kg/m3):
-
Fluid density
- τw (Pa):
-
Skin shear stress on a surface
- Φ (W):
-
Dissipation
- A (m2):
-
Propulsor disk area
- cX (–):
-
Coefficient
- D (N):
-
Drag
- F (N):
-
Force
- H (–):
-
Shape factor
- H* (–):
-
Energy factor
- \( \dot{I} \) (N):
-
Momentum flow
- K (–):
-
Pseudoenergy factor
- P (W):
-
Power
- PK (W):
-
Net propulsor mechanical energy inflow rate
- PP (W):
-
Propulsive power
- PS (W):
-
Net propulsor shaft power
- PV (W):
-
Net pressure volume power
- Q (Pa):
-
Dynamic pressure
- R (–):
-
Wake recovery
- Swet (m2):
-
Wetted area
- T (N):
-
Thrust
- V (m/s):
-
Velocity
- V (m3):
-
Volume
- 0:
-
Far upstream, in freestream
- A:
-
Available
- J:
-
In far downstream jet
- P:
-
At propulsor disk
- P:
-
Profile, pressure
- R:
-
Required
- Rev:
-
Reversible
- w:
-
In the wake
- x:
-
In freestream direction
- ‘:
-
Wake not ingested by propulsor
- “:
-
Isolated fuselage
- REF:
-
Reference
- BLI:
-
Boundary layer ingestion
- CFD:
-
Computational fluid dynamics
- CV:
-
Control volume
- ERC:
-
Exergy recovery coefficient
- ESAR:
-
Energy specific air range
- LCC:
-
Life cycle costs
- NPF:
-
Net propulsive force
- PSC:
-
Power saving coefficient
- TB:
-
Thrust benefit
References
Bolonkin, A.: A high efficiency fuselage propeller (‘Fusefan’) for subsonic aircraft. In: World Aviation Conference, San Francisco, CA, October 19–21 (1999)
Steiner, H.-J., Seitz, A., Wieczorek, K. et al.: Multi-disciplinary design and feasibility study of distributed propulsion systems. In: 28th International Congress of the Aeronautical Sciences, Brisbane, Australia (2012)
Isikveren, A., Seitz, A., Bijewitz, J., et al.: Distributed propulsion and ultra-high by-pass rotor study at aircraft level. Aeronaut. J. 119(1221), 1327–1376 (2015)
Seitz, A., Peter, F., Bijewitz, J. et al.: Concept validation study for fuselage wake-filling propulsion integration. In: 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, September 9–14 (2018)
Stückl, S., van Toor, J., Lobentanzer, H.: VoltAir—the all electric propulsion concept platform—a vision for atmospheric friendly flight. In: 28th Congress of the International Council of the Aeronautical Sciences, Brisbane, Australia, September 23–28 (2012)
Bradley, M.K., Droney, C.K.: Subsonic ultra green aircraft research phase II: N + 4 advanced concept development. NASA/CR-2012-217556. Prepared for Langley Research Center. Hampton, Virginia (2012)
Welstead, J., Felder, J.L.: Conceptual design of a single-aisle turboelectric commercial transport with fuselage boundary layer ingestion. In: 54th AIAA Aerospace Sciences Meeting, San Diego, CA, January 4–8 (2016)
Welstead, J., Felder, J., Guynn, M. et al.: Overview of the NASA STARC-ABL (Rev. B) advanced concept. Presentation (2018)
de la Rosa, E., Hall C., Crichton D.: Special session—towards a silent aircraft challenges in the silent aircraft engine design. In: 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January 8–11 (2007)
Seitz, A.: Flugzeugantriebssystem. German Patent DE200810024463, Issued 2008 (2008)
Drela, M.: Development of the D8 transport configuration. In: 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, June 27–30 (2011)
Armstrong, M.J., Ross, C.A., Blackwelder, M.J., et al.: Trade studies for NASA N3-X turboelectric distributed propulsion system electrical power system architecture. SAE Int. J. Aerosp. 5(2012-01-2163), 325–336 (2012)
MIDAP Study Group: Guide to in-flight thrust measurement of turbojets and fan engines. AGARDograph No. 237 (1979)
Giles, M.B., Cummings, R.M.: Wake integration for three-dimensional flowfield computations: theoretical development. J. Aircr. 36, 2 (1999)
Kim, H., Felder, J.: Control volume analysis of boundary layer ingesting propulsion systems with or without shock wave ahead of the inlet. In: 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, Florida, January 4–7 (2011)
Hardin, L., Tillman, G., Sharma, O. et al.: Aircraft system study of boundary layer ingesting propulsion. In: 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Atlanta, Georgia, July 30–August 1 (2012)
Drela, M.: Power Balance in Aerodynamic Flows. AIAA J. 47(7), 1761–1771 (2009)
Arntz, A.: Civil aircraft aero-thermo-propulsive performance assessment by an exergy analysis of high-fidelity CFD–RANS flow solutions. Dissertation, Universite de Lille (2014)
Hendricks, E.S.: A review of boundary layer ingestion modeling approaches for use in conceptual design. NASA/TM-2018-219926 (2018)
Méheut, M., Bailly, D.: Drag-breakdown methods from wake measurements. AIAA J. 46(4), 847–862 (2008)
van Dam, C.P.: Recent experience with different methods of drag prediction. Prog. Aerosp. Sci. 35(8), 751–798 (1999)
Paparone, L., Tognaccini, R.: Computational fluid dynamics-based drag prediction and decomposition. AIAA J. 41(9), 1647–1657 (2003)
Blumenthal, B.T.: Computational investigation of a boundary layer ingestion propulsion system for the common research model. Master Thesis, The Pennsylvania State University, Department of Aerospace Engineering (2016)
Blumenthal, B.T., Elmiligui, A.A., Geiselhart, K.A. et al.: Computational investigation of a boundary-layer ingesting propulsion system for the common research model. In: AIAA AVIATION Forum, Washington, D.C., USA, June 13–17 (2016)
Gladin, J.C.: Sizing and vehicle matching methodology for boundary layer ingesting propulsion systems. Dissertation, Georgia Institute of Technology (2015)
Hall, D.K., Huang, A.C., Uranga, A., et al.: Boundary layer ingestion propulsion benefit for transport aircraft. J. Propuls. Power 33(5), 1118–1129 (2017)
Hall, D.K., Dowdle, A., Gonzalez, J. et al.: Assessment of a boundary layer ingesting turboelectric aircraft configuration using signomial programming. In: AIAA AVIATION Forum. Atlanta, Georgia, USA, June 25–29 (2018)
Hartuç, T.: Boundary layer ingestion: theoretical and experimental research. Master’s Thesis. Delft University of Technology, Delft, The Netherlands (2015)
Lieu, M.K.: Quantification of the boundary layer ingestion benefit for the D8-series aircraft using a pressure rake system. Master Thesis, MIT, Department of Aeronautics and Astronautics (2015)
Lv, P., Rao, A.G.: Conceptual Analysis of Boundary Layer Ingestion towards aircraft propulsion integration. In: 21st International Symposium on Air Breathing Engines, Busan, Korea, September 9–13 (2013)
Lv, P., Rao, A.G., Ragni, D., Veldhuis, L.: Performance analysis of wake and boundary-layer ingestion for aircraft design. J. Aircraft 53(5), 1517–1526 (2016)
Lv, P., Ragni, D., Hartuc, T., et al.: Experimental investigation of the flow mechanisms associated with a wake-ingesting propulsor. AIAA J. 55(4), 1332–1342 (2017)
Marien, T.V., Welstead, J.R., Jones, S.M.: Vehicle level system impact of boundary layer ingestion for the NASA D8 concept aircraft. In: AIAA SciTech Forum, Kissimmee, Florida, January 8–12 (2018)
Pandya, S.A., Huang, A., Uranga, A. et al.: Computational assessment of the boundary layer ingesting nacelle design of the D8 aircraft. In: AIAA SciTech Forum, National Harbour, Maryland, January 13–17 (2014)
Sands, J., Gladin, J.C., Kestner, B. et al.: Hybrid wing body engine cycle design exploration for boundary layer ingesting (BLI) propulsion systems under design uncertainty. In: 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Atlanta, Georgia, July 30–August 1 (2012)
Sato, S.: The Power Balance Method For Aerodynamic Performance Assessment. Dissertation, MIT, Department of Aeronautics and Astronautics (2012)
Uranga, A., Drela, M., Greitzer, E. et al.: Preliminary experimental assessment of the boundary layer ingestion benefit for the D8 aircraft. In: 52nd AIAA Aerospace Sciences Meeting, National Harbor, Maryland, January 13–17 (2014)
Uranga, A., Drela, M., Greitzer, E.M., et al.: Boundary layer ingestion benefit of the D8 transport aircraft. AIAA J. 55(11), 3693–3708 (2017)
Uranga, A., Drela, M., Hall, D.K., et al.: Analysis of the aerodynamic benefit from boundary layer ingestion for transport aircraft. AIAA J. 56(11), 4271–4281 (2018)
Weed, P.A.: Hybrid wing-body aircraft noise and performance assessment. Master Thesis, MIT, Department of Aeronautics and Astronautics (2010)
Yutko, B.M., Titchener, N., Chambers, J.T. et al.: Conceptual design of a D8 commercial aircraft. In: AIAA AVIATION Forum, Denver, Colorado, June 5–9 (2017)
Arntz, A., Atinault, O., Merlen, A.: Exergy-based formulation for aircraft aeropropulsive performance assessment: theoretical development. AIAA J. 53(6), 1–38 (2014)
Arntz, A., Atinault, O., Destarac, D. et al.: Exergy-based aircraft aeropropulsive performance assessment: CFD application to boundary layer ingestion. In: 32nd AIAA Applied Aerodynamics Conference, Atlanta, USA, June 16–20 (2014b)
Arntz, A., Atinault, O., Destarac, D.: Numerical airframe aerodynamic performance prediction: an exergy point of view. In: 49th International Symposium of Applied Aerodynamics, Lille, France, March 24–26 (2014c)
Arntz, A., Atinault, O.: Exergy-based performance assessment of a blended wing-body with boundary-layer ingestion. AIAA J. 53(12), 3766–3776 (2015)
Arntz, A., Hue, D.: Exergy-based performance assessment of the NASA common research model. AIAA J. 54(1), 88–100 (2016)
Smith, L.H.: Wake ingestion propulsion benefit. J. Propuls. Power 9, 1 (1993)
Rodriguez, D.L.: A multidisciplinary optimization method for designing boundary layer ingesting inlets. Dissertation, Stanford University, Department of Aeronautics and Astronautics (2001)
Elmiligui, A.A., Fredericks, W.J., Guynn, M.D. et al.: Numerical investigation of a fuselage boundary layer ingestion propulsion concept. AIAA (2013)
Wiart, L., Atinault, O., Paluch, B. et al.: Development of NOVA aircraft configurations for large engine integration studies. In: AIAA AVIATION Forum, Dallas, Texas, June 22–25 (2015)
Wiart, L., Atinault, O., Bonifac, J.-C. et al.: Aeropropulsive performance analysis of the NOVA configurations. In: 30th Congress of the International Council of the Aeronautical Sciences, Daejeon, Korea, September 26–29 (2016)
McLean, D.: Understanding Aerodynamics: Arguing from the Real Physics. Wiley, West Sussex (2013)
Daggett, D.L., Kawai, R., Friedman, D.: Blended Wing Body Systems Studies: Boundary Layer Ingestion Inlets with Active Flow Control. NASA (2003)
Kawai, R., Friedman, D., Serrano, L.: Blended Wing Body (BWB) Boundary Layer Ingestion (BLI) Inlet Configuration and System Studies. NASA (2006)
Goldschmied, F.R.: A theoretical aerodynamic analysis of a boundary layer controlled airship hull. Goodyear Aircraft Report GER-6251 (1954)
Bijewitz, J., Seitz, A., Isikveren, A., et al.: Multi-disciplinary design investigation of propulsive fuselage aircraft concepts. Aircraft Eng. Aerosp. Technol. Int. J. 88(2), 257–267 (2016)
Seitz, A., Gologan, C.: Parametric design studies for propulsive fuselage aircraft concepts. CEAS Aeronaut. J. 6(1), 69–82 (2015)
Lundbladh, A., Martensson, H., Petrusson, A. et al.: Installation effects for ultra-high bypass engines. In: 23rd ISABE Conference, Manchester, UK, September 3–8 (2017)
Valencia, E., Nalianda, D., Laskaridis, P., et al.: Methodology to assess the performance of an aircraft concept with distributed propulsion and boundary layer ingestion using a parametric of merit approach. J. Aerosp. Eng. 229(4), 682–693 (2014)
Valencia, E., Laskaridis, P., Singh, R., et al.: Review of the investigation of innovative propulsion system architectures for aircraft. Rev. Polit. 35, 3 (2015)
Goldberg, C., Nalianda, D., MacManus, D. et al.: Installed performance assessment of a boundary layer ingesting distributed propulsion system at design point. In: 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, July 25–27 (2016)
Goldberg, C., Nalianda, D., Laskaridis, P. et al.: Performance assessment of a boundary layer ingesting distributed propulsion system at off-design. In: 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, July 10–12 (2017a)
Lee, B.J., Liou, M.-F., Liou, M.-S.: Conceptual aerodynamic design of a tail-cone thruster system under axi-symmetric inlet distortion. In: Proceedings of ASME Turbo Expo 2018, Oslo, Norway (2018a)
Lee, B.J., Liou, M.-F., Liou, M.-S.: Aerodynamic conceptual design of boundary layer ingestion propulsor systems. Proceedings of ASME Turbo Expo 2018, Oslo, Norway (2018b)
Gray, J.S., Mader, C.A., Kenway, G.K., et al.: Approach to modeling boundary layer ingestion using a fully coupled propulsion-RANS model. In: 58th AIAA/ASCE/AHS/ASC Structure, Structural Dynamics, and Materials Conference, Grapevine, TX, January 9–13 (2017a)
Gray, J.S., Mader, C.A., Kenway, G.K., et al.: Modeling boundary layer ingestion using a coupled aeropropulsive analysis. J. Aircr. 55(3), 1191–1199 (2017)
Gray, J.S., Kenway, G.K., Mader, C.A. et al.: Aeropropulsive design optimization of a turboelectric boundary layer ingestion propulsion system. In: AIAA AVIATION Forum, Atlanta, Georgia, USA, June 25–29 (2018)
Gray, J.S., Martins, J.R.R.A.: Coupled aeropropulsive design optimisation of a boundary-layer ingestion propulsor. Aeronaut. J. 20, 1–17 (2018)
Ordaz, I., Rallabhandi, S.K., Nielsen, E.J. et al.: Mitigation of engine inlet distortion through adjoint-based design. In: 35th AIAA Applied Aerodynamics Conference, Denver, CO, June 5–9 (2017)
Ordaz, I.: Aero-propulsion analysis and design framework. In: Presented at the Propulsion-Airframe Integration Technical Interchange Meeting, Cleveland, Ohio, May 30–31 (2018)
Couilleaux, A., Arntz, A.: Exergy analysis for a CFD-based turbofan exhaust miser performance improvement. In: 53rd 3AF International Conference on Applied Aerodynamics, Salon-de-Provence, France, March 26–28 (2018)
Tailliez, C., Arntz, A.: CFD Assessment of the use of exergy analysis for losses identification in turbomachines flows. In: 53rd 3AF International Conference on Applied Aerodynamics, Salon-de-Provence, France, March 26–28 (2018)
Wiart, L., Negulescu, C.: Exploration of the airbus “Nautilius” engine integration concept. In: 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, September 9–14 (2018)
Seitz, A., Schmitz, O., Isikveren, A.T. et al.: Electrically powered propulsion: comparison and contrast to gas turbines. In: 61. Deutscher Luft- und Raumfahrtkongress, Berlin, DE, September 10–12 (2012)
Plas, A.P., Sargeant, M.A., Crichton, D. et al.: Performance of a boundary layer ingesting (BLI) propulsion system. In: 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January 8–11 (2007)
Plas, A.: Performance of a BLI propulsion system. Master Thesis, MIT, Department of Aeronautics and Astronautics (2006)
Roskam, J.: Airplane Design, Part VIII: Airplane Cost Estimation: Design, Development, Manufacturing and Operating. Design, Analysis and Research Corporation (DARcorporation), Lawrence (2003)
Swift, K., Booker, J.: Process Selection—From Design to Manufacture. Butterworth-Heinemann Publications, Oxford (2003)
Sobieski, J.: Multidisciplinary system optimization by linear decomposition. In: Recent Experiences in Multidisciplinary Analysis and Optimization Symposium held at NASA Langley Research Center, Hampton, Virginia, pp 343–366. NASACP-2327, Part I (1984)
Mistree, F., Lewis, K., Stonis, L.: Selection in the conceptual design of aircraft. In: 5th Symposium on Multidisciplinary Analysis and Optimization (1994)
Seitz, A. and Gologan, C.: Parametric design studies for propulsive fuselage aircraft concepts. In: 4th CEAS Air & Space Conference, Linköping, SW (2013)
Petrusson, A.: Aerodynamic evaluation of nacelles for engines with ultra high bypass ratio. Master Thesis, Chalmers University of Technology, Department of Applied Mechanis (2017)
Acknowledgements
We thank Martijn van Sluis and Biagio Della Corte from Delft University of Technology for providing CFD results within the CENTRELINE project. This work was conducted within the CENTRELINE project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement no. 723242.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Rating of figures of merit
See Table 2.
1.2 Momentum conservation application
Applied to a closed system, Newton’s second law of motion states that the net force acting on a body equals the time rate of change of momentum of the system:
For a body-centered control volume \( {\text{CV}} \) with control surface \( {\text{CS}} \), volume elements \( {\text{d}}V \) and surface area elements \( {\text{d}}A \), the Reynold’s transport theorem for a vector field \( \vec{f} \) is defined as:
When applied to the right-hand side of Eq. (32), the linear momentum equation is derived:
For steady flow, the first term on the right-hand side of Eq. (34) (i.e., the change of momentum inside the control volume over time) becomes 0. The second term equals the momentum integrated over the control surfaces. A combination of Eqs. (32) and (34) for steady flow yields:
The right-hand side of Eq. (35) equals the momentum flow \( \dot{I} \).
The streamwise component of Eq. (35) is applied to all control volumes as defined in Fig. 8. \( F_{\text{p,in,CVi}} \) and \( F_{\text{p,out,CVi}} \) are the axial pressure forces at the inlet and outlet of the control volumes, \( \dot{I}_{\text{in,CVi}} \) and \( \dot{I}_{\text{out,CVi}} \) are the axial momentum flow terms, respectively. \( F_{\text{p,i}} \) and \( F_{\text{v,i}} \) are the integral pressure and viscous forces on the aircraft surfaces in streamwise direction, summed up in the total surface forces \( F_{\text{i}} \) (cf. Fig. 10). \( F_{\text{ST}} \) and \( F_{\text{BL}} \) are the pressure forces on the control surface following the propulsion system streamtube contour, interfacing control volume 1 and 3. In the front part of the fuselage, the streamtube contour lays within the potential flow field (\( F_{\text{ST}} \)), until it crosses the boundary layer (\( F_{\text{BL}} \)) under the assumption that the aft propulsor ingests only a part of the boundary layer.
In the following, the application of the momentum conservation to CV 0 is shown in detail. The application to CV 1 to CV 5 is conducted in a similar manner.
CV 0:
\( \dot{I}_{\text{out,CV0}} = \dot{I}_{\text{out,CV5}} \;{\text{and}}\;\dot{I}_{\text{in,CV0}} = \dot{I}_{\text{in,CV1}} + \dot{I}_{\text{in,CV3}} \), thus
CV 1:
CV 2:
CV 3:
CV 4:
CV 5:
All terms in Eq. (37) can be determined by re-arrangement of Eq. (38) through (42) and by taking into account that
\( \dot{I}_{\text{in,CV2}} = - \dot{I}_{\text{out,CV1}} \), \( F_{\text{p,in,CV2}} = - F_{\text{p,out,CV1}} \) etc.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Habermann, A.L., Bijewitz, J., Seitz, A. et al. Performance bookkeeping for aircraft configurations with fuselage wake-filling propulsion integration. CEAS Aeronaut J 11, 529–551 (2020). https://doi.org/10.1007/s13272-019-00434-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13272-019-00434-w