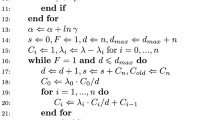An Inhomogeneous Weibull–Hawkes Process to Model Underdispersed Acoustic Cues

Abstract

A Hawkes point process describes self-exciting behaviour where event arrivals are triggered by historic events. These models are increasingly becoming a popular choice in analysing event-type data. Like all other inhomogeneous Poisson point processes, the waiting time between events in a Hawkes process is derived from an exponential distribution with mean one. However, as with many ecological and environmental data, this is an unrealistic assumption. We, therefore, extend and generalise the Hawkes process to account for potential under- or overdispersion in the waiting times between events by assuming the Weibull distribution as the foundation of the waiting times. We apply this model to the acoustic cue production times of sperm whales and show that our Weibull–Hawkes model better captures the inherent underdispersion in the interarrival times of echolocation clicks emitted by these whales.

1 Introduction

A temporal point pattern comprises a series of observed event times over some time period (Daley and Vere-Jones 2003). Such events often occur in clusters, and through using point process methodology, we are able to infer the inherent pattern in their sequences (Diggle 2013). A temporal Hawkes process (Hawkes 1971a, b) is a type of self-exciting model where the occurrence of one event triggers events in the near future. This means that each event immediately increases the rate at which future events occur; the influence of the event diminishes over time.

The self-exciting behaviour of the Hawkes process makes it a particularly useful model for phenomena where events tend to cluster in time. Applications are wide-ranging and to date include seismology (Ogata 1988), finance (Bacry et al. 2015; Hawkes 2018), criminology (Zhuang and Mateu 2019; Park et al. 2021), neuroscience (Reynaud-Bouret et al. 2013) and social media (Zhao et al. 2015). The common theme amongst these applications is that the occurrence of an event (e.g. an earthquake, a large financial trade, or a Tweet) is known to trigger future events (i.e. an aftershock, further transactions, retweets). By using a Hawkes model, the potential causal relationship between events may be inferred. This is because the self-exciting component captures the heightened risk or rate of occurrences immediately following an event.

The phenomenon of event occurrences inducing others is also prevalent throughout environmental, biological and agricultural sciences. Modelling these data as a Hawkes process aids in detecting the clustering and the potentially triggering nature of these events. Accordingly, the Hawkes process has recently begun to see use in these fields, including modelling the spread of invasive species (Balderama et al. 2012; Gupta et al. 2018), forest fires (Tonini et al. 2017; Holbrook et al. 2022), and fisheries stocks (Nakagawa et al. 2019).

The events of a classic Hawkes process are distributed according to an inhomogeneous Poisson process according to a rate that consists of some baseline intensity and a term that accounts for the self-excitement (Hawkes 1971a). However, many natural and ecological events do not occur according to the typically assumed inhomogeneous Poisson process, but are either underdispersed (less variance in the times between events) or overdispersed. For example, the spatial locations of termite mounds (Pringle et al. 2010), pine trees (Kenkel 1988) and pollinated plants (Herrera 2021) are all more regularly spread out than a Poisson point pattern, and the counts of offspring (Brooks et al. 2019) often have less variance than a Poisson distribution. Conversely, overdispersion is common in much ecological count data such as counts of migrating birds (Lehikoinen et al. 2010) and plant species richness (Kleijn et al. 2008).

For an inhomogeneous temporal Poisson process, the compensator at a given point in time point is the expected number of events that have occurred since time zero, see Sect. 2.1. The differences in compensator values between consecutive events are exponentially distributed. Previous work by Berman (1981) allowed the consecutive compensator differences of a temporal point process to instead follow a gamma distribution. There is also a long tradition of using the Weibull distribution to model inter-event times in renewal processes (Lomnicki 1966; Yannaros 1994; Ong et al. 2015). More generally, Lindqvist et al. (2003) developed their trend renewal process, which allows an inhomogeneous temporal point process to use any distribution for the compensator differences whose support is non-negative in place of the exponential. The Weibull distribution has been a common choice as the compensator difference distribution in trend renewal processes, being applied in diverse applications such as medicine (Pietzner and Wienke 2012), volcanic eruptions (Bebbington 2010), and battery reliability (Wang et al. 2019). These previous models, however, do not describe the potentially self-exciting nature of events, as the inhomogeneous “trend function” is not a Hawkes process.

The RHawkes model developed by Wheatley et al. (2016) allows the compensator differences for the baseline, i.e. non-self-excited events only, to come from any distribution with non-negative support. The Weibull–Hawkes process developed by Zhang et al. (2020) again only relaxes the assumption for the baseline events; they define the baseline rate as a power-law function. In both cases, the remaining (self-excited) events are assumed to adhere to the Poisson assumption regarding compensator differences mentioned above.

The different assumptions about baseline and non-baseline events are computationally expensive and suppose some fundamental difference between these two classes of events. This, alongside the exponential waiting time assumption itself, is unrealistic for many situations. This is because (1) in many examples there is no way to reliably distinguish a baseline from a non-baseline event, even when applying methods such as stochastic declustering, and (2) real-world events are often either overdispersed or underdispersed compared to what a inhomogeneous Poisson assumes.

In this paper, we extend the traditional Hawkes process to account for under- or overdispersion in the waiting times between events by modelling all (both baseline and non-baseline) compensator differences using the Weibull distribution, and as an example we fit this model to the acoustic cue production times of sperm whales (Physeter macrocephalus). In Sect. 2 we present our Weibull–Hawkes process and demonstrate, via simulation, the model’s ability to capture both under- and overdispersion. In Sect. 3 we introduce the acoustic cue data and show that the extended Hawkes model captures the inherent underdispersion in the interarrival times of echolocation clicks. In Sect. 4 we discuss how this extension leads to a more realistic and flexible self-exciting model better suited to the typical data structures seen throughout the environmental, biological, and agricultural sciences.

2 Materials and Methods

2.1 A Self-Exciting Temporal Point Process

A Hawkes process assumes that each event immediately increases the rate at which future events may occur, i.e. the occurrence of an event excites others. This self-excitement effect diminishes over time and the rate of events decays to some long-term baseline rate if no further events are observed. For current time t the conditional rate of occurrence is given by an intensity function, $\lambda (t;\cdot )$, which comprises a baseline intensity and a self-excitement term. The self-exciting term typically consists of a summation over all historic events ($\tau _{i} < t$ where $i = 1,..., N$) that is weighted by some specified decay kernel. The conditional intensity of the Hawkes process proposed by Hawkes (1971a) for current time t is given by

$$\begin{aligned} {\lambda (t;\gamma ,\cdot ) = \mu (t;\cdot ) + \gamma \sum _{i: \tau _{i} < t} \nu (t - \tau _i)}. \end{aligned}$$

(1)

Here, $\mu (t;\cdot ) > 0$ is some temporally varying background (baseline) rate and $\nu (t - \tau _i)$ is the historic dependence kernel (which integrates to one). The parameter $\gamma$, termed the branching ratio, gives the expected number of events triggered by any single event. The baseline events are customarily called immigrants and the triggered events children, though in practice it may not be possible to distinguish between the two. Where applicable, this is the terminology we will use during the remainder of the manuscript.

The compensator of a temporal point process, $\Lambda (\tilde{t})$, evaluated at some time $\tilde{t}$ gives the expected number of events in the interval $[0,\tilde{t}]$. For any inhomogeneous Poisson process such as a Hawkes process, the compensator is defined as

$$\begin{aligned} {\Lambda (\tilde{t}) = \int _{0}^{\tilde{t}} \lambda (t)\;{d}t}. \end{aligned}$$

(2)

The random time change theorem (Daley and Vere-Jones 2003) states that if the set of events $[\tau _{1}, \tau _{2},..., \tau _{N}]$ is a realisation of an inhomogeneous Poisson process, then $[\Lambda (\tau _{1}), \Lambda (\tau _{2}),..., \Lambda (\tau _{N})]$ is a realisation of a homogeneous Poisson process with unit rate. We denote the compensator differences as $\delta \Lambda _{i} = \Lambda (\tau _i) - \Lambda (\tau _{i-1})$ for $i = 2,..., N$ and $\delta \Lambda _{1} = \Lambda (\tau _1)$. Under the assumptions above $\delta \Lambda _{i} \sim \text {Exp}(1)$. This is an unrealistic and restrictive assumption for many real-world data, which rarely occur in an independent Poisson manner.

As was discussed in Sect. 1, the exponential compensator assumption for inhomogeneous temporal Poisson processes has previously been relaxed by using Gamma processes (Berman 1981), and more generally, any distribution with non-negative support and unit mean (Lindqvist et al. 2003). For the self-exciting case, Wheatley et al. (2016) relaxes the exponential waiting time assumption for the immigrant points only. That paper developed a renewal Hawkes model where for the immigrant points $\delta \Lambda _{i} \sim \text {Weibull}\,(\rho , k)$ with scale parameter $\rho$ and shape parameter k, see Sect. 2.2. However, the children remain restricted by the assumption of exponential compensator differences. In Sect. 2.2 we extend the Hawkes model to account for under- and overdispersion in the waiting times of all events, both immigrants and children, using the Weibull distribution.

2.2 An Inhomogeneous Weibull–Hawkes Model

In Sect. 2.2.1 we discuss the Weibull distribution and how it can be used to create a family of distributions with mean one. In Sect. 2.2.2 we review the classic Hawkes process with an exponentially decaying kernel, and in Sect. 2.2.3 we present our Weibull–Hawkes model.

2.2.1 The Weibull Distribution

If $T \sim \text {Weibull}\,(\rho , k)$ (for $t \ge 0$), then

$$\begin{aligned} {f(t; \rho , k) = \left( \frac{k}{\rho }\right) \, {\left( \frac{t}{\rho }\right) }^{k-1}\text {exp}{\left( -\frac{t}{\rho } \right) ^{k}}} \end{aligned}$$

(3)

where $\rho > 0$ is the scale parameter and $k > 0$ is a shape parameter that control the spread (stretching/shrinking) and peakedness (peak roundness) of the distribution, respectively. The mean is given by $\rho \Gamma (1 + 1/k)$ where $\Gamma (\cdot )$ is the Gamma function. The hazard (failure) rate function follows a power-law relationship with time and is given by $h(t; \rho , k) = \left( \frac{k}{\rho }\right) \, {\left( \frac{t}{\rho }\right) }^{k-1}$. Note that when $k = 1$, the hazard rate is constant ($\rho ^{-1}$).

Setting $g(k) = \Gamma (1+ 1/k)$ and $\rho = \frac{1}{g(k)}$, the Weibull probability density function given by Eq. (3) becomes

$$\begin{aligned} {f(t; k) = \left( k\,g(k)\right) \;\left( t\,g(k)\right) ^{k-1}\, \text {exp}\,{\left( -t\,g(k)\right) ^k}}. \end{aligned}$$

(4)

Here, k is a dispersion parameter; when $k = 1$ the distribution reduces to an exponential, when $k > 1$ the variance is smaller than that of an exponential, and when $k <1$ it is larger. Thus, the parameter k allows us to model both overdispersion ($k < 1$) and underdispersion ($k > 1$). By setting $\rho$ appropriately, we have ensured that the mean is always one and thus eliminate the need for the second parameter. For $\delta \Lambda _{i} \sim \text {Weibull}(1/g(k), k)$, the log-likelihood, $l\left( g(k), k \mid \varvec{\delta \Lambda }\right)$, is given by

$$\begin{aligned} \begin{array}{rl} l\left( g(k), k \mid \varvec{\delta \Lambda }\right) = &{} N\;\left[ \text {log}(k) + k\;\text {log}(g(k))\right] \; \\ &{}\,+\sum _{i=1}^N (k-1)\;\text {log}(\delta \Lambda _{i})\;-\;(g(k) \delta \Lambda _{i})^k \end{array} \end{aligned}$$

(5)

where N is the number of events.

2.2.2 The Hawkes Process

The intensity of a classic Hawkes process detailed in Hawkes (1971a) with an exponential decay kernel is

$$\begin{aligned} {\lambda (t;\alpha ,\beta ,\cdot ) = \mu (t;\cdot ) + \alpha \sum _{i: \tau _{i} < t} \text {exp}(-\beta (t - \tau _i))}. \end{aligned}$$

(6)

Here, $\alpha$ is the immediate increase in intensity following an event, and $\beta$ is the exponential decay of the intensity over time. The branching ratio [$\gamma$ in Eq. (1)] is $\alpha /\beta$. The log-likelihood for the version of the Hawkes process presented in Eq. (6) is given as follows:

$$\begin{aligned} {l_{H}(\alpha ,\beta ,\cdot \mid \varvec{\tau }) = \sum \limits _{i = 1}^{N} \text {log}\left( \lambda (\tau _i;\alpha ,\beta ,\cdot )\right) - \int \limits _{0}^{T} \lambda \left( t;\alpha ,\beta ,\cdot \right) \;\text {d}t}. \end{aligned}$$

(7)

As noted by Ozaki (1979), this log-likelihood is not always convex and therefore a maximisation algorithm should be run from multiple starting points to ensure that the true maximum has been found.

2.2.3 Proposed Weibull–Hawkes Model

We consider two extension to the Hawkes process, both relaxing the restrictive assumption of an exponential compensator difference distribution. The extensions we propose both make use of the Weibull distribution and allow us to capture/model both under- and overdispersion in waiting times to varying degrees of flexibility. The first model we propose lets $\delta \Lambda _{i} \sim \text {Weibull}(1/g(k), k)$ as in Sect. 2.2.1; that is, the compensator differences follow the Weibull distribution given by Eq. (4), while having an event rate $\lambda (t;\cdot )$ which is the same as the Hawkes process [see Eq. (6)].

The second model we propose is an extension of the one described above where now we use a mixture of two Weibull distributions to model the compensator differences. We denote the first Weibull distribution as having dispersion parameter $k_1$ and mixture weight p. The second Weibull has dispersion parameter $k_2$ and by necessity mixture weight $1-p$. We constrain p to be greater than a half to ensure the model is identifiable. We define the contribution of the first Weibull to the mean as $m_1 = p\;g\;(k_1)\;\rho _1$, where $g(\cdot )$ is defined as in Sect. 2.2.1. Given that the mean of the mixture must be one, we can compute the scale parameter of the first Weibull as $\rho _1 = m_1/\left( p\;g(k_1)\right)$ and that of the second Weibull as $\rho _2 = (1-m_1)/\left( (1-p)\;g(k_2)\right)$. Thus the parameter space is defined by $0<m_1<1$, $0.5<p<1$, $k_1, k_2>0$.

The likelihood of the first Weibull–Hawkes model is the probability of observing no events between time 0 and $\tau _1$, $\tau _1$ and $\tau _2$... $\tau _{N-1}$ and $\tau _{N}$ multiplied by the conditional intensities at $\varvec{\tau }$ (Daley and Vere-Jones 2003; Lindqvist et al. 2003). The probability that there are zero events in the interval $[\tau _{i-1},\tau _{i}]$ is

$$\begin{aligned} 1 - F(\Lambda (\tau _{i};\alpha ,\beta ,\cdot ) - \Lambda (\tau _{i-1};\alpha ,\beta ,\cdot );1/g(k),k) \end{aligned}$$

where F is the c.d.f. of the Weibull distribution given in Eq. (3). Following Eq. 4 of Lindqvist et al. (2003), the conditional intensity at the time $\tau _i$ can be written as

$$\begin{aligned} \lambda _{CI}(\tau _{i};\alpha , \beta , \cdot \mid H_t) = \lambda (\tau _i;\alpha ,\beta ,\cdot )\;h(\Lambda (\tau _{i};\alpha ,\beta ,\cdot ) - \Lambda (\tau _{i-1};\alpha ,\beta ,\cdot ); 1/g(k),k) \end{aligned}$$

(8)

where h(t; 1/g(k), k) is the hazard function of the previously mentioned Weibull distribution. Thus, we can write

$$\begin{aligned} \begin{array}{rl} L_{WH}(g(k), k, \alpha , \beta , \cdot \mid \varvec{\tau }) = &{} \prod \limits _{i=1}^N [1 - F(\Lambda (\tau _{i};\alpha ,\beta ,\cdot ) - \Lambda (\tau _{i-1};\alpha ,\beta ,\cdot );1/g(k),k)]\\ &{} \prod \limits _{i=1}^N \lambda (\tau _i;\alpha ,\beta ,\cdot )\;h[\Lambda (\tau _{i};\alpha ,\beta ,\cdot ) - \Lambda (\tau _{i-1};\alpha ,\beta ,\cdot ); 1/g(k),k] \end{array} \end{aligned}$$

(9)

and by noting the definition of hazard $h(t) = f(t)/(1 - F(t))$, this simplifies to

$$\begin{aligned} L_{WH}(g(k), k, \alpha , \beta , \cdot \mid \varvec{\tau }) =&\prod _{i=1}^N \lambda (\tau _i;\alpha ,\beta ,\cdot ) f(\Lambda (\tau _{i};\alpha ,\beta ,\cdot )\\ \nonumber&\,-\Lambda (\tau _{i-1};\alpha ,\beta ,\cdot ); 1/g(k),k) \end{aligned}$$

(10)

and so we can write the log-likelihood as

$$\begin{aligned} {l_{WH}(g(k), k, \alpha , \beta , \cdot \mid \varvec{\tau },\varvec{\delta \Lambda }) = l(g(k), k \mid \varvec{\delta \Lambda }) + \sum _{i=1}^N \text {log}(\lambda (\tau _i; \alpha , \beta , \cdot ))} \end{aligned}$$

(11)

where $l(g(k), k \mid \varvec{\delta \Lambda })$ is defined by Eq. (5) and $\lambda (t;\alpha ,\beta ,\cdot )$ by Eq. (6).

Alternatively, if one were to use the conditional intensity given by Eq. (8) and substitute this into the likelihood given by Eq. (7), one obtains Eq. (5) in Lindqvist et al. (2003). This equation can be rearranged to give Eq. (6) of the same article, whose first term is equivalent to Eq. (10). We do not need the second term because we have assumed throughout that the process stops at the time of the last event $\tau _N$, which means the second term is always one.

The derivation of the likelihood for our second, mixture model follows the same line of reasoning, except that the distribution referred to by its c.d.f $F(\cdot )$, p.d.f. $f(\cdot )$ and hazard $h(\cdot )$ is now the mixture model parameterised above. Thus, in the final likelihood given by Eq. 11, we substitute $l_M(g(k_1),g(k_2), k_1, k_2, p, m_1)$ for $l(g(k), k \mid \varvec{\delta \Lambda })$. Using the definition of f(t; p, k) in Eq. (3) this can be written as

$$\begin{aligned}{} & {} l_{M}(g(k_1), g(k_2), k_1, k_2, p, m_1, \alpha , \beta , \cdot \mid \varvec{\delta \Lambda })\nonumber \\{} & {} \qquad = \sum _{i=1}^{N} \text {log}[p\;f(\delta \Lambda _{i}, m_1/(p\;g(k_1)), k_1)\nonumber \\{} & {} \qquad \quad +(1-p)\; f(\delta \Lambda _{i}, (1 - m_1)/((1-p) g(k_2)), k_2)] \end{aligned}$$

(12)

Our model is self-exciting and accounts for either under- or overdispersion in waiting times. The self-exciting component captures the heightened instantaneous average rate of occurrences immediately following an event, and the Weibull interarrival times give the model a huge degree of flexibility over a standard Hawkes process.

Figure 1 shows three realisations of this Weibull–Hawkes process, all with $\alpha = 0.5$, $\beta = 1$, and $\mu = 1$. The pattern shown in panel A is simulated with $k = 1$ (i.e. with the typically exponentially distributed waiting times of a Hawkes process); panel B shows the start of simulated point processes with $k=5$ (underdispersed) and $k=0.5$ (overdispersed) while panels C and D show the histograms of compensator differences of the point patterns depicted on panel B. An exponential is a poor fit for both, highlighting the flexibility of our model.

Fig. 1

Top: portion of a sequence of times (blue) from a Hawkes process with $\lambda (t) = 1 + 0.5 \sum _{i: \tau _{i} < t} \text {exp}(-(t - \tau _i))$ and the corresponding intensity (black line). Middle: sequence of times from our Weibull–Hawkes process (see Sect. 2.2.3) with the same formula for $\lambda (t)$, but with dispersion parameters $k=5$ (orange) and $k=0.5$ (green). Bottom: simulated distributions of the compensator differences of both processes. The exponential distribution (blue) is clearly inconsistent with both. See Appendix C for the simulation method (Color figure online)

2.3 Simulation Study

To assess the model performance, we carried out two simulation studies. The two simulation studies use a common baseline intensity $\mu (t) = \mu + B\;\text {s}(t) - C\;\text {sin}(\frac{t}{P})$. We defined $\text {s}(t)$ as 1 when $P\pi< t < 2P\pi$, $3P\pi< t < 4P\pi$, $5P\pi< t < 6P\pi$... and 0 at all other times. We included a constraint $0< C < \mu$. Thus, the baseline rate consists of a constant $\mu$, a sinusoidal component $C\;\text {sin}(\frac{t}{P})$ and a square wave $B\;\text {s}(t)$. The peaks and troughs of the sinusoidal curve and square wave align. For our simulation study we set $\mu = 0.5$, $B = 1$, $C = 0.25$, and $P = 10$. As will be seen in Sect. 3.2, this choice of baseline function has similarities with the function we use in the applied example. The self-excitement had parameter values $\gamma = 0.25$ and 0.75 and $\beta = 0.01$ and 0.1.

For the first study, we simulated from the first proposed Weibull–Hawkes model with values of $k = 0.5, 2/3, 1.5$ and 2 to test under- ($k > 1)$ and overdispersion ($k < 1)$ relative to the exponential assumption ($k = 1$). The second simulation study tested the proposed mixture Weibull–Hawkes model. The same values for the parameters of $\mu (t)$, $\alpha$, $\beta$ and T were used. We set $k_1 = 1.5, 2$ and 3, $k_2 = 0.5$ and 0.75, $p = 0.65$ and 0.85. In each simulation, $p = m_1$.

For every set of parameters, we simulated four different time periods: $T = 400, 1000, 2500$ and 6250. For the first study, there are 64 combinations of parameters and time periods and for each set we generated 250 realisations of our Weibull–Hawkes process for a total of 16,000 simulations. For the second study, we simulated 100 realisations for each of the 192 parameter and time period sets for a total of 19,200 simulations.

Details of the simulation algorithm can be found in Appendix C. Model fitting was carried out using the R package TMB (Kristensen et al. 2016), which allows a user to write a log-likelihood function in C++. Due to the non-convex nature of the likelihood (Ozaki 1979), we maximised the log-likelihood given by Eq. (11) from 20 random starting points. We used the New Zealand eScience Infrastructure (NeSI) server (https://www.nesi.org.nz/) to perform the simulations and fitting, which required 482 h of computing time. The results of this study are given in Sect. 2.4 (Table 1).

2.4 Simulation Study Results

Our simulation studies showed that the bias in the estimates of the parameters of the compensator difference distribution: $k_1$ (or k), $k_2$, p and $m_1$ are low and decrease with sample size. The parameters for the baseline rate and $\beta$ show greater bias, especially in the second mixture model simulation study. The model has some difficulty determining how much of the baseline intensity is comprised of the constant $\mu$ and how much is time-varying (B and C). Some biases do not decrease with sample size; perhaps the period of the pulse wave $\left( B\;\text {s}(t)\right)$ and sinusoidal wave $\left( C\;\text {sin}\left( \frac{t}{P}\right) \right)$ were too short for these waves to be distinguishable. However, on the whole, biases are reasonable and the results give us confidence in the simulation methodology, the likelihood that we derived in Sect. 2.2.3 and that the model can be fitted in a reasonable amount of time. The complete results of our two simulation studies can be found in the GitHub repository https://github.com/ABMvanHelsdingen/WHP. Selected results of the simulation study are plotted in Appendix D, and complete results of our two simulation studies can be found in the GitHub repository https://github.com/ABMvanHelsdingen/WHP.

Table 1 Median biases (%) for each parameter across the four time periods used in the two simulation studies

3 Applied Example

3.1 Acoustic Cue Rate Data

Acoustic cues are emitted by cetaceans for a variety of reasons, including hunting by echolocation (Johnson et al. 2004), communication (Deecke et al. 2005), and mating (Smith et al. 2008). Acoustic cues of cetaceans can be passively recorded by either hydrophones (Zimmer et al. 2008) or by tagging individual whales (Madsen et al. 2002). One example of the latter is a digital acoustic recording tag (DTAG), which are motion and acoustic recording tags that are attached to cetaceans via suction cups (Johnson and Tylack 2003). The tag records sound and also has sensors that measure the dive depth and the animal’s orientation. The sound data are then processed (Shamir et al. 2014), so that sounds emitted by the animal can be distinguished from background noise. The acoustic properties of the cues themselves such as frequency harmonics and power spectra can be used to infer specific behaviours (Mohl et al. 2003; Au et al. 2006) of cetaceans. In addition, the rate of acoustic cues can be used to infer the impact of anthropogenic sounds on behaviour (Tyack et al. 2011; Hawkins and Popper 2016).

A resourceful way of using these data is to estimate animal abundance. To do this, we need to estimate the average cue production rate (Marques et al. 2013) and cues are often considered as having a constant long-term average rate that averages out any other factors such as depth. In previous studies analysing the relationships between cue rates and covariates, the cue data have been binned or aggregated across dive cycles (Stimpert et al. 2015; Warren et al. 2017). This aggregation leads to a huge loss of information. Therefore, we propose treating the acoustic cue times as a temporal point process directly, considering the timestamps of cues as a realisation of some point process. In addition, we propose the use of a self-exciting model to better capture the inherent clustering and potentially contagious nature of echolocation cues.

Figure 2 shows the temporal point pattern of acoustic cues from a single sperm whale alongside its recorded depth (m). A summary of the data over the entire time period considered (approximately 11 h) is given in Table 2. These data were recorded using DTAGs and are part of the ACCURATE project (https://accurate.st-andrews.ac.uk/), which has collated data from over 100 sperm whales. To illustrate our proposed methods, we consider an individual, tag code $\text {sw}03\_253\text {b}$, tagged in the Mediterranean in 2003. Figure 4 in Appendix A shows the distribution of the interclick intervals.

Table 2 Summary statistics for the whale cues, depths, and dive cycles

Fig. 2

Top: depth profile of the whale. Middle: rug plot showing cue times with inset showing individual cue times in a 50 s interval. Bottom: histogram of cue times (each bin is about 160 s long). Note that barely any cues are emitted when the whale is on the surface

The number of acoustic cues emitted by sperm whales is known to increase with dive depth (Stimpert et al. 2015; Warren et al. 2017). Furthermore, there is evidence to suggest that cue rate changes alongside the whale’s rate and direction of descent (Watwood et al. 2006). We found that acoustic cues were more frequent during descents and when the whale was at the bottom of each dive, see Fig. 6 in Appendix B. Acoustic cues occurred at a lower frequency during ascents and virtually never when the whale was at the surface, as the lower panel of Fig. 2 clearly shows. Cues are clearly clustered, see Fig. 6; this is most obvious during the ascent where there were several bursts followed by longer periods of silence.

3.2 Modelling Acoustic Cue Rates

Letting $\text {d}(t)$ be the dive depth in kilometres at time t (i.e. $\text {d}(t) > 0$ when the whale is underwater, available at a frequency of 1 Hz), r(t) denotes the rate of descent calculated using numerical differentiation (i.e. $r(t) > 0$ when descending), and $s(t) = 0$ if $\text {d}(t) > 0.02$ (i.e. $>20$ metres below the surface), $s(t) = 1$; otherwise, we set $\mu (t;\cdot )$ in Eq. (6) to be

$$\begin{aligned} {\mu (t;\varvec{\eta }) = \text {exp}(\eta _0 + \eta _1\text {s}(t) + \eta _{2} \text {d}(t) + \eta _{3} r(t))}. \end{aligned}$$

(13)

Here each $\eta _{j} (j = 0,..., 3)$ is a coefficient of the inhomogeneous baseline rate of cues. As in Eq. (6) the parameter $\alpha$ is the instantaneous increase in intensity when an event occurs and $\beta$ is the decay over time of this self-exciting effect. The branching ratio of events is now $\alpha /\beta$, and we have $\beta \ge \alpha$ so that $\alpha /\beta \le 1$. We also set a constraint $\eta _{1} > 0$ so that the baseline rate when the whale is at the surface ($s(t) = 0$) is less than when it is underwater ($s(t) = 1$). Similar to other studies, we excluded the first complete dive from the point pattern; this is to avoid possible short-term behaviour changes induced by the tagging process (Barlow et al. 2013; Hildebrand et al. 2015). Estimated parameter values for this model are given in Sect. 3.3.

3.3 Modelling Results

We fitted our model to the whale cue data in both frequentist and Bayesian frameworks. For the frequentist results, see Appendix E. To perform model fitting in a Bayesian framework, we used the R package NIMBLE (de Valpine et al. 2017) to run Markov chain Monte Carlo (MCMC) chains. We fitted both the single Weibull and Weibull mixture model in NIMBLE for 50,000 MCMC iterations. We set a burn-in of 10,000 iterations and thinned the chain so that every 4th iteration was retained; thus, we finished with 10,000 samples. This required 58 min of compute time on the NeSI server.

The estimates for both models and the priors we used for Bayesian inference are shown in Table 3. The estimates for $\varvec{\eta }$ are broadly concordant. At the surface, the cue rate ($\text {exp}(\eta _0))$ is close to zero and jumps up when the whale dives below the surface. Estimates of the effect of being underwater ($\eta _1$), depth ($\eta _2$) and rate of descent ($\eta _3$) differ, but are all of the same sign, though the mixture model estimate for $\eta _2$ is indistinguishable from zero.

Table 3 Parameter priors, posterior means and 95% credible intervals for the baseline rate parameters in Eq. (13), the self-excitement parameters from Eq. (6) and the Weibull parameters of Eq. (11) and Eq. (12)

As is evident in Fig. 3, modelling the compensator differences as a single Weibull distribution results in a poor fit, albeit still much better than an exponential. This can be explained by there being a few influential outliers (the maximum value of $\hat{\delta \Lambda _i}$ is 46.71), which necessitate that the value of k be smaller (i.e. a higher variance) than what would be a good fit around the centre of the distribution. With $\hat{k} = 1.53$, we expect $\sim 1.8 \times 10^{-8}$ compensator differences over 10, but we observe 156 such values. When two Weibull distributions are used, the fit is much improved, with about 90% of the mixture being very sharply peaked ($k_1$ = 41.9) and the remaining weight being more dispersed so as to capture the tail. The tail is now much less extreme, with the maximum value of $\hat{\delta \Lambda _i}$ a more reasonable 16.12. However this model does make two markedly different conclusions. Firstly, the estimate of $\eta _2$ is now indistinguishable from zero, i.e. holding the whale’s vertical speed constant, depth may have no direct impact on cue production rate so as long as the whale is at least 20 ms deep. The second is that $\frac{\alpha }{\beta }$ is now much closer to one. In the first model, the expected number of descendants of each cue, $\hat{\beta }/(\hat{\beta } - \hat{\alpha })$, is 12.0, whereas in the second model it is around 100. This insight from the second model would imply that only about 1 % of the cues are baseline, with the rest as the result of self-excitement. It is worth noting, however, that these models do not perform stochastic declustering and therefore we cannot make direct inferences about which cues are baseline and which cues triggered/caused the others.

Fig. 3

Compensator differences ($\delta \Lambda _i$) of the whales cues for both the Weibull and Weibull-Mixture models. The red line is the density of the fitted compensator difference distributions. For the model using a single Weibull distribution, a very long tail, with the maximum value being 46.71, necessitates a lower value of $\hat{k}$ than what would be the best fit around the centre of the distribution (Color figure online)

4 Discussion

Hawkes processes are typically the model of choice for self-exciting event-type data. The trend renewal process introduced by Lindqvist et al. (2003) is a temporal point process that can assume any positive distribution for the waiting times of events; however, there is generally no self-exciting component to the event arrivals. Our proposed Weibull–Hawkes models incorporate both self-excitement and under- or overdispersion in the waiting times, combining these two insights into one integrated framework that adds flexibility to the Hawkes process by applying a specific case of the trend renewal process.

Our simulation studies confirm our model is correctly formulated and that parameter recovery by MLE is feasible and works well. We simulated both under- and overdispersion, different rates of decay of the self-excitement and different branching ratios and got broadly the same results with respect to bias for all these scenarios. While some bias was seen even in the samples with $T=6250$, it should be pointed out that the whales dataset is about an order of magnitude larger, so any issues related to small sample sizes observed in the simulations should not affect our results in Sect. 3.3 to the same degree.

Our model improves upon previous studies of whale cues by using the exact cue times, as opposed to aggregated counts. This additional information makes discerning the level of self-excitement far easier; it is possible to fit Hawkes processes to binned data but this poses various challenges (Shlomovich et al. 2022). Use of deaggregated data also means that it is possible to explore the level of dispersion in the waiting times. Understanding the fine scale details of the sound producing mechanisms may shed light into the ways whales explore and interact with their surroundings. We are able to explore the effects of depth and rate of descent directly, as parameters in the model, rather than more informally through comparing cue rates at different values of $\text {d}(t)$ and $\text {r}(t)$.

Our extensions to the Hawkes process are only a first step and could be refined in many ways. Various different formulations for all three of the baseline rate, self-exciting kernel and compensator differences are imaginable. We have only considered a log-linear baseline intensity function for simplicity, but any other strictly positive function could be considered, for example, nonlinear relationships or the incorporation of other covariates. The self-exciting kernel need not be exponential, though any other function (e.g. a gamma distribution) would prove computationally costly as it would be of $O(N^2)$ time complexity rather than O(N). Finally, functions other than the exponential, Weibull and mixtures of two Weibulls could be used. We have demonstrated that the Weibull distribution can be used as a part of trend renewal process for self-exciting data, but this does not preclude the use of other distributions for both this dataset and more generally.

In many cases, passive acoustic monitoring studies have been interested in a single whale population density estimate for a given time period and area. In that case, a single average cue rate that applies to that time period may be sufficient, even if it might be difficult to estimate the applicable cue rate (Marques et al. 2023). However, if one is interested in making comparisons across time or space, understanding spatio-temporal differences in cue rates is crucial, as assuming a constant cue rate when that is not the case could result in biased inferences, with existing differences in population density being masked, or with spurious differences in density being found. Our model makes progress in this direction by making the cue rate variable across time.

We have presented a model for purely temporal point processes. Thus, spatial information from spatial-temporal point patterns is discarded when using our framework. We anticipate however that our model could be extended to a spatiotemporal point process so that the waiting times between events are under- or overdispersed. This would prove a useful extension to spatiotemporal Hawkes processes (Reinhart 2018) and be especially useful in fields such as agriculture and biology where most point pattern data is spatiotemporal rather than purely temporal.

In conclusion, we have presented a new class of Hawkes processes that relax the Poisson assumptions made in all previous versions of the Hawkes process. Our model has potential to be useful in fields where Poisson assumptions are unrealistic including many natural and environmental sciences. By using our model, researchers can verify if clustering is the result of self-excitement or overdispersion. Conversely, our model can expose self-excitement that might be obscured by the more regular spacing of an underdispersed point pattern.

Appendices

Interarrival Times of Echolocation Clicks

Fig. 4

Interclick intervals, with an exponential distribution of the same mean overlaid (red line). The exponential has a much fatter tail than the observed intervals (Color figure online)

Figure 4 shows the raw waiting times between cues. The distribution is clearly not consistent with an exponential distribution. A main peak at about 0.5 s can be seen, a second peak at about 0.05 s, and a small third peak at about 0.3 s. Evidently, a homogeneous Poisson process will be inadequate for this data.

Figure 5 shows the compensator differences after fitting a traditional Hawkes process. The distribution has a sharp peak around 1 and is completely inconsistent with an exponential distribution with mean 1 as assumed by the random time change theorem (Daley and Vere-Jones 2003).

Fig. 5

Compensator differences ($\delta \Lambda _i$) when a conventional Hawkes process is fitted to the data. The red line is the density of the assumed exponential distribution (Color figure online)

Depths and Cue Times

Figure 6 shows a more granular view of the whale’s behaviour. It is based on Fig. 2, and shows a single, typical dive of the whale, allowing for a closer inspection of how cue rate varies across the dive cycle. Note the clustering evident in the rug plot.

Fig. 6

Top: depths of the whale against time for one of the dives middle: rug plot showing cue times with inset bottom: histogram of cue times. Note that virtually no cues are emitted when the whale is on the surface

Simulation Methodology

Our simulation method has two steps at each iteration i in order to generate an event time $\tau _i$.

• 1. Generate a random value $w_i$ for the compensator difference of the current interval.

• 2. Choose a value for $\tau _i$ so that $w_i = \delta \Lambda _i = \int _{\tau _{i-1}}^{\tau _i} \lambda (t)\;\text {d}t$

Step 1

To simulate from the Weibull distribution, we generate $u_i \sim \text {Uniform}\,(0,1)$. We then compute $w_i = g(k)\;(-\text {log}(u_i))^{1/k}$ where $g(k) = \Gamma (1+ 1/k)$ as defined in Sect. 2.2.1. This can be easily adapted for a mixture of two Weibull distributions, by generating a further variable $v_i \sim \text {Uniform}\,(0,1)$ to determine which of the two Weibull distributions the current interval comes from.

Step 2—constant $\mu (t)$

The equation in Step 2 must be solved numerically. We denote the constant baseline rate $\mu (t)$ as $\mu$. We start by noting that in the period between $\tau _{i-1}$ and $\tau _{i}$ the minimum possible value of $\lambda (t)$ is $\mu$ and the maximum value occurs immediately after $\tau _{i-1}$, which we shall designate as $\lambda (\tau _{i-1} + \epsilon )$. For convenience, we use the notation $T = \tau _i - \tau _{i-1}$.

Using these minimum and maximum values of $\lambda (t)$, we can say that $T < \frac{w_i}{\mu }$ and $T > \frac{w_i}{\lambda (\tau _{i-1} + \epsilon )}$. Denote these lower and upper bounds for T as $T_\text {L}^{(1)}$ and $T_\text {U}^{(1)}$ respectively.

By applying the Newton–Raphson method, we can write:

$$\begin{aligned} {T_\text {L}^{(k+1)} = T_\text {L}^{(k)} - \left( \int \limits _{\tau _{i-1}}^{\tau _{i-1} + T_\text {L}^{(k)}} \lambda (t)\;\text {d}t - w_i\right) \;/\;\lambda \left( \tau _{i-1} + T_\text {L}^{(k)}\right) } \end{aligned}$$

(14)

This equation updates our lower bound, bringing it closer to the true value of T. A similar equation can be written for the upper bound estimates.

If we continually iterate through Eq. (14) for both the lower and upper bounds, eventually $T_\text {L}^k$ and $T_\text {U}^k$ get extremely close. In our experience it often takes ten or fewer iterations for the difference between the bounds to be indistinguishable from zero. The code used to run the simulation study in Sect. 2.3 runs Newton’s method for 10 iterations, and if the difference exceeds a tolerance ($10^{-8}$) runs further batches of 10 iterations until the difference is less than the tolerance.

This works because $\lambda (t)$ is strictly decreasing between events, ensuring that the lower bound is always an underestimate and the upper bound always an overestimate. The two bounds can never cross.

At iteration 1, this method converges immediately (since $\lambda (t) = \mu$ and thus is constant), giving $\tau _1 = w_1/\mu$.

Fig. 7

Bias in maximum likelihood estimates of k (y-axes) for the four different time periods across the four values of k used in the first simulation study. The estimates appear to be asymptotically unbiased and efficient

Step 2—variable $\mu (t)$

When $\mu (t)$ is not constant, we cannot use the Newton–Raphson method, as $\lambda (t)$ may increase without an event occurring. But since $\Lambda (t)$ is strictly increasing, we can use the Bisection method to numerically solve for $\tau _i$.

As before, we need maximum and minimum values of T, and we can write $T > \frac{w_i}{\text {max}\;\mu (t) + \lambda (\tau _{i-1} + \epsilon ) - \mu (\tau _{i-1})}$ and $T < \frac{w_i}{\text {min}\;\mu (t)}$. As before we denote these as $T_\text {L}^{(1)}$ and $T_\text {U}^{(1)}$, respectively. Note that our method requires $\mu (t)$ to be strictly positive.

At each iteration we compute the mean, which we denote as x, of $T_\text {U}^{(k)}$ and $T_\text {L}^{(k)}$, and then $\int _{\tau _{i-1}}^{x} \lambda (t)\;\text {d}t$. If this integral exceeds $w_i$, we know $x > T$ and we set $T_\text {U}^{(k+1)} = x$. Otherwise, $T_\text {L}^{(k+1)} = x$. Iterations continue until the difference is less than a tolerance ($10^{-9}$). Because the difference halves at each iteration, the number of iterations needed can be calculated in advance.

Additional Simulation Study Results

Figures 7, 8, 9 and 10 show, respectively, the bias in estimates of k and $\alpha /\beta$ for the first simulation study, and the bias in $k_1$ and in $\alpha /\beta$ for the second simulation study.

Fig. 8

Bias in maximum likelihood estimates of $\frac{\alpha }{\beta }$ (y-axes) for the four different time periods across the four values of k used in the first simulation study. The y-axis is truncated at 200%

Fig. 9

Bias in maximum likelihood estimates of $k_1$ (y-axes) for the four different time periods across the three values of $k_1$ used in the second simulation study. The estimates are negatively biased in smaller sample sizes, but have little bias in the largest samples ($T = 6250)$

Fig. 10

Bias in maximum likelihood estimates of $\frac{\alpha }{\beta }$ (y-axes) for the four different time periods across the three values of $k_1$ used in the second simulation study. The estimates are unbiased but have a negative skew

Frequentist Analysis

We fitted both a conventional Hawkes process and the model with a single Weibull distribution for the compensator differences in a frequentist framework as well as a Bayesian framework. For our frequentist analysis, we maximised the log-likelihood from 500 different starting points. As with our simulation study, we used the NeSI server and required 59 min of compute time. The maximised log-likelihood was $l = -7119$ for the Weibull–Hawkes process and $l = -13042$ for a conventional Hawkes process.

Parameters for the Weibull–Hawkes model are given in Table 4. The estimates are broadly concordant with the Bayesian analysis presented in Sect. 3, especially for k, $\alpha$ and $\beta$. Estimates for the parameters of the baseline intensity function $\varvec{\eta }$ were less consistent but similar.

Table 4 Parameter MLEs and standard errors for the baseline rate parameters in Eq. (13), the self-excitement parameters from Eq. (6) and the dispersion parameter of Eq. (11)