Abstract
Capture–recapture studies are common for collecting data on wildlife populations. Populations in such studies are often subject to different forms of heterogeneity that may influence their associated demographic rates. We focus on the most challenging of these relating to individual heterogeneity. We consider (i) continuous time-varying individual covariates and (ii) individual random effects. In general, the associated likelihood is not available in closed form but only expressible as an analytically intractable integral. The integration is specified over (i) the unknown individual covariate values (if an individual is not observed, its associated covariate value is also unknown) and (ii) the unobserved random effect terms. Previous approaches to dealing with these issues include numerical integration and Bayesian data augmentation techniques. However, as the number of individuals observed and/or capture occasions increases, these methods can become computationally expensive. We propose a new and efficient approach that approximates the analytically intractable integral in the likelihood via a Laplace approximation. We find that for the situations considered, the Laplace approximation performs as well as, or better, than alternative approaches, yet is substantially more efficient.Supplementary materials accompanying this paper appear on-line
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Capture–recapture surveys are often used when studying wildlife populations to understand the associated population dynamics necessary for management and conservation. These surveys involve repeatedly sampling the population over a series of capture occasions. Observations at each capture occasion may take the form of physical captures and/or visual sightings of animals. Individuals are uniquely identified, using, for example, a ring or tag applied at initial capture or via natural markings. The observed data correspond to the set of capture histories for each individual observed in the study, detailing whether or not they are observed at each capture occasion. Capture–recapture studies may be assumed to be closed or open, dependent on whether the population is constant throughout the study; or may change due to births, deaths and/or migration, respectively. The corresponding parameters of interest typically differ between such studies with closed population models primarily focusing on abundance estimation; while open population models often focus on the estimation of survival probabilities, although these may also extend to abundance. For a review of these data and associated models see for example McCrea and Morgan (2015), Seber and Schofield (2019).
Incorporating heterogeneity in capture–recapture models can be important to model the underlying system processes. Omitting such sources of heterogeneity can lead to biased and/or misleading results (Rosenberg et al. 1995; Schwarz 2001; Chao et al. 2001; White and Cooch 2017). Otis et al. (1978) described three main sources of heterogeneity: temporal, behavioural and individual. In this paper we focus on individual heterogeneity, which can often be incorporated via the use of observable characteristics, such as gender, breeding status or condition. King and McCrea (2019) categorised observed individual covariates into \(2\times 2\) cross-classifications corresponding to continuous/discrete-valued and time-varying/invariant. We focus on the more challenging case of continuous-valued covariates. Missing data often arise for such covariate information due to, for example, imperfect data collection or simply the structure of the experimental design. For example, for stochastic time-varying covariates, if an individual is not observed, the corresponding covariate is also unknown at that time. In general, for continuous-valued covariates, the observed data likelihood is only expressible as an analytically intractable integral leading to model-fitting challenges. Previous model-fitting approaches include using a Bayesian data augmentation (Bonner and Schwarz 2006; King and Brooks 2008; Bonner et al. 2010); an approximate discrete hidden Markov model (Langrock and King 2013); and a two-step multiple imputation approach (Worthington et al. 2015). However, these approaches are computationally expensive and not scalable to large datasets.
Alternatively, unobservable individual heterogeneity can be modelled via individual random effects. These may either be specified as a finite mixture model (Pledger 2000; Pledger et al. 2003); or an infinite mixture model (Coull and Agresti 1999; Dorazio and Royle 2003; King and Brooks 2008). However, we note that identifiability issues may arise in terms of the distributional assumption of this heterogeneity, with different models leading to the same distribution for the observed data (Link 2003, 2006), indicating that some sensitivity analyses are advisable in practice. For the finite case, a closed form expression for the likelihood is available, summing over the mixture components; for the infinite case the necessary integration is generally analytically intractable (though see Dorazio and Royle (2003) for a special case for closed models assuming a Beta distribution). Again, within this paper we focus on the case of continuous-valued individual random effects. A variety of approaches have been applied to fit random effect individual heterogeneity models to data including conditional likelihood (Huggins and Hwang 2011); Bayesian data augmentation (King and Brooks 2008; Royle et al. 2007; Royle 2008); numerical integration (Coull and Agresti 1999; Gimenez and Choquet 2010; White and Cooch 2017) and combined numerical integration and data augmentation (Bonner and Schofield 2014; King et al. 2016). Observed and unobserved heterogeneity can be jointly considered via a mixed model specification, including both covariate information and additional random effects with similar model-fitting tool applied [see, for example, King et al. (2006), Gimenez and Choquet (2010), Stoklosa et al. (2011)].
We develop a computationally efficient Laplace approximation for the analytically intractable integral in the likelihood function in the presence of individual heterogeneity for capture–recapture data, which we subsequently numerically maximise to obtain the MLEs of the parameters. We apply the approach to fit (i) a closed population model with individual random effects (using a higher order Laplace approximation for improved accuracy) and (ii) an open population model with time-varying continuous covariate information. For the open population model, we use the numerical automatic differentiation tool in the R package Template Model Builder (TMB; Kristensen et al. 2016) to approximate the likelihood. TMB builds on the approach of the Automatic Differentiation Model Builder (ADMB) package where the objective function is written in C++. The approach is scalable to both large dimensions and sample size i.e., it is designed to be fast for handling many random effects (\(\approx 10^6\)) and parameters (\(\approx 10^3\)) (Kristensen et al. 2016) since computing the most challenging computation (the second derivatives) is no longer expensive due to the automatic differentiation function within TMB.
In Sect. 2 we introduce the notation and individual heterogeneity models. In Sect. 3 we describe the associated Laplace approximation for the closed and open capture–recapture models we consider. In Sect. 4 we conduct a simulation study of these systems, before analysing two real datasets in Sect. 5. Finally we conclude with a discussion in Sect. 6.
2 Capture–Recapture Models
We begin with a brief description of the general notation for capture–recapture studies and model parameters, before describing the specific models for closed and open populations that we consider in detail with their associated observed data likelihoods.
2.1 Notation
We let \(t=1,\ldots ,T\) denote the capture occasions within the study; and \(i=1,\ldots ,n\) the observed individuals over all the capture occasions. Then, for each individual \(i=1,\ldots ,n\) and capture occasion, \(t=1,\ldots ,T\) we let,
The capture history associated with individual \(i=1,\ldots ,n\) is denoted by \(\varvec{x}_{i}=\{x_{it}:t=1,\ldots ,T\}\); and the set of capture histories \(\varvec{x} = \{x_{it}:i=1,\ldots ,n; t=1,\ldots ,T\}\). Finally, we let \(f_i\) and \(\ell _i\) denote the first and last time individual i is observed, respectively, for \(i=1,\ldots ,n\).
The associated model parameters depend on the specific capture–recapture model being fitted. We describe the general set of parameters and indicate whether they apply to the closed or population models considered within this paper:
-
N = the total population size (closed);
-
\(p_{it}\) = \(\mathbb {P}(\text{ individual } \)i\( \text{ is } \text{ observed } \text{ at } \text{ time } \)t |\( \text{ available } \text{ for } \text{ capture } \text{ at } \text{ time } \)t) (open and closed);
-
\(\phi _{it}\) = \(\mathbb {P}(\text{ individual } \)i\( \text{ is } \text{ alive } \text{ at } \text{ time } \)t+1 |\( \text{ alive } \text{ at } \text{ time } \)t) (open).
We let \(\varvec{p}= \{p_{it}:i=1,\ldots ,N; t=1,\ldots ,T\}\), and similarly for \(\varvec{\phi }\).
We consider the individual heterogeneity model component denoted by \(\varvec{y}= \{\varvec{y}^{\mathrm{obs}},\varvec{y}^{\mathrm{mis}}\}\), where \(\varvec{y}^{\mathrm{obs}}\) and \(\varvec{y}^{\mathrm{mis}}\) denote the observed and unobserved individual heterogeneity components, respectively. For example, \(\varvec{y}^{\mathrm{obs}}\) may correspond to observed covariate values; while \(\varvec{y}^{\mathrm{mis}}\) the missing covariate values or random effect terms. In this paper we assume that \(\varvec{y}^{\mathrm{mis}}\) is continuous-valued. We let \(\varvec{\psi }\) denote the associated individual heterogeneity model parameters; and \(\varvec{\theta }\) the model parameters to be estimated.
The corresponding data are given by \(\{\varvec{x}, \varvec{y}^{\mathrm{obs}}\}\), with associated observed data likelihood,
where \(f(\varvec{x}|\varvec{\theta }, \varvec{y})\) denotes the complete data likelihood; and \(f(\varvec{y}| \varvec{\psi })\) the random effect or covariate model component. This likelihood is, in general, analytically intractable. (If there are discrete-valued elements of \(\varvec{y}^{\mathrm{mis}}\) the integral becomes a summation). We now describe both a closed and open capture–recapture model, considering a continuous-valued random effects model, and time-varying continuous-valued individual covariate model, respectively.
2.2 Closed \(M_h\)-type Models: Unobserved Heterogeneity
We consider the closed models, \(M_{tbh}\), proposed by Otis et al. (1978), where the subscripts correspond to temporal, behavioural and individual heterogeneity, respectively. The subscripts denote which heterogeneities are present in a given model. Additional heterogeneity can be modelled via observed covariates (Stoklosa et al. 2011), but we do not consider this case here. The total population size, N, is the parameter of primary interest. The recapture probabilities, \(p_{it}\), are expressed such that, \(h(p_{it}) = \alpha _t + \lambda S_{it} + \epsilon _i\), where \(S_{it}=0\) if \(t \le f_i\); and \(S_{it}=1\) if \(t > f_i\); and h denotes some function constraining the recapture probabilities to the interval [0, 1]. Within this paper we assume a logistic relationship, so that \(h \equiv \) logit. The \(\alpha _t\) terms correspond to the temporal component; \(\lambda \) the behavioural component and \(\epsilon _i\) the individual random effect term which we assume to be of the form \(\epsilon _i \sim \text {N}(0,\sigma ^2)\). The individual heterogeneity sub-models \(M_h\), \(M_{th}\), \(M_{bh}\) are obtained by setting restrictions on the parameters. For example, in the absence of a behavioural effect \(\lambda = 0\); and when there are no temporal effects \(\alpha _t = \alpha \) for all \(t=1,\ldots ,T\). The conditional likelihood, given the capture probabilities, \(\varvec{p}= \{p_{it}: i=1,\ldots ,N, t=1,\ldots ,T\}\), is of multinomial form (omitting the constant coefficient terms):
However, the capture probabilities are specified as a random effect component. The model parameters are \(\varvec{\theta }= \{N, \varvec{\alpha }, \lambda \}\) with individual heterogeneity model parameters \(\varvec{\psi }= \{\sigma ^2\}\). Thus, assuming there is no additional observed individual covariate information within the study, we have \(\varvec{y}^{\mathrm{obs}} = \emptyset \), and \(\varvec{y}^{\mathrm{mis}} = \{\epsilon _i: i=1,\ldots ,N\}\) . We let \(\varvec{x}_0 = \{x_{01},\ldots ,x_{0T}\}\) denote the unobserved capture history with all entries equal to zero (i.e. \(\varvec{x}_{0t} = 0\) for all \(t=1,\ldots ,T\) and all individuals \(i=n+1,\ldots ,N\)). Further, the associated random effect of an unobserved individual is denoted by \(\epsilon _0\), with associated capture probability at time t given by \(h(p_{0t}) = \alpha _t + \epsilon _0\). The observed data likelihood of Eq. (1) can be expressed as,
where \(f(\epsilon _i|\sigma ^2)\) denotes the density function for the unobserved heterogeneity process; and \(f(\varvec{x}_i|\varvec{\theta }, \epsilon _i)\) the probability of the associated capture history, such that
We note that the likelihood can be written more efficiently by further considering only unique observed capture histories, but for notational simplicity we retain the product over all observed individuals within this expression.
Previous approaches for dealing with the intractable likelihood include the use of Gauss–Hermite quadrature to estimate the integral (Coull and Agresti 1999). White and Cooch (2017) evaluated this approach further via simulation for different parameter values, and concluded that the results were generally unbiased except for relatively low recapture probabilities and/or few capture events. Further, they demonstrated that for larger individual heterogeneity variances a greater number of quadrature points are required to retain accuracy. Alternatively, a Bayesian data augmentation approach has been applied, treating the individual heterogeneity terms as additional parameters (or auxiliary variables) and calculating the joint posterior distribution over both parameters and auxiliary variables. However, in this approach the number of auxiliary variables is also an unknown (it is equal to the unknown parameter, N), leading to the use of a reversible jump algorithm (King and Brooks 2008) or super-population approach (Durban and Elston 2005; Royle et al. 2007). To address these issues King et al. (2016) proposed a computationally efficient semi-complete data likelihood model fitting approach, combining a data augmentation approach for the individual heterogeneity terms of observed individuals, with a numerical integration scheme for the likelihood component corresponding to the unobserved individuals. A similar approach was proposed by Bonner and Schofield (2014), for the case of individual continuous covariates for closed populations (assumed constant within the study period), using a Monte Carlo approach to perform the numerical integration necessary for the likelihood component associated with the unobserved individuals.
2.3 Open Capture–Recapture Models: Observed Heterogeneity
We consider Cormack–Jolly–Seber-type (CJS) models (Cormack 1964; Jolly 1965; Seber 1965) for open populations, which permit entries and exits from the population over the study period. We focus on the case where the survival probabilities are modelled as a function of individual time-varying continuous covariates, to explain the individual and temporal variability.
Notationally, we let \(y_{it}\) denote the covariate value associated with individual \(i=1,\ldots , n\) at time \(t=f_i, \ldots ,T\); and set \(\varvec{y}_i = \{y_{it}:t=f_i,\ldots ,T\}\). The survival probability is specified as a function of the covariate values such that \(h(\phi (y_{it})) = \beta _0 + \beta _1 y_{it}\), for all \(t=f_i,\ldots ,T-1\) and \(i=1,\ldots ,n\), where h denotes some function that maps to the interval [0, 1]; and \(\beta _0\) and \(\beta _1\) denote the corresponding regression parameters. Similarly we may also specify the recapture probabilities to be a function of the covariate such that \(h(p(y_{it})) = \gamma _0 + \gamma _1 y_{it}\), for \(t=f_i+1,\ldots ,T\) and \(i=1,\ldots ,n\), assuming the same functional form for h for simplicity; and where \(\gamma _0\) and \(\gamma _1\) are the associated regression parameters. For notational convenience, we let \(\varvec{\beta }=\{\beta _0, \beta _1\}\) and \(\varvec{\gamma }=\{\gamma _0, \gamma _1\}\). Further we define the stochastic model for the covariate values, assuming a first-order Markovian process, such that, for \(t=f_i,\ldots ,T-1\) and \(i=1,\ldots ,n\),
Clearly, suitable covariate models will be dependent on the given covariate(s) and biological knowledge. We note that in the case where the covariate value may not be observed at initial capture we also need to specify an initial state distribution for the initial covariate values. However, for simplicity, we assume the covariate values at initial capture are known for each individual, as is the case in our case study, but the approach is easily generalisable.
For capture–recapture studies we do not observe all the individual covariate values. Assuming that the covariate model is stochastic, if an individual is unobserved the associated covariate value is, by definition, also unknown; further if an individual is observed, the covariate value may still not be recorded. Finally, we let \(\varvec{\zeta }^1_i\) denote the set of times for which the covariate values are observed for individual i and \(\varvec{\zeta }^0_i\) the set of times following initial capture for which the covariate value is unknown for individual i.
To express the likelihood, we let \(\varvec{y}^{\mathrm{obs}}_i = \{y_{it}: t \in \varvec{\zeta }^1_i\}\) and \(\varvec{y}^{\mathrm{mis}}_i = \{y_{it}: t \in \varvec{\zeta }^0_i\}\) denote the observed and unobserved covariate values associated with individual \(i=1,\ldots ,n\). The full set of observed and unobserved covariate values are \(\varvec{y}^{\mathrm{obs}} = \{\varvec{y}_{i}^{\mathrm{obs}} : i=1,\ldots ,n \}\) and \(\varvec{y}^{\mathrm{mis}} = \{\varvec{y}_{i}^{\mathrm{mis}} : i=1,\ldots ,n\}\). The model parameters are \(\varvec{\theta }= \{\varvec{\beta }, \varvec{\gamma }\}\), with covariate parameters \(\varvec{\psi }= \{\mu _1,\ldots ,\mu _{T-1},\sigma ^2_y\}\). The observed data likelihood in Eq. (1) is given by,
and is again analytically intractable. The term \(f(\varvec{x}_i| \varvec{y}_i, \varvec{\theta })\) denotes the complete data likelihood component corresponding to the probability of the capture history \(\varvec{x}_i\); and \(f(\varvec{y}_i|\varvec{\psi })\) the joint probability density function of the covariate values associated with individual i. The probability of a given capture history, conditional on initial capture and all covariate values \(\varvec{y}_i\), is given by,
where \(\chi _{i \ell _i}\) denotes the probability that individual i is not recaptured again after time \(\ell _i\). We can express \(\chi _{i t}\) via the recursive function, \( \chi _{i t} = 1 - \phi (y_{it}) + \phi (y_{it})(1-p(y_{i t+1}))\chi _{i t+1}, \) such that \(\chi _{i T} = 1\), for all \(i=1,\ldots ,n\). The covariate model component of the observed data likelihood, conditioning on the initial covariate value (which we assume to be known, but can easily be relaxed by the inclusion of an initial state distribution) is given by,
where \(f(y_{i t+1}|y_{it},\varvec{\psi })\) denotes the associated density for the given covariate model.
Previous attempts for dealing with missing covariate values include both classical and Bayesian model-fitting approaches. In particular, Catchpole et al. (2004) derived a conditional likelihood approach, conditioning on only the known observed covariate values. This approach is computationally fast but leads to a (potentially substantial) reduction in the precision of the parameter estimates due to the amount of discarded information (Bonner et al. 2010); and cannot be applied when the observation process parameters (i.e. capture probabilities) are covariate dependent. To use all the available information, Worthington et al. (2015) consider a two-step multiple imputation approach, which involves initially fitting a model to only the observed covariate values and imputing the unobserved covariates before conditioning on these imputed values and using a complete-case likelihood approach for the associated capture histories. Alternatively Langrock and King (2013) numerically approximate the likelihood by finely discretising the integrals and estimate the integral via a hidden Markov model, providing improved parameter estimates. The integral can be made arbitrarily accurate by increasing the level of discretisation. However there is a trade-off between the accuracy of the estimate and the computational expense. Finally, within a Bayesian framework, a data augmentation approach has been applied, treating the missing covariate values as auxiliary variables and sampling from the joint posterior distribution of the parameters and auxiliary variables (Bonner and Schwarz 2006; King et al. 2008).
3 Laplace Approximation
The Laplace approximation is a numerical closed-form approximation of an integral and can be regarded as an alternative form of Gauss–Hermite quadrature (Liu 1994). The underlying idea of the Laplace integration is to approximate the negative log-likelihood by a second (or higher) order Taylor expansion. When the negative-log likelihood is well approximated by a Gaussian curve the Laplace approximation can be shown to have high precision. In particular, in a study from Liu (1994) the standard error of the estimate was shown to be of order \(O(m^{-1})\), where m denotes the number of observations. Adding in further leading terms can further improve the accuracy to the order of \(O(m^{-2})\) (Wong and Li 1992; Breslow and Lin 1995; Raudenbush et al. 2000). Using an analytical expression for the Laplace approximation is generally only feasible when the dimension of the integral is small (for example, of dimension 2 or 3) due to the computational complexity in computing the higher order derivatives. However, numerical approximations of the required derivatives can be obtained using automatic differentiation. In particular we use the Template Model Builder (TMB) automatic differentiation tool developed by Kristensen et al. (2016) that enables the use of the Laplace approximation using a computationally efficient implementation. We apply the Laplace approximation to individual heterogeneity capture–recapture models applying the TMB tool for numerically calculating the derivatives, when these are analytically intractable. We note that Laplace approximations have been used previously for capture–recapture models but within a Bayesian context for approximating the marginal posterior densities of the parameter of interest (Smith 1991; Chavez-Demoulin 1999).
3.1 Closed \(M_h\)-type Models
We consider the general \(M_{tbh}\) model with corresponding likelihood specified in Eq. (2). The integrand of the likelihood can be rewritten in exponential form, such that,
where,
for \(i \in \{0,1,\ldots ,n\}\). Dropping the subscript notation on i for notational brevity, let \(\hat{\epsilon }\) denote the value of \(\epsilon \) that minimises \(g(\varvec{x}, \epsilon |\varvec{\theta }, \sigma ^2)\) given model parameters \(\varvec{\theta }\) and heterogeneity parameter \(\sigma ^2\), so that \(g'(\varvec{x}, \epsilon |\varvec{\theta }, \sigma ^2) = 0\) and \(g''(\varvec{x}, \epsilon |\varvec{\theta }) > 0\). A second-order Taylor series expansion is given by,
Laplace’s method approximates the integrands in Eq. (4) using the properties of normal density functions such that the contribution to the observed data likelihood takes the form,
To improve the accuracy of the approximation, we can also consider a higher-order Laplace approximation involving higher-order derivatives (Raudenbush et al. 2000). We use the fourth-order Taylor expansion to obtain the fourth-order Laplace approximation. Applying the one-dimensional Laplace approximation on the integral yields,
where \(g^{(3)}(.)\) and \(g^{(4)}(.)\) denote the third and fourth derivatives with respect to the random effect term \(\epsilon \). A closed form expression for the fourth-order Laplace approximation is presented in Web Appendix A of the Supplementary Material where we assume the recapture probabilities are specified using the logistic function, so that \(\text{ logit } (p_{it}) = \alpha _t + \lambda S_{it} + \epsilon _i\).
3.2 CJS Model with Individual Time-Varying Continuous Covariates
For the open population CJS model with individual time-varying continuous covariates, the observed data likelihood in Eq. (1) can be expressed in the form,
such that for \(i=1,\ldots ,n\),
Applying the multivariate k-dimension second-order Laplace approximation, we obtain,
where \(\hat{\varvec{y}}^{\mathrm{mis}}_i\) denotes the value of \(\varvec{y}^{\mathrm{mis}}_i\) that minimises \(g(\varvec{x}_i, \varvec{y}_i| \varvec{\theta }, \varvec{\psi })\). There is no closed form for the derivatives (due to the \(\chi \) term) and so we use numerical automatic differentiation function provided in TMB, to evaluate the Laplace approximation for this model.
4 Simulation Study
To assess the performance of the Laplace approximation for both closed and open capture–recapture models we conduct a simulation study, using 1000 datasets for each simulation. For the closed population \(M_{h}\)-type models, we apply both the second and fourth order Laplace approximations (LA2 and LA4, respectively) and compare with a Gauss–Hermite quadrature (GHQ) approximation. For the open population CJS model with covariates we compare the Laplace approximation with an HMM approximation (Langrock and King 2013). All methods use TMB for computational comparability for calculating the MLEs of the parameters.
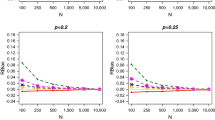
Appendix B of the Supplementary Material provides a detailed discussion of the simulation study and associated results. For the closed population \(M_h\)-type models the MLEs of the parameters, N and \(\sigma \), appear to be slightly negatively biased. However this bias was consistently less for LA4 and GHQ than for LA2. Further, the coverage probabilities for the LA2 approximation were also consistently smaller than the alternative approaches. See Table 1 of Appendix B for further details. We conducted a further simulation study focusing on model \(M_h\) to investigate the performance of the Laplace approximations and GHQ for increasing values of the individual heterogeneity variance, \(\sigma ^2\), as White and Cooch (2017) showed that as \(\sigma ^2\) increases the model-fitting becomes more challenging. Within our study, the LA2 approximation again performs relatively poorly; while the performance of the LA4 and GHQ approaches are very similar in terms of both relative bias and coverage probabilities (see Table 2 of Appendix B). Of further note, for the GHQ approach the width of the confidence interval increases as \(\sigma \) increases. This relationship is not observed for LA4 with similar width confidence intervals across the different values of \(\sigma \), yet both approximations return very similar levels of coverage probabilities for the parameters. For the CJS model we consider a range of scenarios, based on sample size (\(n=200,400\)), capture regimes (\(p=0.5,0.75\)) and length of study \((T=4,6\)). We assume that there is a single covariate and consider two possible covariate models over time corresponding to (i) a random walk; and (ii) a random walk with time-dependent effects. The second-order Laplace approach is compared to the alternative HMM approximation (Langrock and King 2013). For all scenarios, both approaches perform consistently well and similarly in terms of estimating the model parameters (see Tables 3 and 4 of Appendix B).
Finally, we consider the comparative computational expense. The Laplace approximations are consistently faster than the competing methods across all models, however as the model complexity increases, this difference is accentuated. For example, for model \(M_h\) the Laplace approximations are nearly twice as fast at evaluating the log-likelihood function as the given implementation of GHQ; but for model \(M_{th}\) this increases to 8–10 times faster. For CJS-type models the differential in computational expense is even more substantial. For example, the Laplace approximation was often (at least) one order of magnitude faster, and dependent on the size of the data and implementation of the HMM approximation, increases to two orders of magnitude faster. For further discussion, and more specific details regarding computational comparisons, see Appendix B.
5 Examples
We consider two case studies corresponding to the closed \(M_h\)-type models (St. Andrews golf tees data) and open CJS model with individual time-varying continuous covariates (meadow voles). We again compare the Laplace approximation with alternative approaches. All the codes used in these example are provided in the github repository detailed in the information regarding additional Supplementary Material.
5.1 St. Andrews Golf Tees
We consider the St. Andrews golf tees data from Borchers et al. (2002). The dataset consists of \(N=250\) tees differing in size, colour and visibility resulting in individual capture heterogeneity. A total of \(T=8\) independent observers (i.e. capture occasions) were assigned to predefined transects and recorded all golf tees observed. A total of 546 observations were recorded and \(n=162\) unique tees observed in the study (additional size/colour data were not recorded).
Borchers et al. (2002) showed that omitting the presence of individual heterogeneity vastly underestimates the true population size, thus we consider the set of closed population models with individual heterogeneity present. Table 1 provides the estimated population size and \(95\%\) non-parametric bootstrap confidence interval fitted to the four individual heterogeneity \(M_h\)-type models for the Laplace approximations and GHQ approach. In general, the higher order Laplace approximation (LA4) and the GHQ give relatively similar maximum likelihood estimates for N, varying from approximately 242 to 262; while the lower order Laplace approximation (LA2) gives somewhat varying estimates, as previously observed within the simulation study in Sect. 4. The higher order Laplace approximation tends to consistently produce slightly larger estimates of N than the GHQ approach for all individual heterogeneity models. For example, the estimates of N under \(M_h\) model are 251.3 and 242.4 for the LA4 and GHQ approaches, respectively.
The bootstrap confidence intervals for the GHQ approach are noticeably wider than the LA4 approximation, with a consistently substantially larger upper limit (we note that the lower limit is bounded by the number of observed individuals). In particular, the highest upper bound of the LA4 approximation is approximately 310, with the width ranging from 90 to 100; while the lowest upper bound in the GHQ approach is 358 and the widths generally double. King et al. (2008) report a similar uncertainty interval as the LA4 approximation, using a Bayesian approach with a model-averaged 95% credible interval of [194, 288], over the same set of models. Further, the estimate of \(\sigma \) for each of these models is relatively large (approximately 2 for all fitted models). We note that as observed in the second simulation study (see Sect. 4 and Appendix B), as \(\sigma \) increases, the width of the 95% confidence intervals for N using the GHQ approach are increasingly larger than for the Laplace approximations, yet providing comparable coverage probabilities.
Finally, we compared the comparative computational times. In general, the computational speed is fast in terms of absolute time, and on the order of milliseconds for each of the methods. However, comparing the Laplace approximations to GHQ, the Laplace approaches are approximately twice as fast for model \(M_h\), increasing to fives times as fast for model \(M_{tbh}\) (Table 1).
5.2 Meadow Voles
We consider capture–recapture data collected on meadow voles (Microtus pennsylvanicus) at Patuxent Wildlife Research Center, Laurel, Maryland over \(T=4\) capture occasions from 1981 to 1982 (Nichols et al. 1992). A total of 512 voles were observed over the study period. When an individual was observed, its corresponding body mass was also recorded. We follow Bonner and Schwarz (2006) by classifying individuals as immature (body mass \(\le 22\) g) and mature (body mass \(> 22\) g) and consider data only for the mature voles observed for the first time prior to the final capture occasion. This provides a total of \(n=199\) unique capture histories corresponding to a total of 450 observed sightings and associated body mass recordings. We note that approximately 40% of body mass recordings were unknown, following initial capture.
We follow Bonner and Schwarz (2006) and consider the model where the survival and recapture probabilities are dependent on body mass. In particular, we let \(y_{it}\) denote the body mass of individual \(i=1,\ldots ,n\) at time \(t=f_i,\ldots ,T-1\) and set,
Similarly, we specify the model for body mass to be of the form,
for \(i=1,\ldots ,n\) and \(t=f_i+1,\ldots ,T\). The set of model parameters is \(\varvec{\theta }= \{\beta _0,\beta _1,\gamma _0,\gamma _1\}\), and the heterogeneity parameters \(\varvec{\psi }= \{\mu _1,\mu _2,\mu _3,\sigma ^2\}\). All covariate values were recorded when an individual was observed, so we do not need to specify an initial distribution for body mass.
We compared the Laplace approximation, HMM-approximation using 20 intervals (Langrock and King 2013), two-step multiple imputation approach (Worthington et al. 2015) and Bayesian data augmentation approach (as fitted by Bonner and Schwarz 2006). Figure 1 provides the parameter estimates of the fitted CJS model for the different approaches, in terms of MLE/posterior mean and associated 95% confidence/credible interval. All approaches provide generally similar results, and in particular we note that the results for the Laplace approximation and HMM-approximation are very similar. There are however some differences in the results obtained via the two-step multiple imputation approach for the parameters associated with recapture probability in terms of the MLEs and with noticeably larger confidence intervals (the latter is also true for the estimation of \(\sigma \)). Some differences are not unexpected since the regression model parameters are estimated independently by fitting the given covariate model to the observed covariate values only, ignoring the capture observations.
Finally, we compared the associated computational times for each of the different approaches. To obtain the MLE of the parameters, the Laplace approximation takes \(<1\) s; the multiple imputation approach approximately 3 s; and the HMM-approximation approximately 9 s for these data. Thus, using 999 bootstrap replicates to obtain the 95% confidence intervals, the computation times are of the order of approximately 15 min; 45 min and 2.5 h for the Laplace approximation, imputation approach and HMM-approximation, respectively. The Bayesian data augmentation approach using a Markov chain Monte Carlo algorithm will depend on the updating algorithm used, number of iterations required for the Markov chain to converge to the stationary distribution and to obtain reliable posterior summary statistics with small Monte Carlo error following convergence and thus will be comparatively slower, particularly in relation to the fast Laplace approximation.
6 Discussion
In this paper, we describe a Laplace approximation to estimate the analytically intractable observed data likelihood for capture–recapture models in the presence of individual heterogeneity. The complexity of the likelihood function influences the order of the Taylor expansion that can be analytically calculated. For closed population \(M_h\)-type models a fourth-order expression can be analytically derived; whereas for the CJS model with continuous time-varying covariates we use automatic differentiation (via TMB) to obtain the necessary numerical derivatives, as they are analytically intractable. The Laplace approximation for these models provide a reliable and efficient mechanism for evaluating the likelihood function, and hence obtaining the maximum likelihood estimates, and associated confidence intervals.
In particular, comparing this approach to the current “gold-standards”, namely GHQ for \(M_h\)-type models, and an HMM-approximation for the CJS model with continuous covariates, the Laplace approximation consistently performs at least as well but at substantially lower computational cost. However, we note that for the \(M_h\)-type models, the fourth-order Laplace approximation is required for this performance. Further, for the scenarios considered, the coverage probabilities were essentially identical between the fourth-order Laplace approximation and the GHQ approach, yet the width of the associated 95% confidence intervals were significantly larger for the quadrature approach with increasing individual heterogeneity variability (i.e. \(\sigma ^2\)). Wider confidence intervals for increasing variability is also discussed by White and Cooch (2017) when using the quadrature approach. Understanding this apparent difference is the focus of current research. In addition the Laplace approximation is scalable to higher dimensions and thus this approach is potentially a very attractive avenue to pursue for more complex models (for example, in the presence of multiple continuous individual covariates), particularly as the GHQ and the HMM approximation generally suffer from the curse of dimensionality (Langrock and King 2013). Huber et al. (2004) explain that summation-based approaches such as GHQ and HMM may have larger bias when the dimension of integrals increases. The reason of this behaviour is due to GHQ and HMM-approximation being based on pre-specified and fixed quadrature points. These fixed points can easily become too coarse, particular in higher dimensions, such that the peak of the log-likelihood is missed.
Computational efficiency continues to be an important consideration, as models become more complex and/or datasets/studies increase in size. For example, Warton et al. (2015) describe and compare several approaches in terms of speed and accuracy for fitting joint ecological mixed models, including Laplace approximations, adaptive quadrature, data imputation approaches and variational approximations. Within their applications considered, the Laplace approximation was again a very computationally efficient approach, but less accurate for small samples; while adaptive quadrature appeared a reasonable compromise between accuracy and speed. The Expectation–Maximisation (EM) algorithm and Bayesian data augmentation were accurate but relatively slow. Variational approximations, appeared to be as computationally efficient as Laplace approximations whilst also providing moderately accurate estimates. Further, Niku et al. (2019) showed that variational approximations coded in TMB had smaller bias for negative binomial generalized linear latent variable models compared with the second order Laplace approximation. Exploring the use of variational approximations for capture–recapture models is also an area of current research, as well as investigating the robustness of Laplace approximation to models where the individual heterogeneity component is non-Gaussian.
7 Supplementary Material
Web Appendices referenced in Sects. 3.1, 4 and 5.1 are available with this paper in the online Supplementary Material. The codes used in this paper can be assessed at https://github.com/riki-herliansyah/capture-recapture.
References
Bonner S, Schofield M (2014) MC(MC)MC: exploring Monte Carlo integration within MCMC for mark–recapture models with individual covariates. Methods Ecol Evol 5:1305–1315
Bonner SJ, Schwarz CJ (2006) An extension of the Cormack–Jolly–Seber model for continuous covariates with application to Microtus pennsylvanicus. Biometrics 62:142–149
Bonner SJ, Morgan BJT, King R (2010) Continuous covariates in mark–recapture–recovery analysis: a comparison of methods. Biometrics 66:1256–1265
Borchers D, Buckland ST, Zucchini W (2002) Estimating animal abundance: closed populations. Springer, London
Breslow NE, Lin X (1995) Bias correction in generalised linear mixed models with a single component of dispersion. Biometrika 82:12
Catchpole EA, Morgan BJT, Coulson T (2004) Conditional methodology for individual case history data. J R Stat Soc Ser C (Appl Stat) 53:123–131
Chao A, Yip PS, Lee S-M, Chu W (2001) Population size estimation based on estimating functions for closed capture–recapture models. J Stat Plan Inference 92:213–232
Chavez-Demoulin V (1999) Bayesian inference for small-sample capture–recapture data. Biometrika 55:727–731
Cormack RM (1964) Estimates of survival from the sighting of marked animals. Biometrika 51:429–438
Coull BA, Agresti A (1999) The use of mixed logit models to reflect heterogeneity in capture–recapture studies. Biometrics 55:294–301
Dorazio RM, Royle AJ (2003) Mixture models for estimating the size of a closed population when capture rates vary among individuals. Biometrics 59:351–364
Durban JW, Elston DA (2005) Mark–recapture with occasion and individual effects: abundance estimation through Bayesian model selection in a fixed dimensional parameter space. J Agric Biol Environ Stat 10:291–305
Gimenez O, Choquet R (2010) Individual heterogeneity in studies on marked animals using numerical integration: capture–recapture mixed models. Ecology 91:951–957
Huber P, Ronchetti E, Victoria-Feser M-P (2004) Estimation of generalized linear latent variable models. J R Stat Soc Ser B (Stat Methodol) 66:893–908
Huggins R, Hwang W-H (2011) A review of the use of conditional likelihood in capture–recapture experiments. Int Stat Rev 79:385–400
Jolly GM (1965) Explicit estimates from capture–recapture data with both death and immigration-stochastic model. Biometrika 52:225–247
King R, Brooks SP (2008) On the Bayesian estimation of a closed population size in the presence of heterogeneity and model uncertainty. Biometrics 64:816–824
King R, McCrea R (2019) Capture–recapture methods and models: estimating population size. Handbook of statistics, vol 40. Elsevier, pp 33–83
King R, Brooks SP, Morgan BJT, Coulson T (2006) Factors influencing soay sheep survival: a Bayesian analysis. Biometrics 62(1):211–220
King R, Brooks SP, Coulson T (2008) Analyzing complex capture–recapture data in the presence of individual and temporal covariates and model uncertainty. Biometrics 64:1187–1195
King R, McClintock BT, Kidney D, Borchers D (2016) Capture–recapture abundance estimation using a semi-complete data likelihood approach. Ann Appl Stat 10:264–285
Kristensen K, Nielsen A, Berg CW, Skaug H, Bell BM (2016) TMB: automatic differentiation and Laplace approximation. J Stat Softw 70(5):1–21. https://doi.org/10.18637/jss.v070.i05
Langrock R, King R (2013) Maximum likelihood estimation of mark–recapture–recovery models in the presence of continuous covariates. Ann Appl Stat 7:1709–1732
Link WA (2003) Nonidentifiability of population size from capture–recapture data with heterogeneous detection probabilities. Biometrics 59:1123–1130
Link WA (2006) Response to “On identifiability capture-recapture models” by Holzmann, Munk and Zucchini. Biometrics 62:936–939
Liu Q (1994) A note on Gauss–Hermite quadrature. Biometrika 81:7
McCrea RS, Morgan BJT (2015) Analysis of capture–recapture data. CRC Press, Boca Raton
Nichols JD, Sauer JR, Pollock KH, Hestbeck JB (1992) Estimating transition probabilities for stage-based population projection matrices using capture–recapture data. Ecology 73:306–312
Niku J, Brooks W, Herliansyah R, Hui FKC, Taskinen S, Warton DI (2019) Efficient estimation of generalized linear latent variable models. PLoS ONE 14:e0216129
Otis DL, Burnham KP, White GC, Anderson DR (1978) Statistical inference from capture data on closed animal populations. Wildl Monogr 62:1–135
Pledger S (2000) Unified maximum likelihood estimates for closed capture–recapture models using mixtures. Biometrics 56:434–442
Pledger S, Pollock KH, Norris JL (2003) Open capture–recapture models with heterogeneity. I Cormack–Jolly–Seber. Biometrics 59:786–794
Raudenbush SW, Yang M-L, Matheos Y (2000) Maximum likelihood for generalized linear models with nested random effects via high-order, multivariate Laplace approximation. J Comput Gr Stat 9:131–157
Rosenberg DK, Overton WS, Anthony RG (1995) Estimation of animal abundance when capture probabilities are low and heterogeneous. J Wildl Manag 59:252
Royle JA (2008) Modeling individual effects in the Cormack–Jolly–Seber model: a state-space formulation. Biometrics 65:364–370
Royle JA, Dorazio RM, Link WA (2007) Analysis of multinomial models with unknown index using data augmentation. J Comput Gr Stat 16:67–85
Schwarz CJ (2001) The Jolly–Seber model: more than just abundance. J Agric Biol Environ Stat 6:195–205
Seber GAF (1965) A note on the multiple-recapture census. Biometrika 52:249–259
Seber GAF, Schofield MR (2019) Capture–recapture: parameter estimation for open animal populations. In: Statistics for biology and health. Springer, Switzerland
Smith PJ (1991) Bayesian analyses for a multiple capture–recapture model. Biometrika 78:399–407
Stoklosa J, Hwang W-H, Wu S-H, Huggins R (2011) Heterogeneous capture–recapture models with covariates: a partial likelihood approach for closed populations. Biometrics 67(4):1659–1665
Warton DI, Blanchet FG, O’Hara RB, Ovaskainen O, Taskinen S, Walker SC, Hui FK (2015) So many variables: joint modeling in community ecology. Trends Ecol Evol 30:766–779
White GC, Cooch EG (2017) Population abundance estimation with heterogeneous encounter probabilities using numerical integration: individual heterogeneity and abundance estimation. J Wildl Manag 81:322–336
Wong WH, Li B (1992) Laplace expansion for posterior densities of nonlinear functions of parameters. Biometrika 7:393–398
Worthington H, King R, Buckland ST (2015) Analysing mark–recapture–recovery data in the presence of missing covariate data via multiple imputation. J Agric Biol Environ Stat 20:28–46
Acknowledgements
We are grateful to Simon Bonner for providing the vole dataset. RH was supported by the Indonesia Endowment Fund for Education (Lembaga Pengelola Dana Pendidikan-LPDP), Ministry of Finance Republic of Indonesia. RK was supported by the Leverhulme research fellowship RF-2019-299.
Funding
Funding was provided by the Leverhulme research fellowship (Grant Number RF-2019-299), the Indonesia Endowment Fund for Education (Lembaga Pengelola Dana Pendidikan-LPDP), Ministry of Finance Republic of Indonesia.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Herliansyah, R., King, R. & King, S. Laplace Approximations for Capture–Recapture Models in the Presence of Individual Heterogeneity. JABES 27, 401–418 (2022). https://doi.org/10.1007/s13253-022-00486-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13253-022-00486-2