1 Introduction

Basic approaches to evolutionary game theory assume that the individuals are players, strategies are inheritable traits, and fitness constitutes the payoff. However, we can imagine situations where not all individuals that are carriers of the strategy genes are active interacting players. This can occur when sexual reproduction is explicitly considered and only one sex can express the strategies. The classical problem of this type is the evolution of the sex ratio, which was the first problem in evolutionary theory that involved mathematical reasoning. This was done by German biologist Carl Dusing [11]. He argued that the fitness of a female using a given sex ratio strategy could be described by the number of her grandoffspring. In the simplest version derived under assumptions of equal mortality rates and parental expenditures for both sexes, this function can be denoted in the following way:

$$\begin{aligned} W(P_{i} ,\,P)=\frac{k^{2}}{4}(1-P)\left( {\frac{1-P_{i} }{1-P}+\frac{P_{i} }{P}} \right) =\frac{k^{2}}{4}\left( {1-P_{i} +\frac{1-P}{P}P_{i} } \right) , \end{aligned}$$
(1)

where \(P_{i} \) is the individual strategy (offspring’s sex ratio), P is the population sex ratio and k is the average brood size of the female. By the individual strategy, we understand that female control over offspring can be realized by selective abortions; this implies that the female individual can be assumed as the strategic agent. Note that (1) considers only the reproductive success of the focal female as the active strategic agent. The impact of males as passive carriers is not explicitly considered. The interpretation of (1) in the light of the new results will be discussed in this paper in Sects. 3.1 and 4. Similar verbal reasoning was proposed by Fisher (1930). By application of this fitness measure, it can be shown that the average female strategy of 0.5 is evolutionarily stable. This approach to strategic analysis has dominated the game theoretic literature [7, 19, 30, 33, 34]) and can be found in books on population genetics [10, 20]. Sex ratio theory has inspired the development of other theoretic approaches, such as sex allocation theory [8, 36] and local mate competition models ([18]; Schall 2008). However, population genetics provides an alternative way of modelling sex ratio evolution based on the explicit tracing of the gene frequencies, mainly using discrete dynamics ([12, 13, 20] and summarized in [20]) or other methods such as calculation of the ancestral paths [16, 17]. In the population genetic models, evolution of states of subpopulations for both sexes is explicitly described by respective equations. Thus, the analysis is not limited to females as focal individuals as in Dusing’s model (1). The population genetic approach produces different predictions from the basic phenotypic models. It shows that stable population states should be characterized by stable compositions not only of the female but also of the male subpopulation, not simply by the average strategy of females as in basic game theoretic approaches. This leads to the distinction between two classes of modelling approaches, phenotypic and genetic, related to the sex ratio [36].

The genetic models can be analysed and interpreted in the spirit of the ESS approach, i.e., they can be used in the analysis of the fate of the rare mutant in the resident population (see, for example, [9] for the sex ratio case, and in general [14, 22, 23]). However, these approaches do not use core game theoretic notions, such as explicitly derived strategic payoff functions. We can imagine a complementary approach in which basic game theoretic methods (payoff functions associated with continuous replicator dynamics) are extended by description of the underlying genetic structure. In two previous papers [3, 4], an alternative synthetic approach to the modelling of sex ratio evolution was introduced. This was the first application of multipopulation replicator dynamics [2]. The new model focuses on the dynamics of sex ratio evolution and tries to combine the phenotypic strategic approach with an explicit genetic analysis. This new approach also combines game dynamics with sexual reproduction. It explicitly considers parental male individuals as the passive carriers of female sex ratio strategies (similarly to the population genetics models, [20]) that can be expressed by their daughters if they inherit the strategy from the father. This is important, since the rare invading mutants can be not only females but also males.

The first formulation of the model [3] focused on the trajectories of general population parameters (“global” in the sense that they affect the whole population), such as the primary and the secondary sex ratios, and showed that sex ratio evolution dynamics are biphasic. This is caused by the fact that simpler equations describing the male subpopulation and the secondary sex ratio converge to the neighbourhood of their attracting manifolds (nullclines) faster than the nonlinear dynamics of the female subpopulation (however, without separation of timescales). During the second, longer, phase, they follow the changes in their nullclines caused by the ongoing dynamics of the female subpopulation. During the first, shorter, phase, the population converges to equality between the primary and the secondary sex ratios.

In addition, another phenomenon can be observed, which is one of the topics of this paper. During the rapid phase, the male subpopulation is attracted by a unique state, conditional on the current state of the female subpopulation, called the male subpopulation equilibrium (thus the dynamics converge to the neighbourhood of the MSE manifold). This phenomenon is caused by the contribution of an individual to the fitness of individuals of other types (such as different sexes) by producing newborns of their type [3]. This result shows that the role of passive male carriers as fathers, not only as sons, is also very important. This means that the sex ratio of 0.5 cannot be regarded as just an example of the basic, single population evolutionarily stable strategy or state (ESS). However, this interpretation can be found in the basic textbooks [19, 33, 34]. In the sex ratio case, we need notions describing both sexes’ subpopulations and the proportion between them (similarly to the population genetic models).

This riddle was partially solved in the second paper [4], which focused on the selection of genes encoding individual strategies (“local” scope focused on the dynamics of the subpopulations of carriers of the particular strategy genes). Selection of these genes depends only on sex ratios in carrier subpopulations rather than directly on trait values encoded by such genes (this self-regulation process can be called the Fisherian mechanism; see Sections 2 and 3.1 in [4] for details). However, sex ratios in carriers’ subpopulations are determined by the action of female carriers of these genes and female partners of male carriers randomly drawn from the population in a process called the tug of war. This means that the activity of female carriers attracts the sex ratio among carriers of the particular gene to the value encoded by that gene, and the activity of random female partners attracts it to the actual value of the primary sex ratio. Then, the encoded traits are “local variables” affecting only the compositions of carrier subpopulations and are not explicitly visible in the “global” selection dynamics. The Fisherian mechanism and tug of war together constitute a process that can be regarded as double-level selection. Thus, the classical problem of sex ratio evolution is an important example in the current debate on the mechanisms of multilevel selection [25, 26, 32].

A question that arises concerns the role of the MSE phenomenon revealed by the first formulation [3] in the double-level selection process shown by the second formulation [4]. When the MSE state is reached, selection of strategies appears to work according to the values encoded by the genes. (This was shown by Lemma 1 in [3].) The new theory produces predictions similar to the classical theory; however, the mechanistic interpretation of the MSE phenomenon remained a mystery and will be analysed in the present paper. It should be emphasized that the MSE is a specific example of a more general problem. The impact of the passive carriers of unexpressed genes (strategies) on the proliferation of those genes (strategies) may appear in many applications of population genetics and evolutionary game theory. Similar dynamic population equilibria can emerge in problems other than sex ratio evolution, where some fraction of individuals does not exhibit inherited traits but transfer them to their offspring. However, sex ratio evolution is one of the many possible examples of complex self-regulation, where the passive gene carriers play an important role in the underlying mechanisms operating on many levels.

Therefore, the main goal of this paper is to show the importance of the passive carriers in the population processes. We will investigate the relationships between the MSE mechanism from [3] and the dynamic self-regulation mechanisms from [4] (i.e., the Fisherian mechanism and the tug of war) and their relationships in the process of double-level selection. Those results will allow for a comparison of the classical Dusing–Fisher–Shaw–Mohler fitness measure with an analogous static fitness function prepared according to the new approach. The next step is an investigation of the role of the MSE in the adjustment of the sex ratios in carriers’ subpopulations, which will reveal intriguing properties of the MSE manifold.

The following subsections will recall the formal details of the models presented in [3, 4] and briefly summarize the results obtained there. Starting in Sect. 2, new results will be presented.

1.1 Details of the Model

Assume that strategies are expressed by female carriers as in basic game theoretic approaches and in Dusing’s model [11]. There are u arbitrarily chosen individual strategies encoding the sex ratio among newborns of the female, described by \(P_{i} \in [0,1]\). There are \(x_{i} \) female and \(y_{i} \) male carriers of the strategy \(P_{i} \) in the population. Therefore, the population consists of \(x={\sum }_{i}x_{i} \) females and \(y={\sum }_{i}y_{i} \) males. Thus, \(f=[f_{1} ,\ldots ,\,f_{u} ]\) is the vector of frequencies of strategies of the female subpopulation, and \(m=[m_{1} ,\ldots ,\,m_{u} ]\) is an analogous vector for the male subpopulation (where \(f_{i} =x_{i} /x\) and \(\;m_{i} =y_{i} /y)\). \(P=y/(y+x)\) is the fraction of males in the population (a secondary sex ratio), and \({\sum }_{j}f_{j}P_{j} \) is the mean female subpopulation strategy (the primary sex ratio). Assume that each female produces k offspring according to haploid inheritance (with probability 0.5 for gene transfer from the focal parent). However, males are also gene carriers and transfer those genes to their offspring of both sexes. The influence of males can be described by the fitness exchange effect (i.e., daughters of male carriers affect the payoff of female carriers and sons of females affect the payoff of males). This allows for derivation (which is outlined in “Appendix 1”) of the following sex-specific payoff functions, describing explicitly the effects of sexual reproduction:

$$\begin{aligned} W_{m} (P_{i} ,\,P,\,f,\,m)= & {} k\frac{1-P}{2P}\left( {\sum }_{j}f_{j} P_{j} +\frac{f_{i} }{m_{i} }P_{i} \right) \quad -\text { payoff function of males} \end{aligned}$$
(2)
$$\begin{aligned} W_{f} \left( P_{i} ,\,P,\,f,\,m \right)= & {} \frac{k}{2}\left( \left( 1-P_{i} \right) +\frac{m_{i} }{f_{i} }\left( 1-{\sum }_{j}f_{j} P_{j} \right) \right) \, -\text { payoff function of females}\nonumber \\ \end{aligned}$$
(3)

Note that the structure of the above functions, describing growth rates proportional to the average per capita number of produced newborns of the same sex and strategy, explicitly describes the impact of sexual reproduction. Therefore, the obtained replicator dynamics (asexual in general) will also describe sexual reproduction. Now we have all elements needed to formulate the multipopulation replicator dynamics [2]. In the first paper [3], this took the following form:

$$\begin{aligned} \dot{{f}}_{i}= & {} f_{i} \left( {W_{f} (P_{i} ,\,P,\,f,\,m)-\bar{{W}}_{f} \left( {P,\,f,\,m} \right) } \right) \quad \hbox { for } \;i=(1,...,\,u-1),\\ \dot{{m}}_{i}= & {} m_{i} \left( {W_{m} (P_{i} ,\,P,\,f,\,m)-\bar{{W}}_{m} \left( {P,\,f,\,m} \right) } \right) \quad \hbox { for } \;i=(1,...,\,u-1),\\ \dot{{P}}= & {} P\left( {\bar{{W}}_{m} (P,\,f,\,m)-\bar{{W}}\left( {P,\,f,\,m} \right) } \right) , \end{aligned}$$

where \(\bar{{W}}_{m} (P,\,f,\,m)={\sum }_{j}m_{j}W_{m} (P_{i} ,\,P,\,f,\,m)\), \(\;\bar{{W}}_{f} \left( P,\,f,\,m \right) ={\sum }_{j}f_{j}W_{f} \left( P_{i} ,\,P,f,\,m \right) \), \( \bar{{W}}\left( {P,\,f,\,m} \right) =P\bar{{W}}_{m} (P,\,f,\,m)+(1-P)\bar{{W}}_{f} \left( {P,\,f,\,m} \right) \) are the respective average payoff functions of the male, the female and the whole populations (see [3] Appendix D for derivation). This leads to the following system of equations (see [3] Appendix E for the derivation):

$$\begin{aligned} \dot{{f}}_{i}= & {} k\left( \frac{f_{i} }{2}\left( 1-P_{i} \right) +\left( \frac{m_{i} }{2}-f_{i} \right) \,\left( 1-{\sum }_{j}f_{j} P_{j} \right) \right) \quad \hbox { for }\;i=(1,...,\,u-1), \end{aligned}$$
(4)
$$\begin{aligned} \dot{{m}}_{i}= & {} \frac{k}{2}\left( \frac{1-P}{P} \right) \,\left( f_{i} P_{i} -m_{i} {\sum }_{j}f_{j} P_{j} \right) \quad \hbox { for } \;i=(1,...,\,u-1), \end{aligned}$$
(5)
$$\begin{aligned} \dot{{P}}= & {} k(1-P)\left( {\sum }_{j}f_{j} P_{j} -P \right) . \end{aligned}$$
(6)

It was shown that, for biological reasons, we can limit the analysis of the model to values of the primary and the secondary sex ratios over the interval \((0,\,1)\). The above formulation is similar to population genetic models and is focused on the composition of the whole population. Subsystems (5) and (6) have a simple linear form and are rapidly attracted to close neighbourhood of their nullclines, which are male subpopulation equilibrium (discussed in the next section) and the equality of the primary and the secondary sex ratios. After that, during the second phase, the subsystem (4) slowly converges to its equilibrium. The state of the male subpopulation and the secondary sex ratio trace their nullclines, remaining in their close neighbourhood. During the transition between the fast and slow phase, quantitative changes in behaviour of the dynamics of (4) can occur [3]. The system converges to the state with an average female strategy (primary sex ratio) of 0.5 when it is possible (when 0.5 can be a linear combination of the strategy values) or to the monomorphic population of individuals carrying the strategy closest to 0.5. In [4], the model was modified by a change in coordinates where \(G=\left[ {G_{1} ,\ldots ,\,G_{u-1} } \right] \) is the vector of gene frequencies in the whole population (where \(G_{i} =(x_{i} +y_{i} )/(x+y))\) and \(M=[M_{1} ,\ldots ,\,M_{u} ]\) (where \(M_{i} =y_{i} /(x_{i} +y_{i} ))\) is the vector of the sex ratios in the subpopulations of carriers of the same strategy genes. This allows taking the perspective of a gene as a strategic agent. The fitness function of a gene encoding strategy \(P_{i}\) (interpreted as the average payoff of the adult carrier of the ith gene) described in the above coordinates and discussed in detail in Section 2 of [4] and Appendix B in [4] is therefore:

$$\begin{aligned} W_{g} (P_{i} ,\,G,\,M)= & {} M_{i} W_{m} (P_{i} ,G,M)+(1-M_{i} )W_{f} (P_{i} ,G,M)\nonumber \\= & {} \frac{k}{2}\left( \frac{1-P}{P}M_{i} +\left( {1-M_{i} } \right) \right) . \end{aligned}$$
(7)

Note that the fitness function \(W_{g}\) is independent of the value encoded by the individual strategy \(P_{i}\). The fitness of a gene is determined by the sex ratio in a subpopulation of its carriers, \(M_{\mathrm {i}}\). This leads to an alternative form of replicator equations [4]:

$$\begin{aligned} \dot{{G}}_{i}= & {} G_{i} \left( {W_{g} (P_{i} ,G,M)-\bar{{W}}(G,M)} \right) \quad \text {-dynamics of gene frequencies},\\ \dot{{M}}_{i}= & {} M_{i} \left( {W_{m} (P_{i} ,\,G,M)-W_{g} (P_{i} ,P,\,f,\,m)} \right) \quad \text {-dynamics of sex ratios in carrier subpopulations}, \end{aligned}$$

which take the form

$$\begin{aligned} \dot{{G}}_{i}= & {} G_{i} k\left( {\frac{1}{2}-P} \right) \,\left( {\frac{M_{i} }{P}-1} \right) \quad \hbox { for }\;i=(1,\ldots ,\,u-1), \end{aligned}$$
(8)
$$\begin{aligned} \dot{{M}}_{i}= & {} \frac{k}{2}\left( {M_{i} \left( {\frac{1-P}{P}} \right) \,\left( {\bar{{P}}_\mathrm{pr} -M_{i} } \right) +\left( {1-M_{i} } \right) \,\left( {P_{i} -M_{i} } \right) } \right) \quad \hbox { for } \;i=(1,\ldots ,\,u),\nonumber \\ \end{aligned}$$
(9)

where \(\bar{{P}}_\mathrm {pr} ={\sum }_{j}f_{j} P_{j} \). An analysis of the replicator equations based on the fitness function \({W}_{g}\) (see [4] sections 3.1 and 4.2) shows that changes in a gene pool can be described by the following inequalities.

$$\begin{aligned} G_{i} \text { increases when }P< & {} \frac{1}{2}\text { and }P<M_{i} \text { or } P>\frac{1}{2}\text { and }P>M_{i},\nonumber \\ G_{i} \text { decreases when }M_{i}< & {} P<\frac{1}{2}\text { or }M_{i}>P>\frac{1}{2}, \nonumber \\ G_{i} \text { is constant when }G_{i}= & {} 0\text { or }M_{i} =P\text { or } P=\frac{1}{2}. \end{aligned}$$
(10)

This process can be described as the Fisherian mechanism (see sections 3.1 and 4.2 in [4] for details). Thus, gene pool dynamics (8) depends on the current value of the secondary sex ratio P and the sex ratio in the subpopulation of carriers of a gene \(M_{i} \). The signs of the right-hand sides of Eq. (9) are determined by two bracketed terms. The first term \(\left( {\bar{{P}}_\mathrm{pr} -M_{i} } \right) \) is weighted by the fraction of male carriers \(M_{i} \) multiplied by average per capita number of their partners \(\left( {1-P} \right) /P\). The second term \(\left( {P_{i} -M_{i} } \right) \) is weighted by the fraction of female carriers \(\left( {1-M_{i} } \right) \). Thus, the dynamics of parameter \(M_{i}\) (9) is determined by the action of female carriers of strategy \(P_{i}\) as well as partners of male carriers of this strategy in a tug of war mechanism, which means that the activity of female carriers (the second term) attracts \(M_{i}\) to the value encoded by the gene \(P_{i}\) and the action of partners of male carriers (the first term) attracts \(M_{i }\) to the value of the females’ average strategy \(\bar{{P}}_\mathrm{pr} \). In [4], it was shown that for \(P_{i} \in (0,1]\) a unique attracting nullcline exists within the interval \(\left( {\bar{{P}}_\mathrm{pr} ,P_{i} } \right) \). For \(P_{i} =0\), the state \(M_{i }= 0\) can be stable in some specific cases (not important for this study).

1.2 The Male Subpopulation Equilibrium Phenomenon

The role of the male subpopulation composition was shown by population genetic models of sex ratio evolution [12, 13, 20, 29]. In the MSE state (see sections 2.2 and 5.2 in [3] for details), lying on the nullclines of Eq. (5), the condition

$$\begin{aligned} f_{i} P_{i} =m_{i} \bar{{P}}_\mathrm{pr} \end{aligned}$$
(11)

is satisfied for all strategies, and the subpopulation of males is in the state \(m^\mathrm{MSE}=\left[ {f_{1} P_{1} /\bar{{P}}_\mathrm{pr} ,\ldots ,\,f_{u} P_{u} /\bar{{P}}_\mathrm{pr} } \right] \). The dynamics of the female subpopulation are then described by the rules (according to Lemma 1 in [3]):

$$\begin{aligned} f_{i} \text { increases when }\bar{{P}}_\mathrm{pr}< & {} \textstyle {1 \over 2}\text { and } \bar{{P}}_\mathrm{pr}<P_{i} \text { or }\bar{{P}}_\mathrm{pr}>\textstyle {1 \over 2} \text { and }\bar{{P}}_\mathrm{pr}>P_{i} ,\nonumber \\ f_{i} \text { decreases when }P_{i}< & {} \bar{{P}}_\mathrm{pr} <\textstyle {1 \over 2}\text { or }P_{i}>\bar{{P}}_\mathrm{pr} >\textstyle {1 \over 2},\nonumber \\ f_{i} \text { is stable when: }f_{i}= & {} 0\text { or }f_{i} =1\text { or }P_{i} =\bar{{P}}_\mathrm{pr}. \end{aligned}$$
(12)

Note that this mechanism is similar to the Fisherian mechanism of evolution of gene frequencies (10). This suggests that the role of the MSE is important in the process of sex ratio self-regulation. The influence of male carriers is more important for the behaviour of the system than the value of the secondary sex ratio P. The MSE is described by the nonintuitive condition \(f_{i} P_{i} =m_{i} \bar{{P}}_\mathrm{pr} \). This paper will attempt to elucidate the nature of the MSE and specify how it affects the Fisherian and tug of war mechanisms.

1.3 The Goals of the Paper

In this paper, we will analyse three problems related to the framework presented above:

  1. (a)

    We will calculate the equilibria of the tug of war dynamics (9) and analyse its relationships with the MSE equilibrium (11).

  2. (b)

    Using the results from point a) and the gene fitness function (7), we will construct the unbiased static fitness measure and compare it with the simplified approximation based on the assumption of the MSE equilibrium and the classical fitness measure (1).

  3. (c)

    We will analyse the quantitative properties of the MSE phenomenon and explain the underlying feedback mechanism.

Thus, the next section starts the presentation of the new results.

2 MSE as a Dynamic Equilibrium of the Demographic Process

Let us focus on the interpretation of the MSE phenomenon. Some insight into its nature will be revealed below. At the equilibrium of the selection process, the composition of the population (fractions of different strategies and sexes) will reflect the fractions of different types of individuals among newborns being introduced into the population. Thus, for example, the fraction of the male carriers of gene \(P_{i}\) (which is \(y_{i} /N)\) should be equal to the respective proportion of \(P_{i}\) male newborns produced (equal to \(f_{i} P_{i} )\). Note that the summation of the above relationships over all strategies \(\sum {y_{i} } /N=\sum {f_{i} P_{i} } \) leads to the condition \(P=\bar{{P}}_\mathrm{pr} \). Due to this condition, for each strategy, we can rescale the relationship \(y_{i} /N=f_{i} P_{i} \) to the fractions among male newborns and adults by \(y_{i} /\sum {y_{j} } =f_{i} P_{i} /\sum {f_{j} P_{j} } \). In effect, we obtain the MSE condition (11) denoted in the form \(m_{i} =f_{i} P_{i} /\sum {f_{j} P_{j} } \). This means that in the MSE state, the fraction of adult \(P_{i} \) males among all males is equal to the fraction of \(P_{i} \) male newborns among all male juveniles produced by female carriers of the genes. Thus, equality of the primary and secondary sex ratios is closely related to the MSE phenomenon. In the next sections, we will use those conditions together many times to prove interesting relationships.

2.1 The Relationship Between the MSE and the Tug of War Mechanism

As shown in the previous article [4], the sex ratio of the subpopulation of carriers of a given gene is self-regulated by the so-called tug of war mechanism mentioned here at the end of Sect. 1.1; this mechanism is described for each strategy by Eq. (9). Lemma 1 in [4] states that the above dynamics have a single stable restpoint. We can calculate this restpoint, define the symbol \(\Gamma \,=(1-P)/P\) as in [4]. Restpoints of (9) will satisfy the equation:

$$\begin{aligned} M_{i} \left( {\bar{{P}}_\mathrm{pr} -M_{i} } \right) \Gamma \,+\left( {1-M_{i} } \right) \,\left( {P_{i} -M_{i} } \right) =0, \end{aligned}$$

which can be presented in the form

$$\begin{aligned} \left( {1-\Gamma } \right) M_{i}^{2} +\left( {\bar{{P}}_\mathrm{pr} \Gamma -P_{i} -1} \right) M_{i} \,+P_{i} =0, \end{aligned}$$

which collapses to a linear equation with solution \(\tilde{{M}}_{i} \,=P_{i} /\left( {1+P_{i} -\bar{{P}}_\mathrm{pr} } \right) \) for \(\Gamma =1\). Thus, the unique equilibrium from the interior of the interval \((P_{i} ,\bar{{P}}_\mathrm{pr} )\) ([4], Lemma 1a) should be one of the roots of the above quadratic equation. Numerical solutions show that this will be

$$\begin{aligned} \tilde{{M}}_{i} =\frac{P_{i} -\bar{{P}}_\mathrm{pr} \Gamma +1-\sqrt{\left( {\bar{{P}}_\mathrm{pr} \Gamma -P_{i} -1} \right) ^{2}-4P_{i} \left( {1-\Gamma } \right) } }{2\left( {1-\Gamma } \right) }. \end{aligned}$$
(13)

Note that (13) is a monotonically increasing function of \(P_{i} \) for \(\Gamma <1\) and \(\Gamma >1\), which is determined by the factor \(4P_{i} \left( {1-\Gamma } \right) \) in the numerator and factor \(\left( {1-\Gamma } \right) \) in the denominator. A question arises concerning the relationships between the MSE phenomenon and equilibria and the dynamics of the tug of war process. The answer to this problem is described below by the following lemmas. Consider first the form of the MSE from the point of view of the sex ratio in the carrier subpopulation \(M_{i} \).

Lemma 1

The MSE condition (11) for strategy \(P_{i} \), according to the current value of \(\bar{{P}}_\mathrm{pr} \), is equivalent to the following sex ratio among \(P_{i} \) gene carriers:

$$\begin{aligned} \overline{\overline{M}}_{i} =\frac{P_{i} }{\Gamma \bar{{P}}_\mathrm{pr} +P_{i} } \quad \left( {\overline{\overline{M}}_{i} =\frac{P_{i} }{1+P_{i} -\bar{{P}}_\mathrm{pr} }\; \text{ when } \bar{{P}}_\mathrm{pr} =P} \right) . \end{aligned}$$
(14)

For proof, see “Appendix 2”.

Therefore, the MSE state is equivalent to the unique sex ratio in the carrier subpopulation \(\overline{\overline{M}}_{i} \). Let us focus on the role of \(\overline{\overline{M}}_{i} \) in the tug of war process, which is revealed below.

Lemma 2

  1. (a)

    For \(\overline{\overline{M}}_{i} \) and the current value of \(\bar{{P}}_\mathrm{pr} \), the dynamics (9) is attracted by the point

    $$\begin{aligned} \hat{{M}}_{i} =\frac{2P_{i} \bar{{P}}_\mathrm{pr} }{P_{i} +\bar{{P}}_\mathrm{pr}}. \end{aligned}$$
    (15)
  2. (b)

    \(\bar{{\bar{{M}}}}_{i} =\hat{{M}}_{i} \) for all i can be satisfied only when \(\bar{{P}}_\mathrm{pr} =P=0.5\).

For a proof, see “Appendix 3”.

Point a) shows that in general \(\overline{\overline{M}}_{i}\) is not an equilibrium of the tug of war mechanism (which is \(\hat{{M}}_{i} \) when carriers’ sex ratio equals \(\overline{\overline{M}}_{i} )\). Point b) shows the properties of a steady state when the equilibria of the tug of war mechanism are on the MSE manifold. The value of \(\overline{\overline{M}}_{i} \) determined by the MSE of the individual strategy \(P_{i} \) (14) is very important. This parameter is an argument of the fitness function of a gene \(W_{g} \) (7). Let us focus on the relationships between \(\tilde{{M}}_{i} \,\), \(\overline{\overline{M}}_{i} \) and \(\hat{{M}}_{i} \).

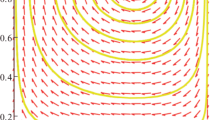
Let us illustrate this problem by numerical examples. Figure 1 shows the trajectories of the gene frequency dynamics (8) and the respective trajectories of the carrier sex ratio dynamics (9). The dynamics of gene frequencies is determined by the underlying dynamics of the carriers’ sex ratios and the secondary sex ratio, according to the rules (10). The growth or decrease in a particular gene frequency is determined by the excess of its carriers’ sex ratio \(M_{i} \,\) from the secondary sex ratio P and the deviation of P from 0.5. The trajectories of the dynamics of the carriers’ sex ratios mainly show the following pattern, depicted in Fig. 2. The trajectory is attracted by the equilibrium of the tug of war mechanism \(\tilde{{M}}_{i} \,\) and follows its changes. The equilibrium \(\tilde{{M}}_{i} \,\) converges to \(\hat{{M}}_{i} \), which is attracted by the MSE manifold represented by \(\overline{\overline{M}}_{i} \). Thus, \(\hat{{M}}_{i} \) can be regarded as the approximation of \(\tilde{{M}}_{i} \,\) in the neighbourhood of the MSE manifold. Therefore, different strategies are attracted by different values of \(\tilde{{M}}_{i} \) (which converge to the respective \(\hat{{M}}_{i} )\), and through these values they can be distinguished by natural selection operating on a second, higher level. We can use this prediction for the construction of the unbiased static fitness measures, free from disadvantages of the classical DFSM fitness measure. This will be the subject of the next section.

Fig. 1
figure 1

Trajectories of the gene frequency dynamics (8) and respective trajectories of the carrier sex ratio dynamics (9) for strategies \(P_{1} =0.1\), \(P_{2} =1\), \(P_{3} =0.7\). The initial conditions are \(G_{1} =0.8\), \(G_{2} =0.13\), \(G_{3} =0.07\) and \(M_{1} =0.9\), \(M_{2} =0.1\), \(M_{3} =0.1\). The growth or decrease in the particular gene frequency is determined by the excess of the ratio \(M_{i}/P\) from 1 and the deviation of P from 0.5 (see Eq. (8))

Full size image
Fig. 2
figure 2

Trajectories of the carriers’ sex ratios. The trajectories converge to the tug of war equilibria \(\tilde{{M}}_{i} \,\) (13), which are attracted to the MSE manifold \(\overline{\overline{M}}_{i} \) (14). With convergence to the MSE, the values \(\tilde{{M}}_{i} \,\) approach the neighbourhoods of their approximations \(\hat{{M}}_{i}\) (15)

Full size image

3 Construction of the Static Fitness Measures

This section examines the results of the classical theory according to the new approach. We can construct static fitness measures using the attractors of the carriers’ sex ratio obtained in the previous section. These fitness measures will assign fitness to the individual strategy under the assumption of equilibrium of the tug of war process. When we substitute \(\tilde{{M}}_{i} \,\) from (13) into the gene fitness function (7), we obtain the following static fitness function based on the assumption that the tug of war process has reached its equilibrium:

$$\begin{aligned} \tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} ,P)=\frac{k}{2}\left( {\frac{\bar{{P}}_\mathrm{pr} \Gamma -P_{i} -1+\sqrt{\left( {\bar{{P}}_\mathrm{pr} \Gamma -P_{i} -1} \right) ^{2}-4P_{i} \left( {1-\Gamma } \right) } }{2}+1} \right) . \end{aligned}$$
(16)

This function is quite complicated. However, in a sufficiently close neighbourhood of the MSE manifold, \(\tilde{{M}}_{i} \,\) (13) can be approximated by \(\hat{{M}}_{i} \,\) (15), which can be substituted into (7). This leads to the approximation of (16) by the much simpler function

$$\begin{aligned} \hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} ,P)=\frac{k}{2}\left( {\frac{2P_{i} \bar{{P}}_\mathrm{pr} }{P_{i} +\bar{{P}}_\mathrm{pr} }(\Gamma -1)+1} \right) . \end{aligned}$$
(17)

The classical static fitness measure (1) (described as the DFSM function in [3]) relies on the number of grand offspring of a female that express her individual strategy. It can be presented as

$$\begin{aligned} W(P_{i} ,P)=\frac{k^{2}}{4}\left( {\left( {1-P_{i} } \right) +P_{i} \Gamma } \right) =\frac{k^{2}}{4}\left( {\left( {\Gamma -1} \right) P_{i} +1} \right) . \end{aligned}$$
(1)

Note that the secondary sex ratio P in the above function describes the state of the population when the offspring of the focal female become mature. An additional assumption of nonoverlapping generations implying \(P=\bar{{P}}_\mathrm{pr} \) allows for the description of (1) as a function of the strategic composition of the population. However, we have shown that the condition \(P=\bar{{P}}_\mathrm{pr} \) in continuous models can be satisfied at an equilibrium of (6) only. This suggests that the condition \(P=\bar{{P}}_\mathrm{pr} \) assumes that offspring will interact only with their peers, and individuals of other generations are disregarded. Thus, in the general case, we can only assume \(P\approx \bar{{P}}_\mathrm{pr} \) as a simplified approximation. However, numerical simulations show that it can be quite good, and the bias is not serious in many cases.

We can now compare fitness function (16) with its approximations (17) and (1) to estimate the bias. Let us assume for simplicity that the mean brood size of a female is \(k=2\), which will remove this parameter from both formulae. In addition, assume for simplicity that \(P\approx \bar{{P}}_\mathrm{pr} \) (then \(\Gamma =(1-\bar{{P}}_\mathrm{pr} )/\bar{{P}}_\mathrm{pr} )\) to reduce the dimensionality of the system. Then, the fitness functions (16), (17) and (1) expressed in parameters \(P_{i} \) and \(\bar{{P}}_\mathrm{pr} \) will have form

$$\begin{aligned} \tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )= & {} \frac{\sqrt{\left( {\bar{{P}}_\mathrm{pr} +P_{i} } \right) ^{2}-\frac{4P_{i} \left( {2\bar{{P}}_\mathrm{pr} -1} \right) }{\bar{{P}}_\mathrm{pr} }} -\left( {\bar{{P}}_\mathrm{pr} +P_{i} } \right) }{2}+1, \end{aligned}$$
(18)
$$\begin{aligned} \hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )= & {} \frac{2P_{i} \bar{{P}}_\mathrm{pr} }{P_{i} +\bar{{P}}_\mathrm{pr} }\left( {\frac{1-\bar{{P}}_\mathrm{pr} }{\bar{{P}}_\mathrm{pr} }-1} \right) +1=\frac{2P_{i} \left( {1-2\bar{{P}}_\mathrm{pr} } \right) }{P_{i} +\bar{{P}}_\mathrm{pr} }+1, \end{aligned}$$
(19)
$$\begin{aligned}&W(P_{i} ,\bar{{P}}_\mathrm{pr} )=\frac{1-2\bar{{P}}_\mathrm{pr} }{\bar{{P}}_\mathrm{pr} }P_{i} +1. \end{aligned}$$
(20)

All three functions are constant and equal to 1 for \(\bar{{P}}_\mathrm{pr} =0.5\); in addition, functions \(\tilde{{W}}\) and W are equal to \(1-P_{i} \) for \(\bar{{P}}_\mathrm{pr} =1\), while function \(\hat{{W}}\) is equal to \(1-\frac{2P_{i} }{P_{i} +1}\).

The classical fitness measure W is a linear function of the parameter \(P_{i} \), whereas the new fitness measure \(\tilde{{W}}\) and its approximation \(\hat{{W}}\) are nonlinear. Figure 3 shows the plots of all three functions. The classical fitness function mainly overestimates the new fitness function \(\tilde{{W}}\), while the approximation \(\hat{{W}}\) always underestimates it. Figure 4 illustrates this bias by plots of overestimation in the case of the classical fitness function W (in cases when W underestimates \(\tilde{{W}}\), the plot shows negative values) and underestimation in the case of the approximation \(\hat{{W}}\) to show the excess of both functions from \(\tilde{{W}}\). It shows that \(\hat{{W}}\) is a good approximation in the neighbourhood of \(\bar{{P}}_\mathrm{pr} =0.5\). The classical DFSM function W is always significantly biased, except for the cases \(\bar{{P}}_\mathrm{pr} =0.5\) and \(\bar{{P}}_\mathrm{pr} =1\) when it is equal to \(\tilde{{W}}\). Thus, the classical fitness function W is a biased approximation, which may have serious implications when modelling detailed population dynamics. The interpretation of the classical DFSM fitness measure as a Malthusian growth rate is problematic from the perspective of the new model. In the relatively wide neighbourhood of the equilibrium value \(\bar{{P}}_\mathrm{pr} =0.5\), the function \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) is a much better approximation.

Fig. 3
figure 3

Plots of the static fitness function \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\), its approximation \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) and the classical DFSM fitness function \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\). The function \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) is bounded, while the function \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\) increases significantly faster than \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\)

Full size image
Fig. 4
figure 4

Functions \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) and \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\) are approximations of \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\). \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) always underestimates \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\), while \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\) mainly overestimates it. The figure shows the plots of underestimation by the function \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) and overestimation by the function \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\) from two different points of view. In the relatively wide neighbourhood of the equilibrium value \(\bar{{P}}_\mathrm{pr} =0.5\), the function \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) is a better approximation than \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\)

Full size image

3.1 Relationships Between Fitness Functions

The DFSM function (1) has an interesting relationship with the gene payoff function (7) and the female payoff function (3).

In the neighbourhood of the MSE manifold (which can be presented in the form \(m_{i} /f_{i} \approx P_{i} /\bar{{P}}_\mathrm{pr} )\), after substitution of the MSE condition and \(P\approx \bar{{P}}_\mathrm{pr} \) into the sex-specific female payoff function (3), we obtain \(W(P_{i} ,\,P)\approx W_{f} k/2\) (where k/2 is the reproductive value of a female). Note that both fitness functions describe the payoff of the focal female. The DFSM function counts offspring of both sexes but disregards the contribution of males from the parental generation. On the other hand, the female payoff function (3) considers the contribution of males from the focal female’s generation, but counts only female offspring. Thus, when multiplied by k/2 to count grand offspring, this function disregards the contribution of males from the offspring generation.

The relationship with the gene payoff (7) is the following: when we assume \(M_{i} =P_{i} \), then we obtain \(W(P_{i} ,\,P)=W_{g} (P,P_{i} )k/2\). This leads to an interesting interpretation. Suppose that a single mutant female produces all carriers of a mutant gene \(P_\mathrm{mut} \) in the next generation according to the expression of her individual strategy. Thus, in the generation of her descendants, there is equality \(M_\mathrm{mut} =P_\mathrm{mut} \), and the reproductive success of a mutant gene in the first generation of descendants is proportional to \(\left( {\Gamma P_\mathrm{mut} +\left( {1-P_\mathrm{mut} } \right) } \right) \). It is clear that the predictions of this function are exactly the same as in the DFSM model. This also supports the compatibility of linearization of a limit case of the population genetic model [29] with the DFSM approach. A problem arises in further generations. For each female carrying mutant gene \(P_\mathrm{mut} \), there is some number of male carriers of the unexpressed gene \(P_\mathrm{mut} \) acting as fathers. The DFSM fitness measure, which is related to the number of a female’s grand offspring, disregards the role of male parents on gene proliferation. Thus, the classical fitness measure can be seriously biased in cases where an entire subpopulation carries a mutant gene, not just a single female. This bias may be strong for strategies close to 1 that produce mostly males.

4 Impact on the Fisherian Selection Mechanism

The gene payoff function (7) leads to the dynamics (8), which leads to the selection rules (10). Now let us look at the simplified models of selection mechanisms, based on the rules (10), implied by the fitness functions (18), (19) and (20). According to (10), the threshold between increase and decrease in a gene frequency \(G_{i} \) is the equality of the actual carriers’ sex ratio \(M_{i} \) and the secondary sex ratio \(P=G_{i} M_{i} \). Straightforward substitution of (13) or (15) or the MSE condition (14) to the condition \(M_{i} =P\), followed by substitution of \(P\approx \bar{{P}}_\mathrm{pr} \) in each case, leads to the same threshold \(P_{i} =\bar{{P}}_\mathrm{pr} \), which is the solution of the obtained equations. (For (13) and (14), there is a second solution \(\bar{{P}}_\mathrm{pr} =1\) that is biologically meaningless.) Thus, in the rules (10), \(P_{i} \) will replace \(M_{i} \) and \(\bar{{P}}_\mathrm{pr} \) will replace P leading to

$$\begin{aligned} G_{i} \text { increases when }\;\bar{{P}}_\mathrm{pr}< & {} \frac{1}{2}\text { and } \bar{{P}}_\mathrm{pr}<P_{i} \hbox { or }\bar{{P}}_\mathrm{pr}>\frac{1}{2}\text { and } \bar{{P}}_\mathrm{pr}>P_{i} ,\nonumber \\ G_{i} \text { decreases when }P_{i}< & {} \bar{{P}}_\mathrm{pr} <\frac{1}{2}\text { or } P_{i}>\bar{{P}}_\mathrm{pr} >\frac{1}{2},\nonumber \\ G_{i} \text { is stable when }G_{i}= & {} 0\text { or }P_{i} =\bar{{P}}_\mathrm{pr} \text { or } \bar{{P}}_\mathrm{pr} =\frac{1}{2}. \end{aligned}$$
(21)

Thus, in the above cases, selection of the genes acts according to the values of individual strategies. However, the selection process at the gene level should be synchronized with the adjustment of the primary sex ratio \(\bar{{P}}_\mathrm{pr} \) determined by the state of the female subpopulation. The relationship between the gene pool and the female subpopulation is \(f_{i} =G_{i} \left( {1-M_{i} } \right) /\left( {1-P} \right) \), which combined with expressions (13) or (15) will be highly complicated. In the case of the MSE state, this relationship is very simple.

Lemma 3

If the MSE condition (11) is satisfied, \(P\approx \bar{{P}}_\mathrm{pr} \) and the population is in a polymorphic state, then

$$\begin{aligned} G_{i} \approx f_{i} (P_{i} +1-\bar{{P}}_\mathrm{pr} ). \end{aligned}$$
(22)

For a proof, see “Appendix 4”.

This result shows that on the MSE manifold, changes in gene frequencies are synchronized with changes in the mean female subpopulation strategy (the primary sex ratio \(\bar{{P}}_\mathrm{pr} )\). This explains the similarity between rules (21) and rules (12). Substitution of the MSE condition into (4) leads to the simplified approximation of the dynamics of the female population [3]

$$\begin{aligned} \dot{{f}}_{i} =kf_{i} \left( {\frac{1}{2}-\bar{{P}}_\mathrm{pr} } \right) \,\left( {\frac{P_{i} }{\bar{{P}}_\mathrm{pr} }-1} \right) \quad \hbox { for } \;i=(1,\ldots ,\,u-1), \end{aligned}$$
(23)

which resembles the gene pool dynamics (8), where \(f_{i} \), \(P_{i} \) and \(\bar{{P}}_\mathrm{pr} \) replace \(G_{i} \), \(M_{i} \) and P. Note that according to the similarity of the DFSM fitness function \(W(P_{i} ,\bar{{P}}_\mathrm{pr} )\) and the female payoff function (3) under the MSE condition (as shown in Sect. 3.1), system (23) can be regarded as the replicator dynamics of the DFSM fitness function. Thus, the selection mechanisms induced by functions \(\tilde{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) and \(\hat{{W}}(P_{i} ,\bar{{P}}_\mathrm{pr} )\) are similar to the mechanism induced by the classical DFSM fitness measure but are not necessarily well synchronized with the adjustment of the primary sex ratio. This synchronization will increase with the convergence to the MSE manifold. Thus, it is time to look more closely at the properties of the MSE manifold, the attractor of those emerging mechanisms.

5 The Effect of the MSE on the Sex-Specific Payoff Functions (2) and (3) and the “Fitness Exchange” Effect

Now let us examine the population structure on the MSE manifold. Since \(\;f_{i} =x_{i} /x\) and \(m_{i} =y_{i} /y\), the MSE condition (11) is equivalent to

$$\begin{aligned} \frac{x}{y}{\sum }_{j}f_{j} P_{j} =\frac{x_{i} }{y_{i} }P_{i} \quad \left( {\Gamma \bar{{P}}_\mathrm{pr} =\Gamma _{i} P_{i} } \right) . \end{aligned}$$
(24)

This means that the product of the number of females per single male x/y and the primary sex ratio in the entire population \({\sum }_{j}f_{j} P_{j} \) is equal to the analogous coefficients for monomorphic subpopulations of carriers of any gene \(P_{i} \). This property can be generalized.

Consider the subpopulation (described by index \(\Lambda )\) consisting of all carriers of arbitrarily chosen strategies. The strategic composition of subpopulation \(\Lambda \) can be described by the vector of strategy indices \(d^{\Lambda }=[d_{1}^{\Lambda } ,\ldots ,\,d_{u^{\Lambda }}^{\Lambda } ]\) (for example, \(d^{\Lambda }=\left[ {1,\,3,\,4} \right] \) means that all carriers of strategies \(P_{1} ,\,P_{3} ,\,P_{4} \) are included in the subpopulation \(\Lambda )\). Assume that \(\Gamma ^{\Lambda }\) is the number of females per single male individual in the subpopulation \(\Lambda \). Analogously, assume that \(\bar{{P}}_\mathrm{pr}^{\Lambda } \) is the mean strategy of females from subpopulation \(\Lambda \) (i.e., the subpopulation primary sex ratio). This leads to the interesting property described by the following lemma.

Lemma 4

When the MSE condition is satisfied, then for every arbitrarily chosen subpopulation \(\Lambda \), the following condition is satisfied:

$$\begin{aligned} \Gamma \bar{{P}}_\mathrm{pr} =\Gamma ^{\Lambda }\bar{{P}}_\mathrm{pr}^{\Lambda }. \end{aligned}$$
(25)

In particular, \(\Gamma \bar{{P}}_\mathrm{pr} =\Gamma ^{i}P_{i} \) for a monomorphic subpopulation of carriers of strategy \(P_{i} \) for which \(\Gamma ^{i}=x_{i} /y_{i} \).

For a proof, see “Appendix 5”.

Note that the transformed MSE condition (24), which is a cornerstone of the above result, contains the term \(x_{i} /y_{i} \) which describes the number of female carriers per single male carrier.

Recall that male and female payoff functions (2) and (3) describe numbers of newborns of the same sex and carrying the same strategy as the focal individual. This term is present in the male sex-specific payoff function (2) and describes the contribution of female carriers to the payoff of a focal male individual. This phenomenon was termed the “fitness exchange” in [3].

Let us examine the form of the payoff functions when a population is in the MSE state. Lemma 5 describes the quantitative properties of the “fitness exchange” mechanism in the MSE state and its impact on sex-specific payoffs.

Lemma 5

When the MSE condition is satisfied and \(P\approx \bar{{P}}_\mathrm{pr} \), then

  1. (i)

    The female contribution is \(\frac{x_{i} }{y_{i} }W_{fm} =\frac{k}{2}\Gamma \bar{{P}}_\mathrm{pr} \) and a male’s payoff (2) has the form

    $$\begin{aligned} \;W_{m} =k\Gamma \bar{{P}}_\mathrm{pr}. \end{aligned}$$
  2. (ii)

    The male contribution is \(\frac{y_{i} }{x_{i} }W_{mf} =\frac{k}{2}\Gamma P_{i} \), and a female’s payoff (3) has the form

    $$\begin{aligned} W_{f} =\frac{k}{2}\left( {\left( {1-P_{i} } \right) +P_{i} \Gamma }\right) . \end{aligned}$$
  3. (iii)

    The MSE condition (11) is equivalent to

    $$\begin{aligned} x_{i} \,P_{i} k=y_{i} \Gamma \bar{{P}}_\mathrm{pr} k, \end{aligned}$$

    which means that all female carriers of gene \(P_{i} \) produce the same number of sons as the partners of all male carriers of that gene.

For a proof, see “Appendix 6”.

In addition, we can generalize point (iii) from Lemma 5 to the following property:

Lemma 6

In the MSE state, the reproductive value of the contribution of the opposite sex gene carriers to the payoff of the focal individual equals the reproductive value of the newborn male carriers produced by that individual.

For a proof, see “Appendix 7”.

It was mentioned in Sect. 3.1 that on the MSE manifold, the female payoff (3) resembles the DFSM payoff function. Here, this is completed by the respective form of the male payoff (2), showing that on the MSE manifold, all males have the same payoff equal to the number of sons of their partners despite the carried gene \(k\Gamma \bar{{P}}_\mathrm{pr} \). Thus, the male payoff is the same for all strategies, while the female payoff depends only on the focal female’s individual strategy. This suggests the existence of a feedback mechanism allowing females to control their payoff by affecting the male subpopulation. The differences in the payoffs between males carrying different genes correspond to the effects of differences in their ”sisters”’ activities (female carriers of the same gene), which is determined by the factor \(x_{i} /y_{i} \) (the number of female carriers per single male carrier). If this factor has a high value, then male carriers of this gene will experience a greater growth rate. However, when the number of male carriers \(y_{i} \) increases, then the factor \(x_{i} /y_{i} \) will decrease (see Fig. 5).

Fig. 5
figure 5

Mechanistic explanation of the male subpopulation equilibrium. Partners of every male produce the same number of offspring carrying his gene ( \(\frac{k}{2}\Gamma \bar{{P}}_\mathrm{pr} )\) , so the differences in payoff are the effects of differences in the activity of female carriers of the same gene. The influence of female carriers is determined by the factor    \(x_{i} /y_{i} \) (the number of female carriers per single male carrier). If this factor has a high value (more females per single male), then male carriers of this gene will have a larger growth rate (this situation is presented in panel a). However, when the number of male carriers \(y_{i} \) increases, then factor \(x_{i} /y_{i} \) will decrease, which will cause a decrease in the influence of female carriers of the gene on the payoff of the average male carrier of the same gene (panel b). This process will lead to an equilibrium state in which the influence of female carriers on all male carriers is the same

Full size image

This will cause a decrease in the influence of female carriers on the payoff of the average male carrier. This process will lead to an equilibrium state in which the influence of female carriers for all male carriers is the same.

How does this mechanism affect the female subpopulation? For different strategies, we will have different values of the factor \(x_{i} /y_{i} \). The contribution of male carriers to female fitness is determined by the coefficient \(y_{i} /x_{i} \) for every strategy (a ratio-dependent mechanism, [1]). Female carriers of different strategies exert continual pressure on the equilibrium state of a male subpopulation by introducing different numbers of new male carriers. In effect, female individuals indirectly control the feedback impact of male carriers on their own fitness.

6 Discussion

Summarizing, in this paper we have shown that the causal chain underlying sex ratio self-regulation towards the value of 0.5 is more complex than was previously thought. The males as the passive carriers play an important role in this process; thus, the analysis cannot be reduced to the females. This phenomenon is the by-product of the convergence of the stable sex ratios in the monomorphic subpopulations of the carriers of the genes encoding the same strategies to the MSE manifold. This means that the trajectories are attracted by the equilibria of the tug of war process (the adjustment of the carriers’ sex ratios by the activity of female strategy carriers and random female partners of male strategy carriers), and those attracting manifolds converge to the MSE manifold. Thus, the results obtained correct the intuitions from [3]. The rapid phase of the dynamics is responsible for the convergence to the equilibria of the tug of war mechanism. Indeed, the dynamics converge to the neighbourhood of the MSE manifold and the equality of the primary and secondary sex ratios, but it will reach them at the global equilibrium of the system. In addition, we have shown that in the neighbourhood of the MSE manifold, the tug of war equilibrium can be approximated by a much simpler formula. Numerical simulations confirm that this approximation can be acceptable. The above result can be used for the derivation of the unbiased static fitness function and its simplified approximation. When the deviation of the sex ratio is not far from the equilibrium value, then the new approximation is better that the classical Dusing–Fisher–Shaw–Mohler fitness function, which is more seriously biased.

On the MSE manifold, selection of the genes is driven by the excess of the encoded individual strategy (phenotypic trait) from the primary sex ratio, and the two variables are equal. The first is the reproductive value of the contribution of the opposite sex gene carriers to the payoff of the focal individual, and the second is the reproductive value of the newborn male carriers produced by that individual. In addition, for all subpopulations containing all carriers of some subset of strategies, there is equality of the products of the number of females per single male and the average strategies of those females. All of those phenomena are revealed by the focus on the passive gene carriers. In problems other than sex ratio evolution, explicit analysis of the impact of the passive carriers can reveal interesting mechanisms.

6.1 The Dusing–Fisher–Shaw–Mohler Model from the Perspective of the New Approach

The classical DFSM fitness measure is based on the reproductive value of the offspring of the focal female, which will be determined by the secondary sex ratio when they become mature. We can describe this fitness measure as a proper frequency-dependent game theoretic payoff (not as in the “playing the field” approach where the environment is not explicitly determined by the population state) by incorporation of the strategic composition. This can be obtained by the simplifying assumption of the equality of the primary and secondary sex ratios. However, numerical simulations show that in continuous models, this assumption holds only at equilibrium. Thus, this approach will be unbiased only in the case of nonoverlapping generations. In other cases, it will disregard the individuals that are not peers of the offspring of the focal female.

Thus, the DFSM fitness measure is equivalent to the reproductive value of the sex-specific female payoff on the MSE manifold. Both of these approaches are biased, simplified approximations of the new approach related to the gene perspective. However, they are compatible with the new approach at the level of the strategic analyses and produce the same game theoretic predictions regarding the female subpopulation. A disadvantage of the classical sex ratio game is the fact that it disregards passive male gene carriers as fathers mating with other females. They are considered only as the sons of “mom’s” [8]. The strategic agent is the female individual. However, invasions of males or mutations in male individuals are possible. This study shows that the DFSM model can be considered as an approximation under the assumption that the male subpopulation is very close to equilibrium and cannot be perturbed. This produces several problems. The first is that the evolutionarily stable equilibrium (the sex ratio of 0.5) is described as a state of the female subpopulation. The male subpopulation is not explicitly considered. However, the new model also shows that the state of the male subpopulation is important, and the sex ratio of 0.5 can be unstable for perturbations of that state [3]. This is an important problem, because the sex ratio game is a basic example of a nonlinear payoff function in every textbook on evolutionary game theory. Thus, the composition of the subpopulation of passive gene carriers should also be considered in the concepts of evolutionary stability. Classical population genetics results support these predictions [12, 13, 20, 29]. In the new approach, the strategic agent is the gene encoding the sex ratio strategy. This perspective is free of the above disadvantages and leads to new interesting predictions, such as the tug of war mechanism and double-level selection. It is also consistent with classical population genetics results. A second problem is a bias in the estimation of reproductive success, which is problematic on the grounds of population dynamics. This is an example of the disadvantage of purely strategic models mentioned by Oster and Rocklin [27]; more on this topic can be found in [6, 35]. In effect, the basic interpretation of the payoff as the Malthusian growth rate is problematic in the case of the classical sex ratio game. (A dynamic model based on Dusing’s approach was discussed in Sect. 4 and can also be found in [24].)

This paper establishes an alternative methodology for derivation of the static fitness functions. It is based on the substitution of the equilibrium of the carriers sex ratio, determined by the encoded strategies and modelled inheritance system, in the gene payoff function describing the Fisherian mechanism. It was shown in this paper that we can derive an unbiased fitness function in this way. It was also shown that it can be approximated by a simpler function that produces a better approximation for relatively small perturbations than the classical DFSM fitness function.

6.2 The Mechanistic Nature of the Convergence to the MSE Manifold

The results presented above attempt to interpret the MSE phenomenon. They suggest that the MSE constitutes a compensatory equilibrium between the production of female carriers of a gene by passive male carriers and the production of male carriers by female individuals. As was mentioned in the introduction, the MSE is an example of a more general class of problems. The MSE is related to population phenomena, such as stable demographic structure or Hardy–Weinberg equilibrium. In the new model, there is no demographic structure. However, existing models that include demographic structure [31] report different behaviours before and after demographic equilibrium is reached. The MSE properties presented in this paper represent effects of haploid inheritance and the assumption that an individual strategy is encoded by a single gene. However, other forms of self-regulation structures are possible for different inheritance systems (diploid or haplodiploid) and different genetic structures (multilocus or polygenic). We can imagine a version of the model where the offspring sex ratio is controlled by males and the females are passive carriers since they cannot apply selective abortions. Here, strategic analysis of phenotypic adaptation meets population genetics. Strictly genetic mechanisms may play important roles in the process of phenotypic selection by determining the values of crucial parameters (e.g., the sex ratio in a carrier subpopulation) that are responsible for the selection of individual strategies. Future extensions of the present model containing more realistic genetics (for example, polygenic and haplodiploid) describing the system observed in some living organism can be tested experimentally, similar to the classical experiments [5, 21]. This situation can also be tested by individual-based models. Similar dynamic equilibria should be observed in every model where there are passive carriers of unexpressed strategy genes. We can imagine many problems, such as the Hawk–Dove game, related to mating conflicts where only the males are active competitors. This problem is not just related to biological models. In economics and social sciences, there are also possible situations where only a part of the population is engaged in the game interaction, and the strategies can be transferred verbally among the passive members of the population. Game theory is focused on individuals who play the games; however, those who do not play the games can also be important.