Abstract
The important biological problem of how groups of animals should allocate themselves between different habitats has been modelled extensively. Such habitat selection models have usually involved infinite well-mixed populations. In particular, the model of allocation over a number of food patches when movement is not costly, the ideal free distribution (IFD) model, is well developed. Here we generalize (and solve) a habitat selection game for a finite structured population. We show that habitat selection in such a structured population can have multiple stable solutions (in contrast to the equivalent IFD model where the solution is unique). We also define and study a “predator dilution game” where unlike in the habitat selection game, individuals prefer to aggregate (to avoid being caught by predators due to the dilution effect) and show that this model has a unique solution when movement is unrestricted.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Animals of many types interact in groups in a number of ways [21]. These might be long-standing social groups, as in the case of many species of primate [41], or packs of wild dogs [45, 46]. Alternatively, they might be more transitional in nature, for instance foragers gathering at a food patch, see Krijger and Sevenster [22] for the case of insects and Steele and Hockey [39] for the case of birds. In long-standing groups, there can be complex social relationships and the individuals often form themselves into dominance hierarchies. In more transitional groups, relationships will generally be simpler if the members of the group have no prior information about the others. This is the case for the foraging examples that we mentioned above, but also in the case of egg laying as in Prokopy and Roitberg [36]. It is this more transitional type of interaction that is the focus of this paper.
For patch foraging, assuming that individuals are free to move between any of the available food patches, at effectively no cost, animals should follow the ideal free distribution (IFD) over the patches. The simplest single species model was developed by Fretwell and Lucas [14], Fretwell [13] (see also [10]), with a closely related model developed by Parker [35]. More complex cases, including for multi-species [15, 23], individuals with different abilities [19, 40] and for more complex payoff functions, including the Allee effect [12, 25], have also been considered.
It has been shown [9, 11, 23] that the IFD is an evolutionarily stable strategy [30]. In all of the models above, the population has been infinite, and all foraging patches are reachable by all individuals. Real populations are finite, of course (although large populations can be well modelled as being infinite), but they generally also contain structure. For instance in the case of the wild dogs of Woodroffe et al [45], individuals will only be able to access a subset of the available places (at least without paying a significant cost). Recently, models of populations which are not well mixed, but have some structure, have been developed to take this into account. Evolutionary graph theory models [1, 2, 5, 26–28, 42, 43] embed standard games such as the prisoner’s dilemma within a graph structure [17, 34, 37]. The interactions within such a structure are restricted to be pairwise, however, and so are unsuited to the type of aggregated situations that we envisage. A more general framework of interactions of populations with restricted movement was introduced in Broom and Rychtář [6]. In that paper, a finite population of individuals distributed themselves over available places subject to their individual restrictions, leading to interactions within the groups on those places, with rewards depending upon the composition of the group, and potentially also on the composition of the groups at other places. More generally the paper introduced a new framework for modelling the evolution of structured populations using multiplayer games (see also [4, 8]). In the current paper, we build upon this model by analysing an important class of models, where an individual’s movements are strategically chosen and its rewards depend only upon the size of its own group.
2 The Territorial Movement Game
2.1 Game Setting
We consider a population of N individuals \(I_{1}, \ldots , I_{N}\) who can move between and potentially interact on a number of M distinct places \(P_{1}, \ldots , P_{M}\). The scenario can be illustrated as bipartite graphs as in Fig. 1 where a link connects an individual \(I_n\) and a place \(P_m\) if and only if the place \(P_m\) can be visited by individual \(I_n\) [6]. A collection of all places \(P_m\) that can be visited by an individual \(I_n\) will be called the territory of \(I_n\) and denoted by \(\mathcal{P}_n = \{m; I_n \hbox { can go to } P_m\}\). Let \(\mathcal{I}_m\) denote the set of individuals that can go to place \(P_m\), i.e. \(\mathcal{I}_m = \{n; I_n \hbox { can go to } P_m\}\), which we shall call the (potential) visitors to \(P_m\). If every individual can go everywhere, we will call the population unstructured.
The individuals play the game as follows. Each individual \(I_n\) chooses a place \(P_m\) in its territory to move to. All individuals make the choice at the same time or, equivalently, without knowledge of what others do. Once the individual has made its choice and visits the place \(P_m\), it receives a reward \(R_m(k_m)\) (sometimes later denoted just by \(R_m\)) that, for the purpose of this paper, depends solely on the place, \(P_m\), and the (total) number of individuals, \(k_m\), occupying the place. Specifically, the reward does not depend on which individuals share the place and how the other individuals are distributed on the other places; we shall call this the local aggregation assumption.
Unpacking this assumption, we are assuming the following. Places can be different of differing quality and of differing accessibility to individuals. Individuals, however, can differ only in the fact that different individuals can (potentially) access different places. This means that once on a particular place, which individuals are there does not affect the payoffs, except through the size of the group. Individuals are only concerned about their immediate payoff, i.e. about what is happening at their current place (and not about what is/or is not happening at other places).
The strategic element of the game involves the movement of the different individuals; each can employ different moving strategies and their aim is to maximize their payoff.
2.2 Game Theoretical Definitions
In the setting of the Territorial Movement Game, we will use the following definitions which are just the appropriate modification of the usual game theoretical notions (see for an example [7]).
An individual pure strategy is the choice of a particular place in a territory.
Given the territorial restrictions, different individuals may have different sets of available strategies to employ.
The occupancy function is a function \(O:\{1,2,\ldots , N\}\rightarrow \{1,2,\ldots , M\}\) where \(P_{O(n)}\) for \(O(n)\in \mathcal{P}_n\) is a place to which an individual \(I_n\) has moved. For every such occupancy function, we define its distribution function as an ordered M-tuple \(\langle k_m\rangle _{m=1}^M\) with \(k_m = |\{n; O(n)=m\}|\) being the number of individuals at place \(P_m\).
We say that two occupancy functions \(O_1\) and \(O_2\) are one move apart (by an individual \(I_{n_0}\)) if \(O_1(n) = O_2(n)\) for all \(n\ne n_0\) while \(O_1(n_0)\ne O_2(n_0)\), i.e. if the difference between the occupancies is exactly in one individual changing its position.
The occupancy function O is termed stable if any individual would receive a lower payoff when it unilaterally changes its position (given the fixed positions of other individuals); i.e. if for every n
The set \(\mathcal{O}\) of occupancy functions is termed a stable set if it is a maximal set with the following properties
-
(i)
if \(O,O'\in \mathcal{O}\), then there is a sequence \(O=O_1, O_2, \ldots , O_k =O'\) of elements in \(\mathcal{O}\) such that each pair \(O_{i}\) and \(O_{i+1}\) is one move apart.
-
(ii)
for all \(O,O'\in \mathcal{O}\) that are one move apart by an individual \(I_{n_0}\), \(R_{O(n_0)}(k_{O(n_0)}) = R_{O'(n_0)}(k'_{O'(n_0)})\),
-
(iii)
for all \(O\in \mathcal{O}\) and \(O'\not \in \mathcal{O}\) that are one move apart, there must be at least one individual \(I_{n_0}\) such that O and \(O'\) are one move apart by \(I_{n_0}\) and \(R_{O(n_0)}(k_{O(n_0)}) > R_{O'(n_0)}(k'_{O'(n_0)})\).
In general it does not make sense to talk about a stable distribution function, as opposed to a stable occupancy function. Two occupancy functions can have the same distribution function, but one may be stable and the other not, because the possible moves depend upon the sets of territories of the individuals at each of the places, which will be different for each occupancy function. The exception is for the well-mixed population, where the territory of each individual is the full set of places, and consequently if an occupancy function is stable, so is any other occupancy function with the same distribution. Thus for the well-mixed population we say that a distribution function is stable if any occupancy function with that distribution function (and hence all of them) is (are) stable.
Often when considering evolutionary game theory, we assume that we have so-called generic games (see for example [3, 7]). Essentially, assuming that payoffs are derived from the natural world with its underlying variation, we can treat each payoff as if it is the realisation of a random variable, and so we ignore special sets of parameters that would occur with probability 0. This is useful, as the most problematic mathematical cases often occur on such parameter sets. In particular, equalities of distinct payoffs can cause problems. Here we shall call a game generic if
i.e. if different patches yield different payoffs (irrespective of the group size) and the same patch yields different payoffs for different group sizes. In subsequent sections, we give results that hold for both generic and non-generic games where we can, but sometimes it has proved necessary to restrict ourselves to consideration of generic games only. We clearly indicate at the appropriate point whether generic games are assumed.
A stable occupancy function is always a stable set (of one element). If payoffs are constant and the population is unstructured, the set of all occupancies is a stable set. If the payoffs are generic, a stable set has only one element, and this element is a stable occupancy function.
In Sect. 2.3, we shall see that there is always at least one stable occupancy function for our game, providing that the local aggregation assumption holds. This is not generally true if it does not hold, as we see in the following example.
Example 1
A stable occupancy function may not exist without the local aggregation assumption. Consider two individuals, a predator and its prey, both of whom can go to one of two available places. The first individual, the predator, wants to be with the prey, but the prey wants to avoid the predator. The predator receives payoff 1 (0) if it is (not) at the same place as the prey, the prey receives 0 (1) if it is (not) at the same place as the predator. Note that the payoffs depend on who else is on the place, not only on the number of occupants. Clearly, no pair of pure strategies form a stable occupancy function.
2.3 Existence of a Stable set for the Territorial Movement Game
Here we show that there is always at least one stable set for the Territorial Movement Game. We will consider two Markov processes on the set of all occupancy functions. For the strong Markov process, we will consider a transition from occupancy O (with a distribution function \(\langle k_m\rangle _{m=1}^M\)) to an occupancy \(O'\) (with a distribution function \(\langle k'_m\rangle _{m=1}^M\)) to be allowable if they are one move apart by \(n_0\) and the individual \(I_{n_0}\) would improve its payoff. Thus, there is a potential transition if and only if there are \(m_1,m_2\in \{1,\ldots , M\}\) such that
-
(i)
\(\mathcal{I}_{m_1}\cap \mathcal{I}_{m_2}\ne \emptyset \), i.e. there is an individual that could go to both \(P_{m_1}\) and \(P_{m_2}\),
-
(ii)
\(k'_{m_1} = k_{m_1}-1\), i.e. the individual is (potentially) leaving \(P_{m_1}\),
-
(iii)
\(k'_{m_2} = k_{m_2}+1\), i.e. the individual is (potentially) coming to \(P_{m_2}\),
-
(iv)
\(R_{m_1}(k_{m_1})<R_{m_2}(k'_{m_2})\), i.e. the payoff the individual gets at \(P_{m_2}\) is higher than the one it got at \(P_{m_1}\) and
-
(v)
\(k'_m = k_m\) for all \(m\ne {m_1},{m_2}\), i.e. nobody else has changed their position.
Note that for the strong process, there cannot be transition from the state O to \(O'\) and from \(O'\) to O for any pair of states. Furthermore in the generic case, there is no potential transition under the strong process if and only if O is stable.
For the weak Markov process, we will consider a transition to be allowable if the conditions (i)–(v) are satisfied, but the inequality in (iv) is not strict. Note that in either process we do not specify the probability of a transition occurring, except that any allowable transition has probability greater than zero.
We shall show the existence of a stable set in two stages.
(a) Let us first define \(\mathcal{A}_s\) to be the set of all absorbing states of the strong Markov process. We claim that \(\mathcal{A}_s\ne \emptyset \).
Suppose that \(\mathcal{A}_s= \emptyset \). Then we could easily find a cycle
\(O_1, O_2, O_3, \ldots , O_T= O_1\) such that transitions can occur from \(O_{i}\) to \(O_{i+1}\) in the strong Markov process. This yields the existence of the sequences \(\langle m_{1,t}\rangle _{t=1}^{T-1}\) and \(\langle m_{2,t+1}\rangle _{t=1}^{T-1}\) such that
corresponding to the fact that at time t there were \(k_{m_{1,t},t}\) individuals in place \(P_{m_{1,t}}\) and one of them was able to improve its position by moving to place \(P_{m_{2,t+1}}\). For every transition at step t, we will have one inequality (3). Let us now look at the sequence \(\langle k_{m,t} \rangle _{t=1}^T\) for a specific m. The sequence is generally constant with occasional jumps by \(\pm 1\). Any time an individual leaves a place \(P_m\), we have \(k_{m,t}>k_{m,t+1} = k_{m,t}-1\), and the term \(R_m(k_{m,t})\) appears on the left-hand side of an inequality (3). Similarly, any time an individual moved to place \(P_m\), \(k_{m,t}<k_{m,t+1} = k_{m,t}+1\), the term \(R_m(k_{m,t+1})\) appears on the right-hand side of an inequality (3). Since the sequence \(\langle k_{m,t} \rangle _{t=1}^T\) begins and ends at \(k_{m,1}\), the term \(R_m(k_{m,t})\) has to appear on the left-hand side of (3) as many times as on the right-hand side of (3). So adding those inequalities together (for all t) yields a contradiction.
So, we have shown that there is at least one occupancy \(O\in \mathcal{A}_s\). If \(O, O'\in \mathcal{A}_s\) are one move apart by an individual \(I_{n_0}\), there is no transition from O to \(O'\) or from \(O'\) to O in the strong Markov process and thus condition (ii) for a stable set is satisfied for all pairs of elements in \(\mathcal{A}_s\). Consequently, when \(O,O'\in \mathcal{A}_s\), there is a transition (both ways) under the weak Markov process between O and \(O'\).
(b) Now, let \(\mathcal{B}_w\subset \mathcal{A}_s\) be the set of occupancies that cannot, after any finite number of transitions in the weak Markov process, reach the set \(\mathcal{A}_s^c\), the complement of \(\mathcal{A}_s\). As above, there must be an occupancy function \(O \in \mathcal{B}_w\); otherwise, we would again get a cycle (and although we could now potentially have equalities in (3), we would have at least one strict inequality).
Since \(\mathcal{B}_w\subset \mathcal{A}_s\), \(\mathcal{B}_w\) satisfies condition (ii) for a stable set. Now assume that it does not satisfy condition (iii), i.e. that there is \(O \in \mathcal{B}_w\) and \(O'\not \in \mathcal{B}_w\), i.e. O and \(O'\) are one move by \(I_{n_0}\) apart so that \(R_{O(n_0)}(k_{O(n_0)}) \le R_{O'(n_0)}(k'_{O'(n_0)})\). But this means that there is a transition from O to \(O'\) in a weak Markov process, and thus, there is a sequence of transitions from O through \(O'\) to an element of \(\mathcal{A}_s^c\), a contradiction with the fact that \(O\in \mathcal{B}_w\).
A maximal “connected” component of \(\mathcal{B}_w\) (i.e. the set of occupancies which one can get from any element of \(\mathcal{B}_w\) by a sequence of changes) is then a stable set.
Remark 1
Here we illustrated with an example the concept of the sets \(\mathcal{A}_s\) and \(\mathcal{B}_w\) from the proof above. Consider 80 individuals with unrestricted movements that can go to two patches with payoffs \(R_1(80)=R_2(80)=1\) and \(R_1(k)=R_2(79-k) = 0\) for \(0\le k\le 79\). Then \(\mathcal{A}_s\) corresponds to the set of all states but \(\langle 79,1\rangle \) or \(\langle 1,79\rangle \) and \(\mathcal{B}_w\) consists of \(\langle 80,0\rangle \) and \(\langle 0,80\rangle \).
Whilst the above results hold for generic and non-generic games, the results from here until the end of Sect. 2.3 apply to generic games only.
Remark 2
For the generic territorial movement game, consider the algorithm “start with any occupancy function, and make transitions as in the strong Markov process until no further moves can be made”. As previously noted, for the generic case this yields a stable occupancy function. However, there may be of the order of \(M^N\) occupancy functions and thus the algorithm can take a long time to finish. We note that which \(O'\) is chosen next will in general depend upon the transition probabilities of the strong Markov process, which would need to be specified.
Unfortunately, it is not the case that the maximum improvement decreases every step and it cannot thus be used as an indicator of the fact that the process is already converging to the stable state. For example, consider a population of two individuals. Individual \(I_1\), currently at \(P_1\) can go to \(P_1\) and \(P_2\), individual \(I_2\), currently at \(P_2\) can go to \(P_2\) and \(P_3\). Let the payoffs be \(R_1(1) = 0.5, R_2(1) = 1, R_2(2)=0.51, R_3(1) = 0.99\). The only improvement that can be made is that individual \(I_1\) moves from place \(P_1\) to place \(P_2\), increasing its payoff by 0.01. That move, however, sharply decreases the payoff of individual \(I_2\) from \(R_2(1)=1\) to \(R_2(2)=0.51\). The next move would be by individual \(I_2\) from \(P_2\) to \(P_3\), increasing its payoff by 0.48 to \(R_3(1) = 0.99\).
Remark 3
An alternative way to show the existence of a stable occupancy function in the special case of the predator dilution game is shown in Sect. 4.3.
We have shown here that there is at least one stable occupancy function, but in general there may be many, as we see in the following example.
Example 2
Consider a game where individuals prefer to be in groups of even numbers, and the payoff to an individual is 1 (0) if it is (not) in a group of even-numbered size. Let there be 2n individuals and m places such that all individuals can go to all places. The number of distributions of individuals over the places is \({2n+m-1 \atopwithdelims ()m-1}\) (see [7] Exercise 9.1). The number of stable distributions can be obtained by sending individuals to places in pairs, yielding \({n+m-1 \atopwithdelims ()m-1}\) stable states. If \(n\gg m\), then the number of distributions is roughly \((2n)^{m-1}/((m-1)!)\) and the number of stable distributions is \((n)^{m-1}/((m-1)!)\) so the proportion of stable distributions is \(2^{1-m}\).
When \(m=2\), the proportion of stable distributions is exactly \((n+1)/(2n+1)\). Thus we can have two-thirds of distributions as stable if we have two individuals on two patches. We conjecture that two-thirds is the largest possible proportion of stable distributions. Note that in this example the proportion of stable occupancy functions for \(n=1, m=2\) is actually 1/2, since the two stable distributions are each associated with a single occupancy function, but the single unstable distribution is associated with two.
3 A Habitat Selection Game
3.1 Game Setting
Consider M places \(P_1, P_2, \ldots , P_M\) and N individuals \(I_1, \ldots , I_N\). If there are \(k_m\) individuals at place \(P_m\), the payoff to each of these individuals will be
where \(B_m>0\) is the basic suitability of place \(P_m\) and \(f_m\) is a nonnegative, increasing and continuous function, with \(f_m(0) = 0\). This corresponds to selecting a habitat to forage on, and as the number of individuals on a given patch increases, the actual yield of the patch decreases. However, the yield does not depend on the particular occupants of the patch. In the unstructured population case where every individual can go everywhere, the game has been described for example in Cressman et al. [10], see also Křivan et al. [23].
3.2 A Unique Distribution in an Unstructured Population
The following reasoning, up until the end of Sect. 3, applies to both generic and non-generic games; note, however, that as shown in Remark 4 below, we do not necessarily have uniqueness in non-generic cases. A known solution to this game for effectively infinite populations is the so-called ideal free distribution [14] (ideal = rational individuals, free = no cost or restriction on movement). Typically, conditional on being at a particular place, the individuals want to be with as few other individuals as possible.
(a) Firstly, we show how to find a solution to the habitat selection game in finite unstructured population. Rather than assuming that individuals all make their choice at the same time, let the individuals choose sequentially. The first individual will choose a place \(P_{m_1}\) that yields the highest payoff; i.e.
Clearly, individual \(I_1\) cannot do any better; and if no other individual arrives, we have the stable occupancy function if there is a strict inequality in (5), i.e. a unique place with best reward. If there are k places which satisfy (5), then there will be a stable set including k distinct occupancy functions. In this case, assuming that \(N\ge k\), the first k individuals must choose the k solutions to (5), since after each choice, the value of the chosen place will decrease, and no longer yield the highest payoff to subsequent individuals. Now, assume that individuals \(I_1, I_2, \ldots , I_i\) made their choices in a sequence, so that there are \(k_m\) individuals at place \(P_m\) and that no individual could do better by unilaterally moving to a different place. The individual \(I_{i+1}\) will pick \(P_{m_{i+1}}\) such that
Clearly, in addition to individual \(I_{i+1}\) being unable to increase its reward, none of the other individuals \(I_j\) for \(j<i+1\) can increase their reward by unilaterally moving to a different place either. Indeed, if \(I_{i+1}\) went to the same place as \(I_j\), then \(I_j\) must be at the best possible position it could now be (otherwise, \(I_{i+1}\) would have chosen a different one). Also, if \(I_j\) is at a different place to \(I_{i+1}\), then it cannot improve its payoff by going anywhere else because the move to any other place had not been optimal for \(I_j\) even before \(I_{i+1}\) arrived (and now the payoff at \(P_{m_{i+1}}\) has become even smaller due to the presence of \(I_{i+1}\), whilst the payoffs at other places have not changed). In this way, we can continue to place the individuals until all have made a choice.
(b) Now we show that while there will usually be many stable occupancy functions (depending on the sequence in which the individuals will make their choice), in unstructured populations and generic games, these will all yield the same distribution \(\langle k_m\rangle _{m=1}^M\).
To see the last statement, assume to the contrary that two stable occupancy functions O and \(O'\) yield different distributions \(\mathbf{k}=\langle k_m\rangle _{m=1}^M\) and \(\mathbf{k'}= \langle k'_m\rangle _{m=1}^M\). Because \(\mathbf{k}\ne \mathbf{k'}\) and \(\sum _m k_m = \sum _m k'_m\), there must be \(m_1\) and \(m_2\) such that \(k_{m_1}>k_{m_1}'\) and \(k_{m_2}<k_{m_2}'\). Since the payoffs \(R_{m_1}\) and \(R_{m_2}\) are monotone, we have
Since O and \(O'\) are stable occupancy functions, we have
Thus, by (7), (8), (9), and (10), we get \(R_{m_1}(k_{m_1})>R_{m_1}(k_{m_1})\) which is a contradiction. Consequently, the stable occupancy functions O and \(O'\) must yield the same distributions \(\mathbf{k}\) and \(\mathbf{k'}\).
Remark 4
In a non-generic game, different occupancies (even in the same stable set) may yield different distributions. For example, consider an unstructured population of three individuals and two places with \(R_1(1)>R_1(2)>R_1(3)=R_2(1)>R_2(2)>R_2(3)\). Then occupancies yielding a distribution \(\langle 3,0\rangle \) and a distribution \(\langle 2,1\rangle \) are both in the same stable set.
Remark 5
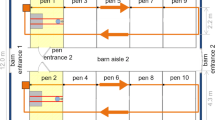
It seems that the same method as presented above would work for the case where individuals could visit only some of the places; the only modification needed being to take the maximum in (5) and (6) only over the allowable places. This is not the case, however, as shown in Fig. 2. Consequently, we have seen that even the well-understood habitat selection game can get more complex if we put restrictions on individual movements.
Method showing the existence for the habitat selection game in an unstructured population cannot be adopted for structured populations. In all instances, we assume that the payoffs are such that \(R_2(1)>R_3(1)>\) \(R_4(1)\) \(>R_1(1)>R_2(2)>\) \(R_3(2)\). a and b show different stable occupancy functions for different orders at which individuals choose their places. c Shows that there is an order under which no stable occupancy is reached (one can still follow the procedures from Sect. 2.3 to reach a stable occupancy function in several steps)
The fact that the habitat selection game (and Territorial Movement Game in general) has a stable occupancy function no matter what the exact structure was shown in Sect. 2.3. There seems to be no clear argument on how to obtain the solution for a general population in this game, however. This is in contrast to the game that we now consider in Sect. 4.
4 A Predator Dilution Game
4.1 Game Setting
Consider M places \(P_1, P_2, \ldots , P_M\) and N individuals \(I_1, \ldots , I_N\) each of which can move to some (but potentially not all) of the places where the payoffs \(R_m(k_m)\) are increasing functions of \(k_m\). This corresponds to the following scenario. Each day each individual selects a place. At some point during the day, a predator arrives in the general area, picks a place at random (i.e. with probability 1 / M) and attempts to eat one individual that is on that place. Each individual at the chosen place \(P_m\) is equally likely to be eaten, with probability \(\lambda _{m}/(1+\lambda _m k_m)\), using the Holling type II predation function Křivan [18], where \(\lambda _m\) corresponds to the rate at which the predator finds any given prey (assuming unit available searching time). If there is no individual present, the predator stays hungry. Note that we assume that, unlike in [24], there is no refuge, i.e. \(\lambda _m>0\) for all m.
The individual payoff for staying at place \(P_m\) is thus
where \(B_m\) is a baseline payoff. Many other payoff functions are possible, as long as \(R_m\) are all increasing functions of \(k_m\).
In contrast to the habitat selection game, the individuals are now better off if they aggregate (although this would not be the case for a Holling type III function, see for example Garay and Móri [16]). In particular, in the special case where all places are of identical quality and individuals can go to all places, there can be M stable occupancy functions (each with a unique distribution), corresponding to all individuals being at a single place (in contrast to the habitat selection game when different stable occupancy functions yield the same distribution).
Note that if we assumed that the predator keeps searching until it finds an occupied patch, the payoff to an individual could depend on the positions of others and thus violate the local aggregation assumption. For example, consider the case with large N and M with \(N\le M\), and a focal individual being alone. The payoff to the focal individual would be different if the others are all together (it will be killed with probability 1 / 2) or if they are all alone (it would be killed with probability 1 / N). For our game defined above, this probability is 1 / M irrespective of the distribution of the others (as long as they are at different places to the focal individual).
4.2 All Solutions to the Predator Dilution Game
Here we present a method of finding all possible stable occupancy functions of the predator dilution game. The methodology in this section applies to generic games only. The fundamental feature of the payoffs is that they increase with group size. Consequently, the individuals will want to aggregate as much as possible. In other words, they will try to fill up an already occupied place to its maximal capacity.
(a) Let us pick a permutation \(\pi \) on indices \(1,2,\ldots , M\) and define the occupancy function O by filling the places to the maximum in the order prescribed by the permutation as follows. We partition \(\{1,2,\ldots ,N\}\) into a disjoint union of \(\{\mathcal{U}^{I}_m; m=1,\ldots , M\}\) where
In the above, \(\mathcal{U}^{I}_1\) corresponds to all individuals that can go to \(P_{\pi (1)}\) and \(\mathcal{U}^{I}_m\) corresponds to all individuals that can go to \(P_{\pi (m)}\) but not to any \(P_{\pi (m')}\) for \(m'<m\). Define
This yields a distribution \(k_{\pi (m)} = |\mathcal{U}^{I}_m|\). To check for the stability of O, first note that an individual in \(P_{\pi (j)}\) cannot physically move to \(P_{\pi (i)}\) for \(i<j\) (since if \(O(n)={\pi (j)}\), then \(n\in \mathcal{U}^{I}_j\) and thus \(n\not \in \mathcal{I}_{\pi (i)}\)). Consequently, an occupancy O will be stable if and only if
(b) We claim that by going through all the permutations \(\pi \), identifying the partitions \(\{\mathcal{U}^{I}_m\}\), defining the occupancy functions by (14) and discarding any non-stable ones (those that do not satisfy (15)), we will get all the stable occupancy functions.
First, it is clear that any occupancy function we get by the above procedure is stable. Conversely, if O is a stable occupancy function with the distribution \(\langle k_m\rangle _{m=1}^M\), consider a permutation \(\pi \) so that the sequence \(\langle R_{\pi (m)}(k_{\pi (m)})\rangle _{m=1}^M\) is decreasing. The place \(P_{\pi (1)}\) must be fully occupied; otherwise, any individual in \(\mathcal{I}_{\pi (1)}\) but not currently at \(P_{\pi (1)}\) would do better by moving to \(P_{\pi (1)}\) since for all m
Consequently, all individuals with \(P_{\pi (1)}\) in their territory must go there. Similarly, the remaining individuals with \(P_{\pi (2)}\) in their territory have to go to \(P_{\pi (2)}\) and so on. So, the above procedure with the permutation \(\pi \) indeed recovers the stable occupancy function D, and any stable distribution which satisfies (15) must have an occupancy function defined by (12) and (13).
4.3 Existence of Stable Occupancy Functions for the Predator Dilution Game
Following Sect. 2, we know that there is at least one stable set (a stable state for the generic game) for the general territorial movement game, and so in particular for the predator dilution game. In Sect. 4.2, we have seen a way of finding all solutions to the predator dilution game, but there may be few or many, and each case needs to be searched one by one. Here we show a method to efficiently find at least one solution to the predator dilution game (particularly useful for large populations/ structures).
The existence of stable occupancy functions for the Territorial Movement Game has been already shown in Sect. 2.3. However, due to the monotonicity of rewards in the predator dilution game, we can provide an explicit recursive method to identify a stable occupancy function.
We will define a permutation \(\pi \) on \(\{1,\ldots , M\}\) as follows. At the beginning, consider that all individuals are unplaced and all places unoccupied, and so define the sets of unoccupied places and unplaced individuals at step 0 as
Then in each recursive step, we find a place that gives its occupants maximal reward (from all unoccupied places) when occupied by a maximum number of (yet unplaced) individuals. This means that once \(\mathcal{V}^{I}_{t-1}\) and \(\mathcal{V}^{P}_{t-1}\) are defined, for some \(t\ge 1\), we pick \(\pi (t)\in \mathcal{V}^{P}_{t-1}\) such that
In principle, in (19) we may have to evaluate \(R_m(0)\) for some m and for simplicity we define it as \(R_{m}(0)=-\infty \). When \(\pi (t)\) is chosen, we define
corresponding to the fact that now place \(P_{\pi (t)}\) is fully occupied and individuals that could go to \(P_{\pi (t)}\) are now placed.
We repeat the process until \(\mathcal{V}^{I}_t=\emptyset \). Since we are filling the places to their maximum, \(\mathcal{V}^{P}_t=\emptyset \) implies \(\mathcal{V}^{I}_t=\emptyset \). Also, each step of the above procedure will make exactly one more place occupied and we are also assigning at least one individual to such a place. Consequently, the procedure is well defined and will stop in no more than \(\min \{N,M\}\) steps. If the above procedure has not defined \(\pi \) on the whole \(\{1,\ldots , M\}\), we will just define \(\pi \) to be the (unique) increasing numerical sequence on the remaining elements.
Once the permutation \(\pi \) is defined, we use it to construct the occupancy function O as done earlier in Sect. 4.2 by (14) together with (12) and (13). The occupancy function O is clearly stable. Indeed, the individuals that go to \(P_{\pi (1)}\) cannot do any better as this place is fully occupied and it is the place that yields a payoff higher than at any other fully (and thus also arbitrarily) occupied place. The individuals at place \(P_{\pi (2)}\) also cannot do any better, because they cannot move to \(P_{\pi (1)}\) but are at the place that is fully occupied and yields the highest reward of all other places occupied fully (and thus also arbitrarily) by those that cannot go to \(P_{\pi (1)}\); and so on.
5 Discussion
In this paper, we have considered the important problem of how groups of animals should allocate themselves between different habitats, introducing a method to model this using a finite population, where the movement of the individuals faces some restriction. We have considered the general case, showing that there is at least one stable population distribution, but there can be many. We have also considered a development of the classical ideal free distribution of optimal foraging to our structure and developed a model of predator dilution; in each case, we have shown how to find the stable occupancy functions (and that the corresponding distribution is unique in the case of unrestricted movement for the generic case).
We have made no explicit mention of evolution for our model. For evolutionary processes involving finite populations, the specific dynamics involved is generally an important factor, and the most important concept is the fixation probability. A generalisation of the ESS to a finite population, involving a combination of the relative fitness of a single mutant individual when compared to the resident fitness and the fixation probability, was considered in Nowak [33]. Alternatively, and perhaps more appropriately for the current model, we could consider an infinite population of individuals, from which random groups of N individuals are selected to play the above game. In this scenario, strategies that we have termed stable occupancy functions would become ESSs (and similarly stable sets would become evolutionarily stable sets). We note, however, that for any complex structure of places and individuals it is unlikely that it would be replicated from group to group within the overall population, and so some more complicated scenario with many possible structures might be needed.
This model reflects real cases where foraging is restricted. An example would be pollinators (as the individuals) and plants (as the places), where each pollinator specialises in a subset of the available plants and some plants specialize for certain pollinators [20, 44]. Here the “territories” of individuals are not physical areas in space, but their own set of host plants. It can also be used to model more general situations, which are not principally about foraging. A range of activities that apply to group-living animals can be regarded in this way, for example taking shelter, or migration (where a “place” would be a migration route) or alternatively mating, where the females may be considered as individuals and the males as “places”. Currently our model is very general, but it is flexible, and there is the potential to develop it to model more species-specific situations.
There are a number of ways that the modelling in this paper can be developed. One can relax the local aggregation assumption as done for example in Maciejewski and Puleo [29] where authors consider a structured population model where different individuals are best suited to different regions of their environment. Also, in this paper we have assumed strategies are pure, so that each individual chooses a place so that given the individuals choices the occupancy function is determined. An interesting question is, can there be mixed strategies, where individuals choose a place according to a probability distribution? We note that a population with only two individuals moving to M patches is a form of bi-matrix game (with special payoffs). ESSs in such games are always pure, following the work of Selten [38]. When can this result be generalised to our multi-player case, meaning that no mixed strategy could be stable? It would also be of interest to consider general, and specific, models on structures of movement with special properties. Models in evolutionary graph theory have focused on such ideas to significant benefit, and there is potential in our model too.
Further, we note that the habitat selection game and the predator dilution game are effectively two extremes of a more general case, in the sense that the ideal group size for the habitat selection game was one (i.e. with no groupmates) and for the predator dilution game individuals prefer to be with as many others as possible. In reality, the ideal group size may typically be somewhere between these two. For example, if individuals are hunters, then a group has to be large enough to catch a large prey animal but not so large that the share of every individual is overly reduced. Similarly, there may be an optimal group size to hide from predators. If the group is too big, the predator dilution effect is strong, but the group may be very visible to potential predators. If the group is too small, the dilution effect is small if the group is found by a predator. Consequently, the optimal group size is neither small nor large.
Thus it would be useful to consider such a generalisation where the best group size is of intermediate value. This would be appropriate for any population which is subject to the Allee effect. This type of situation was modelled in the usual infinite population habitat selection game in Křivan [25] (see also [31, 32]) which demonstrates the strong influence of the Allee effect upon the population dynamics and also upon the spatial distribution of the population. A unique IFD exists for low and high population densities, but there can be up to three IFDs for intermediate densities. Thus even in the case of well-mixed infinite populations, the number of possibilities is large. Thus we do not expect to be able to generate similar complete general results for this case as those we found for the previous two models. Nevertheless we know from Sect. 2.3 that there will always be at least one stable set, and we envisage that some general results can be found, together with approaches to tackle specific models, including finding the stable sets, using the methods we have generated in this paper. It would also be of interest to attempt to combine the analytical methods developed in our paper with those of Křivan [25] for the infinite population unrestricted case.
References
Allen B, Nowak MA (2014) Games on graphs. EMS Surveys Math Sci 1(1):113–151
Antal T, Scheuring I (2006) Fixation of strategies for an evolutionary game in finite populations. Bull Math Biol 68(8):1923–1944
Binmore K, Samuelson L (2001) Can mixed strategies be stable in asymmetric games? J Theor Biol 210(1):1–14
Broom M, Lafaye C, Pattni K, Rychtář J (2015) A study of the dynamics of multi-player games on small networks using territorial interactions. J Math Biol 71(6–7):1551–1574
Broom M, Rychtář J (2008) An analysis of the fixation probability of a mutant on special classes of non-directed graphs. Proc R Soc A Math Phys Eng Sc 464(2098):2609–2627
Broom M, Rychtář J (2012) A general framework for analysing multiplayer games in networks using territorial interactions as a case study. J Theor Biol 302:70–80
Broom M, Rychtář J (2013) Game-theoretical models in biology. CRC Press, Boca Raton
Bruni M, Broom M, Rychtář J (2013) Analysing territorial models on graphs. Involv J Math 7(2):129–149
Cantrell RS, Cosner C, Lou Y (2010) Evolution of dispersal and the ideal free distribution. Math Biosci Eng MBE 7(1):17–36
Cressman R, Křivan V, Garay J (2004) Ideal free distributions, evolutionary games, and population dynamics in multiple-species environments. Am Nat 164(4):473–489
Cressman R, Křivan V (2010) The ideal free distribution as an evolutionarily stable state in density-dependent population games. Oikos 119(8):1231–1242
Cressman R, Tran T (2015) The ideal free distribution and evolutionary stability in habitat selection games with linear fitness and allee effect. Interdis Top Appl Math Springer Model Comput Sci, pp 457–463
Fretwell SD (1972) Populations in a seasonal environment, vol 5. Princeton University Press, Princeton
Fretwell S, Lucas H (1969) On territorial behavior and other factors influencing habitat distribution in birds. Acta Biotheor 19(1):16–32
Garay J, Cressman R, Xu F, Varga Z, Cabello T (2015) Optimal forager against ideal free distributed prey. Am Nat 186(1):111–122
Garay J, Móri T (2010) When is predator’s opportunism remunerative? Commun Ecol 11(2):160–170
Hadjichrysanthou C, Broom M, Rychtář J (2011) Evolutionary games on star graphs under various updating rules. Dyn Games Appl 1(3):386–407
Holling C (1959) The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can Entomol 91(05):293–320
Houston A, McNamara J (1988) The ideal free distribution when competitive abilities differ: an approach based on statistical mechanics. Anim Behav 36(1):166–174
Johnson SD, Steiner KE (2000) Generalization versus specialization in plant pollination systems. Trends Ecol Evol 15(4):140–143
Krause J, Ruxton GD (2002) Living in groups. Oxford University Press, Oxford
Krijger C, Sevenster J (2001) Higher species diversity explained by stronger spatial aggregation across six neotropical drosophila communities. Ecol Lett 4(2):106–115
Křivan V, Cressman R, Schneider C (2008) The ideal free distribution: a review and synthesis of the game-theoretic perspective. Theor Popul Biol 73(3):403–425
Křivan V (2013) Behavioral refuges and predator-prey coexistence. J Theor Biol 339:112–121
Křivan V (2014) The allee-type ideal free distribution. J Math Biol 69(6–7):1497–1513
Lieberman E, Hauert C, Nowak M (2005) Evolutionary dynamics on graphs. Nature 433(7023):312–316
Maciejewski W (2014) Reproductive value in graph-structured populations. J Theor Biol 340:285–293
Maciejewski W, Fu F, Hauert C (2014) Evolutionary game dynamics in populations with heterogenous structures. PLoS Comput Biol 10(4):e1003,567
Maciejewski W, Puleo GJ (2014) Environmental evolutionary graph theory. J Theor Biol 360:117–128
Maynard Smith J (1982) Evolution and the theory of games. Cambridge University Press, Cambridge
Morris DW (1988) Habitat-dependent population regulation and community structure. Evol Ecol 2(3):253–269
Morris DW (2002) Measuring the Allee effect: positive density dependence in small mammals. Ecology 83(1):14–20
Nowak M (2006) Evolutionary dynamics: exploring the equations of life. Belknap Press, Harvard
Ohtsuki H, Hauert C, Lieberman E, Nowak M (2006) A simple rule for the evolution of cooperation on graphs. Nature 441(7092):502
Parker G (1978) Searching for mate. In: Sibly RM, S R (eds) Behavioural ecology: ecological consequences of adaptive behaviour. Blackwells, Oxford, pp 214–244
Prokopy RJ, Roitberg BD (2001) Joining and avoidance behavior in nonsocial insects. Annu Rev Entomol 46(1):631–665
Santos F, Pacheco J (2006) A new route to the evolution of cooperation. J Evol Biol 19(3):726–733
Selten R (1980) A note on evolutionarily stable strategies in asymmetric animal conflicts. J Theor Biol 84:93–101
Steele WK, Hockey PA (1995) Factors influencing rate and success of intraspecific kleptoparasitism among kelp gulls (larus dominicanus). Auk 112(4):847–859
Sutherland W, Parker G (1985) Distribution of unequal competitors. In: Sibly RM, S R (eds) Behavioural ecology: ecological consequences of adaptive behaviour. Blackwells, Oxford, pp 255–274
Voelkl B (2010) The “Hawk-Dove” game and the speed of the evolutionary process in small heterogeneous populations. Games 1(2):103–116
Voorhees B (2013) Birth–death fixation probabilities for structured populations. Proc R Soc Lond A Math Phys Eng Sci R Soc 469:20120248
Voorhees B, Murray A (2013) Fixation probabilities for simple digraphs. Proc R Soc A Math Phys Eng Sci 469(2154):20120,676
Waser NM, Ollerton J (2006) Plant-pollinator interactions: from specialization to generalization. University of Chicago Press, Chicago
Woodroffe R, Ginsberg J, Macdonald D (1997) The African wild dog: status survey and conservation action plan. World Conservation Union, Gland
Woodroffe R, Ginsberg J (1999) Conserving the African wild dog Lycaon pictus. I. Diagnosing and treating causes of decline. Oryx 33(2):132–142
Acknowledgments
This work was supported by funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skodowska-Curie Grant Agreement No 690817. The research was also supported by the Simons Foundation Grant 245400 to J. Rychtář. The authors also would like to thank V. Křivan for his comments and suggestions that helped to improve the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Broom, M., Rychtář, J. Ideal Cost-Free Distributions in Structured Populations for General Payoff Functions. Dyn Games Appl 8, 79–92 (2018). https://doi.org/10.1007/s13235-016-0204-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-016-0204-4