1 Introduction

We analyze strategic interaction in a fishery subject to rarity value, a price-scarcity relationship in which unit prices of a commodity increase sharply as it becomes less and less available (cf., [12]). So in terms of traditional industrial organization, the demand curves shift upwards as scarcity increases; hence, for every quantity offered, a higher market-clearing price is found. In the case of a natural resource, this may induce the following scenario. Once a species becomes rare, its value increases, inducing greater efforts to exploit it, leading to greater rarity, a higher value etc. An Allee effect may then occur, i.e., the population size or density is pushed below a threshold beyond which only negative growth rates exist. [12] list many real-world cases showing that rarity value inducing an anthropogenic Allee effect (AAE) is not an armchair-scientist’s oddity.

In bringing rarity value to the fore, [12] disregarded several subtleties. Their analysis relies on considering unit profits and on agents discounting the future so heavily that the stream of future profits is always sufficiently similar to the prevailing one-shot profits. Also, the influence of one agent on the resource and on the other agents is negligible, but collectively, they can really harm the resource. Finally, to reach the scarcity where price/search costs ratios explode, extended periods of time with negative profits to the agents have to be dealt with. There seems hardly a consistent explanation how this is to be accomplished.

To deal with these subtleties, it is our goal to analyze total profits, i.e., unit profits times quantities, averaged over an infinite period by very patient agents with (possibly) bounded catching capacities in an interactive decision making framework with both short- and long-term strategic externalities in a newly designed Small Fish War.

For this exploratory investigation, we engineered a stochastic gameFootnote 1 by adding a mechanism inducing rarity value, as well as an Allee threshold to the Small Fish War Footnote 2 of [30]. In the original Small Fish War, two agents possess the fishing rights to a body of water, and they have essentially two options, to fish with or without restraint. Restraint in practice may take various forms, e.g., on catching seasons, on quantities caught, on technologies, e.g., boats, nets. Essential is that unrestrained fishing yields a higher immediate catch, but continued unrestrained fishing may lead to decreasing future catches; restrained fishing by both agents is sustainable.

In a Small Fish War, agents wish to maximize their average catches over an infinite time-horizon. There, a ’tragedy of the commons’ ([24]) is curbed, as Pareto-efficient outcomes can be sustained by subgame-perfect equilibria inducing rather high fish stocks. For wide ranges of the model’s parameters, ’perfect restraint’ is never Pareto-efficient.

While examining our new model, we found that it is crucial to make a distinction between strong and weak rarity value, and developed an operational criterion to separate one from the other. We show that a Small Fish War under strong rarity value may exhibit the environmental and economic effects sketched by [12], i.e., Pareto-efficiency either implies ‘no restraint’ or it induces stocks just above the Allee threshold level. It is also without contradiction that our very patient agents (are willing and able to) achieve the necessary scarcity levels to exploit strong rarity value.

Contrasting, very patient agents in a setting with weak rarity value induce ‘almost perfect restraint’ Pareto-efficient equilibria, high sustainable stocks and rewards slightly higher than ‘perfect restraint’ rewards. Errors in assessment of the nature of rarity value may lead to a ‘tragedy of the commons’, i.e., deterioration of the economic and the resource systems, or to a ‘tragedy of the herdsmen’, i.e., missed economic opportunities.

Rarity value leaves room to serve economic and ecological goals simultaneously as many equilibria yield sustainable rewards above ‘perfect restraint.’ This suggests a basis for effective policies for management and conservation of natural resources as [28] attributes ineffectiveness of, for instance, the common fishery policies of the European community, to their biological focus instead of an economic one (see also e.g., [4, 10, 43]). Dangers of strong rarity value, i.e., Pareto-efficient equilibrium behavior targeting the limits of sustainable fish stocks, can be curbed if the resource is managed diligently and strictly, for instance according to The Precautionary Approach of the International Council for the Exploration of the Sea (cf., e.g., [29]).

Next, we review the Small Fish War and then add an Allee effect under the assumption that unit profits are fixed. In Section 3, we examine the combined effects of rarity value and the AAE. Section 4 concludes with a discussion.

2 Small Fish Wars and Impacts of Allee Effects

A Small Fish War is played by players \(A\) and \(B\) at discrete moments in time called stages. Each player has two actions and each stage players choose an action independently and simultaneously. We denote the action set of player \(A\) (\(B\)) by \(J^{A}=\{0,1\} (=J^{B})\) and \(J\equiv J^{A}\times J^{B}.\) Action 1 for either player denotes the action without restraint, e.g., catching with fine-mazed net or catching a high quantity; the other one is the action with a restriction. The payoffs at stage \( t^{\prime }\in \mathbb {N}\) of the play depend on the choices of the players at that stage, and on the relative frequencies with which all actions were actually chosen until then.

Crucial is the current rate of overfishing, i.e., how often the agents have caught without restraint until then. Let \(j_{t}^{A}\left( j_{t}^{B}\right) \) be the action chosen by player \(A (B)\) at stage \(t\ge 2 \), and let \(q\ge 0.\) Define the current rate of overfishing \( \rho _{t}\) recursively by

$$\begin{aligned} \rho _{1}=\rho \in \left[ 0,1\right] ,\quad {\text {and}}\quad \rho _{t}=\frac{q+t-1}{q+t} \rho _{t-1}+\frac{1}{q+t}\left( \frac{j_{t-1}^{A}+j_{t-1}^{B}}{2}\right) . \end{aligned}$$

So, \(\rho \) is the rate of overfishing taken at the start of the period analyzed. A completely untouched system has \(\rho =0;\) a system where overfishing has gone on ‘forever’ has \(\rho \approx 1\). Parameter \(q\) moderates effects of early decisions on the rate. As we focus on long-term horizons, \(\rho \) and \(q\) become irrelevant.

The current fish stock depends on the current rate of overfishing \( \rho _{t}\). Let

$$\begin{aligned} \mu _{t}\equiv 1+\left( 1-\underline{m}\right) \left[ \frac{n_{2}}{ n_{1}-n_{2}}\rho _{t}^{n_{1}}-\frac{n_{1}}{n_{1}-n_{2}}\rho _{t}^{n_{2}} \right] . \end{aligned}$$
(1)

Here, \(\mu _{t}\) is the fish stock (normalized to the unit interval), where \(\mu _{t}=0 \left( \mu _{t}=1\right) \) indicates that the fish stock is depleted (at full capacity). The parameter \(\underline{m}\in \left[ 0,1\right] \) represents the minimal stock due to overexploitation, i.e., if \(\rho _{t}\rightarrow 1,\) then \(\mu _{t}\rightarrow \underline{m}.\) So, (1) determines how the fish stock deteriorates from its maximum due to fishing without restraint. Parameters \( n_{1}>n_{2}>1\) shape the function connecting the normalized fish stocks to the rate of overfishing and are determined by biological and ecological features. Minimal fish stock \(\underline{m}\) depends on technology and the size of the agents.

At each stage, a bi-matrix game is played, and the choices of the players at that stage determine their stage payoffs. Let the stage payoffs at stage \(t\in \mathbb {N}\) be represented by

$$\begin{aligned} \left[ \begin{array}{cc} a\mu _{t},a\mu _{t} &{}\quad b\mu _{t},c\mu _{t} \\ c\mu _{t},b\mu _{t} &{}\quad d\mu _{t},d\mu _{t} \end{array} \right] =\mu _{t}\left[ \begin{array}{cc} a,a &{}\quad b,c \\ c,b &{}\quad d,d \end{array} \right] \text {.} \end{aligned}$$
(2)

If player \(A\) chooses action 0 and \(B\) chooses action \(1, A\)’s stage payoff is \(b\mu _{t}\) and \(B\)’s is \(c\mu _{t}.\) For \(\underline{m}=1,\) we have a standard repeated game.

If both agents never show restraint, then the associated long-run stage payoffs are \(d\underline{m};\) if they show perfect restraint, these payoffs are \(a.\) Next, we make a series of assumptions which guarantees that the problem is a social dilemma (see e.g., [34]). Moreover, the effects of overfishing are not too immediate, yet cannot be postponed indefinitely.

Assumption

Fishing without restraint yields a higher catch in any stage than fishing with restraint, hence \(a<c,b<d\). Two-sided catching without restraint yields higher immediate payoffs than catching with restraint, i.e., \(a<d\). Never restraint gives at most half the long-run stage payoffs associated with ’perfect restraint,’ i.e., \(d\underline{m}\le \frac{a}{2}\); the sharpest decline of the stock occurs for rates of overfishing between 0.25 and 0.75.

2.1 Strategies and Rewards

The sets of all strategies for \(A (B)\) is denoted by \(\mathcal {X}^{A} ( \mathcal {X}^{B})\). The payoff to player \(k, k=A,B,\) at stage \(t,\) is stochastic and depends on the strategy pair \(\left( \pi ,\sigma \right) \in \mathcal {X}^{A}\times \mathcal {X}^{B}\); the expected stage payoff is denoted by \(R_{t}^{k}\left( \pi ,\sigma \right) .\)

The players receive an infinite stream of stage payoffs during the play, and they wish to maximize their average rewards. For a given pair of strategies \( \left( \pi ,\sigma \right) ,\) player \(k\)’s average reward, \(k=A,B,\) is given by \(\gamma ^{k}\left( \pi ,\sigma \right) =\liminf _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}R_{t}^{k}\left( \pi ,\sigma \right) ; \gamma \left( \pi ,\sigma \right) \equiv \left( \gamma ^{A}\left( \pi ,\sigma \right) ,\gamma ^{B}\left( \pi ,\sigma \right) \right) \). First, we focus on rewards from strategies which are pure and jointly-convergent. Then, we extend our analysis to obtain larger sets of feasible rewards.

A strategy is pure, if at each stage a pure action is chosen, i.e., an action is chosen with probability \(1.\) The set of pure strategies for player \(k\) is \(\mathcal {P}^{k}\), and \(\mathcal {P\equiv P} ^{A}\times \mathcal {P}^{B}.\) The strategy pair \(\left( \pi ,\sigma \right) \in \mathcal {X}^{A}\times \mathcal {X}^{B}\) is jointly- convergent if and only if \(z\in \varDelta ^{m\times n}\) exists such that for all \(\varepsilon >0,(i,j)\in J:\)

$$\begin{aligned} \limsup _{t\rightarrow \infty }\Pr _{\pi ,\sigma }\left[ \left| \frac{ \#\{j_{u}^{A}=i\text { and }j_{u}^{B}=j|\text { }1\le u\le t\}}{t} -z_{i+1,j+1}\right| \ge \varepsilon \right] =0, \end{aligned}$$

where \(\varDelta ^{m\times n}\) denotes the set of all nonnegative \(m\times n\) -matrices such that the entries add up to 1\(;\Pr _{\pi ,\sigma }\) denotes the probability under strategy pair \(\left( \pi ,\sigma \right) \). \(\mathcal {JC}\) denotes the set of jointly-convergent strategy pairs. The set of jointly-convergent pure-strategy rewards \(P^{\mathcal {JC}}\) is then the set of pairs of rewards each of which can be obtained by using a pair of jointly-convergent strategies. Under such a pair of strategies, the relative frequency of action pair \(\left( i,j\right) \in J\) converges (with probability 1 in the terminology of Billingsley [6], p. 274) to the number \(z_{i+1,j+1}\).

For jointly-convergent strategies, Eq. (1) and the arguments presented imply that

$$\begin{aligned} \lim _{t\rightarrow \infty }\mu _{t}=1+\left( 1-\underline{m}\right) \left( \frac{n_{2}}{n_{1}-n_{2}}\rho ^{n_{1}}-\frac{n_{1}}{n_{1}-n_{2}}\rho ^{n_{2}}\right) , \end{aligned}$$

where \(\rho \equiv z_{22}+\frac{1}{2}\left( z_{12}+z_{21}\right) .\) So, the expected long-term fish stock converges to a fixed number as well; hence, the bi-matrices representing the stage payoffs in (2) ‘converge’ in the long run, too.

To compute the rewards connected to a pair of jointly-convergent strategies is then a matter of simple ‘book keeping.’ Let

$$\begin{aligned} \varphi (z)\equiv \lim _{t\rightarrow \infty }\mu _{t}\sum _{(i,j)\in J}z_{i+1,j+1}\left( a_{i+1,j+1},b_{i+1,j+1}\right) . \end{aligned}$$

Here, \(\left( a_{i+1,j+1},b_{i+1,j+1}\right) \) is the entry in (2) corresponding to action pair \((i,j)\in J.\) The interpretation of \(\varphi (z) \) is that under jointly-convergent strategy pair \(\left( \pi ,\sigma \right) \), the relative frequency of action pair \((i,j)\in J\) being chosen is \(z_{i+1,j+1}\) and each time this occurs the players receive \( \lim _{t\rightarrow \infty }\mu _{t}\) times the associated entry in (2) in the long run. Hence, the players receive an average amount of \(\varphi (z).\) So, \(\gamma \left( \pi ,\sigma \right) =\varphi (z).\)

2.2 Threats and Equilibria

The strategy pair \(\left( \pi ^{*},\sigma ^{*}\right) \) is an equilibrium, if no player can improve by unilateral deviation. An equilibrium is called subgame-perfect if for each possible state and possible history (even unreached states and histories) the subsequent play corresponds to an equilibrium, i.e., no player can improve by deviating unilaterally from then on. In the construction of equilibria for repeated games, ‘threats’ play an important role. A threat specifies the conditions under which one player will punish the other, as well as the subsequent measures. More details are given in e.g., [31].

We call \(v=\left( v^{A},v^{B}\right) \) the threat-point, where \( v^{A}=\min _{\sigma \in \mathcal {X}^{B}}\max _{\pi \in \mathcal {X}^{A}} \gamma ^{A}(\pi ,\sigma ),\) and \(v^{B}=\min _{\pi \in \mathcal {X} ^{A}}\max _{\sigma \in \mathcal {X}^{B}}\gamma ^{B}(\pi ,\sigma ).\) So, \(v^{A}\) is the highest amount \(A\) can get if \(B\) tries to minimize his average payoffs. Under a pair of individually rational (feasible) rewards, each player receives at least the threat-point reward. We can now present the major result of [30].

Theorem 1

Each pair of rewards in the convex hull of all jointly-convergent pure-strategy rewards giving each player strictly more than the threat-point reward, can be supported by a subgame-perfect equilibrium.

The following consequence of Theorem 1 is illustrated in Fig. 1.

Fig. 1
figure 1

Here, \(\underline{m}=0.1, n_{1}=3,n_{2}=2,a=4, b=3.5, c=6, d=5.5\). PE denotes Pareto- efficient rewards. Left: \(P^{\mathcal {JC}}\) denotes the set of jointly-convergent pure-strategy rewards; CP\(^{\mathcal {JC}}\) is its convex hull. Right: \(E^{\prime }\) represents subgame-perfect equilibrium rewards; \(v\approx (1.925,1.925)\)

Full size image

Corollary 2

Let \(E^{\prime }=\{(x,y)\in P^{\mathcal {JC}}|\left( x,y\right) >v\},\) then all rewards in the convex hull of cl \(E^{\prime }\) (respectively \( E^{\prime })\) can be supported by an equilibrium (respectively a subgame-perfect equilibrium).

This Folk Theorem-type result hinges on the possibility of punishing unilateral deviations, as in e.g., [22]. So, we need history-dependent strategies. To prevent misconception, there is no contradiction between strategy pairs being both jointly-convergent and history-dependent, or for that matter cooperative, e.g., [35, 46, 47], or incentive strategies, or combinations, e.g., [16–19]. Neither is there one between an equilibrium being jointly-convergent and subgame-perfect: If the equilibrium path in the terminology of [25] induces convergence with probability 1, the off-equilibrium part may be of arbitrary sophistication. Finally, equilibrium rewards in the convex hull of \(E^{\prime }\) that do not belong to \(E^{\prime }\) can only be obtained by history-dependent strategies with threats, that are not jointly-convergent.Footnote 3

2.3 A Small Fish War with an Allee Effect

We now introduce an Allee effect into the model. [12] explain: ‘Populations suffering from Allee effects may exhibit negative growth rates at low densities, which drives them to even lower densities and ultimately to extinction.’ [5] define an Allee threshold as the ‘critical population size or density below which the per capita population growth rate becomes negative.’

Let therefore \(Th\) denote an Allee threshold measured in the same dimension as the fish stock. We formalize the explanations above by

$$\begin{aligned} \begin{array}{l} \mu _{t}=1+\left( 1-\underline{m}\right) \left[ \frac{n_{2}}{n_{1}-n_{2}} \rho _{t}^{n_{1}}-\frac{n_{1}}{n_{1}-n_{2}}\rho _{t}^{n_{2}}\right] \; \text { if }\;\mu _{s}\ge \hbox {Th}\;\text { for all }\;s\le t, \\ \mu _{t}\le \left( 1-\theta \right) ^{\gamma \left( t-s^{\prime }\right) } \;\text { for all }\;t\ge s^{\prime }\;\text { if }\;\mu _{s^{\prime }}<\hbox {Th}\;\text { where }\;\gamma \ge 1,\;\theta \in \left( 0,1\right) . \end{array} \end{aligned}$$

The second part above captures the Allee effect in a rather general manner implying that the population decreases (at least) exponentially. Hence, if under strategy pair \(\left( \pi ,\sigma \right) \) the fish stock at any point in time drops below the Allee threshold, then \( \lim _{t\rightarrow \infty }\mu _{t}=0;\) we normalize the associated rewards to \(\gamma \left( \pi ,\sigma \right) =\left( 0,0\right) \) and call them Collapse Rewards, since the resource system as well as the economic system depending on it breaks down.

Figure 2 visualizes sets of rewards under the Allee effect; without this effect, \(P^{\mathcal {JC}}\) would have been ’pointed’ in the southwest as in Fig. 1, it is now ’blunt.’ Equilibrium rewards are quite far removed from the collapse rewards. This means that self-interested rational agents will behave in the interest of the environmental system in order to guarantee high fish stocks staying far above the Allee threshold. The Allee threshold influences the set of equilibrium rewards only if it is rather high, the set of equilibrium strategies is obviously reduced for any level of the threshold.

Fig. 2
figure 2

The same sets \(P^{\mathcal {JC}},\hbox {CP}^{\mathcal {JC}}\backslash P^{\mathcal {JC}},\hbox {PE},E^{\prime }\) for \(\underline{m}=0.01,\hbox {Th}=0.1\) and all other parameters as in Fig. 1. Collapse rewards are \((0,0),\) equilibrium rewards are to the northeast of \(v\approx (1.7675,1.7675)\)

Full size image

We introduce the following notion captured by a single number.

Definition 3

The total relative improvement over perfect restraint \(\varDelta \) is the total symmetric Pareto-efficient rewards minus the total ‘perfect restraint’ rewards relative to the total ‘perfect restraint’ rewards.

For Fig. 1, \(\varDelta \approx \frac{8.11-8}{8}=0.01375,\) for Fig. 2, \( \varDelta \approx \frac{8.09-8}{8}=0.01125.\) The numbers indicate how much the gain of cooperation can be over perfect restraint. So, in both cases these gains are quite limited to just over 1 %.

3 Rarity Value and the Anthropogenic Allee Effect

The Small Fish War and its extension presented implicitly model a situation in which agents sell their catches at a competitive market while incurring fixed-unit search costs, at least fixed with respect to the scarcity of the resource in their fishing environment. Alternatively, if neither prices on the market nor search costs are fixed, then one can regard the model as pertaining to a situation in which unit prices go up approximately in the fashion as the unit search costs do for increasing scarcity.

In some cases, fishermen extract less and less in quantities, but obtain higher and higher revenues. An ongoing real-world example of such an anomaly might be the market for bluefin tuna. Stocks seem to have decreased by 80 % in the 5 years prior to 2007, and prices have sky-rocketed since 2007 especially in the Far East (e.g., [48]). In economics, similar anomalies are known as Veblen and status goods (cf., e.g., [36]), but these are hardly ever linked to animal species facing extinction. [12] model and analyze the latter aspect.

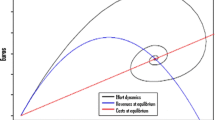
Figure 3 is inspired by a poignant figure from [12]. The unit costs of catching depend on availability, to be captured by the fish stock \(\mu \) in our model (on the horizontal axis). Unit costs increase as the species becomes rarer, i.e., \(\mu \) becomes smaller. Unit prices remain nearly constant between \(\mu =1\) and \(\mu =0.6\), but for lower availability of the fish stock, they go up sharply. The formula for the unit profit curve is

$$\begin{aligned} \begin{array}{c} \pi \left( \mu \right) =p(\mu )-c(\mu )=\frac{4}{3.75}\left( \left( 4+0.75 \frac{1}{\mu ^{2}}\right) -\left( 12-12\mu +\frac{1}{\mu ^{1.5}}\right) \right) . \end{array} \end{aligned}$$
(3)

where \(p\left( \mu \right) \) is the unit price on the market and \(c(\mu )\) is the unit costs given fish stock \(\mu .\) Note that \(\lim _{\mu \downarrow 0}\pi \left( \mu \right) \) does not exist and \(\pi \left( 1\right) =4\) (by scaling).

Fig. 3
figure 3

The unit costs (solid), unit prices (top dashed) and unit profits (bottom dashed) as functions of the level of the fish stock

Full size image

So, unit profits decrease as fish stocks decrease from maximal level as the unit price remains almost constant, but unit search costs increase steadily. If the fish stock continues to fall below approximately \(0.675\), unit profits become negative, i.e., the agents would incur losses by catching fish. However, if the fish stock would fall below approximately \(0.228\), then the unit price driven by scarcity exceeds unit costs again. Moreover, increasing scarcity causes the unit price to increase more than the unit costs from then on.

Figure 4 illustrates the effects of adding Eq. (3) to the model used so far. Since a range with negative unit profits exists, we find negative average rewards. For fish stocks with \(\mu <0.228\) unit, profits increase steadily as fish stocks decline. The Pareto-dominant rewards are the ‘no restraint’ rewards. Note that the latter rewards are located in the southwest in Fig. 1, but in the northeast in Fig. 4. ‘Perfect restraint’ provides relatively high rewards of \(\left( 4,4\right) \), but belongs to the Pareto-efficient set of jointly-convergent pure-strategy rewards in neither figure.

Fig. 4
figure 4

\(P^{\mathcal {JC}}\) for the parameters as before, but with \(\hbox {Th}_\mathrm{AAE}= \underline{m}=0.1\) and \(\pi \). The 250,000 rewards are unevenly distributed, the true set is dense. The system displays strong rarity value as \(\varDelta /\varDelta _\mathrm{Base}\approx 0.34/0.01375.\) Rewards to the ‘North-East’ of \((\overline{v},\overline{v})\) correspond to equilibria

Full size image

Both resource stocks and unit profits change due to overexploitation. To cope with this double effect, we need an additional point of reference.

Definition 4

\(\varDelta _\mathrm{Base}\) is the relative improvement over perfect restraint if unit profits were fixed at ‘base’ level, i.e., for maximal resource stock (\(\mu =1 \)).

Definition 5

The system is said to display weak rarity value if \(\frac{\varDelta }{ \varDelta _\mathrm{Base}}\le 1,\) and strong rarity value otherwise.

So, the system displays strong rarity value if and only if the symmetric Pareto-efficient rewards in the model with rarity value exceed those in the model with prices kept fixed at the level of maximal resource availability.

We have the following result pertaining to the threat-point \(v=\left( v^{A},v^{B}\right) \), the proof is straightforward, therefore omitted.

Lemma 6

For the model introduced, we have \(v^{A},v^{B}\le \overline{v}=\min \left\{ \frac{a}{4},\frac{b}{4}\right\} \cdot \left[ \frac{1}{2}\left( 1+ \underline{m}\right) \right] \cdot \pi _{t}\left( \frac{1}{2}\left( 1+ \underline{m}\right) \right) .\)

Given \(v\le (\overline{v},\overline{v})\), the following is clearly valid in view of Theorem 1.

Corollary 7

Let \(E^{\prime }=\{(x,y)\in P^{\mathcal {JC}}|\left( x,y\right) >( \overline{v},\overline{v})\},\) then each pair of rewards in the convex hull of \(clE^{\prime }\) can be supported by an equilibrium. Moreover, all rewards in \(E^{\prime }\) can be supported by a subgame-perfect equilibrium.

In Fig. 4, the Pareto-optimal equilibrium (‘no restraint’) yields approximately \((5.36,5.36)\) inducing minimal fish stock. Note that \( \frac{\varDelta }{\varDelta _\mathrm{Base}}\approx \frac{0.34}{0.01375}\).

3.1 Rewards, Rarity Value and Parameter Choices

Here, we identify two factors decisive for the sustainability of the resource system. The first one is related to the ‘actual harm’ caused by persistent unrestricted catching. The second is that under the evaluation criterion chosen unit profits are not the real issue, but long-term average total profits.

3.1.1 The Influence of Minimal Fish Stock

In Fig. 5, Pareto-optimal equilibria give rewards quite close to and slightly above 4 and a large proportion of the catches must be restrained. Some equilibrium rewards may be obtained in two different ways by either catching with restraint quite frequently, or by catching without restraint quite frequently. This can be seen in Fig. 5, as the rewards situated in the beak in Fig. 4 have withdrawn into the ‘body of the fish shape,’ visible as the heavy lines in the ‘body’s’ interior. Here,\(\frac{\varDelta }{ \varDelta _\mathrm{Base}}\approx \frac{0.007}{0.0121}=0.578\,51\) so this system displays weak rarity value.

Fig. 5
figure 5

\(P^{\mathcal {JC}}\) for \(\hbox {Th}_\mathrm{AAE}=0.1,\underline{m}= 0.12.\) Here, \(\frac{\varDelta }{\varDelta _\mathrm{Base}}<1,\) so this system displays weak rarity value. Again, all rewards to the North-East of \(\left( \overline{ v},\overline{v}\right) \) can be obtained by an equilibrium

Full size image

For smaller \(\underline{m},\) rarity value effects occur as in the case related to Fig. 4 with the ‘beak’ becoming larger. Hence, if the catching capacity increases (lowering \(\underline{m}\)), the induced unique Pareto-efficient equilibrium yields increasing rewards. So, the agents may bring about the lowest sustainable fish stock deliberately. For \(\underline{m }=0.06,\hbox {Th}_{AAE}=0,\) and all other parameters as before, we found that the Pareto-efficient equilibrium yields \((11.705,11.705)\), and \(\frac{\varDelta }{ \varDelta _\mathrm{Base}}\approx 1.926/0.0116\) which implies strong rarity value.

3.1.2 The Influence of the Unit Profit Function

Unit profits going to infinity is not a necessary condition to induce strong rarity value. This stems from the insight that it is quite irrelevant how the profit function behaves below the technically feasible minimal fish stock level, or the Allee threshold for that matter. The system will either not get there anyway, or the system collapses inducing lower rewards. This strengthens the result mentioned, as infinite unit profits seem quite artificial.

Unit profits going to infinity is not sufficient to obtain strong rarity value, either. Let the unit profits be given by

$$\begin{aligned} \pi ^{\prime }\left( \mu \right) =p(\mu )-c(\mu )=\frac{4}{3.75}\left[ \left( 4+0.75\frac{1}{\mu }\right) -\left( 12-12\mu +\frac{1}{\mu ^{0.5}} \right) \right] . \end{aligned}$$

Qualitatively, \(\pi \) and \(\pi ^{\prime }\) are similar. The significant difference is that even if the catching capacities of the fishermen were unlimited, the price effects do not dominate the quantity effects sufficiently to obtain high rewards. For \(\underline{m}=\hbox {Th}_\mathrm{AAE}=0\) and \(\pi ^{\prime }\) we generated a figure qualitatively equivalent to Fig. 5 with \(\varDelta \approx 0.00067\) whereas \(\varDelta _\mathrm{Base}\approx 0.0107.\) As, \(\frac{ \varDelta }{\varDelta _\mathrm{Base}}\approx \frac{0.00067}{0.0107}=0.062617\), this system displays weak rarity value, even highest scarcity is insufficient to obtain rewards inducing effects leading to the scenario of [12].

3.2 The Anthropogenic Allee Effect

In the Small Fish War with constant prices to which an Allee effect was added, a subset of the jointly-convergent pure-strategy rewards is cut off. Since Allee effects only occur if the fish stock drops below a certain threshold, only lower left-hand-side rewards in \(P^{\mathcal {JC}}\) are affected there. To visualize this effect, please compare Figs. 1 and 2. However, under ‘rarity value’ an Allee effect may be expected to cut off rewards in the upper right-hand corner as the ‘no restraint’ rewards move to the North-East.

Indeed, an analysis of the set of jointly-convergent pure-strategy rewards confirms this intuition. Comparing Figs. 4 and 6 reveals that part of the ‘beak’ in Fig. 4 has disappeared as anticipated, i.e., the AAE eliminates a set of rewards being considerable Pareto improvements over ‘perfect restraint’.

Fig. 6
figure 6

Here, \(\underline{m}=0.1\) and \(\hbox {Th}_\mathrm{AAE}=0.11\), other parameters were taken as before. \(P^{\mathcal {JC}}\) is cut off in the ‘beak’. Equilibrium rewards are to the North-East of \(\left( \overline{v}, \overline{v}\right) \)

Full size image

We found \(\frac{\varDelta }{\varDelta _\mathrm{Base}}\approx \frac{0.125}{0.01375} =9.0909.\) So, despite the AAE removing a set of high-reward equilibria, the Allee threshold is not high enough to turn strong rarity value into the weak variant. As to the sensitivity of strong and weak rarity value to changes in the AAE, for \(\hbox {Th}_\mathrm{AAE}>0.1163\), the system displays weak rarity value, i.e., the remainder of the ‘beak’ disappears completely. So, an increase of the Allee threshold of just under 6 % (\(\frac{0.0063}{0.11}\)) turns strong into weak rarity value.

4 Conclusion and Discussion

The main purpose of this paper was to model rarity value in a Small Fish War ([30]) and examine its consequences. A second goal was to include an Allee effect, i.e., once a population falls below an Allee threshold, only negative growth rates occur. For this purpose, we engineered a stochastic game possessing these features.

Our exploratory investigations reveal that rarity value brings about a very diverse picture. For instance, even if unit profits go to infinity under maximum scarcity, it is by no means guaranteed that the associated rewards constitute even a Pareto improvement over the ‘perfect restraint’ equilibrium. We found it useful to distinguish strong and weak rarity value and developed an operational criterion to separate one from the other. Under weak rarity value, we have a similar result as in the fixed-unit-profits variant: self-interest and sustainability provide no tensions provided agents are sufficiently patient. However, if rewards associated with maximum scarcity are sufficiently high, the economic system and the resource system have ‘conflicting interests’ even for very patient agents. Highest sustainable equilibrium rewards under strong rarity value can only be accomplished by reaching the lowest possible sustainable fish stock.

However, equilibrium behavior need not necessarily imply ruthlessness . Many equilibria induce rewards above the ‘perfect restraint’ rewards for both instances of rarity value with stocks well above the Allee threshold. So, there is room for compromise between ecological and economic maximalistic goals, overcoming the one-sidedness of management policies for natural resources as noted by e.g., [10, 28], thus improving chances of success cf., e.g., [4, 43].

The following matrix gives an overview of the consequences of the complex interplay of factors from economics, biology and technology:

Here, \(\underline{m}\) is the (technologically feasible) minimal fish stock from prolonged overfishing; \(\hbox {Th}_\mathrm{AAE}\) is the threshold of the AAE; \(\varDelta \) is the relative improvement over perfect restraint, i.e., total symmetric Pareto improvements over total ‘perfect restraint’ rewards relative to the total ‘perfect restraint’ rewards, \(\varDelta _\mathrm{Base}\) is the same notion but with profits, prices and costs fixed at the levels associated with maximum availability of the resource. \(\frac{\varDelta }{\varDelta _\mathrm{Base}}>1\left( \frac{\varDelta }{\varDelta _\mathrm{Base}}\le 1\right) \) implies strong (weak) rarity value and \(\mu _{\infty }^\mathrm{PE}\) is the long-term fish stock under the interplay of the parameters if sufficiently patient agents strive for Pareto-efficient equilibria.

In the strong rarity value case, Pareto-efficient behavior may imply flirting with disaster, as the slightest mistake in actions or estimations of the parameters involved, or any change in environmental, ecological or climatic conditions might bring about the AAE. [5] claim that Allee effects may work in combinations. Hence, externalities from other fisheries may push the fish stock targeted over the threshold irrespective of the behavior of the agents. For instance [15], give an overview of negative externalities on own and other fisheries by different types of gear used in the Baltic Sea. Also [33], build a framework to assess damages by marine sand mining on fisheries in Korea, demonstrating that phenomena quite unrelated to any fishery may affect the fish stock targeted.

This indicates that there may be some wisdom in the Precautionary Approach of the International Council for the Exploration of the Sea (ICES) establishing limits on stock levels in order to manage fisheries in a ‘safe’ way (see [29]). Two limits are relevant to our concerns: the biomass limit and the precautionary biomass limit.Footnote 4 The former is the stock level below which the probability of total breakdown is very high and reproductive capacity is reduced. Two variants seem to be possible, one is similar to the scenario pictured with respect to the Allee effect and the second one is similar to the poaching pit (cf., e.g., [11]), in which a ban on fishing may not even be sufficient to guarantee recovery and the species may remain vulnerable to extinction (see also [21]). The latter limit is a level such that if the stocks should fall below it, short-term measures to reduce fishing should suffice for recovery.

If the agents manage the resource according to the precautionary approach (see e.g., [29]), the following overview is appropriate:

Here, we assumed that \(b_{pl},\) the precautionary biomass limit, is rather low, so, \(\hbox {Th}_\mathrm{AAE}<b_{l}<b_{pl}<<1\).

We stacked the cards in favor of sustainability according to common wisdom. Two very patient agents, perfect information, perfect monitoring, absence of stochasticity are factors known to contribute to solving social dilemmas (cf., [34] for an overview) and inducing Pareto-efficient equilibria in repeated and stochastic games. For weak rarity value this can be confirmed indeed, but for the strong variant sustainability of Pareto-optimal behavior may depend crucially on the abstractions made, and in that case must be regarded as unfeasible in practice.

Rarity value is unrelated to increasing marginal returns as studied by [40]. These authors show in a standard model using net present value optimization that increasing marginal returns and weak dependence of marginal costs on stock, induce collapse of schooling fisheries of species with high reproduction rates even if managed by a very patient single agent (‘owner’). Their arguments work in two steps. First, they bring to the fore empirical work showing that for several schooling species limited dependence of marginal costs on stock levels holds, cf., e.g., [13, 39]. Hence, in the case of schooling fisheries marginal returns independent from fish stocks as in e.g., [7], might be more justified than boundlessly increasing marginal harvesting costs for decreasing stock levels as analyzed by [20]. Then, they cite several papers giving a rationale for increasing marginal returns on catching efforts due to positive externalities and technological advances, e.g., [8, 9, 23]. [40] proceed however, with constant unit prices of harvest and constant variable cost independent from stock levels. We suspect that rarity value increases the effects pictured by [40]. The ongoing tragedy of the bluefin tuna brings, in all likelihood, together strong rarity value, increasing marginal returns (tuna is a schooling species), low reproduction rates, and a multitude of myopic agents (instead of few very patient owners).

The quality of information matters, as weak rarity value mistaken for a strong version induces a ‘tragedy of the commons,’ i.e., resource and exploiters suffer both; a strong version mistaken for a weak one induces a ‘tragedy of the herdsmen,’ i.e., the exploiters forfeit considerable income. Classifying rarity value correctly induces ‘no tragedy’ for the weak variant, i.e., resource and exploiters flourish, and a ‘tragedy of the herd’ for the strong one, i.e., the resource suffers. Related, but logically independent, is the issue of imperfect information. For instance, if in a system at the cutting edge of weak and strong rarity value agents wish to achieve a symmetric Pareto-efficient equilibrium, they must have the right information about the system, and perfect information regarding the behavior of the other agent(s).

Our agents are countries, regions, villages or cooperatives of fishermen. It is debatable whether even the latter care sufficiently for the future to induce sustainability (see e.g., [41, 42] for optimistic views), but individual fishermen’s preferences seem too myopic (cf., e.g., [27]). Two agents suffice to model strategic interaction. We did not take more agents because complexities in notation and representation arise, hardly justified by an added value. Figure 7 provides a glimpse of an example of a three-agent Small Fish War.

Fig. 7
figure 7

Rewards obtained by jointly-convergent pure strategies for an extension of the model underlying Fig. 4 to three players

Full size image

We used rather simple (yet quite adaptable) functions to model the effects of overfishing on the resource in deriving our results. We found a three player differential game cohort modelFootnote 5 aiming for a cooperative feedback solution with respect to the discounted reward criterion by [35] for blue fin tuna. The level of sophistication of that contribution may serve as our beacon for future research, yet lacking from it are rarity value and the AAE.

Another self-imposed limitation was the number of stage-game actions. For applied work, more levels or dimensions of restraining measures may require a large number of actions. In case mixing between certain actions is not possible for practical reasons, e.g., it is not easy to switch boats easily, a tree structure in the decisions may be required, yet its subtrees are subject to the present analysis. Adding actions changes nothing to our approach conceptually. We refrained from doing so to economize on notations.

[32] add endogenous stochastic transitions to stochastic games such as Small Fish Wars. That paper’s main purpose is to model hysteresis related to the poaching pit (e.g., [11]), but it may prove useful for modeling the AAE, as well.