Abstract
We discuss combined effects of stochasticity and time delays in finite-population three-player games with two mixed Nash equilibria and a pure one. We show that if basins of attraction of the stable interior equilibrium and the stable pure one are equal, then an arbitrary small time delay makes the pure one stochastically stable. Moreover, if the basin of attraction of the interior equilibrium is bigger than the one of the pure equilibrium, then there exists a critical time delay where the pure equilibrium becomes stochastically stable.
Similar content being viewed by others
1 Introduction
Many social and biological processes can be modeled as systems of interacting individuals within the framework of evolutionary game theory [5, 16, 23, 25, 28, 33, 38, 39]. Although in many models the number of players is very large, their strategic interactions are usually decomposed into a sum of two-player games. However, truly multi-player games naturally appear in many situations. For example, Haigh and Canning [15] discussed a multi-player War of Attrition, Pacheco et al. [30] analyzed a multi-player Stag Hunt game, and Souza et al. [35] and Santos et al. [34] discussed a multi-player Snowdrift game. There have also appeared some systematic studies of multi-player games. Broom et al. [2] defined evolutionarily stable strategies for multi-player games and analyzed their properties, Kim [21] investigated an asymptotic and stochastic stability of Nash equilibria in multi-player games, Bukowski and Miȩkisz [3] provided a classification of symmetric three-player games with two strategies, and fixation probabilities were discussed by Gokhale and Traulsen [10], see also [11, 12].
For certain payoff parameters, such games may have multiple mixed Nash equilibria. For example, in one class of three-player games (discussed here), we have one pure and two mixed Nash equilibria. We are faced with a standard problem of equilibrium selection. We will approach this problem from a dynamical point of view. Let us remark that such a situation may also arise in two-player games in the case where payoff functions are not linear in the population state [33].
It is usually assumed that interactions between individuals take place instantaneously and their effects are immediate. In reality, all social and biological processes take a certain amount of time. It is natural, therefore, to introduce time delays into evolutionary games. It is well known that time delays may cause oscillations in solutions of ordinary differential equations [6, 7, 13, 14, 22]. Effects of time delay in evolutionary games were discussed in [1, 17, 18, 27, 29, 36, 37]. It was shown there that for certain models and time delays (above a critical value where the Hopf bifurcation appears), evolutionary dynamics exhibits oscillations and cycles, and interior equilibria ceased to be asymptotically stable in discrete and continuous replicator dynamics. In particular, Moreira et al. [27] discussed multi-player Stag Hunt game with time delays.
Replicator dynamics describe time evolution of frequencies of strategies in the limit of an infinite number of individuals. However real populations are finite. Stochastic effects connected with random matching of players, mistakes of players, and biological mutations can play a significant role in such systems. Therefore, to describe and analyze their time evolution, one should use stochastic modeling.
For symmetric games with two strategies, a state of the population is given by the number of individuals playing, say, the first strategy. The selection part of the dynamics ensures that if the average payoff of a given strategy is bigger than the average payoff of the other one, then the number of individuals playing the given strategy increases. In the model introduced by Kandori et al. [20], one assumes (as in the standard replicator dynamics) that individuals receive average payoffs weighted by fractions of different strategies present in the population. Players may mutate with a small probability, hence the population may move against a selection pressure. To describe the long-run behavior of such stochastic dynamics, Foster and Young [8] introduced a concept of stochastic stability.
Here we will study how time delays affect stochastic stability of Nash equilibria of evolutionary games. In [27], the authors show that if the time delay is sufficiently large, the oscillations become so big that the population may leave the basin of attraction of the interior evolutionarily stable strategy and converges to the homogeneous state. In our paper we show that one does not need big time delays to make a pure evolutionarily stable strategy stochastically stable. In particular, we will show that if basins of attraction of both Nash equilibria are equal, then an arbitrary small time delay makes the pure one stochastically stable. Moreover, if the basin of attraction of the interior equilibrium is bigger than the one of the pure ones, then there exists a critical time delay where the pure equilibrium becomes stochastically stable.
In Sect. 2, we discuss the simple stochastic dynamics of a three-player game with two interior Nash equilibria. In Sect. 3, we present results concerning stochastic stability in the presence of time delays. Discussion follows in Sect. 4.
2 Stochastic Evolutionary Models in Finite Populations
We consider symmetric three-player games with two strategies, \(A\) and \(B\), given by the following payoff matrices:
where the left matrix gives payoffs for the row player, when the third player uses \(A\), whereas the right matrix provides payoffs in the case of the third individual playing \(B\).
In the well-mixed infinite populations, the expected values (with respect to the fraction of strategies in the population) of the payoffs of strategies are given by
where \(x\) is the frequency of players with the \(A\) strategy. Mixed Nash equilibria are given by solutions of the equation \(f_{A} = f_{B}\). The standard replicator dynamics reads [16, 39]
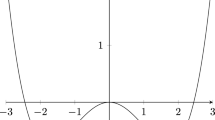
The classification of three-player games with respect to the number of Nash equilibria and evolutionarily stable strategies was provided in [3]. Here we consider games with three Nash equilibria: two mixed ones (an asymptotically stable \(x_{1}\) and an unstable \(x_{2}\)) and an asymptotically stable pure one, \(x_{3}=1\), as it is illustrated in a phase portrait of the replicator dynamics, see Fig. 1a. In general, such a situation arises if \(a>0, c<0, b>|ac|\), then \(x_{1, 2} = \frac{b-c \mp \sqrt{(}b^{2}+ac)}{a+2b-c}\) [3].
To study the effects of stochastic perturbations on the stability of Nash equilibria we will deal with finite-population models. Namely, let us assume that our population consists of \(N\) individuals. The state of the population at any discrete time \(t\) is characterized by the number of individuals, \(z(t)\), playing the strategy \(A\). Now to avoid unnecessary (and non-essential) technicalities, we will choose \(N\) and payoffs such that the Nash equilibria are given by natural numbers and are equal to Nash equilibria in infinite populations. It means that we allow self-interactions, that is \(x=z/N\) in (2.1).
The classical Kandori–Mailath–Rob evolutionary dynamics is described by the following rule [20]:
with the probability \(1-\epsilon \) and with the probability \(\epsilon \) the population moves in the other direction in the first two cases; if \(f_{A}(z_{t}) = f_{B}(z_{t})\), then the number of \(A\)-strategists stays the same with the probability \(1-\epsilon \) and decreases or increases by one at time \(t+1\) with the probability \(\epsilon /2\); if \(z_{t} = 0\), then \(z_{t+1}=0\) with the probability \(1-\epsilon \) and with the probability \(\epsilon \), \(z_{t+1}=1\); if \(z_{t} = N\), then \(z_{t+1}=N\) with the probability \(1-\epsilon \) and with the probability \(\epsilon \), \(z_{t+1}=N-1\).
We have obtained an ergodic Markov chain with the unique stationary probability distribution—stationary state \(\mu _{\epsilon }\). It is easy to see that there are four absorbing states of our dynamics with \(\epsilon =0\): two interior states, \(z_{1}\) and \(z_{2}\), with coexisting strategies; and two homogeneous ones, \(z_{3}=N\) and \(z=0\), the last one is not a Nash equilibrium. Now the question is which absorbing states survive small stochastic perturbations; that is, which are in the support of the zero-\(\epsilon \) limit of \(\mu _{\epsilon }\). The following concept of stochastic stability was introduced in [8].
Definition
A subset of states \(Y\) of a Markov chain with the unique stationary probability distribution \(\mu _{\epsilon }\) is stochastically stable if
It means that along almost any trajectory, for a small mutation level \(\epsilon \), the frequency of visiting \(Y\) is close to 1.
It is clear that in our models the only candidates for stochastically stable states are the asymptotically stable (for \(\epsilon = 0\)) absorbing states \(z_{1}\) and \(z_{3}\). We may also intuitively expect that if the number of steps (mutations or mistakes which happen with the probability \(\epsilon \)) to get out of the basin of attraction of a given state is bigger than the number of steps to get out of the basin of attraction of the other state, then the given state is stochastically stable. The formal proof uses the tree lemma—the special representation of a stationary distribution of an ergodic Markov chain [9], see (4.2) in the Appendix. We get the following theorem.
Theorem 1
\(z_{1}\) is stochastically stable if and only if \(3\sqrt{(}b^{2}+ac) < a+b\).
In our paper we discuss two particular examples.
Example 1
We choose \(a = 12, b = 15, c = -12\), then \(x_{1} = 1/3\) and \(x_{2} = 2/3\) are two mixed Nash equilibria. We set \(N=30\), hence \(z_{1} = 10\) and \(z_{2} = 20\), see Fig. 1b.
Proposition 1
Proof
For every state there is only one rooted tree. In particular, it follows from the fact that \(z_{2} - z_{1} = N - z_{2}\) that trees rooted at \(z_{1}\) and \(z_{3}\) have the same product of probabilities (the system needs the same number of mutations to get out of basins of attraction of both states. The proposition follows from the tree lemma. \(\square \)
Example 2
Here \(a = 8, b = 13, c = -11 \), then \(x_{1} = 1/3\) and \(x_{2} = 22/30\). We set \(N=30\), hence \(z_{1} = 10 \) and \(z_{2} = 22\), see Fig. 1c.
Proposition 2
\(z_{1}\) is stochastically stable.
Proof
Now we have that \(z_{2} - z_{1} > N - z_{2}\). In particular, the tree rooted at \(z_{1}\) has the leading term of the order \(\epsilon ^{12}\) and that of \(z_{3}\) has the order \(\epsilon ^{8}\). In other words, one needs \(12\) mistakes to get out of the basin of attraction of \(x_{1}\) and \(8\) mistakes to get out of the basin of attraction of \(x_{3}\). \(\square \)
Let us mention that three-player games with random matching of players [24, 32] were analyzed in [19]. Dependence of stochastic stability of equilibria on game parameters (payoffs) is much more complex there.
3 Stochastic Models with Time Delays
Now we introduce a time delay \(\tau \) into our stochastic evolutionary models of finite populations. Namely, let
with the probability \(1-\epsilon \) and with the probability \(\epsilon \) the population moves in the other direction in the first two cases; if \(f_{A}(z_{t-\tau }) = f_{B}(z_{t-\tau })\), then the number of \(A\)-strategists decreases or increases by one at time \(t+1\) with the probability \(\epsilon /2\); if \(z_{t} = 0\) or \(N\), then \(z_{t+1}= z_{t}\) with the probability \(\epsilon \) and with the probability \(1 - \epsilon \) the system moves toward the interior.
Let us note that because of the time delay, we have to specify initial conditions for all discrete moments of time \(-\tau \le t \le 0\). To restore the Markov property of our dynamics, we redefine states of our our system to be \(\tau + 1\) tuples \((z_{t-\tau }, z_{t-\tau +1}, \ldots , z_{t})\) at time \(t\). In that way we get a Markov chain with the unique stationary probability distribution. Similar dynamical models with transition probabilities depending upon the finite history are known as high-order Markov chains [4, 31]. By the stochastic stability of a cycle we mean that the set consisting of \(\tau \) \(\tau + 1\) tuples appearing in the cycle is stochastically stable.
Let us assume that \(\tau < z_{2} - z_{1}\). It is easy to see the cycle around \(z_{1}\) with the amplitude \(\tau \) and the time period \(4\tau +2\) is a trajectory of the deterministic part of the dynamics (3.1) that is it is invariant under the deterministic rule (3.1). Moreover, it was proven in [26] that when we start with any consistent initial condition \((z_{0}, z_{-1},\ldots , z_{-\tau })\), that is \(|z_{t}-z_{t-1}| \le 1\), \(t=0,\ldots ,-\tau +1\) and here we additionally assume that \(z_{0}, z_{-1},\ldots , z_{-\tau } <z_{2}\) with not all \(z\)s equal to \(0\), we end up in the cycle in a finite time. It was also proven in [26] that the cycle is stochastically stable.
Now let us observe that once we have oscillations around \(z_{1}\), it is easier to escape the basin of attraction of the cycle. We have the following theorem.
Theorem 2
\(z_{3}=N\) is stochastically stable if and only if \(z_{2} - z_{1} < N - z_{2} + \tau \).
Proof
To leave the basin of attraction of \(z_{1}\) we allow the system to move along the cycle until it reaches the state \(z_{1} + \tau \). Then we need \(z_{2}-z_{1} - \tau \) mutations to reach \(z_{2}\) and then \(n(\tau ) < \tau \) mutations to arrive at the state \(z_{2}+n(\tau )\), then the population will converge to \(z_{3}=N\) by the deterministic dynamics (\(\epsilon = 0\)). It is easy to see that \(n(1)=1, n(2)=1, n(3)=2, n(4)=2, n(5)=2\), and \(n(6)=3.\) To move out of \(z_{3}\) and to arrive at the cycle of \(z_{1}\) one needs \(N-z_{2}+n(\tau )\). The theorem follows from the tree lemma, see (4.2) in the Appendix. \(\square \)
In particular, we have the following propositions:
Proposition 3
In Example 1, \(z_{3}=N\) is stochastically stable for any time delay \(\tau \ge 1\).
Proposition 4
In Example 2, \(z_{3}=N\) is stochastically stable for any time delay \(\tau \ge 5\).
Let us note that the definition of stochastic stability involves two limits. For any fixed but low \(\epsilon \) we take the limit of \(t \rightarrow \infty \) to get the stationary probability distribution and then we take the limit \(\epsilon \rightarrow 0\). It is clear that for a very low \(\epsilon \), if we start with initial conditions close to a non-stochastically stable absorbing state (or cycle) we might need a very long time to arrive near a stochastically stable state (one needs many mistakes and each of them has the probability \(\epsilon \)). Results of stochastic simulations for both examples with initial conditions \(z(-\tau ) = \cdots = z(0) = z_{1} + 1\) and various time delays are presented in Figs. 2 and 3. We expect that bigger the time delay, smaller is the time the population needs to arrive in the neighborhood of the stochastically stable state \(z_{3}\). However, we observe that individual trajectories might not behave that way, see Fig. 2a, d, where the switching time is smaller for \(\tau =1\) than for \(\tau =3\). What should be true is that the average switching time should decrease as the time delay increases. The average switching times (with respect to 1800 simulations) are presented in Fig. 4 and support this statement. Standard deviations of switching times are of the order of averages.
Trajectories of stochastic dynamics in Example 2, \(\epsilon =0.05\), initial conditions \(z(t)=11,-\tau \le t \le 0\) a \(\tau = 5\), b \(\tau = 5\), beginning of a trajectory, c \(\tau =6\), d \(\tau = 6\), beginning of a trajectory, e \(\tau = 6\), a trajectory after a switch, f \(\tau = 7\), g \(\tau = 8\)
4 Discussion
We discussed finite fixed-size populations with a simple stochastic dynamics. More precisely, we studied three-player games with two interior stationary points (mixed Nash equilibria, one asymptotically stable and one unstable in the deterministic discrete replicator dynamics) with coexisting strategies and a stable homogeneous stationary point (pure Nash equilibrium). We showed that if basins of attraction of the stable interior equilibrium and the stable homogeneous one are equal, then an arbitrary small time delay makes the homogeneous one stochastically stable. The reason is that in the presence of a time delay, the interior equilibrium loses its stability—there appears an asymptotically stable cycle—and then it is easier to get out of its basin of attraction by stochastic perturbations. Moreover, if the basin of attraction of the interior equilibrium is bigger than that of the homogeneous one, then there exists a critical time delay where the homogeneous equilibrium becomes stochastically stable.
We would like to emphasize that global stability of the homogeneous equilibrium in our model is a combined effect of both stochasticity and time delays. In the absence of a time delay, the interior equilibrium is stochastically stable, while in the absence of stochastic perturbations, both the homogeneous equilibrium and the cycle around the interior equilibrium are locally asymptotically stable.
Multi-player Stag Hunt game with time delays was recently analyzed in [27]. However, cooperation strategy was not a Nash equilibrium there. The authors concluded that results of their model with time delays reinforced a traditional message that defection is evolutionarily advantageous. In stochastic version of their model we obtain stochastic stability of the defection strategy.
It is important to study effects of time delays and stochasticity in more complex evolutionary systems. In particular, we would like to construct an evolutionary model of social dilemma with stochastic stability of the cooperation strategy. The work is in progress.
References
Alboszta J, Miȩkisz J (2004) Stability of evolutionarily stable strategies in discrete replicator dynamics. J Theor Biol 231:175–179
Broom M, Cannings C, Vickers GT (1997) Multi-player matrix games. Bull Math Biol 59:931–952
Bukowski M, Miȩkisz J (2004) Evolutionary and asymptotic stability in multi-player games with two strategies. Int J Game Theory 33:41–54
Ching WK, Ng MK, Fung ES (2008) Higher-order multivariate Markov chains and their applications. Linear Algebra Appl 428:492–507
Cressman R (2003) Evolutionary dynamics and extensive form games. MIT, Cambridge
Erneux T (2009) Applied delay differential equations. Springer, Berlin
Foryś U (2004) Biological delay systems and the Mikhailov criterion of stability. J Biol Syst 12:1–16
Foster D, Young PH (1990) Stochastic evolutionary game dynamics. Theor Popul Biol 38:219–232
Freidlin M, Wentzell A (1970) On small random perturbations of dynamical systems. Russ Math Surv 25:1–55
Gokhale CS, Traulsen A (2010) Evolutionary games in the multiverse. Proc Natl Acad Sci USA 107:5500–5504
Gokhale CS, Traulsen A (2011) Strategy abundance in evolutionary many-player games with multiple strategies. J Theor Biol 83:180–191
Gokhale CS, Traulsen A (2012) Mutualism and evolutionary multiplayer games: revisiting the Red King. Proc R Soc B 279(1747):4611–4616
Gopalsamy K (1992) Stability and oscillations in delay differential equations of population. Springer, Berlin
Györi I, Ladas G (1991) Oscillation theory of delay differential equations with applications. Clarendon, Oxford
Haigh J, Canning C (1989) The n-person war of attrition. Acta Appl Math 14:59–74
Hofbauer J, Sigmund K (1998) Evolutionary games and population dynamics. Cambridge University Press, Cambridge
Iijima R (2011) Heterogeneous information lags and evolutionary stability. Math Soc Sci 63:83–85
Iijima R (2012) On delayed discrete evolutionary dynamics. J Theor Biol 300:1–6
Kamiński D, Miȩkisz J, Zaborowski M (2005) Stochastic stability in three-player games. Bull Math Biol 67:1195–1205
Kandori M, Mailath GJ, Rob R (1993) Learning, mutation, and long-run equilibria in games. Econometrica 61:29–56
Kim Y (1996) Equilibrium selection in n-person coordination games. Games Econ Behav 15:203–277
Kuang Y (1993) Delay differential equations with applications in population dynamics. Academic Press Inc., San Diego
Maynard Smith J (1982) Evolution and the theory of games. Cambridge University Press, Cambridge
Miȩkisz J (2005) Equilibrium selection in evolutionary games with random matching of players. J Theor Biol 232:47–53
Miȩkisz J (2008) Evolutionary game theory and population dynamics. In: Capasso V, Lachowicz M (eds) Multiscale problems in the life sciences, from microscopic to macroscopic, vol 1940., Lecture Notes in MathematicsSpringer, Berlin, pp 269–316
Miȩkisz J, Wesołowski S (2011) Stochasticity and time delays in evolutionary games. Dyn Games Appl 1:440–448
Moreira JA, Pinheiro FL, Nunes A, Pacheco JM (2012) Evolutionary dynamics of collective action when individual fitness derives from group decisions taken in the past. J Theor Biol 298:8–15
Nowak MA (2006) Evolutionary dynamics. Harvard University Press, Cambridge
Oaku H (2002) Evolution with delay. Jpn Econ Rev 53:114–133
Pacheco JM, Santos FC, Souza MO, Skyrms B (2009b) Evolutionary dynamics of collective action in n-person stag hunt dilemmas. Proc R Soc B 276:315
Raftery AE (1985) A model for high-order Markov chains. J R Stat Soc B 47:528–539
Robson A, Vega-Redondo F (1996) Efficient equilibrium selection in evolutionary games with random matching. J Econ Theory 70:65–92
Sandholm WH (2010) Population games and evolutionary dynamics. MIT, Cambridge
Santos MD, Pinheiro FL, Santos FC, Pacheco JM (2012) Dynamics of N-person snowdrift games in structured populations. J Theor Biol 315:81–86
Souza MO, Pacheco JM, Santos FC (2009) Evolution of cooperation under N-person snowdrift games. J Theor Biol 260:581–588
Tao Y, Wang Z (1997) Effect of time delay and evolutionarily stable strategy. J Theor Biol 187:111–116
Tembine H, Altman E, El-Azouzi R (2007) Assymetric delay in evolutionary games. In: Proceedings of the 2nd international conference on performance evaluation methodologies and tools, ValueTools’07, Article 36
Vega-Redondo F (1996) Evolution, games, and economic behaviour. Oxford University Press, Oxford
Weibull J (1995) Evolutionary game theory. MIT, Cambridge
Acknowledgments
This research was supported in part by PL–Grid Infrastructure. We would like to thank the referees for valuable comments and suggestions, in particular to generalize results and to make extensive stochastic simulations to get average switching times.
Author information
Authors and Affiliations
Corresponding author
Appendix: Stationary Probability Distributions of Ergodic Markov Chains
Appendix: Stationary Probability Distributions of Ergodic Markov Chains
The following tree representation of a unique stationary probability distribution of an ergodic Markov chain was proposed in [9].
Let \((\Omega ,P_{\epsilon })\) be an ergodic Markov chain with a state space \(\Omega \) and transition probabilities given by \(P_{\epsilon }: \Omega \times \Omega \rightarrow [0,1]\). It has the unique stationary probability distribution \(\mu _{\epsilon }\). For \(x \in \Omega \), an \(x\)-tree is a directed graph on \(\Omega \) (connecting all vertices) such that from every \(y \ne x\) there is a unique path to \(x\) and there are no outcoming edges out of \(x\). Denote by \(T(x)\) the set of all \(x\)-trees and let
where \(P_{\epsilon }(y,y')\) is the element of the transition matrix (that is, a conditional probability that the system will be at the state \(y'\) at time \(t+1\) provided it was at state \(y\) at time \(t\)) and the above product is with respect to all edges of the \(x-\)tree \(d\). Here in our paper we assumed that the system follows some deterministic rule with the probability \(1-\epsilon \) and with the probability \(\epsilon \), a mistake is made that moves the system in the other direction hence \(P_{\epsilon }(y,y')\) is equal either to \(1-\epsilon \), \(\epsilon \), or \(0\). Now one can show that (the tree lemma)
for all \(x \in \Omega .\)
It follows from that the stationary probability distribution can be written as the ratio of two polynomials in \(\epsilon \). Hence any non-absorbing state (for \(\epsilon =0\)) has zero probability in the stationary distribution in the zero-\(\epsilon \) limit. Moreover, in order to study the zero-\(\epsilon \) limit of the stationary distribution, it is enough to consider paths between absorbing states. Assume for example, like in our models, that we have two absorbing states (sets): \(x\) and \(y\). Let \(m_{xy}\) be a minimal number of mutations (mistakes) needed to make a transition from the state \(x\) to \(y\) and \(m_{yx}\) the minimal number of mutations to make a transition from \(y\) to \(x\). Then \(q_{\epsilon }(x)\) is of the order \(\epsilon ^{m_{yx}}\) and \(q_{\epsilon }(y)\) is of the order \(\epsilon ^{m_{xy}}\). If for example \(m_{yx}<m_{xy}\), then it follows that \(\lim _{\epsilon \rightarrow 0}\mu _{\epsilon }(x) = 1\), hence \(x\) is stochastically stable.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Miȩkisz, J., Matuszak, M. & Poleszczuk, J. Stochastic Stability in Three-Player Games with Time Delays. Dyn Games Appl 4, 489–498 (2014). https://doi.org/10.1007/s13235-014-0115-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-014-0115-1