Learning Normative Behaviour Through Automated Theorem Proving

Abstract

Reinforcement learning (RL) is a powerful tool for teaching agents goal-directed behaviour in stochastic environments, and many proposed applications involve adopting societal roles which have ethical, legal, or social norms attached to them. Though multiple approaches exist for teaching RL agents norm-compliant behaviour, there are limitations on what normative systems they can accommodate. In this paper we analyse and improve the techniques proposed for use with the Normative Supervisor (Neufeld, et al., 2021)—a module which uses conclusions gleaned from a defeasible deontic logic theorem prover to restrict the behaviour of RL agents. First, we propose a supplementary technique we call violation counting to broaden the range of normative systems we can learn from, thus covering normative conflicts and contrary-to-duty norms. Additionally, we propose an algorithm for constructing a “normative filter”, a function that can be used to implement the addressed techniques without requiring the theorem prover to be run at each step during training or operation, significantly decreasing the overall computational overhead of using the normative supervisor. In order to demonstrate these contributions, we use a computer game-based case study, and thereafter discuss remaining problems to be solved in the conclusion.

1 Introduction

Reinforcement learning (RL) is a powerful tool for teaching autonomous agents goal-directed behaviour in stochastic environments, which has seen substantial advances over the last decades. RL agents are consistently mastering tasks previously relegated to expert humans (e.g., the RL agent that beat the world champion of Go [48], or the agent that plays Starcraft II at the grandmaster level [52]), and the number of application domains for RL agents has continued to expand. Notably, RL is a popular choice for the implementation of robots [29] and autonomous vehicles [46]. [50] emphasizes the notion that technologies integrated in human communities must follow social and moral norms congruent with those communities; as RL agents take up roles more deeply integrated with human society, it becomes imperative that they also can conform to the ethical, legal, and social norms governing society. An autonomous vehicle that does not obey traffic laws would be next to useless.

Constraining RL agents with norms is easier said than done. Though implementing behaviour conforming to a single norm in isolation might be a simple matter (compelling an autonomous vehicle to travel no faster than 50 kph within city limits, for example), when we shift our focus to entire normative systems—which may contain obligations, prohibitions, permissions, counts-as norms, and conflict-resolution mechanisms—we start to encounter problems. For example, how do we implement behaviour in an autonomous vehicle that complies with all regional traffic laws and accompanying social norms, some of which may conflict with or modify each other? Implementing normative behaviour is often more involved than laying out and conforming to a collection of individual, non-interactive constraints. Sometimes, we will need to utilize more complex forms of normative reasoning.

Normative reasoning is the form of reasoning dedicated to correctly drawing conclusions about norms, encompassing the technical demands inherent in reasoning about, for example, law and morality. Norms introduce nuances not found in reasoning strictly dedicated to facts; thus, unique tools have been developed to accommodate these difficulties, largely in the field of deontic logic, a diverse area of study that has yielded a plethora of specialized logics for normative reasoning, along with (to a much lesser extent) tools automating reasoning with these logics. These tools allow us to automate reasoning about norms and the behaviour they should elicit, which in turn can be used to modify the behaviour of autonomous agents such as RL agents. This paper explores this strategy for eliciting normative behaviour from RL agents, analysing and improving on the technique introduced in [37], norm-guided reinforcement learning (NGRL)—a technique that managed to mitigate some of the disadvantages of the approach utilized in [35, 38]. However, NGRL possesses several considerable shortcomings itself—such as an inability to deal with contrary-to-duty (CTD) obligations—which we will address thoroughly in Sect. 3.

1.1 Related Work on Ethical RL

Aligning the behaviour of autonomous agents with human norms is a problem that has been tackled from many angles; RL in particular has been conjectured as a good candidate for implementing behaviour in stochastic environments which is constrained by norms (in contrast to non-learning-based approaches like [19, 20]). There are already many RL techniques aimed toward producing ethical behaviour. These include two main approaches that have been used for teaching RL agents “ethical” (more generally, normative) behaviour: training with human data and training with reward engineering.

Using human demonstrations or feedback to create an ethical utility function is proposed by [6, 39, 42, 54]. However, it may not be feasible to collect enough human data for a given task, and no way has been proposed to verify that this data does indeed depict ethical behaviour; in fact, [54] assumes that most human behaviour is ethical. [5] critiques this approach, noting that the subtleties of many legal systems cannot be represented by a utility function alone (this, of course, also applies to the reward engineering approach as well). In addition, an ethical utility function is not a transparent (often cited as desirable for ethical AI systems [24]) decision-making mechanism. [5] notes pertinently that if there is a problem with the ethical utility function, trying to uncover what has gone wrong will be difficult if not impossible if we can only examine the policy. [39] offers some level of transparency, in that it is clear when the agent switches between a non-ethical and ethical policy, but the opacity of the policy itself is not addressed.

The reward engineering approach entails assigning rewards or punishments to the actions taken by an agent in order to induce compliant behaviour. In developing a reward framework for inducing compliant behaviour, there are two main questions that need to be addressed: (1) which state-action pairs should be assigned a reward or punishment? This comes down to the question: how do we know if an event is compliant or not? And (2) what should the magnitudes of these rewards and punishments be? Much of the literature—for example [1, 9, 31, 43,44,45]—relies to some degree on the manual creation of a reward function. In [1, 9, 31], it is not made clear how we can create this reward function systematically or automatically; [31] and [1] simply assign rewards or punishments to what they deem praiseworthy or transgressive events, and [9] does not tell us how the choice-worthiness function they propose for a given ethical theory should be constructed. [43,44,45], which use multi-objective RL (MORL) over the agent’s primary objective and an ethical objective, do provide us with a direct link from specified moral values to a reward function, but their conception of values and norms is somewhat primitive, and is insufficient for modelling more complex forms of normative reasoning; additionally they assume the existence of what they call an ethical policy (where no violations occur [45]). In [43], norms are conceived of only as non-interacting tuples containing a condition, a deontic modality, the action to which the operator applies, and a penalty.

To some degree, [27] sits outside these two main approaches, and offers an approach (expanded on in e.g. [26, 28]) where norms are represented as linear temporal logic (LTL) formulas; they use the methods proposed in [8] to train an agent that satisfies these formulas with maximal probability. It is acknowledged that norms might come into conflict in this framework (something not considered by the above approaches), and these conflicts are dealt with systematically. However, this technique is specifically defined for model-based RL, where the MDP the agent operates in is already known. It is known that there are limitations to LTL as a language for representing norms (see [13, 36]), and to get around some of these, this technique specifically employs what is called “implicit representation” of norms in [36]. However, among these limitations remain an inability to represent strong permission naturally, cope with obligations/permissions that are conditional on other obligations/permissions, and account for counts-as (or constitutive) norms.

[35] also veers away from these two main approaches, and introduces a normative supervisor utilizing defeasible deontic logic (DDL) for checking the compliance of a trained (model-free) RL agent’s actions in real time, removing those that don’t comply from its arsenal; this proved to be as effective as the approach in [39], and accommodates a much wider array of normative systems [38]. Since the normative supervisor is decoupled from the agent, though, the agent cannot incorporate the norms it is subject to into its planning, and cannot learn to, e.g., avoid situations where compliance is not possible. In addition, the behaviour produced while running the normative supervisor is no longer optimal. This was remedied to some degree in [37], which borrows the model-free MORL approach from [44, 45] and uses the normative supervisor to build a reward function. However, [37] was incapable of dealing with some normative systems, such as those with contrary-to-duty obligations (obligations triggered when another obligation is violated). It was also more generally incapable of determining between two non-compliant actions which was more compliant with the system as a whole. Generally, in the literature on ethical RL, there is a shortage of discussion on how to cope with situations where compliance is not possible; this capability was demonstrated in [35, 38] (as well as in [27]), but this did not carry over to the norm-guided RL (NGRL) presented in [37], as we will demonstrate in Sect. 3.4. We will further argue that the notion of norm violation implicitly espoused by [35, 37, 38] limits what violations can be detected by the normative supervisor.

1.2 Contributions

In this paper, we revisit and offer more extensive analysis of the normative supervisor, employing a more comprehensive definition of normative system violation. We furthermore propose an algorithm that counts the number of violations that occur for a state-action pair $\overline{s}=(s,a)$, and we augment NGRL with what we call violation counting, which allows us to cope with scenarios where compliance is not possible (such as when a contrary-to-duty obligation is triggered). Finally, we propose an algorithm for constructing a “normative filter” which can be used to replace the continual running of the normative supervisor, allowing us to use techniques such as NGRL without calling a theorem prover at every step during training or operation; we will show that using this normative filter dramatically improves training time. Throughout the paper, we make use of a case study, the “Travelling Merchant” (introduced in [36]), to demonstrate the inadequacy of the notion of norm violation implicitly espoused by [35, 37, 38], how regular NGRL fails when faced with contrary-to-duty obligations, how violation counting remedies this issue, and how this technique manages trade-offs between immediate and delayed violations more generally.

In the section immediately following, we will give a brief overview of multi-objective RL, the basic building-blocks of normative systems, and defeasible deontic logic; we will also offer a discussion on compliance and violation, and establish some concepts and notation which we will make use of in later sections. Finally, we introduce the basic mechanics of our case study. In Section 3, we look at the normative supervisor, presenting an overview of its architecture, and the techniques that it can be used to implement. We offer detailed critical analysis of these techniques, including the use of our case study to demonstrate inadequacies. In Section 4, we offer a solution to these problems, by redefining the employed concept of compliance and introducing violation counting. In Section 5 we introduce the normative filter and provide an algorithm for constructing it. In Section 6, we evaluate the techniques presented using our case study. Finally, in Section 7 is a conclusion and brief discussion of remaining issues to be solved in future work.

2 Background

In this section we will discuss the background needed in order to understand the rest of the paper. First, we will review the basics of multi-objective reinforcement learning (MORL). Then, we will discuss normative reasoning with defeasible deontic logic (DDL) and normative system violation, as well as our case study.

2.1 Multi-Objective Reinforcement Learning

The underlying environment of a multi-objective reinforcement learning problem is formalized as a multi-objective Markov decision process (MOMDP). We define a specific type of MOMDP below, where each state is associated with a set of labels:

Definition 1

(MOMDP) A labelled MOMDP is a tuple

$$\begin{aligned} \langle S, A, L, P, \textbf{R}\rangle \end{aligned}$$

where S is a set of states, A is a function $A: S\rightarrow 2^{Act}$ from states to sets of possible actions (where Act is the set of all actions available to the agent), $L:S\rightarrow 2^{AP}$ (where AP is some set of atomic propositions) is a labelling function, $P:S\times Act\times S\rightarrow [0,1]$ is a probability function that gives the probability $P(s,a,s')$ of transitioning from state s to state $s'$ after performing action a, and $\textbf{R}=(R_1,...,R_n)^T$ is a vector of reward functions $R_i: S\times Act \rightarrow \mathbb {R}$.

Single-objective MDPs are simply MDPs for which $\textbf{R}$ is instead a scalar function $R: S\times Act\rightarrow \mathbb {R}$.

Reinforcement learning finds a policy $\pi :S\rightarrow Act$ which designates optimal behaviour; this optimality is determined w.r.t. a vector of value functions $\textbf{V}^{\pi }=(V^{\pi }_1,...,V^{\pi }_n)^T$ defined as:

$$\begin{aligned} V_i^{\pi }(s)=\mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t} r_{t+j} | s_j=s\right] \end{aligned}$$

(1)

which represents the expected cumulative value from state s if policy $\pi$ is followed. Specifically, if $\pi$ generates a trace $(s_0,\pi (s_0)),$ $(s_1,\pi (s_1)),...$, $V_i^{\pi }(s)$ is the expected value of the expression $\sum ^{\infty }_{t=0}\gamma ^{t} r_{t+j}$, where $r_{t+j}=R_{i}(s_{t+j},\pi (s_{t+j}))$, conditional on the input state s being the initial state $s_j$. In the above function, $\gamma \in [0,1)$ is a discount factor (so that rewards in the future do not have as much weight as more immediate rewards).

Generally, for an agent with one objective and therefore one scalar value function $V^{\pi }$, our goal is to find an optimal policy $\pi ^{*}$ from the set of all policies $\Pi$; this is the policy such that:

$$\begin{aligned} V^{\pi ^{*}}(s) = \max _{\pi \in \Pi }V^{\pi }(s) \end{aligned}$$

However, multiple objectives induce a more complex set of semi-optimal policies, where one policy might maximize rewards from $R_{i}$ but not $R_{j}$, for instance. We then turn to the notion of Pareto dominance. A policy strictly dominates another if it results in better outcomes for all objectives. However, in some cases, like in the case of competing objectives, there may be no such policy. Then we look at whether one policy weakly dominates another; that is, the policy results in improvements for some objective(s), but not necessarily all. If we remove from $\Pi$ all strictly dominated policies, the only policies left form the Pareto front (the set of all dominant or incomparable policies). The task of MORL is to find policies in this Pareto front.

Similar to the value function, we can define a vector of Q-functions for each objective, $\textbf{Q}^{\pi }=(Q^{\pi }_1,...,Q^{\pi }_n)^T$, where:

$$\begin{aligned} Q_i^{\pi }(s,a)=\mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t} r_{t+j} | s_j=s, a_j=a\right] \end{aligned}$$

In single-objective RL, the goal of model-free reinforcement learning—reinforcement learning where the underlying MDP is not known—is to learn the Q-function for the optimal policy $\pi ^{*}$, such that

$$\begin{aligned} \pi ^{*}(s)\in \mathop {\mathrm {arg\,max}}\limits _{a\in A(s)}Q(s,a)\ \text { and }\ V^{\pi ^{*}}(s) = \max _{a\in A(s)} Q(s,a) \end{aligned}$$

In Q-learning [53] and related techniques we attempt to learn an optimal Q-function by applying the following rule to update the Q-function during learning (over a transition $(s, a, s')$):

$$\begin{aligned} Q(s, a)\leftarrow (1-\alpha )Q(s, a) + \alpha (R(s,a)+ \gamma \max _{a'\in A(s')}Q(s', a')) \end{aligned}$$

where $\alpha$ is the learning rate, $\gamma$ is the discount factor, and $s'$ is the state observed when the agent transitions from s with action a.

However, with multiple Q-functions, we must learn each $Q_i$ individually and strategically combine them in order ascertain the “optimal” action. [12] presents a MORL method where some objectives can be prioritized over others; [51] describes what they call a “naive approach” to it. This approach, thresholded lexicographic Q-learning (TLQL), is tailored to problems where there is a single objective that must be maximized overall, while all other objectives don’t need to be maximized, but rather must satisfy a threshold. With this technique, we will have a vector of Q-functions $\textbf{Q}=(Q_1,...,Q_n)^T$, along with a vector of thresholds $\textbf{C}=(C_1,...C_n)^T$. Each $C_i$ is a value that we aim to keep $Q_i(s,a)$ at or above, except the last threshold: $C_n=+\infty$. Moreover, we assume that the objective represented by $Q_i(s,a)$ is of higher priority than the objective represented by $Q_j(s,a)$ if $i<j$.

Here, we will work with CQ-values instead of Q-values. A CQ-value is:

$$\begin{aligned} CQ_{i}(s,a)=\min (Q_{i}(s,a), C_{i}) \end{aligned}$$

Then our policy is $\pi (s)\in TLQ(s)$, where TLQ is given by Algorithm 1.

Algorithm 1

TLQ(s)

2.2 Normative Reasoning

We will consider two kinds of norms in this paper: regulative norms and constitutive norms. Regulative norms are obligations, prohibitions, or permissions; in other words, they define what is necessarily the case (in the case of obligations and prohibitions) or possible (as with permissions) in an ideal world. Regulative norms are usually conditional (e.g., “when the light is red, you are obligated to stop”). Conditional obligations are referred to informally as O(p|q) in this paper (with F(p|q) and P(p|q) standing in for prohibitions and permissions respectively).

A constitutive (or counts-as) norm takes the form “in context C, X counts as Y” [47] (which we represent with the shorthand C(X, Y|C)) for some property or event X and Y. In a normative system, constitutive norms facilitate the construction of what Searle calls institutional facts from brute facts or other institutional facts [47]. Brute facts are facts that hold whether or not human institutions (e.g., language, morality) are in place; institutional facts only make sense in the context of human institutions, for example the statement that killing counts as immoral.

With these two types of norms, we can define our simple conception of a normative system:

Definition 2

(Normative System) A normative system is a tuple: $\mathcal {N} = \langle \mathcal {C}, \mathcal {R}, \mu \rangle$ where $\mathcal {C}$ is a set of constitutive norms, $\mathcal {R}$ is a set of regulative norms, and $\mu$ is a conflict resolution mechanism.

In the above definition, what we call the conflict resolution mechanism is a means to resolve normative conflict; it can be, for example, an ordering over prescriptive norms (obligations or prohibitions), or a map from these norms to real numbers. We will discuss one such mechanism momentarily.

It is important to note that the various norms in a normative system may interact with each other and with the conflict resolution mechanism, so even if every regulative norm in a normative system remains individually (ostensibly) unviolated, the normative system may be violated. Consider an example where we have a regulative norm “violating patient privacy is prohibited” and a constitutive norm “accessing file X counts as violating patient privacy”. Now suppose we take the regulative norm on its own and assume the fact “file X has been accessed”. Strictly speaking, this fact does not violate the prohibition; the prohibition refers to violating patient privacy, while the fact refers to accessing a file. It is not until we consider the constitutive norm that we can derive the institutional fact “patient privacy has been violated”, and know that the prohibition has been violated. It is necessary, then, to have a logic for normative reasoning that can handle this interplay. We introduce one below.

2.2.1 DDL Syntax

Propositional defeasible logic [32, 33, 40, 41] is an efficient framework for non-monotonic reasoning, and can be extended with modal operators (e.g. deontic operators, such as obligation). In this section we review the core definitions of the defeasible deontic logic (DDL) presented in [4] and later explored on in [14,15,16,17,18], using as its base deontic modality, obligation O.

Let AP be a set of propositional atoms, $Lit=AP\cup \{\lnot p\ |\ p\in AP\}$ be a set of corresponding literals, and $OLit=\{O(l)|l\in Lit\}$ be a set of modal literals. Then we can define rules:

Definition 3

(Rules [18]) Let r be a label designating a rule:

$$\begin{aligned} r:\ A(r)\hookrightarrow _{*} N(r) \end{aligned}$$

where $A(r)=\{a_{1},..., a_{n}\}$ (a set of literals $\in 2^{Lit\cup OLit}$) is the antecedent, N(r) (a single literal $\in Lit$) is the consequent, $\hookrightarrow _{*}\in \{\rightarrow _{*}, \Rightarrow _{*}, \rightsquigarrow _{*}\}$ is a generic rule symbol, and $*\in \{C, O\}$ gives the mode of each rule.

Rules with the subscript C are constitutive rules, and rules subscripted by O are regulative rules (in which the consequent of the rule is derived in the scope of the deontic operator O, for obligation). Strict rules ($\rightarrow _*$) are rules where the consequent strictly follows from the antecedent without exception; that is, a rule that always holds can be formalized as a strict rule (e.g., $sparrow\rightarrow _C bird$). Defeasible rules ($\Rightarrow _*$) are rules where the consequent usually follows from the antecedent, unless it is refuted by a conflicting rule or a defeater. An example of a defeasible rule would be a default assumption like $bird\Rightarrow _C fly$. Defeaters ($\rightsquigarrow _*$) are rules that can prevent a conclusion from being reached by a defeasible rule; for example we might have a rule like $penguin\rightsquigarrow _C \lnot fly$. Regulative defeaters can used to encode permissive rules. DDL is furthermore equipped with a superiority relation > to resolve conflicts between rules; given two conflicting rules $r_1$ and $r_2$, $r_1>r_2$ indicates that $r_1$ defeats $r_2$ (i.e., if they conflict but are both applicable, only $r_1$ is applied).

From the above, we can define a defeasible theory:

Definition 4

(Defeasible Deontic Theory [14]) A defeasible deontic theory D can be defined by the tuple $\langle F, R^{O}, R^{C}, >\rangle$, where F is a set of facts (i.e., literals l and modal literals O(l)), $R^{O}$ is a set of regulative rules, $R^{C}$ is a set of constitutive rules, and > is a superiority relation over rules.

We can relate this definition to the above definition of a normative system $\mathcal {N}=\langle \mathcal {R}, \mathcal {C}, \mu \rangle$. The overlap between $\mathcal {R}$ and $R^{O}$, and $\mathcal {C}$ and $R^{C}$, is clear. Similarly, we can see that > is an example of a conflict resolution mechanism $\mu$. For this reason, we can think of a defeasible deontic theory as a collection of facts plus a formally defined normative system.

2.2.2 Deduction in DDL

Defeasible proofs are characterized by proof tags. A proof tag is a label applied to a literal and together they constitute a conclusion derived in the proof; there are several types of conclusions we can derive from a defeasible theory. The proof tags are: $+\Delta _{*}$ (definitely provable conclusion), $-\Delta _{*}$ (definitely refuted conclusion), $+\partial _{*}$ (defeasibly provable conclusion), and $-\partial _{*}$ (defeasibly refuted conclusion). For factual conclusions, $*:= C$ and for deontic conclusions, $*:= O$. When we can derive $+\partial _O p$, for example, we have proved that the obligation of p holds defeasibly; $+\partial _O \lnot p$ means the prohibition of p ($\lnot p$ is obligatory) holds defeasibly, while $-\partial _O \lnot p$ means that p is permissible (it is not the case that p is forbidden).

$D\vdash +\Delta _{*} p$ holds if p is a fact or derivable from only facts and strict rules. Conversely, $D\vdash -\Delta _{*} p$ holds if p is neither a fact nor derivable from only strict rules and facts. We will, however, mainly deal with defeasible conclusions.

Let R[p] denote the set of rules with p in the consequent, and for $*\in \{C, O\}$, $R^{*}_{sd}$ the set of strict and defeasible rules.

Definition 5

[Defeasible Provability [32]] Given a defeasible theory D, if $D\vdash +\partial _{*}p$, either $D\vdash +\Delta _{*} p$ or:

• 1. $\exists r\in R^{*}_{sd}[p]$ s.t. for all $a_{i}\in A(r)$ (or $O(a_{i})\in A(r)$), $D\vdash +\partial _{C}a_i$ (or $D\vdash +\partial _{O}a_i$), and

• 2. $D\vdash -\Delta _{*}\lnot p$, and

• 3. $\forall r'\in R^{*}[\lnot p]$, either:

  • 1. $\exists a_i\in A(r')$ (or $O(a_i)\in A(r')$) s.t. $D\vdash -\partial _{C} a_i$ ($D\vdash -\partial _{O} a_i$), or

  • 2. $\exists r''\in R_{sd}^{*}[p]$ s.t. $\forall a_i\in A(r'')$ (or $O(a_i)\in A(r'')$), $D\vdash +\partial _{C} a_i$ (or $D\vdash +\partial _{O}a_i$) and $r''>r'$.

Conversely, $D\vdash -\partial _{*}p$ if $\lnot p$ is defeasibly provable, or an exhaustive search for a constructive proof (where the proofs are constructed as presented in Definition 5) for the literal fails.

Whenever we have a defeasible theory (a set of facts plus a formalized normative system) we can use these conditions to derive conclusions, e.g., obligations $+\partial _O p$ or prohibitions $+\partial _O \lnot p$.

SPINdle. DDL is one of the few deontic logics with a working theorem prover. In particular, SPINdle [30] is an open source theorem prover for defeasible logic; it also accommodates modal defeasible logics, including defeasible deontic logic. This theorem prover generates conclusions from the defeasible theory, with each literal occurring in the theory being assigned a status as definitely provable or refutable, and defeasibly provable or refutable.

2.2.3 Compliance and Violation

We will now discuss the specific paradigm in which we will be working, where we have a normative system $\mathcal {N}=\langle \mathcal {C}, \mathcal {R}, \mu \rangle$ and a state-action pair $\overline{s}=(s,a)$, for which we can construct a defeasible theory $Th(\overline{s}, \mathcal {N})=\langle F_{\overline{s}}, R^{O}, R^{C}, >\rangle$. In this defeasible theory, $R^{O}$ contains the regulative norms in $\mathcal {R}$, $R^C$ contains the constitutive norms in $\mathcal {C}$, and > is a conflict resolution mechanism $\mu$. $F_{\overline{s}}$ contains L(s) (the labels associated with state s), $\lnot p$ for all $p\in AP\setminus L(s)$, and the action proposition $a:=$ “action a is performed”.

Ideally, $\overline{s}$ complies with $\mathcal {N}$; that is, $\overline{s}$ does not incur any violations of $\mathcal {N}$. Violations, informally, occur when something ought to be the case but is not the case [21, 49] and thus, in a simple conception of violation, the violation condition of an obligation O(p) is the case where $O(p)\wedge \lnot p$ is true [25, 34], and we can call $\lnot p$ a violation¹.

In our case, given a state-action pair $\overline{s}=(s, a)$, a violation of $\mathcal {N}$ is going to be the negation of a literal lit in $Th(\overline{s}, \mathcal {N})$. We call the set of violations of $\mathcal {N}$ for $\overline{s}$: $viol(\overline{s},\mathcal {N}) = \{lit\ |\ lit\text { is a violation of }\mathcal {N}\}$. In DDL, we can formally define this set as follows:

Definition 6

(Violation of Normative Systems) Given a state-action pair $\overline{s}=(s, a)$, a violation of $\mathcal {N}$ is a literal $\lnot lit$ such that $Th(\overline{s}, \mathcal {N})\vdash +\partial _{O}lit,\ -\partial _{C}lit$ and the set of violations of $\mathcal {N}$ for $\overline{s}$ is:

$$\begin{aligned} viol(\overline{s},\mathcal {N}) = \{\lnot lit\ |\ Th(\overline{s}, \mathcal {N})\vdash +\partial _{O}lit,\ -\partial _{C}lit\} \end{aligned}$$

(2)

What we are saying with this definition is that a violation of $\mathcal {N}$ occurs when we can prove that lit is obligatory, but we cannot prove that lit is the case; it is specifically the presence of an obligation in a given context, coexisting with the absence of a (brute or institutional) fact reflecting the content of this obligation. Thus, if you ought not spend money, spending money is a violation. If you ought to buy milk, not buying milk is a violation. Based on the characterization of violation presented in, for example, [25, 34], a formal definition of a violation condition in DDL must include the derivation of an obligation of lit (that is, $+\partial _O lit$) and a failure to derive lit (that is, $-\partial _C lit$), hence the definition we have given above.

Note that $Th(\overline{s},\mathcal {N}) \vdash +\partial _{C}\lnot lit$ implies $Th(\overline{s},\mathcal {N}) \vdash -\partial _{C}lit$ [18], so the above definition will also include cases where $Th(\overline{s},\mathcal {N}) \vdash +\partial _{O}lit,$ $+\partial _{C}\lnot lit$; that is, it includes the case where lit is obligatory and we can explicitly prove $\lnot lit$.

When we reason about norms, we often need to also reason about violations. We may come across cases of normative deadlock, where we have a state s such that for all possible actions a, $|viol(\overline{s}=(s,a),\mathcal {N})|>0$. In these cases, we might want to manage what ought to happen when the inevitable violation occurs. For example, consider the case where we have an obligation not to kill, $O(\lnot kill|\top )$, but also an obligation to, if one kills, kill gently O(gentle|kill) [10]. This second obligation is called a contrary-to-duty (CTD) obligation, an obligation (e.g. $O(b|\lnot a)$) triggered when another obligation (e.g. $O(a|\top )$) is violated.

Based on the given notion of violation, we can define a binary compliance function over state-action pairs $\overline{s}$:

$$\begin{aligned} compl_{\mathcal {N}}(\overline{s}) = {\left\{ \begin{array}{ll} 1 &{} viol(\overline{s},\mathcal {N})=\emptyset \\ 0 &{} otherwise \end{array}\right. } \end{aligned}$$

(3)

Finally, we can expand our field of view from the compliance of single state-action pairs to traces generated by specific policies and define an Expected Non-Compliance Count (ENCC):

$$\begin{aligned} ENCC(\pi )=\mathbb {E} \left[ \sum _{t=0}^{\infty } \gamma ^{t} (1-compl_{\mathcal {N}}(\overline{s}_t)) | s_0\in S \right] \end{aligned}$$

(4)

$\overline{s}_0,\overline{s}_1,...$ where $\overline{s}_t = (s_t, \pi (s_t))$ is a trace of state-action pairs generated by following policy $\pi$, and $\gamma \in [0,1)$ is a discount factor; this function gives an expected count of violations occurring over the course of following $\pi$, prioritizing violations occurring in the immediate.

2.3 Case Study: The Pacifist Merchant

Throughout this paper, we will be utilizing a case study to illustrate the effectiveness of various techniques. We have chosen a simple game which allows us to witness the contrast between optimal unconstrained behaviour and optimal normative behaviour via routes taken through a map. We will employ the “Travelling Merchant” environment—first used in [36]—which entails the RL agent, a merchant, traversing a map and collecting resources to sell at a market on the other side of the map. These resources are wood (which can be extracted from trees) and ore (which can be extracted from rocks); in order to collect a resource, the agent must take the actions extract and pickup in a cell where a resource is situated. The agent receives a reward each time it extracts and picks up an object, as well as when it unloads its resources at the market. There are “dangerous” areas on the map where the agent will be attacked by bandits, and then the agent has three choices: it can fight (taking action fight and ending the attack), negotiate (giving up its inventory by using unload, ending the attack), or try to escape (which will often result in failure, and the attack continuing). The agent is rewarded based on how many resources it extracts and picks up, and how many items it arrives at the market with. The agent’s movements are restricted in such a way that mandates it continually move towards its goal (each move must bring it closer to the market), and states are labelled with what kind of cell the agent is in (e.g., $at\_danger$), its immediate surroundings (e.g., $north\_tree$), whether or not it is being attacked (attacked), and what it has in its inventory (e.g. $has\_ore$). A state can be given the labels attacked, $\{at, north, south, east, west\}\_\{tree, wood, rock, ore, danger, home, market\}$, and $has\_\{wood, ore\}$. In Fig. 1, we can see the optimal path for the agent.

Fig. 1

Optimal behaviour for the merchant. Dangerous areas are red, and resources are green. (E) indicates that the agent extracted a resource, (P) that the agent picked up an extracted resource, and (F) that the agent fought bandits

We will be imposing a specific normative system on this RL agent, designated in [36] as “pacifist”. In this normative system, the agent (the “pacifist merchant”) is forbidden from entering the dangerous areas ($O(at\_danger |\top )$, formalized as $obl:\ \Rightarrow _O \lnot at\_danger$), but when it is in danger and being attacked, it is obligated to negotiate ($O(negotiate | at\_danger,$ attacked) or $ctd:\ at\_danger, attacked \Rightarrow _O negotiate$), where unloading one’s inventory counts as negotiating (C(unload,  negotiate|attacked) or $ctsas:\ attacked,$ $unload\rightarrow _C negotiate$).

In the environment presented in Fig. 1, the correct behaviour for the pacifist merchant is to unload when it is forced to enter the first dangerous area, and avoid the second dangerous area altogether (because it is not necessary to pass through it, even though it is more advantageous to do so).

3 The Normative Supervisor

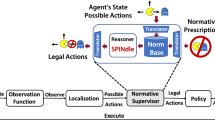
The problem of constraining RL agents is not a new one—there is ample literature on constraining RL agents with Linear Temporal Logic (LTL) specifications representing, e.g., safety constraints (see for example [2, 11, 22, 23]). However, it has been shown that these methods are on their own insufficient for implementing normative behaviour [36]. An alternative to these methods was presented in [35]; the normative supervisor presented there is an external module that can be attached to an RL agent in order to curb its behaviour according to a given normative system $\mathcal {N}$, which we will describe below, adding additional terminology and critical analysis not explored in [35, 37, 38], which were more focused on system architecture and experimental results.

3.1 Architecture

The normative supervisor is composed primarily of (front-end and back-end) translator modules and a reasoner module (see Fig. 2), which we will describe in more detail below.

Fig. 2

The basic architecture of the normative supervisor. Here, the norm base is a knowledge base containing all norms associated with the normative system $\mathcal {N}$

3.1.1 Translators

The translators work together to produce for each state s $Th(s,\mathcal {N})=\langle F_s, R^O, R^C, >\rangle$; the front end translator translates simple statements about the environment into literals to be absorbed into the set of facts $F_s$ (which, unlike $F_{\overline{s}}$ in $Th(\overline{s},\mathcal {N})$, does not specify which action is taken). Generally, we can assume that $F_s = L(s)$, the labels applied to the state s.

Meanwhile, the back-end translator translates regulative and constitutive norms into DDL rules. Generally, the norm O(p|q) is translated as: $r_1:\ q\Rightarrow _O p$ $\in R^O$. Similarly, F(p|q) will be formalized as $r_2:\ q\Rightarrow _{O}\lnot p$ $\in R^O$. As for (strong) permissions, we utilize defeaters and can simply translate the conditional permission P(p|q) as $r_3:\ q\rightsquigarrow _{O} p \in R^O_s$. For the case of normative conflicts, we can simply add an ordered pair to the superiority relation > of $Th(s,\mathcal {N})$. For example, if we have $r_4:q\Rightarrow _O p$ and $r_5:q\Rightarrow _O \lnot p$, where $r_4$ takes priority over $r_5$, we would add $(r_4,r_5)\in>$.

Constitutive norms C(x, y|c) referring to state properties are translated simply as $x,c\rightarrow _C y$, but due to the way the reasoner was configured in [35, 38], constitutive norms referring to actions must be handled differently. We will discuss this below.

Finally, we draw attention to non-concurrence rules – these were not discussed in [35, 38] but are included in the implementation; these are basically rules of the form $C(a, \lnot a'|\top )$ constructed to enforce the fact that the RL agent can only take one action at a time (that is, if a is obligatory, all other actions $a'$ are forbidden). These are automatically included in $Th(s,\mathcal {N})$.

3.1.2 Reasoner

The reasoner is at the core of the normative supervisor, and uses a couple of algorithms to compute sets of what we will call normatively optimal actions for the agent. The first, called ParseCompliant (Algorithm 1 in [38]) (1) returns a single action a if $Th(s,\mathcal {N})\vdash +\partial _O a$, or (2) removes each action a from A(s) such that $Th(s,\mathcal {N})\vdash +\partial _O \lnot a$ to form a set of compliant actions $A_C(s)$.² If $A_C(s)$ is empty, a second algorithm is run, this one called LesserEvil (Algorithm 2 in [38]) which (1) counts the number of applicable rules in $Th(s,\mathcal {N})$ which directly conflict with a for each $a\in A(s)$ and (2) returns the actions a which result in the fewest such conflicts as a set $A_{NC}(s)$. With the output of these algorithms, we can offer a more explicit characterization of normatively optimal actions.

Definition 7

(Normatively Optimal Actions) $A_{\mathcal {N}}(s)$ is the set of normatively optimal actions in state s, defined as:

$$\begin{aligned} A_{\mathcal {N}}(s) = {\left\{ \begin{array}{ll} A_{C}(s) &{} A_{C}(s)\ne \emptyset \\ A_{NC}(s) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(5)

where $A_C(s)$ is the set of actions that comply with $\mathcal {N}$ in state s, and $A_{NC}(s)$ is the set of actions minimally non-compliant with $\mathcal {N}$.

A Simple Notion of Violation. The notion of compliance implicitly employed here is encapsulated by taking an action which is not forbidden. By reconstructing what actions are excluded based on ParseCompliant, we can get the following formal characterization of $A_{C}(s)$:

$$\begin{aligned} A_C(s) = \{a\in A(s)\ |\ Th(s, \mathcal {N})\nvdash +\partial _{O}\lnot a \} \end{aligned}$$

Violations, then, occur when we take an action (represented as an action proposition) which is explicitly forbidden by an applicable regulative rule in $Th(s, \mathcal {N})$.

This definition of $A_C(s)$ requires that we prove that a is forbidden before we can exclude it from the set of compliant actions; in order to do this, we need to be able to propagate prohibitions over facts related by constitutive norms. Because of this, we have to translate constitutive norms over actions a bit strangely. For example, if we have a norm saying that breaking traffic laws is forbidden, and another that says that jaywalking counts as breaking traffic laws, we need to be able to explicitly derive that jaywalking is forbidden. In [35, 37, 38] this is done by encoding each constitutive norm over actions in the case study used as a prohibition triggered by another prohibition. That is, instead of translating the constitutive norm to $jaywalking\rightarrow _C break\_law$ – from which we cannot derive $+\partial _O \lnot jaywalking$—we would have, along with the regulative norm $\Rightarrow _O \lnot break\_law$, another rule $O(\lnot break\_law) \Rightarrow _O \lnot jaywalk$.

Unfortunately, this conception of violation and the accommodations made for it severely limit the expressive range of the normative systems that can be implemented with the normative supervisor, thereby limiting the effectiveness of the normative supervisor for certain applications. We will discuss these issues in more detail in Sect. 3.4.1.

3.2 Online Compliance Checking

In order to elicit compliant behaviour from an RL agent, the algorithms ParseCompliant and LesserEvil can be used together each time an (already-trained) RL agent enters a new state, and the agent’s action function A(s) can be replaced with $A_{\mathcal {N}}(s)$. Thus, when the agent chooses the action with the highest Q-value, it is in fact choosing from the list of normatively optimal actions. This method for correcting the actions of an RL agent is called online compliance checking (OCC) in [37] to contrast the technique presented there, called norm-guided RL (NGRL), which we will discuss momentarily.

OCC has proved effective in curbing RL agent behaviour to conform to a wide variety normative systems. For instance, it was demonstrated in [36] that OCC could easily elicit the correct behaviour for the pacifist merchant.

However, as a technique, OCC is not perfect, and in the next subsection we will motivate the use of NGRL over (or in addition to) OCC.

3.2.1 Limitations of Online Compliance Checking

OCC with the normative supervisor of [35, 38] performs about as well as the agent in [39] when administered the same experiments, where the agent is tasked with playing the game Pac-Man while under the “moral” constraint forbidding the player-character from eating ghosts. Nevertheless, in both [39] and [35, 38] violations still occurred, however infrequently. In [38] it is shown that all of these violations in spite of the normative supervisor occur in states of normative deadlock. It is also notable that in the smaller, simpler environment in [37], the agent’s performance at the simplified Pac-Man game was badly impacted by the use of the OCC; the percentage of games won and average scores plummeted. These two problems are linked; because the normative supervisor is completely decoupled from the agent when used for OCC, the agent does not take the constraints derivable from $\mathcal {N}$ into account while learning optimal behaviour.

To clarify, consider this example presented in [37]: a self-driving car has planned a route, and the normative supervisor is attached to ensure the car does not break any local regulations. The self-driving car eventually comes to a private road, which it is prohibited from passing through; the normative supervisor forces the car to turn around and reroute. If the applicable norms had been incorporated into the agent’s plan from the start, it could have reached its destination much more efficiently. Here, we can extend the example: consider the case where the road leading to the private road is one-way; then, upon coming to the private road, the supervisor must decide whether to proceed or illegally reverse, violating a regulation either way. Thus, the decoupling of the normative supervisor and the policy has the potential to both damage performance and cause normative deadlock unnecessarily.

It was due to these issues that norm-guided reinforcement learning (NGRL) was introduced in [37].

3.3 Norm-Guided Reinforcement Learning

NGRL is an approach to implementing normatively compliant behaviour which largely overcomes the difficulties discussed above in our critique of OCC.

The basic approach is this: given an agent with an objective x (and an associated reward function $R_x(s,a)$), we define a second reward function that assigns punishments when the agent violates a normative system $\mathcal {N}$. We call this second reward function a non-compliance function:

Definition 8

(Non-Compliance Function [37]) A non-compliance function for the normative system $\mathcal {N}$ is a function of the form:

$$\begin{aligned} R_{\mathcal {N},p}(s, a) = {\left\{ \begin{array}{ll} p &{} a\notin A_C(s)\\ 0 &{} otherwise \end{array}\right. } \end{aligned}$$

(6)

where $p\in \mathbb {R}^{-}$.

p from Definition 8 is called the penalty, assigned each time the action taken by the agent is not in $A_C(s)$ (which for now means that the action taken is explicitly forbidden). This automated derivation of conclusions from $Th(s, \mathcal {N})$ solves the first question of the reward engineering approach to teaching normative behaviour, allowing us to dynamically determine the compliance of an action in a given state and, in the case of non-compliance, assign a punishment.

Now, if we have an agent meant to learn objective x with the reward function $R_{x}$, it will do so over $\mathcal {M} = \langle S, A, R_{x}, P\rangle$. Then, if we have a normative system $\mathcal {N}$ we want to subject the agent to while it pursues objective x, we can build an MOMDP we will call a compliance MDP:

Definition 9

(Compliance MDP [37]) Let $\mathcal {M} = \langle S, A, R_{x}, P\rangle$ be a single-objective MDP. Then we can define an associated compliance MDP by introducing a non-compliance function $R_{\mathcal {N},p}(s, a)$ to form the MOMDP:

$$\begin{aligned} \mathcal {M}_{\mathcal {N},p}=\langle S, A, (R_{x}, R_{\mathcal {N},p})^{T}, P\rangle \end{aligned}$$

(7)

NGRL entails finding a policy that is, first and foremost, maximally compliant, but also optimal with respect to the primary objective. Here, the term maximal compliance is a term we substitute for the terminology ethical policy from [37, 44]. We adapt their definitions below:

Definition 10

(Maximally Compliant Policy [44]) Let $\Pi$ be the set of all policies over the compliance MDP $\mathcal {M}_{\mathcal {N},p}$. A policy $\pi ^{*}\in \Pi$ is maximally compliant iff it is optimal with respect to the value function $V^{\pi }_{\mathcal {N},p}$ corresponding to $R_{\mathcal {N},p}$. That is, $\pi ^{*}$ is maximally compliant for $\mathcal {M}_{\mathcal {N},p}$ iff for all s:

$$\begin{aligned} V^{\pi ^{*}}_{\mathcal {N},p}(s)=\max _{\pi \in \Pi }V^{\pi }_{\mathcal {N},p}(s) \end{aligned}$$

(8)

Like in [44], we define within this set of maximally compliant policies those that are optimal with respect to the reward function $R_x$.

Definition 11

(Optimal Maximally Compliant Policy [44]) Let $\Pi _{\mathcal {N}}$ be the set of all maximally compliant policies for $\mathcal {M}_{\mathcal {N},p}$. Then $\pi ^{*}\in \Pi _{\mathcal {N}}$ is optimal maximally compliant for $\mathcal {M}_{\mathcal {N},p}$ iff for all s:

$$\begin{aligned} V_{x}^{\pi ^{*}}(s)=\max _{\pi \in \Pi _{\mathcal {N}}}V^{\pi }_{x}(s) \end{aligned}$$

(9)

There are several ways we can find an optimal maximally compliant policy; in Sect. 2.1 we introduced TLQL, which is what we will adapt for use with compliance MDPs here.

Thus, for $Q_{\mathcal {N},p}$, we must choose a threshold $C_{\mathcal {N},p}$. We choose 0; [37] proved that if a maximally compliant policy exists, setting $C_{\mathcal {N},p}=0$ ensures we learn an optimal maximally-compliant policy.³ Meanwhile, we want to maximize the objective x, so we choose $C_x = +\infty$. With these parameters, we can compute an optimal maximally compliant policy.

3.3.1 The Magnitude of p

In the preceding exposition, we have referenced $R_{\mathcal {N},p}(s,a)$ without specifying a penalty p. [37] proves the following useful theorem:

Theorem 1

If a policy $\pi$ is maximally compliant for the compliance MDP $\mathcal {M}_{\mathcal {N},p}$ for some constant $p\in \mathbb {R}^{-}$, it is maximally compliant for the compliance MDP $\mathcal {M}_{\mathcal {N},q}$ for any $q\in \mathbb {R}^{-}$.

Thus, the value of p is irrelevant, so for the remainder of this discussion we will only deal with the non-compliance function $R_{\mathcal {N}}:= R_{\mathcal {N},-1}$. This answers the second main question we identified for the reward engineering approach.

3.4 Shortcomings of NRGL

In [37], NGRL is shown to remedy the issues we just reviewed in Sect. 3.2.1; their experiments show that NGRL, when used with OCC (that is, NGRL is used to train the agent and OCC is used at operation time), the number of scenarios in which violations were inevitable decreased, and the performance of the agent with respect to its primary objective improved substantially. However, it is notable that NGRL as an individual technique fails to capture certain nuances of normative reasoning, and the expensive process of running OCC at operation time to compensate may not be feasible in all cases. We will discuss the shortcomings of NGRL on its own in more detail below. [37] identifies a couple of potential weaknesses of NGRL, but we will focus on one in particular—its inability to handle normative deadlock in general, and contrary-to-duty obligations in particular.

Consider this simple case we adapt from [37] where we have a normative system $\mathcal {N}=\langle \mathcal {C}, \mathcal {R}, \mu \rangle$ containing a contrary-to-duty obligation, where $\mathcal {R}=\{O(b|\lnot a), O(a|\top )\}$, a and b being action propositions. In DDL these norms can be translated as: $r_{1}:\ \Rightarrow _{O} a$ and $r_{2}:\ \lnot a\Rightarrow _{O} b$. Now, suppose that the agent has two actions available to it in a given state s: they are represented by the action propositions b and c. Now, if the agent could take the action represented by a, it would not receive a penalty from the non-compliance function for violating $r_1$; however, that is not possible. If the agent takes the action represented by b, it will be punished, because $r_1$ along with the non-concurrence rules in $Th(s,\mathcal {N})$ will allow us to derive $+\partial _O \lnot b$, signaling a violation of the above normative system which will trigger a penalty. If the agent takes the action represented by c, the result will be identical. However, choosing b obeys the CTD obligation in the above normative system, and so ideally, we would incentivize the agent to choose this action over c; if we were using OCC, the LesserEvil algorithm would take care of this case, but the non-compliance function does not allow for this nuance.

To verify and illustrate this issue, we trained the Travelling Merchant using NGRL with the pacifist normative system (recall, this is the normative system containing the primary obligation $O(at\_danger|\top )$ and the contrary-to-duty obligation $O(negotiate|at\_danger, attacked)$). We see the learned behaviour in Fig. 3.

Fig. 3

The pacifist merchant’s path after training with NGRL but without OCC. Note that in running this experiment we employed the alternative definition of $A_C(s)$ we will introduce in Sect. 4.1, since the above definition of $A_C(s)$ cannot easily accommodate this normative system (see Sect. 3.4.1)

We can see that the agent takes a path identical to the correct path (see Fig. 4), except for the point at which it enters the dangerous area. The NGRL agent fights instead of negotiating; as we predicted above, the non-compliant action fight is punished just as much as the action unload (both actions in that state have identical $Q_{\mathcal {N}}$-values), and as a result, the contrary-to-duty obligation is not observed (since fight is the more advantageous action for the agent).

Based on the example above, we might find it appropriate to assign graded penalties to violations of a normative system, depending on how much of it is violated; however, this re-introduces the problem of scaling the magnitude of rewards, and we are once again left to attempt to find weights that achieve the behaviour we desire. This is probably a reasonable measure for simple cases, but as soon as we consider more complex normative systems or environments, it can be difficult to predict how rewards with different magnitudes could affect the behaviour of the agent.

An additional shortcoming of NGRL is that it lacks transparency, when compared to OCC. In [35, 38] an event recorder is demonstrated which can be configured to run alongside OCC without additional computational cost. Though we can in theory check the compliance of any given state-action pair with the normative supervisor (and this is indeed done during training), when the agent is actually operating in the environment, it does so by selecting actions based on its Q-function, which retains none of the information from the original normative system (besides how likely we are to incur violations from a given point). If we do encounter an issue with an (ostensibly non-compliant) action a committed in a state s—which we would first have to somehow detect—one approach we can take is to evaluate $Th(\overline{s}, \mathcal {N})$ for $\overline{s} = (s,a)$ with the normative supervisor. If no violations occur, we can assume that the issue is either with what means we used to detect the violation, or with the normative system itself; either the system or the automated implementation is too permissive. Then, we must fix our implementation and retrain the agent from scratch. However, if we encounter violations, we are left to wonder why the agent learned to select a non-compliant action.

Finally, running the normative supervisor at each step during training can incur substantial computational cost. Though a single run is inexpensive (in [37] it is noted that the evaluation of the non-compliance function can be completed in linear time with respect to the size of $Th(s,\mathcal {N})$), in applications that require thousands or even millions of episodes of training, this can be prohibitively expensive. We will discuss a possible remedy for this in Sect. 5.

3.4.1 An Incomplete Notion of Violation

There is an additional problem that proliferates both OCC and NGRL which was not discussed at all in [35, 37, 38]. Since the condition for excluding actions a from $A_C(s)$ is the derivation of $Th(s,\mathcal {N})\vdash +\partial _O \lnot a$, the rules in our normative system must either only reference actions $a\in Act$ (recall that Act is the agent’s action set), or allow us to derive new (concrete) obligations from given abstract obligations. The former disallows constitutive norms over actions which define more abstract actions (e.g., $walk\rightarrow _C move$); for the latter, we must be able to derive $+\partial _O \lnot a$ for every action a that results in a violation (e.g., we need to be able to derive $+\partial _O \lnot walk$ when move is forbidden).

In [35, 37, 38], “strategy rules” essentially express constitutive norms over actions as prohibitions triggered by other prohibitions, so that from the prohibition of some institutional fact we can derive the prohibition of the related brute facts (that is, the actions a of A(s)). So if we have $F(b|\top )$ and $C(a,b|\top )$ for actions a and b (where $a\in A(s)$), the regulative norm will be represented as $\Rightarrow _O \lnot b$ and the constitutive norm will be translated to $O(\lnot b)\Rightarrow _O \lnot a$; if a counts as b, the prohibition of b requires the prohibition of a. But what if our regulative norm is an obligation instead of a prohibition?

Consider the pacifist merchant; in particular, we will look at a slightly modified version where the rule obl (the primary obligation to stay out of the dangerous area) is removed, and we have an additional constitutive norm $C(sing, negotiate| \top )$. Recall that we also have a norm that says O(negotiate| $at\_danger, attacked )$, and another that says C(unload, negotiate|attacked); thus, when the agent is in a dangerous area and is attacked, it is required to negotiate. It can do so by unloading its inventory. However, because of the additional constitutive norm $C(sing, negotiate| \top )$, unloading is not the only action it can take to fulfill the obligation to negotiate anymore. Rather, with the obligation of negotiate the agent is being compelled to unload or sing.

We cannot translate these constitutive norms over actions in a way similar to “strategy rules”, though. $c_1:\ O(negotiate), attacked\Rightarrow _O unload$ is not a good translation of C(unload, negotiate|attacked), because the obligation of negotiate does not simply trigger an obligation of unload. The problem becomes clear if we translate the other constitutive norm the same way ($c_2:\ O(negotiate)\Rightarrow _O sing$) and consider the non-concurrence rules (recall, these are the rules asserting that if one action is obligatory, no other actions can be taken). If $c_1$ is triggered, unload is obligatory and by non-concurrence sing is forbidden. At the same time, $c_2$ can be triggered and so sing is obligatory and by non-concurrence unload is forbidden. We don’t have the means to resolve this conflict—indeed, we shouldn’t have to, because there shouldn’t be a conflict at all here.

We cannot translate this normative system in such a way that we can derive $+\partial _O unload$ and $+\partial _O sing$. We might consider removing the non-concurrence rules, but those are the only means we have for deriving e.g. $+\partial _O \lnot fight$ (which we would need if we are to exclude fight from $A_C(s)$) from the above norms. There may be a generalizable way to translate constitutive norms over actions in cases like this, but the fact that this implicitly given concept of violation forces us to look for non-intuitive and indirect translations for the norms in our normative system suggests that we should take a step back, and reframe the problem with a more conceptually-sound foundation. We do this in the next section.

4 Solution: Violations and Counting Them

In this section, we will introduce solutions to the main issues we identified with NGRL in the last section; that is, we will utilize the explicit, formal characterization of violation given in Sect. 2.2.3 and with it employ a new definition of $A_C(s)$ (as well as a formal definition for $A_{NC}(s)$). We will then reframe the non-compliance function $R_{\mathcal {N}}$ to accommodate our new definition of $A_C(s)$, and introduce a technique we will call violation counting, which we will use to augment NGRL in such a way that accommodates dealing with normative deadlock and contrary-to-duty obligations.

4.1 Redefining Compliance

Before introducing any new techniques, it is important that we address the issues put forward in 3.4.1, which are caused by a fundamental oversight in the normative supervisor’s architecture—the lack of a comprehensive notion of violation to be utilized in the construction of $A_{\mathcal {N}}(s)$. To remedy this we return to our formal definitions for violation-related concepts from Sect. 2.2.3 and redefine $A_C(s)$ and $A_{NC}(s)$.

If we conceive of $A_C(s)$ as the set of actions for which there is an absence of violations (as defined in Definition 6), the following definition arises:

$$\begin{aligned} A_C(s)& = \{a\in A(s)\ |\ viol(\overline{s},\mathcal {N})=\emptyset \} \\& = \{a\in A(s)\ |\ Th(\overline{s},\mathcal {N})\nvdash +\partial _{O}lit, -\partial _{C}lit \} \end{aligned}$$

(10)

In the same vein, we can also provide a formal definition of $A_{NC}(s)$:

$$\begin{aligned} A_{NC}(s) = \mathop {\mathrm {arg\,min}}\limits _{a\in A(s)} |viol(\overline{s},\mathcal {N})| \end{aligned}$$

(11)

Thus, we can compute both $A_C(s)$ and $A_{NC}(s)$ from $viol(\overline{s},\mathcal {N})$. Given $Th(\overline{s},\mathcal {N})$, the computation of $|viol(\overline{s},\mathcal {N})|$ is a simple matter, demonstrated in Algorithm 2.

Algorithm 2

ViolationCount

Our new characterization of violation allows us to translate all constitutive norms C(x, y|c) to $x, c\rightarrow _C y$⁴ (regardless of whether they reference actions or not) and solves the problems presented in Sect. 3.4.1. To demonstrate, if the merchant is being attacked while in danger, we can prove $+\partial _O negotiate$ from the rule ctd; then, if we have the two constitutive norms translated to $unload, attacked\rightarrow _C negotiate$ and $sing\rightarrow _C negotiate$, if actions unload or sing are taken, we will be able to prove $+\Delta _C negotiate$ which implies that $+\partial _C negotiate$, so neither action will be excluded from $A_C(s)$. If we re-introduce the rule $obl:\ \Rightarrow _O \lnot at\_danger$, $at\_danger$ violates obl no matter what action is taken; thus, $A_C(s)$ will be empty. However, because sing and unload do not result in a violation of ctd as well as obl, $A_{NC}(s)=\{sing, unload\}$.

This conception of maximal compliance is much more flexible than the characterization implicitly adopted by [35, 37, 38]. Fortunately, for NGRL we can employ our more comprehensive notion of violation without any additional computational cost (this will be discussed in more detail at the end of Sect. 4.2); moreover, we will find that we can leverage the output of Algorithm 2 to augment NGRL with violation counting, granting the technique the ability to cope with normative deadlock.

4.2 NGRL with Violation Counting

Now that we have a comprehensive definition of what it means for an action to be compliant, we will reframe the non-compliance function (Definition 8). Recall the definition of a non-compliance function:

$$\begin{aligned} R_{\mathcal {N},p}(s, a) = {\left\{ \begin{array}{ll} p &{} a\notin A_C(s)\\ 0 &{} otherwise \end{array}\right. } \end{aligned}$$

where $p\in \mathbb {R}^{-}$ is the penalty. Now that we are defining membership in $A_C(s)$ with the notion of violation presented in Definition 6, the non-compliance function is equivalent to:

$$\begin{aligned} R_{\mathcal {N},p}(s, a) = {\left\{ \begin{array}{ll} p &{} viol(\overline{s},\mathcal {N})\ne \emptyset \\ 0 &{} otherwise \end{array}\right. } \nonumber \\ =p\cdot (1-compl_{\mathcal {N}}(s,a)) \end{aligned}$$

(12)

Once again, we will abbreviate to $R_{\mathcal {N}}$ in practise.

Essentially, this definition of $R_{\mathcal {N},p}$ still entails that p is assigned to state-action pairs $\overline{s}=(s,a)$ such that $a\notin A_C(s)$. However, if we consider our new definition of $A_C(s)$, these are precisely those actions for which there are no violations of $\mathcal {N}$ according to Definition 6.

With this revised non-compliance function, we can establish a link between ENCC—the expected non-compliance count for a policy $\pi$ described in Eq. 4—and maximal compliance (Definition 10). In fact, maximally compliant policies minimize ENCC:

Lemma 1

Let $\Pi$ be the set of all policies over the compliance MDP $\mathcal {M}_{\mathcal {N}}$. Then if $\pi ^*$ is maximally-compliant:

$$\begin{aligned} ENCC(\pi ^*) = \min _{\pi \in \Pi } ENCC(\pi ) \end{aligned}$$

Proof

Suppose $\pi ^*$ is maximally compliant, then we know $V_{\mathcal {N}}^{\pi ^{*}}(s) = \max _{\pi \in \Pi }V_{\mathcal {N}}^{\pi }(s)$. At each step $\overline{s}_t=(s_t, \pi (s_t))$ in a trace generated by a policy $\pi$, the reward awarded to the agent by $R_{\mathcal {N}}$ is equal to $-(1 - compl(s_t, \pi (s_t)))$ (see Eq. 12); then according to Eq. 1 we have the equivalence:

$$\begin{aligned}& \mathbb {E}\left[ \sum ^{\infty }_{t=0}-\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi ^*(s_{t+i}))) | s_i=s\right] \\& \;\; =\max _{\pi \in \Pi } \mathbb {E}\left[ \sum ^{\infty }_{t=0}-\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi (s_{t+i}))) | s_i=s\right] \end{aligned}$$

Then by the linearity of conditional expectation this equation becomes:

$$\begin{aligned}& -\mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi ^*(s_{t+i}))) | s_i=s\right] \\&\;\; = \max _{\pi \in \Pi } - \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl(s_{t+i},\pi (s_{t+i}))) | s_i=s\right] \\& \;\; = - \min _{\pi \in \Pi } \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi (s_{t+i}))) | s_i=s\right] \end{aligned}$$

Or:

$$\begin{aligned}& \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi ^*(s_{t+i}))) | s_i=s\right] \\&\;\; = \min _{\pi \in \Pi } \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi (s_{t+i}))) | s_i=s\right] \end{aligned}$$

Since this equation holds for all $s\in S$, we can say that

$$\begin{aligned}& \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi ^*(s_{t+i}))) | s_{i}\in S \right] \\&\;\; = \min _{\pi \in \Pi } \mathbb {E}\left[ \sum ^{\infty }_{t=0}\gamma ^{t}(1-compl_{\mathcal {N}}(s_{t+i},\pi (s_{t+i}))) | s_i\in S \right] \end{aligned}$$

So we get the equivalence:

$$\begin{aligned} ENCC(\pi ^{*}) = \min _{\pi \in \Pi } ENCC(\pi ) \end{aligned}$$

$\square$

Now, recall that in Sect. 3.4, when we reviewed the shortcomings of NGRL, we demonstrated that it cannot cope with contrary-to-duty obligations or reasoning about normative deadlock. To remedy this, we now introduce violation counting functions.

Definition 12

(Violation Counting Function) A violation counting function for a normative system $\mathcal {N}$ is a function of the form:

$$\begin{aligned} VC_{\mathcal {N}}(s,a) = |viol(\overline{s},\mathcal {N})| \end{aligned}$$

(13)

where $\overline{s}=(s,a)$.

In other words, a violation counting function is a function over state-action pairs to the natural numbers, which outputs the number of violations associated with state-action pair $\overline{s}=(s,a)$ with respect to normative system $\mathcal {N}$. In practise, we can update $VC_{\mathcal {N}}$ every time we update $Q_{\mathcal {N}}$ with values from $R_{\mathcal {N}}$; both $R_{\mathcal {N}}(s,a)$ and $VC_{\mathcal {N}}(s,a)$ can be computed from the output of Algorithm 2.

It is notable that $A_{\mathcal {N}}(s)$ (as defined from the $A_C(s)$ of Eq. 10 and the $A_{NC}(s)$ of Eq. 11) contains precisely those actions which minimize $VC_{\mathcal {N}}$ in the state s.

Proposition 1

For a normative system $\mathcal {N}$, we have:

$$\begin{aligned} A_{\mathcal {N}}(s) = \mathop {\mathrm {arg\,min}}\limits _{a\in A(s)}VC_{\mathcal {N}}(s,a) \end{aligned}$$

(14)

Proof

If the set $A_{C}(s)$ is non-empty, $A_{\mathcal {N}}(s) = A_C(s)$ and the $a\in A_{\mathcal {N}}(s)$ are those $a\in A(s)$ such that for $\overline{s} = (s,a)$, $|viol(\overline{s},\mathcal {N})| = 0$, according to Eq. 10 and Definition 6. Then $\mathop {\mathrm {arg\,min}}\limits _{a\in A(s)} VC_{\mathcal {N}}(s,a)$ are precisely those actions such that $|viol(\overline{s},\mathcal {N})| = 0$, and $A_{\mathcal {N}}(s)=\mathop {\mathrm {arg\,min}}\limits _{a\in A(s)}VC_{\mathcal {N}}(s,a)$.

If $A_{C}(s)$ is empty, $A_{\mathcal {N}}(s)= A_{NC}(s)$, which in turn is equal to:

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{a\in A(s)} |viol(\overline{s},\mathcal {N})| = \mathop {\mathrm {arg\,min}}\limits _{a\in A(s)} VC_{\mathcal {N}}(s,a) \end{aligned}$$

by definition (see Definition 12). So according to Definition 7,

$$\begin{aligned} A_{\mathcal {N}}(s) = \mathop {\mathrm {arg\,min}}\limits _{a\in A(s)}VC_{\mathcal {N}}(s,a) \end{aligned}$$

$\square$

The introduction of the violation counting function into NGRL allows us to in a way mimic the results of using OCC without being forced to use the normative supervisor at runtime; since OCC allows the agent only to select actions from $A_{\mathcal {N}}(s)$, picking actions that minimize $VC_{\mathcal {N}}$ will have the same effect.

Now in order to elicit behaviour aligned with $\mathcal {N}$ as much as possible, we will craft a new policy function based on TLQ(s) (see Algorithm 1). Given the normative Q-function $Q_{\mathcal {N}}$, the primary Q-function $Q_x$, and the violation counting function $VC_{\mathcal {N}}$, we construct the following policy (Algorithm 3) for our agent, which is essentially an augmentation of the thresholded lexicographic Q-learning policy [51] (Algorithm 1) approach used in [37] with $VC_{\mathcal {N}}$.

Algorithm 3

Policy(s)

It is notable that we choose actions that prioritize maximizing $Q_{\mathcal {N}}$; it is only after we have selected those actions which maximize the normative objective that we choose from among them actions that are normatively optimal according to Definition 7 and the redefinitions of $A_C(s)$ and $A_{NC}(s)$ outlined in Sect. 4.1. As a result, they might not be normatively optimal with respect to all actions in A(s). In order to explain this, we need to prove a couple of things.

Firstly, it is clear that this policy, which prioritizes maximizing $Q_{\mathcal {N}}$, is maximally compliant:

Lemma 2

The Policy defined by Algorithm 3 is maximally compliant.

Proof

$Policy(s)\in \mathop {\mathrm {arg\,max}}\limits _{a\in A(s)}Q_{\mathcal {N}}(s,a)$ and so

$$\begin{aligned} V^{Policy}(s)= \max _{a\in A(s)} Q_{\mathcal {N}}(s,a) = \max _{\pi \in \Pi }V_{\mathcal {N}}^{\pi }(s) \end{aligned}$$

So by Definition 10, Policy is maximally compliant. $\square$

Since we have a maximally compliant policy, we can refer back to Lemma 1, and make a statement about the ENCC of the policy.

Proposition 2

The Policy from Algorithm 3 minimizes expected ENCC.

Proof

Lemma 2 shows that Policy is maximally compliant, and Lemma 1 tells us that it has minimal ENCC. $\square$

Proposition 2 shows why Policy prioritizes maximizing $Q_{\mathcal {N}}$ over choosing only actions from $A_{\mathcal {N}}(s)$. Though ideally we will always want to choose actions from $A_{\mathcal {N}}(s)$ (which is $\mathop {\mathrm {arg\,min}}\limits _{a\in A(s)}VC_{\mathcal {N}}(s,a)$ according Proposition 1), policies that choose actions from $\mathop {\mathrm {arg\,max}}\limits _{a\in A(s)}$ $Q_{\mathcal {N}}(s,a)$ minimize the expected count of violations (ENCC) that will occur over the whole trace generated by the policy. This has the effect of prioritizing the overall normative objective over immediate maximal compliance and can minimize violations in the long term. In other words, if we take only actions from $A_{\mathcal {N}}(s)$ we may end up choosing an action that is compliant in the immediate, but results in more violations later on. By using a policy that prioritizes minimizing the ENCC, we can choose actions which minimize violations in the long term, and by further minimizing $VC_{\mathcal {N}}$, we can then exclude the actions which result in the most violations in normative deadlock scenarios. We will see an example of these functionalities at work in Sect. 6.1.

Finally, we note that the adoption of our new definition of violation and the addition of the violation counting function to NGRL does not incur any extra computational cost. DDL conclusions can be computed in linear time with respect to the size of the theory [18], and its theorem prover SPINdle is run only once in Algorithm 2; since both $R_{\mathcal {N}}(s,a)$ and $VC_{\mathcal {N}}(s,a)$ can be computed directly from the output of Algorithm 2, NGRL with violation counting allows us to deal with normative deadlock without requiring additional computations from the theorem prover.

4.2.1 A Reporting Module

We noted in Sect. 3.4 that NGRL has another prominent shortcoming, aside from its inability to deal with normative deadlock; it is not a transparent means of developing normative behaviour (reflecting the criticisms in [5] of the notion of an “ethical utility function”). We noted briefly in Sect. 3.4 that when using OCC, we can employ an event recorder functionality—creating “violation reports” whenever a violation occurs [38]—with no additional computational cost.⁵ These violations reports consist of a formal representation of the environment and the normative system at the time of the violation, along with a list of possible actions and a list of minimally non-compliant actions.

For NGRL with violation counting, we cannot get this information at run time without using the normative supervisor in the operation phase. However, we can configure a reporting module that generates one of these violation reports whenever an action a is chosen such that $VC_{\mathcal {N}}(s,a) >0$; that is, when violations occur, we can reactivate the normative supervisor and run it only in that state, cycling through all possible actions and getting a violation count for each of them; this could be accompanied by a formal representation of $Th(\overline{s}, \mathcal {N})$ for each action a in state s. This is one way we could maintain some transparency in the framework while avoiding running the normative supervisor at each time step at operation time. This does not remedy all the problems mentioned in Sect. 3.4, but it does allow us the means to detect and record violations (and the conditions under which they occured).

5 Constructing a Normative Filter

A persistent issue affecting all techniques utilizing the normative supervisor remains—computational overhead. Running a theorem prover for every state transition is taxing, and the additional computational cost piles up for applications that require a large number of training episodes or have an extended operation time.

This degree of computational overhead is unnecessary—some of these queries to the theorem prover are bound to be redundant, so one way to mitigate this steep computational overhead would be to make sure we never generate conclusions from $Th(\overline{s'},\mathcal {N})$ when we already have generated conclusions from $Th(\overline{s},\mathcal {N})$, where $Th(\overline{s},\mathcal {N})=Th(\overline{s'},\mathcal {N})$. And perhaps the simplest way to do this is to compute the number of violations up front. Shielding—see [2, 23] for examples—involves utilizing an abstraction of the environment and LTL safety specification to synthesize up front a shield, which restricts an RL agent’s actions in such a way that it never takes an action that may lead (up to a certain probability) to an unsafe state. Inspired by this technique (as well as the synthesis technique of [36]) we propose a method for constructing a normative filter up front, through which we can filter actions or rewards and thus perform OCC, NGRL, and NGRL with violation counting, without requiring that we continually run a theorem prover.

Since all we care about in the environment is what labels L(s) are assigned to a given state s, rng(L) ($\subseteq 2^{AP}$) gives us something of a model of the environment (or at least, what of it is relevant to us). We can define equivalence classes for states $[s] = \{s' | s'\in S \text { s.t. } L(s')=L(s)\}\in [S]$, then, and run Algorithm 2, ViolationCount, on $Th(\overline{s},\mathcal {N})$ for each $[s]\in [S]$ and $a\in Act$. We can then use the output to define a function $filter_{\mathcal {N}}:2^{AP}\times Act\rightarrow \mathbb {N}$ which maps subsets of AP and actions to the natural numbers.

Now, to avoid having to compute [S], we could in theory just run ViolationCount on the theory $Th(\Gamma \cup \{a\},\mathcal {N})$ for each $\Gamma \in 2^{AP}$ (where $Th(\Gamma \cup \{a\},\mathcal {N})$ is the theory $Th(\Gamma \cup \{a\},\mathcal {N})=\langle \Gamma \cup \{\lnot p| p\in AP{\setminus } \Gamma \}\cup \{a\}, R^O, R^C, >\rangle$ for regulative rules $R^O$, constitutive rules $R^C$, and superiority relation >). However, $2^{AP}$ may be prohibitively large, and it very well may be the case that there are many $\Gamma \in 2^{AP}$ that do not constitute the labels for any state. In addition, it is possible that some of the atoms in $\Gamma$ are not at all referenced in $R^O\cup R^C$ of $Th(\Gamma \cup \{a\},\mathcal {N})$, and therefore do not impact the conclusions that can be gleaned from $Th(\overline{s},\mathcal {N})$. It therefore makes sense to consider only subsets of $AP_{\mathcal {N}}=AP\cap atoms(R^O\cup R^C)$, where atoms(R) is the set of all atoms occurring in the set of rules R. This still will in many cases constitute an overestimation of which labels we need to consider, and if this set is still prohibitively large, we could find a way to reduce it further by removing $\Gamma$ such that $\Gamma \ne L(s)$ for all s. For the sake of simplicity, we will forego this further reduction and look only at $2^{AP_{\mathcal {N}}}$ in our outline of Algorithm 4.

Algorithm 4

ConstructFilter

It is easy to see that for any $s\in S$, $filter_{\mathcal {N}}(\Gamma , a) = VC_{\mathcal {N}}(s,a)$ if $L(s)=\Gamma$. That means, because of what we have proved in Proposition 1, we can use $filter_{\mathcal {N}}$ to compute $A_{\mathcal {N}}(s)$, and therefore we can use it to perform OCC without having to query the theorem prover. Likewise, $compl_{\mathcal {N}}$ can be computed from $filter_{\mathcal {N}}$, so we can likewise perform NGRL (with or without violation counting) without having to query the theorem prover. Thus, by constructing the normative filter, we enable our agent to use all the techniques that employ the normative supervisor without the significant computational overhead they would normally incur.

Computing the filter is, of course, very computationally expensive itself—but Algorithm 4 only needs to be run once, before training. We will discuss the comparative performance of employing NGRL with the filter and the supervisor in the next section.

6 Final Evaluation

In order to demonstrate the improvements born of adding violation counting to NGRL, along with training using the normative filter, we will now return to the pacifist normative system for the Travelling Merchant as presented in 2.3.

6.1 NGRL with Violation Counting

In Sect. 3.4, we saw how NGRL on its own fails to produce the correct behaviour from the agent. The agent avoids unnecessary violations, but when a violation does occur, it does not obey the contrary-to-duty obligation, choosing to fight (the more advantageous action) rather than unload.

When we run NGRL with violation counting, however, we get exactly the correct behaviour, shown in Fig. 4.

Fig. 4

The pacifist merchant’s path after training with NGRL augmented with violation counting. Note that (U) indicates that the agent unloaded its inventory

To clarify, though in the state s where $at\_danger$ is true $Q_{\mathcal {N}}(s, fight) = Q_{\mathcal {N}}(s, unload)$ (as both actions result in a violation), it is going to be the case that $VC_{\mathcal {N}}(s, fight) > VC_{\mathcal {N}}(s, unload)$, so the action unload is taken.

As a final consideration, in order to demonstrate the advantages of minimizing ENCC, we will consider one more case, where we have changed the environment. Instead of having only two dangerous areas, we have four; in this environment, when the agent is given the choice to enter the second dangerous area, it can either do so (and that is the last violation that will happen), or it can choose not to, and end up forced to pass through two additional dangerous areas. In this environment, choosing to violate the normative system unnecessarily results in fewer violations in the long term, so ideally, the agent would choose that path.

We can see in Fig. 5 that the agent we train with NGRL with violation counting does indeed follow this path, while observing the CTD obligation whenever a violation is incurred.

Fig. 5

The pacifist agent voluntarily violating a norm in order to avoid future violations

6.2 The Normative Filter

The above experiments can also be run using the normative filter we introduced in Sect. 5 (constructed with an implementation of Algorithm 4). The construction of the filter was completed in 484 ms—not an unsubstantial computation time, but again, it only needs to be run once, before training.

It turns out that the improvement in training time is dramatic, however. Below, we provide a table comparing training time using the supervisor with training using the filter.

Table 1 Training time with the supervisor and filter

Table 1 clearly demonstrates the drastic decrease in training time; on average, using the filter reduced training time by 99.54%. Considering that even at only 500 training episodes, the difference in training time is 729.28 ms, the 484 ms it took to construct the filter is seems a very minor cost. This confirms that the use of the normative filter constitutes a significant improvement in training time, when compared to NGRL using the normative supervisor.

7 Conclusion

In this paper, we have reviewed, analysed, and revised the normative supervisor presented in [35, 37, 38]. These papers mostly focus on experimental results, and address the architecture of the normative supervisor through the lens of case studies; to complement and improve the existing work, we have based our analysis and augmentations on a formal characterization of normative system violation.

We began by introducing a formal definition of “normatively optimal actions"—the subset of an agent’s available actions that the normative supervisor is designed to compute. Normatively optimal actions are actions which comply with a normative system, if such actions exist; we extracted a formal (but flawed) characterization of compliant actions from the algorithm from [38] used to compute them, from which we extrapolate an implicitly given definition of violation. After motivating the introduction of NGRL, we provided the basic definitions and results related to this technique, before expanding on the discussion of the technique’s limitations from [37]. Finally, we revisit the definition of violation we inferred and discuss how it fails to accommodate some normative systems.

Earlier, we had presented another definition of normative system violation, more comprehensive and conceptually faithful than the implicit definition we found; we thus adopt this presentation of compliant actions instead. We then provided an algorithm for computing the number of violations of a normative system for a given state-action pair, and returned to NGRL, adding an additional component, a violation counting function—which, together with the non-compliance function fundamental to computing the policy in NGRL (that is, a non-compliance function that accommodates our new definition of violation), can be computed from the algorithm we provided. This violation counting function can be leveraged to overcome one of the main shortcomings of NGRL—its inability to cope with normative deadlock scenarios (in particular, contrary-to-duty obligations). We then specified a policy utilizing the violation counting function and the learned Q-functions corresponding to the agent’s normative and primary objectives. We proved that this policy minimizes the expected total number of violations (discounted) that occur in a trace generated by the policy, while also sorting out actions that are not normatively optimal. As a final improvement—conscious of the significant computational overhead the above techniques incur—we introduced the idea of a normative filter, which allows us to compute ahead of time the means to perform OCC, NGRL, and NGRL with violation counting, without having to query the theorem prover at all following the run of the algorithm.

Finally, we have demonstrated the effectiveness of this approach with a simple case study, which shows violation counting resulting in the observance of a contrary-to-duty obligation (where NGRL alone could not), and furthermore showed that the agent could strategically violate its normative system in order to avoid additional violations later on. We also demonstrated the dramatic decrease in training time that comes with the use of the normative filter, in place of the supervisor.

As for future work, we plan to investigate how to manage the trade-off between the agent’s primary objective and its normative objective. There may be times when fulfilling the primary objective is crucial, and must be pursued in spite of (albeit while minimizing) violations; currently, our technique does not allow for this. In order to accomplish this, we will need to even more closely entwine tools for normative reasoning with the reinforcement learning framework. It may also be possible to expand the approach with weighted violations, so that we can deal with indirect conflicts that cannot be solved with DDL’s superiority relation (such as practical dilemmas where it is impossible to fulfill two norms, one being higher priority than the other, simultaneously, though they do not directly conflict). Additionally, we hope to explore possibilities for including temporal reasoning within the framework; temporal obligations constitute a crucial and challenging subfield of normative reasoning, and the normative supervisor, which strictly employs DDL, cannot accomodate them.