Abstract
Explainable Artificial Intelligence (XAI) has mainly focused on static learning tasks so far. In this paper, we consider XAI in the context of online learning in dynamic environments, such as learning from real-time data streams, where models are learned incrementally and continuously adapted over the course of time. More specifically, we motivate the problem of explaining model change, i.e. explaining the difference between models before and after adaptation, instead of the models themselves. In this regard, we provide the first efficient model-agnostic approach to dynamically detecting, quantifying, and explaining significant model changes. Our approach is based on an adaptation of the well-known Permutation Feature Importance (PFI) measure. It includes two hyperparameters that control the sensitivity and directly influence explanation frequency, so that a human user can adjust the method to individual requirements and application needs. We assess and validate our method’s efficacy on illustrative synthetic data streams with three popular model classes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many contemporary applications of machine learning (ML), predictive models induced from data may no longer be viewed as static objects, because the environments for which the models were initially conceived may change and necessitate adaptations over the course of time [48]. In some scenarios, models may be trained and retrained at fixed intervals to keep up with recent trends and changes in the data. In other, more extreme cases, specific ML models are needed to monitor and incrementally learn from data continuously arriving in real-time. In learning scenarios of that kind, changes in the data generating processes caused by concept drift must be discovered quickly and responded to by model adaptation, so as to maintain predictive performance.
Yet, in many domains, predictive performance alone does no longer suffice for the applicability and acceptance of an ML model. Instead, a certain degree of understanding of the model and its predictions is also required. Novel approaches from the field of Explainable Artificial Intelligence (XAI) provide specific means to explain complex machine learning models to humans [1, 3]. However, current XAI methods are essentially limited to the explanation of static models. If such methods are used to explain models that are learned incrementally, a new explanation needs to be started from scratch each time the model changes. Needless to say, this may become cumbersome over longer time periods and when these models are adjusted only slightly.
In such situations, it is arguably more effective and efficient to build on the user’s current understanding and only explain the difference between a model before and after an adaptation, rather than both versions independently of each other. This idea of explaining model change, which is illustrated in Fig. 1, comes with a couple of challenging research questions.
Illustration of explaining changes of dynamic models directly: Data (rectangles) arriving asynchronously over time lead to models changing over time. If an explanation is necessary at a time step t, then this explanation can be provided by describing the difference of the current model \(h_t\) compared to the latest reference model \(h_r\)
Contribution. We motivate the field of applying XAI in the context of dynamically changing models to explain model change directly. We discuss its applicability and important challenges, which arise when applying XAI on data streams (Sect. 3). More specifically, we propose a time-dependent variant of the well-known Permutation Feature Importance (PFI) explanation approach (Sect. 4). We illustrate our explanation framework through experiments conducted with synthetic data streams.
Related Work. As already mentioned, quite some methods have recently been proposed to explain static machine learning models, such as LIME [36] or SHAP [30, 31]. While these methods provide an appropriate starting point, they are limited to the case of static models. Yet, the need for continuously updated model explanation appears for instance in Explainable Interactive ML [8, 42] as part of human-computer interaction. As neither traditional XAI methods nor approaches from Explainable Interactive ML natively support incremental learning, new methods or extensions are needed. Initial ideas of directly explaining the changes of a model were recently discussed by Hammer and Hüllermeier [20]. They are related to the field of contrast mining and change mining, where changes in two or more data sets are determined using learned patterns from each data set [9]. As a model change is typically caused by a change in the underlying data generating process, our work is also related to the detection and understanding of concept drift in data [44]. For instance, Webb et al. [43, 44] identify features that characterize the concept drift. Moreover, Hinder et al. [22, 23] analyze time-dependent feature dependencies.
2 Explainability and Adaptive Models
In the following, we briefly recall basic concepts of both XAI and incremental learning on data streams. Our focus is on supervised machine learning, i.e., we consider the task of learning a predictive model
mapping from an input or feature space \(\mathscr {X}\) to an output or target space \(\mathscr {Y}\). In the standard (batch) setting, a model of that kind is learned on a dataset D consisting of training examples \((x,y)\in \mathscr {X}\times \mathscr {Y}\). In a streaming scenario (formally introduced in Sect. 2.2), the static data D is replaced by a continuously evolving stream of data, on which a model is learned incrementally.
2.1 Explainability Based on Feature Importance
In general, XAI aims at improving a practitioner’s understanding of a model (1). To this end, various explanation methods have been proposed that address different explanation needs [1, 3, 26, 33]. One way to support understanding of a model h is to quantify the influence of different input variables or features \(X^{(j)}\) on the target variable Y: To what extent does a certain feature determine the predictions by the model h? Obviously, a feature-based explanation of that kind presumes a representation of instances in the form of feature vectors \(X=(X^{(1)}, \ldots , X^{(d)})\), which is a common representation in machine learning. Such feature importance measures are commonly used for creating post-hoc and, often, model-agnostic explanations. Feature-based explanations may be derived locally with methods such as SHAP [31] and LIME [36], or globally for example with SAGE [13].
As a well-known example of a feature-based explanation, we make use of PFI, which is a post-hoc, global, model-agnostic method. The importance of an individual feature is assessed on an explanation dataset \(\tilde{D} = \{ (x_i , y_i) \}_{i=1}^N\) by measuring the (presumably negative) impact that a random permutation of that feature’s values has on the model performance [11]. Thus, given a random permutation \(\pi\) of \(\{1, \ldots , N\}\), the PFI \(\phi ^{(j)}\) for a feature \(X^{(j)}\) is computed as
where \(\tilde{x}_i\) denotes the instance \(x_i\) with the \(j^{th}\) entry \(x_i^{(j)}\) replaced by \(x_{\pi (i)}^{(j)}\), i.e., the entry originally observed in \(x_{\pi (i)}\). The data \(\tilde{D}\) can be taken as part of the training data D but also as extra validation data [33]. In a streaming scenario, where each data sample is commonly used for both testing (first) and training (afterward), this distinction is somewhat blurred.
2.2 Adaptive Models for Data Streams
Data streams are becoming more and more important in industrial applications. They are often linked to the so-called Internet of Things (IoT) [46]. The IoT describes the rising interconnectivity of devices such as industrial machines, vehicles, personal devices, and many more [5]. The installed sensors are generating vast amounts of valuable data streams that can be used to analyze real-time behavior and optimize services for customers. However, traditional batch learning algorithms are not well suited for these scenarios, since IoT devises are often subject to change. Incremental learning algorithms offer an alternative to batch processing that can handle real-time modeling and model updates requiring minimal resources [5]. A data stream may be characterized as a possibly infinite sequence of data observed over time. More formally, for a countable set of observations identified by their time indices \(T \subset [0,\infty )\), e.g. \(T=\mathbb {N}\), the observed data until time t can be defined as
In this setting, traditional batch learning algorithms encounter several obstacles [5]:
-
Data capacity: Data streams provide an unbounded set of training data.
-
High frequency: Observations in data streams may appear in short time intervals and efficient updating of the model is crucial.
-
Concept drift: The data generating process may change over time, either smoothly but perhaps even abruptly, calling for flexible model structures that can be adapted quickly.
Various incremental learning algorithms have been proposed to address these challenges. Incremental learning algorithms rely on a sequence of models \((h_t)_{t \in T}: \mathscr {X} \longrightarrow \mathscr {Y}\), where data up to time point t, \(\mathscr {D}_t\), has been observed to infer model \(h_t\) [20]. In general, the learning algorithm updates the current model upon observation of a new data point and immediately discards the observations afterward. Thus, data capacity constraints are mitigated and the incremental update of the model allows for efficient computation. The field of online or incremental learning has been studied quite intensively in recent years [5, 28]. In the following, we briefly review a few important approaches. Our focus is on (binary) classification, which we also consider in the experiments later on.
Decision Tree (DT). DTs are a class of non-linear learning algorithms that are widely used because of their inherently interpretable structure [21]. A standard DT splits the data according to the value of a feature at each inner node of the tree, and assigns a class label at each leaf node (associated with a certain region in the input space). DTs are built by starting with a single node and recursively splitting leaf nodes by adding informative features, i.e., features increasing the association of subgroups of the data with a unique class label. The tree growing stops when no informative splits can be found anymore, or too few samples are left for splitting. A new split may also be reversed, when new data points no longer support the previous decision.
In the incremental setting, a DT algorithm decides dynamically which partition shall be split after enough samples are available within a particular region [15, 16, 25]. The notion of optimality of a split is usually relaxed to enable more efficient computation. A new split is created when the improvement appears to be significant enough. For instance, Hoeffding trees [15] rely on the Hoeffding bound [24] to determine when to split. Theoretical results are established such that given infinite data, the algorithm approaches the tree that would have been learned in batch mode. In the literature, many variations of Hoeffding trees have been proposed [7, 16, 25, 32]. In practice, while single (sufficiently small) DTs benefit from an inherently interpretable model structure, they lack stability and predictive power. Therefore, ensembles of DTs, called random forests [11], are usually preferred over single trees and serve as powerful black-box models. Random forests can also be applied in the incremental setting [19, 38].
Linear Model (LM). A linear classifier is a model of the form \(x \mapsto I(\langle x, w \rangle > \theta )\), where \(w \in \mathbb {R}^d\) is a weight vector, \(\theta \in \mathbb {R}\) a threshold, and \(I(\cdot )\) denotes the indicator function. Thus, a linear model bisects the input space through a linear hyperplane. LMs are theoretically well understood and appealing due to their simplicity [21].
In the incremental setting, LMs are often trained by stochastic gradient descent (SGD), which is used to gradually update the parameters w based on the training loss and a gradient approximation with the most recent observation [28, 34, 35]. Applications in large-scale learning have shown that linear models trained with SGD perform very efficiently for high-dimensional sparse data [10, 28, 37, 47].
Instance-based Learning (IBL). The notion of instance-based learning refers to a family of machine learning algorithms, which represent a predictive model in an indirect way via a set of stored training examples. Thus, in contrast to model-based methods, IBL algorithms simply store the data itself and defer its processing until a prediction is actually requested. Predictions are then derived by combining the information provided by the stored data, typically accomplished by means of the nearest neighbor (NN) estimation principle [14].
In the data stream scenario, instance-based learning essentially reduces to the maintenance of the training data [41]: every time a new example arrives, the learner needs to decide whether or not this example should be added to the current dataset \(\mathscr {D}_t\), and if other examples should perhaps be removed. Baseline implementations [34, 35] simply rely on a window of recent data points, whereas more complex extensions have been proposed in [27, 40].
2.3 Concept Drift
A common assumption on the context of data streams is a possibly non-stationary data generating distribution [18]. For instance, users may change their behavior in online shopping due to new trends, technical sensors might be replaced by newer technologies, or changes occur due to unknown hidden variables not captured by the model. This phenomenon is referred to as concept drift [39, 45]. More formally, assume \((x_t,y_t) \in \mathscr {X} \times \mathscr {Y}\) is generated by \(P_t\), \(t \in T \subset \mathbb {R}\). Then, concept drift [18] occurs if
Different types of concept drift as described in [29]: Sudden, gradual and incremental drift replace an existing concept over time, whereas reoccurring concepts can reflect seasonal trends
Concept drift may be further distinguished into two components, as \(P_t(x,y) = P_t(x) \times P_t(y \, | \, x)\). A change in \(P_t(y \, | \, x)\), referred to as real drift, is likely to reduce the model’s performance and require a change of the decision boundary.
The underlying distribution can change in different ways over time, as shown in Fig. 2. For sudden, gradual, and incremental drift, the focus typically lies on the pace of the model change and maximizing model performance. Maintaining historical concepts and quickly adapting to the best-suited ones can be beneficial for reoccurring concepts, such as seasonal changes.
Concept drift detection refers to the identification of a point in time where a significant drift takes place. Concept drift detection algorithms often rely on comparing a current and a historical time window of data points. In a supervised learning setting, this comparison can be executed using the model’s dynamic performance within the time windows. A significant decrease in the model’s performance serves as an indicator for concept drift [29]. For instance, ADWIN [6] maintains a dynamic time window and compares sub-windows to detect changes in expected values. ADWIN has been used in many variations, as an accuracy-rate based concept drift detector in classification [6, 29] and within incremental learning algorithms [6, 7, 19] to monitor changes in the model.
Drift learning methods can adapt models actively after drift has been detected, or (passively) adapt models continuously over time. For instance, a DT may grow a separate candidate subtree when a change is detected and may finally replace the associated existing subtree [25]. In contrast, non-parametrical IBL relies on careful maintenance of the stored data points. For instance, in the Self Adjusted Memory (SAM) approach [27], the notion of short- and long-term memory [4] is used to maintain current and previous concepts and convey information from one to the other.
3 Explaining Model Change
While XAI and incremental learning on data streams have both received much attention in recent years [3, 5, 12, 28], the integration of the two, that is, the application of explainability in the setting of incremental learning, remains a significantly understudied field. We will focus on explainability in the context of adaptive model change, as it appears, for example, in incremental learning algorithms. Since adaptive model change is commonly realized by updating an existing model, the question arises whether the model and its corresponding explanations can be updated simultaneously. Furthermore, a user monitoring an autonomous AI system that evolves over time might be primarily interested in an explanation of the model change, rather than an explanation of the overall AI system as a whole. In the following, we will pick up this notion, referred to as explaining model change, and elaborate on its properties in the context of data streams. As pointed out by Hammer and Hüllermeier [20], explaining model change poses challenging questions.
What are suitable representations of models and model change? The question of how to explain a model change strongly depends on the underlying model class, just like the explanation of a model itself. A suitable representation of a model change should admit a certain level of interpretability, which itself highly depends on the updating process. Depending on the model type, some choices will be better suited for analyzing the change of models than others. For instance, neural networks updated by gradient descent will likely change \(h_t\) from one black-box model to another, complicating the analysis of the model change. In contrast, an update of an incremental DT, such as [25], can be viewed as an addition or removal of a certain subtree that acts on a restricted area in the feature space \(\mathscr {X}\). This subtree, given that it is sufficiently small, admits an interpretable structure and may be directly used to characterize the model change. Further, in IBL, the model may be represented as the newly available instances, representing the model change in the feature space.
As an alternative, a user might want to know which features have become less or more important for the predictions in the new model. This change of feature importance could be quantified by global methods like PFI or local methods like SHAP and serve as an explanation of model change in terms of the change of feature relevances. While methods for measuring feature relevance exist for the batch setting, their adaptation for incremental learning is far from obvious, especially because access to training data is limited in the incremental setting.
How to quantify model change? In order to detect, compare, and appropriately react to changes, we need to establish a notion of the magnitude of model change. A natural measure is the expected discrepancy [20], defined as
where \(h_t\) refers to the current model and \(h_r\) to a suitable reference model at different points in time. Since the data distribution on \(\mathscr {X}\) is usually unknown, the expected discrepancy needs to be estimated. One way of finding an estimation is to rely on the empirical distribution of p(x) using the observed samples. However, this approach may lack stability in cases where training data is sparse. Then, it could be more beneficial to assume a specific data distribution on \(\mathscr {X}\) and sample from this distribution.
Furthermore, when establishing measures for model change, one should distinguish between semantic and syntactic model change. Syntactic change refers to a change in the representation of a model \(h_t\), whereas semantic change refers to the actual change of the functional dependency \(\mathscr {X} \longrightarrow \mathscr {Y}\), such as measured by the expected discrepancy. For instance, a DT may change its tree structure completely without changing the function it represents. In general, distinguishing semantic and syntactic model change will highly rely on the traceability of the model change and the model’s representation. While semantic change appears to be more relevant, syntactic change might be more accessible and easier to compute in practice.
How to compute model change efficiently? As efficiency is one of the key challenges in modeling data streams, efficiently computing \(\Delta (h_r,h_t)\) and other explanatory items is crucial. While for incremental learning algorithms the model update may be exploited to compute \(\Delta (h_r,h_t)\) efficiently, explanations are currently mainly computed in the batch setting. In this case, new incremental methods are required. Ideally, the computation of explanations should be able to keep up with the speed of the incremental learning algorithm itself. This task is especially challenging for explanation methods such as SHAP [31], which have a high complexity already in the batch setting.
Again, careful choices of models and representations of change can be beneficial. For instance, it has been shown that SHAP values for DTs can be computed in polynomial time by exploiting the specific tree structure [30]. Hence, incremental versions may benefit from the tree structure as well.
When and how often should a change be explained? An answer to this question depends on the specific objectives of a human user. A detailed and frequent explanation of current changes yields the best representation. However, various limitations must be considered, including the cognitive capacity of the user, who might be overwhelmed by too many updates, as well as computational and storage capacity. Furthermore, noisy data may yield a model change that would soon be reverted, or optimization methods like SGD would oscillate around local optima resulting in uninformative explanations. Ideally, users interacting with the explanation framework should be able to control the system’s sensitivity and adapt it to their personal needs. Higher sensitivity will yield more frequent explanations of more minor changes in the model and increase the cognitive load on the side of the user. Lower sensitivity will yield less frequent explanations of more substantial changes. This could become problematic when important intermediate changes are missed.
4 Agnostic Explanation of Model Change

In the following, we present an efficient and powerful model-agnostic approach as a starting point for explaining model change. Our method relies on the assumption that explanations should be given once a significant change in model performance has been observed. As incremental learning algorithms aim at optimizing model performance, we argue that model change most likely appears when a significant change in model performance is achieved. Significant changes in model performance are commonly used as an indicator of concept drift and we will rely on ADWIN as a well-known error-rate based drift detector [29]. The model performance, for instance, could be measured by the accuracy in the case of classification. The sensitivity of our method can be controlled by a single hyperparameter linked to ADWIN. Furthermore, we introduce another hyperparameter \(\tau\) to prevent uninformative explanations associated with the expected discrepancy.
How to quantify model change? We quantify model change in two ways. First, we measure the change of the model performance of the incremental learning algorithm. Second, we approximate the expected discrepancy \(\Delta (h_r,h_t)\) by
where \(h_t\) is the current model, \(h_r\) the reference model, \(D := D_r \cup D_t\) with \(D_r \subset \mathscr {D}_r\) and \(D_t \subset \mathscr {D}_t\). The subsets \(D_r\) and \(D_t\) (further described below) are used as a representation of the distributions p(x) of the feature space at time r and t to approximate the expectation in (3). To lower the cognitive burden of users interacting with the system, we will provide an explanation only if the expected discrepancy exceeds a threshold parameter \(\tau >0\), i.e. \(\hat{\Delta }_t > \tau\). While \(\hat{\Delta }_t\) estimates the semantic model change directly, the model performance is only indirectly able to quantify it. However, relying on the dynamic model performance could be substantially more efficient, as it can be computed incrementally and does not require an averaging over a large sample. The measurement of expected discrepancy can therefore be seen as a safety measure to guarantee that only significant semantic model changes are explained to the users.
How to compute model change efficiently? We use ADWIN to efficiently monitor significant changes in the model performance. To this end, ADWIN maintains two dynamic time windows and compares the model performance within these. Thereby, only the predictions at each time step are used, which are anyway created in the learning process and no further model evaluations have to be executed. When ADWIN detects a change at time step \(t-K\), we begin collecting the next K training samples for \(D_t\), which results in \(K = |D_t|\). While collecting data, changes detected by ADWIN are ignored. This requires K to be chosen appropriately, such that enough samples for robust estimations can be collected, while changes can still be monitored reliably. After K new samples are observed and collected, we store the last model \(h_t\) and estimate the expected discrepancy \(\hat{\Delta }_t\) to quantify the model change with respect to the reference model \(h_r\) and reference data \(D_r\) according to Equation (4). An explanation (as will be described below) of the change is then presented to the user only if additionally \(\hat{\Delta }_t > \tau\). After an explanation has been presented, we replace the reference model \(h_r\) and the reference data \(D_r\) by the current model \(h_t\) and the collected data \(D_t\).
When and how often should a change be explained? The sensitivity of the method is essentially controlled by the ADWIN parameter \(\delta \in (0,1)\), which describes its confidence value controlling the global false positive-rate [6]. Higher values of \(\delta\) will yield more frequent explanations increasing the cognitive burden of users monitoring the system and the chances of explaining an uninformative change. Small values of \(\delta\) could result in missing important model adaptations. Furthermore, \(\tau\) provides an additional safety measure to prevent uninformative explanations. As already mentioned, \(\delta\) and \(\tau\) are hyperparameters that should be set according to the needs of the user and properties of the current application scenario.
What are suitable representations of models and model change? We propose a model-agnostic approach and make no further assumptions on the representation of \(h_t\). For an explanation, we need to provide more details about the nature of the semantic change, the size of which is estimated by \(\hat{\Delta }_t\). One way of doing this, is to analyze the change in the contribution of each feature in the models \(h_r,h_t\). Using PFI, we compute the feature importance \(\phi ^{(j)}_{t}\) at time t for feature j and \(h_t\) as
As explained in Sect. 2.1, \(\tilde{x}_i\) denotes the instance \(x_i\) with the \(j^{th}\) entry \(x_i^{(j)}\) replaced by \(x_{\pi (i)}^{(j)}\), where \(\pi\) is a permutation of \(\{ 1, \ldots , |D_t|\}\). Our method essentially analyzes how the model performance changes in \(D_t\), when this feature does not contribute any information. We then compute the difference as
and replace \(\phi ^{(j)}_r\) by \(\phi ^{(j)}_t\) for the next explanation iteration. Hence, \(\Delta \phi _t\) yields a magnitude and a direction of the change of the feature importance before and after the model change. Negative values indicate that feature relevance has dropped and positive values that it has increased after the model adaptation.
ADWIN and PFI Change Explanation. One complete explanation iteration of our method is described in Algorithm 1 and illustrated in Fig. 3. We observe each data point \((x_i,y_i)\) consecutively and compute the model prediction \(\hat{y}_i\), the updated model \(h_{i+1}\), and the ADWIN update. When ADWIN detects a change and no data collection is in progress, then \(D_t\) is emptied and \(N=K\) is set to collect the next K samples (including the current one) in \(D_t\). The variable t represents the time step for which an explanation is potentially created from now after N samples are observed, i.e. \(t=i+K\). When the algorithm arrives at the last observation to collect (i.e. \(N=1\) and \(i=t-1\)), the expected discrepancy \(\hat{\Delta }_t\) is computed and compared against the threshold parameter \(\tau\). If the threshold is exceeded, then an explanation is created and presented to the user. In this case, the PFI for each feature is computed using \(D_t\) and the model \(h_t\). Then, the difference \(\Delta \phi _t\) is calculated using the calculated PFI \(\phi _t\) and the previously calculated PFI \(\phi _r\). Afterwards, the variables \(D_r,h_r\) and \(\phi _r\) are replaced by the current variables \(D_t,h_t,\phi _t\) and will be used as the reference model in the next explanation iteration. Finally, the explanation \((t,\hat{\Delta }_t,\Delta \phi _t)\) is presented to the user.
For readability, the initialization of \(h_r,D_r\) and \(\phi _r\) are neglected. These initial objects are computed in the same fashion as their counterparts at time t. The initial data collection iteration is started at the beginning of the training phase of the incremental learning algorithm. However, no explanation is created at the end of the initial data collection. Therefore, r would initially be equal to K. While initializing the reference model, ADWIN is not updated. We note that this initial training phase may be shifted to an arbitrary point in time depending on the application, or the reference can simply be provided by the users.
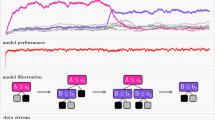
The incremental learning process of a sample adaptive random forest classifier on the STAGGER data stream containing a concept drift: In the initial training phase phase (colored gray) from \(t_0\) to \(t_1\) the first 300 samples are collected (\(D_r\)). The first reference model \(h_r\) is stored at \(t_1\). The concept drift (red line) occurs after 1250 samples. ADWIN detects the concept drift with a delay at \(t_2\) and the first explanation phase starts. Again, the next 300 samples are collected (\(D_t\)) and the first explanation is created for a new updated model \(h_t\) at \(t_3\). The accuracy (classification rate) is calculated prequentially by using every sample first for testing and then for training
5 Experiments
To illustrate our approach of explaining model change, we conduct experiments in the context of binary classification.Footnote 1 We let \(\mathscr {Y} = \{0,1\}\) and \(\Vert \cdot \Vert\) be the one-dimensional Euclidean norm. Accuracy is used to measure model performance. We train three incremental classifiers implemented in the River Python package [34] on synthetic data streams. We train an adaptive random forest [19] (DTs), a SAM-kNN classifier [27] (IBL), and a single-layer perceptron with SGD [34] (LM). During training, we artificially induce a rapid gradual concept drift by switching the data generating distribution of the data streams. Then, the incremental models need to adapt to this concept drift and change their classification functions. We quantify the model change with the expected discrepancy and provide further insights using PFI.
Model Parameters. For the implementation, we rely on River’s [34] default parameters. Hence, the adaptive random forest defaults to 10 trees in the ensemble model with the information gain as a split criterion. The IBL SAM-kNN model considers \(k = 5\) nearest neighbors with distance-weighted estimations using the Euclidean distance as metric. The perceptron is trained with SGD using a learning rate of 1.
Gradual Concept Drift. To illustrate how we can explain model changes, we expose the incremental models to a gradual concept drift. In both experiments, we create two unique data streams and overlay them for the incremental learning task. Each observation at time t has a probability of
to belong to the second data stream. The position and width of the concept drift, where the second data stream begins to dominate, is defined by \(t_d\) and w respectively [34]. As both streams follow distinct classification functions, the concept to be learned by the incremental models switches. This constitutes a real drift described in Sect. 2.3.
5.1 Experiment A: STAGGER Concepts
Our first experiment is based on the STAGGER concepts [17, 39]. STAGGER data streams consist of three features (shape, size, and color) describing an object. Each feature can have only three possible values resulting in 27 unique combinations. Simple classification functions denote what combination of feature values constitute the STAGGER concepts to be learned. We create two data streams with distinct classification functions to induce the actual concept drift. The first classification function returns 1 if the size feature is small and the color feature is red:
Concept A.1:
The function for the second concept returns 1 if the size feature is medium or large:
Concept A.2:
Compared to the first concept, the second no longer depends on the color feature. However, the size feature is inverted, as the values that were previously not describing the concept now define it. An incremental model, thus, has to react to this drastic concept drift by significantly changing its decision surface. In theory, assuming a uniform distribution on the instance space, the magnitude of the expected discrepancy induced by switching from Concept A.1 to Concept A.2 is \(0.\overline{7}\). The theoretical magnitude of the change can be calculated with the symmetric difference of the feature combinations belonging to Concept A.1 and Concept A.2 (\(C_1 \triangle C_2\)). As both concepts are disjunctive, \(C_1 \triangle C_2\) can be calculated by adding the probability of a sample belonging to Concept A.1 \(\left( {3}/{27}\right)\) to the probability of a sample belonging to Concept A.2 \(\left( {18}/{27}\right)\). As illustrated in Fig. 3, we train each model on 2,000 samples in total. In the first 1,250 samples Concept A.1 is dominant, and in the last 750 samples Concept A.2 is dominant, i.e. \(t_d=1250\) in Equation (5). The width w is set to 50.
One-Hot Encoding and PFI Methodology. Each described feature of STAGGER has 3 categories and is implemented by default with a label encoding (0,1,2) in River [34]. To account for the distinct categorical values, we run the learning algorithms with a one-hot encoding (resulting in 9 binary dummy variables, 3 for each feature).
Detecting and Quantifying Model Change. As discussed in Sect. 4, we detect model changes incrementally with ADWIN and verify the change by estimating the expected discrepancy. We choose \(\delta =0.025\) for ADWIN and \(\tau =0.3\) for the expected discrepancy as parameters of our method. Furthermore, our explanation window size is set to \(K=300\). The value of \(\delta\) ensures that the overall false positive rate of ADWIN is below \(2.5 \%\) [6]. Additionally, the value of \(\tau\) is relatively low compared to the theoretical value of \(0.\overline{7}\). As illustrated in Fig. 3, we store the first reference classifier \(h_r := h_{t_1}\) after the initial training phase at \(t_1=300\) with the first 300 observations stored in \(D_r\) together with the computed PFI \(\phi _r := \phi _{t_1}\). The classifier’s accuracy sharply drops after the concept drift at \(k=1250\). This change is recognized by ADWIN with some delay at time step \(t_2\). When ADWIN detects the change, another 300 samples are starting to be stored for \(D_t := D_{t_3}\) until time step \(t_3=t_2+300\). Finally, the updated model \(h_t := h_{t_3}\) is stored after observing all samples at time step \(t_3\). When the expected discrepancy exceeds the sensitivity threshold \(\tau\), the PFI is calculated, and the explanation is presented to the user.
Explaining Model Change. The direct explanation of change between the current model \(h_t\) and the most recent model \(h_r\) consists of the estimated expected discrepancy \(\hat{\Delta }_t\) and the changes of the PFI \(\Delta \phi _t\) for each feature. As discussed in Sect. 4, we calculate \(\phi _t\) based on the stored samples in \(D_t\). Based on this, for each explanation time step t and feature j, the change of a model’s PFI \(\Delta \phi _{t}^{(j)}\) is calculated through the difference of the current model’s PFI \(\phi _{t}^{(j)}\) and the latest reference model’s PFI \(\phi _{r}^{(j)}\). A resulting explanation for the SAM-kNN classifier can be seen in Fig. 4.
Results. We evaluated our experimental setting 100 times for each classifier. The results are summarized in Table 1. For all three reference models, ADWIN reliably detects the concept drift and the approximated expected discrepancy exceeds the threshold of \(\tau = 0.3\). On average, the classifiers change with a magnitude of \(\hat{\Delta }(h_{t_{1}},h_{t_{3}}) = 0.779\), which is very close to the theoretical magnitude of \(0.\overline{7}\). Fig. 4 illustrates a possible explanation for the SAM-kNN model once a substantial model change is presented at time step t. Fig. 4 demonstrates that the classifier adapted to the drift from Concept A.1 to Concept A.2. Whereas the latest reference model \(h_{r}\) assigns a small but equal value to both the size and the color feature, for the current model \(h_{t}\) only the size feature is important. This change is directly stated in the changes of the PFI \(\Delta \phi ^{(\text {size})}_t\) and \(\Delta \phi ^{(\text {color})}_t\). The size feature becomes substantially more important, whereas the color feature completely loses relevance. We further observe that ADWIN in some cases detects changes, when no concept drift is present and the model itself seems stable. These false positives are successfully filtered by our approach, as the estimated discrepancy in this case does not exceed the threshold parameter \(\tau\). In summary, our illustrative experiments demonstrated that our approach can efficiently and reliably identify meaningful points of model change. Furthermore, the change of PFI together with the expected discrepancy of the two versions of a time-dependent model give further insights into the nature of the change and provide convincing reasons to users monitoring the model.
In contrast to the illustrative Experiment A, the second experiment considers a substantially more complicated learning task.
5.2 Experiment B: Agrawal Generator
The learning process of a sample adaptive random forest classifier on the Agrawal data stream with concept drift: The reference phase where \(D_r\) and \(h_r\) is stored includes the first 1000 samples. After the concept drift at \(t_d = 13,333\), the first explanation phase begins when ADWIN detects a change. The phase contains the samples \(D_t\) between \(t_2\) and \(t_3\)
The second experiment is based on a data generator introduced by Agrawal et al. in [2]. The generator creates a data stream consisting of nine features describing credit loan applications. Six features are numeric, one is ordinal, and two are nominal. The target variable describes, if the credit loan has been granted and is created based on different classification functions resulting in binary class labels. Similar to Experiment A, we overlay two of these classification functions to induce a gradual concept drift. The first classification function is given by:
Concept B.1:
The concept depends only on two features (age and salary). For the second classification function, the salary feature is replaced with the ordinal elevel (education level) feature.
Concept B.2:
As illustrated in Fig. 5, we generate 20,000 samples and place the concept drift at time step \(t_d=13,333\) with width \(w=50\). We omit the linear perceptron due its poor performance — the concept obviously requires a nonlinear model. Instead, we rely on the (more powerful) SAM-kNN and adaptive random forest model. For all categorical features we use label encoding. To account for the different ranges of the features, we introduce an incremental standard scaling function, that maintains a moving sample mean and sample variance for each feature to normalize each observation. We set the ADWIN parameter to \(\delta = 0.025\) and the expected discrepancy threshold to \(\tau =0.4\). Our explanation window size is set to \(K=1000\) and the first reference model is stored with \(h_r := h_{t_1}\) after the initial training phase at \(t_1 = 1000\).
Results. We evaluated our experimental setting 50 times for each classifier. The results are summarized in Table 2. For both models, ADWIN reliably detects the concept drift and the approximated expected discrepancy exceeds the threshold. However, the overall accuracy of both models is significantly lower compared to Experiment A, accounting for the increased complexity. In Fig. 5 it can be observed that the accuracy varies over time. This variance of the accuracy is also reflected in more frequent ADWIN alerts. However, our estimation of the expected discrepancy successfully filtered uninformative changes at time points, where no concept drift was present. An explanation created by our method using the adaptive random forest model is shown in Fig. 6. From the visualization it is apparent that the classifier has adapted to the induced concept drift. In accordance to Concept B.1, the reference model \(h_r\) strongly relies on the salary and the age feature. After the drift, the adapted model \(h_t\) prioritizes the elevel feature over the salary feature.
However, the commission feature is also important for the reference model and loses its importance in \(h_t\). Furthermore, age increased its importance from \(h_r\) to \(h_t\), despite being unchanged in the concept definitions. Lastly, several uninformative features appear with small yet non-zero importance values.
Discussion. While the true concepts do not contain the feature commission, our results indicate that model \(h_r\) attributes some importance to the feature, whereas model \(h_t\) did not. This can be explained by the direct dependence of the commission feature on the salary feature. In fact, in the Agrawal dataset, commission is partly composed by the salary feature. It is zero if salary is below 75K and else uniformly distributed from 10k to 75k. Since salary is used in the Concept B.1, the model \(h_r\) has used commission together with salary to build its classification function. This direct dependency also affects the importance of the feature salary, as the missingness of salary may be compensated by the presence of commission. In general, PFI does not account for interactions between features and therefore does not consider the impact of both features being marginalized together. This issue may be solved with other feature importance techniques, such as SHAP [31], which averages the contributions of features over all possible subsets of features.
In Experiment B, the model accuracy is substantially lower than in Experiment A. The imperfectly trained models may result in measurable PFI changes for theoretically uninformative features (e.g., car, zipcode, hvalue, hyears, loan in Fig. 6) that do not contribute any information to the classification. The increase in the PFI value of age may also be explained in this way, despite being unchanged in the concept definition. However, we like to emphasize that a feature’s PFI may also change due to changes in the concept involving other variables. As seen in Table 2, the calculated PFI values also differ among the models, which indicates that each model has a different understanding of the learned concept. As a consequence, any changes in the PFI should be analyzed carefully and taken with a grain of salt unless the model accuracy is sufficiently high. To reduce the cognitive burden of practitioners, their presentation may exclude small importance values that could be caused by noise improving the presentation of Fig 6. However, in presence of multicollinearity this approach may remove underestimated features from the explanations emphasizing the need for further research of suitable XAI methods beyond PFI in the context of explaining model change with feature importances.
6 Conclusion and Further Work
We discussed a general framework for explaining model change yielding a bridge between XAI and adaptive models in the context of incremental learning on data streams. We proposed an efficient method to detect meaningful model changes using well-established techniques of concept drift detection and XAI. Our experimental study, in which we illustrated our approach with a concrete instantiation of the general framework, suggests that we can efficiently detect and describe time-dependent model adaptations. To validate the general applicability, further research needs to be conducted:
-
Complexity. While our experiments illustrate the notion of explaining model change, the used synthetic data streams and induced concept drifts constitute only limited learning scenarios. Further experiments in challenging real-world learning environments are required.
-
Efficiency. While ADWIN provides an efficient way of detecting model change, it does not directly constitute a measure of a semantic model change. Therefore, the expected discrepancy is currently used as a secondary safety measure to decrease the false positive rate of explaining uninformative changes. The expected discrepancy, however, can currently not be computed incrementally. Data for the computation needs to be collected in fixed time frames. Furthermore, while collecting data, no new change can be detected. Synergies of expected discrepancy together with ADWIN or other incremental approaches could further increase the efficiency of detecting semantic model changes.
-
Sensitivity. While we introduced important hyperparameters to control the sensitivity of the dynamic explanation method, we chose them in an application-specific scenario. It remains unclear how users working with adaptive models should choose them in their particular situations. Further cognitive science research could therefore contribute suitable choices of sensitivity levels together with new data-driven techniques.
-
Explanation. Feature importance is only one among many other (generic) approaches to explanation, and PFI only one among many other measure to quantify importance. In more complex scenarios, a simple presentation of the relative feature importances may not satisfy the explanation need of practitioners. For example, too many features may unnecessarily clutter the explanation, thereby increasing the cognitive burden of users. The presentation of our method may further benefit from research in human-computer interaction and data visualization.
In spite of the limited scope of our study and the wealth of open questions, we have shown the importance of explaining model change as a subfield of XAI and sketched the promising research opportunities it offers. While we presented a model-agnostic approach, it is clear that model-specific variants could substantially improve the efficiency and fidelity of explanations. As change is ubiquitous in real-world learning environments, adaptive models will undoubtedly become more prevalent. We strongly believe that incremental explanation methods will significantly contribute towards an effective and efficient understanding of model change.
Notes
Experiments and implementation can be found at: https://github.com/MMschlk/Agnostic-Explanation-of-Model-Change-based-on-Feature-Importance.
References
Adadi A, Berrada M (2018) Peeking inside the black-box: a survey on explainable artificial intelligence (XAI). IEEE Access 6:52138–52160. https://doi.org/10.1109/ACCESS.2018.2870052
Agrawal R, Imielinski T, Swami A (1993) Database mining: a performance perspective. IEEE Trans Knowl Data Eng 5(6):914–925. https://doi.org/10.1109/69.250074
Arrieta AB, Díaz-Rodríguez N, Del Ser J, Bennetot A, Tabik S, Barbado A, Garcia S, Gil-Lopez S, Molina D, Benjamins R, Chatila R, Herrera F (2020) Explainable artificial intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible ai. inform fusion 58(3):82–115. https://doi.org/10.1016/j.inffus.2019.12.012
Atkinson R, Shiffrin R (1968) Human memory: a proposed system and its control processes. In: Psychology of Learning and Motivation, 2, 89–195. Academic Press. https://doi.org/10.1016/S0079-7421(08)60422-3
Bahri M, Bifet A, Gama J, Gomes HM, Maniu S (2021) Data stream analysis: Foundations, major tasks and tools. Wiley Interdisciplin Rev Data Mining Knowl Discovery 11(3):e1405. https://doi.org/10.1002/widm.1405
Bifet A, Gavaldà R (2007) Learning from time-changing data with adaptive windowing. In: Proceedings of International Conference on Data Mining (SIAM), pp. 443–448. https://doi.org/10.1137/1.9781611972771.42
Bifet A, Gavaldà R (2009) Adaptive learning from evolving data sreams. In: Proceedings of International Symposium on Intelligent Data Analysis (IDA), pp. 249–260 . https://doi.org/10.1007/978-3-642-03915-7_22
Biswas R, Barz M, Sonntag D (2020) Towards explanatory interactive image captioning using top-down and bottom-up features, beam search and re-ranking. KI - Künstliche Intelligenz 34(4):571–584. https://doi.org/10.1007/s13218-020-00679-2
Boettcher M (2011) Contrast and change mining. WIREs data mining knowl discovery 1(3):215–230, e1405. https://doi.org/10.1002/widm.27
Bottou L (2010) Large-scale machine learning with stochastic gradient descent. In: Proceedings of international conference on computational statistics (COMPSTAT), pp. 177–186 . https://doi.org/10.1007/978-3-7908-2604-3_16
Breiman L (2001) Random Forests. Mach Learn 45(1):5–32, e1405 https://doi.org/10.1023/A:1010933404324
Burkart N, Huber MF (2021) A larning. J Artif Intellig Res 70:245–317, e1405 https://doi.org/10.1613/jair.1.12228
Covert I, Lundberg SM, Lee SI (2020) Understanding global feature contributions with additive importance measures. In: Proceedings of international conference on neural information processing systems (NeurIPS), pp. 17212–17223
Dasarathy BV (1991) Nearest neighbor (NN) Norms: Nn pattern classification techniques. IEEE Computer Society Press
Domingos P, Hulten G (2000) Mining high-speed data streams. In: Proceedings of International conference on knowledge discovery and data mining (KDD), pp. 71–80 . https://doi.org/10.1145/347090.347107
Gama J, Fernandes R, Rocha R (2006) Decision trees for mining data streams. Intellig Data Anal 10(1):23–45, e1405. https://doi.org/10.3233/IDA-2006-10103
Gama J, Medas P, Castillo G, Rodrigues P (2004) Learning with drift detection. In: Proceedings of Brazilian ligence (SBIA), pp. 286–295 . https://doi.org/10.1007/978-3-540-28645-5_29
Gama J, Žliobaitė I, Bifet A, Pechenizkiy M, Bouchachia A (2014) A survey on concept drift adaptation. ACM Comput Surv 46(4):1–37, e1405. https://doi.org/10.1145/2523813
Gomes HM, Bifet A, Read J, Barddal JP, Enembreck F, Pfharinger B, Holmes G, Abdessalem T (2017) Adaptive random forests for evolving data stream classification. Mach Learn 106(9):1469–1495, e1405. https://doi.org/10.1007/s10994-017-5642-8
Hammer B, Hüllermeier E (2021) Interpretable machine learning: On the problem of explaining model change. In: Proceedings of workshop computation intelligence (CI), pp. 1–10
Hastie T, Tibshirani R, Friedman JH (2009) The elements of statistical learning: Data Mining, Inference, and Prediction, 2 edn. Springer
Hinder F, Hammer B (2020) Counterfactual explanations of concept drift. CoRR. arXiv:2006.12822
Hinder F, Jakob J, Hammer B (2020) Analysis of drifting features. CoRR. arXiv:2012.00499
Hoeffding W (1994) Probability inequalities for sums of bounded random variables. In: The Collected Works of Wassily Hoeffding, pp. 409–426. Springer. https://doi.org/10.1007/978-1-4612-0865-5_26
Hulten G, Spencer L, Domingos P (2001) Mining time-changing data streams. In: Proceedings of International conference on knowledge discovery and data mining (KDD), pp. 97–106 . https://doi.org/10.1145/502512.502529
Linardatos P, Papastefanopoulos V, Kotsiantis S (2020) Explainable AI: A review of machine learning interpretability methods. Entropy. https://doi.org/10.3390/e23010018
Losing V, Hammer B, Wersing H (2016) KNN classifier with self adjusting memory for heterogeneous concept drift. In: Proceedings of international conference on data mining (ICDM), pp. 291–300 . https://doi.org/10.1109/ICDM.2016.0040
Losing V, Hammer B, Wersing H (2018) Incremental on-line learning: a review and comparison of state of the art algorithms. Neurocomputing 275:1261–1274, e1405. https://doi.org/10.1016/j.neucom.2017.06.084
Lu J, Liu A, Dong F, Gu F, Gama J, Zhang G (2018) Learning under concept drift: A Review. IEEE transactions on knowledge and data engineering pp. 2346–2363. https://doi.org/10.1109/TKDE.2018.2876857
Lundberg SM, Erion G, Chen H, DeGrave A, Prutkin JM, Nair B, Katz R, Himmelfarb J, Bansal N, Lee SI (2020) From local explanations to global understanding with explainable AI for Trees. Nat Mach Intellig 2(1):56–67, e1405. https://doi.org/10.1038/s42256-019-0138-9
Lundberg SM, Lee SI (2017) A unified approach to interpreting model predictions. In: Proceedings of international conference on neural information processing systems (NeurIPS), pp. 4768–4777
Manapragada C, Webb GI, Salehi M (2018) Extremely fast decision tree. In: Proceedings of international conference on knowledge discovery and data mining (KDD), pp. 1953–1962 . https://doi.org/10.1145/3219819.3220005
Molnar C (2019) Interpretable machine learning: A Guide for Making Black Box Models Explainable. Lulu.com
Montiel J, Halford M, Mastelini SM, Bolmier G, Sourty R, Vaysse R, Zouitine A, Gomes HM, Read J, Abdessalem T, Bifet A (2020) River: machine learning for streaming data in Python. CoRR. arXiv:2012.04740
Montiel J, Read J, Bifet A, Abdessalem T (2018) Scikit-Multiflow: A multi-output streaming framework. J Mach Learn Res 19(72):1–5
Ribeiro MT, Singh S, Guestrin C (2016) Why Should I Trust You? Explaining the Predictions of Any Classifier. In: Proceedings of international conference on knowledge discovery and data mining (KDD), pp. 1135–1144 . https://doi.org/10.1145/2939672.2939778
Richtárik P, Takáč M (2016) Parallel coordinate descent methods for big data optimization. Math Program 156(1):433–484. https://doi.org/10.1007/s10107-015-0901-6
Saffari A, Leistner C, Santner J, Godec M, Bischof H (2009) On-line Random Forests. In: Proceedings of International conference on computer vision workshops (ICCV Workshops), pp. 1393–1400. IEEE . https://doi.org/10.1109/ICCVW.2009.5457447
Schlimmer JC, Granger RH (1986) Incremental learning from noisy data. Mach Learn 1(3):317–354. https://doi.org/10.1007/BF00116895
Shaker A, Hüllermeier E (2012) IBLStreams: a system for instance-based classification and regression on data streams. Evolv Syst 3(4):235–249. https://doi.org/10.1007/s12530-012-9059-0
Smyth B, McKenna E (2001) Competence models and the maintenance problem. Comput Intellig 17(2):235–249. https://doi.org/10.1111/0824-7935.00142
Teso S, Kersting K (2019) Explanatory interactive machine learning. In: Proceedings of AAAI/ACM Conference on AI, Ethics, and Society (AIES), pp. 239–245. https://doi.org/10.1145/3306618.3314293
Webb GI, Lee LK, Goethals B, Petitjean F (2018) Analyzing concept drift and shift from sample data. Data Min Knowl Discov 32(5):1179–1199. https://doi.org/10.1007/s10618-018-0554-1
Webb GI, Lee LK, Petitjean F, Goethals B (2017) Understanding concept drift. CoRR. arXiv:1704.00362
Widmer G, Kubat M (1996) Learning in the presence of concept drift and hidden contexts. Mach Learn 23(1):69–101. https://doi.org/10.1007/BF00116900
Xu LD, He W, Li S (2014) Internet of things in industries: a survey. IEEE Transact Indust Inform 10(4):2233–2243. https://doi.org/10.1109/TII.2014.2300753
Zhang T (2004) Solving large scale linear prediction problems using stochastic gradient descent algorithms. In: Proceedings of international conference on machine learning (ICML), pp. 116–124 . https://doi.org/10.1145/1015330.1015332
Žliobaitė I, Pechenizkiy M, Gama J (2016) An overview of concept drift applications, pp. 91–114. Springer International Publishing.https://doi.org/10.1007/978-3-319-26989-4_4
Acknowledgement
We gratefully acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation): TRR 318/12021-438445824.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Muschalik, M., Fumagalli, F., Hammer, B. et al. Agnostic Explanation of Model Change based on Feature Importance. Künstl Intell 36, 211–224 (2022). https://doi.org/10.1007/s13218-022-00766-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13218-022-00766-6