Approximate functional differencing

Abstract

Inference on common parameters in panel data models with individual-specific fixed effects is a classic example of Neyman and Scott’s (Econometrica 36:1–32, 1948) incidental parameter problem (IPP). One solution to this IPP is functional differencing (Bonhomme in Econometrica 80(4):1337–1385, 2012), which works when the number of time periods T is fixed (and may be small), but this solution is not applicable to all panel data models of interest. Another solution, which applies to a larger class of models, is “large-T” bias correction [pioneered by Hahn and Kuersteiner (Econometrica 70(4):1639–1657, 2002) and Hahn and Newey (Econometrica 72(4):1295–1319, 2004)], but this is only guaranteed to work well when T is sufficiently large. This paper provides a unified approach that connects these two seemingly disparate solutions to the IPP. In doing so, we provide an approximate version of functional differencing, that is, an approximate solution to the IPP that is applicable to a large class of panel data models even when T is relatively small.

1 Introduction

Panel data offer the potential to account for unobserved heterogeneity, typically through the inclusion of unit-specific parameters; see Arellano (2003) and Arellano and Bonhomme (2011) for reviews. Nonlinear panel data models, however, remain challenging to estimate, precisely because in many models the presence of unit-specific—or “incidental”—parameters makes the maximum likelihood estimator (MLE) of the common parameters inconsistent when the number of observations per unit, T, is finite (Neyman and Scott 1948). The failure of maximum likelihood has prompted two kinds of reactions.

One approach is to look for point-identifying moment conditions that are free of incidental parameters. Such moment conditions can come from a conditional or a marginal likelihood (e.g., Rasch 1960; Lancaster 2000), an invariant likelihood (Moreira 2009), an integrated likelihood (Lancaster 2002), functional differencing (Bonhomme 2012), or from some other reasoning to eliminate the incidental parameters, for example, differencing in linear dynamic models (e.g., Arellano and Bond 1991). This approach is usually model-specific and is “fixed-T”, i.e., it seeks consistent estimation when T is fixed (and usually small). However, point-identifying moment conditions for small T may not exist because point identification simply may fail; see Honoré and Tamer (2006) and Chamberlain (2010) for examples.

The other main approach is motivated by “large-T” arguments and seeks to reduce the large-T bias of the MLE or of the likelihood function itself or its score function (e.g., Hahn and Kuersteiner 2002; Alvarez and Arellano 2003; Hahn and Newey 2004; Arellano and Bonhomme 2009; Bonhomme and Manresa 2015; Dhaene and Jochmans 2015b; Arellano and Hahn 2016; Fernández-Val and Weidner 2016). This approach is less model-specific and may also be applied to models where point identification fails for small T.

The functional differencing method of Bonhomme (2012) provides an algebraic approach to systematically find valid moment conditions in panel models with incidental parameters—if such moment conditions exist. Related ideas are used in Honoré (1992), Hu (2002), Johnson (2004), Kitazawa (2013), Honoré and Weidner (2020), Honoré, Muris and Weidner (2021), and Davezies, D’Haultfoeuille and Mugnier (2022). In this paper, we extend the scope of functional differencing to models where point identification may fail. In such models, exact functional differencing (as in Bonhomme 2012) is not possible, but an approximate version thereof yields moment conditions that are free of incidental parameters and that are approximately valid in the sense that their solution yields a point close to the true common parameter value. Bonhomme’s method relies on the existence of (one or more) zero eigenvalues of a matrix of posterior predictive probabilities (or a posterior predictive density function) defined by the model. Our extension considers the case where all eigenvalues are positive and, therefore, point identification fails, but where some eigenvalues are very close to zero. This occurs as the number of support points of the outcome variable increases. Eigenvalues close to zero then lead to approximate moment conditions obtained as a bias correction of an initially chosen moment condition. The bias correction can be iterated, possibly infinitely many times. In point-identified models, the infinitely iterated bias correction is equivalent to functional differencing. Therefore, approximate functional differencing can be viewed as finite-T inference in point-identified models, and as a large-T iterative bias correction method in models that are not point-identified.

The construction of approximate moment conditions is our main focus. Once such moment conditions are found, estimation follows easily using the (generalized) method of moments, and the discussion of estimation is therefore deferred to later parts of the paper (from Sect. 6).

We illustrate approximate functional differencing in a probit binary choice model. The implementation, including the iteration, is straightforward, only requiring elementary matrix operations. Indeed, one of the contributions of this paper is to show how to iterate score-based bias correction methods for discrete choice panel data relatively efficiently.

After introducing the model setup in Sect. 2, we review the main ideas behind functional differencing in Sect. 3. In Sect. 4 we introduce our novel bias corrections and explain how they relate to functional differencing. Section 5 examines the eigenvalues of the matrix of posterior predictive probabilities in a numerical example. Section 6 briefly discusses estimation. Further numerical illustration of the methods and some Monte Carlo simulation results are presented in Sect. 7. Section 8 discusses some extensions, in particular, a generalization of the estimation method to average effects. Finally, we provide some concluding remarks in Sect. 9.

2 Setup

We observe outcomes $Y_i \in \mathcal{Y}$ and covariates $X_i \in \mathcal{X}$ for units $i=1,\ldots ,n$. We only consider finite outcome sets $\mathcal{Y}$ in this paper, but in principle all our results can be generalized to infinite sets $\mathcal{Y}$. There are also latent variables $A_i \in \mathcal{A}$, which are treated as nuisance parameters. We assume that $(Y_i, X_i, A_i)$, $i=1,\ldots ,n$, are independent and identical draws from a distribution with conditional outcome probabilities

$$\begin{aligned} \textrm{Pr}\left( Y_i= y_i \, \big | \, X_i=x_i, \, A_i = \alpha _i \right) = f\left( y_i \, \big | \, x_i, \alpha _i, \theta _0 \right) , \end{aligned}$$

(1)

where the function $f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right)$ is known (this function specifies “the model”), but the true parameter value $\theta _0 \in \Theta \subset \mathbb {R}^{d_\theta }$ is unknown. Our primary goal in this paper is inference on $\theta _0$.

Let $\pi _0(\alpha _i \,| \,x_i)$ be the true distribution of $A_i$ conditional on $X_i=x_i$. Then, the conditional distribution that can be identified from the data is

$$\begin{aligned} \textrm{Pr}\left( Y_i= y_i \, \big | \, X_i=x_i \right) = \int _\mathcal{A} \, f\left( y_i \, \big | \, x_i, \alpha _i, \theta _0 \right) \, \pi _0(\alpha _i \,| \,x_i) \, \textrm{d} \alpha _i . \end{aligned}$$

(2)

No restrictions are imposed on $\pi _0(\alpha _i \,| \,x_i)$ nor on the marginal distribution of $X_i$, that is, we have a semi-parametric model with unknown parametric component $\theta _0$ and unknown nonparametric component $\pi _0(\alpha _i \,| \,x_i)$.

The setup just described covers many nonlinear panel data models with fixed effects. There, we observe outcomes $Y_{it}$ and covariates $X_{it}$ for unit i over time periods $t=1,\ldots ,T$. For static panel models we then set $Y_i = (Y_{i1},\ldots ,Y_{iT})$ and $X_i = (X_{i1},\ldots ,X_{iT})$, and the model is typically specified as

$$\begin{aligned} f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right) = \prod _{t=1}^T f_*\left( y_{it} \, \big | \, x_{it}, \alpha _i, \theta \right) , \end{aligned}$$

where $f_*\left( y_{it} \, \big | \, x_{it}, \alpha _i, \theta _0 \right) = \textrm{Pr}\left( Y_{it}= y_{it} \, \big | \, X_{it}=x_{it}, \, A_i = \alpha _i \right) .$ Here, $f_*\left( y_{it} \, \big | \, x_{it},\right. \left. \alpha _i, \theta \right)$ often depends on $x_{it}$, $\alpha _i$, $\theta$ only through a single index $x_{it}' \theta + \alpha _i$, where $\theta$ is a regression coefficient vector of the same dimension as $x_{it}$, and $\alpha _i \in \mathbb {R}$ is an individual-specific fixed effect. Of course, $\theta$ may also contain additional parameters (e.g., the variance of the error term in a Tobit model).

For dynamic nonlinear panel models, we usually have to model the dynamics explicitly. For example, we may include a lagged dependent variable in the model. In that case, assuming that $Y_{it}$ at $t=0$ is observed, we have $Y_i = (Y_{i1},\ldots ,Y_{iT})$ and $X_i = (Y_{i0},X_{i1},\ldots ,X_{iT})$, and the model is usually specified as

$$\begin{aligned} f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right) = \prod _{t=1}^T f_*\left( y_{it} \, \big | \,y_{i,t-1}, x_{it}, \alpha _i, \theta \right) , \end{aligned}$$

where $f_*\left( y_{it} \big | y_{i,t-1}, x_{it}, \alpha _i, \theta \right) = \textrm{Pr}\left( Y_{it}= y_{it} \big | Y_{i,t-1}= y_{i,t-1}, \, X_{it}=x_{it}, \, A_i = \alpha _i \right)$. Here, the initial observation $Y_{i0}$ is included in the conditioning variable $X_i$. In this way, the setup in Eqs. (1) and (2) also covers dynamic panel data models.

The setup may also be relevant for applications outside of standard panel data, e.g., pseudo-panels, network models, or games. But one typically needs $Y_i$ to be a vector of more than one outcome to learn anything about $\theta _0$ since, in most models, the value of $\alpha _i$ alone can fully fit any possible outcome value if there is only a single outcome per unit (i.e., if the sample is purely cross-sectional).

The main insights of our paper are therefore applicable more broadly, but our focus will be on panel data. In particular, the following static binary choice panel data model will be our running example throughout the paper.

Example 1A

(Static binary choice panel data model) Consider a static panel data model with $Y_i = (Y_{i1},\ldots ,Y_{iT})$ and $X_i = (X_{i1},\ldots ,X_{iT})$ where the outcomes $Y_{it} \in \{0,1\}$ are generated by

$$\begin{aligned} Y_{it} = \mathbbm {1}(X'_{it} \, \theta _0 + A_i \ge U_{it}) \end{aligned}$$

and the errors $U_{it}$ are independent of $X_i$ and $A_i \in \mathbb {R}$, and are i.i.d. across i and t with cdf F(u). This implies

$$\begin{aligned} f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right) = \prod _{t=1}^T \, [1-F(x'_{it} \,\theta + \alpha _i)]^{1-y_{it}} \, [F(x'_{it} \, \theta + \alpha _i)]^{y_{it}}. \end{aligned}$$

For the probit model, we have $F(u)=\Phi (u)$, where $\Phi$ is the standard normal cdf, and for the logistic model we have $F(u)= (1+e^{-u})^{-1}$. To make the example even more specific, we consider a single binary covariate $X_{it} \in \{0,1\}$ such that for all $i=1,\ldots ,n$ we have

$$\begin{aligned} X_{it} = \mathbbm {1}( t > T_0 ), \end{aligned}$$

for some $T_0 \in \{1,\ldots ,T-1\}$, that is, $X_{it}$ is equal to zero for the initial $T_0$ time periods, and is equal to one for the remaining $T_1 = T-T_0$ time periods. Here $T_0$, and therefore $X_i$, is non-random and constant across i, so we can simply write $f\left( y_i \, \big | \, \alpha _i, \theta \right)$ instead of $f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right)$. The parameter of interest, $\theta _0 \in \mathbb {R}$, is one-dimensional.

Example 1B

(Example 1A reframed) Consider Example 1A, but denote the binary outcomes now as $Y_{it}^* \in \{0,1\}$ and define the outcome $Y_i$ for unit i as the pair

$$\begin{aligned} Y_i = \left( Y_{i,0} , Y_{i,1} \right) := \left( \sum _{t=1}^{T_0} Y^*_{it} , \, \sum _{t=T_0+1}^{T} Y^*_{it} \right) \in \{ 0 ,\ldots ,T_0 \} \times \{0, \ldots ,T_1\} = \mathcal{Y}. \end{aligned}$$

(3)

Here, $Y_{i,0} = \sum _{t=1}^T Y^*_{it} \, (1-X_{it})$ is the number of outcomes for unit i for which $Y_{it}^*=1$ within those time periods that have $X_{it}=0$, while $Y_{i,1} = \sum _{t=1}^T Y^*_{it} \, X_{it}$ is the number of outcomes with $Y_{it}^*=1$ for the time periods with $X_{it}=1$. This implies that

$$\begin{aligned} f\left( y_i \, \big | \, \alpha _i, \theta \right){} & {} = { T_0 \atopwithdelims ()y_{i,0} } [1-F(\alpha _i)]^{T_0 - y_{i,0} } \, [F( \alpha _i)]^{y_{i,0} } { T_1 \atopwithdelims ()y_{i,1}} \\{} & {} \quad \times [1-F(\theta +\alpha _i)]^{T_1 - y_{i,1} } \, [F(\theta + \alpha _i)]^{y_{i,1} }, \end{aligned}$$

where we drop $x_i$ from $f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right)$ since it is non-random and constant across i. The parameter of interest, $\theta _0 \in \mathbb {R}$, is unchanged.

From the perspective of parameter estimation, Example 1B is completely equivalent to Example 1A, because $Y_i$ in Example 1B is a minimal sufficient statistic for the parameters $(\theta _0,\alpha _i)$ in Example 1A. Nevertheless, the outcome space in Example 1A is larger ($|\mathcal{Y}|=2^T$) than the outcome space in Example 1B ($|\mathcal{Y}|=(T_0+1)(T_1+1)$), and this will make a difference in our discussion of moment conditions in these two examples below.

3 Main idea behind functional differencing

We now explain the main idea behind the functional differencing method of Bonhomme (2012). Our presentation is similar to that in Honoré and Weidner (2020). However, our goal here is much closer to that in Bonhomme’s original paper because we want to describe a general estimation method, one that is applicable to a very large class of models, as opposed to obtaining an analytical expression for moment conditions in specific models.

3.1 Exact moment conditions

Consider the model described by (1) and (2), where our goal is to estimate $\theta _0$. Functional differencing (Bonhomme 2012) aims to find moment functions ${\mathfrak m}(y_i,x_i,\theta ) \in \mathbb {R}^{d_{\mathfrak m}}$ such that the model implies, for all $x_i$ and $\alpha _i$, that

$$\begin{aligned} \mathbb {E}\left[ {\mathfrak m}(Y_i , X_i, \theta _0) \, \big | \, X_i=x_i, \, A_i = \alpha _i \right] = 0 \end{aligned}$$

(4)

or, equivalently,

$$\begin{aligned} \sum _{y \in \mathcal{Y}} \, {\mathfrak m}(y , x_i, \theta ) \, f\left( y \, \big | \, x_i, \alpha _i, \theta \right) = 0, \end{aligned}$$

since we want (4) to hold for all possible $\theta _0 \in \Theta$. Verifying that ${\mathfrak m}(y_i,x_i,\theta )$ satisfies this conditional moment condition only requires knowledge of the model $f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right)$, not of the observed data. Note that ${\mathfrak m}(y_i,x_i,\theta )$ does not depend on $\alpha _i$, but nevertheless should have zero mean conditional on any realization $A_i = \alpha _i$. This is a strong requirement, and we will get back to this below.

Once we have found such valid moment functions ${\mathfrak m}(y_i,x_i,\theta )$, we can choose an arbitrary (matrix-valued) function $g(x_i,\theta ) \in \mathbb {R}^{d_m \times d_{\mathfrak m}}$, and define

$$\begin{aligned} m(y_i,x_i,\theta ):= g(x_i,\theta ) \, {\mathfrak m}(y_i, x_i, \theta ), \end{aligned}$$

which is a vector of dimension $d_m$. By the law of iterated expectations, we then obtain, under weak regularity conditions, the unconditional moment condition

$$\begin{aligned} \mathbb {E}\left[ m(Y_i,X_i,\theta _0) \right] = 0, \end{aligned}$$

(5)

which we can use to estimate $\theta _0$ by the generalized method of moments (GMM, Hansen 1982). The nuisance parameters $\alpha _i$ do not feature in the GMM estimation at all, that is, functional differencing provides a solution to the incidental parameter problem (Neyman and Scott 1948).

Of course, the key condition for consistent GMM estimation is that $\mathbb {E}\left[ m(Y_i,X_i,\theta ) \right] \ne 0$ for any $\theta \ne \theta _0$. This identification condition is violated if ${\mathfrak m}(y_i, x_i, \theta )$ does not depend on $\theta$ (a special case of which is ${\mathfrak m}(y_i, x_i, \theta ) = 0$, which is a trivial solution to (4). Hence the moment functions must depend on $\theta$ to be informative about $\theta _0$.

3.1.1 Uninformative moment functions in Example 1A

To give an example of a moment function that is uninformative about $\theta _0$, consider Example 1A. Let t and s be two time periods where $X_{it}=X_{is}$. Let $Y_{i,-(t,s)} \in \{0,1\}^{T-2}$ be the outcome vector $Y_{i}$ from which the outcomes $Y_{it}$ and $Y_{is}$ are dropped. Then, since $X_{it}=X_{is}$, the outcomes $Y_{it}$ and $Y_{is}$ are exchangeable and therefore

$$\begin{aligned} \mathbb {E}\left( Y_{it} \, \big | \, Y_{i,-(t,s)} \right) = \mathbb {E}\left( Y_{is} \, \big | \, Y_{i,-(t,s)} \right) . \end{aligned}$$

This implies that for any function $g: \{0,1\}^{T-2} \rightarrow \mathbb {R}$ the moment function

$$\begin{aligned} {\mathfrak m}(y_i,x_i,\theta ) := \left( y_{it} - y_{is} \right) g(y_{i,-(t,s)}) \end{aligned}$$

(6)

satisfies (4). This moment function does not depend on $\theta$ and is therefore not useful for parameter estimation. (It is useful for model specification testing, but we will not discuss this.)

Furthermore, one can show that every moment function ${\mathfrak m}(y_i,x_i,\theta )$ that satisfies (4) in Example 1A is equal to a corresponding valid moment function in Example 1B plus a linear combination of moment functions of the form (6).¹ Thus, from the perspective of constructing valid moment functions that are informative about $\theta _0$, without loss of generality we can focus on Example 1B instead of Example 1A. Example 1A is useful because it is a completely standard panel model and it gives a simple example of valid moment functions that do not depend on $\theta$. From here onward, however, we will always use Example 1B as our running example.

3.1.2 Informative moment functions in Example 1B for logistic errors

Consider Example 1B with logistic error distribution, $F(u)= (1+e^{-u})^{-1}$. Then, $Y_{i,0} + Y_{i,1}$ is a sufficient statistic for $A_i$, so the distribution of $Y_i$ conditional on $Y_{i,0} + Y_{i,1}$ does not depend on $A_i$. It is well known that this implies that the corresponding conditional MLE of $\theta _0$ is consistent as $n\rightarrow \infty$, for any fixed $T\ge 2$; see, e.g., Rasch (1960), Andersen (1970), and Chamberlain (1980).

Here, instead of considering conditional maximum likelihood, we focus purely on the existence of moment conditions. Let $\bar{y} = (\bar{y}_0,\bar{y}_1) \in \{ 0,\ldots ,T_0 \} \times \{0, \ldots ,T_1\}$ and $\tilde{y} = (\tilde{y}_0,\tilde{y}_1) \in \{ 0,\ldots ,T_0 \} \times \{0, \ldots ,T_1\}$ be two possible realizations of $Y_i$ such that $\bar{y}_0+\bar{y}_1 = \tilde{y}_0 + \tilde{y}_1$ and $\bar{y} \ne \tilde{y}$. Since $Y_{i,0} + Y_{i,1}$ is a sufficient statistic for $A_i$, it must be the case that the ratio

$$\begin{aligned} r(\theta ):= \frac{ f\left( \bar{y} \, \big | \, \alpha _i, \theta \right) }{ f\left( \tilde{y} \, \big | \, \alpha _i, \theta \right) } \end{aligned}$$

does not depend on $\alpha _i$. This implies that

$$\begin{aligned} {\mathfrak m}(y_i , \theta ) := \mathbbm {1}\left\{ y_i = \bar{y} \right\} - r(\theta ) \; \mathbbm {1}\left\{ y_i = \tilde{y} \right\} \end{aligned}$$

(7)

satisfies $\mathbb {E}\left[ {\mathfrak m}(Y_i, \theta _0) \, \big | \, A_i=\alpha _i \right] = 0$. A short calculation gives

$$\begin{aligned} r(\theta ) = { T_0 \atopwithdelims ()\bar{y}_{0} } { T_1 \atopwithdelims ()\bar{y}_{1} } { T_0 \atopwithdelims ()\tilde{y}_{0} }^{-1} { T_1 \atopwithdelims ()\tilde{y}_{1} }^{-1} \exp [(\bar{y}_1 - \tilde{y}_1) \theta ] . \end{aligned}$$

Since we assume $\bar{y} \ne \tilde{y}$, the moment function ${\mathfrak m}(y_i, \theta )$ indeed depends on $\theta$. Furthermore, ${\mathfrak m}(y_i, \theta )$ is strictly monotone in $\theta$ when $y_i=\tilde{y}$ and constant in $\theta$ otherwise, and all outcomes are realized with positive probability. Hence $\mathbb {E}\left[ {\mathfrak m}(Y_i,\theta ) \right]$ is strictly monotone in $\theta$ and the condition $\mathbb {E}\left[ {\mathfrak m}(Y_i,\theta _0) \right] = 0$ uniquely identifies $\theta _0$.

The observation that the existence of a sufficient statistic for the nuisance parameter $A_i$ allows for identification and estimation of $\theta _0$ is quite old (e.g., Rasch 1960). However, the reason that the functional differencing method is truly powerful is that moment functions satisfying (4) and identifying $\theta _0$ may exist even in models where no sufficient statistic for $A_i$ is available. Examples of this are given by Honoré (1992), Hu (2002), Johnson (2004), Kitazawa (2013), Honoré and Weidner (2020), Honoré, Muris and Weidner (2021), and Davezies, D’Haultfoeuille and Mugnier (2022). Bonhomme (2012) provides a computational method for obtaining moment functions ${\mathfrak m}(y_i,x_i,\theta )$ such that (4) holds in a large class of models, while Honoré and Weidner (2020) discuss how to obtain explicit algebraic formulas for moment conditions in specific models. Dobronyi, Gu and Kim (2021) show that additional moment inequalities may exist that contain identifying information on $\theta _0$ that is not contained in the moment equalities.

Our example of a moment function in (7) is convenient and easy to understand, but it is not really representative of the potential complexity of more general moment functions. The papers cited in the previous paragraph give a better view of the true capability of the functional differencing method in more challenging settings.

3.2 Approximate moment conditions

Functional differencing is a very powerful and useful method. Nevertheless, there are many models to which it is not applicable. The reason is that the condition in Eq. (4) is actually quite strong. It requires us to find a function ${\mathfrak m}(Y_i, X_i, \theta )$ that does not depend on $A_i$ at all, but that is supposed to have a conditional mean of zero for any possible realization of $A_i$. In most standard panel data models $A_i$ takes values in $\mathbb {R}$ ($A_i$ can also be a vector), implying that (4) imposes an infinite number of linear restrictions.

It is therefore perhaps unsurprising that there are many panel data models for which (4) has no non-trivial solution at all. In Example 1B we have shown the existence of valid moment functions for the logit model, but it turns out that no valid moment function exists for the probit model when $\theta _0 \ne 0$ (we have verified this non-existence numerically for many values of T and $T_0$).

Instead of trying to find moment functions satisfying (4), and hence (5), exactly, we argue that it can also be fruitful to search for moment functions that satisfy these conditions only approximately, i.e.,

$$\begin{aligned} \mathbb {E}\left[ m(Y_i,X_i,\theta _0) \right] \approx 0 . \end{aligned}$$

(8)

For a given model $f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right)$ we might not be able to find an exact solution to (5), but we might be able to find a very good approximate solution.

Examples of approximate moment conditions are provided by the “large-T” panel data literature, which considers asymptotic sequences where also $T \rightarrow \infty$ (jointly with $n \rightarrow \infty$). To illustrate the insights of this literature, let $\widehat{\alpha }_i(\theta )$ be the MLE of $\alpha _i$ obtained from maximizing $f\left( Y_i \, \big | \, X_i, \alpha _i, \theta \right)$ over $\alpha _i\in \mathcal {A}$, and let $\psi (y_i,x_i,\alpha _i,\theta )$ be a moment function that satisfies $\mathbb {E}[\psi (Y_i,X_i,A_i,\theta _0)]=0$ in model (1), e.g., $\psi (y_i,x_i,\alpha _i,\theta ) = \nabla _{\theta } \left[ \frac{1}{T} \log f\left( y_i \, \big | \, x_i, \alpha _i, \theta \right) \right]$. Then, under standard regularity conditions, $\widehat{\alpha }_i(\theta _0)$ is consistent for $A_i$ as $T \rightarrow \infty$, and a useful approximate moment function is therefore given by $m(y_i,x_i,\theta ) = \psi (y_i,x_i,\widehat{\alpha }_i(\theta ),\theta )$. In this example, the vague approximate statement in (8) can be made precise, namely one can show that, as $T \rightarrow \infty$,

$$\begin{aligned} \mathbb {E}\left[ m(Y_i,X_i,\theta _0) \right] = O(T^{-1}) , \end{aligned}$$

(9)

implying that the estimator of $\theta _0$ obtained from this approximate moment condition also has a bias of order $T^{-1}$. It is possible to correct this bias and obtain moment functions where the right hand side of (9) is of order $T^{-2}$ or smaller, implying an even smaller bias for estimates of $\theta _0$ when T is sufficiently large; see, e.g., Hahn and Newey (2004), Arellano and Hahn (2007, 2016), Arellano and Bonhomme (2009), and Dhaene and Jochmans (2015b). In this paper, we aim for even higher-order bias correction, where the remaining bias is only of order $T^{-q}$, for some integer $q>0$, because we expect better small-T estimation properties from such higher-order corrections, and it allows us to connect the bias correction results with the functional differencing method. However, by correcting the bias in this way, one might very well increase the variance of the resulting estimator for $\theta _0$, as we will see in our Monte Carlo simulations in Sect. 7. The question of how to optimally trade off the bias vs. the variance (using, e.g., a mean squared error criterion function, as in Bonhomme and Weidner 2022) is interesting and could lead to an optimal choice of the bias correction order q, but we will not formalize this in the current paper.

4 Approximate functional differencing

In this section, we answer the following questions: In a model where exactly valid moment functions as in (4) do not exist, is it still possible to construct useful moment functions $m(y_i,x_i,\theta )$ that are approximately valid as in (8)? And if yes, how can we construct such moment functions in a principled way?

4.1 Notation and preliminaries

Our discussion in this section is at the “population level”, that is, for one representative unit i. In the following, we therefore drop the index i throughout. For example, instead of $Y_i$, $X_i$, $A_i$ we simply write Y, X, A.

4.1.1 Prior distribution of the fixed effects

Let $\pi _\textrm{prior}(\alpha \,|\,x)$ be a chosen prior distribution for A, conditional on $X=x$. The prior should integrate to one, that is, $\int _\mathcal{A} \, \pi _\textrm{prior}(\alpha \,| \, x) \, \textrm{d} \alpha = 1$, for all $x \in \mathcal{X}$, but we do not require $\pi _\textrm{prior}$ to be identical to $\pi _0$. We require non-zero prior probability for all points in the support of A, i.e.,

$$\begin{aligned} \pi _\textrm{prior}\left( \alpha \, \,| \,x \right) > 0 , \qquad \text {for all }\alpha \in \mathcal{A} \text { and } x \in \mathcal{X}. \end{aligned}$$

(10)

The prior does not need to depend on x; we may choose $\pi _\textrm{prior}\left( \alpha \, \,| \,x \right) = \pi _\textrm{prior}(\alpha )$, which may be easier to specify in practice, but we allow for general priors $\pi _\textrm{prior}\left( \alpha \, \,| \,x \right)$ in the following.

4.1.2 Posterior distribution of the fixed effects

Given the chosen prior $\pi _\textrm{prior}$, the posterior distribution of A, conditional on $Y=y$ and $X=x$, for given $\theta$, is

$$\begin{aligned} \pi _\textrm{post}(\alpha \,|\, y,x,\theta ) = \frac{ f(y \, | \,x,\alpha ,\theta ) \, \pi _\textrm{prior}(\alpha \,|\,x)}{p_\textrm{prior}(y \, | \, x,\theta )} , \end{aligned}$$

(11)

where $p_\textrm{prior}(y \, |\, x,\theta ) = \int _\mathcal{A} f( y \, | \,x,\theta , \alpha ) \, \pi _\textrm{prior}( \alpha \,|\,x) \, \textrm{d} \alpha$ is the prior predictive probability of outcome y.

4.1.3 Score function

Let $s \,: \, \mathcal{Y} \times \mathcal{X} \times \theta \rightarrow \mathbb {R}^{d_s}$ be some function, which we will call the “score function”. In our numerical illustrations in Sect. 7 we choose the integrated score

$$\begin{aligned} s(y,x,\theta )&= \nabla _\theta \left[ \log \int _\mathcal{A} f(y \,|\, x, \alpha ,\theta ) \pi _\textrm{prior}(\alpha \,|\,x) \, \textrm{d} \alpha \right] \nonumber \\&= \int _\mathcal{A} \left[ \nabla _\theta \, \log f(y \,|\, x, \alpha ,\theta ) \right] \pi _\textrm{post}(\alpha \,|\, y,x,\theta ) \, \textrm{d} \alpha , \end{aligned}$$

(12)

where $d_s=d_\theta$. However, for our construction of moment functions in the following subsection, which is based on a chosen score function, we can actually choose almost any function $s(y,x,\theta )$, as long as it is differentiable in $\theta$ and not identically zero. For example, the profile score $s(y,x,\theta ) = \nabla _\theta \left[ \max _{\alpha \in \mathcal {A}} \log f(y | x, \alpha ,\theta ) \right]$ would be an equally natural choice.

Whatever the choice of $s(y,x,\theta )$, we now rewrite it using matrix notation. Let $n_\mathcal{Y} = | \mathcal{Y}|$ be the number of possible outcomes, and label the elements of the outcome set as $y_{(k)}$, $k=1,\ldots ,n_\mathcal{Y}$, so that $\mathcal{Y}=\left\{ y_{(1)},\ldots ,y_{(n_\mathcal{Y})} \right\}$. For $y \in \mathcal{Y}$, let $\delta (y) = (\delta _1(y),\ldots ,\delta _{n_\mathcal{Y}}(y))'$ be the $n_\mathcal{Y}$-vector with elements $\delta _k(y) = \mathbbm {1}(y = y_{(k)})$, $k=1,\ldots ,n_\mathcal{Y}$, where $\mathbbm {1}(\cdot )$ is the indicator function. Recall that $s(y,x,\theta )$ is a $d_s$-vector. Let $S(x,\theta )$ be the corresponding $d_s \times n_\mathcal{Y}$ matrix with columns $s(y_{(k)},x,\theta )$, $k=1,\ldots ,n_\mathcal{Y}$. Now we can write $s(y,x,\theta )$ as

$$\begin{aligned} s(y,x,\theta ) = S(x,\theta ) \, \delta (y) , \qquad \text {for all }y\in \mathcal {Y} . \end{aligned}$$

(13)

4.1.4 Posterior predictive probability matrix

Given $x \in \mathcal{X}$ and $\theta \in \Theta$, after observing some $y \in \mathcal{Y}$, the posterior predictive probability of observing any “future”$\widetilde{y}\in \mathcal{Y}$ is

$$\begin{aligned} Q( \widetilde{y} \, | \, y,x,\theta ) = \int _\mathcal{A} f \left( \widetilde{y} \, \big | \, x,\alpha ,\theta \right) \pi _\textrm{post} \left( \alpha \, \big | \, y,x,\theta \right) \textrm{d} \alpha . \end{aligned}$$

(14)

Let $Q(x,\theta )$ be the $n_\mathcal{Y} \times n_\mathcal{Y}$ matrix with elements $Q_{k,\ell }(x,\theta ) = Q(y_{(k)} \, | \, y_{(\ell )},x,\theta )$. The following lemma states some properties of the matrix $Q(x,\theta )$ that will be useful later.

Lemma 1

Let $x \in \mathcal{X}$ and $\theta \in \Theta$. Assume that $p_\textrm{prior}(y \, |\, x,\theta ) > 0$ for all $y \in \mathcal{Y}$. Then $Q(x,\theta )$ is diagonalizable and all its eigenvalues are real numbers in the interval [0, 1].

The proof of the lemma is given in the “Appendix”.

4.2 Bias-corrected score functions

We consider the chosen score function $s(y,x,\theta )$ as our first candidate for a moment function $m(y,x,\theta )$ to achieve (8). However, $\mathbb {E} [s(Y,X,\theta _0)]$ need neither be zero nor close to zero. (As discussed above, there are choices of $s(y,x,\theta )$ such that $\mathbb {E} [s(Y,X,\theta _0)]$ is close to zero for large T, but even for those choices $\mathbb {E} [s(Y,X,\theta _0)]$ need not be close to zero for small T.)

Therefore, we aim to “bias-correct” the score by defining an improved score

$$\begin{aligned} s^{(1)}(y,x,\theta ):= s(y,x,\theta ) - b(y,x,\theta ) , \end{aligned}$$

for some correction function $b(y,x,\theta )$. The goal is to choose $b(y,x,\theta )$ such that the elements of $\mathbb {E} [s^{(1)}(Y,X,\theta _0)]$ are smaller than those of $\mathbb {E} [s(Y,X,\theta _0)]$. According to the model we have

$$\begin{aligned} \mathbb {E}\left[ s(Y,X,\theta _0) \, \big | \, X=x, \, A=\alpha \right]&= \sum _{y \in \mathcal{Y}} s(y,x,\theta _0) \, f\left( y \, \big | \, x, \alpha , \theta _0 \right) , \nonumber \\ \mathbb {E}\left[ s(Y,X,\theta _0) \, \big | \, X=x \right]&= \sum _{y \in \mathcal{Y}} s(y,x,\theta _0) \, \int _\mathcal{A} \, f\left( y \, \big | \, x, \alpha , \theta _0 \right) \, \pi _0(\alpha \,| \,x) \, \textrm{d}\alpha . \end{aligned}$$

(15)

We would achieve exact bias correction (i.e., $\mathbb {E} [s^{(1)}(Y,X,\theta _0)] =0$) if we could choose $b(y,x,\theta )$ (or its conditional expectation) equal to $\mathbb {E}[ s(Y,X,\theta _0) \, \big | \, X=x, \, A=\alpha ]$ or equal to $\mathbb {E}[ s(Y,X,\theta _0) \, \big | \, X=x ]$. The first option is infeasible because A is unobserved. The second option is infeasible because $\pi _0(\alpha \,| \,x)$ is unknown.

However, even though A is unobserved, the posterior distribution $\pi _\textrm{post}(\alpha \,|\, y,x,\theta )$ should contain some useful information about A. Inspired by (15) we suggest choosing

$$\begin{aligned} b(y,x,\theta ) = \sum _{\widetilde{y} \in \mathcal{Y}} s(\widetilde{y},x,\theta ) \, \int _\mathcal{A} \, f\left( \widetilde{y} \, \big | \, x, \alpha , \theta \right) \, \pi _\textrm{post}(\alpha \, \big | \, y,x,\theta ) \, \textrm{d} \alpha \,, \end{aligned}$$

where we have replaced $\pi _0(\alpha \,| \,x)$ by $\pi _\textrm{post}(\alpha \,|\, y,x,\theta )$. This gives the bias-corrected score

$$\begin{aligned} s^{(1)}(y,x,\theta )&:= s(y,x,\theta ) - \sum _{\widetilde{y} \in \mathcal{Y}} s(\widetilde{y},x,\theta ) \, \int _\mathcal{A} \, f\left( \widetilde{y} \, \big | \, x, \alpha , \theta \right) \, \pi _\textrm{post}(\alpha \, \big | \, y,x,\theta ) \, \textrm{d} \alpha \nonumber \\&= s(y,x,\theta ) - \sum _{\widetilde{y} \in \mathcal{Y}} s(\widetilde{y},x,\theta ) \, Q(\widetilde{y} \, | \, y,x,\theta ) \nonumber \\&= S(x,\theta ) \, \left[ \mathbbm {I}_{n_\mathcal{Y}} - Q(x,\theta ) \right] \, \delta (y) , \end{aligned}$$

(16)

where $\mathbbm {I}_{n_\mathcal{Y}}$ is the $n_\mathcal{Y}\times n_\mathcal{Y}$ identity matrix. Now, if the expected posterior distribution $\mathbb {E}[ \pi _\textrm{post}(\alpha \, \big | \, Y,X, \theta _0) \, \big | \, X=x ]$ is a good approximation to $\pi _0(\alpha \,| \,x)$, then we expect that $\mathbb {E} [s^{(1)}(Y,X,\theta _0)]$ is indeed smaller than $\mathbb {E} [s(Y,X,\theta _0)]$, that is, $s^{(1)}(y,x,\theta )$ should be a better choice than $s(y,x,\theta )$ as a moment function $m(y,x,\theta )$ satisfying (8). Note also that in the very special case where the prior equals the true distribution of A (i.e., $\pi _\textrm{prior} = \pi _0$), $\mathbb {E}[ \pi _\textrm{post}(\alpha \, \big | \, Y,X,\theta _0) \, \big | \, X=x ]= \pi _0(\alpha \,| \,x)$ and hence $s^{(1)}(Y,X,\theta _0)$ has exactly zero mean regardless of the choice of initial score function.

Of course, generically we still expect that $\mathbb {E} [s^{(1)}(Y,X,\theta _0)] \ne 0$. It is, therefore, natural to iterate the above procedure, that is, to apply the same bias-correction method that we applied to $s(y,x,\theta )$ also to $s^{(1)}(y,x,\theta )$, which gives $s^{(2)}(y,x,\theta )$, and to continue iterating this procedure. Since the bias-correction method applied to $s(y,x,\theta ) = S(x,\theta ) \, \delta (y)$ gives (16), it is easy to see that after $q \in \{1,2,\ldots \}$ iterations of the same bias-correction procedure we obtain

$$\begin{aligned} s^{(q)}(y,x,\theta )&:= S(x,\theta ) \left[ \mathbbm {I}_{n_\mathcal{Y}} - Q(x,\theta ) \right] ^q \, \delta (y) . \end{aligned}$$

(17)

The bias-corrected functions $s^{(q)}(y,x,\theta )$ are the main choices of moment function $m(y,x,\theta )$ that we consider in this paper.

To our knowledge, the bias-corrected scores $s^{(q)}(y,x,\theta )$ have not previously been discussed in the literature. However, as will be explained in Sect. 8.1, these bias-corrected scores are closely related to existing bias-correction methods. In particular, if in (16) we replace the posterior distribution $\pi _\textrm{post}(\alpha \, \big | \, y,x,\theta )$ with a point-mass distribution at the MLE of A for fixed $\theta$, then the profile-score adjustments of Dhaene and Jochmans (2015a) are obtained. In analogy to such existing methods, we make the following conjecture, which is supported by our numerical results in Sect. 7 below for the model in Examples 1A and 1B, and which we presume to hold more generally under appropriate regularity conditions.

Conjecture 1

If we choose the original score function $s(y,x,\theta )$ to be the integrated or profile score, then both $\mathbb {E}\left[ s^{(q)}(Y,X,\theta _0) \right]$ and $\theta _* - \theta _0$ are at most of order $T^{-q-1}$, as $T\rightarrow \infty$ while q is fixed.

From the perspective of the large-T panel literature, we have simply provided another way to achieve and iterate large-T bias correction. What is truly novel, however, is that in the limit $q \rightarrow \infty$, our correction can be directly related to the functional differencing method of Bonhomme (2012), which delivers exact (finite-T) inference results in models to which it is applicable. Our procedure, therefore, interpolates between large-T bias correction and exact finite-T inference.

Remark 1

If the initial score function $s(y,x,\theta )$ is unbiased, that is, if it satisfies the exact moment condition (4) or, equivalently, (5), then the bias correction step (16) does not change the score function at all. More generally, if at any point in the iteration procedure (17) we obtain an unbiased score function, i.e., one for which $\sum _{y \in \mathcal{Y}} \, s^{(q)}(y, x, \theta ) \, f\left( y \, \big | \, x, \alpha , \theta \right) = 0$ for some q, then we have $s^{(r)}(y,x,\theta ) = s^{(q)}(y,x,\theta )$ for all further iterations $r \ge q$. Hence, unbiased score functions correspond to fixed points in our iteration procedure.

4.3 Relation to functional differencing

It turns out that exact functional differencing (Bonhomme 2012) corresponds to choosing

$$\begin{aligned} s_{\infty }(y,x,\theta ):= \lim _{q \rightarrow \infty } s^{(q)}(y,x,\theta ) \end{aligned}$$

as moment functions for estimating $\theta _0$, and the lemma below formalizes this relationship.

Before presenting the lemma, it is useful to rewrite the bias-corrected score function in (17) in terms of the spectral decomposition of $Q(x,\theta )$. Let $\lambda _1(x,\theta ) \ge \ldots \ge \lambda _{n_\mathcal{Y}}(x,\theta )$ be the eigenvalues of $Q(x,\theta )$ sorted in descending order, and let $U(x,\theta )$ be the $n_\mathcal{Y} \times n_\mathcal{Y}$ matrix whose columns are the corresponding right-eigenvectors of $Q(x,\theta )$. Lemma 1 guarantees that $\lambda _k(x,\theta ) \in [0,1]$, for all $k=1,\ldots ,n_\mathcal{Y}$, and that $Q(x,\theta )$ can be diagonalized, that is,

$$\begin{aligned} Q(x,\theta )&= U(x,\theta ) \; \textrm{diag}[ \lambda _k(x,\theta ) ]_{k=1,\ldots ,n_\mathcal{Y}} \; U^{-1}(x,\theta ) . \end{aligned}$$

Now let $h:[0,1] \rightarrow \mathbb {R}$ be a stem function and let $h(\cdot )$ be the associated primary matrix function (Horn and Johnson 1994), so that

$$\begin{aligned} h[ Q(x,\theta ) ]&= U(x,\theta ) \; \textrm{diag}\left\{ h[ \lambda _k(x,\theta ) ] \right\} _{k=1,\ldots ,n_\mathcal{Y}} \; U^{-1}(x,\theta ) . \end{aligned}$$

(18)

That is, applying $h(\cdot )$ to the matrix $Q(x,\theta )$ simply means applying the stem function separately to each eigenvalue of $Q(x,\theta )$ while leaving the eigenvectors unchanged. Every stem function h defines a moment function

$$\begin{aligned} s_h(y,x,\theta )&:= S(x,\theta ) \; h[ Q(x,\theta ) ] \; \delta (y) , \end{aligned}$$

(19)

hence generalizing (17). In particular, the stem function $h_q(\lambda ):= (1-\lambda )^q$ gives the moment function $s^{(q)}(y,x,\theta ) = s_{h_q}(y,x,\theta )$ in (17). In the limit $q \rightarrow \infty$ we obtain $\lim _{q \rightarrow \infty } \, h_q(\lambda ) = \mathbbm {1}\{ \lambda = 0 \}$, for $\lambda \in [0,1]$, and the limiting bias-corrected score function can therefore be written as

$$\begin{aligned} s_{\infty }(y,x,\theta )&= S(x,\theta ) \, h_\infty [ Q(x,\theta ) ] \, \delta (y) ,&h_\infty (\lambda )&:= \mathbbm {1}\{ \lambda = 0 \} . \end{aligned}$$

(20)

Thus, $s_{\infty }(y,x,\theta )$ is obtained by applying the projection $h_\infty [ Q(x,\theta ) ]$ to the original score function $s(y,x,\theta )$. The projection matrix $h_\infty [ Q(x,\theta ) ]$ is obtained according to (18) by giving weight only to eigenvectors of $Q(x,\theta )$ accociated with zero eigenvalues.

Lemma 2

Let $x \in \mathcal{X}$. Suppose that (1) and (10) hold, that $p_\textrm{prior}(y \, |\, x,\theta _0) > 0$ for all $y \in \mathcal{Y}$, and that $f\left( y \, \big | \, x, \alpha , \theta _0 \right)$ is continuous in $\alpha \in \mathcal{A}$. Then

• (i) we have

  $$\begin{aligned}\mathbb {E} \left[ s_{\infty }(Y,X,\theta _0) \, \big | \, X=x, \, A = \alpha \right] = 0 \,, \qquad \text {for all } \alpha \in \mathcal{A} ;\end{aligned}$$

• (ii) the matrix $Q(x,\theta _0)$ has a zero eigenvalue if and only if there exists a non-zero moment function ${\mathfrak m}(y, x, \theta _0) \in \mathbb {R}$ that satisfies

  $$\begin{aligned} \mathbb {E} \left[ {\mathfrak m}(Y, X, \theta _0) \, \big | \, X=x, \, A = \alpha \right] = 0 \,, \qquad \text {for all } \alpha \in \mathcal{A} ; \end{aligned}$$

• (iii) for every moment function ${\mathfrak m}(y, x, \theta _0) \in \mathbb {R}$ that satisfies the condition in part (ii), there exists a function $s(y, x, \theta _0) \in \mathbb {R}$ such that

  $$\begin{aligned} {\mathfrak m}(y, x, \theta _0) = s_{\infty }(y,x,\theta _0) \,,\qquad \text {for all } y \in \mathcal{Y} . \end{aligned}$$

The proof of the lemma is given in the “Appendix”. Note that the true parameter value, $\theta _0$, only takes a special role in Lemma 2 because the expectation $\mathbb {E} \left( \cdot \, | \, X=x, \, A = \alpha \right)$ is evaluated using $f(y | x, \theta _0,\alpha )$, according to (1). If we had written these conditional expectations as explicit sums over $f(y | x, \theta _0,\alpha )$, then we could have replaced $\theta _0$ in the lemma by an arbitrary value $\theta \in \Theta$; that is, there is nothing special about the parameter value $\theta _0$ that generates the data.

Part (i) of the lemma states that $s_{\infty }(y,x,\theta )$ is an exactly valid moment function in the sense of (4). If $Q(x,\theta )$ does not have any zero eigenvalues, then this part of the lemma is a trivial result, because then we simply have $s_{\infty }(y,x,\theta )=0$, which is not useful for estimating $\theta _0$. However, if $Q(x,\theta )$ does have one or more zero eigenvalues, then, for a generic choice of $s(y,x,\theta )$, we have $s_{\infty }(y,x,\theta ) \ne 0$, and part (i) of the lemma becomes non-trivial.

Part (ii) of the lemma states that the existence of a zero eigenvalue of $Q(x,\theta )$ is indeed a necessary and sufficient condition for the existence of an exactly valid moment function in the sense of (4). As explained in the proof, if $Q(x,\theta )$ has a zero eigenvalue, then an exactly valid moment function ${\mathfrak m}(y, x, \theta )$ is simply obtained by the entries of the corresponding left-eigenvector of $Q(x,\theta )$.

Finally, part (iii) of the lemma states that any such exactly valid moment function ${\mathfrak m}(y, x, \theta )$ can be obtained as $\lim _{q\rightarrow \infty }s^{(q)}(y,x,\theta )$, i.e., as the limit of our iterative bias correction scheme above, for some appropriately chosen initial score function $s(y, x, \theta )$. Thus, the set of valid moment functions is identical to the set of all possible limits $s_{\infty }(y,x,\theta )$.

Recall that finding such exactly valid moment functions is the underlying idea of the functional differencing method of Bonhomme (2012). Thus, Lemma 2 establishes a very close relationship between our bias correction method and functional differencing.

Remark 2

If the set $\mathcal{A}$ is finite with cardinality $n_\mathcal{A}=|\mathcal{A}|$, then by construction $\textrm{rank}[Q(x,\theta )]\le n_\mathcal{A}$. Thus, whenever $n_\mathcal{A} < n_\mathcal{Y}$, $Q(x,\theta )$ has $n_\mathcal{Y}- n_\mathcal{A}$ zero eigenvalues, implying that exact moment functions, free of $\alpha$, are available. Notice, however, that this assumes not only that $\alpha$ takes on only a finite number of values, but also that these values are known (they constitute the known set $\mathcal{A}$). By contrast, the literature on discretizing heterogeneity in panel data (e.g., Bonhomme and Manresa 2015; Su, Shi and Phillips 2016; Bonhomme, Lamadon and Manresa 2022) usually considers the support points of A to be unknown. For our purposes, the fact that $\textrm{rank} [Q(x,\theta )] \le n_\mathcal{A}$ matters only in our numerical implementation, where the rank of $Q(x,\theta )$ might be truncated my the discretization of the set $\mathcal{A}$.

5 Eigenvalues of $Q(x,\theta )$: numerical example

Lemma 1 guarantees that all eigenvalues of the matrix $Q(x,\theta )$ lie in the interval [0, 1], and Lemma 2 shows that exact moment conditions that are free of the incidental parameter A are only available if $Q(x,\theta )$ has a zero eigenvalue. However, even in models where $Q(x,\theta )$ does not have a zero eigenvalue, we suggest that calculating the eigenvalues of $Q(x,\theta )$ is generally informative about whether moment conditions exist that are approximately free of the incidental parameters. This is because in typical applications we expect that the distinction between a zero eigenvalue and a very small eigenvalue of $Q(x,\theta )$ should be practically irrelevant, that is, as long as $Q(x,\theta )$ has one or more eigenvalues that are very close to zero, then very good approximate moment conditions in the sense of (8) should exist.

It is difficult to make a general statement about how small an eigenvalue of $Q(x,\theta )$ needs to be to qualify as sufficiently small. However, in a typical model with a sufficiently large number $n_\mathcal{Y}$ of outcomes (which for discrete choice panel data usually requires only moderately large T) one will often have multiple eigenvalues of $Q(x,\theta )$ that are so small (say smaller than $10^{-5}$) that there is little doubt that they can be considered equal to zero for practical purposes.

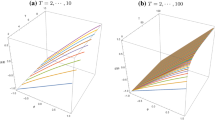
To illustrate this, consider Example 1B with normally distributed errors, $F(u)=\Phi (u)$, even values of T, and $T_0=T_1=T/2$, which implies $n_\mathcal{Y} = (1+T/2)^2$. For the prior distribution of A we choose the standard normal distribution, $\pi _\textrm{prior}(\alpha ) = \phi (\alpha )$.² We then calculate the eigenvalues of the $n_\mathcal{Y} \times n_\mathcal{Y}$ matrix $Q(\theta )$ for $\theta =1$ (there are no longer covariates x in this example as they are assigned non-random values). For $T=2$ we have $n_\mathcal{Y}=4$, and the four eigenvalues of Q(1) are $\lambda _1=1$, $\lambda _2=0.47463$, $\lambda _3=0.10727$, and $\lambda _4 = 0.00016$. For $T=4$ and $T=6$ we have $n_\mathcal{Y}=9$ and $n_\mathcal{Y}=16$, respectively, and the corresponding eigenvalues of Q(1) are plotted in Figs. 1 and 2. Figure 3 plots only the smallest eigenvalues of Q(1) for $T=2,4,\ldots ,20$.

Fig. 1

The eigenvalues $\lambda _j(\theta )$ of the matrix $Q(\theta )$ in Example 1B are plotted for the case $\theta =1$, $T=4$, $T_0=T_1=2$, and where both the error distribution and the prior distribution of A are standard normal. The left and right plots show the same eigenvalues, just with a different scaling of the y-axis

Fig. 2

Same eigenvalue plot as in Fig. 1, but for $T=6$ and $T_0=T_1=3$

Fig. 3

For the same setting as in Fig. 1, but for different values of T (with $T_0=T_1=T/2$), we plot only the smallest eigenvalue of $Q(\theta )$ for $\theta =1$. Notice that the smallest eigenvalue is never zero, that is, Q(1) has full rank for all values of T considered

From these figures, we see that for $T \ge 4$ the smallest eigenvalue of Q(1) is less than $10^{-9}$, which we argue can be considered equal to zero for practical purposes. In Figs. 1 and 2 we see that the largest eigenvalue, $\lambda _1$, is equal to one (because Q(1) is a stochastic matrix), but then the eigenvalues $\lambda _j$ decay exponentially fast as j increases.³

If we were to replace the standard normal distribution of the errors by the standardized logistic cdf $F(u)= (1+e^{-\pi u / \sqrt{3}})^{-1}$ (normalized to have variance one), then the left-hand side (non-logarithmic) plots in Figs. 1 and 2 would look almost identical, but there would be $(T/2)^2$ eigenvalues exactly equal to zero. These zero eigenvalues for the logit model are due to the existence of a sufficient statistic for A and, correspondingly, the existence of exact moment functions (associated with the left null-space of $Q(\theta )$), as discussed in Sect. 3.1 above. Given that the change from standardized logistic errors to standard normal errors is a relatively minor modification of the model, it is not surprising that we see many eigenvalues close to zero in Figs. 1 and 2.

Figure 3 shows that the smallest eigenvalue of Q(1) in this example also decays exponentially fast as T increases.⁴ However, for none of the values of T that we considered here, did we find an exact zero eigenvalue for the static binary choice probit model. We conjecture that this is true for all $T\ge 2$, but we have no proof.⁵

This example illustrates that eigenvalues of $Q(x,\theta )$ very close to zero but not exactly zero may exist in interesting models. When aiming to estimate the parameter $\theta _0$ in a particular model of the form (2), our first recommendation is to calculate the eigenvalues of $Q(x,\theta )$ for some representative values of $\theta$ and x to see if some of them are zero or close to zero. If some are equal to zero, then exact functional differencing (Bonhomme 2012) is applicable. If some are very close to zero, then approximate moment functions (as in (8)) are available.

The eigenvalues of $Q(x,\theta )$ are useful to examine whether exact or approximate moment functions for $\theta$ are available in a given model. However, as explained in Sect. 3.1, the corresponding moment functions also have to depend on $\theta$ to be useful for parameter estimation. For example, the matrix Q(1) in Example 1A has exactly the same non-zero eigenvalues as the matrix Q(1) in Example 1B that we just discussed, but in addition, it has a zero eigenvalue with multiplicity equal to $2^T - (T_0+1)(T_1+1)$, corresponding to the uninformative moment functions in equation (6). As a diagnostic tool, it can also be useful to calculate the matrix Q(x) for the model $f(y | x, \theta _i,\alpha _i)$, which has no common parameters and where both $\theta _i$ and $\alpha _i$ are individual-specific fixed effects (this requires choosing a prior for $\theta$ as well, which may have finite support to keep the computation simple). Every zero eigenvalue of that matrix Q(x) then corresponds to a moment function, for that value of x, that does not depend on $\theta$ (within the range of the chosen prior for $\theta$). The existence of uninformative moment functions (6) in Example 1A, for example, can be detected in this way.

6 Estimation

Suppose we have chosen a prior distribution $\pi _{\textrm{prior}}$, an initial score function $s(y,x,\theta )$, and an order of bias correction, q. This gives the bias-corrected score function $s^{(q)}(y,x,\theta )$ as the moment function $m(y,x,\theta )$ for which the approximate moment condition (8) is assumed to hold. For simplicity, suppose that $d_s=d_{\theta }$, so that the number of moment conditions equals the number of common parameters we want to estimate. We can then define a pseudo-true value $\theta _* \in \Theta$ as the solution of

$$\begin{aligned} \mathbb {E}\left[ m(Y_i,X_i,\theta _*) \right] = 0 . \end{aligned}$$

(21)

The corresponding method of moments estimator $\widehat{\theta }$ satisfies $\frac{1}{n} \sum _{i=1}^n \, m(Y_i,X_i,\widehat{\theta }) = 0.$ Under appropriate regularity conditions, including existence and uniqueness of $\theta _*$, we then have, as $n \rightarrow \infty$,

$$\begin{aligned} \sqrt{n}( \widehat{\theta }- \theta _* ) \; \overset{d}{\rightarrow }\ \; \mathcal{N}(0,V_*) \,, \end{aligned}$$

with asymptotic variance given by

$$\begin{aligned} V_*&= [G'_*]^{-1} \textrm{Var}\left[ m(Y_i,X_i,\theta _*) \right] G^{-1}_* ,&G_*&= \mathbb {E}\left[ \nabla _{\theta } \, m'(Y_i,X_i,\theta _*) \right] . \end{aligned}$$

(22)

In Sect. 7 we will report the bias $\theta _* - \theta _0$ and the asymptotic variance $V_*$ for different choices of moment functions in Example 1B. Note that reporting the bias $\theta _* - \theta _0$ of the parameter estimates is more informative than reporting the bias $\mathbb {E}\left[ m(Y_i,X_i,\theta _0) \right]$ of the moment condition, in particular since the moment condition can be rescaled by an arbitrary factor.

How should q be chosen? If $Q(x,\theta )$ is singular, then a natural choice is $q=\infty$, as described in Sect. 4.3, because this delivers an exactly unbiased moment condition. If $Q(x,\theta )$ is nonsingular but some of its eigenvalues are small, then, recalling our discussion in Sect. 5, our general recommendation is to choose relatively large values of q. The larger the chosen q, the more we rely on the smallest eigenvalues of $Q(x,\theta )$, because contributions to $s^{(q)}(y,x,\theta )$ from larger eigenvalues of $Q(x,\theta )$ are downweighted more heavily as q increases. If none of the eigenvalues $Q(x,\theta )$ is close to zero, then there are no moment conditions that hold approximately in the sense of (8). Yet, even then, setting $q>0$ is likely to improve on $q=0$, even though the remaining bias will still be non-negligible in general. Whatever the eigenvalues of $Q(x,\theta )$ are (and, indeed, whether $Q(x,\theta )$ is singular or not), q is a tuning parameter and a principled way to choose q would be to optimize some criterion, for example, the (estimated) mean squared error of $\widehat{\theta }$. We leave this for further study. In our numerical illustrations in Sect. 7 we just consider finite values of q up to $q=1000$, and $q=\infty$.

7 Asymptotic and finite-sample properties

In this section, we report on asymptotic and finite-sample properties of $\widehat{\theta }$ for different choices of moment functions in the model of Example 1B with standard normal errors (i.e., the panel probit model with a single, binary regressor and fixed effects) and a variation thereof, the model of Example 1A with a continuous regressor. Throughout, we set $\theta _0=1$, we use a standard normal prior (i.e., $\pi _{\textrm{prior}}(\alpha )=\phi (\alpha )$, as in Figs. 1 and 2), we choose the integrated score (12) as the initial score function, and we vary q, the number of iterations of the bias correction procedure.

We first present results on asymptotic and finite-sample biases and variances of $\widehat{\theta }$ for three cases where T is relatively small: Example 1B with $T_{0}=T_{1}=T/2$ and $T\in \{4,6\}$ (Case 1); Example 1B with $T_{0}=1, T_{1}=T-1$ and $T\in \{4,10\}$ (Case 2); Example 1A with a continuous regressor $X_{it}\sim \mathcal {N}(0.5,0.25)$ and $T\in \{4,6\}$ (Case 3). In all three cases we set the true distribution of A equal to $\mathcal {N}(1,1)$ (i.e., $\pi _{0}(\alpha )=\phi (\alpha -1)$); note that this implies that $\pi _{\textrm{prior}}$ is rather different from $\pi _{0}$.

Then, in the setup of Example 1B with standard normal errors, we numerically explore Conjecture 1 by examining the asymptotic bias, $\theta _{*}-\theta _{0}$, for T up to 512, q up to 3, and various choices of $\pi _{0}$ as detailed below.

7.1 Case 1: binary regressor, $T_0=T_1=T/2$

Table 1 reports $\theta _{*}-\theta _{0}$ and $V_{*}$ for the case where $T_{0}=T_{1}=T/2$ and $T\in \{4,6\}$. The uncorrected estimate of $\theta _{0}$ $(q=0)$ has a large positive bias, 0.5050 when $T=4$ and 0.4056 when $T=6$. Bias correction ($q>0$) reduces the bias considerably, though non-monotonically in q. The least bias is attained at $q=\infty$, where the bias is very small: $-0.52\times 10^{-4}$ when $T=4$ and ${-}0.25\times 10^{-10}$ when $T=6$.

Our calculation of $V_{*}$ shows that there is, overall, a bias-variance trade-off in this example. When $T=4$, $V_{*}$ slightly decreases as we move from $q=0$ to $q=1$, but for $q\ge 1$ we see that $V_{*}$ increases in q; when $T=6$, $V_{*}$ increases in q throughout. Strikingly, $V_{*}$ at $q=\infty$ is much larger than, say, at $q=1000$.⁶

Table 1 also reports, for a cross-sectional sample size of $n=1000$, the approximate $\textrm{RMSE}$ of $\widehat{\theta }$ and the approximate coverage rate of the 95% confidence interval with bounds $\widehat{\theta }\pm (n\widehat{V}_{*})^{1/2}\Phi ^{-1}(0.975)$, where $\widehat{V}_{*}$ is the empirical analog to $V_{*}$. The approximate $\textrm{RMSE}$ is calculated as $\textrm{RMSE}=(V_{*}/n+(\theta _{*}-\theta _{0})^{2})^{1/2}$ and the approximate coverage rate as $\textrm{CI}_{0.95}=\Pr [|Z|\le \Phi ^{-1}(0.975)]$ where $Z\sim \mathcal {N}((\theta _{*}-\theta _{0})/(V_{*}/n)^{1/2},1)$. Of course, $\textrm{RMSE}$ and $\textrm{CI}_{0.95}$ follow mechanically from $\theta _{*},V_{*},n$ and heavily depend on the chosen n. For our choice of $n=1000$, when $T=4$, the $\textrm{RMSE}$ is minimized at $q=2$, but this is a rather fortuitous consequence of the bias having a local minimum (in magnitude) at $q=2$. In practice, when T is very small we would not recommend choosing q less than 10, say, because otherwise, the remaining bias is often non-negligible. From $q=10$ or 20 onward, the bias and confidence interval coverage rates are reasonably good. On the other hand, we would also not recommend choosing q to be very large (including $q=\infty$), one reason being asymptotic variance inflation.

We also conducted a real Monte Carlo simulation, under the exact same setup as described (and with $n=1000$ in particular). Table 2 gives the results, based on 1000 Monte Carlo replications. The column “bias” is $\mathbb {E}(\widehat{\theta }-\theta _{0})$ (estimated by Monte Carlo), and the second column is $n\times \textrm{var}(\widehat{\theta })$ (with $\textrm{var}(\widehat{\theta })$ estimated by Monte Carlo), to be compared with $V_{*}$ in Table 1. The columns $\textrm{RMSE}$ and $\textrm{CI}_{0.95}$ are the finite-n $\textrm{RMSE}$ and coverage rate. All the results are close to those in Table 1, confirming that large-n asymptotics provide a good approximation to the finite-n distribution of $\widehat{\theta }$. Note that Table 2 does not report simulation results for $q=\infty$. This is because in some Monte Carlo runs, in particular for $T=6$, it turned out to be too difficult to numerically distinguish between the smallest and the second smallest eigenvalue of $Q(x,\theta )$ and, therefore, to reliably select the eigenvector associated with the smallest eigenvalue. This is another reason not to recommend choosing $q=\infty$.

7.2 Case 2: binary regressor, $T_0=1, T_1=T-1$

There is nothing special about the case $T_0=T_1=T/2$, which we just discussed. Any other $T_0\ge 1$ and $T_1=T-T_0\ge 1$ lead to qualitatively similar results. We illustrate this for the case $T_0=1$ and $T_1=T-1$. Table 3 is similar to Table 1 and reports results for $(T_0,T_1)=(1,T-1)$ with $T\in \{4,10\}$. With $T_0=1$ fixed, we find that the bias for $q=0$ is nearly constant in T (and large), while the bias of the bias-corrected estimates $(q>0)$ decreases in T. Again, the bias is not monotonic in q (it changes sign) and it becomes very small as q becomes sufficiently large, albeit more slowly than in the case $T_0=T_1=T/2$. Table 4 presents the corresponding simulations, showing that the finite-sample results are, again, very close to asymptotic results reported in Table 3.

7.3 Case 3: continuous regressor

Here we illustrate approximate functional differencing in a panel probit model with a single continuous regressor and fixed effects. Apart from the continuity of the regressor, the setup is identical to that in Cases 1 and 2 above. Specifically, we consider Example 1A with $U_{it}\sim \mathcal {N}(0,1)$, $\theta _0=1$, $\pi _{\textrm{prior}}(\alpha )=\phi (\alpha )$, $\pi _{0}(\alpha )=\phi (\alpha -1)$, and the integrated score as initial score. We set $X_{it}\sim \mathcal {N}(0.5,0.25)$, so that $X_{it}$ has the same mean and variance (across t) as the binary regressor in Cases 1 and 2. For $T\in \{4,6\}$ and $n=1000$, we generated a single data set ${X_{it}}$ ($t=1,\ldots ,T$; $i=1,\ldots ,n$) to form $\mathcal {X}=\{X_1,\ldots ,X_n\}$, so the results are to be understood with reference to this $\mathcal {X}$. Table 5 presents the asymptotic biases and variances for q up to 1000. (We do not consider $q=\infty$ here because, even though $\theta _*$ and $\widehat{\theta }$ remain well-defined in the limit $q\rightarrow \infty$, the limiting values are generically determined by a single $X_i\in \mathcal {X}$, that is, estimation would be based on a single observation i, for which $Q(X_i,\theta )$ has the smallest eigenvalue within the sample.) The results are similar to those in Table 1, albeit the asymptotic biases and variances are somewhat larger (for all q). Table 6 presents the corresponding simulation results, which are in line with those in Table 5.

Table 1 Asymptotic biases and variances, and approximate RMSEs and coverage rates ($n=1000$)

Table 2 Simulation results for $n=1000$. Setup as in Table 1. Results based on 1000 Monte Carlo replications

Table 3 Asymptotic biases and variances, and approximate RMSEs and coverage rates ($n=1000$)

Table 4 Simulation results for $n=1000$

Table 5 Asymptotic biases and variances, and approximate RMSEs and coverage rates ($n=1000$)

7.4 Numerical calculations related to Conjecture 1

Table 7 reports bias calculations for larger values of T that support our conjecture about the rate of the bias as T grows. The model is as in Example 1B with standard normal errors, $\pi _{\textrm{prior}}(\alpha )=\phi (\alpha )$, $T_0=T_1=T/2$, and $\theta _0=1$. We calculated the bias, $b_T:=\theta _*-\theta _0$, with $\theta _*$ based on the integrated score, for q up to 3, $T\in \{64,128,256,512\}$, and for five different choices of $\pi _0$: three degenerate distributions, $\delta _z$, with mass 1 at $z\in \{0,1,2\}$ (i.e., $A=z$ is constant); and two uniform distributions, U[0.5, 1.5] and U[0, 2]. (So in all these cases $\pi _{\textrm{prior}}$ is very different from $\pi _0$.) Table 7 gives the bias $b_T$ for the chosen values of T, and also the successive bias ratios $b_{T/2}/b_T$ (the three rightmost columns). If Conjecture 1 is correct, we should see these ratios converge to $2^{q+1}$ as $T\rightarrow \infty$. For comparability, we also report the bias for $q=0$, where the known rate is confirmed: $b_{T/2}/b_T$ converges to 2 for every $\pi _0$, although when $\pi _0=\delta _2$ the convergence to 2 is not yet quite visible. Presumably, this is because then $\pi _0$ and $\pi _{\textrm{prior}}$ are quite different, requiring a larger T for the ratio $b_{T/2}/b_T$ to become stable. For $q=1$, $b_{T/2}/b_T$ is seen to converge to 4 (as conjectured) when $\pi _0\in \{\delta _0,\delta _1,U[0.5,1.5]\}$, while for $\pi _0\in \{\delta _2,U[0,2]\}$ the convergence is less visible. Overall, the picture is a little more blurred for $q=1$ compared to $q=0$. For $q=2$, where $b_{T/2}/b_T$ should converge to 8, we tend to see this convergence for $\pi _0\in \{\delta _0,\delta _1\}$, although the picture is more blurred; but also here the order of magnitude of $b_{T/2}/b_T$ is in line with convergence to 8. Finally, for $q=3$, the picture is even more blurred: we tend to see convergence of $b_{T/2}/b_T$ to 16 only for $\pi _0=\delta _0$, but even here the order of magnitude of $b_{T/2}/b_T$ is not incompatible with convergence to 16 (apart from the case $\pi _0=U[0,2]$, which clearly needs larger values of T for $b_{T/2}/b_T$ to stabilize). Certainly, these numerical calculations are by no means proof of the conjectured rates, but looking at the last column of Table 7, the ratios $b_{T/2}/b_T$ are broadly in line with the conjecture. Note, furthermore, that for any $q\ge 1$ the remaining bias in Table 7 is extremely tiny in most cases, unlike the bias of the maximum integrated likelihood estimator (reported as $q=0$ in the table).

Table 6 Simulation results for $n=1000$

Table 7 Asymptotic bias rates. The model is as in Example 1A with standard normal errors, $T_0=T_1=T/2$, $\pi _{\textrm{prior}}(\alpha )=\phi (\alpha )$, and $\pi _{0}$ as given in the table

8 Some further remarks and ideas

8.1 Alternative bias correction methods

Let $\widehat{\alpha }(y,x,\theta ):= \arg \max _{\alpha \in \mathcal{A}}f\left( y \, \big | \, x, \alpha , \theta \right)$ be the MLE of $\alpha$ for fixed $\theta$. Define $\widetilde{Q}(\widetilde{y} \, | \, y,x,\theta ):= f\left( \widetilde{y} \, \big | \, x, \widehat{\alpha }(y,x,\theta ), \theta \right)$, and let $\widetilde{Q}(x,\theta )$ be the $n_\mathcal{Y} \times n_\mathcal{Y}$ matrix with elements $\widetilde{Q}_{k,\ell }(x,\theta ) = \widetilde{Q}(y_{(k)} \, | \, y_{(\ell )},x,\theta )$, for $k,\ell \in \{1,\ldots ,n_\mathcal{Y}\}$.

Instead of implementing the bias correction of the score as in (16), one could alternatively consider

$$\begin{aligned} \widetilde{s}^{(1)}(y,x,\theta )&:= s(y,x,\theta ) - \sum _{\widetilde{y} \in \mathcal{Y}} s(\widetilde{y},x,\theta ) \, f\left( \widetilde{y} \, \big | \, x, \widehat{\alpha }(y,x,\theta ) , \theta \right) \nonumber \\&= s(y,x,\theta ) - \sum _{\widetilde{y} \in \mathcal{Y}} s(\widetilde{y},x,\theta ) \, \widetilde{Q}(\widetilde{y} \, | \, y,x,\theta ) \nonumber \\&= S(x,\theta ) \, \left[ \mathbbm {I}_{n_\mathcal{Y}} - \widetilde{Q}(x,\theta ) \right] \, \delta (y) . \end{aligned}$$

(23)

This alternative bias correction method is very natural: We simply have subtracted from the original score the expression for the bias in the first line of (15), and replaced the unknown A with the estimator $\widehat{\alpha }(y,x,\theta )$. In fact, this is exactly the “profile-score adjustment” to the score function that is suggested in Dhaene and Jochmans (2015a).

The expression in (23) is identical to that in (16), except that $Q(x,\theta )$ is replaced with $\widetilde{Q}(x,\theta )$. Iterating this alternative bias correction q times therefore also gives the formula in (17) with $Q(x,\theta )$ replaced with $\widetilde{Q}(x,\theta )$. Thus, by the same arguments as before, for large values of q, the corresponding score function $\widetilde{s}^{(q)}(x,\theta )$ will be dominated by contributions from eigenvectors of $\widetilde{Q}(x,\theta )$ that correspond to eigenvalues close to or equal to zero.

It is therefore natural to ask why in our presentation above we have chosen the bias correction in (16) based on the posterior distribution of A instead of the bias correction in (23) based on the MLE of A. The answer is that the matrix $\widetilde{Q}(x,\theta )$ does not have the same convenient algebraic properties as the matrix $Q(x,\theta )$. In particular, none of the parts (i), (ii), (iii) of Lemma 2 would hold if we replaced $Q(x,\theta )$ by $\widetilde{Q}(x,\theta )$, implying that the close relationship between the bias correction in (23) and functional differencing does not generally hold for the alternative bias correction discussed here.

To explain why $\widetilde{Q}(x,\theta )$ does not have these properties, consider the following. For given values of x and $\theta$, assume that there exist two outcomes y and $\bar{y}$ that give the same MLE of A, that is, $\widehat{\alpha }(y,x,\theta ) = \widehat{\alpha }(\bar{y},x,\theta )$. Then, the two columns of $\widetilde{Q}(x,\theta )$ that correspond to y and $\bar{y}$ are identical, and therefore $\widetilde{Q}(x,\theta )$ does not have full rank, implying that it has a zero eigenvalue. The existence of this zero eigenvalue is simply a consequence of $\widehat{\alpha }(y,x,\theta ) = \widehat{\alpha }(\bar{y},x,\theta )$.

Now, in models where there exists a sufficient statistic for A (conditional on X), if the outcomes y and $\bar{y}$ have the same value of the sufficient statistic, then $\widehat{\alpha }(y,x,\theta ) = \widehat{\alpha }(\bar{y},x,\theta )$, and in that case the zero eigenvalue of $\widetilde{Q}(x,\theta )$ just discussed is closely related to functional differencing because the existence of the sufficient statistic generates valid moment functions; recall the example in equation (7).

However, we may also have $\widehat{\alpha }(y,x,\theta ) = \widehat{\alpha }(\bar{y},x,\theta )$ for reasons that have nothing to do with functional differencing. For example, consider Example 1B with normally distributed errors, $T \ge 2$ even, and $T_0=T_1=T/2$. Then, all outcomes y with $y_0 + y_1 = T/2$ have $\widehat{\alpha }(y,\theta )=-\theta /2$. So there are at least $1+T/2$ different outcomes with the same value of $\widehat{\alpha }(y,\theta )$, which implies that $\widetilde{Q}(\theta )$ has at least T/2 zero eigenvalues. But we have found numerically that $Q(\theta )$ does not have zero eigenvalues in this example for $\theta \ne 0$, that is, according to Lemma 2, no exact moment function exists.

This example shows that $Q(x,\theta )$ and $\widetilde{Q}(x,\theta )$ have different algebraic properties, and it explains why we have focused on $Q(x,\theta )$ instead of $\widetilde{Q}(x,\theta )$ in our discussion. Nevertheless, the observation that bias correction can be iterated using the formula in (17) can be useful for alternative methods as well.

8.2 Alternative ways to implement approximate functional differencing

Instead of choosing $s^{(q)}(y,x,\theta )$ as moment function to estimate $\theta _0$, we could alternatively choose the moment function $s_h(y,x,\theta )$ defined by (18) and (19) for some other function $h:[0,1] \rightarrow \mathbb {R}$. In particular, one very natural relaxation of $s_{\infty }(y,x,\theta )$ and $h_\infty (\lambda ) = \mathbbm {1}\{ \lambda = 0 \}$ would be to choose

$$\begin{aligned} h(\lambda )&= K(\lambda /c) , \end{aligned}$$

for some soft-thresholding function $K: [0,\infty ) \rightarrow [0,\infty )$, for example, $K(\xi )=\exp (-\xi )$. The tuning parameter $q \in \{0,1,2,\ldots \}$ is replaced here by the bandwidth parameter $c>0$, which specifies which eigenvalues of $Q(\theta ,x)$ are considered to be close to zero. Regarding the thresholding function, one could in principle consider a simple indicator function $K(\xi )=\mathbbm {1}\{ \xi \le 1 \}$, but since this function is discontinuous, the resulting score function $s_{h}(y,x,\theta )$ defined in (19) would then be discontinuous in $\theta$, so we would not recommend this.

Another possibility to implement approximate functional differencing is to replace the set $\mathcal{A}$ by a finite set $\mathcal{A}_*$ with cardinality $n_\mathcal{A}$ less than $n_\mathcal{Y}$. As explained in Remark 2 above, after this replacement, the matrix $Q(x,\theta )$ will have at least $n_\mathcal{Y}- n_\mathcal{A}$ zero eigenvalues, that is, one can then use the moment function $s_{\infty }(y,x,\theta )$ defined in (20) to implement the MM or GMM estimator. In this case, the key tuning parameter to choose is the number of points $n_\mathcal{A}$ in the set $\mathcal{A}_*$ that “approximates” $\mathcal{A}$.

8.3 Average effect estimation

In models of the form (2) we are often not only interested in the unknown $\theta _0$ but also in functionals of the unknown $\pi _0(\alpha |x)$. In particular, consider average effects of the form

$$\begin{aligned} \mu _0&= \mathbbm {E}\left[ \mu (X,A,\theta _0) \right] = \mathbbm {E}\left[ \int _\mathcal{A} \mu (X, \alpha , \theta _0) \, \pi _0(\alpha \,|\,X) \, \textrm{d}\alpha \right] , \end{aligned}$$

where $\mu ( x,\alpha , \theta )$ is a known function that specifies the average effect of interest. For example, in a panel data model, if we are interested in the average partial effect with respect to the p-th regressor in period t, we could choose $\mu ( x,\alpha , \theta ) = \frac{\partial }{\partial x_{t,p}} \sum _{y \in \mathcal{Y}} y_t f(y | x, \theta ,\alpha )$. For other examples of functionals of the individual-specific effects, see e.g. Arellano and Bonhomme (2012).

We now focus on the problem of estimating $\mu _0$. Therefore, in this subsection, we assume that the problem of estimating $\theta _0$ is already resolved (with corresponding estimator $\widehat{\theta })$, and we focus on the problem that $\pi _0(\alpha |x)$ is unknown when estimating average effects $\mu _0$.

Analogously to the iterated bias-corrected score functions $s^{(q)}(y,x,\theta )$ in (17), we want to define a sequence of estimating functions $w^{(q)}(y,x,\theta )$, $q=0,1,2,\ldots$, such that, for some q,

$$\begin{aligned} \mu _*^{(q)}:= \mathbbm {E}\left[ w^{(q)}(Y,X,\theta _0) \right] \end{aligned}$$

is close to $\mu _0$. The corresponding estimator of $\mu _0$ is

$$\begin{aligned} \widehat{\mu }^{(q)}:= \frac{1}{n} \sum _{i=1}^n w^{(q)} ( Y_i,X_i,\widehat{\theta }) . \end{aligned}$$

Using the posterior distribution in (11), a natural baseline estimating function ($q=0$) is

$$\begin{aligned} w^{(0)}(y,x,\theta ) := \int _\mathcal{A} \mu ( x, \alpha , \theta ) \, \pi _\textrm{post}(\alpha \,|\, y,x,\theta ) \, \textrm{d}\alpha . \end{aligned}$$

The corresponding estimator $\widehat{\mu }^{(0)}$ of $\mu _0$ can again be motivated by “large-T” panel data considerations, where, under regularity conditions, the posterior distribution concentrates around the true value A as $T \rightarrow \infty$.

Let $W(x,\theta )$ be the $n_\mathcal{Y}$-vector with entries $w^{(0)}(y_{(k)},x,\theta )$, $k=1,\ldots ,n_\mathcal{Y}$. Then, the analog of the limiting estimating function in (20), corresponding to $q \rightarrow \infty$, for average effects is

$$\begin{aligned} w^{(\infty )}(y,x,\theta )&:= W'(x,\theta ) \, Q^\dagger (x,\theta ) \, \delta (y) \nonumber \\&= W'(x,\theta ) \; \widetilde{h}^{(\infty )}[ Q(x,\theta ) ] \; \delta (y) ,&\widetilde{h}^{(\infty )}(\lambda )&:= \left\{ \begin{array}{ll} \lambda ^{-1} &{} \text {for } \lambda >0 , \\ 0 &{} \text {for } \lambda =0 , \end{array} \right. \end{aligned}$$

(24)

where $Q^\dagger (x,\theta )$ is a pseudo-inverse of $Q(x,\theta )$, and the application of a function $\widetilde{h}^{(\infty )}:[0,1] \rightarrow \mathbb {R}$ to the matrix $Q(x,\theta )$ was defined in equation (18). The motivation for choosing $w^{(\infty )}(y,x,\theta )$ in this way is that it gives an unbiased estimator of the average effect (i.e., $\mu _*^{(\infty )} = \mu _0$) whenever we can write $\mu ( x, \alpha , \theta ) = \sum _{y \in \mathcal{Y}} \nu (y,x,\theta ) f\left( y \, \big | \, x, \alpha , \theta \right)$ for some function $\nu (y,x,\theta )$.⁷ Of course, average effects with this form of $\mu ( \alpha , x, \theta )$ are a very special case, but they are usually the only cases for which we can expect unbiased estimation of the average effect to be feasible (for fixed T); see also Aguirregabiria and Carro (2021). Notice that we do not assume here that $\mu ( \alpha , x, \theta )$ is of this form, it is just used to motivate (24).

As we have seen before, the non-zero eigenvalues of $Q(x,\theta )$ can be very small, which implies that the pseudo-inverse $Q^\dagger (x,\theta )$ can have very large elements. The corresponding estimator $\widehat{\mu }^{(\infty )}$ based on (24) therefore typically has a very large variance and we do not recommend this estimator in practice. Instead, to balance the bias-variance trade-off of the average effect estimator, some regularization of the pseudo-inverse of $Q(x,\theta )$ in (24) is required. There are various ways to implement regularization, in the same way that there are various ways to implement approximate functional differencing (see Sect. 8.2).

Here, regularization means that we want to find functions $\widetilde{h}_q(\lambda )$ that approximate the inverse function $1/\lambda$ well for large values of $\lambda \in [0,1]$, but that deviate from $1/\lambda$ for values of $\lambda$ close to zero to avoid divergence.⁸ This gives,⁹ for $q\in \{0,1,2,\ldots \}$,

$$\begin{aligned} \widetilde{h}_q(\lambda )&= \sum _{r=0}^q (1-\lambda )^r =\left\{ \begin{array}{ll} \frac{ 1 - (1-\lambda )^{q+1} }{\lambda } &{} \text {for } \lambda >0 , \\ q+1 &{} \text {for } \lambda =0 . \end{array} \right. \end{aligned}$$

(25)

The corresponding estimating function that regularizes $w^{(\infty )}(y,x,\theta )$ is therefore given by

$$\begin{aligned} w^{(q)}(y,x,\theta )&:= W'(x,\theta ) \; \widetilde{h}_q[ Q(x,\theta ) ] \; \delta (y),&\widetilde{h}_q[ Q(x,\theta ) ] = \sum _{r=0}^q \left[ \mathbbm {I}_{n_\mathcal{Y}} - Q(x,\theta ) \right] ^r . \end{aligned}$$

(26)

This is a polynomial in $Q(x,\theta )$, as was the case for $s^{(q)}(y,x,\theta )$. Choosing a value of q that is not too large therefore ensures that the variance of the corresponding estimator $\widehat{\mu }^{(q)}$ remains reasonably small (for fixed q), because we don’t need the pseudo-inverse of $Q(x,\theta )$.

Note also that $w^{(q)}(y,x,\theta )$ and the corresponding estimators $\widehat{\mu }^{(q)}$ have a large-T bias-correction interpretation very similar to $s^{(q)}(y,x,\theta )$. For example, we have $\widetilde{h}_1(\lambda )=2-\lambda$, and therefore

$$\begin{aligned} w^{(1)}(y,x,\theta ) = 2 \, w^{(0)}(y,x,\theta ) - W'(x,\theta ) \; Q(x,\theta ) \; \delta (y) . \end{aligned}$$

We conjecture that the estimator of $\mu _0$ corresponding to only $W'(x,\theta ) Q(x,\theta ) \delta (y)$ has twice the leading order 1/T asymptotic bias of the estimator $\widehat{\mu }^{(0)}$ corresponding to $w^{(0)}(y,x,\theta )$, that is, $w^{(1)}(y,x,\theta )$ is exactly the jackknife linear combination that eliminates the large-T leading order bias in $\widehat{\mu }^{(0)}$; see Dhaene and Jochmans (2015b). Appropriate iterations of this jackknife bias correction also give the estimating functions $w^{(q)}(y,x,\theta )$ for $q>1$.

We are not considering average effects further here. But we found it noteworthy that there is a formalism for average effect calculation that closely mirrors the development of approximate functional differencing for the estimation of $\theta _0$ introduced above. However, this does not imply that we expect the results for average-effect estimation to be necessarily similar to those for the estimation of the common parameters $\theta _0$. In particular, for small values of T, the identified set for the average effects in discrete-choice panel data models tends to be much larger than the identified set of the common parameters (see, e.g., Chernozhukov, Fernández-Val, Hahn and Newey 2013; Davezies, D’Haultfoeuille and Laage 2021; Liu, Poirier and Shiu 2021; Pakel and Weidner 2021). Therefore we expect larger values of T to be required for the point estimators $\widehat{\mu }^{(q)}$ to perform well, and we also expect the bias-variance trade-off in the choice of q to be quite different. For a closely related discussion see Bonhomme and Davezies (2017), and also the section on “Average marginal effects” in the 2010 working paper version of Bonhomme (2012).

9 Conclusions

We have linked the large-T panel data literature with the functional differencing method through a bias correction that converges to functional differencing when iterated. Our numerical illustrations show that in models where exact functional differencing is not possible, one may still apply it approximately to obtain estimates that can be essentially unbiased, even when the number of time periods T is small.

The key element in our construction is the $n_Y \times n_Y$ matrix $Q(x,\theta )$. The eigenvalues of this matrix are informative about whether (approximate) functional differencing is applicable in a given model. The matrix $Q(x,\theta )$ also features prominently in our bias-corrected score functions in (17) and in our regularized estimating functions for average effects in (26). We have assumed a discrete outcome space with a finite number of elements $n_Y$. When the outcome space is infinite, the matrix $Q(x,\theta )$ has to be replaced by the corresponding operator.

The goal of this paper was primarily to introduce and illustrate an approximate version of functional differencing. Future work is needed to better understand the properties of the method and to explore its usefulness in empirical work, both for the estimation of common parameters, which was our primary focus, and for the estimation of average effects, briefly introduced in Sect. 8.3.

A Proofs

Proof of Lemma 1

Define

$$\begin{aligned} \overline{Q}(\widetilde{y} \, | \, y,x,\theta ) = \frac{\int _\mathcal{A} f \left( \widetilde{y} \, \big | \, x,\alpha ,\theta \right) f(y \, | \,x,\alpha ,\theta ) \, \pi _\textrm{prior}(\alpha \,|\,x) \textrm{d} \alpha }{\left[ p_\textrm{prior}(\widetilde{y} \, |\, x,\theta ) \right] ^{1/2} \left[ p_\textrm{prior}( y \, |\, x,\theta ) \right] ^{1/2} } \end{aligned}$$

and let $\overline{Q}(x,\theta )$ be the $n_\mathcal{Y} \times n_\mathcal{Y}$ matrix with elements $\overline{Q}_{k,\ell }(x,\theta ) = \overline{Q}(y_{(k)} \, | \, y_{(\ell )},x,\theta )$. Also define the $n_\mathcal{Y} \times n_\mathcal{Y}$ diagonal matrix

$$\begin{aligned} P_\textrm{prior}( x,\theta ) = \textrm{diag}\left[ p_\textrm{prior}( y_{(k)} \, |\, x,\theta ) \right] _{k=1,\ldots ,n_\mathcal{Y}}. \end{aligned}$$

From (11) and (14) we obtain

$$\begin{aligned} Q( \widetilde{y} \, | \, y,x,\theta )&= \frac{\int _\mathcal{A} f \left( \widetilde{y} \, \big | \, x,\alpha ,\theta \right) f( y \, | \,x,\alpha ,\theta ) \, \pi _\textrm{prior}(\alpha \,|\,x) \textrm{d} \alpha }{p_\textrm{prior}(y \, |\, x,\theta )} \\&= \left[ p_\textrm{prior}( \widetilde{y} \, |\, x,\theta ) \right] ^{1/2} \, \overline{Q}( \widetilde{y} \, | \, y,x,\theta ) \, \left[ p_\textrm{prior}( y \, |\, x,\theta ) \right] ^{-1/2} , \end{aligned}$$

which in matrix notation is

$$\begin{aligned} Q(x,\theta )&= \left[ P_\textrm{prior}( x,\theta ) \right] ^{1/2} \, \overline{Q}(x,\theta ) \, \left[ P_\textrm{prior}( x,\theta ) \right] ^{-1/2} . \end{aligned}$$

This shows that the matrices $Q(x,\theta )$ and $\overline{Q}(x,\theta )$ are similar and therefore have the same eigenvalues.¹⁰ The matrix $\overline{Q}(x,\theta )$ is symmetric and positive semi-definite (by construction), which implies that all its eigenvalues (and therefore all eigenvalues of $Q(x,\theta )$) are non-negative real numbers. Furthermore, $\overline{Q}(x,\theta )$ is diagonalizable because it is symmetric. Hence $Q(x,\theta )$ is also diagonalizable, because it is similar to $\overline{Q}(x,\theta )$.¹¹

In addition, $Q(x,\theta )$ is a stochastic matrix (by construction), which implies that its spectral radius is equal to one, that is, $Q(x,\theta )$ cannot have any eigenvalue larger than one. We thus conclude that all eigenvalues of $Q(x,\theta )$ lie in the interval [0, 1]. $\square$

The following lemma is useful for the proof of Lemma 2, which we present afterward.

Lemma 3

Let the assumptions of Lemma 2 hold. Let $w(y,x,\theta _0) \in \mathbb {R}$ be such that

$$\begin{aligned} \sum _{y \in \mathcal{Y}} w(y,x,\theta _0) \,Q\left( y \, \big | \,\widetilde{y}, x,\theta _0 \right) = 0 \,, \qquad \text {for all } \widetilde{y} \in \mathcal{Y} . \end{aligned}$$

Then

$$\begin{aligned} \sum _{y \in \mathcal{Y}} w(y,x,\theta _0) \,f \left( y \, \big | \, x,\alpha ,\theta _0 \right) = 0 \,, \qquad \text {for all } \alpha \in \mathcal{A} . \end{aligned}$$

Proof of Lemma 3

The $n_\mathcal{Y} \times n_\mathcal{Y}$ diagonal matrix $P_\textrm{prior}( x,\theta _0)$ was defined in the Proof of Lemma 1. In addition, let $F(x,\alpha ,\theta _0)$ and $W(x,\theta _0)$ be the $n_\mathcal{Y}$-vectors with elements $f(y_{(k)} \, | \, x,\alpha ,\theta _0)$ and $w(y_{(k)},x,\theta _0)$, respectively, for $k=1,\ldots ,n_\mathcal{Y}$. Then

$$\begin{aligned} Q(x,\theta _0) = \int _\mathcal{A} F(x,\alpha ,\theta _0) \, F'(x,\alpha ,\theta _0) \, \pi _\textrm{prior}(\alpha \,|\,x) \, \textrm{d}\alpha \, P^{-1}_\textrm{prior}( x,\theta _0) , \end{aligned}$$

(27)

and the condition on $w(y,x,\theta _0)$ in the lemma can be written as

$$\begin{aligned} W'(x,\theta _0) \, Q(x,\theta _0) = 0 . \end{aligned}$$

Plugging in the expression for $Q(x,\theta _0)$ in (27) and multiplying with $P_\textrm{prior}( x,\theta _0) W(x,\theta _0)$ from the right gives

$$\begin{aligned} \int _\mathcal{A} W'(x,\theta _0) \, F(x,\alpha ,\theta _0) \, F'(x,\alpha ,\theta _0) \, W(x,\theta _0) \, \, \pi _\textrm{prior}(\alpha \,|\,x) \, \textrm{d}\alpha = 0 . \end{aligned}$$

Since $W'(x,\theta _0) \, F(x,\alpha ,\theta _0) \, F'(x,\alpha ,\theta _0) \, W(x,\theta _0) \ge 0$ and $\pi _\textrm{prior}(\alpha \,|\,x)>0$ we conclude that

$$\begin{aligned} W'(x,\theta _0) \, F(x,\alpha ,\theta _0) \, F'(x,\alpha ,\theta _0) \, W(x,\theta _0) = 0 , \end{aligned}$$

(28)

for almost all values $\alpha$, except possibly for a set of values $\alpha$ that has measure zero under $\pi _\textrm{prior}(\alpha \,|\,x)$. However, since $f\left( y \, \big | \, x, \alpha , \theta _0 \right)$ is assumed to be continuous in $\alpha$, we conclude that (28) must hold for all $\alpha \in \mathcal{A}$, since any violation on a set of measure zero would require a discontinuity in $\alpha$. Finally, (28) also implies that

$$\begin{aligned} W'(x,\theta _0) \, F(x,\alpha ,\theta _0) = 0 \,, \end{aligned}$$

for all $\alpha \in \mathcal{A}$. This is what we wanted to show, just written in vector notation. $\square$

Proof of Lemma 2

# part (i): Let $U_0(x,\theta _0)$ be the submatrix of $U(x,\theta _0)$ that only contains those columns that are the right-eigenvectors of $Q(x,\theta _0)$ corresponding to the eigenvalues $\lambda _j(x,\theta _0) = 0$. We then have $Q(x,\theta _0) \, U_0(x,\theta _0) = 0.$ Similarly, let $[U^{-1}(x,\theta _0)]_0$ be the submatrix of $U^{-1}(x,\theta _0)$ that only contains the rows that are the left-eigenvectors of $Q(x,\theta _0)$ corresponding to the eigenvalues $\lambda _j(x,\theta _0) = 0$. We then have

$$\begin{aligned}{}[U^{-1}(x,\theta _0)]_0 \, Q(x,\theta _0) = 0 \,, \end{aligned}$$

and according to Lemma 3 this implies

$$\begin{aligned}{}[U^{-1}(x,\theta _0)]_0 \, F(x,\alpha ,\theta _0)&= 0 . \end{aligned}$$

(29)

Next, by using the definition of $s_\infty (y,x,\theta _0)$ and $h_\infty [ Q(x,\theta _0) ]$ in the main text we find

$$\begin{aligned} s_\infty (y,x,\theta _0)&= S(x,\theta _0) \, h_\infty [ Q(x,\theta _0) ] \, \delta (y) \\&= S(x,\theta _0) \, U(x,\theta _0) \; \textrm{diag}\left( \big [ \mathbbm {1}\left\{ \lambda _j(x,\theta _0) = 0 \right\} \big ]_{j=1,\ldots ,n_\mathcal{Y}} \right) \; U^{-1}(x,\theta _0) \, \delta (y) \\&= S(x,\theta _0) \, U_0(x,\theta _0) \; [U^{-1}(x,\theta _0)]_0 \, \delta (y), \end{aligned}$$

and therefore

$$\begin{aligned} \mathbb {E}\left[ s_{\infty }(Y,X,\theta _0) \, \big | \, X=x, \, A = \alpha \right]&= S(x,\theta _0) \, U_0(x,\theta _0) \; [U^{-1}(x,\theta _0)]_0 \, F(x,\alpha ,\theta _0) = 0 , \end{aligned}$$

where in the last step we used (29).

# part (ii): Let ${\mathfrak m}(x,\theta _0)$ be the $n_\mathcal{Y}$-vector with elements ${\mathfrak m}(y_{(k)}, x, \theta _0)$, $k=1,\ldots ,n_\mathcal{Y}$. Then, $\mathbb {E}\left[ {\mathfrak m}(Y, X, \theta _0) \, \big | \, X=x, \, A = \alpha \right] = 0$ can be written in vector notation as

$$\begin{aligned} {\mathfrak m}'(x,\theta _0) \, F(x,\alpha ,\theta _0)&= 0 . \end{aligned}$$

(30)

From the expression of $Q(x,\theta _0)$ in (27) we see that this implies ${\mathfrak m}'(x,\theta _0) Q(x,\theta _0) = 0$, that is, if (30) holds for all $\alpha \in \mathcal{A}$, then $Q(x,\theta _0)$ has a zero eigenvalue with corresponding left-eigenvector ${\mathfrak m}(x,\theta _0)$. This is the “if” part of the statement in part (ii) of the lemma.

Conversely, if $Q(x,\theta _0)$ has a zero eigenvalue, then let ${\mathfrak m}(x,\theta _0)$ be a corresponding left-eigenvector. We then have ${\mathfrak m}'(x,\theta _0) Q(x,\theta _0) = 0$. According to Lemma 3 this implies that (30) holds, or equivalently that $\mathbb {E}\left[ {\mathfrak m}(Y, X, \theta _0) \, \big | \, X=x, \, A = \alpha \right] = 0$. We have thus also shown the “only if” part of the statement in part (ii) of the lemma.

# part (iii): Let ${\mathfrak m}(y, x, \theta _0) \in \mathbb {R}$ be such that $\mathbb {E}\left[ {\mathfrak m}(Y, X, \theta _0) \, \big | \, X=x, \, A = \alpha \right] = 0$. We choose

$$\begin{aligned} s(y, x, \theta _0) = {\mathfrak m}(y, x, \theta _0) . \end{aligned}$$

Using the definition of $s^{(1)}(y,x,\theta )$ in (16) we then find $s^{(1)}(y,x,\theta _0) = {\mathfrak m}(y, x, \theta _0)$, and therefore also

$$\begin{aligned} s^{(q)}(y,x,\theta _0) = {\mathfrak m}(y, x, \theta _0) \,, \end{aligned}$$

for all $q \in \{1,2,\ldots \}$. We therefore also find $s_\infty (y,x,\theta _0) = \lim _{q \rightarrow \infty } s^{(q)}(y,x,\theta _0) = {\mathfrak m}(y, x, \theta _0)$, which is what we wanted to show. $\square$