Abstract
The synthetic control method (SCM) is widely used to evaluate causal effects under quasi-experimental designs. However, SCM suffers from weaknesses that compromise its accuracy, stability and meaningfulness, due to the nested optimization problem of covariate relevance and counterfactual weights. We propose a decoupling of both problems. We evaluate the economic effect of government formation deadlock in Spain-2016 and find that SCM method overestimates the effect by 0.23 pp. Furthermore, we replicate two studies and compare results from standard and decoupled SCM. Decoupled SCM offers higher accuracy and stability, while ensuring the economic meaningfulness of covariates used in building the counterfactual.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since the seminal works of Abadie and Gardeazábal (2003) and Abadie et al. (2010), the synthetic control method (SCM) has been increasingly adopted as a technique to evaluate causal effects under quasi-experimental design (see, among others, Montalvo 2011; Billmeier and Nannicini 2013; Cavallo et al. 2013; Kleven et al. 2013; Bohn et al. 2014; Percoco 2015; Acemoglu et al. 2016; Kreif et al. 2016; Albalate and Bel 2020; Sun et al. 2019). The method provides a practical solution to the evaluation of case studies in which either only a single unit or very few aggregate units are treated (countries, regions, cities, etc.) and it is considered one of the most influential recent contributions to empirical policy evaluation (for instance, Athey and Imbens 2017, p. 9). The SCM creates a hypothetical counterfactual (the synthetic unit) by taking the weighted average of pre-intervention outcomes from selected donors (control units). The impact of treatment is quantified by the simple difference between the treated unit and its synthetic cohort after the treatment (post-treatment period).
As discussed in a series of papers by its pioneering authors (see Abadie and Gardeazábal 2003; Abadie et al. 2010, 2015; Abadie and L’Hour 2019), the SCM has two main advantages over other methods, such as regression-based counterfactuals or nearest-neighbor matching. First, by being constrained to nonnegative weights that need to sum one, it does not impose a fixed number of matches and ensures sparsity, while avoiding negative weights or weights greater than one that would imply an unchecked extrapolation outside the support of the data and complicate the interpretation of the estimate. Second, weights are calculated to minimize the discrepancies between the treated unit and the synthetic control in the outcome and the values of certain matching variables or covariates. Thus, the SCM is intended to ensure that the synthetic unit reproduces the control unit not only in terms of the outcome, but also in terms of the drivers that explain the evolution of the outcome of the treated unit before treatment.
In spite of the influential contribution made by the SCM, the method suffers from some weaknesses that, if not properly addressed, may erode the reliability and robustness of its causal estimates and, consequently, of its policy implications. For instance, Ferman et al. (2020) have highlighted that lack of guidance on how to choose covariates gives researchers specification-searching opportunities that directly influence the choice of comparison units and therefore the signification of the results. Abadie (2020) also pointed out that even assuming a proper set of covariates and a counterfactual that matches the treated unit, interpolation biases may arise if this matching is obtained by averaging donors that have large differences in covariates but compensate each other to match the treated unit. As stated by Albalate et al. (2020), the bilevel optimization design of the SCM and its NP-hardFootnote 1 nature helps to explain why quasi-experimental methods for estimating covariate importance under the SCM are unstable and highly dependent on the donor pool, thus affecting weight estimation.
The contribution of this paper is twofold. First, we develop a proposal of decoupling synthetic control methods, to overcome the limitations of the bilevel design of the SCM. Our approach is simpler and more operational, since it breaks down the NP-hard problem of the nested optimization into two independent problems of quadratic optimization with linear constraints. The method we propose ensures robustness of the estimation of both covariate importance and the weights. By decoupling the estimation of covariate importance from that of weights, it minimizes interpolation biases and guarantees economic sense. To estimate covariate importance, we use a new methodology for estimating feature importance suggested by Lundberg and Lee (2017; 2019): SHapley Additive exPlanation (SHAP) Values. This method allows us to analyze the marginal effects and average contribution of the different features of a model, even in the case of nonparametric models. Thus, we can obtain sound estimates for each unit of the relation of the different covariates with the outcome and define a distance between the donor pool and the treated unit in terms of how covariates influence the outcome. To estimate weights, the procedure we use minimizes quadratic error in the pre-treatment outcome, restricting the donor pool to the most similar units to the treated unit. Roughly speaking, we obtain a synthetic control that is the benchmark that best reproduces the pre-treatment outcome and whose behavior is explained by the same factors that explain the treated unit.
Second, to illustrate the main advantages of our proposal, we apply both methods to an evaluation of the causal economic effects of the 10-month-long government formation impasse in Spain, after the December 2015 elections. In line with the approach taken by Albalate and Bel (2020) for the 18-month government formation deadlock in Belgium, we use the SCM to build an appropriate counterfactual to identify and isolate the gap between Spain’s actual GDP per capita growth rate and the rate at which it would have grown without a government formation deadlock. Our results indicate that the growth rate was not affected by government deadlock, ruling out any damage to the economy attributable to the institutional impasse. Moreover, as a robustness check of the advantages of the decoupled synthetic control method, we use our methodology to reproduce two previous studies: the impact of German reunification (analyzed in Abadie et al. 2015) and the effect of tobacco control programs in California (Abadie et al. 2010).
The rest of this paper is organized as follows: First, we describe the standard SCM and we evaluate its stability, consistency and economic meaningfulness. In light of the limitations identified, in Sect. 3 we propose a new decoupled SHAP-distance synthetic control method (DSD-SCM) that overcomes the limitations of the standard SCM. In Sect. 4, we apply both methods to the estimation of the causal economic effects of a long government formation deadlock in Spain between December 2015 and October 2016. We discuss the findings, focusing on the magnitude of the differences between the two methods (SCM vs. DSD-SCM), the advantages of the DSD-SCM, and the economic implications of the impasse. In Sect. 5, we present the replication of two case studies, as a robustness check of the improvements of our methodology with respect to the original synthetic control. Concretely, we replicate the analysis of the impact of German Reunification and of the effect of the tobacco control program in California. In Sect. 6, we offer our main conclusions and considerations about the new method proposed.
2 The synthetic control method: an evaluation of its stability, consistency and meaningfulness
The synthetic control method builds a counterfactual of a specific treated unit as a weighted average of a number of control units (the so-called donor pool), to reproduce what would have been its performance if it had not been exposed to the treatment and to identify, by its difference with respect to reality, the causal effect of the policy. In this section, we first describe the main features of the SCM, and then, we evaluate its consistency and stability.
2.1 The working of the SCM
The SCM assumes there are J control units and observations during T periods (pre-treatment). Let \(X_{TU}\) be a (\(K\times 1\)) vector of the outcome growth predictors of the treated unit (the covariates). Let \(X = (X_1,\ldots , X_J)\) be a (\(K \times J\)) matrix which contains the values of the same variables for the J possible control units. Both \(X_{TU}\) and X could include pre-treatment observations of the dependent variable. Let V be a diagonal matrix with nonnegative components reflecting the relative importance of the different growth predictors. Let \(Y_{TU}\) be a (\(T \times 1\)) vector whose elements are the values of the outcome of the treated unit for the T periods, and \(Y = (Y_1,\ldots , Y_J)\) a (\(T\times J\)) matrix whose elements are the values of the outcome of the control units. Then, the counterfactual is built as \(Y W^{*}\), where \(W^{*} = (w_1^{*},\ldots , w_J^{*})\) is a (\(J \times 1\)) vector containing the weights of the control units in the counterfactual. \(W^{*}\) is chosen to minimize the objective function \( D(W) = (X_{TU} - XW)'V(X_{TU} - XW)\), subject to \(w_i \ge 0\) and \(\sum _{i=1}^{J} w_i = 1\).
V is chosen as \( V = {\mathrm{arg min}}_{V \in \mathcal {V}} (Y_{TU} - YW^{*}(V))'(Y_{TU} - YW^{*}(V))\), where \(\mathcal {V}\) is the set of all nonnegative diagonal \((K \times K)\) matrices, whose Euclidean norm is one. Notice that V is the key element for determining \(W^{*}\) and avoiding interpolation biases, since it defines the relative importance of the adjustment of each covariate in the counterfactual.
Several contributions have recently been made aimed at extending the scope of use of the SCM and improving its accuracy and robustness. As regards the former, Powell (2018) suggested a way to estimate policy effects when the outcomes of the treated unit lie outside the convex hull of the outcomes of the other units. Since the treated unit may be part of a synthetic control for a non-treated unit, the post-treatment outcome differences for these units are informative of the policy effect. In recent studies, the SCM has been extended to contexts with disaggregated data, where samples contain large numbers of treated and untreated units, and interest lies in the average effect of the treatment among the treated (see Abadie and L’Hour 2019). Building synthetic controls for each of the treated units as opposed to a synthetic control for the average treated unit has been proposed in order to minimize interpolation biases.
To increase SCM accuracy and robustness, studies have addressed three issues: the role of covariates, the estimation of weights, and the best way to gauge the uncertainty of the estimated treatment effect. As regards the first of these, Doudchenko and Imbens (2016), Gobillon and Magnac (2016) and Kaul et al. (2015) showed that high accuracy can only be achieved if lagged outcomes are included as covariates. However, by so doing, other covariates may become irrelevant, which could lead to interpolation bias if the set of pre-treatment outcomes is not long enough (Botosaru and Bruno (2019)), or if there is an imperfect pre-treatment fit (Arkhangelsky et al. 2018). Ferman et al. (2020) have also highlighted that this lack of guidance on how to choose covariates gives researchers specification-searching opportunities that directly influence the choice of comparison units and the signification of the results. Indeed, they showed that with few pre-treatment periods (between 10 and 30), a researcher would have substantial opportunities to select statistically significant specifications even when the null hypothesis is true. Moreover, Klobner et al. (2015) showed that the current SCM suffers from high numerical instability in covariate importance and weights.
Studies of the estimation of weights have proposed different strategies to reduce interpolation biases. Hastie et al. (2009), and Hastie et al. (2015) combined a Lasso and Ridge regularization to capture a preference for a small number of nonzero weights, as well as for smaller weights. Likewise, Abadie and L’Hour (2019) introduced a penalization parameter that trades off pairwise matching discrepancies with respect to the characteristics of each unit in the synthetic control against matching discrepancies with respect to the characteristics of the synthetic control unit as a whole.
Finally, to gauge the uncertainty of the estimated treatment effect, the SCM compares the estimated treatment effect with the “effects” estimated from placebo tests in which the treatment is randomly assigned to a control unit (see Abadie and Gardeazábal 2003). Building multiple synthetic controls by leaving countries out of the optimal control has also been proposed (Abadie and L’Hour 2019). In this regard, Xu (2017) proposed a parametric bootstrap procedure to obtain confidence intervals of the estimates of the treatment effect.
Following Albalate et al. (2020), in the next subsection, we show that the bilevel design of the SCM is at the root cause of the main concerns related to its stability, consistency and meaningfulness.
2.2 An evaluation of the SCM as a bilevel problem
The SCM is characterized as a bilevel problem. Such problems are optimization problems (upper level) that contain another optimization problem as a constraint (lower level).
Definition 1
For the upper-level objective function \(F : \mathrm{I\!R}^n \times \mathrm{I\!R}^m \rightarrow \mathrm{I\!R}\) and lower-level objective function \(f : \mathrm{I\!R}^n \times \mathrm{I\!R}^m \rightarrow \mathrm{I\!R} \) the bilevel problem is given by
where \(G_k : X_U \times X_L \rightarrow \mathrm{I\!R}\), \(k = 1,\ldots , K\) denote the upper-level constraints, and \(g_j : X_U \times X_L \rightarrow \mathrm{I\!R}\) represent the lower-level constraints, respectively. Equality constraints may also exist that have been avoided for brevity.
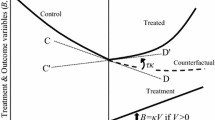
Figure 1 illustrates a general bilevel problem. Given a \(x_u\) vector, \(x_l^{*}\) is the optimal lower-level vector for the lower-level optimization. But, as seen in the figure, the solution \((x_l^{*}, x_u)\) is not optimal for the upper-level optimization given \(x_l^{*}\).
The SCM proposed by Abadie et Gardeazabal is a bilevel optimization problem of the form:
Bilevel programming is known to be strongly NP-hard (Hansen et al. 1992), and it has been proven that merely evaluating a solution for optimality is also a NP-hard task (Vicente et al. 1994). Moreover, the hierarchical structure may introduce difficulties such as non-convexity and disconnectedness (that is, that the solution set can be separated into two disjoint sets) even for simpler instances of bilevel optimization, which may cause solutions to be highly unstable to small perturbations and the algorithm to converge to different local optima.
In the particular case of the SCM method, the flaws of bilevel optimization imply that the solution V can be completely arbitrary and highly unstable to small perturbations. As a result, weights are also unstable and V does not offer reliable insights in terms of economic meaningfulness since it can be driven by interpolation biases. In Appendix I (supplementary materials), we illustrate the aforementioned flaws with two simple examples.
In Sect. 6, we present an empirical assessment of the numerical instability for the case study of Spain’s government deadlock. As seen there, current implementation of the SCM method can lead to very unstable results just by removing or adding to the donor pool units that are given no weights in the synthetic control. Although this is clearly counterintuitive and should not be possible, it is due to the fact that the implementation of the optimization problem is done using an interior point method (Abadie et al. 2011). That is, weights can be given values close to zero, but not zero. Thus, although the final result is presented as 0, the real value for the algorithm could be of the order of \(10^{-7}\) or \(10^{-8}\) (depending on the margin parameter given to the function). Therefore, removing units with zero weight in the solution is equivalent to introduce a very small perturbation, which, as we have showed, can be devastating in terms of optimal parameters and goodness of fit.
3 The decoupled SHAP-distance-based synthetic control method
The aim of this section is to propose and present a modification of the SCM that can guarantee economic meaningfulness and the stability of feature importance, at the same time as it increases the robustness of the estimation of weights and treatment effect. Our proposal is coined as the decoupled SHAP-distance synthetic control method (DSD-SCM) and is designed as an operational alternative to the use of the SCM that involves less complexity than the standard approach due to the NP-hard nature of bilevel optimization and guarantees higher stability and economic sense.
In the previous section, we showed that the minimization problem of SCM is defined over covariates and that feature importance estimation is nested to weights, potentially leading to considerable instability and a lack of economic meaningfulness. Therefore, we propose decoupling feature importance from weight estimation by defining the optimization problem of the SCM as a minimization of the error in the pre-treatment outcome adjustment, conditional to using units that are as similar as possible to the treatment unit. As highlighted by Abadie (2020), donors’ similarity to the treated unit is one of the most critical requirements for the synthetic method to be an appropriate tool for policy evaluation. Hence, we also present a concrete methodology for feature estimation and unit similarity that guarantees economic sense and stability, the regularized SHAP-based distance. However, other distances or previous expert knowledge on the feature importance would also be worth considering.
3.1 Optimization function
Let us note by \(d(X_{TU}, X_i)\) a distance between the treated unit and the unit i, dependent on their respective vector of covariates \(X_{TU}\), \(X_i\). The vector of weights \(W^{*}\) in our modified method is chosen as
subject to \(W > 0\) and \(\sum _{i = 1}^l w_i = 1\). \(\tilde{Y}^t\) is a vector that contains the outcome in time t of the top L most similar units to the treated unit. This optimization problem is a minimization of a quadratic and positive-definite function with linear constraints. The number L of units is chosen to balance the potential trade-off between a pure minimization of the adjustment error and the similarity to the treated unit. We require all the units entering the synthetic control to be similar to the treated unit so as to minimize interpolation biases (as suggested in Abadie et al. (2015), Abadie (2020)). Roughly speaking, this is equivalent to saying that, for example, what most resembles a medium-size house is not the average of a small and a big house, but the average of two medium-size houses.
As we will see next, in our procedure the distance function is not linked to the weights, which in the SCM contributed to increasing instability and reducing economic meaningfulness, but determined independently through an econometric model that involves another quadratic minimization.
Notice that the choice of L is not uniquely determined and depends on several conditionings. For example, the stronger the relation between the covariates and output evolution, the more sense it makes to choose a lower value of L. In the next section, we present a method for assessing the importance of L and for choosing an adequate value.
3.2 SHAP-based distance
Intuitively, we would like to consider that a unit is similar to the treated unit if their outcomes evolved in a similar way before the treatment and for similar reasons. For example, a 99% correlation in the evolution of GDP per capita between two countries would tell us nothing about their similarity if one has an economy based on natural resources that grew because of a hike in petrol prices, whereas the other’s growth was attributable to manufacturing exports. In short, to define a distance between units it is critical we understand the relationship between their outcome and their covariates. To do so, we propose the following methodology. First, we build a model of the evolution of the outcome using the covariates as explanatory variables. Second, we use one of the newest and most popular methods of model interpretation to estimate the average marginal contribution of each feature to each prediction of the model: the SHapley Additive exPlanation or SHAP values. Finally, by estimating the SHAP values, we are able to define a distance based on feature importance and average contributions to outcome evolution.
3.2.1 Outcome evolution model
Let us note the growth rate of unit i by \(g_i^t = \frac{Y_i^t-Y_i^{t-1}}{Y_i^{t-1}}\), where \(i \in \{1,\ldots , J,TU\}\). Recall that \(Y_{TU}\) is the \((T \times 1)\) vector containing the values of the outcome for the treated unit, and \(Y = (Y_{1},{\ldots } Y_{J})\) the \((T \times J)\) matrix with values of the outcome for the control units.
Let us consider \(G(X_i^s|s \in \{1,\ldots ,t \})\) a model for \(g^{t}\), that is \(G(X^s_{i}|t \in \{1,\ldots ,T \}) = g_i^{t} + \varepsilon _{t}\), where \(\varepsilon _{t}\) is the error term at time t. Notice that G is a model that depends on covariates, and for which no concrete functional form is required. It could be a linear model, but also a nonlinear and even a nonparametric model, such as a gradient boosting tree.Footnote 2 It may also include past information from covariates. It is important to highlight that the robustness, stability and consistency of the variable importance are inherited by the properties of the modeling technique G. For instance, if we use OLS, under the hypothesis of homoscedasticity, no autocorrelation, and normality of the error terms, estimates are consistent, efficient and non-biased. As we will see in the empirical illustrations in Sects. 4 and 5, the decoupling ensures that the importance attributed to each variable is stable and practically does not change even if we add or remove countries from the donor pool, while it is highly unstable for the original SCM.
3.2.2 Shapley additive explanation values
SHAP values have been proposed as a unified framework for assigning feature importance to parametric and nonparametric models (Lundberg and Lee 2017 and Lundberg and Lee 2019). Roughly speaking, given an instance x, the SHAP value of feature i on x corresponds to the marginal impact of feature i on the output of the model, with respect to other instances that share some of the features with x but not i.
Formally, let us consider the subset S of the set of input variables V and \(G_x(S) = E[G(x) | x_S]\) the expected value of the model G conditioned on the subset of input features S. Then, SHAP values are the combination of these conditional expectations:
where the combinations are needed because for nonlinear functions the order in which features are introduced matters. For a linear model \(G(x) = \sum _{i = 1}^{k} \alpha _i x_i\), the SHAP value is straightforward: \(\phi _j(x) = \alpha _j(\hat{x}_j - E(x_j))\). Notice that model estimation, which is required for the SHAP value, is based on a quadratic minimization, which consists of the second quadratic problem of the DSD-SCM.
Figure 2 shows how the SHAP values explain the output of a function f as a sum of the effects \(\psi _i\) of each feature being introduced into a conditional expectation.
3.2.3 Feature importance and SHAP-based distance
Let us note by \(\phi _m(X_{1}^t)\) the SHAP value of the covariate m for the treated unit at time t. Then, we can estimate the relative importance of the covariate m in the outcome evolution of the treated unit, \(RI_m\), as:
where J is the total number of covariates and T the total number of observations.
Therefore, we can define V as the diagonal matrix such that \(V_{mm} = RI_m\). This matrix has economic sense, because it is exactly estimating the importance of each covariate on the outcome evolution of the treated unit before the treatment. It is also stable in the sense that it relies on the stability of parameter estimation or model inclusion of the different variables. Thus, features whose relation with outcome is less robust will tend to not be considered (for example, discarded in a linear model if their p value is lower than 0.1 or 0.05) or be assigned lower relevance.
Having estimated V, let define \(AC_m^{i}\) the average contribution of feature m in outcome evolution for unit i:
Then, we can define the SHAP distance between non-treated unit \(U_i\) and the treated unit TU as:
where \(AC^{i} = (AC_1^{i},\ldots , AC_J^{i})\) and \(AC^{TU} = (AC_1^{TU},\ldots , AC_J^{TU})\) are the vectors containing the average contributions of the covariates for unit \(U_i\) and the treated unit TU.
3.2.4 Choice of the size of the restricted pool
Given L, let us note by W(L) the solution of (1) and by \(R^2(L)\) as the \(R-squared\)Footnote 3 of the synthetic control \(Y(L) = W(L)\tilde{Y}\). Let us note by \(l \le L\) the number of units that have a positive weight in W(L). Let us define the covariate distance between the treated unit and Y(L) as \(d(L) = \frac{\sum _{i=1}^{l(L)} d(X_{TU}, X_i)}{l(L)}\). Since units are ordered by similarity, given \(L_1 > L_2\), we have that \(d(L_1) \ge d(L_2)\) and \(R^2(L_1) \ge R^2(L_2)\). The higher the number of units, the larger the distance and the higher the goodness of fit. Hence, \(d(J) \ge d(L)\) and \(R^2(J) \ge R^2(L)\) for \(L \in 1,\ldots , J\). Notice that, in particular, W(J) is equivalent to the constrained regression synthetic method suggested in Doudchenko and Imbens (2016)
Let us define also the error loss of L as the ratio
and the similarity gain as
The error loss is the ratio between the error of the counterfactual Y(L) and the best potential counterfactual in terms of goodness of fit, Y(J). The similarity gain captures the relative increase in similarity between Y(L) and the treated unit, with respect the similarity between Y(J) and the treated. The lower the EL the better, since this means the goodness of fit is near to the maximum possible. Likewise, the higher the SG the better, since this means that the countries in the synthetic control are closer to the treated unit. As we stated in Sect. 3.2.1, L sets a threshold in terms of goodness of fit with respect to similarity loss (or, conversely, in terms of error loss with respect similarity gain) for a new unit to be considered in the counterfactual. Therefore, we propose finding the optimal value of L as the value L, which minimizes the ELSG (error loss–similarity gain) ratio. That is:
where \(L_{\nu }\) is the minimum L such that \(R^2(L_{\nu }) > \nu R^2(J)\). That is, values of L that ensure at less a certain level of goodness of fit, to prevent degenerated cases where the distance is almost no related with outcome (for \(L = J\), the ELSG ratio is defined as \(\infty \)). We recommend using \(\nu = 0.9\) or 0.95. By doing so, it is guaranteed that the goodness of fit of the DSD-SCM will be equal to or higher than that of the SCM, unless the SCM uses all pre-treatment outcomes as the only covariates, and control units that do not resemble the treated unit in the underlying drivers of the outcome. As highlighted in Abadie (2020), the asymptotic bias of the SC estimator should be small in situations where one would expect to have a close-to-perfect fit for a large pre-treatment period. Hence, ensuring that pre-treatment fit is (in general) at least as in the original SC ensures also that any bias in the estimation of the treatment effect is expected to be lower.
Notice that, in comparison with other extensions that limit the donor pool for regularization purposes, such as the best subset selection procedure described in Doudchenko and Imbens (2016), our restriction is primarily linked to similarity. Therefore, in our method, the role of the distance is to offer practical guidance for the applied researcher on the reliability of the estimates, specially in cases where the pre-treatment period is not that large, and in which could be biases in the estimation. For example, if the goodness of fit of the outcome model is low, similarity between units is expected to be less reliable, the number L is expected to be closer to J, and therefore, the researcher may include additional covariates to minimize the risk of interpolation biases, or be more cautious about the conclusions derived from the estimation of the treatment effect. In particular, this reduces the risk of using specification search, because it makes it clear whether the similarity function between units is accurate or not.
Although we have presented here the SHAP distance, any other distance that ensures economic and statistical sense might be used. The main contribution of our proposal is the decoupling of the minimization involved in the original SCM, which helps to prevent instability and biases in the estimates.
4 Empirical illustration: the economic effects of the government formation deadlock in Spain, 2016
Although hardly new, lengthy government formation processes in parliamentary regimes after a general election are becoming more usual in Europe. In the last two decades, there have been seven cases of government formation deadlocks lasting more than three months: six months in Belgium after the June 2007 election, eighteen months after the June 2010 election and sixteen months after the May 2019 election, both of them again in Belgium, ten months in Spain after the December 2015 election and ten months after the April 2019 election, seven months in the Netherlands after the March 2017 election, and six months in Germany after the September 2017 election.
Contrary to widespread claims that government deadlocks and the associated political instability harm a country’s growth by disrupting economic policies that might otherwise promote better performance (Alesina et al. 1996; Angelopoulos and Economides 2008; Aisen and Veiga 2013), studies of recent impasses provide evidence that this might not always be the case. Using the SCM to build an appropriate counterfactual to reproduce Belgium’s economic growth if it had had a full-powered government, Albalate and Bel (2020) reported a nonnegative effect on economic growth during the 18 months of government deadlock in that country following the June 2010 election. The study suggests that certain characteristics peculiar to Belgium could be behind this (perhaps) counterintuitive result. First, the country’s highly decentralized multilevel governance, which assigns a considerable number of functions and powers to the communities and regions, at the same time as the European Union’s institutions have absorbed some of the core functions performed by conventional Member States (Bouckaert and Brans 2012; Hooghe 2012). Second, the existence of robust, efficient institutions, outside government, that played a positive role in protecting the economy from the difficulties of the impasse. Third, the delay in fiscal consolidation that could have caused higher short-term economic growth than might otherwise have been expected.
4.1 Spain’s political deadlock
The general election held in Spain on December 20, 2015, resulted in a fragmented political landscape following the emergence of two new political parties: Podemos (left-wing) and Ciudadanos (Cs) (right-wing). In spite of winning the election, the Partido Popular (PP) (right-wing), who ruled Spain with an absolute majority between 2011 and 2015, lost 63 seats and got 123 seats, far from the 176 needed for the majority. Due to the numerous corruption cases in which leading members of the PP were then embroiled, the other main right-wing party, Cs, refused to facilitate a right-wing government and offered their votes to the Partido Socialista Obrero Española (PSOE). Together the two parties controlled 130 of the chamber’s 350 seats and needed either the support of Podemos (69 seats) or the abstention of the PP. Neither of the two requirements was met, and fresh elections were held in June 2016. The 2016 election results reinforced the position of the PP, which won 14 additional seats, totaling 137. However, it was still not enough to form a government. After two months of negotiations, Cs (along with the Coalición Canaria, a right-wing regional party in the Canary Islands) announced their support for Mariano Rajoy, PP’s candidate for the Presidency. With 170 votes and the controversial abstention of the PSOE, Rajoy was re-elected President of Spain on October 29, 2016, ending a ten-month-long deadlock.
Despite this period of impasse and the limited powers of a caretaker government, Spain’s economic performance did not appear to suffer greatly. Indeed, even the Spanish Central Bank (Banco de España) published an article in 2017 estimating the negative effect of the political uncertainty of the previous year at just 0.1% of GDP, although this result was not statistically significant (see Gil, Pérez and Urtasun, 2017). If we observe the GDP growth rate (Fig. 3), Spain’s performance during 2016 was slightly higher than the EU average, and better than the euro area average, as it had been in 2015. However, as Albalate and Bel (2020) discuss in their evaluation of the 18-month government deadlock in Belgium, this comparison tells us only how Spain’s performance compared to that of the other countries of Europe, but it offers no causal insights as to how it might have performed had it had a full-powered government. Thus, we need to build a counterfactual to reproduce how Spain would have performed in the absence of its government formation deadlock.
4.2 Results with the standard synthetic control method
To evaluate the robustness and meaningfulness of the SCM and the advantages of implementing our proposed DSD-SCM alternative, we compare the estimates provided by the two methods of the causal effects of this political deadlock. First, we apply the standard SCM, with and without outcome lags in the covariates, to show that in both cases covariate importance is highly unstable, highly dependent on the donor pool and lacking in economic meaningfulness. Second, we implement our proposed SHAP-distance based synthetic control method to show how this approach addresses and avoids the main weaknesses of SCM, providing more stable, accurate and meaningful estimates.
The donor pool used in the comparison includes a sample of the EU-28 countries. Malta and Luxembourg had to be excluded given the amount of missing data for some of the key predictors used in the analysis. Belgium was excluded since it was also affected by a lengthy government deadlock between 2010 and 2011, and Ireland because of the marked change in GDP pc in 2014 (26.3% growth rate) due to the reallocation of the intellectual property of large multinational firms.
Tables 1 and 2 report the pre-treatment values of several variables typically associated with a country’s growth potential and used as covariates, as well as their relative importance, for the case without and with lagged outcomes. Table 3 presents the weight matrix for the donor pool, where the synthetic weight is the country weight assigned to each country. When the lagged outcomes are not included, the synthetic Spain is made up of the four main contributors: Portugal (33.5%), France (30.7%), Greece (23.3%), and Italy (12.0%). Finland also plays a role, but only a minor one (0.4%). When using this counterfactual to predict Spain’s GDP per capita from 2001 to 2015, R\(^{2}\) is 92.60% and the mean absolute percentage error (MAPE) is 0.64%. When initial and final outcomes are included, the results are quite similar. The main contributors remain the same, although their relative importance changes. The minor role played by Finland disappears, and instead, Denmark (3.7%) and Sweden (2.6%) enter the synthetic control. The goodness of fit improves slightly (R\(^{2}\) = 93.44%) and the MAPE remains unchanged at 0.64.
Figure 4 shows the GDP per capita evolution of the real and synthetic Spain built with and without lagged outcomes. In both cases, the growth rate during the 2016 deadlock was around 1.8 percentage points (p.p.) higher than expected, while in 2017 and 2018 the gap was reduced to 0.4 and 0.1 p.p., respectively.
To evaluate the robustness of the SCM, two placebo tests have been widely used: in-time and in-space. In the former, the SCM is applied considering that the treatment occurred in an earlier timeframe (i.e., the treatment is reassigned to occur during the pre-treatment period) and so the control is built using observations up to this new moment in time. The test examines the uncertainty associated with making a prediction after the last observation considered for the estimation. In the in-space test, the SCM is applied to the control units as if they too had been treated at the same moment of time as the treated unit. Hence, it tests the uncertainty associated with the volatility of outcomes of the control units during the treatment.
However, neither of these two tests evaluates the stability of covariate importance and weights, and their economic foundations, which are the main ideas on which the SCM is based. Even if the methodology passes the in-time and in-space placebo tests, it would be difficult to rely on its results if, for example, V had no relation with economic theory. Moreover, if a placebo test fails to confirm robustness, it is unable to tell us whether it is because the treatment had no significant effect or because the methodology was not properly applied and its accuracy could be improved (for example, by adding new covariates).
Here, therefore, we analyze the stability and economic meaningfulness of covariate importance and weights and show that SCM does not guarantee any of them, even in those cases when the methodology passes the placebo tests.
As Fig. 4 shows, in this particular case, including lagged outcomes has almost no impact in terms of the goodness of fit and the estimation of the treatment effect. Nonetheless, as recognized elsewhere, including Doudchenko and Imbens (2016), Gobillon and Magnac (2016) and Kaul et al. (2015), variable importance is greatly affected, and the covariates become almost irrelevant (Tables 1 and 2). This might not, however, be important in terms of the economic foundations and robustness of V. If the covariates reflect the economy drivers, they could also be influencing lagged outcomes in the sense that countries with more similar values for these covariates would also have similar outcomes. This means that the importance of the covariates could be hidden behind the lagged outcomes; the only problem being that the inclusion of lagged outcomes makes it almost impossible to gain any economic insights from V and to judge whether the estimations are the result of an interpolation bias.
However, here, an analysis of V shows that its estimation is neither consistent with the economic foundations nor is it stable. First, if we turn our attention to the SCM without lagged outcomes, the most important variables are openness (54.1%) and low education (26.0%), while unemployment, investment and debt have almost no influence (4.2, 1.1 and 0%, respectively). The Spanish economy’s cumulative growth per capita in real terms from 2000 to 2007 was 2.8 p.p. higher than that of the euro area, driven mainly by exceptionally high levels of investment due to the housing bubble (Akin et al. 2014). Total investment in Spain averaged 27.7% of GDP from 2000 to 2007, 5.2 p.p. higher than in the euro area. Once the crisis began, investment dropped significantly, reaching a minimum of 17.4% in 2013, almost 13 p.p. lower than its maximum in 2006. In the euro area, the fall in investment was much lower: from a maximum of 23.4% in 2007 to a minimum of 19.7% in 2013. Unemployment more than tripled, from 8.2% in 2007 to a maximum of 27% in the first quarter of 2013, the highest level in the euro area. As a result, Spain’s public debt almost tripled, growing from 35.8% of GDP in 2007 to 99.3% in 2015. In the euro area, however, the increase was much lower, from 65.9 to 90.8%.
Thus, it has no solid economic foundations to devise a similarity measure with respect to Spain that assigns no importance to debt, unemployment and investment, while at the same time assigning almost 70% of the importance to the degree of openness and the percentage of the population with a low education. Openness, for example, remained largely stable before and during the crisis. In the period 2000–2007, imports and exports accounted for 56.2% of GDP, while in 2008–2015 they represented 58.2%. In conclusion, openness and low education levels are not assigned a high level of importance because they are the main drivers of Spain’s economy, but rather because a number of countries whose real GDP per capita evolution correlated highly with Spain’s presented similar levels of openness and low education (see Appendix II in supplementary materials).
Secondly, because of the interpolation bias, covariate importance, weights and goodness of fit are highly unstable and dependent on the donor pool (as in Klobner et al. (2015)). Table 4 shows the average importance and standard deviation for 100 simulations after removing three countries from the donor pool that were assigned no weights in the synthetic Spain. The standard deviation is higher than 50% of the average importance estimation for almost all covariates, both with and without lagged outcomes. As a result, the distance between the synthetic and real Spain is modified and, so, the weights are adjusted accordingly (Table 5). Yet, weight instability may not necessarily compromise the SCM. Indeed, it might just be the result of the fact that the donors are so similar to each other that a small perturbation in V modifies the selection of one of them into the control. However, as Table 6 shows, the goodness of fit is significantly affected for the SCM without lagged outcomes and slightly affected for SCM with lagged outcomes.
Given the high instability of the goodness of fit without lagged outcomes, the SCM does not pass the in-time placebo test using 2012 as the treatment (Fig. 5). However, the same does not hold true for the SCM with lagged outcomes. Yet, in both cases, the placebo test fails to provide any information as to why the methodology works properly or not, or whether it can be improved.
In conclusion, we have shown, first, that covariate importance may not be consistent with economic theory and provide no meaningful insights; second, that this lack of meaning is due to interpolation biases that make estimations highly unstable and dependent on irrelevant countries (i.e., countries with no weight) in the donor pool; and, third, that although including lagged outcomes may make the results more robust in terms of goodness of fit, it does not solve the problem of meaning and stability of covariate importance. Moreover, it also tends to make the other covariates irrelevant, thus compromising the main idea behind the SCM. Finally, we have also shown that standard robustness checks, such as the in-time placebo test, may be unable to identify these flaws and to suggest any strategy to improve the results.
4.3 Results with the decoupled SHAP-distance synthetic control
In this subsection, we build the synthetic Spain adhering to the strategy described in Section III, that is we build a model of GDP per capita growth, define a distance using SHAP values, select a regularization parameter and estimate optimal weights. We consider a linear model of the GDP per capita growth rate from 2001 to 2015, using as our explanatory variables the covariates used in the previous subsection and all the countries in the donor pool including Spain. The results are presented in Table 7 (variables with gr indicate growth rates of the covariate). Note that while the covariates are able to explain 73.33% of the variation in economic growth, around 25% of the variation remains unexplained. Thus, a synthetic control that relies solely on the covariates would not be sufficiently accurate or robust.
Table 8 shows the feature importance of the different covariates of economic growth in Spain and the donor pool. According to the DSD-SCM results, Spain’s economic evolution has been characterized primarily by high levels of unemployment and debt growth. Conditional convergence has had a much lower impact on Spain than it has had on the donor pool, mainly because Spain’s GDP was already very close to the average of the selected countries (a 6% difference, on average, during the period). Using covariate importance, we define the distance between countries in the donor pool and Spain as in (2), but normalizing to be between 0 and 1. The corresponding results are presented in Table 9.
Based on the ELSG ratio (as described in Section II.B), the optimal L is 6. Restricting the donor pool to the six most similar countries reduces the number of units in the counterfactual from six (case with no restriction) to four, almost halves the distance with respect to the treated unit (from 0.21 to 0.11) and implies a loss of only 0.45 p.p. in R\(^{2}\) with respect to the counterfactual that uses all the units in the donor pool (96.84% vs 96.39%). It is worth pointing out that even in the case of no regularization, the average distance of countries in the synthetic control is much lower than the average distance of those in the donor pool (0.21 vs. 0.33). This means that the more similar countries are to Spain, the more likely they are to be selected.
When using the DSD-SCM with \(L^{*} = 6\), the counterfactual consists of Portugal (34.5%), UK (27.5%), Italy (19.4%), and Greece (18.2%). The R\(^{2}\) is 96.39% and the MAPE 0.42%. Notice that this counterfactual uses fewer countries than the standard method and obtains between 3 and 4 additional percentage points in R\(^{2}\). Hence, the DSD-SCM ensures greater economic meaningfulness of feature importance and achieves better results while reducing the number of parameters.
Figure 6 shows the different counterfactuals we have built. In all cases, growth in 2016 was higher than expected, lying in a range between 1.58 p.p. (DSD-SCM) and 1.81 p.p. (SCM without lagged outcomes). Thus, SCM overestimates the effect of the Spanish deadlock by a 0.23 p.p. However, our primary goal was to provide a more robust method. As Table 10 shows, the covariate importance estimates are highly stable, with standard deviations of 2 p.p. As a result, in all simulations, the same countries are selected and assigned the same weights.
Finally, Fig. 7 shows the results of the in-time placebo test. In the case of the in-space placebo test, we excluded countries whose MAPE for 2001–2015 was three times higher than Spain’s. Thus, countries with an MAPE greater than 1.2% were excluded when we compared the base model to the best placebos (with eight countries surviving). The comparison showed a difference in the average treatment effect in 2016 for placebo countries of - 0.006 p.p. in the growth rate and of 0.92 p.p. in the standard deviation. The treatment effect for Spain is estimated at 1.58, which is higher than 0 at a 7.8% confidence level, assuming a normal distribution of the placebo estimates.
5 Robustness check: the German reunification and the effect of tobacco control programs in California
5.1 German Reunification
Abadie et al. (2015) evaluate the impact of the German Reunification in 1991 on GDP per capita, considering 1971 to 1980 as the pre-treatment period and 16 OECD countries as the donor pool. They considered five covariates: trade openness, inflation rate, industry share, schooling levels, and invest ment rate. We replicate the analysis using the DSD-SCM.
As investment rate and schooling levels are given on 5-year basis, we build the model of GDP growth in 5-year basis, starting from 1970. As can be seen in Table 11, only inflation and initial GDP (conditional convergence) are relevant. Thus, including other covariates would not ensure capturing similarity in economic growth dynamics, since those drivers are not statistically relevant. The relative importance for West Germany for inflation is 11.4% and for conditional convergence 88.6%. This explains why GDP has to be used as a covariate in Abadie et al. (2015): only by including conditional convergence a reasonable fit in terms of outcome can be achieved.
The best ELSG ratio is achieved with L = 7. The counterfactual consists of 40.4% Austria, 33.3% USA, 19.8% Netherlands, and 6.5% France. The MAPE is 0.64%. In comparison, the counterfactual in the original paper consists of 6 countries (42% Austria, 22% USA, 16% Japan, 11% Switzerland, and 9% Netherlands) and its MAPE is 0.85%. Notice that the counterfactual with the decoupled method has less units and higher goodness of fit. Both counterfactuals share 3 units, which account for 93.5% of the importance in the decoupled and 73% in the original synthetic method. Remarkably, France, which is the 6th most similar country to West Germany according to the similarity distance in Abadie et al. (2015), does not belong to the original counterfactual, while it has a 6.5% weight in the DSD-SCM. Japan and Switzerland, which have a positive weight in the original counterfactual, are among the less similar countries (10th and 13th, respectively). Thus, the original counterfactual is build with countries that the method considers not to be similar to the treated unit. If we applied the decoupled method with the original distance, we get that the best ELSG ratio is achieved with \(L = 9\) units, instead of seven, and the counterfactual would be exactly the same as the one built with the SHAP distance. As explained in Sect. 3.2.4, the larger the number of similar units needed for the second step of the decoupled method, the lower the reliability of the similarity measure. Hence, decoupling the problem allows to identify the lower economic sense of the distance built in the nested optimization.
Figure 8 shows the results. Both methods estimate a clear negative impact, but they differ in the estimation. Concretely, GDP per capita in West Germany in 2003 was 4283.5 USD lower that it would have been without the Reunification according to the DSD-SCM, while the difference accounted for 3379.3 USD in the original estimation. It is worth mentioning that other extensions of the synthetic control method, such as the constrained regression or the best–subset (Doudchenko and Imbens 2016) discussed in Sect. 3.2, also find a negative impact, although lower than the estimated by the decoupled synthetic. Concretely, the impact in year 1995 for these extensions lays between 790 and 1019 USD, while in our case is 1301 USD.
Moreover, results obtained with the decoupled synthetic method are also robust to placebo test in time and space, as can be seen in Figs. 9 and 10. The placebo test in time considered a placebo re-unification effect from 1985 to 1990. For the placebo in space, all units with a MAPE lower than three times that of the decoupled synthetic were considered.
In conclusion, the comparison between the original synthetic control method and our decoupled version in the German re-unification shows that while both methods get a similar conclusion, the decoupled ensures higher economic sense and stability in the similarity measure between countries (for instance, using the distance metric of the original synthetic would require the top 9 most similar countries instead of the top 7 to get the same goodness of fit) and achieves higher goodness of fit.
5.2 California’s tobacco control program
Abadie et al. (2010) estimate the effect of California’s Tobacco Control Program implemented in 1988, in terms of per capita cigarettes sales. They use annual state-level panel data from the period 1970 to 2000. They consider the following covariates: income per capita (in natural logarithm), beer consumption, percentage of population aged 15–24, and the average retail price of a cigarettes pack. In order to increase the goodness of fit of the counterfactual, they are also forced to include three lagged outcomes: cigarettes sales in 1975, 1980 and 1988. The donor pool consists of 38 states where no control program or cigarettes’ tax raise was implemented during the period of analysis. The counterfactual build using the SCM consists of 5 states: Utah (33.4%), Nevada (23.4%), Montana (19.9%), Colorado (16.4%), and Connecticut (6.9%). Remarkably, 95% of the covariate importance is given to previous lagged outcomes. Indeed, authors highlight that the counterfactual does not reproduce covariates such as GDP per capita because they are given a very small weight, meaning that it does not have substantial power predicting the per capita cigarette consumption. Actually, none of the covariates is given more than 3% weight, which compromises the main idea of covariates. That is why, for instance, the two most relevant states in the counterfactual, Utah and Nevada, are among the less similar to California, according to the distance estimated in the study. Concretely, they are ranked the 34th and 35th out of 38, respectively. Hence, a counterfactual is built where covariates are not relevant (only lagged outcomes) and the units are not similar to the treated unit.
We reproduce the analysis by using the DSD-SCM. Table 12 shows the estimated parameters for the model of cigarettes consumption per capita (in natural logarithm), using only non-lagged outcome covariates. The relative importance based on SHAP values for the covariates is: 55.7% for retail price, 31.8% for income per capita, 10.4% for the percentage of young people, and 2.0% for beer consumption.
The best ELSG ratio is achieved with a restricted pool of the 30th most similar states. Notice that a large number of donor states is needed, indicating that the distance metric might not be accurate. The counterfactual consists of 40.3% Utah, 21.0% Nevada, 16.5% Montana, 9.0% Colorado, 9.0% Nebraska, and 4.2% New Hampshire. The MAPE is 0.98%, compared to a 1.05% in the original synthetic. Both counterfactuals share 4 states, which account for around 90% of the total relevance, although the relative weights are slightly different. However, the choice of the states in this second counterfactual is more meaningful. For instance, Utah is the 15th most similar according to the SHAP-based distance, instead of the 34th. As can be seen in Fig. 11, both methods estimate that by the year 2000 annual per capita cigarette sales in California was about 26 packs lower than what they would have been in the absence of the program, although the impact is slightly larger (0.55 packs) according to the decoupled synthetic.
Finally, Figs. 12 and 13 show the results of the placebo tests. While the placebo in space shows that the decrease in California was clearly larger than in the other states, as in the original study and other extensions (see Doudchenko and Imbens 2016), the placebo test in time shows a 7% decrease in 4 years, even when no legislation was passed. Hence, it suggests that, at least partially, the effect observed in California, although significantly larger than in the rest of states, might be caused by other factors than the tobacco program. It is important to highlight that in the original paper by Abadie, Diamond and Hainmueller, no placebo test was provided. However, when applying the original methodology, the placebo test also fails, and even more than in the decoupled version (10% decrease, instead of 7% with the decoupled), due to the poor performance of the similarity measure, as discussed before. Figure 14 show the results.
As in the German reunification case, the decoupled synthetic method ensures higher economic sense and stability in the similarity measure between countries and achieves higher goodness of fit. Furthermore, it gives a clear guidance on why results should be taken cautiously, as seen in the placebo test in time. Because the similarity metric is not highly accurate, units that are not similar to the treated unit have to be considered as part of the counterfactual to get a proper goodness of fit of the pre-treatment period.
6 Conclusion
The synthetic control method has been an influential innovation in quasi-experimental design, combining as it does elements of matching and difference-in-differences, and providing a systematic approach to building a counterfactual. Similarly, it offers new opportunities for evaluating causal treatment effects in single—or in very few—aggregate units of interest. The method’s impact on the empirical policy evaluation literature has been far-reaching and continues to grow, with its application in an increasing number of disciplines, including economics, political science, epidemiology, transportation, engineering, etc.
The SCM is credited with many advantages, including its transparency, sparsity and interpretability. Nevertheless, we have shown that it also suffers from a number of critical drawbacks and limitations, some of them directly derived from its bilevel nature. In short, we have shown that (1) the covariate importance may not be consistent with economic theory, thus eroding the model’s meaningfulness; (2) estimates are unstable—due to the interpolation bias and the nested nature of the optimization problem—and overly dependent on irrelevant countries in the donor pool; and (3) including lagged outcomes does not solve the problem of meaning and the stability of covariate importance—even if the goodness of fit improves—but rather it makes other covariates irrelevant, compromising the main idea underpinning the SCM.
As an alternative to the SCM, we have proposed the decoupled SHAP-distance synthetic control method (DSD-SCM), which overcomes the main limitations of the standard method by decoupling feature importance from weight estimation and by providing a new methodology for feature estimation and unit similarity that ensure meaningfulness and stability.
Here, both methods were used to evaluate the effects on GDP growth of a ten-month government formation deadlock in Spain and to re-estimate the impact of German Reunification in West Germany GDP per capita (Abadie et al. 2015) and the effect of the tobacco control program in California (Abadie et al. 2011). Regarding the first case study, we provide evidence, consistent with Albalate and Bel (2020), refuting the negative economic effects of lengthy impasses in government formation. Thus, not only did Spain’s economy not suffer any damage, but it actually benefited by 1.58 p.p.; however, and more importantly in the context of this paper, the SCM overestimates these causal effects by 0.23 p.p. with respect to the DSD-SCM.
Moreover, we have demonstrated that the DSD-SCM is a more stable, accurate and meaningful method than the standard SCM. Concerning the second and third cases of study, we show that the DSD-SCM provides a better counterfactual, both in terms of fitting and similarity of the units with respect to the treated unit. Both methods provide similar conclusions. Namely, that German Reunification had a significant and negative impact in West Germany GDP per capita and that the tobacco control program reduced tobacco consumption. For the German reunification, the gap estimate with the DSD-SCM is 27% larger (904.3 USD) than with the original method, while for the tobacco consumption the difference between the two methods is less than 5% (0.5 packs).
After almost two decades of being first proposed, the SCM has shown to be a very useful method for policy evaluation. Some weaknesses of the originally proposed version has been diagnosed and corrections suggested, so that results obtained can be more precise, robust and meaningful. This has been the main objective of this research. Future research should try to further improve SCM, by focusing on how to assess the similarity between units in the donor pool and the treated unit.
Notes
A problem is set to be NP-hard if an algorithm for solving it can be translated into one for solving any non-deterministic polynomial time problem. That is, NP-problems are those which cannot be solved (with certainty) in polynomial time. See Arora and Barak (2007) for a detailed review and discussion of complexity theory.
Gradient boosting trees are models that combine into a single prediction a sequence of models, called base learners, in which each subsequent base learner focuses on the residual error of the previous base learners. Often, these base learners are decision trees or stumps.
\(R-squared\) is defined as in a linear model: \(R^2(W) = 1 - \frac{(Y_{TU} - WY)'(Y_{TU} - WY)}{ (Y_{TU} - \bar{Y}_{TU})'(Y_{TU} - \bar{Y}_{TU})}\), where \(\bar{Y}_{TU}\) is the mean value of the outcome of the treated unit in the pre-treatment period. Notice that \(R-squared\) is not necessarily defined between 0 and 1, since there is no constant and W is nested to V to solve the covariate adjustment. Hence, \(R-squared\) could even be negative, since the adjustment of \(Y_{TU}\) by WY could be worse than using \(\bar{Y}_{TU}.\)
References
Abadie A (2020) Using synthetic controls: feasibility, data requirements, and methodological aspects. J Econ Lit 59:391–425
Abadie A, Gardeazábal J (2003) The economic costs of conflict: a case study of the Basque country. Am Econ Rev 93(1):113–132
Abadie A, Diamond A, Hainmueller J (2010) Synthetic control methods for comparative case studies: estimating the effect of California’s tobacco control program. J Am Stat Assoc 105(490):493–505
Abadie A, Diamond A, Hainmueller J (2011) Synth: an R package for synthetic control methods in comparative case studies. J Stat Softw 42(13):1–17
Abadie A, Diamond A, Hainmueller J (2015) Comparative politics and the synthetic control method. Am J Polit Sci 59(2):495–510
Abadie A, L’Hour J (2019) A penalized synthetic control estimator for disaggregated data. http://economics.mit.edu/files/18642 Accessed from 18 Feb 2020
Acemoglu D, Johnson S, Kermani A, Kwak J, Mitton T (2016) The value of connections in turbulent times: evidence from the United States. J Financ Econ 121(2):368–391
Aisen A, Veiga FJ (2013) How does political instability affect economic growth? Eur J Polit Econ 29:151–167
Akin O, Montalvo JG, García-Villar J, Peydró JL, Raya JM (2014) The real estate and credit bubble: evidence from Spain. SERIEs J Span Econ Assoc 5:223–243
Albalate D, Bel G (2020) Do government formation deadlocks really damage economic growth? Evidence from history’s longest period of government formation impasse. Governance 33(1):155–171
Albalate D, Bel G, Mazaira-Font F (2020) Ensuring Stability, accuracy and meaningfulness in synthetic control methods: the regularized SHAP-distance method. IREA-B, Working Paper 2020-05, posted 26 April 2020
Alesina A, Ozler S, Roubini N, Swagel P (1996) Political instability and economic growth. J Econ Growth 1(2):189–211
Angelopoulos K, Economides G (2008) Fiscal policy, rent seeking, and growth under electoral uncertainty: theory and evidence from the OECD. Can J Econ 41(4):1375–1405
Arkhangelsky D, Athey S, Hirshberg D, Imbens GW, Wager S (2018) Synthetic difference in differences, arXiv e-prints, p. arXiv:1812.09970
Arora S, Barak B (2007) Computational Complexity: A Modern Approach. Cambridge University Press, NP, Cambridge
Athey S, Imbens GW (2017) The state of applied econometrics: causality and policy evaluation. J Econ Perspect 31(2):3–32
Billmeier A, Nannicini T (2013) Assessing economic liberalization episodes: a synthetic control approach. Rev Econ Stat 95(3):983–1001
Bohn S, Lofstrom M, Raphael S (2014) Did the 2007 legal Arizona workers act reduce the State’s unauthorized immigrant population? Rev Econ Stat 96(2):258–269
Bouckaert G, Brans M (2012) Governing without government: lessons from Belgium’s Caretaker Government. Governance 25(2):173–176
Botosaru I, Bruno F (2019) On the role of covariates in the synthetic control method. Econ J 22(2):117–130
Cavallo E, Galiani S, Noy I, Pantano J (2013) Catastrophic natural disasters and economic growth. Rev Econ Stat 95(5):1549–1561
Doudchenko N, Imbens GW (2016) Balancing, regression, difference-in-differences and synthetic control methods: a synthesis. NBER Working Papers, 22791
Ferman B, Pinto C, Possebom V (2020) Cherry picking with synthetic controls. J Policy Anal Manag 39(2):510–532
Gobillon L, Magnac T (2016) Regional policy evaluation: interactive fixed effects and synthetic controls. Rev Econ Stat 98(3):535–551
Hansen P, Jaumard B, Savard G (1992) New branch-and-bound rules for linear bilevel programming. SIAM J Sci Stat Comput 13(5):1194–1217
Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning: data mining, inference, and prediction, 2nd edn. Springer-Verlag, New York
Hastie T, Tibshirani R, Wainwright M (2015) Statistical learning with sparsity: the lasso and generalizations. CRC Press, NP, Florida
Hooghe M (2012) Does multi-level governance reduce the need for national government? Eur Polit Sci 11(1):90–95
Kaul A, Klößner S, Pfeifer G, Schieler M (2015) Synthetic control methods: never use all pre-intervention outcomes together with covariates. MPRA Paper 83790, University Library of Munich, Germany
Kleven HJ, Landais C, Saez E (2013) Taxation and international migration of superstars: evidence from the European football market. Am Econ Rev 103(5):1892–1924
Klobner S, Ashok K, Pfeifer G (2018) Comparative politics and the synthetic control method revisited: a note on Abadie. Swiss J Econ Stat 154(1):651–667
Kreif N, Richard G, Hangartner D, Turner A, Nikolova S, Sutton M (2016) Examination of the synthetic control method for evaluating health policies with multiple treated units. Health Econ 25(12):1514–528
Lundberg SM, Lee S (2017) A unified approach to interpreting model predictions. Adv Neural Inf Process Syst NIPS Proc 30:1–10
Lundberg S, Lee s, (2019) Consistent individualized feature attribution for tree ensembles. arXiv:1802.03888v3. Accessed from 15 Feb 2020
Montalvo JG (2011) Voting after the bombings: a natural experiment on the effect of terrorist attacks on democratic elections. Rev Econ Stat 93(4):1146–54
Percoco M (2015) Heterogeneity in the reaction of traffic flows to road pricing: a synthetic control approach applied to Milan. Transportation 42:1063–79
Sun J, Wang F, Yin H, Zhang B (2019) Money talks: the environmental impact of China’s green credit policy. J Policy Anal Manag 38(3):653–680
Vicente L, Savardand G, Júdice J (1994) Descent approaches for quadratic bilevel programming. J Optim Theory Appl 81(2):379–99
Xu Y (2017) Generalized synthetic control method: causal inference with interactive fixed effects models. Polit Anal 25(1):57–76
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has benefited from financial support provided by the Spanish Ministry of Science and Innovation (PID2019-104319RB-I00).
Appendix I: examples of instability associated with the bilevel nature of the SCM
Appendix I: examples of instability associated with the bilevel nature of the SCM
The first example shows that if the treated lies inside the convex hull defined by the untreated units, then any solution \(W^{*}\) of the lower-level problem is insensitive to V . As a consequence, any arbitrary V will do. The second illustrates the high dependency between \(W^{*}\) and V and to what extent nesting both estimations can lead to highly unstable results. As the SCM does not control for this instability, if no prior outcomes are included as covariate variables there is no guarantee at all that results will have proper goodness of fit. But if prior outcomes are included, as shown in Sect. 4, then there is no guarantee that interpolation bias is avoided.
Example 1: V completely arbitrary
Let us note by W(V) the set of W that are solution of the lower-level problem, given V. Let us note by \(\Omega = \{(W^{1}, V^{1}) .., (W^{s}, V^{s})\}\) the set of weights and feature importance matrix such that \(X_{TU}^i = W^{j}X^{i}\) for at least some covariate i but not all of them and that \(W^{j}\) is a solution of the lower-level optimization, that is, \(W^{j}\in W(V^{j})\). Let us consider that there exists \(W^{*}\) such that \(X_{TU} = W^{*}X\). Then:
-
(i)
For any V, \(W^{*} \in W(V)\)
-
(ii)
The optimal solution (or solutions) of the SCM problem is the solution of the problem
$$\begin{aligned} \min _{(W,V)\in \Omega \cup (W^{*},V^{*})} (Y_{TU} - WY)'(Y_{TU} - WY) \end{aligned}$$
In particular, if \(W^{*}\) adjust better \(Y_{TU}\) than any \(W^{j} \in \Omega \), the solution of the SCM admits any arbitrary V.
Proof
-
(i)
Given that \(X_{TU} = W^{*}X\), we have that \(D(W^{*}) \equiv (X_{TU} - W^{*}X)^{'}V^{'}(X_{TU} - W^{*}X) = 0\) for any V. Since the lower-level function D is nonnegative for any positive semi-definite matrix V, \(W^{*} \in W(V)\) for any positive semi-definite V.
-
(ii)
Let us consider \(V \notin \{V^{1},\ldots , V^{s}\}\). Let us assume that there exists \(\hat{W} \ne W^{*}\) such that \(\hat{W} \in W(V)\). Since \(D(W^{*}) = 0\) and \(W \in W(V)\), then \(D(\hat{W}) = 0\). But since V is positive semi-definite, there has to exists at least one covariate i such that \(X^i_{TU} = \hat{W}X^{i}\), and that is impossible because \(V \notin \{V^{1},\ldots , V^{s}\}\). Thus, for any \(W \in W(V)\) with \(V \notin \Omega \), \(W = W^{*}\). Therefore, the solution of the bilevel problem has to be a pair \((W, V) \in \Omega \cup (W^{*},V)\) that minimizes the upper-level problem.
\(\square \)
Example 2: V unstable and driven by interpolation biases
Let us consider a donor pool formed by 15 units with 3 covariates each one: \(X_i = (C^1_i,C^2_i,C^3_i)\), where \(C^j_i\) is the average value of the covariate j for the unit i during the time period. Let us consider that the covariates are distributed as:
Let us consider that the growth rate of \(X_i\) for the period t, \(\gamma _{i,t}\), is defined as:
where \(\hat{C}^j_i = \frac{C^j_i - min(C^j)}{max(C^j) - min(C^j)}\) and \(\varepsilon _t \sim N(0, 0.02)\).
Thus, we are ensuring that covariates are related to output, since growth rates depend on covariates. All units are given the same output value at \(t= 0\), that for simplicity we take as 1. Therefore, \(Y_i^0 = 1\) and
Let us define the treated unit as:
where \(\{X_i, Y_i\}\), \(\{X_j, Y_j\}\) are two randomly selected donors such that \(C_{i,j}^1 < 0.5\), \(C_{i,j}^2 < 0.5\), and the correlation between \(Y_i\) and \(Y_j\) is higher than 0.7. Notice that the treated unit is related to donors in terms of output and covariates.
Figure SM1 shows four examples of simulated results. In each graph, it is represented the \(R-squared\) value of the synthetic unit in the z axis when feature importance is \(V = (x,y, 1-x-y)\). As can be seen, the upper-level problem (the sum of squares, which is a linear transformation of the \(R^2\)) is highly non-convex and there are multiple local optima. Moreover, small variations in V can lead to huge changes in \(R^2\). For example, in the first figure, the maximum \(R^2\) is 0.948 and corresponds to \(x = 0\) and \(y = 1\). However, a small perturbation can lead to the lowest \(R^2\), - 0.212, at \(x = 0.05\) and \(y = 0.95\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Albalate, D., Bel, G. & Mazaira-Font, F.A. Decoupling synthetic control methods to ensure stability, accuracy and meaningfulness. SERIEs 12, 549–584 (2021). https://doi.org/10.1007/s13209-021-00242-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-021-00242-8