Score-driven currency exchange rate seasonality as applied to the Guatemalan Quetzal/US Dollar

Abstract

In this paper we introduce new Dynamic Conditional Score (DCS) models for the Skew-Gen-t (Skewed Generalized t) and NIG (Normal-Inverse Gaussian) distributions as alternatives to the recent DCS models for the Student’s-t and EGB2 (Exponential Generalized Beta of the second kind) distributions, respectively. The DCS models we propose include stochastic local level, stochastic seasonality, and irregular components with DCS-EGARCH (Exponential Generalized Autoregressive Conditional Heteroscedasticity) volatility dynamics. DCS models are robust to extreme observations, whereas standard financial time series models are not. We use data from the Guatemalan Quetzal (GTQ) to United States Dollar (USD) exchange rate for the period of 4th January 1994–30th June 2017. This dataset exhibits significant rises and falls in the GTQ/USD that lead to extreme observations, stochastic seasonality with dynamic amplitude, and volatility dynamics. These seasonality dynamics of the GTQ/USD are related to the Guatemalan trade-related currency movements, receipt and payment of foreign loans, and remittance payments of Guatemalans working abroad. We show that the in-sample statistical performance of the DCS-Skew-Gen-t and the DCS-NIG models is superior to that of the DCS-t and the DCS-EGB2 models, respectively. Furthermore, we show that the statistical performance of all DCS models is superior to that of the standard financial time series model.

Introduction

Historically, Guatemala has ranked among the largest exporters of several agricultural products worldwide. According to the United States Dollar (USD) value of sugar exports, Guatemala is the fourth ranked country in the world, for example, with a value of USD826.2 million during 2017 (that is 3% of total sugar exports worldwide, following Brazil with 41.3%, Thailand with 9.4% and France with 4.9%). Guatemala is the fourteenth ranked country for coffee exports worldwide, with a value of USD748.6 million during 2017 (that is 2.3% of total coffee exports worldwide, following Ethiopia with 2.9%, United States with 2.7% and the Netherlands with 2.3%). Moreover, Guatemala is the fifth ranked country for banana exports worldwide, with a value of USD882.3 million during 2017 (that is 7.1% of total banana exports worldwide, following Ecuador with 24.6%, Belgium with 8.5%, Costa Rica with 8.4% and Colombia with 7.4%). We also highlight that Guatemala is the top cardamom producing country worldwide, with a total value of exports of USD277.1 million during 2016 (that is 55.7% of total cardamom exports worldwide, followed by Nepal with 12.4%, India with 8.7% and the United Arab Emirates with 6.2%). The sugarcane, coffee, banana and cardamom production in Guatemala has a seasonal component related to weather conditions. Therefore, the export-related currency movements of these products may lead to an exchange rate seasonality (i.e. annual seasonality) of the Guatemalan Quetzal (GTQ) to USD (GTQ/USD) exchange rate.

During the last two decades, the relative importance of sugar, coffee, banana and cardamom exports, out of Guatemala’s total exports, has decreased significantly (source: Bank of Guatemala, http://www.banguat.gob.gt; see notes of Table 4). This suggests that the impact of the export-related seasonality effects on the GTQ/USD exchange rate may have decreased over time. During the same period, the relative importance of the receipt and payment of foreign loans, and remittance payments to Guatemala (as a fraction of total foreign currency movements of the country) has increased significantly. As the receipt and payment of foreign loans and the remittance payments to Guatemala do not involve significant exchange rate seasonality components (i.e. annual seasonality), the increase in the relative importance of those currency movements may indirectly lower the amplitude of GTQ/USD exchange rate seasonality.

The aforementioned issues motivated the present work and we focus on the in-sample analysis of the GTQ/USD exchange rate $p_{t}$. We evaluate the historical evolution of stochastic seasonality effects in the GTQ/USD exchange rate for the sample period of 4th January 1994–30th June 2017. We use information on (1) Guatemalan export-related currency movements, (2) import-related currency movements, (3) receipt of Guatemalan USD loans, (4) payment of Guatemalan USD loans, and (5) remittance payments of Guatemalan citizens who are working abroad. To study the stochastic seasonality component of the GTQ/USD exchange rate, we suggest using the new Dynamic Conditional Score (DCS) models (Creal et al. 2013; Harvey 2013) that include both stochastic local level $\mu _{t}$ and stochastic seasonality $s_{t}$ components. The new DCS models are flexible and they allow stochastic dynamics in the local level $\mu _{t}$ component, the seasonality $s_{t}$ component, and the irregular $v_{t}$ component, within the decomposition of the GTQ/USD exchange rate: $p_{t} = \mu _{t} + s_{t} + v_{t}$.

The use of the DCS models for the time series sample in the present study is motivated by the GTQ/USD time series that exhibits: (1) significant rises and falls that lead to extreme observations, (2) a significant stochastic seasonality component (i.e. annual seasonality) with dynamic amplitude, and (3) significant volatility dynamics. DCS models are robust to extreme observations. Therefore, the new DCS models for the GTQ/USD exchange rate may be more adequate for an effective in-sample measurement of the stochastic seasonality component than the standard financial time series models (i.e. the latter are less robust to extreme observations). Our paper makes several contributions to the body of DCS literature.

Firstly, we introduce the new DCS-Skew-Gen-t (Skewed Generalized t distribution) model with (1) stochastic local level $\mu _{t}$, (2) stochastic seasonality $s_{t}$, and (3) DCS-EGARCH (Exponential Generalized Autoregressive Conditional Heteroscedasticity) (Harvey 2013) scale dynamics for the irregular component $v_{t}$. The statistical performance of the DCS-Skew-Gen-t model is superior to that of the DCS Student’s-t model (hereinafter, DCS-t) (Harvey 2013; Harvey and Luati 2014), according to all Log-Likelihood (LL)-based metrics of this paper.

Secondly, we introduce the new DCS-NIG (Normal-Inverse Gaussian distribution) model (Barndorff-Nielsen and Halgreen 1977) with (1) stochastic local level $\mu _{t}$, (2) stochastic seasonality $s_{t}$, and (3) DCS-EGARCH scale dynamics for the irregular component $v_{t}$. The statistical performance of the DCS-NIG model is superior to that of the DCS-EGB2 (Exponential Generalized Beta distribution of the second kind) model (Caivano et al. 2016), according to the LL-based parsimony metrics.

In this paper, we suggest two new DCS models because their terms, which do the updating, transform extreme observations in a similar way to the benchmark DCS models, as described in the literature: (1) For both the DCS-t and DCS-Skew-Gen-t models, the most extreme observations are trimmed by local level and seasonality (updating terms), and extreme observations in scale (updating term) are Winsorized; (2) For both the DCS-EGB2 and DCS-NIG models, local level and seasonality (updating terms) perform Winsorizing of extreme observations, and scale (updating term) transforms extreme observations according to a linear function. The type of transformation of extreme observations that is more appropriate for local level, stochastic seasonality and volatility, is an open question in the relevant body of DCS literature.

Thirdly, we compare the DCS models with a standard financial time series model that de- composes the GTQ/USD exchange rate to the three components: stochastic local level $\mu _{t}$, stochastic seasonality $s_{t}$, and irregular $v_{t}$. We find that all of the DCS models in this paper present a statistical performance that is superior to that of the standard model.

The remainder of this paper is organized as follows. Section 2 reviews the literature on DCS models. Section 3 presents the econometric framework. Section 4 describes the dataset. Section 5 presents the empirical results. Section 6 concludes.

Review of the literature on DCS models

DCS models are observation-driven time series models (Cox et al. 1981), in which each dynamic equation is updated by the conditional score of the LL (hereinafter, score function) with respect to a dynamic parameter. The score function discounts the effects of previous observations when the dynamic equations of the DCS model are updated. Thus, DCS models are robust to extreme values in the irregular component (Creal et al. 2013; Harvey 2013). Those models can be applied to the study of I(0) (e.g. financial returns, real GDP growth) or I(1) (e.g. exchange rate level, real GDP level) times series variables (see Hamilton 1994).

The first example of DCS models is Beta-t-EGARCH (Harvey and Chakravarty 2008), which is an outlier-robust alternative to the GARCH model (Engle 1982; Bollerslev 1986). With respect to Beta-t-EGARCH, we refer to the recent applications of Blazsek and Villatoro (2015), Blazsek and Mendoza (2016), and Blazsek and Monteros (2017). Another example of DCS models is QAR (Harvey 2013), which is a nonlinear and outlier-robust alternative to the AR Moving Average (ARMA) model (Box and Jenkins 1970). An additional recent example of DCS models is QVAR (Blazsek et al. 2017, 2018b), which is a nonlinear and outlier-robust alternative to the VARMA model (see, for example, Lütkepohl 2005).

We also refer to the following recent models from the body of DCS literature: Blazsek and Escribano (2016a) suggest a DCS count panel data model, which is an alternative to the dynamic count panel data models of Blundell et al. (2002), Wooldridge (2005), and Blazsek and Escribano (2010, 2016b). Ayala et al. (2017) suggest DCS-EGARCH models with score-driven shape parameters, which are extensions of the DCS-EGARCH models with constant shape (see, for example, Harvey 2013). Blazsek and Ho (2017) introduce the Markov regime-switching Beta-t-EGARCH model. Blazsek et al. (2018c) compare single-regime and regime-switching Beta-t-EGARCH, Skew-Gen-t-EGARCH, EGB2-EGARCH and NIG-EGARCH volatility models. Ayala and Blazsek (2018a, b) use new DCS copula models for financial portfolios, by considering score-driven Clayton, rotated Clayton, Frank, Gaussian, Gumbel, rotated Gumbel, Plackett, and Student’s t copulas.

Related to the new DCS models with stochastic local level and stochastic seasonality components that are suggested in the present paper, we refer to the works of Harvey (2013) and Harvey and Luati (2014), who introduce the dynamic Student’s-t location model that includes stochastic local level and stochastic seasonality components. More recently, Caivano et al. (2016) introduce the dynamic EGB2 location model, which includes stochastic local level and stochastic seasonality components. Caivano et al. (2016) compare the dynamic Student’s-t location and the dynamic EGB2 location models, and demonstrate that extreme observations are discounted in different ways in those models. For the Student’s-t location model, the score function converges to zero as $|v_{t}| \rightarrow \infty$, which is described as a soft form of trimming. For the EGB2 location model, the score function converges to a positive or negative non-zero value as $|v_{t}| \rightarrow \infty$, which is described as a soft form of Winsorizing.

We also refer to a related recent work of Blazsek and Hernández (2018), who apply DCS-t, DCS-Gen-t (Generalized t distribution) and DCS-EGB2 models of stochastic local level, stochastic seasonality and EGARCH-driven irregular components, to spot electricity prices from El Salvador, Guatemala and Panama that exhibit significant rises and falls.

Econometric framework

DCS models with local level and seasonality

The DCS models of this paper are formulated as: $p_{t}=\mu _{t}+s_{t}+v_{t}=\mu _{t}+s_{t}+\exp (\lambda _{t})\epsilon _{t}$ for days $t=1,\ldots ,T$, where T is the number of observations. The model includes three score-driven components: stochastic local level component $\mu _{t}$, stochastic annual seasonality component $s_{t}$, and irregular component $v_{t}$. The irregular component is the product of a dynamic scale parameter $\exp (\lambda _{t})$ and a standardized error term $\epsilon _{t}$.

For $\epsilon _{t}$, we use the Student’s-t, Skew-Gen-t, EGB2 and NIG distributions (we present the corresponding density functions in Sect. 3.3). For these probability distributions, the updating terms of the DCS equations either trim or Winsorize the extreme observations, or transform them according to a linear function. Due to these transformations, the DCS models for the GTQ/USD currency exchange rate of the present paper are robust to extreme observations.

Firstly, the local level component $\mu _{t}=\mu _{t-1}+\delta u_{\mu ,t-1}$ is updated by the scaled score function $u_{\mu ,t}$ with respect to $\mu _{t}$ ($u_{\mu ,t}$ is defined in Sect. 3.3). We initialize $\mu _{t}$ by using the first observation $p_{1}$. As an alternative, we also consider the use of parameter $\mu _{0}$ to initialize $\mu _{t}$. We obtain very similar results for both cases, thus, in this paper we only report results for $\mu _{1}=p_{1}$. With respect to these alternatives of initialization, we refer to the work of Harvey (2013, p. 76).

Secondly, the annual seasonality component is $s_{t}=D'_{t}\rho _{t}=(D_{\text {Jan},t},D_{\text {Feb},t},\ldots ,D_{\text {Dec},t})'\rho _{t}$, where the monthly dummies $D_{j,t}$ with $j\in \{\text {Jan},\ldots ,\text {Dec}\}$ select an element from the $12 \times 1$ vector of dynamic variables $\rho _{t}$. The vector $\rho _{t}$ is formulated as $\rho _{t}=\rho _{t-1}+\gamma _{t} u_{\mu ,t-1}$. Vector $\rho _{t}$ is updated by the scaled score function $u_{\mu ,t}$ with respect to $\mu _{t}$ (Sect. 3.3), and $u_{\mu ,t}$ is multiplied by the $12 \times 1$ vector of dynamic parameters $\gamma _{t}$. Each element of the $\gamma _{t}$ vector is given by $\gamma _{jt}=\gamma _{j}$ for $D_{jt}=1$ and $\gamma _{jt}=-\gamma _{j}/(12-1)$ for $D_{jt}=0$, where $\gamma _{j}$ with $j\in \{\text {Jan},\ldots ,\text {Dec}\}$ are seasonality parameters to be estimated. This specification ensures that the sum of the seasonality parameters is zero, hence, $s_{t}$ has mean zero and it is effectively separated from $\mu _{t}$.

We initialize $\rho _{t}$ by estimating the equation $p_{t}=a+b t+c_{\text {Jan}} D_{\text {Jan},t}+\cdots +c_{\text {Dec}} D_{\text {Dec},t}+\epsilon _{t}$, under the restriction $c_{\text {Jan}}+\cdots +c_{\text {Dec}}=0$. Due to this restriction multicollinearity is avoided, thus, all parameters are identified in the equation. For the estimation, we use data from the first year of the full data window (i.e. the first 259 observations of the GTQ/USD exchange rate sample from year 1994), and we estimate the parameters by using the Non-linear Least Squares (NLS) method. The initial values of $\rho _{t}$ are the NLS estimates of $(c_{\text {Jan}},\ldots ,c_{\text {Dec}})'$. With respect to this method of initialization, we refer to the work of Harvey (2013, p. 80).

In the DCS models of this paper, the same scaled score function updates both the local level and the seasonality components. Therefore, the local level and seasonality shocks are correlated. The DCS models with stochastic local level and stochastic seasonality of this paper are alternatives to the recent Unobserved Components Model (UCM) of Hindrayanto et al. (2018) that uses correlated shocks for the local level and seasonality components.

Thirdly, we model the time-varying scale of the irregular component $v_{t}$ by using the DCS-EGARCH(1,1) model $\lambda _{t}=\omega +\beta \lambda _{t-1}+\alpha u_{\lambda ,t-1}$, which is updated by the score function $u_{\lambda ,t}$ with respect to $\lambda _{t}$ ($u_{\lambda ,t}$ is defined in Sect. 3.3). DCS-EGARCH models for the Student’s-t, Skew-Gen-t, EGB2 and NIG distributions are named Beta-t-EGARCH (Harvey and Chakravarty 2008), Skew-Gen-t-EGARCH (Harvey and Lange 2017), EGB2-EGARCH (Caivano and Harvey 2014) and NIG-EGARCH (Blazsek et al. 2018c), respectively. We initialize $\lambda _{t}$ by using parameter $\lambda _{0}$. As an alternative, we also consider DCS-EGARCH with leverage effects (Harvey 2013). However, we find that the parameter that measures leverage effects is not significantly different from zero for the GTQ/USD dataset that is used in this paper.

Motivated by the works of Dacorogna et al. (1993) and Andersen and Bollerslev (1998), we also consider a seasonality component in volatility. We add the seasonality component ${\tilde{s}}_{t}$ into scale, as follows: $p_{t}=\mu _{t}+s_{t}+v_{t}=\mu _{t}+s_{t}+\exp (\lambda _{t}+{\tilde{s}}_{t})\epsilon _{t}$, where we use the Student’s t, Skew-Gen-t, EGB2 and NIG distributions for $\epsilon _{t}$. The seasonality component is specified as ${\tilde{s}}_{t}=D'_{t}{\tilde{\rho }}_{t}=(D_{\text {Jan},t},D_{\text {Feb},t},\ldots ,D_{\text {Dec},t})'{\tilde{\rho }}_{t}$ and ${\tilde{\rho }}_{t}={\tilde{\rho }}_{t-1}+\kappa _{t} u_{\lambda ,t-1}$. Each element of the $\kappa _{t}$ vector is given by $\kappa _{jt}=\kappa _{j}$ for $D_{jt}=1$ and $\kappa _{jt}=-\kappa _{j}/(12-1)$ for $D_{jt}=0$, where $\kappa _{j}$ with $j\in \{\text {Jan},\ldots ,\text {Dec}\}$ are parameters to be estimated. This specification ensures that the sum of the seasonality parameters is zero, hence, ${\tilde{s}}_{t}$ has mean zero and it is effectively separated from $\lambda _{t}$. We do not report results for these extended DCS specifications with seasonal volatility, because the ML estimator does not converge to an optimum for the GTQ/USD currency exchange rate dataset of the present paper. Nevertheless, this specification may be helpful in future applications for currency exchange rates involving stochastic seasonality and extreme observations.

Standard financial time series model with local level and seasonality

The standard financial time series model is formulated as: $p_{t}=\mu _{t}+s_{t}+v_{t}=\mu _{t}+s_{t}+\lambda ^{1/2}_{t}\epsilon _{t}$ for days $t=1,\ldots ,T$. We use the same notation for the local level, seasonality and irregular components as for the DCS models, and for the error term we use $\epsilon _{t} \sim N(0,1)$.

Firstly, the local level component is $\mu _{t}=\mu _{t-1}+\delta v_{t-1}$ (our motivation for using this updating term is outlined in Sect. 3.3). We initialize $\mu _{t}$ by using the first observation $p_{1}$. As an alternative, we also consider the use of parameter $\mu _{0}$ to initialize $\mu _{t}$. We obtain very similar results for both cases, thus, in this paper we only report results for $\mu _{1}=p_{1}$.

Secondly, the annual seasonality component is $s_{t}=D'_{t}\rho _{t}=(D_{\text {Jan},t},D_{\text {Feb},t},\ldots ,D_{\text {Dec},t})'\rho _{t}$, where the monthly dummies $D_{j,t}$ with $j\in \{\text {Jan},\ldots ,\text {Dec}\}$ select an element from the $12 \times 1$ vector of dynamic variables $\rho _{t}$. The vector $\rho _{t}$ is formulated as $\rho _{t}=\rho _{t-1}+\gamma _{t} v_{t-1}$ (Sect. 3.3). We initialize $\rho _{t}$ in the same way as for the DCS models. Each element of the $\gamma _{t}$ vector is given by $\gamma _{jt}=\gamma _{j}$ for $D_{jt}=1$ and $\gamma _{jt}=-\gamma _{j}/(12-1)$ for $D_{jt}=0$, where $\gamma _{j}$ with $j\in \{\text {Jan},\ldots ,\text {Dec}\}$ are seasonality parameters to be estimated. This specification ensures that $s_{t}$ is centred at zero.

Thirdly, we model the conditional variance of $v_{t}$ by using the classic GARCH(1,1) specification $\lambda _{t}=\omega +\beta \lambda _{t-1}+\alpha v_{t-1}^{2}$. We initialize $\lambda _{t}$ by using parameter $\lambda _{0}$.

Conditional densities, score functions and updating terms

We use four probability distributions for $\epsilon _{t}$ in the DCS models. In this section, for each alternative, we present the log conditional density of $p_{t}$, and the score functions $u_{\mu ,t}$ and $u_{\lambda ,t}$. Furthermore, in this section we also present the log conditional density of $p_{t}$ and the properties of the updating terms of $\mu _{t}$ and $\lambda _{t}$ for the standard financial time series model.

Firstly, $\epsilon _{t} \sim t[0,1,\exp (\nu )+2]$ is the Student’s t-distribution, where $\nu \in {\mathbb {R}}$ influences tail-thickness. The degrees of freedom $\exp (\nu )+2$ parameter specification ensures finite conditional variance for $p_{t}$. The log conditional density of $p_{t}$ is

$$\begin{aligned} \ln f(p_{t}|p_{1},\ldots ,p_{t-1})= & {} \ln \Gamma \left[ \frac{\exp (\nu )+3}{2}\right] -\ln \Gamma \left[ \frac{\exp (\nu )+2}{2}\right] \nonumber \\&-\frac{\ln (\pi )+\ln [\exp (\nu )+2]}{2}-\lambda _{t} \nonumber \\&-\frac{\exp (\nu )+3}{2}\ln \left\{ 1+\frac{\epsilon _{t}^{2}}{\exp (\nu )+2}\right\} \end{aligned}$$

(1)

where $\Gamma (x)$ is the gamma function. The score function with respect to $\mu _{t}$ is given by

$$\begin{aligned} \frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \mu _{t}}= & {} \frac{[\exp (\nu )+2]\exp (\lambda _{t})\epsilon _{t}}{\epsilon _{t}^{2}+\exp (\nu )+2}\times \frac{\exp (\nu )+3}{[\exp (\nu )+2]\exp (2\lambda _{t})}\nonumber \\= & {} u_{\mu ,t} \times \frac{\exp (\nu )+3}{[\exp (\nu )+2]\exp (2\lambda _{t})} \end{aligned}$$

(2)

where the scaled score function $u_{\mu ,t}$ is defined according to the last equality. The $u_{\mu ,t}$ term trims extreme observations, because $u_{\mu ,t} \rightarrow _{p} 0$ when $|\epsilon _{t}| \rightarrow \infty$. The discounting that is undertaken by $u_{\mu ,t}$ is identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results). The updating term $v_{t}$ that is used in the local level and stochastic seasonality equations of the standard financial time series model is a limiting special case of the scaled score function $u_{\mu ,t}$, because:

$$\begin{aligned} u_{\mu ,t}=\frac{[\exp (\nu )+2]\exp (\lambda _{t})\epsilon _{t}}{\epsilon _{t}^{2}+\exp (\nu )+2}= \frac{\exp (\lambda _{t})\epsilon _{t}}{[\exp (\nu )+2]^{-1}\epsilon _{t}^{2}+1} \longrightarrow _{p} \exp (\lambda _{t})\epsilon _{t}=v_{t} \end{aligned}$$

(3)

as $\nu \rightarrow \infty$. Related to this, we also note that under the same limit $t[0,1,\exp (\nu )+2] \rightarrow _{d} N(0,1)$, i.e. the standardized error term of the standard financial time series model is obtained. The score function $u_{\lambda ,t}$ is

$$\begin{aligned} u_{\lambda ,t}=\frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \lambda _{t}} =\frac{[\exp (\nu )+3]\epsilon _{t}^{2}}{\exp (\nu )+2+\epsilon _{t}^{2}}-1 \end{aligned}$$

(4)

The updating term $u_{\lambda ,t}$ Winsorizes extreme observations, because $u_{\lambda ,t} \rightarrow _{p} c$ ($c>0$ is a real number) when $|\epsilon _{t}| \rightarrow \infty$. The discounting that is undertaken by $u_{\lambda ,t}$ is identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results). We also show the limiting case for $u_{\lambda ,t}$ when $\nu \rightarrow \infty$:

$$\begin{aligned} u_{\lambda ,t}=\frac{[\exp (\nu )+3]\epsilon _{t}^{2}}{\exp (\nu )+2+\epsilon _{t}^{2}}-1 \longrightarrow _{p} \epsilon _{t}^{2}-1=\exp (-2\lambda _{t})v_{t}^{2}-1 \end{aligned}$$

(5)

as $\nu \rightarrow \infty$. The last equality shows that $u_{\lambda ,t}$ performs a quadratic transformation of $v_{t}$ for the limiting case, as per the conditional variance equation in the standard financial time series model.

Secondly, $\epsilon _{t} \sim \text {Skew-Gen-}t[0,1,\text {tanh}(\tau ),\exp (\nu )+2,\exp (\eta )]$ (McDonald and Michelfelder 2017), where $\text {tanh}(x)$ is the hyperbolic tangent function, and $\tau \in {\mathbb {R}}$, $\nu \in {\mathbb {R}}$ and $\eta \in {\mathbb {R}}$ influence the asymmetry, tail-thickness and peakedness, respectively. The Skew-Get-t distribution is a generalization of the Student’s t distribution. By setting $\text {tanh}(\tau )=0$ and $\exp (\eta )=2$, Skew-Get-t coincides with Student’s t. The degrees of freedom $\exp (\nu )+2$ specification ensures finite conditional variance for $p_{t}$, as for the Student’s t distribution. The log-density of $p_{t}$ is

$$\begin{aligned}&\ln f(p_{t}|p_{1},\ldots ,p_{t-1}) = \eta -\lambda _{t}-\ln (2)-\frac{\ln [\exp (\nu )+2]}{\exp (\eta )}-\ln \Gamma \left[ \frac{\exp (\nu )+2}{\exp (\eta )}\right] \nonumber \\&\qquad -\ln \Gamma [\exp (-\eta )]+\ln \Gamma \left[ \frac{\exp (\nu )+3}{\exp (\eta )}\right] \nonumber \\&\qquad -\frac{\exp (\nu )+3}{\exp (\eta )}\ln \left\{ 1+\frac{|\epsilon _{t}|^{\exp (\eta )}}{[1+\text {tanh}(\tau )\text {sgn}(\epsilon _{t})]^{\exp (\eta )} \times [\exp (\nu )+2]} \right\} \end{aligned}$$

(6)

where $\text {sgn}(x)$ is the signum function. The score function with respect to $\mu _{t}$ is given by

$$\begin{aligned}&\frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \mu _{t}}=\frac{[\exp (\nu )+2]\exp (\lambda _{t})\epsilon _{t}|\epsilon _{t}|^{\exp (\eta )-2}}{|\epsilon _{t}|^{\exp (\eta )}+ [1+\text {tanh}(\tau )\text {sgn}(\epsilon _{t})]^{\exp (\eta )}[\exp (\nu )+2]}\nonumber \\&\quad \quad \quad \times \frac{\exp (\nu )+3}{[\exp (\nu )+2]\exp (2\lambda _{t})}=u_{\mu ,t} \times \frac{\exp (\nu )+3}{[\exp (\nu )+2]\exp (2\lambda _{t})} \end{aligned}$$

(7)

where the scaled score function $u_{\mu ,t}$ is defined according to the second equality. The $u_{\mu ,t}$ term trims extreme observations, because $u_{\mu ,t} \rightarrow _{p} 0$ when $|\epsilon _{t}| \rightarrow \infty$. The discounting that is undertaken by $u_{\mu ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results). The score function $u_{\lambda ,t}$ is

$$\begin{aligned} u_{\lambda ,t}= & {} \frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \lambda _{t}}\nonumber \\= & {} \frac{|\epsilon _{t}|^{\exp (\eta )}[\exp (\nu )+3]}{|\epsilon _{t}|^{\exp (\eta )}+[1+\text {tanh}(\tau )\text {sgn}(\epsilon _{t})]^{\exp (\eta )}[\exp (\nu )+2]}-1 \end{aligned}$$

(8)

The updating term $u_{\lambda ,t}$ Winsorizes extreme observations, because $u_{\lambda ,t} \rightarrow _{p} c_{1}$ when $\epsilon _{t} \rightarrow -\infty$ and $u_{\lambda ,t} \rightarrow _{p} c_{2}$ when $\epsilon _{t} \rightarrow +\infty$ ($c_{1}>0$ and $c_{2}>0$ are real numbers). The Winsorizing that is undertaken by $u_{\lambda ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results).

Thirdly, $\epsilon _{t} \sim \text {EGB2}[0,1,\exp (\xi ),\exp (\zeta )]$, where $\xi \in {\mathbb {R}}$ and $\zeta \in {\mathbb {R}}$ influence both asymmetry and tail-thickness. The log conditional density of $p_{t}$ is

$$\begin{aligned}&\ln f(p_{t}|p_{1},\ldots ,p_{t-1})= \exp (\xi )\epsilon _{t} -\lambda _{t} -\ln \Gamma [\exp (\xi )]-\ln \Gamma [\exp (\zeta )]\nonumber \\&\quad +\ln \Gamma [\exp (\xi )+\exp (\zeta )]-[\exp (\xi )+\exp (\zeta )]\ln [1+\exp (\epsilon _{t})] \end{aligned}$$

(9)

The score function with respect to $\mu _{t}$ is given by

$$\begin{aligned} \frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \mu _{t}}= u_{\mu ,t} \times \{\Psi ^{(1)}[\exp (\xi )]+\Psi ^{(1)}[\exp (\zeta )]\}\exp (2\lambda _{t}) \end{aligned}$$

(10)

where the scaled score function $u_{\mu ,t}$ is defined as:

$$\begin{aligned} u_{\mu ,t}= & {} \{\Psi ^{(1)}[\exp (\xi )] +\Psi ^{(1)}[\exp (\zeta )]\}\exp (\lambda _{t}) \nonumber \\&\left\{ [\exp (\xi )+\exp (\zeta )]\frac{\exp (\epsilon _{t})}{\exp (\epsilon _{t})+1}-\exp (\xi )\right\} \end{aligned}$$

(11)

where $\Psi ^{(1)}(x)$ is the trigamma function. The $u_{\mu ,t}$ term Winsorizes extreme observations, because $u_{\mu ,t} \rightarrow _{p} c_{1}$ when $\epsilon _{t} \rightarrow -\infty$ and $u_{\mu ,t} \rightarrow _{p} c_{2}$ when $\epsilon _{t} \rightarrow +\infty$ ($c_{1}<0$ and $c_{2}>0$ are a real numbers). The discounting that is undertaken by $u_{\mu ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results). The score function $u_{\lambda ,t}$ is

$$\begin{aligned} u_{\lambda ,t}=\frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \lambda _{t}}= [\exp (\xi )+\exp (\zeta )]\frac{\epsilon _{t}\exp (\epsilon _{t})}{\exp (\epsilon _{t})+1} -\exp (\xi )\epsilon _{t}-1 \end{aligned}$$

(12)

The updating term $u_{\lambda ,t}$ transforms extreme observations according to a linear increasing function, because $u_{\lambda ,t} \rightarrow _{p} \infty$ in a linear manner when $|\epsilon _{t}| \rightarrow \infty$. The linear transformation that is undertaken by $u_{\lambda ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results).

Fourthly, $\epsilon _{t}\sim \text {NIG}[0,1,\exp (\nu ),\exp (\nu )\text {tanh}(\eta )]$, where $\nu \in {\mathbb {R}}$ and $\eta \in {\mathbb {R}}$ influence tail-thickness and asymmetry, respectively. The log conditional density of $p_{t}$ is

$$\begin{aligned}&\ln f(p_{t}|p_{1},\ldots ,p_{t-1})= \nu -\lambda _{t}-\ln (\pi )+\exp (\nu )[1-\text {tanh}^{2}(\eta )]^{1/2}\nonumber \\&\quad +\exp (\nu )\text {tanh}(\eta )\epsilon _{t} +\ln K^{(1)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] -\frac{1}{2}\ln \big (1+\epsilon _{t}^{2}\big ) \end{aligned}$$

(13)

where $K^{(1)}(x)$ is the modified Bessel function of the second kind of order 1. The score function with respect to $\mu _{t}$ is given by

$$\begin{aligned}&\frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \mu _{t}} = -\exp (\nu -\lambda _{t})\text {tanh}(\eta )+\frac{\epsilon _{t}}{\exp (\lambda _{t})\big (1+\epsilon _{t}^{2}\big )}\nonumber \\&\qquad +\frac{\exp (\nu -\lambda _{t})\epsilon _{t}}{\sqrt{1+\epsilon _{t}^{2}}}\times \frac{K^{(0)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] +K^{(2)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] }{2K^{(1)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] } \qquad \end{aligned}$$

(14)

and the scaled score function $u_{\mu ,t}$ is defined as:

$$\begin{aligned} u_{\mu ,t}=\frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \mu _{t}} \times \exp (2\lambda _{t}) \end{aligned}$$

(15)

where $K^{(0)}(x)$ and $K^{(2)}(x)$ are the modified Bessel functions of the second kind of orders 0 and 2, respectively. The $u_{\mu ,t}$ term Winsorizes extreme observations, because $u_{\mu ,t} \rightarrow _{p} c_{1}$ when $\epsilon _{t} \rightarrow -\infty$ and $u_{\mu ,t} \rightarrow _{p} c_{2}$ when $\epsilon _{t} \rightarrow +\infty$ ($c_{1}<0$ and $c_{2}>0$ are real numbers). The discounting that is undertaken by $u_{\mu ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results). The score function $u_{\lambda ,t}$ is

$$\begin{aligned} u_{\lambda ,t}= & {} \frac{\partial \ln f(p_{t}|p_{1},\ldots ,p_{t-1})}{\partial \lambda _{t}} =-1-\exp (\nu )\text {tanh}(\eta )\epsilon _{t} +\frac{\epsilon _{t}^{2}}{1+\epsilon _{t}^{2}}\nonumber \\&+\frac{\exp (\nu )\epsilon _{t}^{2}}{\sqrt{1+\epsilon _{t}^{2}}}\times \frac{K^{(0)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] +K^{(2)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] }{2K^{(1)}\left[ \exp (\nu )\sqrt{1+\epsilon _{t}^{2}}\right] } \end{aligned}$$

(16)

The updating term $u_{\lambda ,t}$ transforms extreme observations according to a linear increasing function, because $u_{\lambda ,t} \rightarrow _{p} \infty$ in a linear manner when $|\epsilon _{t}| \rightarrow \pm \infty$. The linear transformation that is undertaken by $u_{\lambda ,t}$ is not identical for the positive and negative sides of the probability distribution (see Sect. 5 for empirical results).

Finally, we also present the log-density of $p_{t}$ for the standard financial time series model:

$$\begin{aligned} \ln f(p_{t}|p_{1},\ldots ,p_{t-1})= -\frac{1}{2}\ln (2\pi \lambda _{t})-\frac{1}{2}\epsilon _{t}^{2} \end{aligned}$$

(17)

The updating terms of the equations $\mu _{t}=\mu _{t-1}+\delta v_{t-1}$ and $\lambda _{t}=\omega +\beta \lambda _{t-1}+\alpha v_{t-1}^{2}$ perform linear and quadratic transformations of $\epsilon _{t}$, respectively. For both $\mu _{t}$ and $\lambda _{t}$, the updating terms go to infinity when $|\epsilon _{t}| \rightarrow \infty$. The linear and quadratic transformations that are undertaken by the updating terms are identical for the positive and negative sides of the probability distribution. Compared to the DCS specifications, the standard financial time series model does not discount extreme observations. We highlight the fact that extreme observations are accentuated in GARCH by the quadratic transformation of shocks, possibly leading to an overestimation of volatility after extreme observations (Blazsek et al. 2018a).

Statistical inference

The DCS specifications of this paper are estimated by using the Maximum Likelihood (ML) method (see, for example, Davidson and MacKinnon 2003). The ML estimator is given by

$$\begin{aligned} {\hat{\Theta }}_{\text {ML}}=\arg \max _{\Theta }\text {LL}(p_{1},\ldots ,p_{T};\Theta ) =\arg \max _{\Theta }\sum _{t=1}^{T}\ln f(p_{t}|p_{1},\ldots ,p_{t-1};\Theta )\nonumber \\ \end{aligned}$$

(18)

where $\Theta$ denotes the vector of parameters. We estimate the components $\mu _{t}$, $s_{t}$ and $v_{t}$ jointly, under the initialization methods of $\mu _{t}$, $s_{t}$ and $\lambda _{t}$ that are presented in Sect. 3.1 (see also Harvey 2013). The standard errors of parameters are estimated by using the inverse information matrix (Creal et al. 2013; Harvey 2013). For some parameters, we estimate their transformed values. We use the delta method to estimate the standard errors for those parameters (see, for example, Davidson and MacKinnon 2003).

For the DCS models of this paper, we use results from the work of Harvey (2013) for the conditions of consistency and asymptotic normality of the ML estimates. For the local level and stochastic seasonality equations, the dynamic parameters of the $\mu _{t}$ and $\rho _{t}$ equations are set to one, instead of being estimated. Therefore, the asymptotic properties of the ML estimator hold for those cases (Harvey 2013). With respect to the dynamic log-scale equation, we define the statistic $C_{\lambda }= \beta ^{2}+2\beta \alpha E(\partial u_{\lambda ,t}/\partial \lambda _{t})+\alpha ^{2}E[(\partial u_{\lambda ,t}/\partial \lambda _{t})^{2}]$ (Harvey 2013). We estimate $C_{\lambda }$ numerically for each DCS specification of the present paper. Firstly, the partial derivatives of the score function with respect to $\lambda _{t}$ are computed numerically. Secondly, the Augmented Dickey and Fuller (1979) (hereinafter, ADF) is performed for each $\partial u_{\lambda ,t}/\partial \lambda _{t}$ time series, in order to justify the use of the sample average estimator for the expectations. For all cases, the ADF test indicates that $\partial u_{\lambda ,t}/\partial \lambda _{t}$ forms a covariance stationary time series. Thus, the sample average is a consistent estimator of the expected value (see, for example, Hamilton 1994). Two conditions for DCS-EGARCH(1,1) are $|\beta |<1$ and $C_{\lambda }<1$.

For the standard financial time series model: (1) we use the ML estimator, (2) we estimate the standard errors of parameters by using the inverse information matrix, and (3) we use the delta method for the transformed parameters. Even if the $\epsilon _{t} \sim N(0,1)$ assumption does not hold, we still get consistent and asymptotically normal estimates of the parameters in accordance with the Quasi-ML (QML) results of Gouriéroux et al. (1984). For the local level and stochastic seasonality equations, the dynamic parameters of the $\mu _{t}$ and $\rho _{t}$ equations are not estimated but are set to one. Therefore, the asymptotic properties of ML hold for those cases. For GARCH, a sufficient condition for the asymptotic properties of ML is $\alpha +\beta <1$.

Table 1 Descriptive statistics

Data

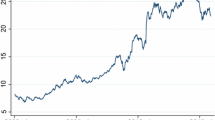
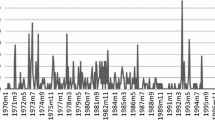
We use GTQ/USD exchange rate data that are obtained from the Bank of Guatemala (see related details in the notes of Table 1). The GTQ/USD exchange rate $p_{t}$ is available from 6th November 1989, when GTQ/USD started to float in the foreign currency market. Until 1994, the Bank of Guatemala used a pegged float exchange rate regime, for which the rate was allowed to fluctuate within a specific band. For the period of 6th November 1989 to 31st December 1993, the GTQ/USD time series shows constant level periods with zero volatility, step function-like evolution in other periods, and significant rises or falls on some days (Fig. 1a, b). Thus, the DCS models of this paper are not adequate for the GTQ/USD time series of this period.

From 1994, a managed float exchange rate regime was introduced, and GTQ/USD became more volatile. In 1997 and 1998, GTQ depreciated in relation to the effects of the Asian Financial Crisis and the Russian Financial Crisis, respectively (Fig. 1c, d). In 1999, both demand and price of the goods exported from Guatemala decreased significantly, and GTQ depreciated significantly again (Fig. 1c, d) due to a negative current account and a negative capital account in the same year. As a consequence, the Bank of Guatemala intervened in the GTQ/USD exchange rate market in August 1999. In May 2001, the Congress of the Republic of Guatemala approved the Law of Free Foreign Currency Transactions (Act No: 94-2000), and created the Institutional Foreign Currency Market (hereinafter, we use the Spanish language acronym of MID). Those institutions that participate in the MID are obliged to report all foreign currency transactions, on a daily basis, to the Bank of Guatemala. The current exchange rate regime in Guatemala allows the participation of the Bank of Guatemala in the MID. Since 2006, the rules of intervention by the Bank of Guatemala are officially published, and are known by the participants of the MID.

Fig. 1

Source of data Bank of Guatemala

GTQ/USD level $p_{t}$ and GTQ/USD log-return $\ln (p_{t}/p_{t-1})$

In this paper, we use data for the period of 4th January 1994–30th June 2017 (Fig. 1c, d). The Bank of Guatemala reports bid and ask prices for GTQ/USD for seven days of the week (Guatemalan banks are open seven days in every week). We use the average of bid and ask prices for each day. We use data for every Monday to Friday from the data window. We do not include bank holidays and weekends in the dataset, since the MID undertakes foreign currency transactions only from Monday to Friday (thus, GTQ/USD does not change during the weekend). As an extension of our models, we also consider a weekly stochastic seasonality component for the GTQ/USD currency exchange rate time series data of this paper. We do not report those results, because weekly seasonality is not significantly different from zero.

We present descriptive statistics for the GTQ/USD level $p_{t}$ and the GTQ/USD log-return $\ln (p_{t}/p_{t-1})$ time series in Table 1. We also present results for the ADF test in Table 1, which suggest that $p_{t}$ is a I(1) process, and thus motivate the use of the local level component with unit root in the DCS model. Further, in Table 1, we present the mean $p_{t}$ for each month of the year. Those mean $p_{t}$ estimates indicate the following annual seasonality effects: (1) strengthening GTQ from December to May; (2) relatively stable GTQ from June to August; (3) weakening GTQ from September to November. These results motivate the use of the annual seasonality component $s_{t}$ in the DCS model. Significant rises and falls in GTQ/USD are also observed in Fig. 1c, which motivate the use of different DCS specifications that discount extreme observations in a different manner. Finally, significant volatility clustering is observed in Fig. 1d, which motivates the use of DCS-EGARCH.

Empirical results

Statistical performance

The ML parameter estimates and model diagnostics are presented in Table 2. For all DCS specifications, the ML conditions for local level and stochastic seasonality are satisfied since the dynamic parameters are set to one. Moreover, the EGARCH estimates support the consistency and asymptotic normality of ML (i.e. $|\beta |<1$ and $C_{\lambda }<1$) (Table 2). With respect to the standard financial time series model, we find statistically significant parameters for the local level, stochastic seasonality and irregular components (Table 2). For the standard model, the ML conditions for local level and stochastic seasonality are satisfied and the estimate of $\alpha +\beta$ is less than one, which supports the asymptotic properties of ML (Table 2).

Table 2 Parameter estimates and model diagnostics

Fig. 2

Updating terms for DCS and standard financial time series models; estimated for the GTQ/USD time series. Notes Each updating term is presented as a function of the error term $\epsilon _{t}$

We use the following metrics to compare statistical performance: LL, Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and Hannan-Quinn Criterion (HQC). According to AIC, BIC and HQC, the in-sample statistical performance of the DCS-Skew-Gen-t model is superior to that of all the alternatives of this paper (Table 2). We also perform a Likelihood-Ratio (LR) test for non-nested models (Vuong 1989). In the LR test, we estimate the linear regression $d_{t}=c+\epsilon _{t}$, where $d_{t}$ is the difference between the log-densities of two models for day t. We estimate this equation by using the OLS-HAC (Ordinary Least Squares - Heteroscedasticity and Autocorrelation Consistent) estimator (Newey and West 1987). In Table 2, we report three different LR test results: (1) LR1 compares the LLs of all alternatives with that of the DCS-Skew-Gen-t model (i.e. the model with the highest LL estimate). According to the results, the LL of the DCS-Skew-Gen-t model is significantly higher than the LLs of the alternative models. (2) LR2 compares the LLs of all alternatives with that of the standard financial time series model (i.e. the model with the lowest LL estimate). According to the results, the LLs of all DCS models are significantly higher than the LL of the standard financial time series model. (3) LR3 compares the LLs of those DCS models that undertake trimming in the location equation (i.e. the recent DCS-t model and the new DCS-Skew-Gen-t model), and also compares the LLs of those DCS models that undertake Winsorizing in the location equation (i.e. the recent DCS-EGB2 model and the new DCS-NIG model). According to the results, the LL of the DCS-Skew-Gen-t model is significantly higher than the LL of DCS-t model, while the LLs of DCS-EGB2 and DCS-NIG models do not differ significantly.

The properties of the scaled score functions and score functions that update the local level and log-scale of $p_{t}$ are important with respect to the likelihood-based performance of alternative DCS models. In the following, we present those properties in the empirical analysis that can be related to the mathematical details of those updating terms (Sect. 3.3). The updating terms $u_{\mu ,t}$ and $u_{\lambda ,t}$ of the DCS-t, DCS-Skew-Gen-t, DCS-EGB2 and DCS-NIG models are presented in Fig. 2a–d, respectively, as functions of $\epsilon _{t}$. We evaluate $u_{\mu ,t}$ and $u_{\lambda ,t}$ by using the ML estimates of the shape parameters, and for $\lambda _{t}$ we use its unconditional mean estimate ${\hat{\omega }}/(1-{\hat{\beta }})$. We also present in Fig. 2e, f the updating terms of the local level $\mu _{t}$ and the conditional variance $\lambda _{t}$ equations for the standard financial time series model. For the evaluation of the updating term of $\lambda _{t}$, we use the ML estimate of its unconditional mean: ${\hat{\omega }}/(1-{\hat{\alpha }}-{\hat{\beta }})$.

For the DCS-t and DCS-Skew-Gen-t models, $u_{\mu ,t}$ undertakes a smooth form of trimming (Fig. 2a). For the greater part of the support of the probability distribution, the DCS-Skew-Gen-t model discounts more observations than the DCS-t model (the only exception is for a small negative interval in the central part of the distribution) (Fig. 2a). Furthermore, for the DCS-t and DCS-Skew-Gen-t models, $u_{\lambda ,t}$ undertakes a smooth form of Winsorizing (Fig. 2b). In the central part of the distribution, observations are discounted in similar ways for the DCS-t and DCS-Skew-Gen-t models (Fig. 2b). In the extreme parts of the distribution, observations are discounted more for the DCS-Skew-Gen-t model than for the DCS-t model (Fig. 2b). All LL-based metrics of Table 2 suggest that the discounting of extreme values for the DCS-Skew-Gen-t model is more effective than the discounting of extreme values for the DCS-t model.

For the DCS-EGB2 and DCS-NIG models, $u_{\mu ,t}$ undertakes a smooth form of Winsorizing (Fig. 2c), and $u_{\lambda ,t}$ increases linearly as $|\epsilon _{t}| \rightarrow \infty$ (Fig. 2d). We find that, for both $u_{\mu ,t}$ and $u_{\lambda ,t}$, observations are discounted more for the DCS-EGB2 model than for the DCS-NIG model (Fig. 2c, d). Moreover, for both the DCS-EGB2 and DCS-NIG models, observations are discounted differently with respect to the left and right tails of the distribution (i.e. observations in the right tail are discounted more than observations in the left tail by both $u_{\mu ,t}$ and $u_{\lambda ,t}$) (Fig. 2c, d). The AIC, BIC and HQC metrics presented in Table 2 suggest that the discounting of extreme values for the DCS-NIG model is more effective than the discounting of extreme values for the DCS-EGB2 model.

With respect to the updating terms of conditional mean $\mu _{t}$ and conditional variance $\lambda _{t}$ for the standard financial time series model, in Fig. 2e, f we present that extreme values in the noise $\epsilon _{t}$ are transformed according to linear and quadratic functions, respectively, for the empirical GTQ/USD exchange rate dataset. All LL-based metrics of Table 2 suggest that the discounting of extreme values for the DCS models is more effective than the transformation of extreme values for the standard financial time series model.

Stochastic seasonality component

For the GTQ/USD exchange rate, significant stochastic annual seasonality $s_{t}$ estimates are shown in Fig. 3a–d for the DCS-t, DCS-Skew-Gen-t, DCS-EGB2 and DCS-NIG models, respectively. We also present those seasonality $s_{t}$ estimates for the standard financial time series model in Fig. 3e. With respect to the economic significance of seasonality effects, for the highest local maximum and lowest local minimum points of $s_{t}$, we estimate approximately $+2\%$ and $-1.5\%$, respectively, for $s_{t}/p_{t}$. The amplitude of seasonality is time-varying. However, for the greater part of the sample period, with respect to the local maximum and local minimum values of $s_{t}$, we estimate at least $+\,0.8\%$ and $-\,0.8\%$, respectively, for $s_{t}/p_{t}$.

Fig. 3

GTQ/USD stochastic annual seasonality component $s_{t}$ for the period of 4th January 1994–30th June 2017

The presence of the annual seasonality component is against the efficiency of the GTQ/USD exchange rate market. The currency market does not eliminate the GTQ/USD seasonality, because the bid and ask exchange rates for clients, that are offered by financial institutions in Guatemala, are such that it is impossible to obtain profits based on the seasonal movements. As an example, we refer to the bid and ask exchange rates offered by Banco Industrial for 12 November 2018. With respect to total assets in 31 December 2017, Banco Industrial is the largest bank in Guatemala (source: Superintendency of Banks, Guatemala). The corresponding bid and ask prices are 7.60 GTQ/USD and 7.80 GTQ/USD, respectively. According to those prices, the bid-ask spread to the mean GTQ/USD ratio is 2.6%, which is higher than the seasonality amplitude that is estimated for any year of the sample period. This example for the relative bid-ask spread is also representative for other Guatemalan financial institutions, for any year of the sample period.

The annual seasonality component can be explained by the evolution of agricultural product exports within each year. During the period of December to May, the amount of USD entering Guatemala increases due to coffee, sugar, banana and cardamom exports. Therefore, during the period of December to May, GTQ becomes stronger with respect to USD (Fig. 3). For the period of June to August, the GTQ/USD exchange rate is relatively stable. For the period of September to November, the amount of USD entering Guatemala reduces due to the finish of agricultural product harvests. As a consequence, during the period of September to November, GTQ becomes weaker with respect to USD (Fig. 3).

Table 3 Total exports from Guatemala and total imports to Guatemala

Fig. 4

Source of data Bank of Guatemala

Relative importance of specific foreign currency movements. Notes R1 is 1994–2000 (solid thin); R2 is 2001–2008 (dashed thin); R3 is 2009–2016 (solid thick)

According to Fig. 3a, b, the seasonality components are very similar for the DCS-t and DCS-Skew-Gen-t models. Moreover, the seasonality components are also very similar for the DCS-EGB2, DCS-NIG and standard models. For the DCS-t and DCS-Skew-Gen-t models, which have superior statistical performance to the competing alternatives, the estimated seasonality component has a relatively high amplitude for the period of 2001–2017. The amplitude of the annual seasonality component of GTQ/USD is dynamic (Fig. 3). We identify three regimes with different amplitudes: (R1) 1994–2000; (R2) 2001–2008; (R3) 2009–2017 (Fig. 3). In the remainder of this section, we present several economic reasons for those regimes.

Table 4 Exports of the main agricultural products of Guatemala

Firstly, in Table 3, we present the evolution of total exports from Guatemala and total imports to Guatemala, for the period of 1993–2016. The growth rate of total exports from Guatemala decreases over time: the mean growth rates of total exports for (R1), (R2) and (R3) are 15.1%, 7.8% and 3.4%, respectively (Table 3). This reduction in the growth rate of total exports suggests a decreasing amplitude of the annual seasonality for periods (R1)–(R3).

Secondly, the relative importance of total exports, with respect to total currency inflows and outflows, decreases for the data window. In Fig. 4, we present the relative importance of the following foreign currency movements for (R1), (R2) and (R3): (1) total exports from Guatemala (Fig. 4a); (2) total imports to Guatemala (Fig. 4b); (3) receipt of loans to Guatemala (Fig. 4c); (4) payment of loans from Guatemala (Fig. 4d); (5) remittance payments to Guatemala (Fig. 4e). For all cases, we compute relative importance with respect to the sum of total inflows and total outflows of foreign currency, and we estimate average relative importance separately for each month. We find that the relative importance of total exports, on average, significantly decreases from (R1) to (R2) and (R3) (Fig. 4a). Furthermore, we also find that the relative importance of loans and remittance payments that do not have a significant seasonality component, on average, significantly increases from (R1) to (R3) (Fig. 4c–e). These results also support the reducing amplitude of GTQ/USD seasonality for the data window.

Thirdly, a further explanation for the decreasing amplitude of the annual seasonality component is the reduction of the relative importance of agricultural product exports within total exports. In Table 4, we present the export income from coffee, sugar, banana and cardamom, which, as aforementioned, are the main agricultural export products of Guatemala. The relative importance of these products reduces significantly during the period of 1994–2016.

These results suggest that the stochastic seasonality component of the GTQ/USD currency exchange rate is significant, both from the statistical and economic points of view, for the period of 1994–2008. The results also suggest that the amplitude of this stochastic seasonality component has decreased for the period of 2009–2017, due to the reduced relative importance of agricultural exports of Guatemala.

Conclusions

We have studied the stochastic seasonality of the GTQ/USD currency exchange rate, by using daily exchange rate data for the period of January 1994–June 2017. For this period, when a managed float currency exchange rate regime has been used in Guatemala, reliable GTQ/USD exchange rate data are available from the Bank of Guatemala.

The seasonality analysis of this paper is motivated by the significant agricultural exports of Guatemala, which lead to significant foreign currency inflows after the harvest periods in every year. The seasonality analysis is also motivated by: (1) the relative importance of agricultural exports in Guatemala has decreased during the past decade, while (2) the relative importance of the non-seasonal receipt of loans, payment of loans and remittance payments to Guatemala have increased during the same period. We have found that the stochastic seasonality of the GTQ/USD exchange rate is significant, both statistically and economically. We have explained the changing amplitude for the period of January 1994–June 2017 by the following points: (1) reducing growth rate of total exports; (2) reducing relative importance of total exports, and increasing relative importance of non-seasonal foreign currency movements (i.e. loans and remittance payments); (3) reducing relative importance of agricultural product exports to total exports.

In the in-sample statistical analysis of this paper, we have introduced the DCS-Skew-Gen-t and DCS-NIG models that include stochastic local level, stochastic seasonality, and irregular components with DCS-EGARCH scale dynamics. Those models are alternatives to the DCS-t and DCS-EGB2 models, respectively. We have also compared the statistical performance of the DCS models with the performance of a standard financial time series model that includes GARCH volatility dynamics. We have focused on the in-sample analysis of the GTQ/USD exchange rate and we have not performed out-of-sample analyses, because the models used in the present paper aim to examine particular empirical features of the historical time series of GTQ/USD exchange rates, such as seasonality and different volatility regimes.

The statistical performance of DCS models is related to the score functions that update the local level and log-scale equations. We have presented the properties of the updating terms of all DCS models. We have shown the trimming, Winsorizing or linear transformation of extreme observations for each DCS updating term. As a consequence, DCS models are robust to extreme observations. We have compared the DCS updating terms with the linear and quadratic updating terms of the standard financial time series model. We have shown that the standard model is not robust to extreme observations. We have found that (1) the DCS-Skew-Gen-t model is superior to all alternatives, (2) all DCS models are superior to the standard financial time series model, (3) the DCS-Skew-Gen-t model is superior to the DCS-t model, (4) the DCS-NIG model is superior to the DCS-EGB2 model according to AIC, BIC and HQC, and (5) the LLs of the DCS-NIG and DCS-EGB2 models do not differ significantly.

The new methodologies of the present work involve the stochastic analyses of the level and seasonality components of currency exchange rate, and we also propose the use of a new stochastic seasonality model in currency exchange rate volatility. Those outlier-robust new methods may be applied in future analyses of currency exchange rates by, for example, central bankers, policy makers, international organizations, private firms and financial investors.