Abstract
This paper identifies patterns of cross-sectional and temporal price dispersion—in the Spanish online grocery retail market—and evaluates the extent to which search costs and chain heterogeneity explain such dispersion. We build a data set comprising 836,074 prices for the most popular grocery products sold online by Spanish national chains at different locations. Our results show that price dispersion is still present (albeit to a lesser extent) even after controlling for chain heterogeneity and that it persists over time. We structurally estimate search costs distributions for two different baskets of goods using price data while accounting for vertical product differentiation. The analysis suggests that the extent of search is low. According to our estimates more than two thirds of consumers do not compare prices among supermarkets. We also find that more frequently purchased products have lower search cost and also lower price–cost margins.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Price dispersion arises when stores in the same market set different prices for the same homogenous good (Hopkins 2008). Different sources of heterogeneity among sellers as well as information frictions explain much of the price dispersion observed in many markets (Lach 2002; Baye et al. 2006). First, store differentiation (e.g., discount retailers versus well-established national chains) may lead to some stores persistently selling their products at a lower price level than others in the same market. Second, when some consumers are perfectly informed about market prices while others are not, price dispersion could arise as a mixed-strategy equilibrium outcome (Stigler 1961; Varian 1980).Footnote 1 In this case, stores’ relative positions in the price distribution change over time—which makes it more difficult for consumers to identify the lowest-price store (Chandra and Tappata 2011). These two accounts are not mutually exclusive and may, when taken together, explain observed price dispersion. In fact, price dispersion remains after store differentiation is controlled for (Lach 2002; Baye et al. 2006).
Price dispersion is a common feature of the grocery retail sector (Zhao 2006). Supermarket chains typically differ in the services offered (i.e., in terms of product assortment, shipping services, return policies, Web design, etc.), and the strategy of unannounced, short-term reductions in the prices of certain products (i.e., sales) is frequently employed. Thus chain differentiation and search frictions might explain price dispersion in grocery markets.
In the case of online shopping, store differentiation appears to be less relevant and consumer search costs look lower than the costs of a “physical” search (Janssen et al. 2007); hence one might expect a reduction of price dispersion in the online context.Footnote 2 Nonetheless, empirical evidence suggests that price dispersion remains even when consumers can easily access price information on homogeneous products from retailers’ Web pages or price comparison websites (Brynjolfsson and Smith 2000; Baye et al. 2004a, b; Ellison and Ellison 2009).
The aim of this empirical paper is to shed some light on price dispersion and search behavior in the Spanish online grocery sector. In Spain, online grocery sales represent a low yet growing share of the total grocery market. Most brick-and-mortar chains have already committed to this e-grocery segment, and most supermarket chains are increasing the number of services offered online. At the same time, the last few years have seen the deployment in Spain of several online price comparison applications that have significantly increased the price information available to consumers.Footnote 3 The empirical analysis is based on price information obtained from the comparison site Soysuper.com. The data cover a period of 182 days—from 1 October 2013 through 31 March 2014—and include 836,074 price observations. However, this data source does not reveal either the quantities sold online or the market shares of the respective grocery chains.
We therefore follow the literature that estimates the search cost distribution when only prices are observed while accounting for chain heterogeneity. In particular, we follow the approach of Wildenbeest (2011) who, building on Hong and Shum (2006) and Moraga-González and Wildenbeest (2008), allows for the estimation of search costs using only price data while accounting for vertical product differentiation.
Competition among supermarket stores is highly localized—even for online shopping. Supermarket websites might differ among locations in terms of product availability and prices.Footnote 4 Hence we consider four distinct markets that are geographically distant from each other: Madrid, Barcelona, Málaga, and Vigo. We follow the literature that deals with search costs in the grocery market and estimate those costs for two baskets of goods: one that includes frequently purchased products (beverages, breakfast and cereals, dairy products, pantry, and personal care and household) and another that includes only alcoholic drinks (beer, wine, and spirits), which we assume is purchased less frequently. Each basket includes identical products (at the bar-code level) in all stores. Yet to the extent that online grocery chains remain heterogeneous in terms of reputation and/or range and level of services, the baskets cannot be viewed as homogeneous products.
As a preview of our results, we observe that price dispersion is still present (albeit to a lesser extent) even after we control for chain heterogeneity, and it persists over time. We find that chain heterogeneity explains much of the observed price dispersion and also that supermarkets’ relative positions in the price ranking do not remain constant over time. These observed patterns suggest that price dispersion may be due to chain differentiation and mixed strategies, which justifies estimating search costs based on a model of utility competition (as in Wildenbeest 2011).
The estimated extent of search is low: across markets, more than two thirds of consumers search just once despite the low cost of searching. Overall, these results are in line with similar studies of the retail food market in other countries (e.g., France, the United Kingdom). In addition, our findings also indicate that the products purchased more frequently tend to entail lower search costs and are likely also to have lower price–cost margins.
The rest of this paper proceeds as follows. In Sect. 2 we discuss several empirical studies that measure price dispersion and search cost. Section 3 describes our data, and Sect. 4 presents empirical evidence of price dispersion in Spanish grocery markets. In Sect. 5 we provide details on our model and estimation strategy; the estimation results follow in Sect. 6. We conclude with a summary of our findings in Sect. 7.
2 Empirical literature on price dispersion and search cost
There is a burgeoning empirical literature that seeks to explain the sources of price dispersion. On the one hand, there are studies measuring price dispersion for a single product category; examples include orange juice (Berck et al. 2008), gasoline (Barron et al. 2004; Chandra and Tappata 2011), books and CDs (Brynjolfsson and Smith 2000; Brynjolfsson et al. 2010), spare parts for cars (Delgado and Waterson 2003), computer and electronic products (Baye et al. 2004a, b; Ellison and Ellison 2009), and airline tickets (Bachis and Piga 2011; Orlov 2011).Footnote 5
On the other hand, some studies compare price dispersion across different products with the goal of establishing empirical regularities that could help to identify the sources of price dispersion. For example, Lach (2002) compares goods of different price levels and finds that higher-priced products exhibit greater price dispersion. Sorensen (2000) compares prescription drugs purchased at different frequencies and reports that price dispersion is negatively correlated with the frequency of purchase.
The price data used in these studies are from different sources. However, recent years have seen a greater number of studies using Internet-sourced data—obtained either directly from retailer websites or indirectly from price comparison websites. See, for example, Clay et al. (2001), Brown and Goolsbee (2002), Baye et al. (2004a, b), Ellison and Ellison (2009), and Cavallo (2017, 2018).
The theoretical approach based on non-sequential consumer search has become increasingly popular in these empirical studies. Thus, for instance, Burdett and Judd (1983) propose a model under which price dispersion can be sustained in equilibrium provided that some consumers observe multiple prices while other consumers observe only one price; this asymmetric distribution of price information is attributed to search costs. Departing from this idea, Hong and Shum (2006) propose a model for estimating search cost distributions—by means of an empirical likelihood estimation procedure—when only price data are observed. Moraga-González and Wildenbeest (2008) modify Hong and Shum’s approach by introducing a maximum likelihood estimator.
Wildenbeest (2011) introduces vertical product differentiation and search costs to explain price dispersion in the grocery retail industry. In that paper, search cost estimation is based on a basket of grocery items from the four leading UK retailers over a 12-week period 2008. In his model, each firm has its own price distribution because firms are heterogeneous in terms of overall quality; this setup accounts not only for price dispersion across firms but also for the observation that some firms have persistently higher average prices than others. Wildenbeest’s findings suggest that nearly two thirds of the observed price variation is explained by supermarket heterogeneity. Hence, ignoring the vertical product differentiation component could lead to overestimation of search frictions. In addition, search intensity is low: 7 in 10 consumers visit only one supermarket.
Following Wildenbeest’s (2011) approach, Richards et al. (2016) use online grocery price data from four large retailers in the United Kingdom to estimate search costs for consumers who engage in multi-product shopping. Their results confirm the finding of low search intensity; 4 out of 5 consumers search only once when shopping for products in multiple categories, and even larger share search only once when shopping for a single category of product.
Hortaçsu and Syverson (2004) analyze the mutual funds industry while assuming that consumers have identical tastes but different search costs. De los Santos et al. (2012) utilize a large data set on Web-browsing and purchasing behavior to test how well various search models capture actual consumer search behavior. Dubois and Perrone (2015) extend the model of Hortaçsu and Syverson to allow for heterogeneous consumer preferences; thus, products are differentiated both vertically and horizontally. Dubois and Perrone use also data derived from observed shopping behavior, since they examine all store visits made by households within a certain period of time. Seiler (2013) proposes a structural model, with imperfect information, that accounts for both inventory holdings and searching. This author uses a consumer-level panel data set (Kantar Worldpanel UK) on laundry detergent and reports that consumers are unaware of its price on 70% of their shopping trips that involve purchasing that product.
In short, results reported in the empirical literature on search costs suggest that consumer search behavior is limited.
3 Data description
Our data set consists of daily posted prices (in euros) for a total of 237 branded products in the categories of beverages, breakfast and cereals, dairy products, pantry, and personal care and household; we excluded fresh food and store brands to ensure comparability between supermarkets. The product prices were provided by the online price aggregator Soysuper.com and were selected based on that site’s popularity index.Footnote 6
The data set identifies products in great detail. Two products are considered to be different if they have different bar codes; for example, whole milk and low-fat milk of the same brand are viewed as different products, for which separate prices are recorded. We also distinguish between the same product being sold either in packs or individually. We identify each chain–product–store combination with a specific product code (SPC); thus, for example, a 500g box of Corn Flakes Kellogs stocked by Auchan and Carrefour in Madrid and Barcelona is represented by four distinct SPCs, each with its own time series of daily prices. Hence identical products have different SPCs depending on the store at which they are sold.
Prices were recorded daily, from 1 October 2013 through 31 March 2014 (182 days), at four locations across Spain: Madrid, Barcelona, Málaga, and Vigo.Footnote 7 The total number of price observations is 836,074. These prices were collected from the product postings on websites of the main Spanish supermarket chains (Auchan, Carrefour, El Corte Inglés, Eroski, and Mercadona)Footnote 8 and of a regional chain (Condis) that operates only in Catalonia (see Table 8 in the “Appendix”).
The average Spanish household’s expenditures on food products amounted to €123.50 per month in 2014.Footnote 9 According to the Report on Food Consumer Habits in Spain (2014) from the Spanish Agriculture and Food Ministery (MAPAMA 2014), consumers’ shopping habits depend on which products they want to buy. Fresh products are purchased more often, typically at specialized shops or small supermarkets, and consumers are more concerned about the quality than the price of such products. In contrast, the standardized products purchased during “primary shopping” (beverages, dairy, cereals, etc.) are often bought in large quantities and at larger stores, such as supermarkets or superstores.
We estimate search costs for two shopping baskets: the basic basket that includes 30 products included in all categories and the occasional one that includes only alcoholic beverages. Tables 9 and 10 list the items included in each basket as well as their prices. We assume that the basic basket are purchased with higher frequency than the occasional one.
4 Evidence of price dispersion
Varian (1980) was among the first to distinguish between spatial and temporal price dispersion. Spatial price dispersion implies that the firm’s place in the price distribution does not necessarily change over time. In our context, any permanent price differences could be explained by store differentiation as price dispersion should diminish over time if consumers can learn (from experience) that some firms consistently offer lower prices than others. Temporal price dispersion arises when the store’s position in a price-based ranking changes over time. In what follows we discuss both types of price dispersion in our data.
4.1 Spatial price dispersion
We measure price dispersion as the (log of) deviations in price from the daily mean (Lach 2002); that is, \(g_{ijlt}=\log p_{ijlt}-\log \bar{ p}_{ilt}\). Here \(p_{_{ijlt}}\) denotes the price of item i in chain j at location l on day t, and, \(\bar{p}_{ilt}\) is the mean price across stores of item i at location l on day t, for \(i=1,\ldots ,237\), \(j=1,\ldots ,6\), \(l=1,\ldots ,4\), and \(t=1,\ldots ,182\).
Part of the dispersion observed in prices may be explained by product differentiation. Although we compare goods with the same physical characteristics, these goods are sold at different stores and also on different days. As a result, the products are not homogenous. We therefore assume that identical products in different locations are not substitutes—since the distance between cities is great enough that we can view them as distinct markets.
Following Lach (2002), we remove from prices any heterogeneity due to the supermarket chain, location, or time. For this purpose we run item-by-item regressions of prices (measured as log deviations from the daily mean) on the fixed effects of supermarket chain and location, on the interaction between those effects, and on a time effect. We estimate the following equation for each item i, \(g_{ijlt}=\mu +\alpha _{j}+\beta _{l}+\alpha _{j}\times \beta _{l}+\gamma _{t}+\varepsilon _{ijlt}\) ; here \(\alpha _{j}\)is a supermarket-chain fixed effect that is common across products and locations, \(\beta _{l}\) is a location fixed effect, and \( \gamma _{t}\) is a time effect. The residuals of these regressions represent the price of a homogeneous product after controlling for time-invariant, store-specific effects and for the price fluctuations common to all stores. This method of deriving homogeneous prices is now standard in the literature (see e.g. Sorensen 2000; Lach 2002; Zhao 2006; Dubois and Perrone 2015).
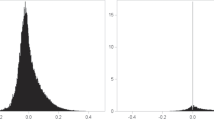
Figure 1 plots the empirical density function for the spatial dispersion of observed prices (solid line) and of homogeneous prices pooled over products, stores, and days (dashed line).Footnote 10
This figure reveals that prices exhibit considerable dispersion. Most observed prices fluctuate between − 10% and \(+\) 10% of the mean and, as expected, are relatively more dispersed than are the homogeneous prices. The empirical literature has documented that the magnitude of price dispersion varies as a function of product characteristics (price level, purchase frequency, etc.). Table 1 reports several measures of price dispersion by product categories.
The table’s first two data columns give the standard deviations of the observed and homogeneous (residual) prices, and the last four columns report the 5th and 95th percentiles of each distribution. For all categories, spatial price dispersion drops significantly—in terms of both the standard deviation and the quantiles—when we control for observed product heterogeneity. Nevertheless, some dispersion persists even when prices are homogeneous. Results are somewhat heterogeneous with respect to product categories. The pantry category and the breakfast and cereals category exhibit the most price dispersion, since their standard deviations are the highest; prices for dairy products exhibit the least dispersion.
4.2 Temporal price dispersion
We observe temporal price dispersion when the identity of the store offering the lowest (and highest) price varies over time. If stores’ relative positions in the price distribution remain constant, then dispersed prices could simply reflect store heterogeneity. However, if the ranking by prices varies over time then price dispersion might rather be the result of costly consumer search. In this latter case, firms change their prices so that buyers cannot identify the “cheapest” store overall.
Temporal price dispersion is measured by comparing how stores’ prices are ranked over time. We define rr (rank reversal) as the number of changes in price-rank position for a given product i sold at supermarket j over \( \tau \) days.Footnote 11 Thus, we write, \(rr_{i}^{j}=\frac{1}{T}\sum _{t=\tau +1}^{T}I(r_{it}^{j}\ne r_{it-\tau }^{j})\); here \(r_{it}^{j}\) denotes the position of the supermarket j in the price ranking of item i on day t in a given location, and \(r_{it-\tau }\) denotes its position \(\tau \) days earlier. Now we can define the average ranking change for supermarket j at a given location as the average of rank changes among all products: \(RR^{j}= \frac{1}{N}\sum _{i=1}^{N}rr_{i}\). Although rank changes on two successive days may be small, the extent of change increase with the time interval.
Table 2 reports the average rank changes in prices between two observations with a time lag of 1, 10, and 30 days in Barcelona, Madrid, Málaga, and Vigo. A change in ranking position indicates a price change in at least one chain’s stores. However, a given supermarket can change a price without its rank changing and can also see its rank change without changing any prices—that is, provided some competitor does.
The table suggests that stores change their relative position in the price rankings as the time lag increases. The four first columns (one under each location) show that stores price rankings barely change between two consecutive days. Yet with a 10-day (resp. 30-day) time lag, the average percentage change approaches or exceeds 20% (resp. 35%). The exception to this pattern is Auchan, which is in the same position of the ranking most of the time. We shall see that their prices are always the lowest.Footnote 12
Price rankings that fluctuate make it more difficult for consumers to find the best deal, and chances are nearly 4 in 10 that relative prices for a given product will have changed within the past month. It follows that consumers must update their information about prices rather frequently if they want to continue paying the least amount possible.
5 Using price data to estimate consumer search costs
The empirical evidence described so far suggests that part of the dispersion observed in prices may be explained by store differentiation, although our evidence is consistent also with imperfect information about prices. To the extent that supermarkets change their prices and thus their positions in the ranking, it is more difficult for consumers to learn about prices. In this section we estimate search costs as well as the proportion of consumers who compare prices when grocery shopping; for that purpose we use the available information about prices while accounting for supermarket chain heterogeneity.
We follow previous papers in this literature by considering the price of a basket of products rather than individual product prices, and we assemble two different baskets of goods. The basic basket includes those branded products—from various categories—most often included on consumer shopping lists and the occasional basket includes only alcoholic beverages. We estimate the search costs for the two baskets in four geographical markets.
5.1 The model
In estimating search costs, we use the nonsequential search model developed by Wildenbeest (2011)Footnote 13. In this model firms compete directly in the utility space, which implies that the supermarket strategy space is reduced from two dimensions (quality and price) to a single utility dimension. This approach enables us to incorporate chain differentiation into the model.
Suppose there are N supermarkets offering a homogeneous good (a basket of groceries) to imperfectly informed consumers at a particular location. Supermarkets sell this “good” at a unit cost of \(r_{j}\).
Consumers share a common utility function and have identical preferences regarding quality; however, their search costs differ (as in Hortaçsu and Syverson 2004). We can write
where \(\upsilon _{j}\) is the consumer’s valuation of buying the good from supermarket j at a given location. This valuation has the additively separable structure \(\upsilon (s_{j})=x+s_{j}\); here x denotes the common consumers’ valuation of the homogeneous good independent of store quality, \( s_{j}\) is the supermarket’s level of services or quality (Wildenbeest 2011), and \(p_{j}\) is the basket’s price.
Because the consumers in our setup all have the same utility function, a supermarket determines its quality level \(s_{j}\) by maximizing the price–cost margin: \(p_{j}-r_{j}=p(s_{j})-r(s_{j})=\upsilon (s_{j})-r(s_{j})-u,\) for a given utility level u. By Euler’s theorem, the total cost of quality inputs exhausts quality-related output; that is, \( r(s_{j})=s_{j}\).Footnote 14 As a consequence, the valuation cost markup does not depend on store quality: \(\upsilon (s_{j})-r(s_{j})=x+s_{j}-r(s_{j})=x\). We can therefore focus on symmetric mixed-strategy equilibria in utility levels, where the supermarket’s strategy is given by a common utility distribution function L(u).
Consumers search nonsequentially. That is, a consumers takes supermarkets’ strategies as given and decides on the optimal number \(k\ge 1\) of stores to visit, after which he buys from the store that gives him the highest utility.Footnote 15 A consumer’s search cost c is assumed to be a random draw from a common atomless distribution G(c) with support \((0,\infty )\) and positive density g(c).
Consumer search behavior should be optimal in this sense: the net benefit of searching k times should be greater than that of searching either \(k-1\) or \(k+1\) times; and the expected utility from searching should exceed its expected cost (\(k\cdot c\)). The search cost of a consumer who is indifferent between searching k and \(k+1\) times,
is decreasing in k. The share \(q_{k}\) of consumers who sample k prices is then
which implies:
Here \(G(c_{0})=1\), so every search cost is lower than \(c_{0}\); and \( G(c_{N})=0\), so \(c_{N}\) is the minimum search cost.
Supermarket j’s expected profit from offering utility level \(u_{j}\) is
given expected consumer behavior \(q_{k}\) and the distribution function L(u) . Here \(x-u_{j}=p_{j}-r_{j}\) is the price–cost margin of each supermarket that implicitly sets a price p. The summation captures the expected sales quantity, which depends on: (i) the proportion \(q_{k}\) of consumers searching k times; (ii) the likelihood k / N of consumers observing the utility of firm j; and (iii) the probability \(L(u_{j})^{k-1}\) that, at utility level \(u_{j}\), the firm offers the highest utility level of all the k firms searched.
In this setting, a price dispersion equilibrium is possible only when there exists a positive (though not certain) likelihood of a consumer observing only one price.Footnote 16 The characterization of the equilibrium utility distribution in mixed strategies implies that the supermarket should be indifferent about what level of utility to set in the support of L(u) (Burdett and Judd 1983). In particular, the supermarket should be indifferent between (a) offering a utility of zero by setting \(\bar{p}_{j}=\upsilon _{j}\) and selling only to uninformed consumers (i.e., those who search just once) and (b) setting any other utility level in the support of L(u), \(u>0= \underline{u}\):
where the right-hand side is the expected profit when offering zero utility. In this case, if firms offer the maximum utility (\(u=\overline{u}\)) then \(L( \overline{u})=1\) (all utility levels are below the maximum); hence the maximum utility is given by
Our aim is to estimate the points \(\{q_{k},c_{k}\}_{k=1}^{n}\) via maximum likelihood, as in Moraga-González and Wildenbeest (2008). The equilibrium distribution of utilities, L(u), can only be implicitly defined, but the density function can be derived from the first-order conditions of expected profit maximization:
these conditions are then used to define the log-likelihood function \( LL=\sum _{i=2}^{T}\log l(u_{i})\). Here T is the total number of observations, the minimum utility is zero, and all utilities are arranged in ascending order: \(\underline{u}=u_{1}<u_{2}<\cdots <u_{T}=\overline{u}\). Thus we have \(L(\overline{u})=1\) and \(L(\underline{u})=0\).
We can use this characterization of optimal searching behavior to rewrite the search cost as follows:
Further simplification is possible if we put \(y=L(u)\), so that \(dy=l(u)\,du\) and \(u=L^{-1}(y)=u(y)\); then
If we now use the same change of variable in the equilibrium profit equation y yields
from which the equality \(u(y)=x-\frac{x\mu _{1}}{\sum _{k=1}^{N}k\mu _{k}y^{k-1}}\) followsFootnote 17.
5.2 Estimation strategy
The first step is to estimate utilities. Toward that end, we assume that consumers differ in their search costs but have the same preferences regarding chain characteristics.Footnote 18 Thus consumers in a given location derive utility from buying the homogeneous basket at store j according to \( u_{j}=v_{j}-p_{j}\), where \(v_{j}\) is the valuation of buying the basket at store j and \(p_{j}\) is that basket’s price. Utilities are then defined as prices adjusted by the heterogeneity between stores (services provided, quality, etc.). Consumers know their valuation of a good but do not know its price. Hence they must obtain information about basket prices at a number of supermarkets in accordance with their search costs.
We rewrite the preceding paragraph’s equation as \(p_{j}=v_{j}-u_{j}\), which can be estimated via a fixed-effects regression on prices. Then \( p_{j}=\alpha +\gamma _{j}+u_{j}\), where \(\alpha \) is a constant, \(\gamma _{j} \) is a store fixed effect, and the (negative of) disturbance \(u_{j}\) represents utility.
After deriving the estimated utilities, we proceed as in Moraga-González and Wildenbeest (2008).Footnote 19 The maximum likelihood (ML) problem is given by
The term M is the number of price data points at each location, and \( L(u_{j})\) solves
and
and using the fact that \(q_{N}=1-\sum _{k=1}^{N-1}q_{k}\). That is, the ML estimator yields estimates of the proportion \(q_{k}\) (\(k=1,\ldots ,N\)) of consumers who are searching, and we can recover the search costs from those estimates.Footnote 20
6 Results
In order to estimate search costs we select two different baskets of products. First, a “basic” basket that includes the most frequently purchased grocery products. And the “occasional” basket, a basket containing only alcoholic beverages (wine, beer, and spirits).Footnote 21 These products are assumed to be purchased less frequently and most of them are not included in the basic basket.
6.1 Price dispersion: basic basket
The basic basket of goods includes regularly purchased items (according to Soysuper.com’s popularity index) in five product categories (beverages, breakfast and cereals, dairy products, pantry, and household and personal care), for which we have a complete series of prices across all the chains at all locations. Because each product in this basket is branded, we can view the basket as a completely homogenous good. Supermarkets are assumed to be especially interested in the pricing of these highly popular products.
Our basic shopping basket (which excludes fresh groceries) contains 30 items, most of which are purchased as part of primary shopping. The basket price is the sum of all individual prices weighted by category—that is, according to the household monthly expenditures reported by the Spanish Household Budget Survey, 2013. Its total cost range from €57.55 (Auchan) to €69.32 (El Corte Inglés) and averages about €67 (see Table 3).Footnote 22 The difference between the most and the least expensive basket is €11.80, but this difference varies across supermarkets. Auchan has the greatest intra-firm price dispersion, ranging between €58 and €64; the basket price at Carrefour exhibits very little variation (€66.80–€68.50). El Corte Inglés and Eroski have the highest prices. Price differences among stores belonging to the same chain are small in all chains except Auchan. Mercadona is the chain that exibit lower intra-chain price dispersion, which suggests that most of its prices are centralized at the chain level.Footnote 23
If store characteristics do not change (at least in the short term) and if price dispersion reflects chains differentiation, then we should expect supermarkets to set prices in a manner that preserves their ranking position. Thus, high-quality supermarkets will nearly always set relatively high prices. Of course, if the position of stores in the price distribution remains constant then it is easier for consumers to learn about prices.
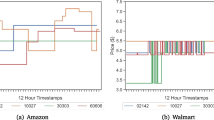
In Fig. 2, Panel A provides information on the daily price of the basic basket for the six supermarkets in Barcelona. Auchan is clearly the supermarket with the lowest basket price, yet its prices change frequently. The ranking of the other supermarkets varies, although El Corte Inglés usually has the highest prices and Mercadona the lowest—especially in the last month sampled, when the latter chain initiated a price-cutting campaign. Stores revise their pricing often but do not change prices synchronously; that is, the length of time between price changes differs across chains. In sum, Panel A suggest that some chains have consistently lower prices (and/or prices that change more frequently) than other chains. Panel B displays information on consumer utility, which is estimated as the negative of the residuals from a regression of prices on store fixed effects; the resulting value can be interpreted as the price of the homogeneous good after controlling for chain heterogeneity.Footnote 24 This panel shows that no single supermarket yields utilities that are consistently higher or lower than the others. Although positions in the ranking of utilities seldom change daily, there is considerable longer-term fluctuation.
Table 4 reports the percentage of time that the price and the utility spend in each quartile (at the Barcelona location).
From the table’s first four columns we observe that Auchan is the only supermarket that have occupied the first quartile for the entire study period; in other words, it was always among the lowest-priced stores. Mercadona was located in the two first quartiles for almost two thirds of the period. At the other extreme, Eroski was the most expensive supermarket 88% of the time and El Corte Inglés was among the least expensive only 2.7% of the time. Carrefour was usually located in the second quartile, and Condis was most often located in the third quartile. Looking at the distribution of utilities (last four columns of the table), we can see that there is less concentration in particular quartiles because the distribution of utilities is more spread out. These observed patterns support the notion that price dispersion is due to mixed strategies in combination with chain heterogeneity. In other words, each chain has its own price distribution from which to draw and—depending on the extent of firm heterogeneity—the respective supports of those distributions may overlap.
6.2 Search cost estimates for the basic basket
We use the basket prices to estimate the model’s parameters.Footnote 25 We are mainly interested in estimating the proportion of consumers who search and calculating their search costs, that is, \(\{q_{k},c_{k}\}_{k=1}^{n}\). The estimation results, which are obtained using the ML procedure described previously, are presented in Table 5.
We first estimate utilities by running the chain–fixed-effects regression of prices separately for each location. The resulting \(R^{2}\) values indicate that, in all locations, more than the 90% of the variation in prices is explained by chain dummies.
The first three rows of Table 5 report the estimated proportion of consumers searching one time (\(q_{1}\)) or two times (\(q_{2}\)). The estimated share of consumers who search once or twice is about 90% in all locations, but the percentage of consumers who search all local stores is never more than 4.4%. These results might indicate that there are no significant differences in search costs among the respective consumers from different locations, although the proportion of those who search only once is lower in Vigo and higher in Barcelona. Search costs may reflect the opportunity cost of time (which directly affects the cost of acquiring information) and/or other consumer characteristics (e.g., education, age).
Unfortunately we cannot analyze how search costs vary among consumers within each city as we have not information about consumer characteristics. For example, Dubois and Perrone (2015) find that, across income levels, there are no consistent differences in the proportion of individuals who engage in searching when shopping. On the other hand, De los Santos (2017) using data on consumers shopping for books online finds that consumers with higher-income individuals devoting less time to search.
Our results are in line with those reported in other papers. With regard to UK grocery items, Wildenbeest (2011) finds that most of the observed price variation is explained by supermarket heterogeneity and that the estimated amount of searching is low. He reports that 71% of consumers search only once, 91% search either once or twice, and only 8% of consumers compare all prices. Richards et al. (2016) show that 84% of consumers search only one store when shopping for products in many categories at the same time. Using data from France on food expenditures, Dubois and Perrone (2015) confirm that consumers observe only a few prices before making a purchase.
Estimated search costs are low. We estimate that, the search cost of a consumer who searches just once range from €0.45, in Málga and €0.61 in Madrid. So for these consumers we can only infer that their search cost should have been at least of this amount in order to rationalize their behavior. Similarly, for consumers who search twice the search costs should have been at least €0.27 in Málaga and €0.37 in Madrid. Consumers who are comparing more than two prices should have been lower search costs. Such low search costs are similar to those found by Wildenbeest (2011), who calculates that the search cost of consumers who do not search should have been at least €0.27 for that behavior to be rational.
The estimated maximum price–cost margins \((v_{j}-r_{j})\) range from €5.78 in Vigo to €9.72 in Barcelona, which translates into a maximum margin below 10% in all locations—except in Barcelona. We remark that, in this last location, consumers search less than elsewhere, which could explain the higher margins in that city. Estimated margins in the United Kingdom range between 8 and 9%.
6.3 Price dispersion: occasional basket
Our results could be affected by the particular products selected for the shopping basket. All the products in our basic basket are among the most frequently purchased, so it is fair to suppose that consumers have more information about them. We therefore put together a substantially different basket containing only alcoholic beverages (wine, beer, and spirits). These products are assumed to be purchased less frequently, and most of them are not included in the basket basket.Footnote 26
The average cost of this basket is approximately €72, and its price dispersion is greater than that of the basic food basket. As Table 6 shows, the price ranges from €62.59 at Auchan to €76.28 at Eroski—a difference of almost 20%. Auchan remains the supermarket with the lowest prices (just as for the basic basket), but now Eroski (rather than El Corte Inglés; cf. Table 3) is, on average, the most expensive supermarket.
Figure 3 plots (once again, for Barcelona) the evolution of our occasional basket’s price and utility. The patterns are strongly similar to those observed for the basic basket (cf. Fig. 2). Although Auchan is again always the least expensive supermarket, there is variability in the price ranking of the other supermarkets. Panel B of the figure shows that utility rankings (calculated as the negative of the residuals) change more frequently than do prices and that no supermarket exhibits a consistent ranking.
6.4 Search cost estimates for the occasional basket
We first regress prices on store fixed effects to obtain the utilities. For most locations, these fixed effects explain more than 75% of observed price variability, as Table 7 shows.
The estimated portion of consumers who search only once ranges from 65% to 71%, although the differences are not statistically significant among cities. Search costs are higher than for the basic basket. We estimate that, the search cost of a consumer who searches just once range from €1, in Málaga and €1.1 in the rest of locations. So consumers search cost should have been larger than this amount in order to rationalize their behavior.
The maximum estimated price–cost margin ranges between 15 and 18%, values that are also higher than for the basic basket.
So in comparison with the basic basket, the occasional basket is characterized by greater price dispersion, higher search costs, and higher margins. These results accord with those in Sorensen (2000), who establishes that prices of repeatedly purchased prescriptions—for which search benefits are expected to be high—exhibit relatively low price–cost margins and relatively less price dispersion.
7 Conclusions
The aim of this empirical paper is to identify patterns of cross-sectional and temporal price dispersion, and to assess the role played by search costs and chain differentiation in that dispersion. We build a price data set of grocery and household products often included on Spanish consumers’ shopping lists and sold at the main Spanish supermarket chains.
Quantifying search costs is a relevant question from the perspective of competition policy. As Waterson (2003) shows, traditional policies that fail to incorporate search costs will likely be less effective than other policies at enhancing competition. In fact, consumer information about prices is a necessary condition for markets to be truly competitive. If consumers never engaged in price comparison, then the monopoly price would prevail in equilibrium (Diamond 1971); however, price dispersion will be an equilibrium in markets where at least some consumers search more than once (Burdett and Judd 1983). Regulations that aim to promote competition must therefore account for the distortions due to informational restrictions. For instance, Stahl (1989) shows that—in the presence of search costs—firm entry does not necessarily improve consumer welfare. Similarly, Lach and Moraga-González (2017) find that consumer surplus always (although weakly) decreases with increased competition. For those agencies tasked with devising competition policy, another consideration should be retailer practices that aim to confuse or mislead consumers (Ellison and Ellison 2009).
Analyzing consumer search in online markets could also yield insights into traditional, brick-and-mortar retail behavior. Consumer access to prices through supermarket websites or price comparison sites (e.g., Soysuper.com) has reduced search costs for both online and offline retail consumers. Customers can easily check prices before they shop and also while they shop.
We find that some chains have persistently lower prices than others, even as prices change frequently. This empirical evidence suggests that both search frictions and chain differentiation help explain price dispersion in Spanish grocery markets. We estimate the distribution of consumer search costs for different baskets of goods sold in different geographical markets. For that purpose we employ the model proposed by Burdett and Judd (1983) and modified—to account for vertical product differentiation—by Wildenbeest (2011). We find (for Barcelona) that about 90% of the observed variation in prices is due to chain fixed effects and that the estimated share of consumers searching only once is 84% and such behavior is economically rational only when search costs amounted to at least €0.57. Our regression results also indicate that the more frequently purchased products tend to have lower price dispersion and lower price–cost margins.
Finally, our results are in line with findings previously reported in the literature on the retail food market in other countries—for instance, France and the United Kingdom. Moreover, are consistent with the Ministry of the Environment and Rural and Marine Affairs (MARM 2011) survey where 84% of interviewed Spanish consumers consider themselves to be fairly loyal to a supermarket and 48.4% of them always buy without comparing prices.
Notes
Consumer access to prices—through supermarket websites or price comparison sites—may reduce search costs both for online and for offline retail consumers, since customers can easily check prices before or even while they shop. Baye et al. (2013) examine the evolution of product search since the pre-Internet era.
E.g. carritus.com, tudespensa.com, Soysuper.com, and komparing.com (among others), with responsive web designs.
A shopper who logs on to a supermarket’s website must check for whether delivery is available in her postal zone; since these zones are matched up to the nearest warehouse, prices (and also product availability) may well differ by location.
For a review of the research on price dispersion, see Baye et al. (2006).
This index is based on three factors: the frequency that a product is purchased in comparison with all products purchased online; the frequency with which a product is added to the basket as compared with all products added to baskets; and the number of supermarkets selling the focal product on their respective Web pages.
Madrid and Barcelona are home to (respectively) 3,165,235 and 1,602,386 inhabitants. Málaga and Vigo are located, respectively, in the south (Andalucía region) and northwest (Galicia region) of Spain and have 566,913 and 294,997 residents. Average annual income per capita among the four cities differs, but not by much: €35,090 in Barcelona, €36,636 in Madrid, €24,405 in Málaga, and €29,654 in Vigo.
Aggregate revenue of the five national chains accounted for 72.2% of the net sales of main food chains (CNC 2011).
See the Report on Food Consumer Habits in Spain (MAPAMA 2014) from the Spanish Agriculture and Food Ministry. Fresh products (fresh fruit, vegetables, meat, fish, eggs, and fresh bread) represent a 44.5% of those expenditures, which means that €69.5were spent each month on non–fresh food products.
Because our measure of price dispersion averages to zero each day, all variation in the kernel density is cross-sectional for each day and at each location.
See Chandra and Tappata (2011) for a similar rank-reversal statistic.
Annual reports on supermarket prices published by the Spanish consumer organization (OCU) indicate that Auchan has been the lowest-price national chain in Spain: https://www.ocu.org/consumo-familia/supermercados/informe/cadenas-mas-baratas and https://elpais.com/economia/2017/09/25/actualidad/1506360054_741892.html (both accessed 29 September 2017).
See Moraga-González et al. (2017) for an analysis of the equilibrium’s existence and uniqueness.
Under perfect competition, supermarkets obtain quality input factors and the quality production function exhibits constant returns to scale.
A condition that partially characterizes a symmetric equilibrium in the utility space is that some consumers search only once (at no cost) while others search more than once (see Burdett and Judd 1983).
The intuition for this claim is that, if all consumers did compare the prices at different stores, then each firm would set a price equal to their unit cost.
Moraga-Gonzalez et al. (2013) show that the model described here is nonparametrically identified if the number of searches does not tend to infinity.
This assumption implies, for example, that all consumers would prefer shopping at Eroski or El Corte Inglés than at Auchan if prices were identical across supermarket chains.
The estimates are derived while assuming that firms play a stationary repeated game of finite horizon, so the data in each period should reflect the equilibrium of the static game analyzed previously (cf. Moraga-González and Wildenbeest 2008). For the estimation we select price observations every 10 days to avoid serial correlation.
The maximum likelihood estimator was programmed using MATLAB and the optimization procedure with its TOMLAB solver package.
Products included in the bakets must be sold in all supermarkets and in all locations during the entire study period (else comparisons would not be possible). We exclude not only products that are almost identical (e.g., we include low-fat milk but neither whole milk nor skim milk) but also different sizes of the same product (e.g., 2l vs. 500ml Coca-Cola). When confronted with similar products, we made a random selection to determine which should be included in the basket.
Table 9 (in the “Appendix”) reports the average price and the price dispersion of each product included in the basic basket.
See González (2017) for a discussion of pricing strategies at the chain level.
We normalize minimum utility to zero adding a constant. Estimates of the search cost distribution do not change when a constant is added because the differences between utilities remain invariant.
One assumption of the theoretical model is that price observations could be uncorrelated. We check for serial correlation and calculate the autocorrelation function for the basket in each store–location pair. Not surprisingly, the autocorrelation between two consecutive days is fairly high; yet autocorrelations calculated with a 10-day lag between price observations are not significantly different from zero. So when estimating search costs, we use price observations separated by 10 days.
Table 10 gives the average price (and price dispersion) of each product in this basket. The basket price is the sum of all individual prices weighted by subcategory (according to the Spanish Household Budget Survey, 2013). The share of expenditures on these three groups is 38.7% (beer), 43.9% (wine) and 17.4% (spirits). The specific items included in each category were chosen among those available in the six supermarkets at the four locations.
References
Bachis E, Piga CA (2011) Low-cost airlines and online price dispersion. Int J Ind Organ 29(6):655–667
Barron JM, Taylor BA, Umbeck JR (2004) Number of sellers, average prices and price dispersion. Int J Ind Organ 22(8–9):1041–1066
Baye MR, Morgan J (2001) Information gatekeepers on the Internet and the competitiveness of homogeneous product markets. Am Econ Rev 91(3):454–474
Baye MR, Morgan J, Scholten P (2004a) Temporal price dispersion: evidence from an online consumer electronics market. J Interact Mark 18(4):101–115
Baye MR, Morgan J, Scholten P (2004b) Price dispersion in the small and in the large: evidence from an Internet price comparison site. J Ind Econ 52(4):463–496
Baye MR, Morgan J, Scholten P (2006) Information, search and price dispersion. In: Hendershott T (ed) Handbook of economics and information systems, vol 1. Elsevier Press, Amsterdam, pp 323–371
Baye MR, De los Santos B, Wildenbeest MR (2013) The evolution of product search. J Law Econ Policy 9:201–221
Berck P, Brown J, Perloff JM, Villas-Boas SB (2008) Sales: test of theories on causality and timing. Int J Ind Organ 26(6):1257–1273
Brown JR, Goolsbee A (2002) Does the Internet make markets more competitive? Evidence from the life insurance industry. J Polit Econ 110(3):481–507
Brynjolfsson E, Smith MD (2000) Frictionless commerce? A comparison of Internet and conventional retailers. Manag Sci 46(4):563–585
Brynjolfsson E, Dick AA, Smith MD (2010) A nearly perfect market? Differentiation versus price in consumer choice. Quant Mark Econ 8:1–33
Burdett K, Judd K (1983) Equilibrium price dispersion. Econometrica 51(4):955–969
Carlson JA, McAfee RP (1983) Discrete equilibrium price dispersion. J Polit Econ 91(3):480–493
Cavallo A (2017) Are online and offline prices similar? Evidence from multi-channel retailers. Am Econ Rev 107(1):283–303
Cavallo A (2018) Scraped data and sticky prices. Rev Econ Stat. https://doi.org/10.1162/REST_a_00652
Chandra A, Tappata M (2011) Consumer search and dynamic price dispersion: an application to gasoline markets. RAND J Econ 42(4):681–704
Clay K, Krishnan R, Wolff E (2001) Prices and price dispersion on the web: evidence from online book industry. J Ind Econ 49(3):521–539
Comisión Nacional de la Competencia (CNC) (2011) Report on the relations between manufacturers and retailers in the food sector
Dana JD (1994) Learning in an equilibrium search model. Int Econ Rev 35(3):745–771
De los Santos B (2017) Consumers search on Internet (Manuscript). http://babur.people.clemson.edu/research/Consumer_Search_on_the_Internet.pdf. Accessed 23 Jan 2018
De los Santos B, Hortaçsu A, Wildenbeest MR (2012) Testing models of consumer search using data on web browsing and purchasing behavior. Am Econ Rev 102(6):2955–2980
Delgado J, Waterson M (2003) Tyre price dispersion across retail outlets in the UK. J Ind Econ 51(4):491–509
Diamond PA (1971) A model of price adjustment. J Econ Theory 3(2):156–158
Dubois P, Perrone H (2015) Price dispersion and search costs: the roles of imperfect information and product differentiation (Manuscript)
Edelman B (2012) Using Internet data for economic research. J Econ Perspect 26(2):189–206
Ellison G, Ellison SF (2009) Search, obfuscation and price elasticities on the Internet. Econometrica 77(2):427–452
González X (2017) Chain heterogeneity and price-setting behavior: evidence from e-grocery retailers. Electron Commer Res Appl 26:62–72
Hong H, Shum M (2006) Using price distributions to estimate search costs. RAND J Econ 37(2):257–275
Hopkins E (2008) Price dispersion. In: Durlauf SN, Blume LE (eds) The new palgrave dictionary of economics. Palgrave Macmillan, London
Hortaçsu A, Syverson C (2004) Product differentiation, search costs and competition in the mutual fund industry: a case study of S&P 500 index funds. Quart J Econ 119(2):403–456
Janssen M, Moraga-González JL (2004) Strategic pricing, consumer search and the number of firms. Rev Econ Stud 71(4):1089–1118
Janssen M, Moraga-González JL, Wildenbeest MR (2005) Truly costly sequential search and oligopolistic pricing. Int J Ind Organ 23(5–6):451–466
Janssen M, Moraga-González JL, Wildenbeest MR, Brousseau E, Curien N (2007) Consumer search and pricing behavior in Internet markets. In: Brousseau E, Curien N (eds) Internet and digital economics. Cambridge University Press, Cambridge, pp 460–483
Lach S (2002) Existence and persistence of price dispersion: an empirical analysis. Rev Econ Stat 84(3):433–444
Lach S, Moraga-González JL (2017) Asymmetric price effects of competition. J Ind Econ 65(4):767–803
MAPAMA (2014) Informe sobre el consumo alimentario en España, 2014. Ministerio de Agricultura, Pesca, Alimentación y Medio Ambiente. http://www.mapama.gob.es/es/alimentacion/temas/consumo-y-comercializacion-y-distribucion-alimentaria/dic14_tcm7-382143.pdf. Accessed 29 Sept 2017
MARM (2011) Estudio de mercado. Observatorio del consumo y la distribució n alimentaria, Ministerio de Medio Ambiente y Medio Rural y Marino
Moraga-González JL, Wildenbeest MR (2008) Maximum likelihood estimation of search costs. Eur Econ Rev 52(5):820–848
Moraga-Gonzalez JL, Sandor Z, Wildenbeest M (2013) Semi-nonparametric estimation of consumer search costs. J Appl Econ 28:1205–1223
Moraga-González JL, Sandor Z, Wildenbeest M (2017) Non-sequential search equilibrium with search cost heterogeneity. Int J Ind Organ 50:392–414
Orlov E (2011) How does the Internet influence price dispersion? Evidence from the airline industry. J Ind Econ 59(1):21–37
Richards T, Hamilton SF, Allender W (2016) Search and price dispersion in online grocery markets. Int J Ind Organ 47:255–281
Rosenthal RW (1980) A model in which an increase in the number of sellers leads to a higher price. Econometrica 48(6):1575–1579
Seiler S (2013) The impact of search costs on consumer behaviour: a dynamic approach. Quant Mark Econ 11:155–203
Sorensen AT (2000) Equilibrium price dispersion in retail markets for prescription drugs. J Polit Econ 108(4):833–850
Stahl DO (1989) Oligopolistic pricing with sequential consumer search. Am Econ Rev 79(4):700–712
Stigler G (1961) The economics of information. J Polit Econ 69(3):213–225
Varian HR (1980) A model of sales. Am Econ Rev 70(4):651–659
Waterson M (2003) The role of consumers in competition and competition policy. Int J Ind Organ 21(2):129–150
Wildenbeest MR (2011) An empirical model of search with vertically differentiated products. RAND J Econ 42(4):729–757
Zhao Y (2006) Price dispersion in the grocery market. J Bus 79(3):1175–1192
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank J. L. Moraga, M. J. Moral, C. Pazó and two anonymous reviewers for their valuable comments and suggestions as well as Claudia Martínez-Boubeta for excellent research assistance. The paper has also benefited presentations at Munich (EARIE 43rd annual conference) and Alicante (XXX Jornadas de Economía Industrial conference). We thank Marta Esteve and Diego Kuperman from Soysuper for providing data and technical assistance. All remaining errors are our own responsability. Financial support from Ministerio de Economía y Competitividad and FEDER (ECO2015-69334-R) is gratefully acknowledged.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
González, X., Miles-Touya, D. Price dispersion, chain heterogeneity, and search in online grocery markets. SERIEs 9, 115–139 (2018). https://doi.org/10.1007/s13209-018-0172-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-018-0172-6