Prices and promotions in U.S. retail markets

Abstract

We provide generalizable results on the price and promotion tactics employed in the U.S. retail grocery industry. First, we document a large degree of price dispersion for UPCs and brands across stores, both nationally and at the local market level. Base price differences across stores and price promotions contribute to the overall price variance, and we show how to decompose the price variance into base price and promotion components. Second, we document that a large percentage of the variation in prices and promotion tactics across stores can be explained by retail chain and especially market/chain factors, whereas market factors explain only smaller percentage of the variation. Third, we show that the chain-level price and promotions similarity can be explained by similarity in demand. In particular, a large percentage of the variance in price elasticities and promotion effects can be explained by retail chain and especially market/retail chain factors. Further, price elasticities and promotion effects across stores of the same chain are hard to distinguish from the chain-market-level mean, and cross-price elasticities are typically imprecisely estimated. These findings suggest that retail managers may plausibly consider price discrimination across stores to be infeasible.

Appendices

Appendix

A Data description: Details

2.1 A.1 UPCs and UPC versions

The RMS scanner data record sales units and prices at the week-level, separately for all stores and UPCs. Over time, a UPC can be reassigned to a different product. Therefore, the Kilts Center for Marketing also provides a version code (upc_ver_uc) such that the combination of the UPC and UPC version code uniquely identifies a product.³⁴ A change of the brand name (description) is one of the reasons why a new UPC version is created. Sometimes, a new UPC version reflects a different spelling or abbreviation of the brand name, for example “MOUNTAIN DEW R” versus “MTN DEW R.” We attempt to identify and correct all such instances.

In the paper we only refer to UPCs, with the understanding that at the most disaggregated level a product is characterized by a unique combination of a UPC and UPC version code.

2.2 A.2 Product size (revenue) distribution

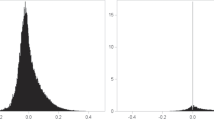
Between 2008 and 2010 the RMS data include information on 967,832 products (UPCs).³⁵ A large percentage of the total sales revenue is concentrated among a relatively small number of products. To illustrate, in Fig. 17 we rank all products based on total revenue between 2008 and 2010 and plot the cumulative revenue of the top N products on the y-axis. For example, the top 1,000 products account for 20.7 percent, the top 10,000 products account for 56.5, and the top 50,000 products account for 89.3 percent of the total revenue in the 2008-2010 data, respectively.

2.3 A.3 Product assortments

We document the distribution of product and brand availability across stores and retail chains in our sample. We classify a product (brand) as available in a specific store or retail chain if it was sold in the store or chain at least once during 2010.

Figure 18 displays the distribution of store availability for brands (column one) and products (column two). The histograms are shown separately for the top 100 (based on total revenue), top 1,000, top 10,000, and—at the bottom of the figure— for all brands and products included in the analysis. The median product in the top 100 group is sold in 12,771 stores, whereas the corresponding median brand is sold in 15,985 stores, representing 93% of all 17,184 stores. Hence, the top products and in particular the top brands are widely available. However, even the top 100 products and brands are not consistently available across all stores, indicating differences in store-level assortment choices. Also, the top brands are more consistently available across stores than products, implying assortment differences whereby stores that carry the same brand offer the brand in different pack sizes or forms (e.g. cans versus bottles). Whereas the top 100 and also top 1,000 products and brands are widely available, the corresponding distributions for the top 10,000 and all products and brands indicate a smaller degree of availability across stores. For example, the median product among all products in the sample is available at 3,854 stores, and the median brand is available at 5,281 stores, i.e. 31% of all stores. Overall, we find that assortments across stores tend to be somewhat specialized, with the exception of top-selling products and brands that are typically available at a vast majority of all stores and chains.

The distributions of brand and product availability across retail chains, shown in columns three and four of Fig. 18, are similar to the corresponding distributions across stores. In particular, whereas the top-selling brand and products are widely available (for example, the median brand among the top 100 is sold in 76 out of 81 retail chains), availability is much more limited among the top 10,000 and among all brands and products in the sample. Compared to the store availability distributions, however, the differences across the top and bottom groups are less pronounced. For example, the median brand among all brands in the sample is still available in the majority of retail chains (45 out of 81). In particular, the brand availability distribution for all brands exhibits a pronounced bi-modal shape, indicating a mass of brands available at most retailers and a mass of brands available at a very limited number of retail chains.

2.4 A.4 Private label products

The Nielsen data contain both national brand and private label products. However, the brand description of private label products is always “CTL BR” (control brand), and hence we do not know the brand name under which the product is sold. Also, we cannot infer the brand name based on the store where the product was sold because the name of the retail chain that the store belongs to is not revealed. However, we know the product (UPC) description of a product, such as “CTL BR RS BRAN RTE” for a private label Raisin Bran product in the ready-to-eat breakfast cereal category.

In our analysis we treat all private label UPCs as the same product if they share the same product description and contain the same volume. In particular, we treat such UPCs as the same product even if the UPCs are different. The UPCs are typically different because the product is sold by different retail chains, whereas the product itself of often physically identical because it is produced by the same manufacturer that supplies multiple retailers. Even if the product is identical the packaging and specific brand name (e.g. “Kroger Raisin Bran”) will differ across retailers. Hence, treating different private label UPCs as the same product is not entirely innocuous, but it is the best we can do to compare the price dispersion of national brands to the price dispersion of private label products across retail chains.

Table 1 shows the percentage of observations accounted for by private label products. Private label products account for 10.8 percent of all price observations and 15.4 percent of total revenue.

B Additional price dispersion results

3.1 B.1 Price dispersion: Sensitivity analysis

We calculate two alternative dispersion statistics that are related to the standard deviation of log-prices. First, the distribution of percentage price differences can be measured using the standard deviation of prices normalized relative to the mean price (nationally or at the market level), $p_{jst}/\bar {p}_{jmt}$, which is the approach used in Kaplan and Menzio (2015). Second, we can report the square root of the variance of log-prices calculated using the following approach:

$$ \begin{array}{@{}rcl@{}} \text{var}(\log(p_{jst})|m) & =&\frac{1}{N_{jmt}}\sum\limits_{s\in\mathcal{S}_{jmt}}(\log(p_{jst})-\overline{\log(p_{jmt})})^{2}, \\ \text{var}(\log(p_{jst})) & =&\frac{1}{N_{jt}}\sum\limits_{m\in\mathcal{M}}N_{jmt}\text{var}(\log(p_{jst})|m). \end{array} $$

(5)

Note that we do not use Bessel’s correction in these two variance formulas. This approach is equivalent to demeaning each $\log (p_{jst})$ observation with respect to the average log price in market m, and then calculating the variance over all observations. We include this approach because it is more closely related to the variance decomposition in Section 6.

Summary statistics for these two alternative approach are shown in Table 7, separately for products defined as UPCs and brands. As expected the difference between the dispersion statistics based on the standard deviation of log prices and the standard deviation of normalized prices is negligible. On the other hand, the standard deviation calculated as the square root of Eq. 5 is slightly larger at the DMA and 3-digit ZIP code level compared to the standard deviation of the log of prices. Overall, our main conclusions are unchanged using these two alternative dispersion statistics.

Table 7 Additional price and base price dispersion statistics

3.2 B.2 Comparison to Kaplan and Menzio 2015

Our results are not directly comparable to Kaplan and Menzio (2015) because their work is based on different data and a substantially smaller number of products, as we already discussed in Section 2. Also, they measure price dispersion using the standard deviation of prices normalized relative to the market-average price level, $p_{jst}/\bar {p}_{jmt}$, whereas our main price dispersion measure is the standard deviation of log prices. However, as expected, the different dispersion statistics yield almost identical dispersion measures (see the sensitivity analysis in Appendix A) and hence they are not a source of differences in the results.

Kaplan and Menzio (2015) report that the standard deviation of normalized prices for the mean UPC at the Scantrack/quarter level is 0.19. In our data, the corresponding standard deviation is 0.10 for the median UPC at the 3-digit ZIP code/week level and 0.12 at the the Scantrack/week level. Hence, the price dispersion of identical products at a given moment in time is substantially smaller than the dispersion level that Kaplan and Menzio report at the quarter level for a small product sample. Comparable brand-level results are not reported in Kaplan and Menzio (2015).³⁶

C Base prices and promotions: Details

4.1 C.1 Choice of promotion threshold $\bar {\delta }$

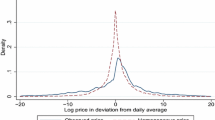
Assuming that every event when the price of a product is strictly less than the base price is a price promotion, we could define the promotion indicator as $D_{jst}=\mathbb {I}\{\delta _{jst}>0\}$. However, it is unlikely that any brand or category manager designs a price promotion that offers only a negligible price discount. Hence, to find a suitable threshold value $\bar {\delta }$ to use in our analysis we examine the distribution of the percentage price discounts, δ_jst, pooled across all products, stores, and weeks when p_jst < b_jst ⇔ δ_jst > 0. This distribution is shown in the top right panel of Fig. 4 and summarized in Table 3. The median percentage price discount across all events is 17.7%. There are instances of small percentage price discounts, but the overall incidence of such events is small. For example, in only slightly less than 10% of all events the price discount is less than 5%, 0 < δ_jst < 0.05. It is implausible that these observations represent a planned price promotion. Rather, such observations are likely due to measurement error in either the price or base price. Such measurement error can arise due to differences between the promotional calendar in a store and the Nielsen RMS definition of a week. For example, suppose a product was offered at a 20 percent price discount during a two week period starting on a Monday and ending on Sunday, May 30. Because a week in the RMS data ends on a Saturday, the RMS week that begins on May 30 and ends on Saturday, June 4 will include one day when the product was offered at the 20 percent price discount and six days when the product was sold at the regular (base) price. The data report the average price over these seven days, which is an average over the promoted and non-promoted prices. The inferred percentage price discount, δ_jst, is likely to be small in this example, and it will not accurately represent the promotional price discount. In order to ameliorate measurement error we use the threshold of $\bar {\delta }=0.05$, as discussed in Section 5.2.

4.2 C.2 Calculation of percent volume sold on promotion and lift factors

The percentage of product volume that is sold during a promotional period is given by

$$ \nu_{js}=\frac{{\sum}_{t\in\mathcal{T}_{js},D_{jst}=1}q_{jst}}{{\sum}_{t\in\mathcal{T}_{js}}q_{jst}}. $$

Here, q_jst is the number of product j units sold in store s in week t. To calculate a corresponding product-level statistic, ν_j, we take a weighted average of ν_js over all stores s, with weights N_js, the number of observations for store s.

The lift factor (promotion multiplier) is given by

$$ L_{js}=\frac{\frac{{\sum}_{t\in\mathcal{T}_{js},D_{jst}=1}q_{jst}}{N_{js}^{D}}}{\frac{{\sum}_{t\in\mathcal{T}_{js},D_{jst}=0}q_{jst}}{N_{js}-N_{js}^{D}}}. $$

Alternatively, we could calculate L_js using the predicted volume in the absence of a promotion in the denominator, based on a demand model or a weighted average of the observed non-promoted volume. To obtain a product-level lift factor L_j we aggregate over L_js using the same approach that we use to aggregate the volume percentages.

D Derivation of price variance decompositions

All decompositions are performed at the product level, hence we drop the subscript j. ${\mathscr{M}}$ is the set of all markets, $\mathcal {S}_{m}$ is the set of all stores in market $m\in {\mathscr{M}},$ and $\mathcal {S}=\cup _{m\in {\mathscr{M}}}\mathcal {S}_{m}$ is the set of all stores. For each store s we observe prices in periods $t\in \mathcal {T}_{s}.$ Correspondingly, S_m is the number of stores in market m, $S={\sum }_{m\in {\mathscr{M}}}S_{m}$ is the number of all stores, and N_s is the number of observations for stores s. Then the total number of observations is $N={\sum }_{s\in \mathcal {S}}N_{s}$, and the number of observations in market m is $N_{m}={\sum }_{s\in \mathcal {S}_{m}}N_{s}$.

Define the overall (national) average price, the average price in market m, and the average price in stores s:

$$ \begin{array}{@{}rcl@{}} \bar{p} & =&\frac{1}{N}\sum\limits_{s\in\mathcal{S}}\sum\limits_{t\in\mathcal{T}_{s}}p_{st},\\ \bar{p}_{m} & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}p_{st},\\ \bar{p}_{s} & =&\frac{1}{N_{s}}\sum\limits_{t\in\mathcal{T}_{s}}p_{st}. \end{array} $$

Similarly, define the average base price in market m and the average base price in store s :

$$ \begin{array}{@{}rcl@{}} \bar{b}_{m} & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}b_{st},\\ \bar{b}_{s} & =&\frac{1}{N_{s}}\sum\limits_{t\in\mathcal{T}_{s}}b_{st}. \end{array} $$

Our goal is to provide a decomposition for the overall variance of prices,

$$ \begin{array}{@{}rcl@{}} \text{var}(p_{st})=\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p})^{2}. \end{array} $$

5.1 D.1 Basic decomposition

Define

$$ \begin{array}{@{}rcl@{}} \text{var}(\bar{p}_{m}) & =&\frac{1}{N}\sum\limits_{m\in\mathcal{M}}N_{m}(\bar{p}_{m}-\bar{p})^{2},\\ \text{var}(\bar{p}_{s}|m) & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}N_{s}(\bar{p}_{s}-\bar{p}_{m})^{2},\\ \text{var}(p_{st}|s) & =&\frac{1}{N_{s}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{s})^{2}. \end{array} $$

var(p_m) is the variance of average market-level prices across markets, $\text {var}(\bar {p}_{s}|m)$ is the within-market variance of average store-level prices, and var(p_st|s) is the within-store variance of prices over time. Note that var(p_m) and $\text {var}(\bar {p}_{s}|m)$ are calculated as weighted averages, using the number of observations in each market and the number of observations for each store as weights.

We first decompose the overall variance of prices, var(p_st), into an across-market and a within-market term:

$$ \begin{array}{@{}rcl@{}} \text{var}(p_{st}) & =&\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p})^{2} \\ & =&\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m}+\bar{p}_{m}-\bar{p})^{2} \\ & =&\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}{\sum}_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2}+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(\bar{p}_{m}-\bar{p})^{2} \\ & =&\text{var}(\bar{p}_{m})+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2}. \end{array} $$

(6)

Note that the third line in this formula follows because

$$ \begin{array}{@{}rcl@{}} \sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st} - \bar{p}_{m})(\bar{p}_{m} - \bar{p}) & = \displaystyle\sum\limits_{m\in\mathcal{M}}(\bar{p}_{m} - \bar{p})\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st} - \bar{p}_{m})=0. \end{array} $$

To further decompose the within-market term, note that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{s}+\bar{p}_{s}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{s})^{2}+\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(\bar{p}_{s}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(p_{st}|s)+N_{m}\text{var}(\bar{p}_{s}|m). \end{array} $$

(7)

Here, to derive the second line we used

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{s})(\bar{p}_{s}-\bar{p}_{m}) =\sum\limits_{s\in\mathcal{S}_{m}}(\bar{p}_{s}-\bar{p}_{m})\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{s})=0. \end{array} $$

Substituting (7) in Eq. 6, we obtain the desired decomposition of the overall price variance into the variance of average market-level prices, the weighted average of the within-market variances of average store-level prices, and the weighted average of the within-store variances of prices:

$$ \begin{array}{@{}rcl@{}} \text{var}(p_{st}) & =&\text{var}(\bar{p}_{m})+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} \\ & =&\text{var}(\bar{p}_{m})+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}N_{m}\text{var}(\bar{p}_{s}|m)+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(p_{st}|s) \\ & =&\text{var}(\bar{p}_{m})+\frac{1}{N}\sum\limits_{m\in\mathcal{M}}N_{m}\text{var}(\bar{p}_{s}|m)+\frac{1}{N}\sum\limits_{s\in\mathcal{S}}N_{s}\text{var}(p_{st}|s). \end{array} $$

(8)

5.2 D.2 Decomposition into base price and promotion components

We start with an alternative decomposition of the within-market term (7):

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} & =& \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-b_{st}+b_{st}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-b_{st})^{2}+\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{p}_{m})^{2}\\ &&+2\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-b_{st})(b_{st}-\bar{p}_{m}). \end{array} $$

(9)

Note that

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{p}_{m})^{2} & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{b}_{m}+\bar{b}_{m}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{b}_{m})^{2}+N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{b}_{s}+\bar{b}_{s}-\bar{b}_{m})^{2}+N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-\bar{b}_{s})^{2} + \sum\limits_{s\in\mathcal{S}_{m}}N_{s}(\bar{b}_{s}-\bar{b}_{m})^{2} + N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & =&\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(b_{st}|s)+N_{m}\text{var}(\bar{b}_{s}|m)+N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2}. \end{array} $$

(10)

Substituting (10) in (9) and rearranging terms, we obtain

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} & =&N_{m}\text{var}(\bar{b}_{s}|m)+\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(b_{st}|s) \\ & +&N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2}+\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-p_{st})^{2} \\ & -&2\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-p_{st})(b_{st}-\bar{p}_{m}). \end{array} $$

(11)

Define

$$ \begin{array}{@{}rcl@{}} \text{var}(b_{st}-p_{st}|m) & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}\left( (b_{st}-p_{st})-(\bar{b}_{m}-\bar{p}_{m})\right)^{2} \\ & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-p_{st})^{2}-(\bar{b}_{m}-\bar{p}_{m})^{2}. \end{array} $$

(12)

Rearranging (12) and substituting in Eq. 11, we obtain

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} & =&N_{m}\text{var}(\bar{b}_{s}|m)+\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(b_{st}|s) \\ & +&N_{m}\text{var}(b_{st}-p_{st}|m)+2N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & -&2\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}-p_{st})(b_{st}-\bar{p}_{m}). \end{array} $$

(13)

Define the within-market covariance between the promotional price discounts, b_st − p_st, and the difference between the store-level base price and the average market price, $b_{st}-\bar {p}$:

$$ \begin{array}{@{}rcl@{}} \text{cov}(b_{st}-p_{st},b_{st}-\bar{p}_{m}|m) & =&\frac{1}{N_{m}}\sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}\left( (b_{st}-p_{st})-(\bar{b}_{m}-\bar{p}_{m})\right)\\ &&\times\left( (b_{st}-\bar{p}_{m})-(\bar{b}_{m}-\bar{p}_{m})\right) \\ & =&\frac{1}{N_{m}}\!\sum\limits_{s\in\mathcal{S}_{m}}\!\sum\limits_{t\in\mathcal{T}_{s}}(b_{st}\! - \!p_{st})(b_{st}\! - \!\bar{p}_{m})\! - \!(\bar{b}_{m}\! - \!\bar{p}_{m})^{2}. \end{array} $$

(14)

Rearranging and substituting (14) in Eq. 13, we then obtain

$$ \begin{array}{@{}rcl@{}} \sum\limits_{s\in\mathcal{S}_{m}}\sum\limits_{t\in\mathcal{T}_{s}}(p_{st}-\bar{p}_{m})^{2} & =&N_{m}\text{var}(\bar{b}_{s}|m)+\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(b_{st}|s) \\ & +&N_{m}\text{var}(b_{st}-p_{st}|m)+2N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & -&2N_{m}\text{cov}(b_{st}-p_{st},b_{st}-\bar{p}_{m}|m)-2N_{m}(\bar{b}_{m}-\bar{p}_{m})^{2} \\ & =&N_{m}\text{var}(\bar{b}_{s}|m)+\sum\limits_{s\in\mathcal{S}_{m}}N_{s}\text{var}(b_{st}|s) \\ & +&\!\!N_{m}\text{var}(b_{st}\! - \!p_{st}|m) - 2N_{m}\text{cov}(b_{st}\! - \!p_{st},b_{st}\! - \!\bar{p}_{m}|m). \end{array} $$

(15)

Finally, we substitute (15) in Eq. 6 and note that $\text {cov}(b_{st}-p_{st},b_{st}-\bar {p}_{m}|m)=\text {cov}(b_{st}-p_{st},b_{st}|m)$ to obtain the variance decomposition:

$$ \begin{array}{@{}rcl@{}} \text{var}(p_{st}) & =&\text{var}(\bar{p}_{m}) \\ & +&\frac{1}{N}\sum\limits_{m\in\mathcal{M}}N_{m}\text{var}(\bar{b}_{s}|m)+\frac{1}{N}\sum\limits_{s\in\mathcal{S}}N_{s}\text{var}(b_{st}|s) \\ & +&\frac{1}{N}\!\sum\limits_{m\in\mathcal{M}}N_{m}\text{var}(b_{st} - p_{st}|m) - 2\frac{1}{N}\!\sum\limits_{m\in\mathcal{M}}\!N_{m}\text{cov}(b_{st} - p_{st},\!b_{st}|m). \end{array} $$

(16)

5.3 D.3 Example: Price promotions may decrease the overall price variance

We focus only on price variation within one market. Assume that base prices in each store s are constant over time, $b_{st}\equiv \bar {b}_{s},$ and uniformly distributed around the mean base price $\bar {b}$ on the interval $[\bar {b}-\nu ,\bar {b}+\nu ].$ Suppose that only stores with above average base prices, $b_{st}=\bar {b}_{s}>\bar {b}$, promote the product, and that the promoted price is always $p_{st}=\bar {b}.$ All stores with base prices $b_{st}=\bar {b}_{s}\leq \bar {b}$ always sell the product at the base price, p_st = b_st. Define the promotion indicator $D_{st}=\mathbb {I}\{p_{st}<b_{st}\}$ (this corresponds to the promotion definition in Section 5.2 with a threshold $\bar {\delta }=0$). The incidence of promotions is constant, $\pi \equiv \Pr \{D_{st}=1|b_{st}>\bar {b}\}$. There is a continuum of stores with mass 1, and promotions are independent across stores and across time periods.

The mean price is given by:

$$ \begin{array}{@{}rcl@{}} \mathbb{E}[p_{st}] & =&\frac{1}{2}\mathbb{E}[p_{st}|b_{st}\leq\bar{b}]+\frac{1}{2}\left( (1-\pi)\mathbb{E}[p_{st}|D_{st}=0,b_{st}>\bar{b}]+\pi\mathbb{E}[p_{st}|D_{st}=1,b_{st}>\bar{b}]\right)\\ & =&\frac{1}{2}\left( \bar{b}-\frac{\nu}{2}\right)+\frac{1}{2}\left( (1-\pi)\left( \bar{b}+\frac{\nu}{2}\right)+\pi\bar{b}\right)\\ & =&\bar{b}-\frac{\pi\nu}{4}. \end{array} $$

The across-store variance of base prices is given by the variance of a uniform distribution,

$$ \text{var}(\bar{b}_{s})=\frac{\nu^{2}}{3}. $$

To derive the variance of the promotional price discounts we first calculate

$$ \begin{array}{@{}rcl@{}} \mathbb{E}\left[(b_{st}-p_{st})^{2}\right] & =&\frac{1}{2}\pi\mathbb{E}\left[(b_{st}-p_{st})^{2}|D_{st}=1,b_{st}>\bar{b}\right]\\ & =&\frac{1}{2}\pi\mathbb{E}\left[(b_{st}-\bar{b})^{2}|D_{st}=1,b_{st}>\bar{b}\right]\\ & =&\frac{1}{2}\pi{\int}_{\bar{b}}^{\bar{b}+\nu}(x-\bar{b})^{2}\frac{1}{\nu}dx\\ & =&\frac{\pi\nu^{2}}{6}. \end{array} $$

Similarly, to derive the covariance between the promotional price discounts and the base prices we use the expression for $\mathbb {E}\left [(b_{st}-p_{st})^{2}\right ]$ above to obtain

$$ \begin{array}{@{}rcl@{}} \mathbb{E}\left[(b_{st}-p_{st})(b_{st}-\bar{b})\right] & =&\frac{1}{2}\pi\mathbb{E}\left[(b_{st}-p_{st})(b_{st}-\bar{b})|D_{st}=1,b_{st}>\bar{b}\right]\\ & =&\frac{1}{2}\pi\mathbb{E}\left[(b_{st}-\bar{b})^{2}|D_{st}=1,b_{st}>\bar{b}\right]\\ & =&\frac{\pi\nu^{2}}{6}. \end{array} $$

Also, the squared difference between the mean base price and shelf price is:

$$ (\bar{b}-\bar{p})^{2}=\frac{\pi^{2}\nu^{2}}{16}. $$

Hence,

$$ \begin{array}{@{}rcl@{}} \text{var}(b_{st}-p_{st}) & =&\mathbb{E}\left[(b_{st}-p_{st})^{2}\right]-(\bar{b}-\bar{p})^{2}\\ & =&\frac{\pi\nu^{2}}{6}-\frac{\pi^{2}\nu^{2}}{16}. \end{array} $$

Also,

$$ \begin{array}{@{}rcl@{}} \text{cov}(b_{st}-p_{st},b_{st}) & =&\text{cov}(b_{st}-p_{st},b_{st}-\bar{b})\\ & =&\mathbb{E}\left[(b_{st}-p_{st})(b_{st}-\bar{b})\right]\\ & =&\frac{\pi\nu^{2}}{6}. \end{array} $$

Combining the three components we obtain the variance of prices,

$$ \begin{array}{@{}rcl@{}} \text{var}(p_{st}) & =&\text{var}(\bar{b}_{s})+\text{var}(b_{st}-p_{st})-2\text{cov}(b_{st}-p_{st},b_{st})\\ & =&\frac{\nu^{2}}{3}+\frac{\pi\nu^{2}}{6}-\frac{\pi^{2}\nu^{2}}{16}-2\frac{\pi\nu^{2}}{6}\\ & =&\nu^{2}\left( \frac{1}{3}-\frac{\pi}{6}-\frac{\pi^{2}}{16}\right). \end{array} $$

The EDLP vs. Hi-Lo adjustment factor is positive if π > 0 and strictly increasing in π, and the variance of prices is strictly decreasing in the frequency of promotions, π:

$$ \text{var}(p_{st})=v^{2}\left( \frac{1}{3}-\frac{\pi}{6}-\frac{\pi^{2}}{16}\right). $$

E Visualization of price similarity using principal component analysis

We examine the similarity of pricing patterns across stores based on the whole time series of store-level prices. For product j, we observe the vector of prices $\boldsymbol {p}_{s}=(p_{s1},\dots ,p_{sT})$ for each store $s\in \mathcal {S}$ and over the prior 2008-2010 (we suppress the index j for notational simplicity). The sample of prices for product j then consists of $\boldsymbol {p}_{1},\dots ,\boldsymbol {p}_{S}.$ Our goal is to visualize the price vectors p_s, which is not directly feasible given the dimensionality of p_s. Instead, we conduct a principal components analysis (PCA) of the store-level price vectors. PCA is an unsupervised dimensionality reduction technique that allows us to represent each p_s in a low-dimensional space while maintaining as much of the original information (variance) contained in p_s as possible.³⁷

We perform a PCA for the top 1,000 products (UPCs) in our sample, based on total revenue rank. We only choose these top products because we need to be able to consistently observe the weekly prices, p_st, across stores for the analysis to be feasible. For smaller products there is a larger incidence of missing values.

The top panel in Fig. 20 displays box plots of the percentage of the price variance that is explained by the first twenty principal components. Each box plot shows the distribution (weighted by total product revenue) of these percentages across the products in our sample. The first principal component explains 20% of the price variance for the median product, and all the first five principal components explain at least 5% of the price variance. In the bottom panel of Fig. 20 we display box plots of the cumulative percentage of the price variance explained by the top principal components. The top five principal components explain 53% and the top ten principal components explain 68% of the price variance for the median product. Hence, a large percentage of the information in the original store-level price vectors over the 2008-2010 period can be explained by a small number of principal components. A representation of the original, high-dimensional price data in a low-dimensional space is therefore meaningful.

Following the case of Tide HE Liquid Laundry Detergent (100 oz) in Figs. 7 and 8, we present additional examples in Fig. 21, including Prilosec (42 count), Pepsi (12 oz cans 12 pack), and private-label milk (2 percent, 1 gallon). In this graph we only include the store-level price vectors for a subset of all retail chains. For Prilosec and Pepsi we find a pattern that is similar to the case of Tide laundry detergent—a large degree of price similarity within retail chains and a significantly smaller degree of price similarity at the market level. The case of private-label milk is quite different, however, as there is much heterogeneity in prices both at the chain and the market level.

F Overview of promotion coordination

To provide an overview of promotion coordination we summarize the percentage of all stores in a retail chain that promote a specific product during week t.

Promotions are captured using the indicator D_jst ∈{0, 1}, such that D_jst = 1 if product j is promoted in store s in week t. We calculate the chain/market level promotion percentage for product j:

$$ \phi_{jcmt}=\frac{{\sum}_{s\in\mathcal{S}_{jcmt}}D_{jst}}{|\mathcal{S}_{jcmt}|}. $$

$\mathcal {S}_{jcmt}$ includes the stores that belong to retail chain c in market m and carry product j in week t, and $|\mathcal {S}_{jcmt}|$ is the corresponding number of stores.

The graphs in the top row of Fig. 22 display histograms of the promotion percentages ϕ_jcmt, pooled over all products, chains, markets, and time periods between 2008 and 2010 (Table 11 contains detailed summary statistics). The distributions are weighted using total product revenue weights. We display the promotion percentage distributions conditional on ϕ_jcmt > 0, i.e. weeks when at least one store in chain c and market m promotes the product, to avoid that the histograms are dominated by large mass points at 0. The percentage of observations when none of the stores promoted the product, ϕ_jcmt = 0, is indicated separately at the bottom of each graph. We define markets as DMAs to ensure that the chains have a sufficiently large number of stores in a local market.³⁸ To see why this is important consider the case when a chain has only one local store. Then the promotion percentage is always 0 or 1, indicating perfect promotion coordination. For the same reason, we summarize the promotion percentage distributions only for observations when the retail chain c carries the product in at least five stores in the local market.

The top row in Fig. 22 shows the promotion percentage distributions for all products (left panel) and the top 1,000 products as measured by annual, national product revenue (right panel). Both histograms reveal a large mass point at 1, indicating perfect promotion coordination. The promotion percentages, conditional on ϕ_jcmt > 0, are overall larger among the top 1,000 products, with a median of 0.548 compared to a median of 0.41 for all products. This indicates a larger degree of promotion coordination among the top-selling products, although the percentage of ϕ_jcmt = 0 observations is smaller for the top 1,000 products: 55.1% versus 62.2% among all products. However, the latter finding may simply reflect an overall higher promotion frequency among the top 1,000 products, not a smaller degree of coordination on weeks when none of the stores in the chain promote the product.

Although suggestive of promotion coordination, the overall extent of promotion coordination conveyed by Fig. 22 is difficult to assess without a comparison to a baseline where promotions are not coordinated. To provide such a baseline we simulate data assuming that promotions are chosen independently across stores. For each product j and stores s we calculate the promotion frequency π_js using the 2008-2010 data, as in Section 5.2. For each store s and week t we then draw a promotion indicator $\tilde {D}_{jst}$ from a Bernoulli distribution with success probability π_js. The distributions of promotion percentages for the simulated data are shown in the second row of Fig. 22. The histograms indicate a much smaller degree of promotion coordination compared to the observed promotion percentages. The median promotion percentage among all products in the simulated data is 0.200, compared to 0.41 in the actual data, and the corresponding percentages among the top 1,000 products are 0.279 in the simulated data versus 0.548 in the observed data. Indeed, the displayed distributions understate the difference between the simulated and the original data because they are conditional on ϕ_jcmt > 0, and hence do not reveal the large difference in observations where none of the stores in a chain promotes a product. In the observed data, ϕ_jcmt = 0 for 62.2% of all observations, compared to 28.3% of all observations in the simulated data.

The distributions in the top rows of Fig. 22 are based on observations at the chain/market level in a given week, conditional on at least one store in the chain promoting product j. This leads to an asymmetry between observations with highly coordinated promotions and observations with a small number of stores promoting a product. For example, suppose that all promotions were perfectly coordinated within a retail chain, such that ϕ_jcmt = 1 in the week when the promotion is held. Suppose there were some small differences in the timing of the end date of the promotion across stores in the chain, such that a small number of stores would still offer the promotion for a few days in week t + 1. Then each perfectly coordinated promotion observation, ϕ_jcmt = 1, would have an associated observation with a small, positive ϕ_{jcm, t+ 1} value, suggesting that perfectly coordinated promotion events were as frequent as almost completely uncoordinated promotion events. Hence, as an alternative summary of promotion coordination we associate each store-level promotion event, D_jst = 1, with the corresponding promotion percentage, ϕ_jcmt, and display the distribution of the promotion percentages based on all store level observations such that D_jst = 1. This is equivalent to displaying the distribution of ϕ_jcmt weighted by the number of stores that promote product j in chain c and market m in week t. The results are shown in the third row of Fig. 22 (Table 11 contains detailed numbers), and strongly indicate that store-level promotions are coordinated at the chain-market level. Furthermore, the differences between the actual and simulated data, shown in the bottom row of Fig. 22, are large.

G Bayesian hierarchical demand model

This section provides an overview of the Bayesian hierarchical linear regression model to estimate the brand/store-level demand parameters. See Rossi et al. (2005), Chapter 3.7, for a detailed exposition of the model and the MCMC sampling approach.

The goal is to obtain the posterior distribution of the demand parameters for brand j and store s in model (4). The store-level parameter vector 𝜃_js = (α_js,β_js, γ_js) includes the intercept, α_js, the own and cross-price elasticities, β_jks, and the promotion parameters, γ_jks. We do not estimate the large number of 3-digit ZIP code/time fixed effects, τ_j(s, t), as part of the Bayesian hierarchical model. Instead, we first project all variables in the demand model, $\log (1+q_{jst})$, $\log (p_{kst})$, and D_kst, on the fixed effects. We then use the residuals from this projection to estimate the store-level demand parameters in the model:

$$ \begin{array}{@{}rcl@{}} \widetilde{\log(1+q_{jst})} & =&\alpha_{js}+\sum\limits_{k\in\mathcal{J}_{js}}{\upbeta}_{jks}\widetilde{\log(p_{kst})}+\sum\limits_{k\in\mathcal{J}_{js}}\gamma_{jks}\widetilde{D_{kst}}+\epsilon_{jst},\\ \epsilon_{jst} & \sim& N(0,\sigma_{js}^{2}). \end{array} $$

(17)

𝜖_jst is i.i.d. across stores and time. From now on we drop the brand index j to simplify the notation.

We specify a normal first-stage prior or population distribution for the the store-level demand parameters, 𝜃_s:

$$ \theta_{s}\sim N(\mu,V_{\theta}). $$

The parameter vectors for different stores are conditionally independent, given μ and V_𝜃. More flexible priors are possible, such as a mixture of normal distributions, which has been used in the literature (Rossi et al., 2005).

We further specify the second-stage prior distribution of V_𝜃 and μ:

$$ \begin{array}{@{}rcl@{}} V_{\theta} & \sim&\text{IW}(\nu,V),\\ \mu|V_{\theta} & \sim& N(\bar{\mu},V_{\theta}\otimes A^{-1}). \end{array} $$

IW denotes an inverse Wishart distribution. The error term variances, ${\sigma _{s}^{2}}$, are independent draws from an inverse chi-squared distribution,

$$ {\sigma_{s}^{2}}\sim\frac{\nu_{\epsilon}{r_{s}^{2}}}{\chi_{\nu_{\epsilon}}^{2}}. $$

Here, ν_𝜖 denotes the degrees of freedom and ${r_{s}^{2}}$ is a scale parameter.

The MCMC algorithm to obtain the posterior distribution of the model parameters is performed using Peter Rossi’s bayesm package³⁹ in R. We run the algorithm using the default settings for the hyper-parameters in the bayesm package. These settings allow for a diffuse prior:

$$ \begin{array}{@{}rcl@{}} v & =&3+n,\\ V & =&\nu I_{n},\\ \bar{\mu} & =&0,\\ A & =&0.01,\\ \nu_{\epsilon} & =&3,\\ {r_{s}^{2}} & =&\text{var}(\widetilde{\log(1+q_{st})}). \end{array} $$

Here, n is the dimension of the parameter vector 𝜃_s.

We choose a chain length of 20,000 (after 2,000 initial burn-in draws) and keep every 10th draw to calculate the posterior means and the 95% credible intervals of the parameters. A visual inspection of the trace plots for a large number of randomly selected parameters (across brands and stores) indicates convergence of the chain.

H Causal price and promotion effects: Sensitivity analysis

Price and promotion endogeneity occurs if the retail chains set prices or promotions based on demand shocks that are observed to them but not to us. To avoid endogeneity bias we include time-invariant store fixed effects α_js in the demand model (4). The store fixed effects account for systematic demand differences across stores that are associated with systematic differences in prices and promotions. Further, we include the market/time fixed effects τ_j(s, t) to account for demand shocks and brand-specific trends in demand at a narrowly defined geographic level.

Table 8 Retail chain and store descriptive statistics

Table 9 Details of price variance decompositions

Table 10 Percentage of variance of prices, promotion frequency, and promotion depth explained by market and chain factors

Table 11 Promotion coordination: Summary statistics for promotion percentages

Table 12 Own-price coefficient estimates

Table 13 Percentage of variance in estimated own-price elasticities and own-promotion effects explained by market and chain factors

We can interpret the price and promotion estimates as causal if (i) τ_j(s, t) captures all time-varying demand components that may be correlated with p_kst and D_kst, (ii) there is variation in the price and promotion changes over time across stores, and (iii) the difference in price and promotion changes across stores reflects store or chain-specific changes in costs, wholesale prices, markups, or other factors that affect prices and promotion but not directly demand. These assumptions are not directly testable, but we can perform an analysis to indicate if our estimates are sensitive to the inclusion and exact specification of the fixed effects. Thus, we first estimate demand without fixed effects, and then including τ_j(s, t) defined at the 3-digit ZIP code/quarter, 3-digit ZIP code/month, and 3-digit ZIP code/week levels.

The estimated distributions of the price effects are shown in Fig. 24 and summarized in Table 12. The median elasticity estimate is -1.767 in the model without fixed effects, -1.924 in the model with 3-digit ZIP code/quarter fixed effects, -1.93 with 3-digit ZIP code/month fixed effects, and -1.859 with 3-digit ZIP code/week fixed effects. Hence, controlling for time fixed effects at the local market level moderately changes the distribution of the estimates, and the direction of this change is consistent with price endogeneity if positive demand shocks are correlated with higher prices. However, the elasticity estimates are not particularly sensitive to the exact choice of fixed effects, and the direction of the change in the estimated elasticities when we use year-month or year-week fixed effects instead of year-quarter fixed effects is not indicative of a price endogeneity problem. For a severe price endogeneity problem to exist it would have to be true that there are high-frequency demand shocks that occur at level that is more local than a 3-digit ZIP code area, and that the store or chain managers are able to predict these shocks and correspondingly change prices. This seems a priori implausible, and in particular such localized price-setting is inconsistent with the strong similarity in price and promotion patterns at the retail chain level that we document.

Fig. 15

Predicted base prices, Tide liquid laundry detergent (70 oz)

Fig. 16

Predicted base prices, Kellogg’s Raisin Bran (20 oz)

Fig. 17

Cumulative revenue for top 100,000 products

Fig. 18

Product and brand availability across stores and retail chains. Note: The graph displays the distribution of the number of stores (the two columns to the left) and chains (the two columns to the right) at which a product or brand is available. The median of each distribution is indicated using a vertical line. A product (brand) is classified as available if it was sold at least once in a store or chain in 2010. The sample includes 17,184 stores and 81 retail chains

Fig. 19

Base prices dispersion statistics: Brand-level base prices

Fig. 20

Percentage and cumulate percentage of price variance explained by principal component

Fig. 21

Projected store-level price vectors colored by retail chain and DMA

Fig. 22

Distribution of chain/DMA promotion percentages

Fig. 23

Promotion coordination regression results: Promotion incidence and inside and outside promotion percentages

Fig. 24

Own-price elasticity estimates for different fixed effects definitions