Abstract
We propose a simple behavioral model to analyze situations where (1) a group of agents repeatedly plays a public goods game within a network structure and (2) each agent only observes the past behavior of her neighbors, but is affected by the decisions of the whole group. The model assumes that agents are imperfect conditional cooperators, that they infer unobserved contributions assuming imperfect conditional cooperation by others, and that they have some degree of bounded rationality. We show that our model approximates quite accurately regularities derived from public goods game experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A public goods game is an example of an economic situation in which individual and collective interests are not aligned. Therefore, the Nash equilibrium prediction leads to a suboptimal collective outcome. The experimental evidence strongly suggests that subjects act on a reciprocal basis, following the lines first suggested by Sugden (1984). In her experiment, Croson (2007) finds a simple reciprocity pattern: subjects try to match the average contribution, rather than the minimum or the maximum (see also Fischbacher et al. 2001). In a recent study, Fischbacher and Gächter (2010) find that conditional cooperation is imperfect; participants systematically fall short of matching others’ contributions by a relatively small, but significant margin.
Conditional cooperation requires information about others’ contributions. Recent experimental literature analyzed how limited information about other subjects’ contributions shapes their decisions (Fatas et al. 2010, 2014; Leibbrandt et al. 2014; and Carpenter et al. 2012). These papers manipulate the level to which agents observe the contributions of others modeling groups as informational networks. The whole group still provides the public good, but you may get different information about the decisions of the other group members. Note that this is a major difference with respect to the standard theoretical literature on public goods in networks (as in Bramoullé and Kranton 2007, where agents only benefit from the contributions of her neighbors). The main finding in the experimental analysis of network structures is that contributions are lower in incomplete networks, and some incomplete networks (the star) significantly outperform others (the circle or the line).
Both the Nash prediction and the conditional cooperation logic described above are unable to explain these differences across networks. In this paper we propose a simple behavioral model that assumes that (1) agents are imperfect conditional cooperators and that (2) agents predict unobserved contributions assuming imperfect conditional cooperation by others. By introducing two additional behavioral assumptions (we consider that players only react to the most recent experience and that they have a limited level of rationality) we keep the model purposely simple and stop its recursive nature.Footnote 1
This simple formulation is enough to reveal a connection between imperfect conditional cooperation and the presence of decay, one of the main ingredients in some influential models of network formation (e.g., Jackson and Wolinsky 1996, or Bala and Goyal 2000).Footnote 2 In these models, the decay represents frictions that determine the value of the externalities generated by individual links. In our formulation, the decay factor will coincide with the parameter capturing the imperfect conditional cooperation.
Besides this theoretical connection, our model captures the differences in contributions across networks. Interestingly, it also predicts well the decisions of players with the same numbers of neighbors (i.e., nodes with the same degree) in different networks. We simulate our model and compare the results to the evidence derived from the experimental results by Fatas et al. (2010) in which groups of four subjects repeatedly play a public goods game within different network structures (the complete network, the circle, the line and the star). In our simulations, we estimate the imperfect conditional cooperation parameter and fit the model to predict behavior in every incomplete network, relative to a quite natural benchmark: the complete network.
Our results show that the model offers a good approximation to the dynamic evolution of contributions in different incomplete networks. Moreover, it also fits well with a range of different players’ network positions (defined by their connectivity to other players). Rather than describing precise behavioral rules, the model provides a simple but powerful analytical basis for the deterioration of information, and cooperation, in networks. Our results suggest that the incompleteness of the network erodes conditional cooperation by making more difficult for subjects to get accurate information about the decisions of the other group members.
The remainder of the paper is organized as follows. Section 2 presents the model. In Sect. 3 we describe the experiment. Section 4 describes our simulations procedures. Section 5 compares the results. Finally, Sect. 6 concludes.
2 The model
Let \(N = \{1,{\ldots },n\}\) be a group of agents and \(g\) a network (set of links) comprised of the elements of \(N\). We assume that \(g\) is undirected, i.e., if an agent is linked to another, the later is also linked to the former. Given \(g\), the distance between two agents \(i,j\in N,\) denoted by \(d(i,j)\) is the (minimum) number of links that separates them.Footnote 3 For each \(i\in N,\) we denote by \(N_i (g)\) the set of \(i\)’s neighbors in \(g\in G.\) Time is discrete \(t\in \{1,\ldots ,T\}.\) At each \(t\), each \(i\in N\) (simultaneously) decides a contribution to a public good, \(c_i (t)\in [0,m],\) where \(m>\) 0. Previously to this choice, \(i\) learns \(c_j (t-1)\) for each \(j\in N_i (g)\). The payoff to player \(i\) at period \(t\) is determined by
where \(a \in ( {1/ n,1})\).Footnote 4
As already anticipated, we propose a dynamics based on two assumptions: agents are imperfect conditional cooperators, and believe that others also behave in the same way. Specifically, in order to define precisely imperfect conditional cooperation, we consider that each player would like to match the average contribution of the other members of the group, but only partially.
Assumption 1 (A1) Agents are imperfect conditional cooperators.
Put in other words, (A1) states that, at each \(t >\) 1, each player aims to contribute \(\delta \in (0,1)\) times the average contribution of the remaining players of the group in the previous period.
In the complete network, all agents can directly apply the rule (by taking the average contribution of the remaining players in the previous round). However, in the incomplete networks there are players that need to infer the contributions of other members of the group.
Assumption 2 (A2) Agents infer unobserved contributions assuming imperfect conditional cooperation by others.
To illustrate this assumption consider a player, say \(i\), that does not observe \(j\)’s contribution but observes the contribution of some neighbors of \(j\). Player \(i\) knows that \(j\) observes these contributions and, given (A2) believes that player \(j\) also behaves as an imperfect conditional cooperator. Therefore, given her available information, player \(i\)’s inference for \(j\)’s contribution is \(\delta \) times the average contribution of these commonly observed neighbors.
Note that, in this formulation, we are implicitly making two additional assumptions:
Assumption 3 (A3) Players have bounded memory.
Specifically, (A3) states that when, at some period \(t\), players infer the contribution of a non-observed agent (at period \(t-1\)), they only use the information they have from period \(t-1\). In other words, agents have bounded memory and only use the information from the previous round.Footnote 5
Example 1
To illustrate this point, consider three agents (\(i\), \(j\) and \(k)\) arranged in a line, (\(i\) linked to \(j\), \(j\) linked to \(i\) and \(k\), and \(k\) linked to \(j)\). When agent \(i\) infers the contribution of \(k\) at period \(t-1\), in principle, she should use \(\delta \) times the contribution of \(j\) at period \(t-2\) (from the belief that, in period \(t-1\), \(k\) responded as an imperfect conditional cooperator to \(j\)’s behavior in the former round). However, by (A3) we consider that \(i\) relies instead on the contribution of \(j\) at the immediately previous period.
Assumption 4 (A4) Agents have a limited level of rationality.
Specifically, when players infer the (former) contribution of a non-observed agent located at distance two in the network, they believe that such an agent has acted as an imperfect conditional cooperator to the (average) contribution of their common neighbors (i.e., those players that are commonly observed), but they are myopicin the sense that they do not take into account that such a player, like themselves, also infers in the same fashion the contributions of those agents that she cannot directly observe.
Example 1 (continuation) To illustrate this point, consider the former case of players \(i\), \(j\) and \(k\) arranged in a line. When \(i\) infers the contribution of \(k\) at period \(t-1\), by (A4) we assume that \(i\) only considers that \(k\) responds to \(j\)’s previous contribution, and does not incorporate into his prediction for \(k\)’s contribution the fact that \(k\) did also form expectations on \(i\)’s former contributions in order to choose her own ones.
The following example shows how players infer others’ contributions and make their own choices in a network where all pairs of players are at distance at most two.
Example 2 (the star) Let \(n=4\), and assume that player 1 is linked to players 2, 3 and 4 and that players 2, 3 and 4 are only linked to player 1.Footnote 6 Consider that \(\delta =\) 0.9 and that at period 1 all players contribute 50. Then, player 1 (the center), who observes all others’ former contributions, can directly apply the rule (A1), i.e., average them and apply the (decay) factor \(\delta =\) 0.9 and, therefore, contributes 45 at period 2. Consider now a spoke player, for instance, player 2. Player 2 observes player 1’s former contribution and, therefore, can use it in order to calculate the average, but she does also need to infer players 3 and 4’s former contributions. Player 2 is aware of the fact that player 3, like herself, observes player 1’s former contribution and, moreover, she believes that player 3 is also an imperfect conditional cooperator ( and will react by applying factor \(\delta \) to what she observes). Thus, by (A2)–(A4), at period 2, player 2’s inference of player 3’s former contribution is 0.9 times player 1’s former contribution, i.e., 45 (the inference for player’s 4 contribution is analogous). Given this process, by (A1), player 2 contributes 42 at period 2.
This process can be recursively extended to infer contributions of players that are at distance higher than two. Indeed, we can generalize the process above by replacing the role played by the contributions of “the common neighbors” (i.e., commonly observed agents) in the inferences of the contributions of the non-observed agents located at distance 2. When the distance is higher, we replace them by the contributions of those players’ neighbors that are closer to the non-observed agent in the network, taking into account the distance between them. For instance, consider now 4 players arranged in a line: player 1 linked to player 2, player 2 linked to players 1 and 3, player 3 linked to players 2 and 4, and player 4 linked to player 3 (see Table 1 below). Consider player 1, who is at distance three from player 4. Given (A2), player 1 believes that player 4 reacts as an imperfect conditional cooperator to what she observes, i.e., to player 3’s contribution. Thus, given (A2)–(A4) player 1’s inference for player 4’s former contribution is \(\delta \) times her prediction for player 3’s former contribution, i.e., \(\delta ^2\) times player 2’s former contribution.
Thus, assumptions (A2)–(A4) have the following technical implication: In order to infer \(j\)’s former behavior, \(i\) applies a decay factor \(\delta \) to \(k\)’s contribution per link that separates \(k\) from \(j\), being \(k\) the neighbor of \(i\) that is located in the (shortest) path between \(i\) and \(j\) (if there are more than one shortest path, \(i\) averages the contributions of the respective neighbors). Hence, if \(k\) and \(j\) are very close, \(i\)’s inference on \(j\)’s behavior is close to \(k\)’s contribution whereas if they are far away, \(i\)’s prediction is close to zero. Formally, at period t, once a player \(i\in N\) has observed the contribution of her neighbors, for all \(j\in N\backslash \){\(i\)} the inference of \(i\) on \(j\)’s contribution at period \(t-1\) is:
where \(\delta \in (0,1)\) and \(N_{i,j} =\arg \min _{k\in N_i (g)} d(k,j).\)Footnote 7
Hence, given (A1)–(A4), the dynamics of contributions is governed by the following system of difference equations:
Remark 1
Our behavioral model does not attempt to describe how players start contributing in different networks in VCM games, but rather to show how imperfect conditional cooperation is strongly consistent with the dynamics of contributions in incomplete networks. This is the reason why (2) is not defined for \(t=1\) (since in the first period the neighbors’ contributions are not observed) and, therefore, our model remains open with respect to the initial contributions. To close the model, we shall match the initial contributions to those coming from experimental data, in order to run the simulations and compare the dynamics across different networks and types of players (see Sect. 4).
Theoretical implications
In this framework, the evolution of the contribution levels depends on the degree of imperfectness in agents’ contribution patterns and how it spreads through the (incomplete) networks. In this sense, there are two forces that affect to this spread and that, therefore, may determine whether cooperation can be sufficiently sustained across time: the average connectivity (total number of links) and the presence of highly connected players (distribution of links).
On the one hand, if there are many links, players in general directly observe many others, which make them not to discount too much these others’ contributions when acting as imperfect conditional cooperators.
On the other hand, having highly connected players can be important to sustain cooperation. These players directly observe many others (and, therefore, are expected to produce high contribution levels since they do not discount very much these others’ contributions). At the same time these highly connected players are the reference point of many (less connected) players to behave as conditional cooperators. Thus, they can act as coordinators that avoid that contribution levels fall too fast.
We investigate which of these two forces dominates. To this aim, we consider the same four network structures studied by Fatas et al. (2010): The complete network, the circle, the star and the line, depicted in Table 1 above. The complete network (the baseline treatment) has the maximum number of links and, at the same time, all the players are maximally connected. Thus, our model predicts that the complete network should produce the highest contribution levels. On the other extreme is the line, which has the lowest number of links (across connected networks) and, at the same time, does not have any maximally connected player. This network is expected to yield the lowest contribution levels. In between, we have the circle and the star. The star has less links (the same than the line) but has one maximally connected player (the center), whereas the circle has more links but no maximally connected player.
The experimental evidence derived from Fatas et al. (2010) shows that, indeed, the complete network and the line respectively produce the maximum and minimum contribution levels. Moreover they obtain that the star outperforms the line, and produces similar outcomes to the complete network, which suggests that it is the distribution, rather than the total amount of information what matter to sustain contributions to the public good. The circle produces lower average contribution levels than the star and higher than the line, but these differences are not found to be significant. As we shall see, our simulations offer quite a good approximation to the evolution of the experimental data, which suggests that a pattern of imperfect conditional cooperation can be appropriate to explain behavior in public good games played in networks.
Finally, if we focus on the specific case of the star network, we note that our model predicts a peculiar “oscillating” dynamics due to the presence of a central (highly connected) player and a group of peripheral players: Although contributions decrease over time (due to the imperfect conditional cooperation assumption), the slope varies from one period to another due to the asymmetric informational regime of the center and the spokes.
To illustrate the source of this dynamics in the star, assume a situation where all players start contributing the same amount (say \(k\)) at period 1. Initially, the dynamics leads to lower contributions of the spokes than the center at period 2 (due to the limited observability of the spokes). The average drop of the contributions is sharp due to the higher number of spokes. The next period, the drop of the contributions of the spokes (reacting to a relatively higher contribution of the center) is softer than the drop of the contribution the center (reacting to relatively lower contributions of the spokes at period 2). This makes that the drop of the average contribution is now softer (again due to the higher number of spokes). This “oscillating dynamics” then repeats over time (from odd to even periods). This argument is formalized in the following lemma, which provides the analytic solution of the system of difference equations (3) for this specific case. The proof is in Appendix A2.
Lemma 1
Let n \(=\) 4 and g be the star network. If \(c_1 (1)=c_2 (1)=c_3 (1)=c_4 (1)=k,\) then, assuming (A1)–(A4), the players’ contributions at each \(t\ge 1\) are as follows:Footnote 8
-
If t is odd, \(c_1 (t)=c_2 (t)=c_3 (t)=c_4 (t)=k\delta ^{t-1}\left( {\sqrt{\frac{1+2\delta }{3}} }\right) ^{t-1}\)
-
If t is even, \(c_1 (t)=k\delta ^{t-1}\left( {\sqrt{\frac{1+2\delta }{3}} }\right) ^{t-2}\) and \(c_2 (t)=c_3 (t)=c_4 (t)=k\delta ^{t-1}\left( {\sqrt{\frac{1+2\delta }{3}} }\right) ^t\)
Thus, across time the star is expected to yield a volatile behavior. As we shall see, this special behavior is reflected both in the experimental data and the simulations: There is a trend to decrease contributions across time in all networks, but in the star we observe that this occurs relatively more abruptly (with more pronounced peaks).
3 The experimental design
The experiment was conducted at LINEEX (Laboratory for Research in Experimental Economics), at the University of Valencia. The participants were 144 business and economics undergraduate students, all of them inexperienced in public goods games experiments or network experiments.
We consider groups of 4 subjects (\(n=4\)). The experiment consists of four treatments. Each treatment corresponds to a network: the complete network (N1), the circle (N2), the line (N3) and the star (N4), depicted in Table 1.
We follow a partners matching, that is, the group composition is kept constant. Moreover, each subject’s position within a network is randomly determined at the beginning of the experiment and fixed throughout the experiment.
The experiment was computerized using z-tree (Fischbacher 2007). Along the experiment subjects play the Voluntary Contribution Mechanism (VCM) game for 20 rounds, with payoffs defined by (1), where \(n=4\), \(m=50\) and \(a=0.5\). In this game, links involve the information about others’ contributions.Footnote 9 After each round, the computer screen of each subject displays her initial endowment, the contribution of the group members linked to her and her earnings.Footnote 10 In Fig. 1 we present z-tree screen shots.
We ran 8 sessions (two for each treatment) and no subject participated in more than one session. Specifically, 36 subjects participated in treatment N1 (\(6+3\) groups, in two sessions), 36 subjects participated in N2 (\(6+3\) groups), 40 subjects participated in N3 (\(6+4\) groups), and 32 subjects participated in N4 (\(6+2\) groups). The average payment was around 14€ and, on average, a session lasted around 50 min, including the initial instructions and the payment of subjects.
4 Simulations
In analogy to the experiment, we focus on the case of four players (\(n=\) 4), and the network structures represented in Table 1 (N1, N2, N3, and N4). We also set \(T=\) 20, \(m=\) 50 and \(a=\) 0.5.
We simulate the model considering the initial conditions derived from each of the experimental groups. We obtain one simulation per group and, then, average them. In particular, we calculate the average contribution that each subject who participated in the experiment made in the first block of five rounds, which serves as initial conditions for the simulation of each group.Footnote 11 The initial contributions therefore reflect: (1) how agents perceive the network structure (the network and their position in the network) and (2) how this structure affects to their initial behavior.
5 Results
In Table 2, we report the average contribution in each network given from the experimental data and compare it to the results of the simulations of our model for \(\delta \) = 0.97057 (within brackets). We have calibrated \(\delta \) using the experimental data of our sessions for the complete network. In the complete network, where each agent observes all others’ contributions, \(\delta \) purely measures the degree of imperfectness in the subjects’ pattern of conditional cooperation (A1). This contrasts with the other incomplete networks, where additional assumptions are needed. Hence, we select the parameter value that better fits the data for the complete network treatments, and use it to simulate [using (2), (3)] the evolution of the contributions of each experimental group.
In Table 2, we present this comparison disaggregating by types of players (players with different degree). Note that, given our set of networks (see Table 1), there are players with degree 1 (T1 players, with one link), degree 2 (T2 players, with two links), and degree 3 (T3 players, with three links).Footnote 12
Contributions across networks and types observed in the experiment (Table 2) are significantly different from a statistically point of view. As reported in Fatas et al. (2010),Footnote 13 contributions in the line network are significantly lower than in the complete and star networks across types, even if we control for first-round decisions and lagged contributions. Contributions in the circle network are never significantly different from contributions in the other three networks.
The econometric analysis of differences between types reveals an interesting pattern. Differences between players with the same number of links in the same heterogeneous network can only be explained using decisions in the first round and the conditional cooperation dynamics (see Table 4 in page 408 of Fatas et al. 2010). In both the line and the star networks, conditional cooperation, measured by the lagged average contribution of the other players in the group, is significantly and positively driving contributions. Interestingly, a similar result is obtained when the comparison is made across networks, for the same players’ types, with the exception of T1 players (with only one link): only decisions in the star network are significantly larger than in the line for T1 players (see Table 5 in page 409 of Fatas et al. 2010).
Table 2 shows that the outcomes of the simulations with \(\delta \) close to 1 (\(\delta \) = 0.97057) are very similar to the experimental results.Footnote 14 In our view, the model captures the effect of incompleteness in a very accurate way, both across networks (N1, N2, N3 and N4) and types of players (T1, T2 and T3).
In Fig. 2, we analyze the same comparison (simulation vs. experimental data) across the 20 rounds of play. Again, at each round the average contribution in N1 is normalized to 1. We present this comparison by pairs of graphs: The graphs on the left correspond to the simulations (\(\delta \) = 0.97057), and those on the right correspond to the experimental data. The first pair of graphs shows the evolution of the average contribution across networks (N1, N2, N2 and N4). Then, we compare the (average) contributions of each type of player (T1, T2 and T3) across different networks: T1 players in N3 and N4; T2 players in N2 and N3; and, finally, T3 players in N1 and N4.
As Fig. 2 reveals, our stylized model offers good approximations to the regularities derived from the experimental data: a small degree of imperfectness in the conditional cooperation pattern (associated to \(\delta \) = 0.97057) suffices to capture the dynamics of the experiment. This result holds both when we analyze the evolution of contributions across networks and when we compare the behavior of players with the same degree (same type) located in different networks.
As we can observe in Fig. 2, the complete network and the line produce, respectively, the highest and lowest contribution levels across time, both in the simulations and in the experiment. We also observe that the star yields similar outcomes to the complete network, whereas the outcomes of the circle are in between those of the complete network and the line. This suggests that it is the distribution of links (presence of highly connected players), rather than the total amount of information, what matters to sustain contributions to the public good.
We also note in Fig. 2 that the star presents a (relatively) more volatile (cyclical) behavior than the other networks. This holds both at the aggregate level and when we study the evolution of behavior of different types, which confirms the theoretical implications of our model regarding this asymmetric case of one (highly connected) central player and a group of peripheral players.
Finally, we note that in all networks, the experimental data present a sharp decline of contributions in the final rounds that is not reflected in the simulations. This abrupt decline is due to the end-game effect (typical of many experiments) that erodes the possibilities of cooperation, and that is not included in the assumptions of our model.
6 Conclusion
This paper provides a new application for decay (interpreted as the degree of imperfectness in the pattern of conditional cooperation) in networks. Rather than determining the (reduction in the) value of the externalities generated by individual links, we use the decay to model the accuracy losses associated to the network incompleteness in a public goods environment.
From our assumptions, there are two main forces that can affect to which extent the imperfectness of conditional cooperation spreads through the network (decay) and that, therefore, may determine whether cooperation can be sufficiently sustained across time: the average connectivity (total number of links) and the presence of highly connected players (distribution of links). Our results (both the experimental data and the simulations) suggest that it is the network architecture (in particular, the presence of highly connected players), rather than the total amount of information, what fosters higher contribution levels.
Moreover, the fit of the outcomes of our model to the experimental data suggests that, in a social dilemma situation, the incompleteness of the network structure may effectively erode conditional cooperation, by making more difficult for subjects to get accurate information about the decisions of the other group members.
Finally, it is worth mentioning that to some extent our paper is related to the recent literature on rank-based behavioral models (see, e.g., Boyce et al. 2010), in the sense that networks can matter as they provide the subjects with information to locate themselves within the ranking of contributions. To illustrate this point note, for instance, that to be able to observe the central player of a star is very informative, since such a player knows the complete ranking of contributions, as compared, for example, to the more central agents in the line. In our view, a deeper and systematic analysis of the connections between informational networks and rank-based behavioral models is a very interesting topic that merits future research.
Notes
More complex models that extend this recursive nature are interesting, and they left for future research.
As conventionally, if there is no path of links between \(i\) and \(j\), we set \(d(i\),\(j)\) at \(\infty \).
In this context, if we assumed that players are selfish, the unique subgame perfect Nash equilibrium would result in the inefficient outcome where all players contribute zero at every period.
Recency effects, meaning that people tend to rely on the most recent experiences to take their decisions, are a robust phenomenon in cognitive psychology (see, for instance, Jones and Sieck 2003 and Fatas et al. 2011). Recent studies suggest that the most recent trial has significantly larger effect than previous experiences, but all previous experiences have an approximately the same effect independently of their recency. Nevo and Erev (2012) refer to this pattern as the “very recent effect”. In these lines, we simply assume that subjects rely on the immediate experience, and disregard other (former) information.
This network is depicted in Table 1 below.
Note that if \(j\in N_i (g),\) then \(N_{i,j} =\{j\}\) and, since \(d(i,j)\) = 1, \(\hat{c}_{i,j} (t-1)=c_j (t-1).\) Note also that, if \(i\) and \(j\) do not belong to the same component (\(i.e.\), if they are not linked through a path of links), then \(d(i\),\(j)\) is set at \(\infty \) (cf. Footnote 3) and, by (2), \(\hat{c}_{i,j} (t-1)=0,\) i.e., the Nash equilibrium prediction.
Note that, since \(\delta <1, \, \sqrt{\frac{1+2\delta }{3}} <1\) and, therefore, \(\left( {\sqrt{\frac{1+2\delta }{3}} }\right) ^{t-2}>\left( {\sqrt{\frac{1+2\delta }{3}} }\right) ^t.\)
A copy of the instructions, translated into English, can be found in the Appendix.
Note that having information about the own payoff provides all agents with the possibility derive from it (by making some calculations) the average contribution of the other members of the group in the previous round, regardless which information about contributions they get from the network. Thus, if players used this information, there should be no observed differences in the dynamics across networks nor across types of players. Since this is in contrast to the regularities observed in Fatas et al. (2010), we assume that agents do not make use of the information about payoffs to infer former contributions and that they rely instead only on the information about others’ contributions that they get from the network. This somehow extends the bounded rationality assumption made in (A4).
Similar results are obtained when the initial conditions are directly taken from round 1. However, the simulations fit the experimental data more accurately when we take as starting point the average of the first block of five rounds. This reduces the typical noise and confusion faced by subjects in the very first round of the experiment, which can be remarkable when there are no trial rounds (as it is the case in our experiment).
Specifically, N1 consists of four T3 players, N2 consists of four T2 players, N3 consists of two T2 players and two T1 players, and N4 consists of one T3 player and three T1 players.
See Tables 2 and 3 in pages 405 and 406.
We believe our theory is not designed to be econometrically tested in the laboratory. As a deterministic model, the model generates a set of powerful intuitions about how different types of agents behave in different incomplete networks. In order to provide a basic measure of the model’s goodness of fit, and given that for each experimental group there is a simulated one for which the initial contribution of each simulated agent is the average contribution of the corresponding experimental subject in the first five rounds, a comparison using Wilcoxon matched-pairs signed-rank tests at the group level can be done. We do not observe any significant difference between the experimental data and the simulation generated by our model neither when we use all the rounds, nor when we focus in rounds 6 to 20 or in the second half of the experiment. The results of the tests, together with some descriptive statistics of the simulations, are included in the appendix (see Table 3).
We provide the experimental instruction of the star treatment. The instructions of the other treatments (complete network, circle and line) are analogous and just differ in point 4. Instructions are translated from Spanish. Original instructions are available from authors upon request.
References
Bala B, Goyal S (2000) A non-cooperative model of network formation. Econometrica 68:1181–1229
Boyce CJ, Brown GDA (2010) Money and happiness rank of income, not income, affects life satisfaction. Psychol Sci 21(4):471–475
Bramoullé Y, Kranton R (2007) Public goods in networks. J Econ Theory 135:478–494
Carpenter J, Kariv S, Schotter A (2012) Network architecture. Cooperation and punishment in public good experiments. Rev Econ Design 16:93–118
Croson R (2007) Theories of commitment. Altruism and reciprocity: evidence from linear public goods games. Econ Inq 45:199–216
Fatas E, Jimenez-Jimenez F, Morales AJ (2011) Controlling for initial endowment and experience in binary choice tasks. J Risk Uncertain 43:227–243
Fatas E, Meléndez-Jiménez MA (2010) An experimental analysis of team production in networks. Exp Econ 13:399–411
Fatas E, Meléndez-Jiménez MA, Solaz H (2014) Social hierarchies: a laboratory study on punishment patterns across Networks. mimeo.
Feri F (2007) Stochastic stability in networks with decay. J Econ Theory 135:442–457
Feri F, Meléndez-Jiménez MA (2013) Coordination in evolving networks with endogenous decay. J Evol Econ 23:955–1000
Fischbacher U (2007) z-Tree: Zurich toolbox for ready-made economic experiments. Exp Econ 10(2):171–178
Fischbacher U, Gächter S, Fehr E (2001) Are people conditionally cooperative? Evidence from a public goods experiment. Econ Lett 71(3):397–404
Fischbacher U, Gächter S (2010) Social preferences, beliefs, and the dynamics off free riding in public good experiments. Am Econ Rev 100(1):541–556
Galeotti A, Goyal S (2006) Network formation with heterogeneous players. Games Econ Behav 54:353–372
Hojman D, Szeidl A (2008) Core and periphery in networks. J Econ Theory 139(1):295–309
Jackson MO, Rogers BW (2005) The economics of small worlds. J Econ Euro Assoc (Papers and Proceedings) 3:617–627
Jackson MO, Wolinsky A (1996) A strategic model of social and economic networks. J Econ Theory 71:44–74
Jones M, Sieck WR (2003) Learning myopia: an adaptive recency effect in category learning. J Exp Psychol Learn Memory Cogn 29(4):626–640
Leibbrandt A, Ramalingam A, Sääksvuori L, Walker JM (2014) Incomplete punishment networks in public goods games: experimental evidence. Exp Econ, forthcoming
Nevo I, Erev I (2012) On surprise, change, and the effect of recent outcomes. Front Psychol 3 (art. 24), 1–9
Sugden R (1984) Reciprocity: the supply of public goods through voluntary contributions. Econ J 94:772–787
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors thankfully acknowledge the support of the Spanish Ministry of Economy and Competitiveness (Grant ECO2011-26996), the Regional Government of Andalusia (Grants SEJ2009-4794 and SEJ2011-8065), and the ESRC Network for Integrated Behavioral Science.
Appendix
Appendix
1.1 A1: Experimental instructions Footnote 15
The aim of this Experiment is to study how individuals make decisions in certain contexts. The instructions are simple. If you follow them carefully you will earn a non-negligible amount of money in cash at the end of the experiment. Individual payments will remain private, as nobody will know the other participants’ payments. Any communication among you is strictly forbidden and will result in an immediate exclusion from the Experiment.
-
1.
The experiment consists on 20 rounds. In each round you are member of the same group of four participants. Group composition is randomly determined at the beginning of the experiment and does not vary along it. You will not know the identities of the other group members.
-
2.
At the beginning of the experiment, you will be assigned a player number, which can be 1, 2, 3 or 4. This number will not change along all the experiment. Therefore, in your group there will be a player 1, a player 2, a player 3 and a player 4. You will be one of them.
-
3.
At each round, each participant receives an endowment of 50 ECUS. Your unique decision consists on choosing how many of them you assign to the Group Account. The remaining ECUS will remain in you Private Account.
-
4.
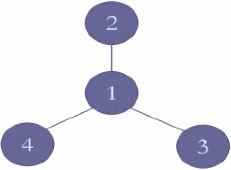
After these decisions are made, each participant will receive information about the assignments to the Group Account made by some other group members. This information is summarized in the following figure:
-
Player 1 will observe the assignments of players 2, 3 and 4
-
Player 2 will observe the assignment of player 1
-
Player 3 will observe the assignment of player 1
-
Player 4 will observe the assignment of player 1
-
-
5.
Your round profits comes both from the group and private accounts. To calculate the benefit of the Group Account we first sum the assignments that all group members have made to the Group Account (i.e., we sum the assignments of players 1, 2, 3 and 4 to the Group Account). This sum of assignments to the Group Account is multiplied by 2, and divided in 4 equal shares (one share for each member of the group).
-
6.
The Private Account benefit equals your assignment to the Private Account and does not depend on the decisions made by the other players.
-
7.
To summarize, your benefit in a given round is determined as follows:

-
8.
At the end of every round, you will get information about current and past profits. The information consists of the benefit you obtain from the Group Account, the benefit you obtain from the Private Account, your total individual benefit and your accumulated benefit up to that moment.
-
9.
At the beginning of the experiment, just by showing up, you will start with an accumulated benefit of 500 ECU (Experimental Currency Units). The benefits that you obtain during the experiments will be added to that amount. At the end of the experiment your cumulative profits (plus the showing-up fee) will be privately paid in cash at the exchange rate of 100 ECU = €1.
1.2 A2: The star with homogeneous initial conditions
Proof of Lemma 1 We analytically solve the system of difference equations given by (3) for the star network when \(c_1 (1)=c_2 (1)=c_3 (1)=c_4 (1)=k.\) Since in the star, assuming homogeneous initial conditions and given (3), all the spokes are in an identical situation at every period, it holds that, for all \(t\ge 1, \quad c_2 (t)=c_3 (t)=c_4 (t),\) Therefore, we have a system of two difference equations, given by:
Substituting (5) into (4), we get the following 2\(\mathrm{nd}\) order difference equation
Whose characteristic equation has two real roots: \(\pm \delta \cdot \sqrt{\frac{1+2\delta }{3}} \). Thus, we get the following solution for the difference equation:
where \(\alpha ,\beta \) are constants. To get the values of \(\alpha \) and \(\beta \), we rely on the fact that \(c_1 (1)=c_2 (1)=k\) and that, by (5), \(c_2(2)=k \delta \dot{\frac{1+2\delta }{3}}\). Thus, evaluating (6) at \(t=\) 1 and \(t=\) 2, we get the following system of equations:
Which yields the following solution
Introducing these values in (6) we get the solution for \(c_2 (t)\):
and, then, using (4), we get the analytic solution for \(c_1 (t)\):
We can simplify (7), (8) just by noting that whether \(t\) is odd or even determines the sign of the terms \((-1)^t\) and \((-1)^{t-1}\), and the lemma directly follows. Q.E.D.
1.3 A3: Additional tables
See Table 3.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Fatas, E., Meléndez-Jiménez, M.A., Morales, A.J. et al. Public goods and decay in networks. SERIEs 6, 73–90 (2015). https://doi.org/10.1007/s13209-014-0114-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-014-0114-x