Abstract
This paper extends the (Lucas, Bell J Econ 9:508–523,1978) model of occupational choices by individuals with different skills, beyond the simple options of self-employment or wage-employment, by including a second choice for the self-employed. That is, an option to hire employees and so become self-employed with employees (SEWEs), or to be self-employed without employees (SEWNEs). We solve for the market equilibrium and examine the sensitivity of relative sizes of occupational groups, and of the level of productivity, to changes in the exogenous parameters. The results show that the positive (negative) association between number of SEWEs (SEWNEs) and productivity, observed in the Spanish data, can be explained, under certain conditions, as the result of cross-region and time differences in average skills. These findings point to the importance of distinguishing between SEWEs and SEWNEs in drawing valid conclusions concerning any link between entrepreneurship and economic development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper considers the determinants of occupation structure in economies where individuals who differ in skills make occupational choices in response to monetary incentives. We model an economy where heterogeneous individuals choose either to work as salaried employees, to be self-employed and not hire employees (SEWNEs), or to be self-employed and hire employees (SEWEs). The market equilibrium from individual occupational choices determines the relative size of each occupation group, as well as the average productivity of the economy (our indicator of welfare). We examine the sensitivity of the occupational structure and average productivity to changes in certain exogenous parameters of the model and relate the theoretical predictions to empirical regularities observed in the relationship between self-employment rates and economic development, in general, and particularly for the Spanish economy.
Our paper is motivated by the observation that existing models of occupational choice ignore the decision of the self-employed to hire employees, or not, and limit occupational choice to employers and employees. The theoretical distinction between SEWEs and SEWNEs is empirically relevant first, because the number of self-employed working on their own is larger than the number of employers, even in a developed country such as Spain; ignoring the SEWNEs, the model is clearly incomplete. Second, because the sign of the association between self-employment rates and productivity in the pool of Spanish cross-region and time-variant data is positive for SEWEs and negative for SEWNEs. Since self-employment rates are a common measure of entrepreneurial activity, this paper presents the different conclusions that can be drawn on the association between entrepreneurship and economic development, depending on the type of self-employment considered and contributes to the literature on entrepreneurial heterogeneity and its implications for economic development.
Early models of occupational choice (Lucas 1978; Rosen 1982; Jovanovic 1994) ignore the realistic alternative of working alone as own-account self-employed. Existing models also differ in assumptions about individual skills and production and organization technologies. In certain papers, such as Lucas (1978), and others that followed, individuals differ in entrepreneurial skills and production takes place with labour and capital inputs in organizationally irrelevant firms. Rosen (1982) extended the Lucas model to an economy where individuals differ in general skills that are converted into either entrepreneurial or operational skills. In Rosen model production involves only labour inputs from entrepreneurs and employees (no capital input) and the organization of production within firms is the relevant economic variable that explains the observed increasing and convex relationship between the size of firms and the managers’ compensations. To the best of our knowledge, our paper is the first that, in addition to considering three occupational choices, models and solves market equilibrium from occupational choices in an economy where individuals differ in general skills, the production inputs involve direct labour and capital services, and the organizational structure matters for overall production efficiency.
The empirical relevance of the model presented in this paper explains the heterogeneity observed in the population of entrepreneurs and provides theoretical support to the evidence that not all entrepreneur types exhibit the same association with indicators of economic development, such as per capita income. The interest in heterogeneity among entrepreneurs stems from the work of Baumol (1990), who classified entrepreneurship into productive, unproductive, and destructive, with empirical support for the distinction being subsequently provided by van Stel and Storey (2004) and Sobel (2008). The GEM (2006) study also made the distinction between necessity and opportunity entrepreneurs. Our paper separates entrepreneurs into those who work on their own (SEWNEs) and those who hire employees (SEWEs), and provides empirical evidence from Spain (and other countries) of the empirical relevance of this distinction.
Over the years, there has arisen a body of literature that seeks to link general indicators of entrepreneurship with economic development (Wennekers et al. 2005; Audretsch et al. 2006, but there is also considerable theoretical and empirical work emphasising that the strength of this link depends on the “type” of entrepreneurship. This has led to the conclusion that not all types of entrepreneurs contribute equally to economic output (Lerner and Schoar 2010). In fact, the evidence leads to contradictory conclusions. On the one hand, there is a strong negative association between self-employment rates and per capita income found in cross-country studies (Kuznets 1971; Iyigun and Owen 1999; Gollin 2008) that raises doubts about the presumed positive link between entrepreneurship and economic development. On the other, there is empirical evidence that productivity growth is greater in economies with a larger share of self-employed (Salas-Fumás and Sanchez-Asin 2013).
Our paper aims to provide new insights into the potential causal effects of entrepreneurship on economic development. In this respect, the paper is similar to Gollin (2008) but with certain important differences. First, Gollin assumes, as does Lucas (1978), that individuals in the economy differ in entrepreneurial skills and that the internal organization of firms is irrelevant. Furthermore, Gollin does not solve for equilibrium with three occupational choices, even though the own-account self-employed are included in the theoretical model. In this paper, individuals differ in general skill, the internal organization of firms affects the average productivity of the economy, and the relative size of each occupational group is explicitly calculated. Comparative static analysis clarifies the relationship between entrepreneurship and economic development, showing that there are cases where each type of entrepreneur, SEWEs and SEWNEs, responds differently to changes in the exogenous parameters.
The paper is also related to recent empirical work that calibrates the parameters of production technologies and distribution of skills in economies where individuals make occupational choices: Gollin (2008) for Japan; Poschke (2011) for the USA; Garicano et al. (2013) for France, and Braguinsky et al. (2011) for Portugal.Footnote 1 We add Spain to the list of countries, but our interest is in explaining occupational structure and its evolution over time. We observe that the rate of SEWEs increases over time, while the rate of SEWNEs decreases.Footnote 2 Since the average productivity of the Spanish economy also increases during the same time period, Spain is an example of the theoretical result, where the rate of one type of entrepreneur is positively correlated over time with average productivity, the SEWEs, and the other type, the SEWNEs, is negatively correlated. These results continue to hold when we combine time and cross-section data from the Spanish regions. We also find that the time-increasing lower bound in the distribution of skills (due to, for example, improvements in education levels of the population) is an important driver of the cross-regional and over-time evolution of occupational rates and productivity for the Spanish economy in the period (1980–2006).Footnote 3 This result is connected to other recent evidence on the human capital of entrepreneurs as a driver of economic growth (Gennaioli et al. 2013).
Another related literature includes work that explains the actual occupational choice using individual level data (Evans and Jovanovic 1989; Evans and Leighton 1989; Carrasco 1999; Dunn and Holtz-Eakin 2000; Dawson et al. 2009). These authors model individual occupation decisions and changes in occupation over time, taking account of individual characteristics such as wealth and wealth constraints, education levels, family background, prior work experience, preferences for independent work, and so on. In this paper, a single attribute, the level of general skill, summarizes all individual characteristics. Our objective is to explain the market equilibrium solutions that result from individual decisions, not the prediction of the occupational choice of a particular individual.
The rest of the paper is organised as follows. In Sect. 2, we model the general results on the equilibrium share of entrepreneurs and output when individuals differ in general skills. Section 3 compares the determinants of equilibrium self-employment rates and productivity with both two and three occupational choice models. In Sect. 4, we use the calibrated model to explain the observed self-employment rates and productivity for the Spanish economy over time, and for 18 Spanish Autonomous Communities (AACC). The conclusions summarise our main results and point to areas for further study.
2 The equilibrium number of self-employed and of direct workers
In this section, we first model the production function for entrepreneurs who hire employees, SEWEs, and for those who work on their own, SEWNEs; next, we solve for the equilibrium occupational groups, and total output produced in an economy with three occupational choices.
2.1 The production functions
Our starting point for the production function is Rosen (1982), who models the output from joint production of an entrepreneur together with several employees, each with a level of general skill. The entrepreneur performs two functions, making strategic and organizational decisions, and supervising the work of employees. The employees perform operational activities and the input in performing each task is the working time weighted by the respective level of skill. Rosen assumes, as does Lucas (1978), that the strategic and organizational decisions of entrepreneurs are one-shot decisions and their quality, which depends on the skills of the entrepreneur, will have an impact on the productivity of all employees under the direction of the entrepreneur. Thus, the level of skill of the entrepreneur enters into the production function as one of the total factor productivity (TFP) components in a positive and increasing way. The difference from Lucas is that Rosen explicitly considers another function of the entrepreneur, namely the supervision of the employees. This supervision is performed on a job-by-job basis and is affected by scale diseconomies that, in turn, depend on the internal organization of the firm. The entrepreneur decides how to allocate the limited quality-weighted working time among employees so that total output is maximized. The scale diseconomies in the supervision of employees imply decreasing returns to scale from increasing the number of employees that, in turn, limit the size of the firm.
In our model, individuals differ in their level of general skill according to a known probability distribution. The formulation of the production function for an entrepreneur who hires employees involves two steps. In the first, the entrepreneur allocates supervision time to transform the general skills of employees into the maximum level of operational skills to be used as production input. In the second step, the quality-adjusted operational skills are combined with the capital input to produce the final output. The TFP of inputs labour and capital is affected by the skill of the entrepreneur through the quality of the strategic decisions.
More formally, let \(t_{i}\) be the amount of time the entrepreneur assigns to an employee \(i\) with general skills \(q_{i}\). The output defined in terms of quality-adjusted operational skills \(l_{i}\), jointly produced by a worker of skill \(q_{i}\) and an entrepreneur with general skill \(q\), is then given by \(l_i =f(qt_i;q_i)\) for all \(i\) hired by the entrepreneur, where \(f()\) is a linear homogeneous, increasing and concave function of inputs \(qt_{i}\) and \(q_{i}\). The total quality-adjusted operational skills of the employees under the direction of an entrepreneur of skill \(q\) is \(\sum \nolimits _i {l_i =\sum \nolimits _i {f(qt_i;q_i)}} \). The entrepreneur will allocate working time \(T\) among workers to maximize output. Rosen (1982) shows that the linear homogeneity property of the function \(f()\) implies that the optimal allocation of the entrepreneur’s working time will satisfy the conditions, \(t_{i}/q_{i}=T/Q\) where \(\sum t_{i} = T\) and \(Q = \sum q_{i}\). The linear homogeneity implies that in the optimal solution entrepreneurs assign more of their time to more able direct workers (\(t_{i}/q_{i}\) constant to all \(i\)).
Then the maximum operational skill obtained by the entrepreneur with skill \(q\) is
where the function \(\phi (x)=f(x,1)\) satisfies the conditions \(\phi {'}(x)>0,\phi {''}(x)<0\) given that \(f{'}(x)>0\) and \(f{''}(x)<0\). The aggregate operational skills then depend on the sum of general skills supplied by the employees, \(q_{1}+q_{2}+\dots +q_{n}\), and on the general skills supplied by the entrepreneur, \(q\). After their combination with the entrepreneurs’ time, the general skills \(q_{i}\) and \(q_{j}\) applied to operational tasks become perfect substitutes.Footnote 4 The intermediate output function \(L()\) exhibits decreasing returns in \(Q\), even though the function \(f()\) exhibits constant returns.Footnote 5 This occurs because large amounts of resources share a fixed amount of the entrepreneur’s time and skills (\(q\) is a fixed factor). The diminishing returns also affect the variable \(q\) in \(Q\phi (qT/Q)\) although, together with \(g(q)\), returns may be increasing.
The final output produced by an individual SEWE involves the inputs of quality-adjusted operational skills \(L(q; Q)\) and capital services, \(K\), together with the entrepreneurial input that contributes to the total productivity of operational skills and capital services. We express the entrepreneurial input by the function \(g(q)\), increasing in \(q\). The production function that gives the total output produced is given by
In the remainder of the paper, the entrepreneur who hires employees is identified as SEWE, the working time \(T\) is normalized to 1, and the functional forms used in the analysis are of the Cob–Douglas form with constant returns to scale. If, \(f(qt_{i};q_{i})=(qt_{i})^{\beta }{q_{i}^{1-\beta }}\), where \(\beta \) is a parameter (\(0<\beta <1)\), then the operational skills from the entrepreneurs and employees is \(L(q;Q)= q^{\beta } Q^{1-\beta }\). The output produced by the SEWE is given by
where \(g(q)=q^{\tau }, \tau >0\) by assumption ; \(\mu \) is the elasticity of output to capital services; \(\theta \) is an exogenous total factor productivity parameter the same for all production units of the economy, and \(\rho =( {1-\beta })( {1-\mu }), \alpha =\tau +\beta ( {1-\mu })\).
The self-employed individual with no employees, SEWNE, combines skills \(q\) with capital services \(K\) and also benefits from the scale economies of entrepreneurial skills. Since there are no employees, the entrepreneur does not get involved in supervision activities and we assume that one unit of general skill of the self-employed transforms into one unit of operational skill. The production function is given by \(Y=h(q)H(q,K)\), where \(H()\) is the aggregator function of skills and capital services. The production technology of SEWNEs may or may not be the same as that used by SEWEs. Blau (1987) argues in favour of different technologies for SEWNEs based on the empirical observation that the rates of SEWNE differ across industries. Gollin (2008) also allows for different production technologies, this time assuming different TFP parameter \(\theta \) for SEWEs and for SEWNEs. In this paper, we assume the same production technology except for scale economies from skills that may be different, \(h(q)=q^\varphi \) , where \(\varphi \) may be equal to or different from \(\tau \). The production function of a full-time SEWNE is as follows:
where \(\upsilon =\varphi +1-\mu \). Under constant returns to scale, in the combination of operational skills and capital services, the SEWNE will be full-time self-employed. Under decreasing returns, it could be the case that a self-employed individual may choose to work part-time as an employee.
2.2 Distribution of skills
Let \(\Gamma (q)\) be the cumulative distribution of general skills \(q\) in the population, for \(q>0\). Then \(\Gamma (q)\) is the proportion of those with skills less than or equal to \(q\). We assume a Pareto probability distribution:
where \(a\) and \(b\) are non-negative parameters and \(a>2\).Footnote 6 The Pareto distribution implies an asymmetric distribution of skills in the working population always decreasing with \(q\). The expected value and variance of skills are a function of \(a\) and \(b\): \(E(q)=ab/(a-1)\) and \(\hbox {Var}(q)=ab^2/[{(a-1)^2(a-2)}]\). Expected skill increases with \(b\) but decreases with \(a\). On the other hand, the coefficient of variation \(SD( q)/E( q)=1/[{a(a-2)}]^{1/2}\) is independent of \(b\) and decreasing with \(a.\)
2.3 Market equilibrium
In the economy, there is a perfectly elastic supply of capital services at rental price (interest rate and depreciation) equal to \(r\). The price per unit of general skill, \(w\), will be determined as part of the market equilibrium. An individual with skill \(q\) will make occupational choices comparing the profits from working as a SEWE, the rents working as a SEWNE, and the salaries earned as an employee. We now calculate the profits, rents and salaries for the production functions given above.
Given the production technology (2) an individual with skills \(q\) will earn a maximum profit as SEWE:
The profit maximizing demand of general skills and capital services are, respectively,
where \(\gamma =\rho +\mu <1\).
The same individual with skills \(q\) working as SEWNE earns a rent:
An individual with skills \(q\) will earn a \(\hbox {Salary}= w\cdot q\) working as an employee.
The individual will make the occupational choice that maximizes income. If many individuals choose to work as employees, then the price of skills will go down, profits will increase, and some individuals will shift to work as SEWEs. Then the demand for and the price of skills will increase, reducing profits and increasing the salaries of employees. In market equilibrium, no individual will change occupation and the supply of operational skills by employees will be equal to the demand by employers.
The equilibrium with three occupational choices is characterized as follows. First, there is a level of general skills \(z\) for which the individual with this skill will be indifferent between being a SEWE and a SEWNE: \(\Pi (w,r;\mathbf{z})=R(r;\mathbf{z})\):
For each market price of skills \(w\) equation (7) solves for \(z(w)\) that maps the price with the indifferent level of skill \(z\) (\(z(w)\) is non-negative and increasing with \(w\) from the convexity properties of the two profit functions). For skill values \(q>z(w)\), profits as a SEWE are higher than profits as a SEWNE, so an individual with greater skills will choose to be a SEWE.
Second, there is a level of skills \(y\) for which the individual with this skill will be indifferent between being a SEWNE and a salaried employee, \(R(r,y)=wy\):
The convexity of the profit function implies that \(R(r,q)\) will intersect the compensation of salaried employees, \(w q,\) from below, so individuals with skills lower than \(y(w)\) that solves (8) choose to work as salaried employees, whereas those with skills between \(y(w)\) and \(z(w)\) choose to be SEWNEs.
The third condition for the market equilibrium is that the price of skills solves the condition that supply is equal to demand. The supply of skills is equal to the sum of general skills from all individuals who choose to work as employees. The demand for skills for operational jobs of an employer with skills \(q\) is given by (5). The demand for skills will be equal to the sum of demands from all employers (those with skills greater than \(z^{*})\):
Solving this equation for \(Q^*\) given in (5) and taking into account (7) and (8), the supply equal to demand condition is written as a function of y, as follows:
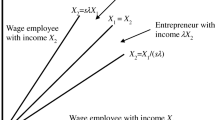
The solutions to Eqs. (7), (8) and (9), when they exist, give the level of general skills \(z^{*}\) at which individuals are indifferent between SEWE and SEWNE; the skills at which individuals are indifferent between SEWNE and salaried employee, \(y^{*}\); and the market clearing price per unit of skill, \(w^{*}\). Substituting these critical skill values into the distribution function of skills, \(\Gamma (q)\) we obtain the equilibrium number of individuals in each occupational choice in the equilibrium: employees, \(\Gamma ( {y^*})=1-\left( {\frac{b}{y^*}}\right) ^a\), SEWEs, \(1-\Gamma ({z^*})=\left( {\frac{b}{z^*}}\right) ^a\), and SEWNEs, \((1-\Gamma ( {y^*}))-(1-\Gamma ( {z^*}))=\left( {\frac{b}{y^*}}\right) ^a-\left( {\frac{b}{z^*}}\right) ^a\). The average span of control of the economy, ASC, is the ratio between number of employees and number of SEWEs: \(\hbox {ASC}=\frac{1-( {b/y^*})^a}{( {b/z^*})^a}\). Figure 1 illustrates in a graphical way the occupational groups in the market equilibrium solution.
The market equilibrium with three occupational choices. The figure plots the wage for salaried workers and the profit functions of SEWEs, \(\Pi \)(), and the rents for SEWNEs, \(R ()\), as a function of the general skills of individuals. Those with skills from \(0\) to \(y^*\) will prefer to be a salaried worker, those with skills between \(y^*\) and \(z^*\) will choose to be SEWNE, and those with ability above \(z^*\) will choose to be SEWE. The market equilibrium requires that at the threshold skill values the supply of operational skills is equal to the demand
Finally, the total output produced is equal to the output produced by the SEWEs and the output from SEWNEs:
3 Comparative static analysis of the equilibrium results
We now present some properties of the equilibrium solution.
Result 1. The market equilibrium exists if \((1-\gamma )a-\alpha =\beta (1-\mu )(a-1)-\tau >0\) and \(\varphi \le \tau \).
Equilibrium requires that Eqs. (7), (8), and (9) have a solution and that the values of \(y^*\) and \(z^*\) satisfy the conditions \(b<y^*< z^*\). The left-hand side of (9) is always positive since \(b <y^*\). Therefore, the right-hand side must also be positive. A necessary and sufficient condition is that \((1-\gamma )a-\alpha =\beta (1-\mu )(a-1)-\tau >0\).
From Eq. (9) \({\left( {\frac{b}{{{y^*}}}} \right) ^{a - 1}} = \frac{1}{{1 + X}}\) and
The term \(X\) is positive under the restrictions imposed on the parameters and consequently we prove that \(y^*\) is greater than \(b\).
Since the first term is greater than 1, a sufficient condition for \(z^{*}>y^*\) is that \(\varphi \le \tau \).
Result 2.
-
(a)
The proportion of individuals in each occupational group, employees, SEWEs and SEWNEs, in the market equilibrium from occupational choices, is independent of the productivity parameter \(\theta \) and of the cost of capital \(r\).
-
(b)
When the production technology of SEWEs and SEWNEs is the same, \(\tau =\varphi \), the proportions of individuals in each occupational group in the market equilibrium is independent of parameter \(b\) of the distribution of skills.
-
(c)
When \(\tau >\varphi \) then the number of SEWEs increases and the number of SEWNEs decreases as the parameter \(b\) of the distribution of skills increases.
Result 2a follows from (9) and (11)], and we see that they are independent of \(\theta \) and \(r\). When \(\tau =\varphi \), the power of \(y\) on the right-hand side of (9) is equal to \(-(a-1)\) and, therefore, \((b/y^*)\) is independent of \(b\). From (11), \((b/z^*)\) will also be independent of \(b\). Consequently, the number of SEWEs and the number of SEWNEs, in the equilibrium, are independent of \(b\) (Result 2b).
To prove Result 2c first notice that the power of \(y\) on the right-hand side of (9) is greater than \(-(a-1)\) when \(\tau >\varphi \). When the assumptions of the model hold, comparative static analysis shows that \(y^*\) decreases with \(b\). From (11) \(z^*\) will also decrease with \(b\) but since the power of \(y\) in (11) is less than 1 it decreases proportionally less than \(y^*\). Therefore, in the equilibrium, the number of SEWEs, \(\small {\left( {\frac{b}{z^*}}\right) ^a}\), increases and the number of SEWNEs, \(\small {\left( {\frac{b}{y^*}}\right) ^a-\left( {\frac{b}{z^*}}\right) ^a}\), decreases with \(b\).
3.1 Relationship with the literature
Lucas (1978) proved that, in an economy with only two occupational choices, and a production technology with elasticity of substitution between labor and capital equal to 1, the equilibrium number of entrepreneurs is independent of the capital to labor ratio. Lucas takes the ratio of capital to labour for the whole economy as exogenous and allows it to vary over time. In our model, the capital input is endogenous and we assume that entrepreneurs face a perfectly elastic supply of capital at an exogenously given rental price \(r\). We have solved the market equilibrium restricting to only two occupational choices (Eqs. (7) and (8) are merged into one, with \(y = z)\) and the results confirm the Lucas prediction for the case of the exogenous rental price of capital.
With three occupational choices, the independence between the occupational structure and the exogenous rental price of capital also depends on the assumptions about the production technologies of SEWEs and SEWNEs. In our economy, the production technology of SEWEs and SEWNEs is the same, and the terms with the cost of capital \(r\) cancel out in solving for the equilibrium solution. If, for example, we would allow for different elasticity of output to capital in the two production functions, then the sizes of occupational groups in the equilibrium will depend on \(r\).
Jovanovic (1994) proved, with two occupational choices, that occupational equilibrium is independent of an exogenous TFP parameter for homogeneous production functions. The intuition, which also applies to our model with three choices, is that higher TFP affects both equilibrium salary and equilibrium profits. Therefore, the level of skill at which individuals are indifferent between one occupation and the other does not change with changes in the exogenous TFP. In the three choices equilibrium, this result also requires that the parameter \(\theta \) enters equally in the production functions of SEWEs and SEWNEs. Gollin (2008) assumes a different TFP parameter in the production function of employers and of own-account self-employed; under this assumption, the independence between equilibrium occupational groups and \(\theta \) no longer holds. Naturally, in equilibrium, the occupational group with higher TFP increases its relative size compared to the size when the productivities are equal.
Result 2b says that when \(\tau =\varphi \), changes in the lower bound of distribution of skills \(b\) do not affect the relative size of the occupational groups, in equilibrium, and output increases with \(b\). This result also holds for any feasible value of \(\tau \) when only two choices, employer or employee, are allowed. When the contributions of skills to the total factor productivity term are the same for SEWNEs and for SEWEs, and the other assumptions hold, higher average skills from higher values of \(b\) (recall that the coefficient of variation remains constant) have similar implications for equilibrium than changes in the exogenous TFP parameter \(\theta \): rents in all occupational groups change proportionally and the sizes of occupational groups remain unchanged. When \(\tau >\varphi \) so the contributions of skills to the TFP term are higher for the SEWEs than for the SEWNEs, then higher average skills in the population from increasing \(b\) give more employers and less own-account self-employed in equilibrium (Result 2c). One reason why the SEWNEs may have lower contributions to TFP from skills than the SEWEs is that the former perform two unrelated functions, working on operational tasks and making entrepreneurial decisions, so their specialization is lower than that of the SEWEs.
4 Occupational choices and productivity: empirical evidence from Spain and other economies
We now highlight the empirical significance of the distinction between SEWNEs and SEWEs, one of the main interests of this paper. For this purpose, we use Spanish data on occupational groups and output per occupied person and productivity, both across regions and over time. The data separate the self-employed in own-account self-employed and employers, and separate salaried employees into those who occupy top management positions, managers, and other salaried employees. The National Statistical Office has collected the data with the same methodology in all of the 18 Spanish Autonomous Communities (AACC). The managers perform similar entrepreneurial and management functions as the employers, so we add the two groups of employers and managers to get what in the model is referred to as SEWEs.
4.1 Self-employment and productivity in Spain: 1980–2005
Table 1 shows the absolute and the relative numbers of all occupied persons in Spain, disaggregated in four occupational groups: Employees (excluding managers), Employers, Managers, and Own-Account Self-Employed. The data shown come from Spanish official statistics on occupations (Encuesta de Población Activa) and correspond to every fifth year in the period 1980–2005, although they are available for each of the years. Employers are the self-employed with employees and Own-Account Self-Employedare the self-employed who do not hire employees. Managers, although they are salaried employees, perform similar entrepreneurial and managerial functions to the employers, and so the SEWEs will include Employers + Managers. The own-account self-employed coincides with the SEWNEs. The last column of Table 1 shows the year average labor productivity of the Spanish economy in thousands of PPP 2005 dollars. Although not shown, we have similar information for each of the AACC and each year.
The proportion of Employees in 2005 was 10 percentage points higher than in 1980. The SEWEs, employers and managers together, also increase over time, from 4.5 % of total employment in 1980 to 6.7 % in 2005. Of this total, the proportion of managers rose from 20 % in 1980 to 28 % in 2005. The opposite trend occurs in the rate of SEWNEs, which falls from over 20 % in 1980 to less than 10 % in 2005. Labor productivity increases over time, but at different rates. In the period 1980–1995, productivity grows at an average annual rate of 2.5 %; in the period 1995–2005 it grows at an annual rate of less than 0.5 %.
We are interested in examining the over-time and cross-region observed values of occupational groups and productivity in Spain, under the lens of our three occupational choices model. For this purpose, we calibrate the values of the parameters of the model with data from the Spanish economy for the years 2000–2005. This calibration sets the size of each occupational group at values of 6.5 % SEWEs, 11.5 % SEWNEs, and 82 % employees. Since there are more parameters than reference values used in the calibration, we set certain parameters from the outset, make certain assumptions, and simulate the equilibrium values of the relative sizes of occupational groups to obtain the remaining parameter values. The values of \(\theta \) and \(\tau \) are normalized to 1, \(\theta =\tau =1\). To obtain the user cost of capital \(r\), we estimate a real interest rate of 4 % and a depreciation rate of 8 %, based on the average cost of debt and depreciation rates of Spanish firms in years 2000–2005 (Central de Balances, Banco de España)Footnote 7; therefore \(r=0.12\). From the model, the term \((1-\beta )(1-\mu )\) corresponds to the proportion of salaries of employees in the output produced by the SEWEs; in the profit-maximizing solution, the ratio of cost of capital services in total output, \((r K^{*})/Y^{*}\) is equal to \(\mu \), and \(\beta (1-\mu )\) is the proportion of profits that are the compensation of entrepreneurs.
The national accounts do not separate gross value added into compensation of entrepreneurs and employees, and cost of capital services. From the accounting statements of business corporations in the years 2000–2005, we estimate a ratio of fixed operating assets plus inventories over gross value added approximately equal to \(K^{*}/Y^{*} = 2\); since \(r\) is set equal to 0.12, the calibrated value of the elasticity of output to capital services is set to \(\mu =0.25\). The same accounting data indicates that labour costs represent 52 % of the gross value added. We do not know what part of this proportion corresponds to the salaries paid to managers and possibly business owners. If the compensation of business owners and managers represents 10 percentage points, the compensation of non-management employees would be 42 % of the value added; this would imply a value of \(\beta =0.45 ((1-0.45)(1-0.25)=0.42)\).
We still have to calibrate parameters \(a\) and \(b\) of the distribution of skills, and parameter \(\varphi \) of the scale economies of skills for SEWNEs. The value of parameter \(a\) is obtained from the size distribution of Spanish firms together with the values of the parameters set above (see Appendix); the base value is 4.7. The values of parameters \(b\) and \(\varphi \) are obtained from simulations (for the remaining parameters set at the values given before), with the restriction that the equilibrium values of the SEWEs and of the SEWNEs are equal to the observed values of 6.5 and 11.5 %, giving us \(b=1.6\) and \(\varphi = 0.60\). We have conducted simulations for different values of the parameters \(\beta \) and \(\mu \) around their values in the base case scenario, to verify the robustness of the results to the choice of the base values. The simulations prove that there is no realistic combination of parameters with the restriction \(\tau =\varphi \) that replicates the observed data on self-employment rates.
4.2 Explaining the time evolution and cross-regional differences in occupational groups and productivity
We observe from Table 1 that the proportion of employers and managers increases over time, while the proportion of self-employed with no employees decreases over time. The table also shows a positive time trend in labor productivity. Therefore, from the aggregated data, it appears that the underlying changes in the Spanish economy in the period under examination cause a positive (negative) association between SEWEs (SEWNEs) and average productivity. We now examine whether this regularity also holds with the across-region and time-variant data from the Spanish AACC. For this purpose, we estimate a regression model of occupational rates as a function of average productivity, controlling for unemployment rates and for time and region fixed effects, using the AACC data. The results of the estimation are shown in Table 2. The initial empirical regularity is confirmed: average productivity is positively associated with the rate of SEWEs and negatively associated with the rate of SEWNEs. If self-employment rates are an indicator of entrepreneurship, the Spanish data show that the sign of the association between entrepreneurship and average productivity differs, depending on the indicator of entrepreneurship used in the analysis.
What could cause the observed pattern of associations between self-employment rates and productivity? When \(\tau >\, \varphi \), Result 2 predicts that higher values of parameter \(b\) imply higher (lower) rates of SEWEs (SEWNEs) and higher output. Therefore, regional differences in parameter \(b\) of the distribution of skills, and differences over time, can explain the observed empirical regularities. To see if there is any other parameter whose cross-region and time variations may explain the observed regularities in the Spanish data, we have performed a comparative static analysis on the equilibrium for changes in the values of the parameters, \(r\) and \(\theta \). The results, not reported, confirm that the empirical evidence is consistent only with changes in \(b\).
Figure 2a plots the predicted market equilibrium occupational rates (Eqs. (7), (8) and (9)) and Fig. 2b shows the predicted average productivity (Eq. (10)) for selected values of parameter \(b\), and the remaining parameters at their base values. The values of \(b\) are \(b= 1.40\) in 1980 to \(b=1.66\) in 2006, with a per year increase of 0.01. In the two figures, we also plot occupational rates (observed and adjusted after removing the variations in SEWNEs resulting from the time evolution of unemployment ratesFootnote 8) and observed productivity, respectively, in the period 1980–2006. Figure 2a, b is complemented with Fig. 3 that shows the occupational rates predicted as market equilibrium for different values of \(b\) in the interval 1.4 and 1.6, and observed rates from all AACC and years.
a Observed (dots), predicted as a function of unemployment rates (dashed line), and simulated (continuous line) self-employment rates in Spain, for changes in parameter \(b\) that determine the average level of entrepreneurial skills; other values of the parameters: \(\varphi =0.60, \beta =0.40, \mu =0.25, r= 0.12, \theta =1\) and \(a=5.0\). b Observed (dots) and simulated (continuous line) for labor productivity in logs in Spain (real GDP per hour worked. Converted to US dollars using 2005 PPPs—2005 US dollars), for changes in parameter \(b\) that determine the average level of entrepreneurial skills; other parameters of the simulation: \(\varphi =0.60, \beta =0.40, \mu = 0.25, r= 0.12, \theta =1\) and \(a=5.0\)
From Figs. 2a and 3, we conclude that time variations and cross-regional variations in the lower bound of the distribution of skills explain rather well the cross-regional differences and time variations in the sizes of occupational groups. The skills values are not observable, but they are reasonably related to the educational levels of the population. Data on educational levels for the Spanish working population show that, in 1980, the proportion of individuals with a level of primary education or less was 78 %. In 2005, that proportion declines to 16 %. In the same time period, the average duration of formal education of the working population increases from 7 to 11 years. Differences in average years of formal education across the AACC are significant and are maintained over time (Congregado et al. 2008). Cross-region and time variations in educational levels may then explain the observed cross-section and time differences in occupational groups in the Spanish data.
Observed pair values of log of productivity and self-employment rates (dots) with data from Spanish AACC and time. Plot of the fitted OLS regression lines of self-employment rates as a function of productivity. Plot of simulated pair values of productivity and self-employment for the market equilibrium calculated for the rest of the parameters at their base levels
Higher average skills in the population from higher values of \(b\), from 1.44 to 1.66, also imply higher average productivity over time (Fig. 2b). In fact, the calculations show that output per occupied person increases at an average constant rate of 1.6 % per period. Table 1 shows that the actual cumulative annual productivity growth rate is 1.7 %, but the actual increase in productivity is not homogeneous over time: 2.5 % annual growth in 1980–1995 and 0.5 % in 1995–2000. As for the sources of the increase in productivity, the conventional analysis distinguishes between the contribution from higher capital per occupied person, and the contribution from improvements in exogenous TFP. Unofficial statistics indicate that capital per capita increased at a cumulative annual rate of 3.8 % in the period 1980–1995, and at an annual rate of 0.3 % in the period 1995–2005; the annual cumulative growth rate in TFP is 0.2 % in 1980–1995 and \(-\)0.1 % in the period 1995–2005 (Banco de España).Footnote 9
In our analysis, the TFP component of the production function involves two terms, the parameter \(\theta \) that summarizes the general technical progress of the economy, common to all production units, and the functions \(g(q)\) and \(h(q)\) that capture the contribution of skills to the quality of the entrepreneur’s decisions. We take parameter \(\theta \) as exogenous and the values of \(q\), the skills of entrepreneurs, will vary with the distribution of skills. As for the contribution to productivity of capital deepening, notice that in our model the demands of capital and labour (as supplier of operational skills), are endogenous values given by Eqs. (5) and (6). The ratio of optimal capital to optimal demand of operational skills, the capital to direct labor ratio, increases with \(w^{*}\), the price of skills, and decreases with the cost of capital, \(r\). Result 2 above gives that higher values of \(b\) imply higher \(y^{*}\) and, from (7), higher price of skills, \(w^{*}\), in equilibrium. Therefore, as average skills increase, we expect a higher ratio of capital to direct labour in the economy.
Lucas (1978) assumes an exogenous increase in capital per occupied person over time, in parallel with general economic progress. Our analysis can explain this time trend in capital deepening as the result of time-increasing average skills from higher values of \(b\), and non-increasing cost of capital \(r\).
The actual data on output and productivity growth for the Spanish economy suggest that there are two differentiated periods in the dynamics of change in the Spanish economy, until 1995, and afterwards. One explanation of this can be that parameter \(b\) does not change at a constant annual rate in every time period. First, the educational levels in the Spanish population improved relatively more in the first years of the period than in the later ones. Second, beginning in the late 1990s, Spain saw an important increase in the number of low-skilled jobs in construction and personal services that probably lowered the mean and increased the dispersion in the distribution of skill. In fact, Table 1 and Fig. 2a show stagnation in the rate of employers and managers after 1995. However, other sources of structural change in the economy, different from changes in the distribution of skills (foreign direct investment, public infrastructure, better management, etc.) cannot be excluded as factors affecting productivity and occupational groups.
4.3 Other evidence on self-employment rates and productivity
Homogeneous data for all countries and over time on individuals in each occupational group, similar to that available for Spain and the individual AACCs, are not available. The International Labor Organization (ILO) publishes data on self-employment rates, distinguishing between SEWEs and SEWNEs for certain OECD countries and years (21 countries with scattered observations in the years 1987–2008). The rate of SEWEs (SEWNEs) in the ILO data ranges from 1.08 % (3.22 %) to 15.12 % (27.4 %). A preliminary examination of the association between the rates of each group of self-employed and per capita income of the specific countries confirms a positive association between SEWEs and productivity and a negative association between SEWNEs and productivity, in line with the results of data from the Spanish AACCs shown in Table 2.Footnote 10
As for the USA, Hipple (2004) reports that around 20 % (slightly decreasing over time) of the unincorporated self-employed hire salaried employees, while nothing is said about the number of employers among the incorporated self-employed. Most of the self-employed without employees will then be in the group of the unincorporated, and it is reasonable to assume that the number of incorporated self-employed gives a lower bound in the number of self-employed with employees in the US. The incorporated self-employed in the US were 2.9 % of total employment in 1990, increasing to 3.6 % in 2003 (Hipple 2004). On the other hand, the unincorporated self-employed were 8.5 % in 1990, declining to 7.5 % in 2003. During this period, productivity per worker in the US economy increased from $58,829 in 1990 to $73,199 in 2003 (price levels and PPP $2005). The time evolution of self-employment rates and productivity in the US, appear, therefore, to be broadly in line with what we observe in Spain: higher (lower) rates of SEWEs (SEWNEs) as average productivity increases over time.
5 Conclusion
This paper emphasises the importance of disaggregating or “unpacking” the concept of entrepreneurship to better understand the nature, if any, of the relationship between entrepreneurship and economic development. Theoretically, the paper extends Rosen’s (1982) model of individual occupational choice, with general skills, and diseconomies in the internal organization of firms, in two ways: including capital services as an additional input of production, and allowing for own-account self-employment. Solving for the new market equilibrium, we find the determinants of the relative sizes of each occupational group, and of the average productivity of the economy. The comparative static analysis on the equilibrium solution provides new insights into the explanation of heterogeneity within entrepreneurial individuals and how such heterogeneity relates to per capita income of the economy.
Taking self-employment as a proxy for entrepreneurship, our key theoretical distinction is between two forms of self-employment: where individuals employ only themselves (SEWNEs) and where they employ others (SEWEs). We explain that this choice depends on the skill level of the individual and that these skills vary between individuals. We then show that output (productivity) in the economy is not only a function of technological and organizational parameters, but also a function of parameters of the distribution of skills.
The observed variability in self-employment rates and productivity across time and space reflect variations in these parameters. However, certain parameters are difficult to observe so it is vital for policy makers to know whether all forms of entrepreneurship/self-employment impact equally on productivity. To address this, we specify the conditions under which higher rates of SEWEs lead to enhanced productivity, whereas higher rates of SEWNEs lower productivity. We also argue that, over time, although total self-employment rates (SEWEs + SEWNEs) may rise or fall, the key influence on productivity is the absolute number and proportion of SEWEs.
Our theoretical model provides a good explanation of self-employment rates and productivity in the Spanish regions in the period 1980–2006. First, we calibrate the parameters of the model and find that the scale economies from skills in entrepreneurial jobs are higher in the group of SEWEs than in the group of SEWNEs. Second, we observe that shifts to the right in the distribution of general skills over time, reflecting improved education for example, increase average output per worker. Simultaneously, the shift also changes occupation composition, with more people having the skills to become employers and managers and less becoming SEWNEs. The higher wages resulting from higher average skills then make it relatively more attractive for the less able SEWNEs to hire employees, and the higher profits generated by SEWEs make it more attractive for them to hire ex-SEWNEs as employees. The reduction in SEWNEs is greater than the increase in SEWEs, so total self-employment decreases over time at a decreasing rate (at higher values of average skills and productivity, the total self-employed rate levels off). This explains the convex and decreasing relationship between total self-employment rates and productivity.
This “unpacking” of entrepreneurship appears to be theoretically and empirically robust and provides an opportunity for further work. For example, the model could be extended to include other technologies and other distributions of skills. Another worthwhile extension would be to incorporate the uncertainty faced by individuals over their skills, and the role of learning by experience (Jovanovic 1982; Hopenhayn 1992). In this way, the model presented in this paper could be converted from static to dynamic (Salas-Fumás and Sanchez-Asin 2013). A final area for development could be to incorporate our approach with occupational-choice models using individual level data. The incorporation of personal characteristics such as education, gender, family and ethnic background, income, preferences for independent work, etc., could also provide useful insights.
However, what remains beyond question is the simple assertion that greater entrepreneurial resources continuously and consistently enhance productivity growth. Our finding, that certain forms of entrepreneurship are linked to economic development, while others are not, has considerable implications for public policy, pointing to the economic implications of ensuring that there is a strong alignment between skills and the choice of self-employment. So, for example, those individuals with skills below a threshold level who become SEWEs are more likely to fail in their business venture. Equally, an economy in which there are many individuals with the skills to become a SEWE but who choose to become a SEWNE leads to an under-performance of the whole economy. There is a public policy role in aligning skills with entrepreneurial choice.
Finally, it is important to emphasize that the current model explicitly excludes changes in attitudes of individuals over time. The key change that emerges from the Spanish case is in the distribution of skills in the working population shifting to the right, almost certainly reflecting improvements in education. From a policy perspective, this suggests that the emphasis should be on enabling more individuals to acquire the basic skills, general and specific, to operate a business and employ others, rather than on the currently fashionable trend to create entrepreneurial mindsets or attitudes.
Notes
Poschke (2009) explains the existence of two groups of entrepreneurs, one at the lowest end of the distribution of skills and another at the upper end, as the consequence of uncertainty about the productivity of start-up projects and differences in individuals’ ability to search for good projects. Our model assumes certainty.
In Rosen’s (1982) model of the internal organization of firms, the only problem that needs to be solved is who will be self-employed and who will be an employee; the matching of entrepreneurs and workers is irrelevant. Garicano (2000) and Garicano and Rossi-Hansberg (2006) model the market equilibrium from occupational choices in knowledge hierarchies that involve optimal matching.
The organizational diseconomies result from the limited time of the entrepreneur that is available for coordination and supervision on a person-by-person basis, and from the loss of control. Thus, the span of control inside firms is limited (Calvo and Wellisz 1979; Rosen 1982), while the loss of control limits the number of organizational layers (Williamson 1967; Calvo and Wellisz 1978).
The Pareto distribution has been used to empirically describe the distribution of the sizes of firms (Simon and Bonini 1958) and was used by Lucas (1978) to illustrate certain of his theoretical results; the scale economies of ability imply a match between the distribution of ability and the distribution of sizes of firms.
Rates of SEWNEs can be affected by the unemployment rate if the occupational choice is conditioned by the need to find an occupation, and not to respond to a business opportunity. The model does not explain self-employment by necessity and this is why unemployment-adjusted rates of SEWNEs are appropriate to use in the context of the model.
The regression of self-employment rates on per-capita income (in purchasing power parity), controlling for the unemployment rate, with the OECD data, gives an estimated coefficient of 4.2 (\(p<0.01\)) for SEWEs and of \(-\)0.97 (\(p<0.05\)) for SEWNEs.
References
Audretsch D, Keilbach M, Lehmann E (2006) Entrepreneurship and economic growth. Oxford University Press, Oxford
Antras P, Garicano L, Rossi-Hansberg E (2006) Off-shoring in a knowledge economy. Q J Econ 121(1): 31–77
Baumol WJ (1990) Entrepreneurship: productive, unproductive, and destructive. J Polit Econ 98(5):893–921 (part 1)
Blau D (1987) A time series analysis of self-employment in the US. J Polit Econ 95(3):445–467
Braguinsky S, Branstetter L, Regateiro A (2011), The incredible shrinking of Portuguese firms, NBER working paper series, No. WP 17265. National Bureau of Economic Research, Cambridge. http://www.nber.org/papers/w17265
Burstein A, Monge-Naranjo A (2007) Foreign know-how, firm control, and the income of developing countries, NBER working paper series, No. W15129. National Bureau of Economic Research, Cambridge. http://www.nber.org/papers/w13073
Calvo G, Wellisz S (1978) Supervision. Loss of control and the optimal size of the firm. J Polit Econ 87:943–952
Calvo G, Wellisz S (1979) Hierarchy. Ability and income distribution. J Polit Econ 87:991–1010
Carrasco R (1999) Transitions to and from self-employment in Spain: an empirical analysis. Oxford Bull Econ Stat 61(3):315–341
Congregado E, Hernández L, Millán JM, Raymond JL, Roig JL, Salas V, Sánchez-Asín JJ, Serrano L (2008) El Capital Humano de los Emprendedores en España, Fundación Bancaja
Dawson ChJ, Henley A, Latreille PL (2009) Why do individuals choose self-employment, IZA Discussion Paper No. 3974. http://ssrn.com/abstract=1336091
Dunn T, Holtz-Eakin D (2000) Financial capital, human capital, and the transition to self-employment: evidence from intergenerational links. J Labor Econ 18(2):282–305
Eeckhout J, Jovanovic B (2012) Occupational choice and development. J Econ Theory 147(2):657–683
Evans D, Leighton LS (1989) Some empirical aspects of entrepreneurship. Am Econ Rev 79(3):519–535
Evans DS, Jovanovic B (1989) An estimated model of entrepreneurial choice under liquidity constraints. J Polit Econ 97(4):808–827
Garicano L (2000) Hierarchies and the organization of knowledge in production. J Polit Econ 108(5):874–904
Garicano L, Rossi-Hansberg E (2006) Organization and inequality in a knowledge economy. Q J Econ 121(4):1383–1435
Garicano L, LeLarge C, Van Reenen J (2013) Firm size distortions and the productivity distribution: evidence from France. National Bureau of Economic Research, NBER Working Paper No 18841
GEM (2006) Global entrepreneurship monitor, GEM 2006 results. http://www3.babson.edu/eship/upload/gem_2006_global_report.pdf
Gennaioli N, La Porta R, Lopez-de-Silanes F, Shleifer A (2013) Human capital and regional development. Q J Econ 128(1):105–164
Gollin D (2008) Nobody’s business but my own: self-employment and small enterprise in economic development. J Monetary Econ 55(2):219–233
Hipple S (2004) Self-employment in the United States: an update. Mon. Labor Rev 127(July):13–23
Hopenhayn HA (1992) Entry, exit, and firm dynamics in long run equilibrium. Econometrica 60(5):1127–1150
Iyigun M, Owen A (1999) Entrepreneurs, professionals and growth. J Econ Growth 4(2):213–232
Jovanovic B (1982) Selection and the evolution of industry. Econometrica 50(May):649–670
Jovanovic B (1994) Firm formation with heterogeneous management and labor skills. Small Bus Econ 6(3):185–191
Kuznets S (1971) Economic growth of nations: total output and production structure. Belknap Press of Harvard University Press, Cambridge
Lerner J, Schoar A (eds) (2010) International differences in entrepreneurship. National Bureau of Economic Research, University of Chicago Press, Chicago
Lucas R (1978) On the size distribution of business firms. Bell J Econ 9(2):508–523
Parker S, Robson M (2004) Explaining international variations in self-employment: evidence from a panel of OECD countries. South Econ J 71(2):287–301
Poschke M (2009) Who becomes an entrepreneur?. Labour Market Prospects and Occupational Choice, IZA Discussion Paper 3816
Poschke M (2011) The firm size distribution across countries and skill-biased change in entrepreneurial technology, Mimeo
Rees H, Shah A (1986) An empirical analysis of self-employment in the UK. J Appl Econ 1:95–108
Rosen S (1982) Authority, control, and the distribution of earnings. Bell J Econ 13(2):311–323
Salas-Fumás V, Sanchez-Asin JJ (2013) The management functions of entrepreneurs and countries’ productivity growth. Appl Econ 45(17):2349–2360 (available online: 12 Apr 2012)
Simon HA, Bonini CP (1958) The size distribution of business firms. Am Econ Rev 48(4):607–617
Sobel RS (2008) Testing Baumol: institutional quality and the productivity of entrepreneurship. J Business Venturing 23(6):641–655
van Stel AJ, Storey DJ (2004) The link between firm births and job creation: is there a Upas Tree effect? Reg Stud 38(8):893–909
Wennekers S, van Stel A, Thurik R, Reynolds P (2005) Nascent entrepreneurship and the level of economic development’. Small Bus Econ 24(3):293–309
Williamson O (1967) Hierarchical control and optimal firm’s size. J Polit Econ 75(2):123–138
Acknowledgments
We gratefully acknowledge the comments of María Callejón, Oscar Gutierrez-Arnaiz, Francisco Ruiz-Aliseda, three anonymous referees, and the Journal editor regarding a previous version of this paper, and the technical support of David González Ibáñez in the simulation of the equilibrium solutions. The Spanish authors acknowledge financial support from project ECO2009-13158 MICINN-PLAN NACIONAL I+D. This paper is also part of the results obtained in the framework of the CREVALOR Group of Research, acknowledged and financed by DGA-FSE.
Author information
Authors and Affiliations
Corresponding author
Appendix: Calibration of parameter \(a\) of the distribution of skills with Spanish data
Appendix: Calibration of parameter \(a\) of the distribution of skills with Spanish data
One of the parameters of the model is parameter \(a\), capturing the dispersion in the amount of skills in the working population. The dispersion in skills translates in the market equilibrium into dispersion in the span of control among employers. The natural data from which to calibrate the value of \(a\) would be the dispersion in the amount of operational skills per employer, but that information is not available. We use instead information on the distribution of sizes of firms, where size is measured in number of employees. Since all the operational skills are interchangeable, one single price per unit, the number of employees will be proportional to the amount of operational skills, and it can be expected that the vast majority of employers will conduct business through an incorporated company.
From (5), the amount of operational skills per individual that choose SEWE is written as
where \(M=[ {( {\frac{\mu }{r}})^\mu ( {\frac{\rho }{w}})^{1-\sigma }} ]^{\frac{1}{1-\gamma }}\). The cumulative value is
where \(\sigma =\frac{(1-\gamma )a-\alpha }{1-\gamma }\) is a positive constant from the restrictions on the values of the parameters imposed by Eq. (8).
When \(q\) tends to infinity, the cumulative number of skills is \(N^*\):
The cumulative distribution of employees, \(n\), per SEWE/ firm is
The cumulative distribution of the number of SEWEs is
Therefore, \([ {1-\Gamma (q)}]^{\frac{1}{a}}=\frac{z^*}{q}.\) Substituting in (12),
1.1 Empirical data on distribution of employees per sizes of firms
The data on the distribution of firms and employees per firms come from the DIRCE (2002), but the pattern of the distributions remains very stable over time (Table 3).
There are more firms without employees (52.6 %) than firms with employees (47.4 %). Firms with one or two employees represent 55.8 % of the firms with employees, but they employ only 8.8 % of the total number of employees. Firms with 100 or more employees are 0.34 % of the total, but they employ almost 39 % of the employees.
From Eq. (14) we have \(\sigma /a = \hbox {Ln} [1- H(n)] /\hbox {Ln} [1- \Gamma (q)]\). For example, considering the cumulative values of firms and employees up to the size class of nine employees, the value of \(\sigma /a\) would be equal to \(\hbox {Ln} (1-0.271)/\hbox {Ln}(1-0.87)= 0.154\). Repeating the calculation for the other size classes, we obtain the values of 0.113 (up to 2 employees), 0.190 (up to 59) and 0.17 (up to 99). The average of these values gives \(\sigma /a =0.15\).
On the other hand, from the theoretical model (and \(\tau =1\)) we know that \(\alpha = 1+\beta (1-\mu \)) and \(1-\gamma =\beta (1-\mu )\). Substituting in \(\sigma \) we obtain \(\sigma /a =0.15\) so we can solve for the value of \(a=\frac{1+\beta (1-\mu )}{\beta (1-\mu )(1-\sigma /a)}\). Substituting the calibrated values of \(\beta =0.45, \mu =0.25\) and \(\sigma /a =0.15\), we obtain \(a=4.7\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Salas-Fumás, V., Sanchez-Asin, J.J. & Storey, D. Occupational choice, number of entrepreneurs and output: theory and empirical evidence with Spanish data. SERIEs 5, 1–24 (2014). https://doi.org/10.1007/s13209-013-0103-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13209-013-0103-5