Introduction

Spin transfer torque (STT)-based magnetoresistive random access memory (MRAM) has shown enormous promise among the next generation of non-volatile memories due to its scalability, high operation speed and unlimited endurance (Slonczewski 1996; Berger 1978, 1996; Tsoi et al. 1998; Myers et al. 1999; Kiselev et al. 2003; Tserkovnyak et al. 2005; Albert et al. 2000). STT-MRAM cell normally consists of an MTJ and a transistor as access device. In a typical MTJ device there are two ferromagnetic (FM) layers separated by an insulating tunneling barrier (MgO). One of the FM layers has fixed magnetization direction and the other layer has a variable magnetization which can be made to align either parallel (P) or anti-parallel (AP) with respect to the fixed layer. When current flows through the MTJ, the FM absorbs angular momentum from the electrons and creates a torque which flips the magnetization of the free layer. Logical value of memory bit is stored by the spin orientation of free layer. However, the issue with STT-MRAM is that the current required for switching is relatively large (107–108 A/cm2) and hence relatively large transistors are required to drive it, thus limiting the information storage density in this technology.

In this paper we study properties of a novel, bi-directional MTJ stack consisting of antiparallel fixed layers proposed in (A. Raychowdhury “Numerical Analysis of a Novel MTJ Stack for High Readability and Writability”, IEEE 2011) and compare the switching times with perpendicular anisotropy version. We also explore the variations of switching time on the dimensions of the free layer and spacer.

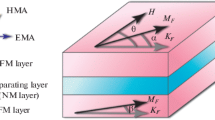
The proposed MTJ stack is presented in Fig. 1. It is a multilayer stack structure with two antiparallel fixed layers at the top and bottom of the stack perpendicularly polarized in +z and -z directions, respectively, and a system of coupled, perpendicularly polarized-free layers is sandwiched between these two fixed layers. The spacer separating fixed layers from the free layers is insulating tunneling barrier (MgO) and the spacer which separates free layers is metallic (Ru, Cu).

Fig. 1
figure 1

Schematic diagram of the bidirectional MTJ stack. Two ferromagnetic, free layers separated by an Ru layer sandwiched between antiparallel fixed layers

Full size image

Switching dynamics

Switching in perpendicular DBSAF-AP MTJ device proceeds as follows (Fig. 2). Initially, perpendicularly polarized electron current is injected through the stack for P to AP switching. The top free layer injects up-spin electrons thus exerting torque on the bottom free layer. Furthermore, the fixed layer at the bottom reflects the up-spin electrons, which are transmitted through the bottom free layer causing magnetization of the bottom free layer to flip in +z direction thus entering a metastable stage in which both free layers have magnetization in the same direction (+z). If the current is stopped at this stage, magnetization of TFL switches in −z direction to attain stability and hence completes the transition to AP (Fig. 2b). For switching from AP to P, current is injected from the opposite direction. Initially, the magnetization of the bottom free layer flips leading to a ferromagnetic state of the two free layers, which is metastable, and then again current is stopped and top free layer switches in +z direction again returning to P state. The total switching time is the total time taken in P-to-AP transition (tr + tf). However, switching from metastable stages to complete the transition is very slow. Switching speed can be enhanced by injecting the current in the opposite direction at stage 2 (Fig. 2a). To achieve the bipolar nature of the current a 1T-1R bitcell was suggested in (Raychowdhury 2011) which allows a selector transistor to drive the MTJ. In this way, the polarities of the voltages on the source line, word line and bit line are controlled.

Fig. 2
figure 2

Switching of the p-MTJ memory stack with Mz vs. switching time curvea for current-assisted switchingb for self-switching after the intermediate stage

Full size image

Micromagnetic simulations

We use the micromagnetic simulator OOMMF to simulate the magnetization dynamics of the coupled free layers as we apply spin-polarized current pulse. However, we simulate only the system of coupled free layers alone ignoring any dipolar field from the fixed layers. In a real MTJ device, this can be achieved by using a synthetic antiferromagnetic fixed layer (Leal and Kryder 1998). The parameters used are saturation magnetization Ms = 1,400 × 103 A/m, uniform exchange constant A = 30 × 1012 J/m and anisotropy constant K1 = 5 × 103 J/m3. Time evolver in OOMMF integrates the Landau–Lifshitz–Gilbert ODE augmented with a spin momentum term (Xiao et al. 2004).

$$ \frac{dm}{dt} = - \left| \gamma \right|m \times Heff + \alpha \left({m \times \frac{dm}{dt}} \right) + \left| \gamma \right|\beta\epsilon \left({m \times mp \times m} \right) - \left| \gamma \right|\beta \epsilon \prime m \times mp, $$
(1)

where m is the reduced magnetization, M/Ms, γ is the Gilbert gyromagnetic ratio, \( \beta = |\frac{\hbar }{{\mu {\text{e}}}}|\frac{\text{J}}{{{\text{df}} \times {\text{Ms}}}} \), mp is the (unit) polarization direction of spin-polarized current, df is the free layer thickness, P is the spin polarization, J is the current charge density, \( \epsilon = \frac{P \wedge}{{({\wedge^2} + 1) + ({\wedge^2} - 1)(m.mp)}} \) which represents the dependence of the spin polarization on m and ϵ’ is the secondary spin transfer term. For simplicity we take value of ∧ to be 1 as it has been done in previous studies (Nikonov et al. 2010) we assume P to be 0.4.ϵ′ is taken to be 0.06, since field-like-torque is taken to be 30 % of the STT term in Eq. (1) (Nikonov et al. 2010), P is assumed to be 0.4 and value taken for α is 0.01. Polarization direction of spin-polarized current mp is taken to be (0, 0, 1). Since we assumed that the fixed layer magnetization can be pinned by coupling to an adjacent antiferromagnetic free layer we can ignore the spin transfer torque that acts on fixed layers.

Simulation of the stack is performed for pulses of amplitudes ranging from 1 × 107 A/cm2 to 4 × 107 A/cm2 in steps of 1 × 107 A/cm2 to study the effect of STT on MTJ device. Cell size of 1 × 1 × 0.1 nm3 is chosen. Reducing the cell size further does not affect the dynamics, significantly. The effect of temperature is not considered, which means that any stochastic effect due to random thermal motion or process variability is not taken into account. To initiate switching, we disorient the initial magnetization configuration of free layer slightly by 0.5°. This disorientation is present in MTJs at finite temperature due to inherent thermal agitation of magnetic moments.

Magnetization dynamics of bi-directional MTJ stack are studied for current-assisted switching as well as self-switching. We choose 40 nm × 20 nm as the cell footprint while the spacer and free-layer thickness is varied to study their effects on the switching time. First we study the dependence of switching time on the current density. As the current density increases, the switching time first decreases and then increases. The relaxation time (tf) is much more than the rise time (tr) and hence switching time depends mostly on tf for this case.

In case of current-assisted switching, tr and tf are almost of same magnitude and switching is almost symmetric (Fig. 2a). Switching from parallel (P) to anti-parallel (AP) configuration is compared for in-plane DBSAF and perpendicular DBSAF. The free layers’ thickness is 2 nm and spacer thickness is 2 nm (Fig. 3), the switching time versus current density curves for the perpendicular DBSAF clearly lies below the one for in-plane DBSAF. To understand why p-MTJs switch faster and to understand the variation of switching time on variation of free layer thickness we should know the dependence of intrinsic switching current density Jc on the magnetization of free layer Ms and the thickness of the free layer df. For a macrospin model at zero temperature (Sun 2000; Koch et al. 2004; Sun et al. 2004; Sun 2006), the intrinsic current density Jc which is required to reverse the magnetization in a MTJ can be expressed as:

Fig. 3
figure 3

P to AP switching to compare the switching speed between in-plane DBSAF and perpendicular DBSAF

Full size image
$$ {\text{Jc}} = \frac{{2{\text{e}} \times \alpha \times {\text{Ms}} \times {\text{df}} \times \left( {{\text{H }} + {\text{Hk }} + 2\pi {\text{Ms}}} \right)}}{\hbar \eta } $$
(2)

where H is the applied field along the easy axis, α is the damping constant, η is the spin transfer efficiency and Hk is the effective anisotropy field. When spin-polarized current is greater than Jc the stable magnetization state of the free layer becomes unstable causing it to either reverse or enter into a precessional state. For p-MTJs we use a free layer with perpendicular anisotropy with Hk⊥ > 4πMs. Since the magnetization is out of the plane it eliminates the 2πMs term in Eq. (2) (Huai 2008). From Fig. 3 it can be observed that switching time of the perpendicular DBSAF for the same current applied is much less than the in-plane DBSAF.

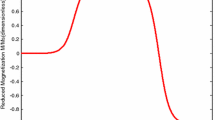
Next the dependence of switching time on dimensions of the MTJ was studied. The free layer thickness was varied from 1 to 2 nm and the switching time for different current densities was observed. It can be noted from Fig. 4 that for the same current applied, switching time for MTJ with df = 1 nm is lesser as compared to stack with df = 2 nm. From Eq. (2), Jc is proportional to the thickness of the free layer df, hence the smaller value of Jc can be achieved by reducing df. But the thermal activation energy is proportional to the free-layer volume, so when free-layer thickness becomes very small, thermal activation energy becomes an important issue. Hence there is a trade-off relationship between Jc and thermal activation energy. Composite free layers consisting of two ferromagnetic layers with various types of coupling have been proposed in (Ochiai et al. 2005; Hayakawa 2006; Hayakawa et al. 2008; Ichimura et al. 2009; Yen et al. 2008; Yao et al. 2008; Lee et al. 2009). We varied spacer thickness from 0.5 to 4 nm in steps of 0.5 nm but no significant variation on switching time was observed. We also studied dependence of switching time on coupling strength. Coupling strength dependence was studied for the values of sigma −1 × 103, −1 × 102, and −1 × 101. It was observed that on increasing coupling strength, overall magnetization settles at a lesser value than 1 when spin-polarized current is applied. On increasing the coupling strength further, the overall magnetization settles at a much lower value (Fig. 5).

Fig. 4
figure 4

Plot to study dependence of switching time on free-layer thickness (df)

Full size image
Fig. 5
figure 5

Semi-logarithmic plot to study dependence of switching time on coupling strength (sigma)

Full size image

If the bi-directional MTJ stack is exposed to negative polarity current while switching from metastable state to stable state for a period longer than the switching time, then the bottom free layer eventually switches again to −z direction leading to another metastable state (Fig. 6). This leads to an unintentional switching event and a write failure. To avoid this, a timing margin is necessary. A design to significantly reduce this failure has been proposed (Raychowdhury 2011).

Fig. 6
figure 6

Mz vs. time graph showing that MTJ goes to another metastable state on continuation of negative pulse

Full size image

Conclusion

We investigated the switching speed of a perpendicular DBSAF-AP MTJ device and compared it with an already proposed in-plane device. Using micromagnetic simulations we observed significant reduction in switching time in p-MTJ as compared to the in-plane. We also explored the switching time dependence on the dimensions of the device and observed that reducing the free-layer thickness reduces the switching time for the same current applied. No significant variation was observed when spacer thickness was varied. On increasing the coupling strength between the composite-free layers, the overall magnetization starts settling at a value lower than 1. This value reduces further on increasing coupling strength.