Introduction

Spin transfer torque (STT)-based magnetoresistive random access memory (MRAM) is emerging as a promising memory technology for the next generation due to its scalability, high operation speed and unlimited endurance [1–16]. However, the challenge with STT-MRAM is that the current required for switching is relatively large (107–108 A/cm2) and hence relatively large transistors are required to drive them and power consumption is also high, thus limiting the information storage density in this technology. Cobalt-based Heusler compounds are reported to have the advantage of low mismatch of lattice constant, high spin polarization factor and high tunneling magneto resistance (TMR) ratio. [17, 18]. In 1903, Heusler reported that Cu–Mn alloy can be turned into a ferromagnetic material by the addition of a sp element e.g., Al, In, Sn, Sb or Bi even though there is no ferromagnetic element in the alloy. The reason for the ferromagnetism in these alloys is the double-exchange mechanism between neighboring magnetic ions. They are characterized by rich electronic and magnetic properties such as shape memory and half metallic behavior [19]. They are interesting candidates for spintronic devices due to their large magnetization, high magnetic critical temperatures and half metallicity. It has been shown that for critical current required for switching in MTJs J c can be reduced by employing materials with values of M s and α lesser than that of CoFeB MTJs in free layers. In this work, we use Co2MnSi (CMS) and Co2FeAl0.4Si0.6 (CFAS) as the material in the free layer for the MTJ stack used in [20] with perpendicular anisotropy. Both these Heusler alloys have low M s and α values and hence are expected to show faster switching. We show significant reduction in switching time for the same switching current densities. We also compare the TMRs of the structures using most general model proposed by Julliere.

Micromagnetic model

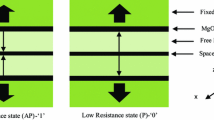
For the Heusler alloy-based MTJs, we expect significant reduction in the switching current density due to lower saturation magnetization (M s) values, smaller Gilbert damping constant (α) and higher spin polarization factor (P). We have used micromagnetic simulation tool OOMMF for detailed analysis of switching dynamics. Material parameters for different alloys used are provided in Table 1 [21, 22]. We have used a perpendicular DBSAF-AP MTJ stack as used in earlier works [20] for simulations and varied parameters accordingly for the different alloys used. The stack consists of two (antiparallel) fixed layers on the top. Below the fixed layers are (two for the two fixed layers) MgO tunnel barrier layers and below the MgO tunnel barriers are (two) synthetic antiferromagnetic free layers separated by Ruthenium.

Table 1 Material parameters for different alloys used in micromagnetic simulation
Full size table

OOMMF uses a time evolver that integrates a Landau–Lifshitz–Gilbert ODE with a spin momentum term. For simplicity we have neglected perpendicular spin torque terms in our calculations.

$$\frac{{{\text{d}}m}}{{{\text{d}}t}} = - \gamma_{0} \; \times \;m\; \times \;H_{\text{eff}} \; + \;\alpha \; \times \;m\; \times \;\frac{{{\text{d}}m}}{{{\text{d}}t}} + T_{\text{STT}}$$
(1)

where m is reduced magnetization M/M s, \(\alpha\) is damping constant, γ 0 is Gilbert gyromagnetic ratio, \(H_{\text{eff}} \; = \;H_{\text{ext}} \; + \; \, H_{\text{exchange}} \; + \; \, H_{\text{demag}} \; + \; \, H_{\text{dip}} \; + \; \, H_{\text{anisotropy}} ,\beta \; = \;|\frac{\hbar }{\mu e}|\frac{\text{J}}{{d_{f} \; \times \;M_{\text{s}} }}\). Here, H eff is the effective field which includes contributions due to external applied magnetic field H ext which is zero in this case, the exchange field H exchange, the dipolar field due to fixed layers H dip, the demagnetization field H demag and the anisotropy induced field H anisotropy. The Eq. (1) has three torque terms on the right hand side. First term is the torque on free layer due to sum total of all magnetic fields, the second term is the damping torque which acts as a friction force impeding the motion and is proportional to the velocity of the motion while the third term is the torque produced due to spin polarized current and is given by \(T_{\text{STT}} = \left| \gamma \right|\beta \varepsilon \left( {m \times m_{p} \times m} \right)\) in which ε is the effective spin polarization efficiency factor and is given by \(\varepsilon = \frac{{P \wedge^{2} }}{{( \wedge^{2} + 1) + ( \wedge^{2} - 1)(m.m_{\text{p}} )}}\). Here, P is the spin polarization, J is the current charge density and m p is the unit polarization direction of spin polarized current and d f is the thickness of the free layer. As we can see that T STT is inversely proportional to saturation magnetization (M s) and directly proportional to spin polarization factor (P). So lesser switching time is expected from Heusler alloy-based MTJs for the same switching current applied. Also for a macrospin model at zero temperature the critical current density which is required to reverse the magnetization in a MTJ can be expressed as :

$$J_{\text{c}} = \frac{{2e \times \alpha \times M_{\text{s}} \times d_{\text{f}} \times (H_{\text{ext}} + H_{\text{anisotropy}} + 2\pi M_{\text{s}} )}}{\hbar P}$$
(2)

From Eq. (2) it can be easily noticed that to reduce the critical current density a material which has lower value of M s, and α and higher P values should be preferred. Reducing thickness of free layer can also reduce the J c but after a certain thickness the thermal stability of STTRAM bit gets compromised. For a stable bit, an energy barrier of about 60 k B T (k B is Boltzmann’s constant and T is temperature in Kelvins) is required for 10 years retention. In this work, we have concentrated on the current densities and confirmed our assumptions using simulations. We have also calculated and compared the stability constants for the same free layer thickness for all three materials and showed its dependence on free layer volume.

Switching dynamics

Switching magnetization in the MTJ structure under study proceeds as follows. We inject perpendicularly polarized current in the top free layer (TFL). Initially the magnetization of the TFL is in the same direction (+z) as the spin polarization of the electrons injected. Up-spin electrons conduct thorough the metallic Ru layer and are injected in the bottom free layer (BFL). Initial magnetization of the BFL is in −z direction due to RKKY coupling. The up-spin electrons injected exert torque on the BFL, also there are reflected up-spin electrons from the bottom pinned layer (BPL) which has its magnetization pinned in the −z direction. If the current density is large enough the torque on the BFL is enough to flip the magnetization of the BFL in the +z direction and enters in a metastable state where both the free layers have magnetization in the same direction +z in this case. If we stop the current at this stage then magnetization of TFL switches in −z direction by itself to reach in another stable state (AP). The time taken to switch from P to metastable state is t r and the time taken to switch from metastable state to AP is t f. However, the switching from metastable state to stable AP states is too slow (t f > > t r) as compared to switching from P to metastable state so to assist switching from metastable state to AP state we reverse the direction of the current after the metastable state is reached. If the bi-directional MTJ stack is exposed to negative polarity current while switching from metastable state to stable state for a period longer than the switching time, then the BFL eventually switches again to −z direction leading to another metastable state. This leads to an unintentional switching event and a write failure. To avoid this, a timing margin is necessary. A design to significantly reduce this failure has been proposed. [20] For switching from AP to P current is injected from the opposite direction and hence the electrons injected this time have spin in −z direction and they exert torque on the BFL to flip its magnetization in −z direction leading to another metastable state in which both the free layers have their magnetization in −z direction and then again we reverse the direction of current at metastable state to switch back to P state.

Micromagnetic simulation results and discussion

For comparing the switching dynamics two cobalt-based Heusler alloys are selected which have values of M s and α less than that of cobalt and high spin polarization factor P. Co2MnSi (CMS) and Co2Fe0.4Al0.6 (CFAS) are chosen as the ferromagnetic material to design coupled free layers. We simulate the given device by applying current pulses of amplitudes ranging from 1 × 107 to 5 × 107 A/cm2 in steps of 1 × 107 A/cm2 to study the effect of STT and compare the dynamics of different materials. The dimensions of the free layers in device used are 40 × 20 × 2 nm3. The cell size chosen for simulation is 1 × 1 × 0.1 nm3. Figure 1 shows the magnetization switching from P to AP state for the Cobalt-based MTJ for current density of 2 × 108 A/cm2. At the beginning device is in P state and since both the free layers have magnetizations in opposite direction the overall reduced magnetization m is equal to zero and when a spin polarized current is applied the device reaches the metastable state and at this stage m becomes equal to 1. Then the polarity is reversed to reach stable AP configuration and m again reduces to zero. However, as discussed earlier if the current is not stopped after the AP state the device goes into another metastable state as shown in the Fig. 1 and the overall reduced magnetization becomes equal to −1. Figure 2 compares the switching dynamics of the three materials used to design free layers at the same current density of 2 × 108 A/cm2. As expected the material with lowest value of M s and α (CMS) shows the fastest switching and the material with highest value of M s and α shows slowest switching. To show the comparison more precisely, we have studied the switching of all the three devices by varying the current density and plotting the switching time versus current density for all of them.

Fig. 1
figure 1

Magnetization versus time plot to understand the switching dynamics

Full size image
Fig. 2
figure 2

Plot to compare the switching dynamics of different materials used for J = 2 × 108 A/cm2

Full size image

As can be observed from Fig. 3 for the same current density applied switching time for CMS is lowest while it is highest for Cobalt. We expected similar results from theoretical analysis since the spin transfer torque is inversely proportional to M 2s and directly proportional to P and we can see from the Table 1 that the CMS has the lowest value of M s.

Fig. 3
figure 3

Switching time versus current density plot to compare the switching speed in Cobalt, CMS and CFAS

Full size image

Stability analysis was done for the three materials used by comparing the energy difference (∆E) between two states P and AP. As mentioned earlier for 10-year data retention an energy difference of about 60 k B T is required (Fig. 4) [23]. Thermal stability of STTRAM bit often sets trade-off between maximum storage density and data retention requirement. We have shown in Fig. 5 that ∆E decreases on decreasing the density of free layer by decreasing its thickness. To show the dependence of ∆E on the volume of the free layer we have compared ∆E for the thickness values of 1 and 2 nm and found that for 1 nm ∆E < k B T for T = 300 K while ∆E for 2 nm thick free layer is almost 100 times k B T and hence satisfies the requirement for data retention. In Figs. 5 the plots show variation of total energy with time while the switching takes place. The two minima, first one at t = 0 s and the second one after the maxima, correspond to stable P and AP states, respectively. We have also compared the ∆E values for Cobalt, CMS and CFAS free layers having thickness 2 nm and observed that ∆E is maximum for CFAS and minimum for CMS free layer. The following observation can be explained using Eq. (3).

Fig. 4
figure 4

Plot to compare stability by comparing ∆E of different materials used

Full size image
Fig. 5
figure 5

Plot to study the dependence of ∆E on free layer thickness

Full size image
$$\Delta E = \frac{{\mu \; \times \;M_{\text{s}} \; \times \;V\; \times \;H_{k} }}{2}$$
(3)

where H k is the effective magnetic anisotropy field, \(\mu\) is the permeability of free space, V is the volume of the free layer. Effective anisotropy field is directly proportional to uniaxial anisotropic constant K1. So the energy difference ∆E depends on the product of saturation magnetization M s and K1. We can observe from the parameters given in Table 1 that the product has the maximum value for CFAS and minimum value for CMS, so CFAS should have the maximum ∆E for fixed volume of free layer and it is confirmed from the simulation results obtained. Though the switching is fastest in CMS-based MTJ due to lowest M s and high P, CFAS-based MTJ shows the highest stability due to high value of anisotropic constant K1. For a better comparison between the two current density and stability constants (∆E/k B T) curve can be plotted and one which has lower current density at same stability constant should be preferred.

TMR calculations

Resistance of a MTJ depends on the angle between the magnetization directions of the free layer and the pinned layer since in the transport between the majority and minority spin states the tunneling which occurs depends on the spin. In the tunneling process, the electrons maintain their spin direction and the probability that an electron with a certain spin will tunnel through the barrier from the pinned layer to free layer depends on the number of states with the same spin direction available in free layer. So the probability of tunneling is not equal for both parallel and antiparallel states since they correspond to different density of state. Tunnel magnetoresistance (TMR) is defined as:

$$\frac{\Delta R}{R} = \frac{{R_{\text{AP}} - R_{\text{P}} }}{{R_{\text{P}} }}$$
(4)

where R P and R AP are the resistance for parallel (P) and antiparallel (AP) magnetic configurations, respectively. In this study, we calculate the TMR of a simple MTJ structure with in-plane anisotropy. There are only two ferromagnetic layers with a tunneling barrier between them. One of the ferromagnetic layers has its magnetization fixed and is called reference layer or pinned layer while the magnetization of other layer is not fixed and is free to rotate. We have used the simplest model proposed by Julliere to calculate the TMR of the materials used and compared them. Though we compared TMRs for a simple MTJ stack using a simple model we expect similar results will hold in case of multilayered MTJ stack such as DBSAF MTJ stack used for studying dynamics.

In the Julliere model to explain the TMR [24], it depends only on the spin polarization of the ferromagnetic material used in pinned and free layers and is given by,

$$\frac{\Delta R}{R} = \frac{{2P_{1} P_{2} }}{{1 - P_{1} P_{2} }}$$
(5)

where P 1 and P 2 are spin polarization of pinned and free layer, respectively. In this case, same ferromagnetic material is used in both pinned and free layers so P 1 is equal to P 2. TMR values are calculated for CoFeB-, CMS- and CFAS-based MTJs and are given in Table 2. As it can be observed from the table a higher P value means a higher TMR so we can conclude Heusler alloy-based MTJs are expected to show higher TMR values than the Co-based MTJs. These results for TMR are for making a comparison and based on the simplest model for calculation and so are not highly accurate. A high TMR is essential for high readability of MTJs, and hence from this observation, Heusler alloys are much better option to use as the ferromagnetic material in MTJs. It has also been reported that CMS produces high TMR values at low temperatures and its TMR value decreases with increasing temperature while CFAS is reported to have high TMR values for all temperature and is weakly dependent on temperature [25].

Table 2 TMR values for Cobalt, CMS and CFAS-based in-plane MTJs
Full size table

Conclusion

We performed detailed micromagnetic simulations to study the advantages and disadvantages of Heusler alloy-based perpendicular double barrier synthetic antiferromagnetic magnetic tunnel junctions. Their low saturation magnetization (M s) values and high spin polarization (P) lead to faster switching as compared to Cobalt-based MTJs. However, due to low M s thermal stability of the bit is compromised. In this study, we used CMS and CFAS Heusler alloys as the material to fabricate free layers and compared them with Cobalt-based free layers. Switching in CMS is fastest among the three while its thermal stability is lowest for the same free layer thickness. Switching of CFAS free layer is faster than Cobalt but is slow when compared to CMS free layer while its thermal stability is highest due to high value of crystalline anisotropy constant K1. We also compare TMR of in-plane simple MTJ based on Jullier model for all the three materials and observe that the TMR of CFAS MTJ is highest.