Unsteady mixed convection flow of nanofluid on a rotating cone with magnetic field

Abstract

In this article, we have presented the unsteady flow of a rotating nanofluid in a rotating cone in the presence of magnetic field. The highly nonlinear coupled partial differential equations are simplified with the help of suitable similarity transformations. The reduced nonlinear coupled equations are solved analytically with the help of homotopy analysis method. The physical features of the parameters of interest are discussed by plotting graphs and through tables.

Introduction

The study of flow over cone-shaped bodies is often encountered in many engineering applications. Only limited attentions have been focused to this kind of study. Mixed convection flow is another important subject which has fascinated the attention of several researchers due to its fundamental applications. Solar central receivers exposed to wind currents, electronic devices cooled by fans, nuclear reactors cooled during emergency shutdown, heat exchangers placed in a low velocity environment are some of the applications of mixed convection flow. The study of convective heat transfer in a rotating flows over a rotating cone is also very important phenomena for the thermal design of various types of equipment’s such as rotating heat exchanger, spin stabilized missiles, containers of nuclear waste disposal and geothermal reservoirs (Tien 1960; Lin and Lin 1987). Initially, Heiring and Grosh (1963) studied the steady mixed convection from a vertical cone for Pr = 0.7. They applied similarity transformation which shows that Buoyancy parameter is the dominant dimensionless parameter that would set the three regions, specifically forced, free and mixed convection. Further, Himasekhar et al. (1989) presented the similarity solution of the mixed convection flow over a vertical rotating cone in a fluid for a wide range of Prandtl numbers. Anilkumar and Roy (2004) have investigated the self-similar solutions of an unsteady mixed convection flow over a rotating cone in a rotating viscous fluid. They found that similar solutions are only possible when angular velocity is inversely proportional to time. Boundary layer on a rotating cones, disks and axisymmetric surfaces with a concentrated heat surface has been given by Wang and Kleinstreur (1990). Non-similar solutions to the heat transfer in unsteady mixed convection flows from a vertical cone is presented by Ishak et al. (2010).

The study of magnetohydrodynamic flows in the presence of heat transfer in the form of either mixed convection or natural convection is important in number of technological and industrial applications (Aldoss 1996; bararnia et al. 2009). Such applications include the production of steel, aluminium, high performance super alloys or crystals. In crystal growth, the magnetic fields are used to suppress the convective motion induced by the arising strong fluxes to control the flow in the melt and consequently the crystal quality. Recently, Kakarantzas (2009) have examined the magnetohydrodynamic natural convection in a vertical cylinder cavity with sinusoidal upper wall temperature.

Recently nanofluids have attracted great interest because of reports of greatly enhanced thermal properties. These fluids are solid–liquid composite materials made of solid nanoparticles or nanofibers with a size of 1–100 nm suspended in liquid. Buongiorno (2006) and Kakaç and Pramuanjaroenkij (2009) have investigated a comprehensive survey of convective transporting nanofluids. Khan and Pop (2010) analyzed the development of the steady boundary layer flow, heat transfer and nanoparticle fraction over a stretching surface in a nanofluid. More recently, various problems about nanofluids are investigated by other researchers (Buongiorno 2006; Makinde and Aziz 2011; Hojjat et al. 2010; Bachok et al. 2010; Kakaç and Pramuanjaroenkij 2009; Khan and Pop 2010; Nadeem and Lee 2012; Nadeem and Haq 2012; Duangthongsuk and Wongwises 2007, 2008; Hojjat et al. 2010).

The objective of the present paper was to analyze the development in the unsteady mixed convection MHD rotating nanofluid flow on a rotating cone. The viscous flow equations for unsteady flow are presented along with heat and mass transfer analysis. The governing highly nonlinear coupled partial differential equations are first transformed to coupled ordinary differential equations using the similarity transformations and then solved analytically with the help of homotopy analysis method (Liao 2003, 2004, 2005, 2009; Liao and Cheung 2003; Abbasbandy 2006, 2008; Abbasbandy and Samadian 2008; Ellahi and Riaz 2010; Ellahi and Afzal 2009; Nadeem et al. 2010; Nadeem and Hussain 2009; Nadeem and Saleem 2013). The influences of different physical parameters are also presented and discussed graphically. Finally, our analytical and previous numerical results are in excellent agreement.

Mathematical formulation

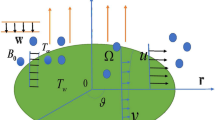
We have considered an unsteady axisymmetric incompressible flow of nanofluid over a rotating cone in a rotating fluid in the presence of MHD. We have taken the rectangular curvilinear fixed coordinate system. Let u, v and w be the velocity components along x (tangential), y (circumferential or azimuthal) and z (normal) directions, respectively. Both the fluid and the cone are in a rigid body rotation about the axis of cone with time-dependent angular velocity Ω either in some or reverse directions, due to which unsteadiness produces in the fluid flow. A constant magnetic field is applied in the normal direction, i.e., in the z direction. The induced magnetic field is considered to be negligible because of small magnetic Reynolds number. Further there is no electric field. The wall temperature T_w and wall concentration C_w are constant functions. Geometry of the problem is shown in Fig. 1.

Fig. 1

Geometry of the problem

The boundary layer equations of motion, temperature and concentration in the presence of nanoparticles are

$$ \frac{\partial u}{\partial x} + \frac{u}{x} + \frac{\partial w}{\partial z} = 0, $$

(1)

$$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + w\frac{\partial u}{\partial z} - \frac{{v^{2} }}{x} = - \frac{{v_{e}^{2} }}{x} + \nu \frac{{\partial^{2} u}}{{\partial z^{2} }} + g\beta \cos \alpha^{ * } (T - T_{\infty } ) + g\beta^{ * } \cos \alpha^{ * } (C - C_{\infty } ) - \frac{\sigma }{\rho }B^{2} u, $$

(2)

$$ \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + w\frac{\partial v}{\partial z} + \frac{uv}{x} = \frac{{\partial v_{e} }}{\partial t} + \nu \frac{{\partial^{2} v}}{{\partial z^{2} }} - \frac{\sigma }{\rho }B^{2} (v - v_{e} ), $$

(3)

$$ (\rho c)_{\text{f}} \left( {\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + w\frac{\partial T}{\partial z}} \right) = \kappa \frac{{\partial^{2} T}}{{\partial z^{2} }} + (\rho c)_{\text{p}} \left[ {D_{\text{B}} \frac{\partial C}{\partial z}\frac{\partial T}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right], $$

(4)

$$ \frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + w\frac{\partial C}{\partial z} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }}, $$

(5)

where Eq. (1) is the continuity equation, Eqs. (2) and (3) are the momentum equations, and Eqs. (4) and (5) are the temperature and nanoparticle concentration equations. In the above equations, k is the thermal diffusivity, $\alpha^{ * }$ is the semi-vertical angle of the cone, ν is the kinematic viscosity, ρ is the density, β and $\beta^{ * }$are the volumetric coefficient of expansion for temperature and concentration, respectively, C_∞ and T_∞ are the free-stream concentration and temperature, respectively, (ρc)_p is the nanoparticle heat capacity, (ρc)_f is the base fluid heat capacity, D_B is the Brownian diffusion coefficient, D_T is the thermophoretic diffusion coefficient. Applying the similarity transformations and non-dimensional variables given in Anilkumar and Roy (2004), Eqs. (1)–(5) with the boundary conditions for prescribed wall temperature (PWT) case can be expressed as

$$ f^{\prime \prime \prime } - ff^{\prime \prime } + \frac{1}{2}f^{\prime 2} - 2(g^{2} - (1 - \alpha_{1} )^{2} ) - 2\lambda_{1} (\theta + N\phi ) - s\left( {f^{\prime } + \frac{1}{2}\eta f^{\prime \prime } } \right) - Mf^{\prime } = 0, $$

(6)

$$ g^{\prime \prime } - (fg^{\prime } - gf^{\prime } ) + s\left( {1 - \alpha_{1} - g - \frac{1}{2}\eta g^{\prime } } \right) - M(g - 1 + \alpha_{1} ) = 0, $$

(7)

$$ \frac{1}{\Pr }\theta^{\prime \prime } - \left( {f\theta^{\prime } - f^{\prime } \frac{\theta }{2}} \right) - s(2\theta + 2^{ - 1} \eta \theta^{\prime } ) + Nb\phi^{\prime } \theta^{\prime } + Nt\theta^{\prime 2} = 0, $$

(8)

$$ \phi^{\prime \prime } - {\text{Le}}\left\{ {\left( {f\varphi^{\prime } - f^{\prime } \frac{\phi }{2}} \right) - s(2\phi + 2^{ - 1} \eta \phi^{\prime } )} \right\} + \frac{\text{Nt}}{\text{Nb}}\theta^{\prime \prime } = 0. $$

(9)

$$ \begin{aligned} f(\eta ) & = 0 = f^{\prime } (\eta ), \, g(\eta ) = \alpha_{1} , \, \theta (\eta ) = \phi (\eta ) = 1,\quad {\text{when }}\eta = 0 \\ f^{\prime } (\eta ) & = 0 \, ,g(\eta ) = 1 - \alpha_{1} , \, \theta (\eta ) = \phi (\eta ) = 0,\quad {\text{as}}\quad \eta \to \infty . \\ \end{aligned} $$

(10)

For prescribed heat flux (PHF) case, Eqs. (1)–(5) with the boundary conditions are stated as

$$ F^{\prime \prime \prime } - FF^{\prime \prime } + 2^{ - 1} F^{\prime 2} - 2(G^{2} - (1 - \alpha_{1} )^{2} ) - 2\lambda_{1}^{*} (\Uptheta + N^{*} \Upphi ) - s(F^{\prime } + 2^{ - 1} \eta F^{\prime \prime } ) - MF^{\prime } = 0, $$

(11)

$$ G^{\prime \prime } - (FG^{\prime } - GF^{\prime } ) + S(1 - \alpha_{1} - G - 2^{ - 1} \eta G^{\prime } ) - M(G - 1 + \alpha_{1} ) = 0, $$

(12)

$$ \frac{1}{\Pr }\Uptheta^{\prime \prime } - \left( {F\Uptheta^{\prime } - F^{\prime } \frac{\Uptheta }{2}} \right) - s\left( {2\Uptheta + 2^{ - 1} \eta \Uptheta^{\prime } } \right) + {\text{Nb}}\Upphi^{\prime } \Uptheta^{\prime } + {\text{Nt}}\Uptheta^{\prime 2} = 0, $$

(13)

$$ \Upphi^{\prime \prime } - Le\left\{ {\left( {F\Upphi^{\prime } - F^{\prime } \frac{\Upphi }{2}} \right) - s(2\Upphi + 2^{ - 1} \eta \Upphi^{\prime } )} \right\} + \frac{Nt}{Nb}\Uptheta^{\prime \prime } = 0. $$

(14)

$$ \begin{aligned} F(\eta ) & = 0 = F^{\prime } (\eta ),G(\eta ) = \alpha_{1} ,\Uptheta^{\prime } (\eta ) = \Upphi^{\prime } (\eta ) = - 1,\quad {\text{when}}\quad \eta = 0 \\ F^{\prime } (\eta ) & = 0,G(\eta ) = 1 - \alpha_{1} ,\Uptheta (\eta ) = \Upphi (\eta ) = 0,\quad {\text{as}}\quad \eta \to \infty \\ \end{aligned} $$

(15)

where

$$ \begin{gathered} v_{e} = \Upomega_{2} x\sin \alpha^{ * } (1 - st^{ * } )^{ - 1} ,\eta = \left( {\frac{{\Upomega \sin \alpha^{ * } }}{v}} \right)^{{\tfrac{1}{2}}} (1 - st^{ * } )^{{ - \tfrac{1}{2}}} z, \hfill \\ t^{ * } = (\Upomega \sin \alpha^{ * } )t,u(t,x,z) = - 2^{ - 1} \Upomega x\sin \alpha^{ * } (1 - st^{ * } )^{ - 1} f^{\prime } (\eta ), \hfill \\ v(t,x,z) = \Upomega x\sin \alpha^{ * } (1 - st^{ * } )^{ - 1} g(\eta ),w(t,x,z) = (v\Upomega \sin \alpha^{ * } )^{{\tfrac{1}{2}}} (1 - st^{ * } )^{{ - \tfrac{1}{2}}} f(\eta ), \hfill \\ T(t,x,z) - T_{\infty } = (T_{\text{w}} - T_{\infty } )\theta (\eta ),T_{\text{w}} - T_{\infty } = (T_{0} - T_{\infty } )\left( \frac{x}{L} \right)(1 - st^{ * } )^{ - 2} , \hfill \\ C(t,x,z) - C_{\infty } = (C_{\text{w}} - C_{\infty } )\varphi (\eta ),(C_{\text{w}} - C_{\infty } ) = (C_{0} - C_{\infty } )\left( \frac{x}{L} \right)(1 - st^{ * } )^{ - 2} , \hfill \\ {\text{Gr}}_{1} = g\beta \cos \alpha^{ * } (T_{0} - T_{\infty } )\frac{{L^{3} }}{{v^{2} }},{\text{Re}}_{L} = \Upomega \sin \alpha^{ * } \frac{{L^{2} }}{v},\lambda_{1} = \frac{{{\text{Gr}}_{1} }}{{{\text{Re}}_{L}^{2} }} \hfill \\ Gr_{2} = g\beta^{*} \cos \alpha^{ * } (C_{0} - C_{\infty } )\frac{{L^{3} }}{{v^{2} }},\lambda_{2} = \frac{{{\text{Gr}}_{2} }}{{{\text{Re}}_{L}^{2} }},N = \frac{{ \, \lambda_{2} }}{{ \, \lambda_{1} }} \hfill \\ \alpha_{1} = \frac{{\Upomega_{1} }}{\Upomega },\Pr = \frac{v}{\alpha },M = \frac{{\sigma B_{0}^{2} }}{\rho }(\Upomega \sin \alpha^{ * } )^{ - 1} (1 - st^{ * } ),N^{*} = \frac{{ \, \lambda^{*}_{2} }}{{ \, \lambda^{*}_{1} }},\lambda_{1}^{*} = \frac{{{\text{Gr}}_{1}^{*} }}{{\text{Re}_{L}^{2} }} \hfill \\ \lambda_{2}^{*} = \frac{{{\text{Gr}}_{2}^{*} }}{{{\text{Re}}_{L}^{2} }},{\text{Gr}}_{1}^{*} = g\beta^{*} \cos \alpha^{ * } (q_{0} )\frac{{L^{4} }}{{\kappa v^{2} }},{\text{Gr}}_{2}^{*} = g\beta^{*} \cos \alpha^{ * } \left( {\mathop {m_{0} }\limits^{.} } \right)\frac{{L^{4} }}{{\rho Dv^{2} }} \hfill \\ {\text{Nb}} = \frac{{(\rho c)_{\text{p}} D_{\text{B}} (C_{\text{w}} - C_{\infty } )}}{{\nu (\rho c)_{\text{f}} }},{\text{Nt}} = \frac{{(\rho c)_{\text{p}} D_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\nu (\rho c)_{\text{f}} T_{\infty } }},{\text{ Le}} = \frac{\nu }{{D_{\text{B}} }}. \hfill \\ \end{gathered} $$

Here α₁ is the ratio of angular velocity of the cone to the composite angular velocity, λ₁ and $\lambda_{1}^{*}$ are the buoyancy force parameter for PWT and PHF cases, respectively, Nand N^* are the ratio of the Grashof numbers for PWT and PHF cases, respectively. It is zero for chemical diffusion, infinite for the thermal diffusion, positive when the buoyancy forces due to temperature and concentration difference act in the same direction and vice versa. s is the unsteady parameter. The flow is accelerating if s > 0 provided st^* < 1 and the flow is retarding, if s < 0. Further α₁ = 0 shows that the fluid is rotating and the cone is at rest, moreover, the fluid and the cone are rotating with equal angular velocity in the same direction for α₁ = 0.5, and for α₁ = 1, only the cone is in rotation. Nb, Nt, M and Le denote the Brownian motion parameter, thermophoresis parameter, non-dimensional magnetic parameter and Lewis number, respectively.

The physical quantities of interest in this problem are the local skin-friction coefficients, Nusselt number and the local Sherwood number, which are defined for the PWT case as

$$ C_{fx} = \frac{{\left[ {2\mu \left( {\frac{\partial u}{\partial z}} \right)} \right]_{z = 0} }}{{\rho \left[ {\Upomega x\sin \alpha^{ * } (1 - st^{ * } )^{ - 1} } \right]^{2} }} = - Re_{x}^{ - 1/2} f^{\prime \prime } (0), $$

$$ C_{fy} = - \frac{{\left[ {2\mu \left( {\frac{\partial v}{\partial z}} \right)} \right]_{z = 0} }}{{\rho \left[ {\Upomega x\sin \alpha^{ * } (1 - st^{ * } )^{ - 1} } \right]^{2} }} = - Re_{x}^{ - 1/2} g^{\prime } (0), $$

or

$$ \begin{aligned} C_{fx} Re_{x}^{1/2} & = - f^{\prime \prime } (0), \\ C_{fy} Re_{x}^{1/2} & = - g^{\prime } (0), \\ \end{aligned} $$

(16)

$$ \begin{aligned} {\text{Nu}}\,Re_{x}^{ - 1/2} & = - \theta^{\prime } (0), \\ {\text{Sh}}\,Re_{x}^{ - 1/2} & = - \varphi^{\prime } (0). \\ \end{aligned} $$

(17)

Solution of the problem

The highly nonlinear coupled ordinary differential equations for PWT case will be solved analytically by homotopy analysis method (HAM). According to HAM procedure, we express f(η), g(η), θ(η) and ϕ(η) by a set of base functions

$$ \left\{ {\eta^{k} \exp ( - n\eta )\left| {k \ge 0,n \ge 0} \right.} \right\}, $$

(18)

in the form

$$ f(\eta ) = a_{0,0}^{0} + \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {a_{m,n}^{k} \eta^{k} \exp ( - n\eta )} } , $$

(19)

$$ g(\eta ) = b_{0,0}^{0} + \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {b_{m,n}^{k} \eta^{k} \exp ( - n\eta )} } , $$

(20)

$$ \theta (\eta ) = \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {c_{m,n}^{k} \eta^{k} \exp ( - n\eta )} } , $$

(21)

$$ \phi (\eta ) = \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 0}^{\infty } {d_{m,n}^{k} \eta^{k} \exp ( - n\eta )} } , $$

(22)

in which $a_{m,n}^{k} ,b_{m,n}^{k} ,c_{m,n}^{k} ,d_{m,n}^{k}$ are the coefficients. Based on the rule of solution expressions and the boundary conditions, one can choose the initial guesses f₀, g₀, θ₀, and ϕ₀ as follows:

$$ f_{0} (\eta ) = 0, $$

(23)

$$ g_{0} (\eta ) = (1 - \alpha_{1} ) + (2\alpha_{1} - 1)\exp ( - \eta ), $$

(24)

$$ \theta_{0} (\eta ) = \exp ( - \eta ), $$

(25)

$$ \phi_{0} (\eta ) = \exp ( - \eta ). $$

(26)

The auxiliary linear operators are

$$ \pounds_{f} = \frac{{{\text{d}}^{3} f}}{{{\text{d}}\eta^{3} }} - \frac{{{\text{d}}f}}{{{\text{d}}\eta }}, $$

(27)

$$ \pounds_{g} = \frac{{{\text{d}}^{2} g}}{{{\text{d}}\eta^{2} }} + \frac{{{\text{d}}g}}{{{\text{d}}\eta }}, $$

(28)

$$ \pounds_{\theta } = \frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} - \theta , $$

(29)

$$ \pounds_{\varphi } = \frac{{{\text{d}}^{2} \phi }}{{{\text{d}}\eta^{2} }} - \phi , $$

(30)

which satisfy

$$ \pounds_{f} [C_{1} + C_{2} \exp (\eta ) + C_{3} \exp ( - \eta )] = 0, $$

(31)

$$ \pounds_{g} [C_{4} + C_{5} \exp ( - \eta )] = 0, $$

(32)

$$ \pounds_{\theta } [C_{6} \exp (\eta ) + C_{7} \exp ( - \eta )] = 0, $$

(33)

$$ \pounds_{\phi } [C_{8} \exp (\eta ) + C_{9} \exp ( - \eta )] = 0, $$

(34)

where C _i (i = 1–9) are arbitrary constants.

If $p \in [0,1]$ is an embedding parameter and $\hbar_{f} ,\hbar_{g} ,\hbar_{\theta }$ and $\hbar_{\phi }$ indicate the non-zero auxiliary parameters, respectively, then the zeroth order deformation problems are

$$ (1 - p)\pounds_{f} [\hat{f}(\eta ;p) - \hat{f}_{0} (\eta )] = p\hbar_{f} N_{f} [\hat{f}(\eta ;p),\hat{g}(\eta ;p),\hat{\theta }(\eta ;p),\hat{\phi }(\eta ;p)], $$

(35)

$$ (1 - p)\pounds_{g} [\hat{g}(\eta ;p) - \hat{g}_{0} (\eta )] = p\hbar_{g} N_{g} [\hat{f}(\eta ;p),\hat{g}(\eta ;p)], $$

(36)

$$ (1 - p)\pounds_{\theta } [\hat{\theta }(\eta ;p) - \hat{\theta }_{0} (\eta )] = p\hbar_{\theta } N_{\theta } [\hat{f}(\eta ;p),\hat{\theta }(\eta ;p)], $$

(37)

$$ (1 - p)\pounds_{\varphi } [\hat{\phi }(\eta ;p) - \hat{\phi }_{0} (\eta )] = p\hbar_{\phi } N_{\phi } [\hat{f}(\eta ;p),\hat{\phi }(\eta ;p)], $$

(38)

$$ \hat{f}(0;p) = 0 = \hat{f}^{\prime } (0;p),\quad \hat{g}(0;p) = \alpha_{1} ,\quad \hat{\theta }(0;p) = \hat{\phi }(0;p) = 1, $$

(39)

$$ \hat{f}^{\prime } (\infty ;p) = 0,\quad \hat{g}(\infty ;p) = 1 - \alpha_{1} ,\quad \hat{\theta }(\infty ;p) = \hat{\phi }(\infty ;p) = 0, $$

(40)

in which

$$ \begin{aligned} N_{f} [\hat{f}(\eta ;p),\hat{g}(\eta ;p),\hat{\theta }(\eta ;p),\hat{\phi }(\eta ;p)] & = \frac{{\partial^{3} \hat{f}(\eta ;p)}}{{\partial \eta^{3} }} - \hat{f}(\eta ;p)\frac{{\partial^{2} \hat{f}(\eta ;p)}}{{\partial \eta^{2} }} + \frac{1}{2}\left( {\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta }} \right)^{2} \\ & \quad - M\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta } - 2[(\hat{g}(\eta ;p))^{2} - (1 - \alpha_{1} )^{2} ] \\ & \quad - 2\lambda_{1} (\hat{\theta }(\eta ;p) + N_{1} \hat{\phi }(\eta ;p)) \\ & \quad - s\left( {\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta } + \frac{1}{2}\eta \frac{{\partial^{2} \hat{f}(\eta ;p)}}{{\partial \eta^{2} }}} \right), \\ \end{aligned} $$

(41)

$$ \begin{aligned} N_{g} [\hat{g}(\eta ;p),\hat{f}(\eta ;p)] & = \frac{{\partial^{2} \hat{g}(\eta ;p)}}{{\partial \eta^{2} }} - \left[ {\hat{f}(\eta ;p)\frac{{\partial \hat{g}(\eta ;p)}}{\partial \eta } - \hat{g}(\eta ;p)\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta }} \right] \\ & \quad + s\left( {1 - \alpha_{1} - \hat{g}(\eta ;p) - \frac{1}{2}\eta \frac{{\partial \hat{g}(\eta ;p)}}{\partial \eta }} \right) \\ & \quad - M(\hat{g}(\eta ;p) - 1 + \alpha_{1} )), \\ \end{aligned} $$

(42)

$$ \begin{aligned} N_{\theta } [\hat{\theta }(\eta ;p),\hat{f}(\eta ;p)] & = \frac{1}{\Pr }\frac{{\partial^{2} \hat{\theta }(\eta ;p)}}{{\partial \eta^{2} }} - \left( {\hat{f}(\eta ;p)\frac{{\partial \hat{\theta }(\eta ;p)}}{\partial \eta } - \frac{1}{2}\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta }\hat{\theta }(\eta ;p)} \right) \\ & \quad - s\left( {2\hat{\theta }(\eta ;p) + \frac{1}{2}\eta \frac{{\partial \hat{\theta }(\eta ;p)}}{\partial \eta }} \right) + {\text{Nb}}\frac{{\partial \hat{\phi }(\eta ;p)}}{\partial \eta }\frac{{\partial \hat{\theta }(\eta ;p)}}{\partial \eta } + {\text{Nt}}\left( {\frac{{\partial \hat{\theta }(\eta ;p)}}{\partial \eta }} \right)^{2} , \\ \end{aligned} $$

(43)

$$ \begin{aligned} N_{\varphi } [\hat{\phi }(\eta ;p),\hat{f}(\eta ;p)] & = \frac{{\partial^{2} \hat{\phi }(\eta ;p)}}{{\partial \eta^{2} }} - {\text{Le}}\left\{ {\left( {\hat{f}(\eta ;p)\frac{{\partial \hat{\phi }(\eta ;p)}}{\partial \eta } - \frac{1}{2}\frac{{\partial \hat{f}(\eta ;p)}}{\partial \eta }\hat{\phi }(\eta ;p)} \right) - s\left( {2\hat{\varphi }(\eta ;p) + \frac{1}{2}\eta \frac{{\partial \hat{\varphi }(\eta ;p)}}{\partial \eta }} \right)} \right\} \\ & \quad + \frac{\text{Nt}}{\text{Nb}}\frac{{\partial^{2} \hat{\theta }(\eta ;p)}}{{\partial \eta^{2} }}. \\ \end{aligned} $$

(44)

For p = 0 and p = 1,  we have

$$ \hat{f}(\eta ;0) = f_{0} (\eta ),\quad \, \hat{f}(\eta ;1) = f(\eta ), $$

(45)

$$ \hat{g}(\eta ;0) = g_{0} (\eta ),\quad \hat{g}(\eta ;1) = g(\eta ), $$

(46)

$$ \hat{\theta }(\eta ;0) = \theta_{0} (\eta ),\quad \hat{\theta }(\eta ;1) = \theta (\eta ), $$

(47)

$$ \hat{\phi }(\eta ;0) = \varphi_{0} (\eta ),\quad \hat{\phi }(\eta ;1) = \phi (\eta ). $$

(48)

By Taylor theorem

$$ \hat{f}(\eta ;p) = f_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {f_{m} (\eta )p^{m} } , $$

(49)

$$ \hat{g}(\eta ;p) = g_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {g_{m} (\eta )p^{m} } , $$

(50)

$$ \hat{\theta }(\eta ;p) = \theta_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {\theta_{m} (\eta )p^{m} } , $$

(51)

$$ \hat{\phi }(\eta ;p) = \phi_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {\phi_{m} (\eta )p^{m} } , $$

(52)

$$ \begin{aligned} f_{m} (\eta ) & = \left. {\frac{1}{m!}\frac{{\partial^{m} f(\eta ;p)}}{{\partial \eta^{m} }}} \right|_{p = 0} ,g_{m} (\eta ) = \left. {\frac{1}{m!}\frac{{\partial^{m} g(\eta ;p)}}{{\partial \eta^{m} }}} \right|_{p = 0} , \\ \theta_{m} (\eta ) & = \left. {\frac{1}{m!}\frac{{\partial^{m} \theta (\eta ;p)}}{{\partial \eta^{m} }}} \right|_{p = 0} ,\phi_{m} (\eta ) = \left. {\frac{1}{m!}\frac{{\partial^{m} \phi (\eta ;p)}}{{\partial \eta^{m} }}} \right|_{p = 0} , \\ \end{aligned} $$

(53)

and

$$ f(\eta ) = f_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {f_{m} (\eta )} , $$

(54)

$$ g(\eta ) = g_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {g_{m} (\eta )} , $$

(55)

$$ \theta (\eta ) = \theta_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {\theta_{m} (\eta )} , $$

(56)

$$ \phi (\eta ) = \phi_{0} (\eta ) + \sum\limits_{m = 1}^{\infty } {\phi_{m} (\eta )} . $$

(57)

The mth-order deformation problems are defined as

$$ \pounds_{f} [f_{m} (\eta ) - \chi_{m} f_{m - 1} (\eta )] = \hbar_{f} R_{m}^{f} (\eta ), $$

(58)

$$ \pounds_{g} [g_{m} (\eta ) - \chi_{m} g_{m - 1} (\eta )] = \hbar_{g} R_{m}^{g} (\eta ), $$

(59)

$$ \pounds_{\theta } [\theta_{m} (\eta ) - \chi_{m} \theta_{m - 1} (\eta )] = \hbar_{\theta } R_{m}^{\theta } (\eta ), $$

(60)

$$ \pounds_{\phi } [\phi_{m} (\eta ) - \chi_{m} \phi_{m - 1} (\eta )] = \hbar_{\phi } R_{m}^{\phi } (\eta ), $$

(61)

$$ f_{m} (0) = f_{m}^{\prime } (0) = g_{m} (0) = \theta_{m} (0) = \varphi_{m} (0) = 0, $$

(62)

$$ f_{m}^{\prime } (\infty ) = g_{m} (\infty ) = \theta_{m} (\infty ) = \varphi_{m} (\infty ) = 0, $$

(63)

where

$$ \begin{aligned} R_{m}^{f} (\eta ) & = f_{m - 1}^{\prime \prime \prime } - \sum\limits_{k = 0}^{m - 1} {f_{k} f_{m - 1 - k}^{''} } + \frac{1}{2}\sum\limits_{k = 0}^{m - 1} {f_{k}^{\prime } f_{m - 1 - k}^{\prime } } - 2\left[ {\sum\limits_{k = 0}^{m - 1} {g_{k} g_{m - 1 - k} } - (1 - \alpha_{1} )^{2} (1 - \chi_{m} )} \right] \\ & \quad - 2\lambda_{1} (\theta_{m - 1} + N_{1} \phi_{m - 1} ) - s\left( {f_{m - 1}^{\prime } + \frac{1}{2}\eta f_{m - 1}^{\prime \prime \prime } } \right) - Mf_{m - 1}^{\prime } , \\ \end{aligned} $$

(64)

$$ \begin{aligned} R_{m}^{g} (\eta ) & = g_{m - 1}^{\prime \prime } - \sum\limits_{k = 0}^{m - 1} {\left[ {f_{k} g_{m - 1 - k}^{\prime } - g_{k} f_{m - 1 - k}^{\prime } } \right]} + s\left[ {(1 - \alpha_{1} )(1 - \chi_{m} ) - g_{m - 1} - \frac{1}{2}\eta g_{m - 1}^{\prime } } \right] \\ & \quad - M(g_{m - 1} - 1 - \alpha_{1} ) \\ \end{aligned} $$

(65)

$$ \begin{aligned} R_{m}^{\theta } (\eta ) & = \frac{1}{\Pr }\theta_{m - 1}^{\prime \prime } - \sum\limits_{k = 0}^{m - 1} {\left[ {f_{k} \theta_{m - 1 - k}^{\prime } - \frac{1}{2}\theta_{k} f_{m - 1 - k}^{\prime } } \right]} - s\left( {2\theta_{m - 1} + \frac{1}{2}\eta \theta_{m - 1}^{\prime } } \right) + {\text{Nb}}\sum\limits_{k = 0}^{m - 1} {\phi_{k}^{\prime } \theta_{m - 1 - k}^{\prime } } \\ & \quad + {\text{Nt}}\sum\limits_{k = 0}^{m - 1} {\theta_{k}^{\prime } \theta_{m - 1 - k}^{\prime } } , \\ \end{aligned} $$

(66)

$$ R_{m}^{\phi } (\eta ) = \phi_{m - 1}^{\prime \prime } - {\text{Le}}\left\{ {\sum\limits_{k = 0}^{m - 1} {\left[ {f_{k} \phi_{m - 1 - k}^{\prime } - \frac{1}{2}\phi_{k} f_{m - 1 - k}^{\prime } } \right]} - s\left( {2\phi_{m - 1} + \frac{1}{2}\eta \phi_{m - 1}^{\prime } } \right)} \right\} + \frac{\text{Nt}}{\text{Nb}}\theta_{m - 1}^{\prime \prime } , $$

(67)

$$ \chi_{m} = \left\{ {\begin{array}{*{20}c} {0 \, m \le 1,} \\ {1 \, m > 1.} \\ \end{array} } \right. $$

(68)

The general solution of Eqs. (58)–(61) can be written as

$$ f_{m} (\eta ) = f_{m}^{ * } (\eta ) + C_{1} + C_{2} \exp (\eta ) + C_{3} \exp ( - \eta ), $$

(69)

$$ g_{m} (\eta ) = g_{m}^{ * } (\eta ) + C_{4} + C_{5} \exp ( - \eta ), $$

(70)

$$ \theta_{m} (\eta ) = \theta_{m}^{ * } (\eta ) + C_{6} \exp (\eta ) + C_{7} \exp ( - \eta ), $$

(71)

$$ \phi_{m} (\eta ) = \phi_{m}^{ * } (\eta ) + C_{8} \exp (\eta ) + C_{9} \exp ( - \eta ), $$

(72)

where $f_{m}^{ * } (\eta ),g_{m}^{ * } (\eta ),\theta_{m}^{ * } (\eta )$ and $\phi_{m}^{ * } (\eta )$ are the special solutions.

The numerical data of these solutions have been computed and presented through graphs and tables.

Convergence of the homotopy solutions

Analytical solutions to the governing ordinary differential Eqs. (6)–(9) with boundary conditions (10) are obtained using HAM. The series solutions depend on the non-zero auxiliary parameters $\hbar_{f} ,\hbar_{g} ,\hbar_{\theta }$ and $\hbar_{\phi }$ which can adjust and control the convergence of the HAM solutions. The range of admissible values of auxiliary parameters is seen by plotting $\hbar {\text{ - curve}}$ of the functions $f^{\prime \prime } (0),g^{\prime } (0),\theta^{\prime } (0)$ and $\phi^{\prime } (0)$ for 10-order of approximations in Figs. 2 and 3. It is found that the range of permissible values of $\hbar_{f} ,\hbar_{g} ,\hbar_{\theta }$ and $\hbar_{\phi }$ is $- 1.1 \le \hbar_{f} \le - 0.4$, $- 1.1 \le \hbar_{g} \le - 0.5$, $- 1.3 \le \hbar_{\theta } \le - 0.4,$ and $- 1.0 \le \hbar_{\phi } \le - 0.4$. Also, our computation shows that the series solution converges in the whole region of η when $\hbar_{f} = \hbar_{g} = \hbar_{\theta } = \hbar_{\phi } = - 0.8.$

Fig. 2

ℏ-Curve of f″ (0) and g′ (0) at 10th approximation (PWT case)

Fig. 3

ℏ-Curve for θ′(0) and φ′(0) at 10th approximation (PWT case)

The convergence (Table 1) is prepared for each of the function up to 30th order of approximation. It is found that the convergence is achieved up to 15th order of approximation.

Table 1 Convergence of HAM solution for different order of approximations

Results and discussion

The main focus of this section is to observe the effects of emerging parameters on the velocity, temperature and concentration fields for PWT case. The effects of variations are depicted in Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14. The variation of tangential velocity $-f^{\prime }$ for combined effects of α₁ and λ₁ is plotted in Fig. 4. The fluid and the cone are rotating with equal angular velocity in the same direction for α₁ = 0.5. The positive Buoyancy force (i.e., λ₁ = 1), which behaves as favorable pressure gradient, is responsible for the flow. For α₁ > 0.5, the velocity $-f^{\prime }$ increases its magnitude; further the behavior is opposite when α₁ < 0.5. The velocity $- f^{\prime }$ decreases with the increase in M, whereas the boundary layer thickness decreases (see Fig. 5). Thus, we say that magnetic field causes the reduction of boundary layer. In Fig. 6, it is seen that with the increase of α₁, azimuthal velocity g (η) decreases for α₁ > 0.5, but the behavior is opposite for α₁ < 0.5. Figure 7 illustrates that both the velocity and boundary layer thickness increase with the increasing M. The variation of Nb on temperature profile is plotted in Fig. 8. It is clear from the figure that with an increase in Nb, the temperature increases. The effects of Nt on temperature profile are seen in Fig. 9. It is seen that temperature profile increases with the increase in Nt. Figure 10 explains the effects of Pr on temperature profile θ. It is found that thermal boundary layer thickness decreases with the increasing Pr. Temperature profile has a small change with an increase in Le (see Fig. 11). It is depicted from Fig. 12 that concentration profile decreases with the increasing Nb. However, with increase in Nt, concentration profile increases and th layer thickness reduces (see Fig. 13). The behavior of Le on concentration profile is plotted in Fig. 14. It is inferred that concentration profile decreases as Le increase. It is depicted that our series solutions are in good agreement with the numerical results reported by Anilkumar and Roy (2004) in the absence of Nb, Nt and M (see Table 2). The skin-friction coefficients are an increasing function of λ₁, and N. On the other hand, the variation is opposite for M (see Table 3). Table 4 provides the numerical values of Nusselt number $- \theta^{\prime } (0)$ and Sherwood number $- \phi^{\prime } (0)$ for various values of Nb, Nt, Pr and Le, respectively. From Table 4, it is obvious that the Nusselt number $- \theta^{\prime } (0)$ decreases with the increasing Nb, Nt, and Le. However, increases by an increase in Pr. Further we have seen that the Sherwood number $- \phi^{\prime } (0)$ have an increasing behavior with an increase in Nb and Le but decreases with an increase in Nt and Pr. Since the equations for both PWT case and PHF case have almost the same structure, the results for PHF case are ignored.

Fig. 4

Variation of α₁ and λ₁ on −f′ when N = 1, Pr = 0.7, Nb = 0.1, Nt = 0.1, Le = 4, M = 1, s = 0.5

Fig. 5

Variation of M on −f′ when λ₁ = 1, α₁ = 0.6 N = 1, Pr = 0.7, Nb = 0.1, Nt = 0.1, Le = 4, s = 0.5

Fig. 6

Variation of α₁ and λ₁ on g when N = 1,  Pr = 0.7,  Nb = 0.1,  Nt = 0.1,  Le = 4, M = 1, s = 0.5

Fig. 7

Variation of M on g when λ₁ = 1, α₁ = 0.6, N = 1,  Pr = 0.7, Nb = 0.1, Nt = 0.1,  Le = 4, s = 0.5

Fig. 8

Variation of Brownian motion parameter Nb on temperature θ when λ₁ = 1, α₁ = 0.6, N = 1, Pr = 0.7, M = 1, Nt = 0.1, Le = 4, s = 0.5

Fig. 9

Variation of thermophoresis parameter Nt on temperature θ when λ₁ = 1, α₁ = 0.6, N = 1,  Pr = 0.7, Nb = 0.1, M = 1, Le = 4, s = 0.5

Fig. 10

Variation of Prandtl number Pr on temperature θ when λ₁ = 1, α₁ = 0.6, N = 1, M = 1, Nb = 0.1, Nt = 0.1, Le = 4, s = 0.5

Fig. 11

Variation of Lewis number Le on temperature θ when λ₁ = 1, α₁ = 0.6, N = 1,  Pr = 0.7, Nb = 0.1, Nt = 0.1, M = 1, s = 0.5

Fig. 12

Variation of thermophoresis parameter Nb on concentration ϕ when λ₁ = 1, α₁ = 0.6, N = 1, Pr = 0.7, M = 1, Nt = 0.1, Le = 4, s = 0.5

Fig. 13

Variation of thermophoresis parameter Nt on concentration ϕ when λ₁ = 1, α₁ = 0.6, N = 1, Pr = 0.7, Nb = 0.1, M = 1, Le = 4, s = 0.5

Fig. 14

Variation of Lewis number Le on concentration ϕ when λ₁ = 1, α₁ = 0.6, N = 1, Pr = 0.7, Nb = 0.1, Nt = 0.1, M = 1, s = 0.5

Table 2 Comparison of the results [−f″(0), −g′(0), −θ′(0)] with those of Anilkumar and Roy (2004)

Table 3 Values of skin-friction coefficients for different parameters

Table 4 Values of Nusselt number and Sherwood number for different pertinent parameters

Concluding remarks

Unsteady mixed convection flow of a rotating nanofluid over a rotating cone is studied in the presence of magnetic field. The solutions are carried out by a well-known analytical method HAM. The velocity $- f^{\prime } (\eta )$ is an increasing function of α₁. The behavior of M on velocities $( - f^{\prime } (\eta )^{\prime } ,g(\eta ))$ is just opposite. The effect of Pr is to decrease the temperature profile θ. The temperature profile θ increases as Nb, Nt and Le increase. The influence of Nb and Nt are opposite for concentration field ϕ. The concentration field ϕ decreases with the increasing Le. Skin-friction coefficients show an increasing behavior with an increase in the ratio of buoyancy force N. Our present results are in good agreement with the previous results available in Anilkumar and Roy (2004).