Introduction

The main energy inputs in the Brazilian chemical sector are electricity (28%), natural gas and fuel oil (35%). Figure 1 shows the energy consumption in 2014 [16].

Fig. 1
figure 1

Consumption structure in Brazilian chemical industry

Full size image

Electric motor consumes electricity to drive rotating equipments such as pumps and compressors. This equipment is responsible for 60% of the total electricity consumption in petrochemical industries [45].

Purchase contracts of this electricity in Brazil often have fixed minimum and maximum consumption values called take or pay and upper limit. If the minimum contract value is not consumed or the upper limit is crossed, the difference can be sold or purchased on open market.

Brazilian Electric Energy Trading Chamber (CCEE—Camara de Comercialização de Energia Elétrica) regulates the buying market and free energy sales in Brazil. This agency publishes the prices that should be established in energy trading between the Brazilian contracts.

The energy price is called differences settlement price (PLD – Preço de Liquidação de(das) Diferenças) and is weekly variable, based on the regional costs incurred in generating operations, transmission and electricity distribution period [7].

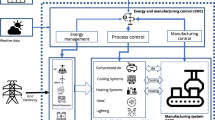
The other two major energy inputs of chemical industry, fuel oil and natural gas are consumed in furnaces and boilers. These equipments account for 70% of fuel consumption [45]. The downstream from the furnaces generate steam at a super high pressure, about 12 MPa [10]. Additional boilers generate steam at a high pressure, typically about 5 MPa. Figure 2 illustrates a typical steam system of an ethylene unit.

Fig. 2
figure 2

Steam system scheme

Full size image

Enterprise-wide optimization

The essence of enterprise-wide optimization (EWO) is to integrate the electricity and fuel supply areas and optimize the decision-making. Using models or simulation software, it is possible to speed up the information processing and analyse the multi criteria parameters for a better decision. It is a tool that can generate energy savings and several petrochemical companies have been using it [18].

However, Bunse et al. [6] state a gap between studies in the area of energy efficiency academically developed and actually applied. Many authors [11, 12, 14, 15, 21, 33] discuss the reasons for this gap. Some of the causes are: decision based on pay back and not by energy impact, limitation of investment capital, low prioritization of these projects by the industries [15], lack of information [39], measurement difficulties after implementation [13].

In addition to all of these issues, studies have identified deficiencies in the energy management system (EMS) as barriers to energy efficiency improvements [36, 40, 43]).

Energy management is defined by Blackstone [3] as a function of planning, organizing and processes controlling providing an efficient utilities service. It can bring benefits to the industry in terms of economy, environment and social issues [8, 24].

In this context, public policy, dollar value, market price value (PLD), contracts and the efficiency of each equipment influence the cost of energy utility sources. With so many influences that range in a short time, as illustrated in Fig. 3, the support tool can be a mixed integer linear programming (MILP). This simplifies the decision-making in these devices with multiple criteria in relation to energy consumption .

Fig. 3
figure 3

Decision-making

Full size image

MILP refers to a mathematical programming with discrete and continuous variables governed by linear equations in objective function and model constraints. It is a tool to assist energy performance in petrochemical business [23].

Papoulias and Grossmann [32] presented MILP for constant process heat and power demand for a site. The following equations show this superstructure-based design approach:

$$ \hbox{min} C = \left( {\alpha_{1} } \right)y + \left( {\alpha_{2} } \right)y_{d} + \left( \beta \right)x_{c} $$
(1)
$$ E_{1} y_{d} + E_{2} x_{c} = e $$
(2)
$$ d_{L} \le D_{1} y + D_{2} y_{d} + D_{3} x_{c} \le d_{U} $$
(3)
$$ x_{c} \ge 0 $$
(4)

where C is the cost function to be optimized, y and y d are binary vectors, x c is the vector of continuous variables; α 1 , α 2 , β, are cost vectors associated with the binary and continuous variables; e, d L , d U and E 1 , E 2 , D 1, D 2, D 3 are vectors and matrices that define the constraints set of the problem, respectively.

EWO presents a duality between robustness and accuracy of the model. According to Omun et al. [31], MILP is favored because it has sufficient flexibility and robustness to handle this duality.

According to Merkert et al. [27], MILP is a technology that can address operational issues related to energy. According to this author, the technique has evolved over the past two decades and today it can solve a wide range of problems based on reduction by a factor of a million in solution time. It can be an important tool in decision-making in rapidly changing market scenarios.

According to Li et al. [26] by applying MILP methodology, it is possible to reduce up to 8% the total operating cost of an ethylene plant in China. Pfenninger et al. [35] describe that the current models need to seek solutions for energy of the twenty-first century systems. Additionally, Hesamzadeh et al. [19] describe the benefits of modeling for a short-term energy management due to high variations of electricity prices in the energy market.

Framework and mathematical model formulation

The framework adopted to obtain the set of the model equations consists of the stages presented in Fig. 4.

Fig. 4
figure 4

Framework stages

Full size image

Stage 1 Setting up the degrees of freedom is the first stage of the framework. All the equipment that have double drive with steam turbines and electric motors should be listed. Generation and distribution steam system, such as boilers, furnaces and steam pressure control valves are the typical degrees of freedom necessary in this stage.

Stage 2 The next stage is the assembling of the model equations to determine the objective function [Eq. (1)], which is given by the individual contribution of each model equation.

Stage 3 At this stage, the physical and operational constraints of the plant were checked to incorporate them as model limitations [Eqs. (2), (3) and (4)]. These limitations are necessary to define boundary conditions and to ensure model consistency and its feasibility.

Stage 4 Implement the equations in software and development of optimization platform. This platform can be developed in Excel® and shall contain all the equations and constraints. A combination of discrete and continuous variables defines this model as MILP.

For modeling and solving this typical system, numerous softwares can be used [28]. In the industrial area, LINDO system application, What’s best, proved to be appropriate and effective, for example, solving mathematical problems in the industrial city water reuse [1] and industrial zone waste heat reuse for combined heat and power generation [41].

For solving, the Branch and bound (BB or B&B) method can be used. It is an algorithm developed for solving discrete, continuous and combined optimization problems. The method was first proposed by Land and Doig [25] for discrete programming and has been improved and applied for MILP models solutions in power supply system optimizations [48], in operational planning of cogeneration plants [17] or even in production of fuel from urban solid waste [30].

Stage 5 The model should be tested. Actual operating data should be used to evaluate if the model suggestions are consistent and applicable.

Worldwide, trend of energy consumption in chemical sector can grow up to 50% by 2030, according to the study of Utrecht University in Netherlands [5].

Companies have sought for energy efficiency. For example, in countries like Italy [34], Canada [20], Sweden [29], Nigeria [44], United States [2], Germany and Colombia [22], China [47], Japan [42], Thailand [38] and Poland [46]. This reinforces the importance of the subject in the global energy context.

According to Santana et al. [37], energy in Brazil is a typical bottleneck. The energetic cost of a typical petrochemical plant in Brazil like BRASKEM(Braskem), for example, represents 13.4% of total product costs [4]. According to CNI [9], the energy costs in Brazilian industry grew by 3.8% between the first and second quarters of 2014 and continue in upward trend.

The aim of this study is to identify opportunities to increase energy efficiency at the management of energy resources for drive rotating equipment in a Brazilian petrochemical industry, using MILP for support in decision-making with multiple criteria. The model studied should subsidize energy input optimal choice based on the minimization of total consumption and reduction of energy costs.

Specific objectives are:

  • Validation of modeling using MILP and its adherence with real values.

  • Assess models’ solution time and prove its robustness as a decision-maker in rapidly changing market scenarios, as stated by Merkert et al. [27].

  • Evaluate potential for energy efficiency and financial gains at time series analysis.

  • Conduct a comparative analysis between uses of optimization model on a monthly or daily basis.

Methodology of the framework application

The following equipment constitutes the degrees of freedom of the model:

  • heaters that generate steam;

  • boilers;

  • turbines that has extraction and condensation options;

  • turbines that has motor equivalent;

  • steam pressure control valves.

Following equation  is the objective function (C) of this problem, which represents the total energy consumption

$$ C = EE + F $$
(5)

where EE is the electricity cost and F the fuel cost. The electricity cost is based on three parts shown in Eq. (6): the electricity purchased by normal contract (EE NC) and electricity purchased and sold at open market (EE POM , EE SOM)

$$ EE = EE_{\text{NC}} - EE_{\text{POM}} + EE_{\text{SOM}} $$
(6)

Equation (7) describes the electricity cost according to each power device (P i) and the electricity price ($ EE), where “i” represents the equipment in operation triggered by electric motor

$$ EE = \mathop \sum \limits_{0}^{i} P_{i} *\$_{\text{EE}} $$
(7)

If the EE value is above the upper contract limit, it is necessary to purchase it at open market and if EE value is lower than take or pay contract, it is possible to sell it at open market, defining EE POM and EE SOM values.

Total power consumption is based on the equipment with motor drive in operation. For this setting, the model must use a binary function that defines equipment activation. For the binary function, 0 represents equipment off and 1 is equivalent to engine on.

Equation (8) calculates the power of each motor depending on its power measured (P mi) multiplied by the binary factor (y Mi)

$$ P_{\text{i}} = P_{\text{mi}} *y_{\text{Mi}} $$
(8)

When all the electricity calculation is done, it is necessary to obtain the fuel equations. Equation (9) shows the fuel cost (F) depending on the fuel consumption (W F) and the fuel price ($ F)

$$ F = W_{\text{F}} *\$_{\text{F}} $$
(9)

The fuel flow consumption is defined by the steam flow necessary to drive the turbines in operation. Equation (10) shows fuel consumption (W F) depending on the steam flow (W Si) multiplying fuel consumption factor for steam generating (F SG)

$$ W_{\text{F}} = \mathop \sum \limits_{0}^{i} W_{\text{Si}} *F_{\text{SG}} $$
(10)

Steam consumption is defined by the equipment with turbine drive in operation. The same logic should be followed, using binary functions to define trigger by turbines.

Equation (11) shows measurement vapor flow of each turbine (W Smi) multiplied by the turbine binary factor (y Ti)

$$ W_{\text{Si}} = W_{\text{Smi}} \, \times \,y_{\text{Ti}} $$
(11)

Continuing to follow the framework, in this industry context, it is necessary to evaluate these constraints:

  • Historical turbine flow limits:

    • steam admission;

    • steam extraction;

    • condensation.

  • Pressure control steam valves capacity limits;

  • steam generation capacity limits;

  • electrical system contract limits;

  • number of equipments needed for a specific operation by its function;

  • equipment on maintenance;

  • ensure that the demands of other consumers of the steam system are respected.

The next stage is the coherency model test. For example, if electrical energy efficiency is high and its price is low, the model should suggest the use of electric motors. If specific consumption of fuel and its price are low, the model should suggest the use of turbines.

The strategy of solution adopted was the Branch and bound method. Starting from scheduling solutions as roots of a tree, the algorithm will compare previous analyzed solutions and generate its bounds. The optimal solution is found after evaluating all candidate solutions.

Financial gain (G f) is obtained by subtracting total energy consumption on a current real situation (C CUR) by the total energy consumption on an optimized condition (C OPT), as shown in the following equation:

$$ G_{\text{f}} = C_{\text{CUR}} - C_{\text{OPT}} $$
(12)

After obtaining the financial gain value, it can be converted to energy gain as shown in the following equation:

$$ G_{\text{e}} = {\raise0.7ex\hbox{${G_{\text{f}} }$} \!\mathord{\left/ {\vphantom {{G_{\text{f}} } {(\$_{\text{e}} \, \times \,{\text{MP}})}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(\$_{\text{e}} \, \times \,{\text{MP}})}$}} $$
(13)

where energy gain (G e) can be obtained from the price paid by energy ($ e) and the marketable petrochemicals (MP).

When all equations of the mathematical model were obtained, simulations were realized to achieve the minimum value of the total energy cost, represented by the objective function. It used What’s Best LINDO System as a solver for the optimization problem.

As a result of each simulation, new operational conditions were suggested. These new operational values were implemented on the plant to validate the operational continuity. Some simulations did not converge and the unit had periods out of production to turnaround. These outlier results were manually excluded from the database.

However, several factors influence the model that fluctuate over time, and on different timescales. For example, the dollar rate changes daily, the PLD is adjusted weekly and the energy operational demand varies randomly. Therefore, one of the objectives of this work was to evaluate the schedule through which new minimized objective functions must be obtained.

To achieve this purpose, it was chosen to simulate the model using historical data with monthly and daily time basis, to assess the gain frequency and maximum gain obtained on each tested time basis.

Results and discussion

The first simulation presents the new operational conditions obtained by the model simulation in Table 1. In the right column of the table, the filled circles represent the equipment put into operation and the blank circles represent the devices removed from service. The values of binary functions of turbines (y Ti) and motors (y Mi) used in the model are also presented.

Table 1 Model suggestions—Feb/2014
Full size table

For this particular simulation result, the model suggests to remove four turbines and operate with only one. To guarantee steam balance when the operating turbines were removed, variations in steam extraction turbines were needed.

In this scenario, energy gains were quantified at around US$ 11,000/day, equivalent to 1.4 GJ/t. The model solution time for this optimization was 10 s.

After model’s coherence consolidation, the simulation was performed once a month during the period comprehended from January 2013 to March 2015, to evaluate potential gains that MILP could present.

Figure 5 presents the historical values of energy and financial gains in this period. The dark line represents financial gains and shows a maximum value of US$ 12,800/day. The gray line represents energy gains and shows a maximum value of 1.7 GJ/t.

Fig. 5
figure 5

Potential gains over time (one day per month)

Full size image

It is possible to observe in Fig. 5 that for some days of some months, the model was executed and the gain was zero, for example, April, May and June of 2013. So it is assumed that for these situations, the degrees of freedom of the operational conditions were optimized.

When the gain value (G f) is zero, it means that objective function in current real condition (C CUR) is equal to objective function at optimum condition (C OPT) according to Eq. (12). Therefore, the objective function simulated value for the energy total cost is equal to the real plant value, indicating the model coherency and accuracy. This estate validates the modeling using MILP and proves its adherence with real values.

To evaluate the financial and energy potential gains of model application on a daily basis, new simulations were performed from January 2013 until May 2015, and the results are presented in Figs. 6 and 7.

Fig. 6
figure 6

Potential energy gains over time (once a day)

Full size image
Fig. 7
figure 7

Potential financial gains over time (once a day)

Full size image

The dark line in Fig. 7. represents financial gains and shows a maximum value of US$ 23,300/day. The gray line in Fig. 6 represents energy gains and shows a maximum value of 3.0 GJ/t.

The model solution time for these optimizations was 12 s on average, indicating the model’s robustness.

It can be calculated from Figs. 5, 6 and 7 that the maximum values of potential gains were 81% greater when the model was performed on a daily basis. This value is obtained by taking the maximum financial gain from Fig. 7 and dividing it by the maximum financial gain from Fig. 5.

From Fig. 7, it can be seen that the average earning potential is 1500 US$/day with a standard deviation of 3000 US$/day. In other words, this earning can be very high or very low. This average is only to have an order of magnitude of the potential gains. Annualizing this value represents an average gain of 556,000 US$/year.

In addition, a daily basis performance presents the potential gains in periods where a month basis simulation could not. For example, like in the period between March to June of 2013, November 2013, December 2013, June 2014 and July 2014.

Conclusion

For the tested conditions, the use of MILP proves to be possible to achieve energy efficiency gains from the optimal decision-making by analyzing the best configuration of rotating equipment drivers. Real gains from the model application were around 11,000 US$/day. From historical data, an average earning potential of 1500 US$/day, representing an average gain of 556,000 US$/year was observed Therefore, the standard deviation is high, so this value should be used carefully.

MILP is effective in this multi criteria decision-making scenario. It is accurate because matched with real values and robustness shows a small solution time of 12 s on average. Due to the temporal variations of multicriteria parameters of this decision-making, it was possible to confirm the importance of a rapid response tool and its implementation as often as possible, since potential gains by running the model once a day were 81% higher than running it once a month.

This framework presents the application’s potential for use in other industrial plants. To be effective, it is necessary to have similar degrees of freedom shown in the methodology section. The stages must be followed as described, but special attention should be paid to the particular degrees of freedom definition, preparation of equations and constraints of each industrial plant.