Introduction

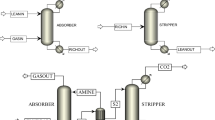
Disulfide oil (DSO) is a byproduct of demercaptanization unit from LPG by Merox process [1]. During this process, mercaptan (R-SH) is converted to mercaptide salt (R-S−Na+) in a reaction with NaOH, as shown in Eq. (1). It is then converted to disulfide in the presence of catalysts and in combination with oxygen, as shown in Eq. (2) [2]. Schematic of Merox process is shown in Fig. 1 [3]:

$${\text{RSH}} + {\text{NaOH }} \to {\text{NaSR}} + {\text{H}}_{2} {\text{O}}$$
(1)
$$4{\text{NaSR}} + {\text{O}}_{2} + 2{\text{H}}_{2} {\text{O }}\mathop \to \limits^{{{\text{Cat}}.}} 2{\text{RSSR}} + 4{\text{NaOH}} .$$
(2)
Fig. 1
figure 1

Schematic of Merox process [3]

Full size image

DSO is a chemical mixture with general chemical formula as RSSR’, in which two alkyl groups have been connected to a sulfur–sulfur connective link [4, 5]. These chemicals are usually a combination of dimethyl disulfide (DMDS), diethyl disulfide (DEDS), and methyl ethyl disulfide [6]. Table 1 presents typical composition of a DSO stream in a Fajr Jam gas refining complex (FJGRC) located in Bushehr province, around 60 km away from northern Persian Gulf coastline, Iran.

Table 1 DSO composition
Full size table

This is highly flammable at room temperature with yellowish color and unpleasant odor like garlic. Adverse effects of DSO on humans, animals, plants, and aquatic culture have identified it as a hazardous material. It is a potential source of cancer, threatens fertility, and also may cause skin irritation and inflammation [6, 7]. There is not any common practical application for DSO so far. It is known as a low-grade byproduct that usually stored or burned once production [8]. Its storage would make a serious problem as any leakage into water and soil will cause irreparable consequences. Burning DSO, on the other hand, emits toxic gases such as H2S, CO, CO2, and carbonyl compounds [6]. Regarding to statistics announced by gas refineries, considerable portion of emitted greenhouse gases (GHG) belongs to incinerators. Therefore, according to the world commitment legislation for GHG reduction, any effort in case of decreasing environmental pollutants or changing their user would be of paramount importance.

Some applications are proposed for disulfide component during recent years, e.g., removal of asphaltene and solid sulfur compounds from oil wells [5, 9] and production of cyclic compounds such as thiophene [10,11,12]. In some literature, adding DSO to hydrocarbon cutoff such as gas condensate in gas refineries presented as an alternative which not only eliminates the DSO burning and storage problems but also improves its economic aspect [13]. However, this would restrict the usage of such mixture as on-road diesel fuel due to the worldwide sulfur content limitations. Since, environmental regulations in Europe in 2009 have forced petroleum industries to reduce their sulfur contents to 10 ppm [8].

It should be taking into account that the main purpose of mixing DSO and condensate is increase in DSO price. Adding gas condensate to DSO may facilitate its exportation. In addition, as it was mentioned before, this mixture can be utilized as asphaltene solvent in enhanced oil recovery processes. Therefore, knowledge of physical properties such as density, viscosity, surface tension, and excess molar volume of DSO and gas condensate along with their mixtures can play a vital role in equipment design [14].

Rare literature was found on studying properties of this mixture. Based on searches, the current work would be likely done for the first time. Few studies have focused on measurement physical properties of either DSO or condensate separately; however, more elaboration was focused on modeling of these products. For instance, Dyusengaliev et al. studied on extraction of DMDS, diethyl methyl disulfide, and DEDS from DSO produced in Tengiz Gas Refinery in Kazakhstan [15]. Sokolsky et al. also investigated the structural and chemical characteristics of this byproduct [16]. Dysangaliev et al. reported density, boiling point, refractive index, sulfur content, solubility in different solvents, and geometrical structure of DSO produced in Tengiz Gas Refinery [17]. Taheri et al. focused on biological elimination of DSO from soil using several bacterial strains [6]. Kornetova et al. recently studied on solubility of wax and asphaltene components via DSO as solvent. It was found that DSO was not enough to dissolve these materials except in combination with surfactants and aromatic hydrocarbons [18]. In case of gas condensate, Zhang et al. studied some properties of gas condensate of Karachaganak reservoir, including PVT properties and interfacial tension [19]. Bonyadi and Esmaeilzadeh predicted density of several gas condensates using Esmaeilzadeh–Roshanfekr (ER) and Peng–Robinson (PR) equations of state (EOS) and compared with PVT observations. They found that ER-EOS was more reliable than PR-EOS to predict density of the studied gas condensate [20]. In addition, Nikookar et al. used Dashtizadeh–Pazuki–Taghikhani–Ghotbi (DPTG) EOS for a better prediction of gas condensate density [21].

In this study, density, viscosity, and surface tension of DSO and gas condensate mixtures are measured with different volume fractions and temperature range of 283.15–318.15 K, followed by presenting a mathematical approach to predict these physical properties. In addition, excess properties such as molar volume, viscosity deviations, excess Gibbs free energy, and surface tension are calculated, as well.

Materials and methods

DSO and gas condensate were provided from Fajr Jam gas refinery company, Bushehr, Iran. Physical properties of these products as well as gas condensate constituents are given in Tables 2 and 3, respectively.

Table 2 Properties of DSO and gas condensate samples
Full size table
Table 3 Gas condensate components of Fajr jam gas refining complex (FJGRC)
Full size table

Mixtures of DSO and gas condensate were prepared in a range of 0–100% v/v with 10% steps using volumetric glass flasks (Simax, Germany, ± 0.06 ml uncertainty) and micropipette (Brand, Germany, ± 0.001 ml accuracy) at room temperature and atmospheric pressure. The taken volume of each sample is checked gravimetrically according to their initial densities by an AND balance with ± 10−4 g resolution (GR-300). The mixtures were miscible in all volumetric ratios. However, to assure well mixing, blending is performed using a magnetic stirrer for almost 1 min. All measurements were conducted immediately after sample preparation to avoid any disturbance in volume ratio and composition upon vaporization.

Viscometer SVM3000 (Anton Paar) were utilized to measure density, and kinetic and dynamic viscosities of DSO and gas condensate mixtures according to ASTM D7042 [22] with the precision of ± 10−4 g cm−3 and ± 10−5 mPa s, respectively. The main part of device includes two nested cylinders; the internal one rotates mechanically at 4000 rpm. Maximum 5 ml of sample is required to conduct the measurement. A small syringe is used to inject the samples into viscometer. Each sample is analyzed at atmospheric pressure and temperatures range of 283.15–318.15 K with 5-degree steps. Temperature adjustment is performed by controlling device screen. The viscometer automatically performs tests in triplicates and results that are shown finally are the average values.

Surface tension of mixtures was measured by a digital tensiometer (TD1C, Lauda) with Du Noüy ring method according to ASTM D1331-14 [23], which measures contact surface of liquid mixture with gas phase (air) at room temperature and atmospheric pressure with the precision of ± 0.01 mN m−1. The device is calibrated using double-distilled water and extra pure methanol. After pouring sample into cup of the device, the ring is sunk into liquid followed by swiping it up gently. As the ring is coming out of liquid sample, the device records increasing force exerted to ring by surface of sample. The maximum force recorded is exactly where the junction between ring and sample is broken and known as surface tension. Due to handheld nature of the device, tests are conducted manually in duplicates and confidence intervals (CI) of 95% determine for each sample.

Results and discussion

Density and viscosity of DSO and gas condensate

Figures 2, 3 shows measured density and viscosity of DSO and gas condensate before mixing, respectively. These pure properties are used for predicting properties of mixture.

Fig. 2
figure 2

Viscosity µ of gas condensate and DSO as a function of temperature T. Measured viscosities: solid triangle, gas condensate; solid circle, DSO and dotted line, and correlated viscosities

Full size image
Fig. 3
figure 3

Density ρ of gas condensate and DSO as a function of temperature T. Measured densities: solid triangle, gas condensate; solid circle, DSO and dotted line, and correlated densities

Full size image

An empirical exponential-type equation as Eq. (3) was proposed to predict viscosity of gas condensate and DSO versus temperatures. The general form of correlation of viscosity versus temperature has been proposed in the literature [24], while the coefficients were optimized. The coefficients in the following equations were achieved using nonlinear optimization technique and least square method in MATLAB programming software (2010A) with the aim of achieving maximum R-square:

$$\mu = a_{1} \exp \left( {a_{2} T} \right),$$
(3)

where μ is viscosity in mPa s and T is absolute temperature in K. Constants, a1 and a2, are dimensionless and achieved through optimization. Final adjusted parameters of Eq. (3) for DSO and gas condensate are given in Table 4. Predicted viscosities based on Eq. (3) are showed in Fig. 2.

Table 4 Constants of viscosity and density equations for gas condensate and DSO
Full size table

As seen, the measured viscosity decreased by increasing in temperature. The average absolute relative error (AARE) of 0.37 and 0.34% was obtained for gas condensate and DSO, respectively. The AARE is calculated by the following equation [25]:

$$\% {\text{AARE}} = \frac{100}{n} \mathop \sum \limits_{i = 1}^{N} \frac{{|P_{\text{pred}} - P_{ \exp } |}}{{P_{ \exp } }},$$
(4)

where P is the desired property. Density of gas condensate and DSO was measured at the same temperature range, and Eq. (5) was proposed to predict gas condensate and DSO densities versus temperature. This equation was inspired from a general linear correlation reported by Kariznovi et al. [24]:

$$\rho = a_{3} T + a_{4} ,$$
(5)

where ρ is density in kg m−3. Constants, a 3 and a 4 were optimized for each product and shown in Table 4. Measured and predicted densities of gas condensate and DSO at the studied temperatures were showed in Fig. 3.

The AARE values of 0.03 and 0.01% were obtained for gas condensate and DSO, respectively.

Density, viscosity, and surface tension of gas condensate–DSO mixture

Density and viscosity of gas condensate and DSO mixtures were measured at different volume fractions and temperatures range of 283.15–318.15 K. Equations (6) and (7) are proposed to predict density and viscosity of mixtures, respectively. The main principle of such correlation development can be found in Mohamadi-Baghmolaei et al. study [26]:

$$\rho = 0.3153\left( {T + 9.299} \right)\left( {w_{{{\text{cond}} .}} + 0.3512} \right)\left( {w_{{{\text{cond}} .}} - 3.911} \right) + 1147,$$
(6)

where w cond. is gas condensate mass fraction. Results shown in Fig. 4 indicate a good agreement between the experimental and predicted data with AARE of 0.38%. Table 5 also reports the obtained experimental data at the entire range of studied temperatures.

Fig. 4
figure 4

Gas condensate–DSO mixture density ρ as a function of temperature T at various gas condensate volume fractions. Points show experimental observations and the dotted curve shows the correlation results

Full size image
Table 5 Density ρ/kg m−3 of gas condensate (1) + DSO (2)
Full size table

It is clear from Fig. 4 that density of mixture decreased by increasing in gas condensate volume fraction as well as temperature. However, effect of volume fraction on fluid density is much more tangible than temperature. In addition, all density variations versus temperature and volume fractions are linear with high precision. The proposed mathematical model for the prediction of gas condensate–DSO mixture viscosity is shown by the following equation:

$$\mu = \frac{{2.497 \times 10^{7} }}{{T(w_{{{\text{cond}}.}} + T)(4.973 w_{{{\text{cond}}.}} + T - 9.423)}} - 0.1976.$$
(7)

The mixture volume fractions and temperatures were the same as those of density. Results are shown in Figs. 5 and 6. In addition, Table 6 shows the obtained experimental viscosities at temperatures between 283.15 and 318.15 K.

Fig. 5
figure 5

Residual (experimental versus predicted values) viscosities of gas condensate and DSO mixtures under different gas condensate volume fractions and temperatures

Full size image
Fig. 6
figure 6

Experimental viscosities µ of gas condensate and DSO mixtures at different temperatures T

Full size image
Table 6 Viscosity µ/mPa.s of gas condensate (1) + DSO (2)
Full size table

In Fig. 5, the predicted viscosities are plotted versus the measured ones. It can be clearly seen that the data deviations at each temperature decreased by increase in temperature, so that the R-squared values at the temperature of 283.15 and 318.15 K were achieved 0.0105 and 0.9925, respectively. This phenomenon could be interpreted by weakening of the interaction forces between molecules by increasing temperature [27]. The AARE value for the figure, however, was calculated 0.76% that is negligible enough to assume accurate correlation. The decreasing trend of mixture viscosity versus temperature is also evident from Fig. 5 and Table 6. The experimental viscosities at the studied temperatures and three gas condensate volume fractions are shown in Fig. 6. As can be seen, the viscosity versus temperature has an exponentially trend for all volume fractions. Although temperature has a significant impact on mixture viscosity, volume fraction has minor effect insofar as the three plotted lines in Fig. 6 are overlapped.

As mentioned, variation of surface tension was measured experimentally at room temperature and atmospheric pressure for the whole range of volume fractions in duplicates. This property was also predicted by Eq. (8) for all mixtures:

$$\ln (\sigma /{\text{mN}}\;{\text{m}}^{ - 1} ) = x_{1} \ln \sigma_{1} + x_{2} \ln \sigma_{2} - 0.1984 x_{1} x_{2} ,$$
(8)

where \(\sigma\) is surface tension in mN m−1 and x is mole fraction. The subscripts 1 and 2 in Eq. (8) and the following equations refer to gas condensate and DSO, respectively. Both experimental and predicted surface tensions were plotted in Fig. 7 and the AARE obtained 0.95%.

Fig. 7
figure 7

Experimental and predicted surface tension σ at 298.15 K and different gas condensate mole fractions x 1

Full size image

As can be seen from Fig. 7 and Table 7, surface tension of DSO and gas condensate mixture decreased by increase in gas condensate volume fraction. Experimental data reported in Table 7 were also supplemented by standard deviation values for two replications. The predicted data by Eq. (8) were also listed in Table 7.

Table 7 Surface tension σ/mN m−1 of gas condensate (1) + DSO (2) at 298.15 K
Full size table

Excess properties

Excess molar volume can be calculated by experimental densities of pure and mixture materials. This property is determined for a binary mixture by the following equation [27,28,29]:

$$V^{\text{E}} = \frac{{x_{1} M_{1} + x_{2} M_{2} }}{\rho } - \left( {\frac{{x_{1} M_{1} }}{{\rho_{1} }} + \frac{{x_{2} M_{2} }}{{\rho_{2} }}} \right),$$
(9)

where V E is excess molar volume in m3.mol−1 and M is molar mass in kg mol−1. The Redlich–Kister equation is used to predict the excess molar property of gas condensate–DSO mixture [30]:

$$P = x_{1} \left( {1 - x_{1} } \right)\sum\limits_{i = 0}^{n} {A_{\text{i}} \left( {1 - x_{1} } \right)^{i} } ,$$
(10)

where P is the desired property and A is a regulator coefficient. The subscript i is an integer number considered three in this study. Figure 8 illustrates graphical trend of excess molar volume \(V^{\text{E}}\) in more detail. As can be seen, the excess molar volumes are positive for all molar ranges. This phenomenon is likely arising from the interaction effects occurred by mixing condensate and DSO which results in breaking of chemical bonds and increase the total volume after mixing, leading to excess molar volume greater than zero [28]. While the negative excess molar volume may suggest strong interactions such as hydrogen bond between molecules of a mixture [27], the positive value for excess molar volume was also observed by AlTuwaim et al. for different binary mixtures of N,N-dimethylformamide in combination with 1-pentanol, 1-hexanol, and 1-heptanol separately [31]. Moreover, Narendra et al. [32] and Kumari et al. [33] found the same trend for anisaldehyde + cresols and acetic acid + toluene mixtures, respectively. The height of curves of excess molar volume illustrated in Fig. 8 increases by increasing temperature that can be attributed to bond breaking and volume expansion by temperature [27,28,29, 34,35,36].

Fig. 8
figure 8

Excess molar volumes V E for the gas condensate and DSO mixtures as a function of gas condensate mole fraction x 1. Points show experimental observations and the dotted curve shows the Redlich–Kister fitting

Full size image

Having viscosity of gas condensate and DSO as well as their mixture, the viscosity deviation can be obtained using Eq. (11) as follows [27, 28, 34, 35]:

$$\Delta \mu = \mu - (x_{1} \mu_{1} + (1 - x_{1} )\mu_{2} ),$$
(11)

where Δµ is viscosity deviation in mPa s. Prediction of this property was conducted using Redlich–Kister equation, as well. Figure 9 illustrates the experimental and predicted viscosity deviations at different gas condensate mole fraction and temperatures.

Fig. 9
figure 9

Viscosity deviations Δµ for gas condensate and DSO mixtures as a function of gas condensate mole fraction x 1. Points show experimental observations and the dotted curve shows the Redlich–Kister fitting

Full size image

From Fig. 9, it can be observed that viscosity deviations of mixture represent a W-shape trend for all mole fractions and temperatures in which the negative parts appeared at low (0 < x 1 < 0.3) and high (0.8 < x 1 < 1) mole fractions. This may be due to the disruption of molecular order of the dilute component which results in the random separation of molecules of the dilute component within the more concentrated one. The positive viscosity deviation, on the other hand, may be due to intermolecular Van der Waals attraction force as well as interactions between permanent and induced dipoles [28]. The other remarkable point that can be concluded from Fig. 9 is reduction in the difference between positive and negative viscosity deviation values by increasing in temperature. The same behavior was observed by Esteban et al. for a binary mixture of solketal and n-hexadecane [28]. The S-shape behavior was also observed for viscosity deviations in a binary mixture, where a downward peak appeared in early part of the chart and an upward one in late part or vice versa. For instance, similar trends were reported by Kapadi et al. [34] for ethanolamine and water mixture and by and Gómez Marigliano and Solimo [37] for formamide and 1-propanol mixture.

Deviation of excess Gibbs free energy (\(\Delta G^{\text{E}}\)) is considered as another important mixture property and can be determined by Eq. (12) for a binary mixture [28]:

$$\Delta G^{\text{E}} = RT[\ln \left( {\mu V} \right) - ((x_{1} \ln (\mu_{1} V_{1} ) + (1 - x_{1} )\ln (\mu_{2} V_{2} ))],$$
(12)

where ΔG E is deviation of excess Gibbs free energy in J mol−1 and R is gas constant in J mol−1 K−1. The molar volume of mixture is also calculated via Eq. (13):

$$V = \frac{{x_{1} M_{1} + x_{2} M_{2} }}{\rho }.$$
(13)

Deviation of excess Gibbs free energy of mixture calculated by Eq. (12) and predicted data fitted by Redlich–Kister equation is shown in Fig. 10.

Fig. 10
figure 10

Deviation of the excess Gibbs free energy ΔG E for gas condensate and DSO mixtures as a function of gas condensate mole fraction x 1. Points show experimental observations and the dotted curve shows the Redlich–Kister fitting

Full size image

It is clear from Fig. 10 that the deviation of excess Gibbs free energy contains both negative and positive parts, forming a W-shape trend. The positive part can be attributed to domination of specific interactions between constituent molecules of mixture, while the negative values imply the dominance of dispersion forces [27, 28, 34]. Esteban et al. found a similar trend for binary mixture of n-hexadecane and solketal [28].

Excess surface tension is determined by the following equation [28]:

$$\sigma^{\text{E}} = \sigma - (x_{1} \sigma_{1} + (1 - x_{1} )\sigma_{2} ),$$
(14)

where σ E is excess surface tension in mN m−1.

The Redlich–Kister equation was also presented to fit the data obtained by Eq. (14). Figure 11 illustrates experimental and predicted excess surface tension.

Fig. 11
figure 11

Excess surface tension σ E for gas condensate and DSO mixtures as a function of gas condensate mole fraction x 1, at 298.15 K. The solid triangle and dotted line show experimental and Redlich–Kister fitting

Full size image

According to Fig. 11, excess surface tension values are negative in all range of gas condensate mole fractions. It may be assumed that concentration of the component with lower surface tension may be higher at the surface than bulk of liquid mixture [28, 38]. Similar trends were observed by Esteban et al. for a binary mixture consisted of n-hexadecane + solketal [28] and Azizian and Hemmati for ethanol + ethylene glycol system [39]. Moreover, Yue and Liu found such a downward dome-shaped graph for several binary systems of n-heptane and ethanol as well as 2,2,4-trimethylpentane mixed with ethanol, propanol, 1-pentanol, 1-hexanol, and 1-heptanol [38].

The whole coefficients of Redlich–Kister equation achieved for the prediction properties of excess molar volume, viscosity deviation, deviation of the excess Gibbs free energy, and surface tension for the studied mixture are listed in Table 8.

Table 8 Coefficients of the Redlich–Kister equations
Full size table

Conclusion

In this work, density, viscosity, and surface tension of DSO and gas condensate mixture were measured and modeled by empirical equations. It was found that the AARE% were less than 1% for all properties. Furthermore, excess properties such as excess molar volume (V E), viscosity deviation (\(\Delta \mu\)), deviation of excess Gibb’s free energy (\(\Delta G^{\text{E}}\)), and excess surface tension (σ E) of the studied mixture were determined using experimental data and modeled by Redlich–Kister. It was finally observed that excess molar volume was positive in all range of mixture composition, while both the viscosity and Gibbs free energy deviations unveiled simultaneous positive and negative behavior at different mixture concentration. Negative values were also obtained for excess surface tension in all studied mole fractions.