Introduction

The demand for hydrocarbons is increasing day by day, although there is some support from other resources. It is well established that most of the residual oil remains unextracted due to the lack of proper understanding of the flow behavior phenomenon (Ahammad 2014). It is important to determine the accurate measurement of flow rate and pressure drop at the near wellbore to enhance the reservoir productivity index (Byrne et al. 2009; Ahammad et al. 2024). The change of flow pattern from laminar to turbulent mainly happens near the wellbore region (Tang et al. 2017). In addition, near-wellbore fluid flow is also affected by formation damage that occurs during drilling, completion, work-over operations, and stimulation. Thus, the studies of reservoir flow phenomena at the near-wellbore must include formation damage mechanisms (Ding 2011).

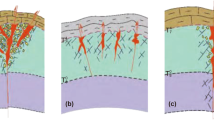
Furthermore, the virgin reservoir has two flow regions: the reservoir region and the wellbore region. On the other hand, in the real situation, the total reservoir fluid flow can be divided into three regions, such as the reservoir region, the formation damage region (the skin region), and the wellbore region. The significance of formation damage is depicted in Fig. 1. (Chaudhry 2004). It is clearly visible in Fig. 1a and b, that how the difference of pressure drop changes at the near-wellbore due to the skin region. It is because of damages to the reservoir formation in Fig. 1b. In the petroleum industry, skin factor is used to evaluate the degree of influence of formation permeability around the wellbore where the formation damages happen (Liu et al. 2016; Ahammad 2019).

The fluid flow in the reservoir and damage region is considered laminar, whereas fluid flow in the wellbore is turbulent (Ahammad et al. 2019; Sabea and Al-Fatlawi 2022). Chupin et al. (2007) nicely pointed out five more extra challenging situations that arise near the wellbore flow phenomena. Among those, the change of flow pattern from steady to unsteady at the near wellbore and gas-water coning in the near wellbore may have an effect on the downstream operation.

The modeling of fluid flows through three main regions, such as the reservoir region, skin zone, and wellbore region, in an integrated way is the main challenge in this field. Therefore, an integrated model is required to simulate the flow dynamics with a single model theoretically or computationally to understand the phenomena accurately.

In this regard, many investigations have been performed to address the issues encountered in simulating the hydrocarbon flow from reservoirs into wellbores, considering different types of aspects (Byrne et al. 2011; Azadi et al. 2016; Mahmood and Al-Fatlawi 2022). Vicente et al. (2000) have studied the coupling of wellbore-reservoir flow with two independent equations for each region in the case of single-phase gas flow. They have used conservation of mass and Darcy’s law in the reservoir flow, and for isothermal conditions, mass and momentum are used to simulate the flow. They have developed a coupling technique for the transient case by preserving the continuous pressure equation and mass balance condition. They have also identified that the boundary conditions have a significant influence on the accuracy and stability of the numerical solution. Chupin et al. (2007) have developed an integrated wellbore-reservoir model to investigate the liquid loading in a gas well. They identified that the flow could be unsteady in some situations. The formation damage zone has been ignored in their investigation. Tang et al. (2017) have introduced an integrated wellbore-reservoir model with a drift-flux approach for the interface of two domains to study liquid flow phenomena in oil industries. The Darcy equation has been considered as momentum conservation in their modeling. Karimi-Fard and Durlofsky (2010) have proposed a coupling technique for a reservoir model by utilizing productivity indices for transient numerical upscaling procedures. In their case, the boundary conditions in the near wellbore model remained unchanged. This could lead to misleading results, for example, multiphase flow problems. Cheng et al. (2022) have developed a near-wellbore coupling model to investigate multiphysics phenomena for two phase flow systems. Geomechanics deformation has been taken into consideration, but with the Darcy equation. Gao et al. (2016) have studied numerical investigation for the coupling of multi-layers of a reservoir, and they have concluded that the challenges of connecting injector and producer layers. Also, it has been identified that coupling the multi-layer has raised concerns about computational cost due to the occurrence of actual flow size.

The real flow situations occur at the millimeter scale, whereas some models use the full size of the reservoirs with a larger grid size. In those cases, the grid size is greater than the diameter of the perforated tunnels. Thus, the numerical simulations to capture the flow at the millimeter scale suffer huge computational complexity (Ahammad and Alam 2017). This type of computational cost is analyzed in detail by Ahammad (2014) and Ahammad et al. (2024). Despite the challenges, the CFD simulation facility is promoting research on this topic.

Furthermore, towards the development of an integrated model for reservoir simulations, the numerical approximations have to face boundary conditions issues due to the change of phase for more than one flow region. During the modeling of integrated reservoirs, there exists a sharp interface between two domains, such as porous-porous or porous-fluid interfaces, and a "critical boundary" between the reservoir-perforated tunnel and the perforated tunnel-wellbore. Thus, numerical simulations have to overcome the challenges of convergence and stability criteria (Ding 2011). The modeling of boundary conditions and the interface of two domains is another challenge in integrated wellbore-reservoir modeling.

The research that has been done so far to unify the reservoirs of the well has not yet been able to excavate inside the combination of the three zones of the flow together. Most of the researchers have focused on simulation or porous areas or reservoir aspects of well flow. Some researchers have used the model with simplistic assumptions, for example, the Darcy equation as a momentum equation, ignoring the interaction between reservoir and well. Therefore, the actual situation of the production of hydrocarbon reservoirs can be associated with errors (Liao et al. 2021).

The present studies focus on two novel ideas for advancing current knowledge of simulating an integrated wellbore-reservoir model, including formation damage regions. Here, the first principle of conservation laws is considered based on the 3D Navier–Stokes equations to simulate the impact of formation damage. Then the simulation of reservoir fluid flows is attempted for a coupled wellbore-reservoir model with Navier–Stokes equations using a conservative flux technique for the interface condition. Second, in the simulation process, a CFD approach is considered in which the velocity and the pressure are simultaneously coupled into a single system of equations that is solved by an algebraic multigrid technique. An advantage of this CFD approach is its robustness, flexibility, and accuracy. It takes advantage of modern high-performance computing architecture, thereby bringing the fastest CFD methods to the field of oil, gas, and energy technology will explore new windows of research.

Fig. 1
figure 1

Idealized reservoir with vertical wellbore: (a) the sketch of a undamaged reservoir and (b) reservoir with skin zone (source: Chaudhry 2004)

Full size image

Methodology

Governing equation for flow through porous media

Hydrocarbon transportation through reservoir followed three main categories of flow regimes. These include the Darcy or creeping flow regime in the reservoir, Forchheimer flow regime at the near wellbore, and fully turbulent flow regime in the wellbore. These flows can be analyzed by modeling the topology of the porous medium. The detail mathematical derivation of the model equations can be found in De Lemos (2012). The Darcy and Forchheimer forces are included in the present model to utilize the flow in a coupled manner. Following (Ahammad et al. 2017; Ahammad 2019) Navier-Stokes equations for slightly incompressible flow are considered to investigate the flow behavior.

$$\begin{aligned}{} & {} \frac{\partial (\phi \rho )}{\partial t} + \frac{\partial (\rho u_j)}{\partial x_j} =0, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \rho \left( \frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j}\right) =-\frac{\partial P}{\partial x_i} + \frac{\partial \tau _{ij}}{\partial x_i}+\rho g_i+ \mathcal {F}_i~, i,j=1,2,3. \end{aligned}$$
(2)

where \(\tau _{ij}=\mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right)\) and the momentum sink \(\mathcal {F}_i\) can be expressed as a combination of Darcy and Forchheimer forces due to flow through porous media. It is well established that, the Forchheimer term has notable influence on the near wellbore fluid flow since it represents the inertial force (De Lemos 2012).The total momentum sink due to porous media is defined as

$$\begin{aligned} \mathcal {F}_i=-\frac{\mu }{{\mathcal {K}}}u_i - \beta \frac{\rho }{2} |\varvec{u}| u_i~, \end{aligned}$$
(3)

where loss coefficient, \(\beta\), is modeled by following Khaniaminjan and Goudarzi (2008) as

$$\begin{aligned} \beta =\frac{17.2\times 10^{10}}{{{\mathcal {K}}^{1.76}}}. \end{aligned}$$
(4)

Boundary conditions

An integrated wellbore-reservoir model is considered for the present CFD simulations. The dimensions of the computational model and other parameters are listed in Tables 1 and 2. respectively. The inlet and outlet are assumed at the outer boundary of the domain and at the wellhead of the wellbore as exhibited in Fig. 2. The mathematical forms of the boundary conditions are described as follows: inlet boundary condition is chosen for the present CFD simulations as

$$\begin{aligned} P(r,t)=P_0, t\ge 0, \end{aligned}$$

The outlet boundary condition is

$$\begin{aligned} r\frac{\partial P}{\partial r}=\frac{q\mu }{2\pi {{\mathcal {K}} }h}, t> 0, \end{aligned}$$

where a constant flow rate is presented.

Further, we assume uniform pressure in the reservoir initially, thus,

$$\begin{aligned} P(r,0)=P_0, r_w \le r \le r_e. \end{aligned}$$

The upper and lower boundary of the simulation model domain are considered as walls, so no slip boundary condition is used here.

Pressure calculation technique

Analytical solution of Darcy model

The Darcy model describes the fluid flow through porous media i.e. flow through oil and gas reservoir. Assuming the flow is steady-state, and linear in the reservoir then classical Darcy model has the form

$$\begin{aligned} \frac{\partial P}{\partial x_i }=-\frac{\mu }{{\mathcal {K}}}u_i~. \end{aligned}$$
(5)

The Eq. (5) can be written in polar coordinate for the isotropic reservoir, as

$$\begin{aligned} \frac{\partial P}{\partial r}=-\frac{q\mu }{2\pi r{{\mathcal {K}} }h},~~ r\epsilon [r_w, r_e]. \end{aligned}$$
(6)

The theoretical solution of Darcy equation in the case of steady state condition can be achieved by integration of Eq. (6) and which leads to  (Economides 2013)

$$\begin{aligned} P = P_{w}+\frac{q\mu }{h{\mathcal {K}}}ln\left( \frac{r}{r_w}\right) , \end{aligned}$$
(7)

where the reservoir radius, wellbore radius, wellbore pressure, reservoir pressure and height of the reservoir are expressed by \(r, r_w, P_w, P\) and h respectively. This equation can be written for the oilfield units as (Economides 2013)

$$\begin{aligned} P=P_{w}+ 141.22\frac{Bq\mu }{h{\mathcal {K}}}ln\left( \frac{r}{r_w}\right) . \end{aligned}$$
(8)

Analytical solution of pressure diffusivity equation

The reservoir fluid flows mostly radial direction towards the wellbore, thus the mass conservation equation for flow to the radial direction with true velocity is

$$\begin{aligned} \frac{\partial }{\partial t}(\phi \rho ) +\frac{\partial }{r \partial r}(r u \rho )=0. \end{aligned}$$
(9)

Pressure diffusivity equation can be derived from the first principal of mass conservation law by combining with Darcy equation. Thus, for a slightly compressible and radially symmetric flow in an oil reservoir, the spatio-temporal reservoir pressure is given by the well-known solution of pressure diffusivity equation as (Economides 2013; Razminia et al. 2014)

$$\begin{aligned} \frac{\partial ^2P}{\partial r^2}+\frac{1}{r}\frac{\partial P}{\partial r} + c_r\left( \frac{\partial P}{\partial r}\right) ^2= \frac{\phi \mu c_t}{\mathcal {K}}\frac{\partial P}{\partial t}. \end{aligned}$$
(10)

Total compressibility,

$$\begin{aligned} c_t= c_r+c_f \end{aligned}$$

where \(c_r=\frac{1}{\phi }\frac{\partial \phi }{\partial P}\) is rock compressibility and \(c_f=\frac{1}{\rho }\frac{\partial \rho }{\partial P}\) is fluid compressibility.

The Eq. (10) is a nonlinear partial differential equation in nature. It is not straight forward to find an analytical solution of this equation. By neglecting the nonlinear term in Eq. (10) if pressure variation is small (Azin et al. 2017), then the Eq. (10) becomes

$$\begin{aligned} \frac{\partial ^2P}{\partial r^2}+\frac{1}{r}\frac{\partial P}{\partial r} = \frac{1}{\chi }\frac{\partial P}{\partial t}, \end{aligned}$$
(11)

It is referred to as the pressure diffusivity equation, where \(\chi = \frac{\mathcal {K}}{\phi \mu c_t}\). The solution to this equation yields pressure data for any point r in the domain at any given time t.

In order to create the model equation and get the analytical solution, the following presumptions are taken into consideration. The requirements for reservoir include: (i) being isotropic and homogeneous in all directions; (ii) producing at a constant flow rate; (iii) having a wellbore radius very small compare to reservoir radius; (iv) having uniform initial pressure in the reservoir and draining at infinite area (i.e., \(P \rightarrow P_0\) as \(r \rightarrow \infty\)). With these assumptions, the pressure diffusivity Eq. (11) can be used to compute pressure analytically as

$$\begin{aligned} P(r,t)=P_0 - \frac{q\mu }{4\pi \mathcal {K}h}ln\left( \frac{2.25t\chi }{r^2}\right) . \end{aligned}$$

The above equation becomes in the form of field unit by converting the respective variables in oilfield units as (Economides 2013)

$$\begin{aligned} P(r,t)=P_0 - \frac{162.6Bq\mu }{\mathcal {K}h} \left( log_{10}\left( \frac{t\chi }{r^2}\right) -3.23\right) . \end{aligned}$$
(12)

CFD model of oil reservoir

Fig. 2
figure 2

Computational geometry of a typical reservoir with skin zone: (a) 3D view and (b) top view

Full size image

In the CFD modeling, a vertical wellbore of radius \(r_w\) and a reservoir of radius \(r_e\) is considered and depicted in Fig. 2. where the wellbore is parallel to the z-axis. The annulus region around the wellbore represents formation damage, which is called the ‘skin zone’ in this article. Table 1 provides the necessary field measurement regarding the wellbore-reservoir system, and Table 2. presents the other modeling parameters as well. Note that, the outer boundary of the reservoir is usually far away from the well, and typically the ratio of the reservoir radius and wellbore radius can be expressed as \(r_e/r_w \ge 3000\)—a CFD mesh of which is difficult to be resolved with modern computing resources. In the present work, we have developed a CFD simulation framework for the near wellbore region, where we have truncated the outer boundary of the model reservoir with ratio \(r_e/r_w \ge 28\). To ensure that the CFD model enforces the most appropriate boundary condition at \(r\rightarrow r_e\), the following assumptions are adopted.

  1. (i)

    There is a steady flow of a slightly compressible reservoir fluid far away from the well at \(r > r_e\).

  2. (ii)

    The pressure in the outer region is given by the solution of the pressure diffusivity equation under the assumption of radial symmetry.

  3. (iii)

    The mass flow across the outer boundary is continuous when the actual reservoir is truncated to the computational reservoir.

  4. (iv)

    Under these assumptions, we expect that the CFD simulation is equivalent to the field-scale reservoir flow near the wellbore if all other parameters are consistent with the field measurements.

Table 1 Parameter values used for the computational domain
Full size table

Numerical technique to simulate integrated wellbore-reservoir model

The element-based finite volume technique to simulate complex domain is kind of tricky. At first, meshes of the desired domain needs to generate, then the discretization can be executed using the meshes. In this methodology, it is expected to conserve the mass, momentum, and other desired quantities on the generated mesh (Larsson et al. 2010). The upwind method on a higher resolution is applied for the spatial discretization and implicit backward Euler scheme is used for time integration. The overall scheme is unconditionally stable (Pletcher et al. 2012). In this methodology, optimal mesh size helps to obtain the faster converge solutions. The collocated grid offers the advantage of translating the created mesh from one coordinate system to another in the complicated domain system. The values of all desired variables are computed at the cell centers (ANSYS 2016) in the collocated grid layout. Moreover, the same locations are used to store the scalar and vector variables. Thus, the system requires less computational cost (Abbasi et al. 2013). The commercial software ANSYS TM CFX 17.2 developed the collocated grid in the numerical process. Despite of the advantage of this methodology, there is a possibility of the pressure–velocity decoupling issue (Rhie and Chow 1983). This issue can overcome by applying interpolation method (Ahammad et al. 2019; Abbasi et al. 2013) The velocity-pressure coupling solver is performed to simulate the problem in this study. Utilizing the benefits of an algebraic multigrid method, the system of linear equations is resolved. By merging the finer mesh, the algebraic multigrid approach assists in transforming the discrete equation system on a coarse mesh. During the iterations, this technique is used on a virtual grid layout, and mesh refinement is performed until an accurate solution is reached. As a result, this technique’s processing cost decreases as convergence rates rise. This is as a result of just solving the discretization of the non-linear equations once on a finer mesh (Pletcher et al. 2012). Utilizing the benefits of this approach, the entire computational process is implemented on the ANSYS TM CFX 17.2 platform for the current study.

The flow chart of the solution process of the transient problem is exhibited in the Fig. 3. The algorithm is summarized as:

  • Step 1 Setting the initial values for the parameters, such as \(\Delta t\).

  • Step 2 Involves taking the updated values of u, v, w, and P.

  • Step 3 Involves applying the Rhie and Chow interpolation technique for u, v, w, and P.

  • Step 4 Involves solving the coupled system of equations for u, v, w, and P.

  • Step 5 Utilizing the algebraic multigrid approach, the solution process is accelerated until the convergence criteria are reached.

  • Step 6 Find solutions for the remaining interesting variables.

  • Step 7 Stop when the solution time reaches its maximum value; if not, continue steps 2 through 7 in reverse order.

Fig. 3
figure 3

Flow chart for pressure based coupled solver

Full size image

Interface modeling for integrated wellbore-reservoir

In the modeling of integrated wellbore-reservoir, there are mainly two interfaces: porous-porous and porous-fluid. The size of the respective domains also different so sometimes size of the grid may be different. All these factors make the interface modeling more challenging than usual. General Grid Interface (GGI) algorithm connects the resultant surfaces on either side of an interface. Moreover, the GGI algorithm employs an automatic surface trimming function to connect mismatched surfaces. This approach helps GGI algorithm to successfully define interface where the surface on one side of the interface is larger than the other side. In addition, the treatment of the interface fluxes is fully implicit and conservative in mass, momentum, and other species. Thus, it allows to apply the multi-grid solver directly, with the same level of robustness or convergence rate (ANSYS 2016). ANSYS TM CFX 17.2 have implemented GGI to investigation the rotor/stator interaction for rotating machinery. We attempt to implement this technique in the integrated wellbore-reservoir modeling in the petroleum industries with conservative mass flux interface condition.

Results and discussions

CFD model verification

The present CFD model setup is verified for two cases: one with the Darcy equation and another with the pressure diffusivity equation. The details are described in the following sections.

Verification with the Darcy equation

Reservoir simulation plays a crucial role in the oil and gas industry by providing insights into the complex processes occurring in underground reservoirs. Here, a simple case is considered to verify the present CFD setup with available data in the literature. The simulation is performed only in the reservoir region, i.e. excluding the wellbore in the CFD mesh in this case, and there is no formation damage in the reservoir. The model is linear (\(\beta =0\)) i.e. no Forchheimer force is acting here. This simulation helps to verify the present results with the solution of the Darcy equation. The pressure contour plot of the present simulation using Navier-Stokes Equations (NSE) for a steady-state condition is presented in Fig. 4a. A pressure profile is drawn along a horizontal line of the CFD domain to compare with the solution of the Darcy equation, and the results are illustrated in Fig. 4b. As seen in Fig. 4b, the present CFD simulation using NSE has excellent agreement with the analytical solution of Darcy equation (Eq. 8) for the steady-state flow condition. In other words, a CFD model is designed with a velocity-pressure coupling solver for an oil and gas reservoir, and the present CFD model predicts the flow as accurately as it is predicted by the Darcy model. The same validation approach was followed by Molina and Tyagi (2015). The next validation is performed for integrated wellbore-reservoir modeling, which is a unique from of available data in the literature, for example, Molina and Tyagi (2015).

Fig. 4
figure 4

Comparison of present model with the analytical solution of Darcy equation for an idealized reservoir (without wellbore for CFD simulation): (a) pressure contour plot of the present CFD set up, (b) comparison of pressure profiles (\(\beta =0\) and \(q= 474.36 ~[\text {bbl/day}]\) )

Full size image
Table 2 Parameter values used for the simulations in this paper. The data for computational domain and relative variables are adapted from (Molina and Tyagi 2015)
Full size table

Verification with pressure diffusivity equation for integrated wellbore-reservoir

Fig. 5
figure 5

Pressure profile distribution of a reservoir without skin zone (i.e. \(\mathcal {K}_s=0[\hbox {mD}],\) and \(\mathcal {K}_r=250[\hbox {mD}]\)), (a) pressure contour plot, (b) comparison of pressure profile with analytical solution of pressure diffusivity equation for (\(\beta _r=1.035\times 10^8 [{\hbox {ft}^{-1}}]\) and \(q= 300.00 ~[{\hbox {bbl/day}}]\))

Full size image

The numerical technique is described in previous section, where a coupled CFD solver for the integrated wellbore-reservoir model is developed. In this process, the pressure and the velocity are obtained by solving a linear system of the equation at each time step. Here, the wellbore and reservoir are modeled in a coupled manner, as described in Fig. 2, where the wellbore is a fluid zone and the reservoir is a porous zone without any formation damage. The parameter values are listed in Table 2. with the loss coefficient as \(\beta _r= 1.035\times 10^8 [{\hbox {ft}^{-1}}]\) and flow rate, \(q=300~[\hbox {bbl/day}]\) and reservoir formation permeability is \(\mathcal {K}_r=250 [\hbox {mD}]\). The simulated pressure contour is plotted on the vertical planes \(y = 0,\) passing through the center of the wellbore and illustrated in Fig. 5a. The result indicates that the assumption of radial symmetry of the flow in the outer region implies that the near wellbore flow remains approximately symmetric unless there is a perturbation. The CFD prediction of the near wellbore pressure distribution should follow the pressure distribution predicted by the pressure diffusivity model. The pressure profile of the simulation using NSE is drawn along a horizontal line of the reservoir model. The analytical solution of the pressure diffusivity equation is compared with the CFD simulation using NSE and presented in Fig. 5b. The results have good agreement except at the wellbore end. The slight decline of pressure drop at the wellbore end is because, the extra term in the pressure diffusivity equation is neglected to make it simple to get the analytical solution. This verification indicates that the field-scale distribution of reservoir pressure can be simulated accurately and efficiently by the implicit CFD method presented in this article.

Verification with inflow performance relation for integrated wellbore-reservoir

The relationship between the reservoir’s bottom hole pressure and the well production rate, or i.e. the flow rate at the wellhead, is known as the inflow performance relationship, or IPR. A case is taken into account with the parameter values listed in Table 2. the equation for the IPR curve without skin zone leads to (Economides 2013)

$$\begin{aligned} P_w=1200 - \frac{q}{3.46}\left( log_{10}t+4.65\right) . \end{aligned}$$
(13)
Fig. 6
figure 6

Inflow performance analysis with IPR curves for the reservoir without any skin zone

Full size image

Three different flow rates such as \(q = 100, 200,\) and \(300~[\text {bbl/day}]\) are tested to investigate the inflow performance, and the simulations are performed for a fixed time, \(t=150~[\text {sec}].\) The bottom hole pressures for the simulations using NSE are calculated at the final time, and the data are compared with the theoretical solution of IPR (Eq. 13) and the results are presented in Fig. 6. It has been noticed that the CFD simulations by NSE have a good agreement with the theoretical solution of the IPR curve, except for a slight deviation when flow rate increases. The reason for the slight deviation may be that flow becomes non-linear at a higher flow rate. This result indicates that the CFD model with NSE is capable of simulating reservoir flow like other models.

Integrated wellbore-reservoir model with formation damage

In the previous section, the ability of present model for integrated wellbore-reservoir modeling is demonstrated without formation damage. In this section, the integrated wellbore-reservoir model is extended with a skin zone near the wellbore, i.e., three zones such as reservoir, skin zone near wellbore and wellbore zone. A simulation is conducted with the skin zone permeability \(\mathcal {K}_s=50[\text {mD}]\), reservoir formation permeability \(\mathcal {K}_r=250[\text {mD}]\) and flow rate is \(q=300~[\text {bbl/day}].\) The contour plot and pressure profile of the simulations are presented in Fig. 7. It is noticed that the pressure gradually decreases in the reservoir region and suddenly drops at the skin zone. The current simulation is compared with the analytical solution for PD, where only formation permeability is considered. The CFD result matches with the analytical solution until the beginning of the skin zone. There is no combined analytical solution for both zones, thus, deviation is observed at the skin zone. Note that, the sudden pressure drop in the skin zone is clearly noticeable in Fig. 7b. This indicates the influence of the skin zone on hydrocarbon transportation to the wellbore. The comparison of flow behavior with or without formation damage is discussed in the next section.

Fig. 7
figure 7

Comparison of pressure profiles of an idealised reservoir with an integrated wellbore-reservoir including formation damage where idealsied reservoir permeability, \(\mathcal {K}=250[\text {mD}]\)), skin zone permeability (i.e. \(\mathcal {K}_s=50[\text {mD}],\) and reservoir formation permeability, \(\mathcal {K}_r=250[\text {mD}]\)): (a) pressure contour plot, (b) comparison of pressure profile with analytical solution of pressure diffusivity equation for (\(\beta =1.035\times 10^8 [\text {ft}^{-1}]\) and \(q= 300.00 ~[\text {bbl/day}]\))

Full size image

Comparison of integrated wellbore-reservoir with and without formation damage

Two scenarios, such as an idealized instance without a skin zone and a formation damage case with a skin zone, are investigated in this study. This means, in the first case, there is only one porous zone with reservoir formation permeability, \(\mathcal {K}=250~[\text {mD}]\) and the second one with \(\mathcal {K}_s=50~[\text {mD}]\) for skin zone i.e. permeability of the damage zone at near the wellbore and \(\mathcal {K}_r=250~[\text {mD}]\) for reservoir area. The parameter values are listed in Table 2. With flow rate, \(q=300~[\text {bbl/day}]\) for both cases. In the previous section, It is observed that for both cases, pressure is gradually decreasing towards the wellbore surface. In the case of formation damage, the pressure is suddenly dropped (see, Fig. 7b) at the skin zone, which agrees with the convention. Further investigation is performed by analyzing the pressure contours of both simulations at the reservoir area, skin zone, and wellbore region. The comparative results are displayed in Fig. 8, where the first column is for the undamaged (Ideal) reservoir and the second column is for the damaged reservoir. In this figure, the first row represents the pressure contour at the wellbore region for both cases (Fig. 8a and b). Having the same parameters except at the skin zone, it is seen that the pressure drop at the wellbore for the damage zone is much higher than the undamaged zone. The second row expresses the pressure contour of the fluid flow through the skin zone and without the skin zone (Fig. 8c and d). Here, pressure at the reservoir and skin zone interface for both cases is observed to be the same, but the pressure drop across the skin zone is higher than without the skin zone. This indicates that when initial fluid moves from the skin zone to the wellbore, fluid from the reservoir may not enter into skin zone at the same rate due to damage, so pressure dropped at the skin zone does not increase much. The last row (Fig. 8e and  f) represents the pressure contour for the reservoir area in both cases. The pressure changes along the reservoir in both cases are almost the same. These findings are quantified with the analytical solution of the pressure diffusivity equation for the idealized case. In this regard, the pressure profiles are drawn along the horizontal line of the reservoir for both simulations. The results are exhibited in Fig. 9. with the analytical solution of the pressure diffusivity equation. In this figure, it is clearly seen that there are pressure levels in the three regions. The pressure profiles at the reservoir region for the present CFD using NSE matches with the analytical solution of PD as shown in the previous section. The pressure drop is higher in the skin zone (more discussion in the following section), as seen in the contour plot, and the wellbore pressures remain steady in both cases as there is no drag force due to porous media.

Fig. 8
figure 8

Pressure contour plot for integrated wellbore-reservoir model. First row: (a) wellbore region without skin effect and (b) wellbore region with skin effect. Second row: (c) skin zone without its effect and (d) skin zone with its effect. Third row: (e) reservoir area without skin effect and (f) reservoir area with skin effect. All parameters are same except skin zone i.e. \(\mathcal {K}_r=250~[\text {mD}]\) & \(\mathcal {K}_s=50~[\text {mD}]\)

Full size image
Fig. 9
figure 9

Comparison of pressure profile of the undamaged reservoir and damage reservoir with the analytical solution of PD to quantify the results presented in Fig. 8

Full size image

Flow direction for integrated wellbore-reservoir with and without formation damage

Fig. 10
figure 10

Stream lines plot of the integrated wellbore-reservoir model representing flow direction: (a) without skin zone, (b) with skin zone

Full size image

Now, the flow direction is investigated for an integrated wellbore-reservoir in both cases, i.e., with formation damage and without formation damage. This is performed by presenting streamline plots. The streamlines are plotted along a plane \(y=0\) and presented in Fig. 10. for both cases. In both cases, it is observed that, fluids are flowing from the reservoir end towards the wellbore and moving to the wellhead. This indicates that fluid flows radially towards the wellbore, and along the wellbore, it moves vertically to the wellhead. Moreover, fluid velocity for the idealized case remains the same in the reservoir, whereas fluid velocity increases at the damage zone due to the drag of porous media. In both cases, velocity is higher at the surface level of the reservoir in the wellbore. This point of investigation helps to understand the change of phase of flow phenomena and has a good agreement with the analysis of different flow regimes in Kundu et al. (2014). Moreover, this study indicates that the integrated wellbore-reservoir model performs as desired.

Performance of integrated wellbore-reservoir model

In this section, the performance of the model for different parameters such as flow rates, different skin zones, and reservoir formations is studied.

Integrated wellbore-reservoir with different production rate

In this case, four different production rates are considered to investigate the performance of the present integrated wellbore-reservoir model in terms of pressure drop at the wellbore. The parameter values are listed in Table 2 and we chose \(\mathcal {K}_r = 250~[\text {mD}]\) and \(\phi _r = 25 \%\) for the reservoir area, and \(\mathcal {K}_s= 50~[\text {mD}]\) and \(\phi _s= 10 \%\) for the skin zone in these simulations. Pressure profiles are drawn along a horizontal line of the reservoir for all cases, and results are displayed in Fig. 11. Here, the same behavior is observed as pressure decreases gradually within the reservoir and a sudden drop occurs at the skin zone. This phenomenon was already explained in the previous section and verified with the analytical solution of the pressure diffusivity equation. Moreover, the pressure at the wellbore is higher for a higher production rate and lower for a low production rate, as recorded. This indicates that pressure drop increases with respect to production rate within the same skin zone. This analysis could help to estimate the reservoir life.

Fig. 11
figure 11

Investigation of pressure drop for the different flow conditions for integrated wellbore-reservoir model

Full size image

Integrated wellbore-reservoir study for different skin zones

The skin zone causes alterations in the flow or pressure drop behavior near the wellbore (Dake 2001). This section explains the effect of the skin zone on the flow at the wellbore for the model of an integrated welbore-reservoir. In this investigation, three types of skin zone characteristics, such as skin zone permeability, \(\mathcal {K}_s= 150, 100\), and \(50~[\text {mD}]\) with porosity, \(\phi _s=10 \%\) are considered, and the respective loss coefficients, \(\beta = 2.541\times 10^{7},~5.179\times 10^{7}\) and \(1.758\times 10^{8}~ [\text {ft}^{-1}]\) are calculated following Eq. (4), and all other parameters are chosen from Table 2. Using Hawkin’s formula (Hawkins Jr et al. 1956; Terry et al. 2014): \(s=\left( \frac{\mathcal {K}_r}{\mathcal {K}_s}-1\right) ln\left( \frac{r_s}{r_w}\right)\) for skin factor, the three values of \(s=6.63,~2.49,\) and  1.11 are considered for the skin zone permeability, \(\mathcal {K}_s= 150, 100\), and \(50[\text {mD}]\) respectively. These skin factors are within the range of skin factors used by Zhang et al. (2021) for the study of gas pressure with turbulent terms in the model. The positive skin factor means the negative impact on flow rate and pressure drop at the wellbore, and vice-versa, moreover, skin factor zero means the ideal case. The impact of skin factor on the pressure drop at the wellbore is examined following (Al-Rbeawi 2016). The pressure contour plots are presented in Fig. 12. For all three cases. The current results are quantified by the pressure profiles for these contour plots in Fig. 13. It is noticed that a higher pressure drop occurs for a higher skin factor, i.e. low permeability of the skin zone. The pressure drop increases gradually with the increasing permeability of the skin zone, and in all cases, the pressure profile remains the same in the reservoir region.

Fig. 12
figure 12

Pressure contour plots for fixed reservoir formation with different skin zones such as skin permeability: (a) \(\mathcal {K}_s= 150~[\text {mD}]\), (b) \(\mathcal {K}_s= 100~[\text {mD}]\), and (c) \(\mathcal {K}_s= 50~[\text {mD}]\)

Full size image
Fig. 13
figure 13

Effect of different skin zones on pressure drop, the pressure profiles are drawn along a horizontal line of the domain for the simulations presented in Fig. 12

Full size image

Integrated wellbore-reservoir study for different reservoir formation

The permeability of the hydrocarbon transportation medium is one of the influential parameters of the reservoir that describes the ability of fluids to flow through reservoir formation (Sun et al. 2021). Hereinafter, the performance of the present model is investigated for the different reservoir formations. Three types of reservoir formations with permeability, \(\mathcal {K}_r=250, 400\) and \(500~[\text {mD}]\) are taken into consideration while keeping skin zone permeability fixed as \(\mathcal {K}_s=50~[\text {mD}]\) for all three cases, and other parameters are mentioned in Table 2. With \(q = 300~[\text {bbl/day}]\). More attention is given to investigating the influence of formation permeability on the change in fluid pressure through the medium instead of focusing on verification here. In Fig. 14, it is observed that bottom-hole pressure decreases more for the lower permeable formation compared to the higher. By observing the contour plot, it is difficult to understand the pressure drop across the reservoir to the skin zone. The pressure profiles are drawn by following the process as before, and the results are illustrated in Fig. 15. In the pressure profile graph, there are three zones: reservoir area, skin zone, and wellbore area. The pressure drop of the reservoir up to the skin surface (\(r_s=0.2~[m]\)) is higher for the low-permeable formation. This is the reason for the pressure drop at the wellbore, rather than the skin zone effect here. Given that skin zone permeability is constant across all three scenarios, it is interesting to note that the differential pressure across the skin is nearly identical in each case. The entire phenomena aligns with the state of nature and is consistent with the conclusions of the analytical solution of the pressure diffusivity equation presented in section before it. The analysis verifies that an integrated wellbore-reservoir system with various formation characteristics can be modeled using the current CFD setup with 3D Navier–Stokes equations.

Fig. 14
figure 14

Pressure contour plots for fixed skin zone with different reservoir formations permeability such as: (a) \(\mathcal {K}_r= 250~[\text {mD}]\), (b) \(\mathcal {K}_r= 400~[\text {mD}]\), and (c) \(\mathcal {K}_r= 500~[\text {mD}]\)

Full size image
Fig. 15
figure 15

Effect of different reservoir formation permeability on pressure drop, the pressure profiles are drawn along a horizontal line of the domain for the simulations presented in Fig. 14

Full size image

Conclusions

In this study, an integrated wellbore-reservoir model is developed with efficient CFD methodology for the petroleum industry. The present CFD facilities offer usable tools to help understand reservoir flow behavior. The present study successfully investigates the formulation of an integrated wellbore-reservoir model. The model is validated with analytical solutions to the pressure diffusivity equation, and inflow performance relation curve, and other models. The findings of present investigation can be summarized as follows:

  • 3D Navier–Stokes equations are successfully applied to model the fluid flow at the porous–porous and porous-fluid interfaces.

  • The General Grid Interface (GGI) technique helps to handle the complex boundary condition in this model.

  • The use of a pressure-based velocity coupling solver accelerates the robustness of the solution.

  • The present model enables the study of all three regions with a single equation using appropriate interface conditions. The model performs as expected for three cases: different flow rates, skin zones, and reservoir formations.

  • The present development hits the new window to enhance the reservoir simulators by including all of the possible forces, such as viscous forces, surface forces, etc.

  • The successful validation of the inflow performance relations curve indicates that this integrated reservoir - wellbore model can help in understanding reservoir performance.

Finally, this model can be extended to realistic reservoir conditions and can be further verified with field data. Moreover, it can be easily extended for multiphase flow studies with appropriate interface conditions.