Introduction

With the rapid advances of the oil and gas exploration and development, ultra-deep oil and gas resources have become the hot spot of the exploration and development around the world (Tong et al. 2018). As the ultra-deep formations have the high thermal evolution, the oil and gas resources are dominated by natural gas. The ultra-deep natural gas resources are abundant in China, which are buried at more than 4500 m (Li et al. 2021). There are several ultra-deep natural gas reservoirs discovered and put into development in China in recent years, such as Puguang, Kuqa, Yuanba and Anyue reservoirs (Zhang et al. 2019). Ultra-deep natural gas reservoirs are playing significant roles in gas reserves and production increase in China, which is becoming increasingly more important in the strategic exploration position. According to the statistics from the fourth oil/gas resource evaluation, PetroChina's geological reserves of ultra-deep natural gas were 2.86 × 1012 m3, and there are huge exploration and development potentials (Li et al. 2020). Consequently, accelerating ultra-deep natural gas exploration and development is significantly necessary to ensure stable gas supply and national energy security.

The exploration and development of ultra-deep natural gas reservoirs are faced with the complex environments of high temperature, high pressure and high in situ stress, and there exist the complex multiphysics-coupled processes of the fluid flow between the reservoir and the wellbore (Selvadurai et al. 2018; Lei et al. 2021). The mechanical deformation due to the changes of fluid pressure in reservoirs is an important aspect that should be considered in the reservoir depletion (Sangnimnuan et al. 2021). The gas production of gas reservoirs generally leads to the decrease in fluid pressure and the increase in effective overburden load on the reservoir rocks. As the gas production extracts, the successive increase in effective overburden load will conversely compact the reservoir rocks and thus result in the change of the reservoir stress state (Chin et al. 2000; Susan et al. 2003). And thus, the accurate gas production prediction in the reservoirs requires both coupled fluid flow and mechanical deformation modeling. The coupled flow and geomechanical simulations in the porous reservoirs have recently been investigated by a number of researchers (Settari et al. 2001; Jha et al. 2007; Huang et al. 2013). The iteratively coupled approach in which each code solves its own governing equations and the two codes was proposed by using a porosity correction term (Settari and Mourits, 1998). Gutierrez et al. (2004) mentioned the importance of coupling geomechanical deformation to multiphase flow in the porous reservoirs. A finite element model was proposed to simulate two-phase flow and solid deformation in a dual-porosity medium (Nair et al. 2005). Yang et al. (2014) developed a fully coupled geomechanics and multiphase flow solver that can model the processes of rock deformation and multiphase flow in the heterogeneous porous media. Ma et al. (2020) used a coupled two-phase flow and geomechanical model to understand methane production during the CO2-enhanced coalbed methane. Consequently, considering the coupling of geomechanics and fluid flow is crucial for the aforementioned phenomena and performing the accurate simulations in the porous reservoirs.

In the depletion of ultra-deep natural gas reservoirs, the reservoir deformation caused by overburden pressure results in considerable change of porosity and permeability, which will affect the reservoir production performance. The pore pressure decline results in the rise in effective stress, subsequently compacts pore structure geometry and reduces reservoir porosity and intrinsic permeability (Ren et al. 2016). It has been widely recognized that the near-wellbore flow behavior has a huge impact on gas productivity (Ding 2010). Ding (2011) proposed a new technique for the coupled modeling of the near-wellbore and the reservoir simulator, and the near-wellbore flow behavior was modeled using the fine grids. Huang and Ghassemi (2012) considered that the gas production in tight gas reservoirs declines rapidly in a manner that was believed to be closely related to the evolution of fracture aperture and permeability. Hemmingsen et al. (2019) developed the multiphase coupling of a reservoir simulator and fluid dynamics for wellbore flow and investigated the issues from the simultaneous simulation for the near and far well flow behavior. Although there are a few studies conducted on the coupled wellbore-reservoir flow in the porous reservoirs, the coupled geomechanics and fluid flow modeling in ultra-deep natural gas reservoirs are still lacking. The ultra-deep natural gas reservoirs were located in the conditions with high temperature, high pressure and high in situ stress. Therefore, there is a significant necessity to understand the coupled geomechanics and fluid flow behavior on these extreme conditions so as to optimize extraction conditions and ultimately maximize gas productivity in ultra-deep natural gas reservoirs.

In this study, a mathematic model was developed to describe the coupled fluid flow and geomechanics deformation caused by pore pressure in ultra-deep natural gas reservoirs. The stress dependency of the porosity and permeability as well as geomechanics deformation was considered in the models, and the models were then implemented and solved in the COMSOL Multiphysics based on the finite element method. The models were verified by the reservoir depletion from Dabei gas field in China, and the reservoir fluid flow and well-head pressure were analyzed. Furthermore, the effects of reservoir properties and production parameters on gas production, near-wellbore pore pressure and permeability evolution were discussed.

Methods of the coupled modeling

Fluid flow equations

According to the mass conservation law, the general mass conservation equations for an immiscible two-phase fluid (e.g., water and gas) flow in a porous reservoir can be expressed as (Shen et al. 2015; Ma et al. 2017a)

$$\frac{{\partial m_{\alpha } }}{\partial t} + \nabla \cdot \left( {\rho_{\alpha } u_{\alpha } } \right) = Q_{\alpha }$$
(1)
$${{\varvec{u}}}_{\alpha }=-\frac{k{k}_{r\alpha }}{{\mu }_{\alpha }}\nabla {p}_{\alpha }$$
(2)

where \({m}_{\alpha }\) is the fluid flow mass (kg); \(t\) is the time (s);\({\rho }_{\alpha }\) is the fluid density (kg/m3); \({{\varvec{u}}}_{\alpha }\) is the fluid velocity (m/s); \({Q}_{\alpha }\) is the flow source or sink term (\(\alpha =\mathrm{water or gas}\)); \(k\) and \({k}_{r\alpha }\) are the apparent permeability (m2) and the relative permeability, respectively; \({\mu }_{\alpha }\) is the fluid viscosity (m2/s); \({p}_{\alpha }\) is the pore pressure (Pa).

Assuming the reservoir a single porosity and permeability medium, the water and gas mass can be written as (Webb 1998)

$${m}_{w}={S}_{w}{\rho }_{w}\phi$$
(3)
$${m}_{g}={S}_{g}{\rho }_{g}\phi$$
(4)

where \({m}_{w}\) and \({m}_{g}\) are the water and gas mass (kg), respectively; \({S}_{w}\) and \({S}_{g}\) are the water and gas saturation, respectively; \({\rho }_{w}\) and \({\rho }_{g}\) are the water and gas density (kg/m3), respectively;\(\phi\) is the reservoir porosity.

Substituting Eqs. (2), (3) and (4) into (1), the mass conservation equations that describe fluid flow in the porous reservoir can be expressed as

$$\frac{\partial }{\partial t}\left( {S_{w} \rho_{w} \phi } \right) + \nabla \cdot \left( { - \rho_{w} \frac{{kk_{{{\text{rw}}}} }}{{\mu_{w} }}\nabla p_{w} } \right) = Q_{w}$$
(5)
$$\frac{\partial }{\partial t}\left( {S_{g} \rho_{g} \phi } \right) + \nabla \cdot \left( { - \rho_{g} \frac{{kk_{{{\text{rg}}}} }}{{\mu_{g} }}\nabla p_{g} } \right) = Q_{g}$$
(6)

For the water and gas phase system in the porous reservoir, the saturations and capillary pressures are defined as

$${S}_{w}+{S}_{g}=1$$
(7)
$${p}_{c}={p}_{g}-{p}_{w}$$
(8)

where \({p}_{c}\) is the capillary pressure (Pa), which is the function of saturation. According to the previous studies (Rutqvist et al. 2001; Ma et al. 2017b), the relationships between the capillary pressure, the saturation and the relative permeability can be expressed as

$${p}_{c}={p}_{e}{({s}_{e})}^{-1/\lambda }$$
(9)
$${k}_{\mathrm{rg}}={\left(1-{s}_{e}\right)}^{2}(1-{{s}_{e}}^{2})$$
(10)
$${k}_{\mathrm{rw}}=\sqrt{{s}_{e}}{\left\{1-{\left(1-{{s}_{e}}^{1/m}\right)}^{m}\right\}}^{2}$$
(11)
$${s}_{e}=\frac{{S}_{w}-{S}_{\mathrm{wr}}}{1-{S}_{\mathrm{wr}}-{S}_{\mathrm{gr}}}$$
(12)

where \({p}_{e}\) is the entry pressure (Pa); \({s}_{e}\) is the effective saturation; \(\lambda\) is the coefficient related to the pore size distribution; \({S}_{\mathrm{wr}}\) and \({S}_{\mathrm{gr}}\) are the residual water saturation and the residual gas saturation, respectively.

Porosity and permeability models

In the reservoir depletion, the reservoir rock deformation caused by overburden pressure results in the considerable porosity and permeability changes. The porosity and permeability models considering the reservoir rock deformation can be expressed as (Ma et al. 2017b)

$$\phi =\alpha +\left({\phi }_{0}-\alpha \right)exp\left(-\frac{\Delta {\sigma }^{^{\prime}}}{K}\right)$$
(13)
$$\frac{k}{{k}_{0}}={\left(\frac{\phi }{{\phi }_{0}}\right)}^{3}={\left\{\frac{\alpha }{{\phi }_{0}}+\frac{\left({\phi }_{0}-\alpha \right)}{{\phi }_{0}}exp\left(-\frac{\Delta {\sigma }^{^{\prime}}}{K}\right)\right\}}^{3}$$
(14)

where \({\phi }_{0}\) and \({k}_{0}\) are the initial porosity and the initial permeability (m2), respectively; \(\alpha\) is the Biot coefficient; \({\sigma }^{^{\prime}}\) is the effective mean stress (Pa).

Geomechanical model for rock deformation

According to the pore elastic constitutive relationship and considering the volume strain caused by the reservoir exploitation, the geomechanical model for rock deformation can be expressed as ( Rutqvist et al. 2001)

$$\sigma = \sigma^{\prime} - \alpha Ip = D:\varepsilon - \alpha Ip$$
(15)
$$p={S}_{w}{p}_{w}+{S}_{g}{p}_{g}={S}_{w}\left({p}_{g}-{p}_{c}\right)+{S}_{g}{p}_{g}={p}_{g}-{S}_{w}{p}_{c}$$
(16)
$$D = \frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1 - \nu } \\ \nu \\ \nu \\ \end{array} } \\ 0 \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} \nu \\ {1 - \nu } \\ \nu \\ \end{array} } \\ 0 \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} \nu \\ 0 \\ {1 - \nu } \\ \end{array} } \\ 0 \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {\left( {1 - 2\nu } \right)/2} \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ {\left( {1 - 2\nu } \right)/2} \\ 0 \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ 0 \\ {\left( {1 - 2\nu } \right)/2} \\ \end{array} } \right]$$
(17)

where \({\varvec{\sigma}}\) and \({{\varvec{\sigma}}}^{\mathrm{^{\prime}}}\) are the total stress and the effective stress (Pa), respectively; \({\varvec{\varepsilon}}\) is the volume strain; \({\varvec{D}}\) is the tangential stiffness; \(I\) is the pore pressure tensor,which is the unit matrix; \(p\) is the mean pore pressure (Pa); E and ν are the rock Young's modulus and the Poisson's ratio, respectively.

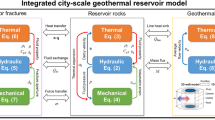
In this study, Eqs. (5), (6), (13), (14) and (15) are the coupled models for fluid flow and reservoir rock deformation. These above equations are implemented and then solved with the COMSOL Multiphysics. A pre-arranged COMSOL geomechanics module is selected to solve the geomechanical model with Eq. (15), and then, the immiscible two-phase fluid flow is implemented with Eqs. (5) and (6) using the COMSOL General Form PDE interface illustrated in Fig. 1.

Fig. 1
figure 1

Schematic of solving the coupled model of fluid flow and rock deformation with COMSOL

Full size image
Fig. 2
figure 2

Locations and structural units of the Dabei gas field

Full size image

Model validation

Model description

The Dabei gas field is located in the west of Kuqa Depression in the northern margin of the Tarim Basin, which is illustrated in Fig. 1, and it is one of the most complex and deep continental condensate gas fields in China (Zhang et al. 2011). The gas-bearing layer is the sandstone of Cretaceous Bashijiqike Formation, which belongs to low porosity and low permeability reservoirs (Guo et al. 2016; Zhu et al. 2019). The gas field with the complex geological structure is characterized by high temperature, high pressure and strong heterogeneity. The reservoir porosity is usually from 0.03 to 0.09 with an average value of 0.6, and the reservoir permeability generally ranges from 0.01 mD to 1 mD. In order to understand the gas production behavior of the near-wellbore and reservoir in ultra-deep natural gas reservoirs, the reservoir depletion from Dabei gas field was considered in this study. The finite element numerical tool named COMSOL Multiphysics was used to construct and solve the numerical reservoir model. The geometry of the reservoir model was 1000 m (length) × 1000 m (width) × 100 m (height), with a production well in the model center (Fig. 2). The wellbore diameter was 18 cm, and the plan view of the numerical reservoir model is illustrated in Fig. 3. The lateral directions were constrained for outer boundaries. For the gas flow setting, the gas reservoir was initially saturated with gas at some certain pressure, and a constant production pressure was applied on the wellbore boundary, but its values vary with the reservoir depletion. The detailed reservoir properties used in the simulation are listed in Table 1. In this study, the water and gas relative permeability curves in the reservoir are illustrated in Fig. 4a based on the experimental results, and the capillary pressure curve used in the reservoir is shown in Fig. 4b.

Fig. 3
figure 3

Schematic diagram of the numerical geometry model

Full size image
Table 1 Reservoir properties used in the simulation
Full size table
Fig. 4
figure 4

Relative permeability curves for reservoir system (a) and capillary pressure (b)

Full size image

Model validation with the history data

In this study, to validate the applicability of the current model in gas and water production in ultra-deep naturel gas reservoirs, the field data of Dabei gas field are used to validate the numerical simulation results based on the reservoir model. For the numerical simulation, all the actual conditions are adopted, and the wellhead pressure is also come from the field data. The comparison between the field data and the numerical simulation results is illustrated in Fig. 5. From the result of Fig. 5, it can be seen that the gas and water production rates with the numerical simulation are in good agreement with those obtained from the field data. It implies that the numerical results can reflect the field production data accurately. Thus, the numerical reservoir model can be used to analyze the near-wellbore change and production performance in ultra-deep naturel gas reservoirs.

Fig. 5
figure 5

Comparison between simulation results and field data

Full size image

Discussions

Effect of the reservoir porosity

The reservoir porosity is the void space in the reservoir rock that can store the fluids, which determines the reservoir storage capacity (Postnikova et al. 2021). The effects of the reservoir porosity between 0.03 and 0.09 on the evolution of gas production rate, near-wellbore pore pressure and permeability have been conducted in this study. Figure 6 shows the evolution of gas production rate, near-wellbore pore pressure and permeability under different magnitudes of the reservoir porosity. As illustrated in Fig. 6, the simulation results of gas production rate evolution regarding different porosities show that porosity plays an important role in the gas production rate during the reservoir depletion. The gas production rate gradually decreases with time, and the peak value of gas production rate increases with increasing porosity. With the linear increase in porosity, the gas production rate increases nonlinearly, and this is due to the effect of the reservoir rock deformation coupling. When φ = 0.09, the maximum gas rate is approximately 30.0 × 104m3/d, and it quickly jumps to 28.6 × 104m3/d and 25.6 × 104m3/d for the φ = 0.06 and φ = 0.03, respectively. After 1000 days, the gas production rate is 24.4 × 104m3/d, 23.4 × 104m3/d and 20.9 × 104m3/d for the φ = 0.09, φ = 0.06 and φ = 0.03 cases, respectively. The near-wellbore pore pressure decreases rapidly with time and tends to be balanced, and the time to reach equilibrium is the shortest for the φ = 0.03 case. It is mainly because that the lower porosity will have the higher pore pressure, and it will result in the larger rock deformation of reservoir structure. Due to the large deformation of pore structure, the permeability greatly will reduce with time.

Fig. 6
figure 6

Evolution of gas production rate, near-wellbore pore pressure (a) and permeability (b) under different magnitudes of reservoir porosity

Full size image

Effect of the reservoir permeability

The reservoir permeability is the key factor in assessing the hydrocarbon productivity of ultra-deep natural gas reservoirs, which measures the capacity of the formation to transmit fluid in reservoirs (Selvadurai et al. 2018; Bohnsack et al. 2020). In order to analyze the effect of the reservoir permeability, the values of the reservoir permeability from 0.5 mD to 2 mD are considered in the numerical reservoir model. The evolutions of gas production rate, near-wellbore pore pressure and porosity under different magnitudes of reservoir permeability are illustrated in Fig. 7. From the result of Fig. 7, it can be seen that there is an increase from 0.5 mD to 2 mD significantly that enhances the gas production rate. For instance, when the permeability is 2 mD, the gas production rate reaches the peak value of 56.1 × 104m3/d, but it decreases to 14.2 × 104m3/d when the permeability is 0.5 mD. With the linear increase in permeability, the gas production rate increases linearly. With the depletion of ultra-deep natural gas reservoirs, the near-wellbore pore pressure and porosity decrease rapidly with time and tend to be balanced. The rock deformation in reservoirs caused by permeability is very small, but the permeability evolution affects greatly the gas production rate during the development of ultra-deep natural gas reservoirs.

Fig. 7
figure 7

Evolution of gas production rate, near-wellbore pore pressure (a) and porosity (b) under different magnitudes of reservoir permeability

Full size image

Effect of gas production rates

The gas production rate is a significant parameter in the gas reservoir depletion which can affect the productive life and the ultimate recovery factor in reservoirs (Høyland et al. 1989). To determine the effect of different gas production rates on the fluid flow in ultra-deep natural gas reservoirs, the gas production rates between 24 × 104m3/d and 39 × 104m3/d are conducted in the numerical reservoir model. Figure 8 shows the evolution of gas production rate, near-wellbore pore pressure and permeability under different magnitudes of gas production rate. As illustrated in Fig. 8, it can be seen that with the increase in the gas production rate, the reservoir porosity decreases. This is due to the influence of reservoir rock deformation coupling. The greater the gas production rate is, the greater the pressure drop is, and the more obvious the reservoir rock deformation is, which results in the smaller reservoir porosity. With the depletion of ultra-deep natural gas reservoirs, the greater the gas production rate is, the near-wellbore pore pressure and permeability decrease rapidly and tend to balance with time. It implies that the gas production rate has a great impact on the rock deformation in reservoirs, and too high gas production rate is not conducive to the stable production capacity in the reservoir depletion.

Fig. 8
figure 8

Evolution of gas production rate, near-wellbore pore pressure (a) and permeability (b) under different magnitudes of gas production rate

Full size image

Effect of Young's modulus and Poisson's ratio

The rock Young's modulus and Poisson's ratio describe the rock deformation response under the deformation condition, which considers as the significant mechanical properties and can be used to predict the geomechanical behavior in the reservoir depletion (Villeneuve et al. 2011; Zhang et al. 2014). In order to understand the effects of Young's modulus and Poisson's ratio, the low, medium and high deformation of Young's modulus and Poisson's ratio are conducted in the numerical reservoir model (Table 2). Under these conditions, the evolutions of gas production rate, near-wellbore pore pressure and permeability under different magnitudes of Young's modulus and Poisson's ratio are evaluated, respectively.

Table 2 Different Young's modulus and Poisson's ratios
Full size table

Figure 9 illustrates the evolutions of gas production rate, near-wellbore pore pressure and permeability under different magnitudes of Young's modulus and Poisson's ratio. From the result of Fig. 9, an increasing deformability increase from high to low reduces the time used to reach peak value and enhances the gas production rates. For instance, when the deformability is low (E = 7GPa, ν = 0.28), the gas production rate needs only 10 days to reach the peak of 29.6 × 104m3/d, but it increases to 10 days when the deformability is high and its peak value dwindles to 27.3 × 104 m3/d. With the increase in the deformability, the gas production rate decreases rapidly. The near-wellbore pore pressure decreases rapidly with time and tends to be balanced. The higher deformability has the higher near-wellbore pore pressure pore pressure. Due to the larger deformation of reservoir pore structure, the permeability gradually decreases with.

Fig. 9
figure 9

Evolution of gas production rate, near-wellbore pore pressure (a) and permeability (b) under different magnitudes of Young's modulus and Poisson's ratio

Full size image

Conclusions

In this study, a fully coupled model was developed to describe the coupled behavior between gas water two-phase flow and reservoir poromechanics in ultra-deep natural gas reservoirs. The stress-dependent porosity and permeability models as well as geomechanics deformation were considered in the model, which was implemented and solved in the COMSOL Multiphysics. The numerical model was validated by the reservoir depletion from Dabei gas field in China. Furthermore, the effects of reservoir properties and production parameters on gas production, near-wellbore pore pressure and permeability evolution were discussed. The main conclusions were as the following: (1) Based on the geological characteristics of ultra-deep natural gas reservoirs, considering the mechanical deformation of reservoir rocks, the gas–water two-phase flow and the reasonable mass exchange term between the two flows, a multiphysics-coupling model of the near-wellbore and reservoir can be established. (2) The gas and water production rates with the numerical simulation are in good agreement with those obtained from the field data, and it implies that the numerical models can reflect the field production data. Consequently, the numerical reservoir model can be used to analyze the near-wellbore change and production performance in ultra-deep naturel gas reservoirs. (3) With the increase in porosity, permeability and Young’s modulus, the gas production rate increases nonlinearly, which is due to the coupling effect of reservoir rock deformation. The lower the porosity is, the greater the near-wellbore pore pressure is and the larger the rock deformation is. The permeability evolution has little effect on reservoir rock deformation, but has a great influence on the gas production rate in the reservoir depletion. With the increase in the gas production rate, the reservoir porosity decreases, and the greater the gas production rate is, and the near-wellbore pore pressure is and permeability decreases rapidly and tends to balance with time. The higher the deformation capacity of reservoir rock is, the greater the near-wellbore pore pressure is. The reason is due to the gradual reduction in reservoir permeability resulting from the large deformation of reservoir pore structure.