Introduction

As important reservoirs of oil and gas resources, carbonate reservoirs are important in international oil and gas exploration (Tian et al. 2019; Issoufou et al. 2021). Recently, unconventional oil and gas exploration in China has made rapid progress. Owing to the industrial and strategic value of tight carbonate reservoirs, their oil and gas exploration and development has garnered increasing attention (Cao et al. 2020; Zhai et al. 2023). Carbonate rocks have more complex pore systems and stronger heterogeneity than clastic rocks (Michie et al. 2014). Generally, porosity less than 10% and permeability less than 1mD are taken as the criteria for categorizing tight reservoirs (Zou et al. 2015). Under the background of generally ultralow rock physical properties of tight reservoirs, the evaluation and identification of high-quality reservoirs has become a key challenge in oil and gas exploration and development (Zheng et al. 2020).

The evaluation of reservoir classification is important in the comprehensive geological evaluation of gas reservoir reserves and grades. Recently, research on tight reservoirs in different regions has been performed and certain achievements in the classification, evaluation, and prediction of high-quality reservoirs have been made. Currently, the widely recognized carbonate reservoir classification evaluation methods mainly include grading evaluation by combining oil and gas productivity with reservoir physical parameter statistics (Li et al. 2021a, b; Ali et al. 2015). The pore structure parameters determined using high-pressure mercury intrusion, nuclear magnetic resonance, and other analysis and testing methods are used to conduct grading evaluation based on the relative content of pores of different grades (Li et al. 2021a, b; Qin et al. 2015; Guo et al. 2011; Fan et al. 2019). A study to classify and evaluate carbonate reservoirs was performed by studying the contribution of intergranular pores to reservoir physical properties (Dou et al. 2011). Different methods have their own applicability, advantages, and disadvantages. The wide application of various technologies has made the reservoir classification and evaluation develop from single to comprehensive. However, the above methods are mostly affected by subjective experience and the lack of modular and quantitative decision-making process and ignore fracture control on the quality of carbonate reservoirs, which has great limitations. The spatial distribution and research of dolomite reservoirs in different regions must be strengthened. Selecting appropriate evaluation parameters and methods based on the characteristics of different classification evaluation objects and the purpose of classification evaluation at different stages is crucial.

Fracture can be the reservoir space and migration channel of oil and gas, which makes it an important research content of fractured reservoirs. As the most effective method for fracture evaluation, imaging logging is limited in its application scope owing to its high cost. Conversely, conventional logging data are characterized by low cost, complete data, and wide application. Therefore, researchers have conducted extensive research in identifying fractures and calculating fracture porosity using logging data (Ghasem et al. 2020; Hussein 2022; Yasin et al. 2022; Zhang et al. 2021). However, in practice, it is difficult to accurately identify the occurrence and distribution density of fractures for tight storage. The actual geological conditions are complex and diverse. Using simple linear models to predict fractures has the disadvantages of large errors and a low recognition rate. Caianiello (1961) first proposed the use of the artificial neural network. In the oil and gas exploration field, the artificial neural network method has been applied to logging identification, diagenetic facies identification, seismic attribute characteristics, and engineering development (Cao and Liang 2002; Tariq et al. 2021; Chen et al. 2022; Abdulaziz et al. 2022). The backpropagation (BP) neural network method enables the machine model to learn from experience, identify the complex correlation between various datasets, and extract key information to improve the accuracy of reservoir fracture identification (Brenjkar et al. 2021). Compared to other machine learning models, BP neural networks have the ability to achieve complex nonlinear mapping, thereby solving problems with complex internal mechanisms. Suitable for complex and highly fractured reservoirs, minimizing the risk of oil and gas exploration (Dev and Eden 2019; Adibifard et al. 2014). From these advantages, machine learning can be applied to carbonate reservoir quality assessment.

The Ordos Basin is the second-largest gas basin in China. Carbonate reservoirs in the middle Ordovician Majiagou Formation in the central part of the basin are highly developed and rich in natural gas resources (Cai et al. 2020). Among them, in 1996, the Ma55 gas reservoir was discovered and is one of the most important gas reservoirs of Ordovician carbonate rocks that contributes to the productivity of the Paleozoic gas reservoirs. Fractures formed by multistage tectonic movement in the Ma55 subsegment control oil and gas migration, and the fractures associated with these fractures also form high-quality reservoir space for oil and gas. Recently, there have been many achievements in this area. Currently, the basic description of the sedimentary environment, pore characteristics, and diagenesis are the main focus of research (Wei et al. 2021a, b; Fu et al. 2019; Wei et al. 2021a, b). Thus, evaluation technology is relatively comprehensive; however, there is still unclear understanding of the control parameters of high-quality reservoirs. The difficulties in reservoir evaluation caused by this have greatly hindered progress in subsequent oil and gas exploration.

To solve the above problems, the microporosity and diagenesis of the tight carbonate reservoir were comprehensively studied using casting thin section analysis, rock physical property analysis, and capillary pressure test data. The BP neural network algorithm is used to identify and predict the fractures in the reservoir. Based on the above evaluation, there are four types of reservoirs. Through the quantitative analysis of the analytic hierarchy process, the reservoir quality distribution map of the study area is generated by integrating the above reservoir influencing factors, which provides a plan and basis for the fine exploration and development of tight carbonate reservoirs.

Geological setting

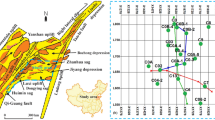
The Ordos Basin is located in the western part of North China that is 600-km long the north to south, 50–100 km wide from the east to west and covers an area of ~ 50,000 km2. It is a cratonic rectangular tectonic basin with complex changes (Fig. 1a). According to the distribution form of the basin, it can be divided into six primary structural units: Yimeng uplift, Weibei uplift, western Shanxi spoiler belt, Yishan slope, Tianhuan syncline, and western margin thrust fault structural belt. The Sulige gas field is located in the north of the middle of the Ordos Basin, which belongs to the north of the Yishan slope belt. In terms of region, Suligemiao is the regional boundary, extending to Etuoke Banner in the west and adjacent to the Jingbian gas field in the south (Fig. 1b). The study area is located in the east of the Sulige gas field, with an area of 65 km2 (Fig. 1c). The Upper Paleozoic strata developed from top to bottom, including Permian Taiyuan Formation, Carboniferous Benxi Formation, and Ordovician Majiagou Formation. The 5th member of the Majiagou Formation (M5) can be divided into 10 submembers (M51, M52, …, M510) based on petrology and sedimentary cycles (Yang et al. 2011). The research horizon is the Ma5 submember of the Majiagou Formation of the Ordovician System, with a reserve of 2.17 billion m3 and a buried depth of 3100–3160 m (Fig. 1d). It is a typical carbonate lithologic gas reservoir.

Fig. 1
figure 1

a Location of the Ordos Basin in China, b tectonic units of the Ordos Basin, c well location map of the study area, and d stratigraphic column of the Majiagou Formation in the study area

Full size image

Methods

This study comprehensively studied the characteristics of tight carbonate reservoirs using core samples, cast thin sections, physical properties testing, and capillary pressure testing data. Based on well logging data, use the BP neural network algorithm in machine learning to identify and predict fractures in reservoirs. Compare and verify the recognition results with logging imaging. Finally, through quantitative analysis using the Analytic Hierarchy Process, a comprehensive evaluation map of the reservoir in the study area was generated by integrating the aforementioned influencing factors of the reservoir (Fig. 2).

Fig. 2
figure 2

Reservoir evaluation process based on fracture identification and Analytic Hierarchy Process

Full size image

Data acquisition

Samples were taken from carbonate rock cores of the Ma55 submember in the east of Sulige. To eliminate the interference of impurities and organic matter and ensure the reliability of the test results, the test samples were taken with a microdrill after hand specimen observation. Test and analysis include slice identification (74 pieces), physical property test (33 pieces), and capillary pressure test (20 pieces).

Samples for thin section analysis were taken from 15 coring wells in the study area, such as SD39-62C1 and SD40-66. Subsequently, the thin sections were stained with a mixed solution of alizarin red and potassium ferricyanide and observed under a DMLP-217400 high power microscope to distinguish the rock composition, pore, and throat (Table 1) at 15–20℃.

Table 1 Partial thin slice identification samples
Full size table

Based on the measurement method of rock porosity and permeability under overburden pressure SY/T 6385-2016, porosity and permeability measurements were performed with Ultrapore-300 and PoroPDP-200 at the Institute of Sedimentary Geology, Chengdu University of Technology (Table 2). During sample processing, the extremely low deviation of sample length and diameter was ensured, along with the accuracy of test results by prolonging the time of the test process. The slippage effect refers to the phenomenon where the gas molecules near the surface of the channel wall have a non-zero flow velocity during the process of gas seepage through the medium channel (Wang et al. 2008). The larger the slip factor, the greater the slip effect. Due to the existence of the slip effect, the calculation of permeability using Darcy's law is not accurate, so a Kirschner correction was performed. The error of permeability measurement value should not exceed ± 3%, and the accuracy should be 0.001 × 10−3 μm2.

Table 2 Partial overburden porosity and permeability analysis samples
Full size table

In the State Key Laboratory of Oil and Gas Reservoir Geology and Development Engineering of Chengdu University of Technology, high-pressure mercury was injected into 20 core plugs from six coring wells using an AutoPore IV9500 mercury injection meter at 0–227 MPa based on the industrial standard SY/T5346-2005 (China).

Moreover, imaging logging data of 4 wells and logging curve data of 32 wells were collected from PetroChina Changqing Oilfield Company.

Fracture identification by the backpropagation neural network

The fracture identification accuracy of conventional logging is usually ~ 50%, which cannot effectively characterize the fracture attribute characteristics. Hence, the BP neural network method was adopted herein based on logging multifactor identification. The neural network is used to learn the sample data of multiple input logging curves and the learning model is built. The generalization performance of the model is enhanced by continuously improving the parameters of the model. Finally, fractures can be identified through the trained model.

Sample data processing

Various logging interpretation methods are usually used for reservoir evaluation; however, different logging data have different sensitivities to reservoir fracture development and corresponding response characteristics (Deng et al. 2009). In general, five logging curves, namely, acoustic transit time (AC), compensated neutron (CNL), caliper (CAL), density (DEM), and shallow detection induction logging (RLLD), have a large contribution rate to fracture density and the least impact on each other (Deng et al. 2006; Lan et al. 2020). Hence, they are selected for BP neural network modeling. After removing obvious abnormal data points, the logging curve was normalized before substituting it into the network. As shown in Eq. 1, the linear normalization method was adopted for logging curves such as AC. Some data are shown in Table 3

$$\begin{array}{c}R=\frac{V-{V}_{min}}{{V}_{max}-{V}_{min}},\#\end{array}$$
(1)

where R is the normalized value, V is the measured data of logging curve, Vmin is the minimum value, and Vmax is the maximum value.

Table 3 Some training samples after normalization
Full size table

Establishing the backpropagation neural network model

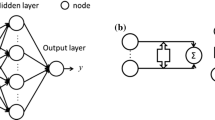
The BP neural network method, also known as the error reverse transfer algorithm, is composed of the input layer, hidden layer, and output layer. It is a mathematical structure model imitating biological neurons. The method has three stages. First, in positive signal transmission, the data in the learning sample enters the neural network model through the input layer and is output by the output layer after being processed by the neurons in the hidden layer. Second, in reverse error transfer, the error is compared between the actual output and the expected output and the gradient descent method is used to adjust the weight of each layer of neurons. Third, in cyclic iteration, the above process is repeated until the output error reaches a satisfactory accuracy or the number of iterations reaches the preset value (Fig. 3).

Fig. 3
figure 3

Structure of the BP neural network model

Full size image

In the second process, the Bayesian regularization method is used to optimize the model to improve the generalization ability of the BP neural network. As shown in Formula (2) (Jorjani et al. 2008), each node in the output layer and hidden layer will mainly be used as the sum point and the input from each node in the previous layer will be merged and modified.

$$\begin{array}{c}{s}_{i}=\sum_{j=1}^{m}{x}_{i}{w}_{ij}+{b}_{j},\#\end{array}$$
(2)

where si is the net input of the hidden layer or output layer to node (neuron) j, xi are the inputs to node j, wij are the weights representing the strength or weakness of the connection between the ith and jth nodes, and bj is the bias or threshold associated with node j.

For nonlinear relations, hyperbolic tangent sigmoid (tansig) and logarithmic sigmoid (logsig) with outputs between [0,1] and [− 1, 1] are commonly used transfer function types in the hidden layer of artificial neural networks.

These functions are shown in Eqs. (3) and (4), respectively.

$$\begin{array}{c}f\left({s}_{i}\right)=\frac{{e}^{{s}_{j}}-{e}^{-{s}_{j}}}{1+{e}^{-{s}_{j}}}\#\end{array}$$
(3)
$$\begin{array}{c}f\left({s}_{i}\right)=\frac{1}{1+{e}^{-{s}_{j}}},\#\end{array}$$
(4)

where f (si) is the output of the node, i.e., the input of the next layer.

Model validation

The network model obtained after network training has a fixed connection weight value and weight coefficient, and the model needs to be tested through validation data. To verify the network model, this paper mainly compares the calculation results of imaging logging data with the original imaging interpretation results after verifying the data network forward operation.

Fine classification evaluation method of the reservoir based on the analytic hierarchy process

The classification and evaluation of carbonate reservoirs are a process from macro to micro, from qualitative to quantitative. The indicators involved are complex, and the parameters are obtained in various ways. Hence, it is a complex process. In actual operation, the proportion of each evaluation index will change accordingly based on different geological conditions. To solve this problem, the analytic hierarchy process (AHP) is introduced.

Establishing the evaluation index hierarchy

The AHP is a process of modeling and quantifying the decision-making thinking process of decision makers for complex systems. With this method, decision makers can obtain the weight of different schemes by decomposing complex problems into several levels and factors and comparing and calculating the factors to provide a basis for the best choice (Lian 2007).

Assume that the target layer is layer A, which only includes one factor, namely, the evaluation of the tight carbonate reservoir; the highest criterion layer under it is layer B, with n factors. The lower subcriteria level varies from place to place (Fig. 4). The lines between layers indicate that the connected lower layer factors contribute to the upper layer factors, and all the lower layer factors contribute to the target layer, thus forming a hierarchical structure that is subdivided from top to bottom and assembled from bottom to top.

Fig. 4
figure 4

AHP index hierarchy

Full size image

Build judgment matrix

In the hierarchical construction, each element of the same layer belonging to each element of the upper layer is compared in pairs to compare its importance to the criteria and quantified based on the scale specified in advance to form a matrix, i.e., a judgment matrix. For n indicators of B at the same level, judgment matrix A can be obtained by comparing them in pairs. The element is aij = bi/bj, where aij represents the ratio of the importance or contribution of criterion bi to bj for target A, and the relative importance is determined by the 1–9-bit scale method.

Hierarchical ranking and consistency check

Hierarchical ranking can be attributed to the problem of calculating the eigenvalues and eigenvectors of the judgment matrix. The maximum eigenvalue \({\lambda }_{max}\) of judgment matrix B and the corresponding normalized eigenvector W is calculated, where W = (W1, W2,…, Wn) is the single sorting weight of B1, B2,…, Bn for the elements of the upper level. The basic steps are as follows.

Each column vector of matrix \(\mathbf{B}={\left({b}_{ij}\right)}_{n\times m}\) is normalized.

$$\begin{array}{c}{\widetilde{W}}_{ij}=\frac{{b}_{ij}}{\sum_{i=1}^{n}{b}_{ij}}\#\end{array}$$
(5)

The \({\widetilde{W}}_{ij}\) are sum by row.

$$\begin{array}{c}{\widetilde{W}}_{i}=\sum_{j=1}^{n}{\widetilde{W}}_{ij}\#\end{array}$$
(6)

\({\widetilde{W}}_{i}\) is normalized.

$$\begin{array}{c}{W}_{i}=\frac{{\widetilde{W}}_{i}}{\sum_{i=1}^{n}{\widetilde{W}}_{i}}\#\end{array}$$
(7)

Subsequently, there is eigenvector \(\widetilde{W}\)= (\({W}_{1}\), \({W}_{2}\)…\({W}_{n}\)). Finally, the maximum eigenvalue is calculated, corresponding to the eigenvector \({\lambda }_{max}\) approximate value of

$$\begin{array}{c}{\lambda }_{max}=\frac{1}{n}\sum_{i=1}^{n}\frac{{\left(AW\right)}_{i}}{{W}_{i}}.\#\end{array}$$
(8)

Maximum characteristic value \({\lambda }_{max}\) is used to check the consistency of the judgment matrix, i.e., to check the rationality of the matrix and define the consistency index \(CI=\frac{{\lambda }_{max}-n}{n-1}\), which measures the degree of inconsistency of the judgment matrix. To judge whether matrix B is consistent, CI is compared with the average random consistency index RI, and CR = CI/RI is the random consistency ratio of the judgment matrix. If CR < 0.10, the matrix is considered to have satisfactory consistency. Finally, the composite weight of reservoir evaluation index is obtained.

Results

Sedimentary characteristics

The study area is generally located in tidal flat facies and evaporation tidal flat facies. The Ma55 sedimentation period is in the relative regression period. The water body is relatively deep, the seawater salinity is generally low, the rock type mainly develops micrite limestone, and the intertidal granular beach is locally developed. In addition, owing to underwater uplift in some areas, the terrain is relatively high and the water body is shallow, and thus, muddy powder crystal dolomite containing gypsum pseudocrystal is developed. During the period from Ma553 to Ma552, it is generally in the intertidal subtidal sedimentary environment, mainly developing some ash flats and ash cloud flats, reflecting the underwater low-energy environment. Local uplift, evaporation and dolomitization, forming some debris shoals (Fig. 5). Since Ma551, the sea level has decreased greatly, the exposed parts of the platform have increased, and the development range of cloud flat and beach body has become wider.

Fig. 5
figure 5

Sedimentary mode of the transverse section of the Ma55 member

Full size image

Rock type

The Ma55 submember is carbonate deposit, and reservoir rock types can be divided into limestone and dolomite and further subdivided into eight types of combination. Microcrystalline limestone, granular limestone, laminated limestone, argillaceous limestone, and karst breccia limestone are the types of limestone. Crystalline dolomite, residual texture dolomite, and calcareous dolomite are the types of dolomite. Dolomite grains are mostly powder crystal and above, and the maximum can reach medium crystal, while microcrystalline dolomite is not developed. The Ma55 submember is strongly controlled by sedimentation. Dolomite is mainly the product of two dolomitization processes, namely, quasicontemporaneous dolomitization and burial dolomitization, and its plane distribution is lenticular (Fig. 6).

Fig. 6
figure 6

Plan distribution of dolomite in sublayer Ma551

Full size image

Physical characteristics of the reservoir

Porosity and permeability characteristics

Based on the statistical analysis of 170 reservoir samples, the Ma55 submember in the study area belongs to an ultralow porosity and ultralow permeability reservoir. Porosity is mainly distributed from 2 to 10%, accounting for 70.71% of the total samples. Permeability is mainly distributed in 0–1 × 10−3 μm2, accounting for 71.43% of the total samples. A porosity of 0.1–11.19% (average 4.27%) and a permeability distribution of 0.01–38.89 × 10−3 μm2 (average 2.72 × 10−3 μm2) are calculated for sublayer M551. For the Ma552 sublayer, a porosity of 0.22–12.02% (average 4.67%) and permeability distribution of 0.01–32.36 × 10−3 μm2 (mean 3.83 × 10−3 μm2) are calculated. For the Ma553 sublayer, a porosity of 0.2–13.86% (average 4.82%) and permeability distribution of 0.01–83.28 × 10−3 μm2 (mean 4.61 × 10−3 μm2) are measured (Figs. 7, 8).

Fig. 7
figure 7

Porosity (a) and permeability (b) distribution of the submember Ma55 reservoir

Full size image
Fig. 8
figure 8

Vertical distribution characteristics of porosity (a) and permeability (b) of the submember Ma55 reservoir

Full size image

Porosity and permeability characteristics of reservoirs with different lithologies

Using statistical analysis, the porosities of the medium crystal, fine crystal, and silty dolomite are 5.17–13.1% (average 9.48%) and their permeabilities are 0.0096–5.28 × 10−3 μm2 (average 1.8 × 10−3 μm2). This is the best physical properties of all reservoir rock types and high-quality reservoirs in this study area. However, microcrystalline limestone and microcrystalline dolomitic limestone have low porosity and permeability and basically no have storage capacity (Table 4).

Table 4 Statistics of the physical properties of the reservoir with different lithologies
Full size table

Reservoir space and pore throat structure characteristics

Type of reservoir space

The reservoir space of carbonate rocks can be grouped into primary pores, secondary pores, and fractures. Using core observation and thin section identification, it is believed that the pore types of the Ma55 member in the study area include both the pores retained during sedimentation and the pores formed during diagenesis. The primary pores are mainly bird eye pores, the secondary pores are mainly intercrystalline pores and dissolution pores, and other secondary pores are relatively rare.

The bird eye holes in the study area are distributed in muddy limestone and muddy dolomite in the supratidal zone. The bird eye structure is formed after the air bubbles dry and shrink, and some of them are filled with sparry calcite or gypsum to form bird eye holes (Fig. 9A). Most of the pores are round with a pore size of 0.8–2.5 μm.

Fig. 9
figure 9

Types of different reservoir spaces: a SD39-57 3131.02 m, bird eye holes. b SD37-58 3113.87 m, intergranular pore. c SD39-62C1 3107.45 m, karst cave. d SD345 3981.8 m, silty fine crystalline dolomite and karst fissure. e SD39-57 3125.83 m, microfracture. f SD39-62C1 3129.74 m, structural joints

Full size image

Intercrystalline pores can be seen in the medium crystal, fine crystal, and silty dolomite (Fig. 9B), and pore sizes are 5–25 μm. Most of the pores are polyhedral or tetrahedral, most of them are unfilled, and a few are filled with mud, with porosities of 1–20%. The better and more complete the crystal form of dolomite is, the more developed its pores will be. The solution pores, caves, and fractures account for a large proportion in the Ma55 submember, usually accounting for 17–46%, mainly in dolomite and limestone (Fig. 9C). The pore size of the dissolved pore is 50–200 μm, that of the karst cave is usually 1–3 μm (2–4 μm), and the pores are irregular and round and partially unfilled and partially filled with calcite, gypsum, and quartz. The maximum surface porosity is 17% (average 1.8%). Some solution pores and cavities are developed in places with more intergranular pores, and some are developed in places where sutures and solution fractures are connected with the outside world.

Open fractures are the main structural fractures, which are the products of tectonic movement (Fig. 9d–f). The occurrence probability of the samples is 18.6%, and most of them are not filled with other substances. The edge broken particles caused by stress can be occasionally seen at the edge of these cracks. The reservoir performance will be greatly improved when the fracture connects with the solution hole or solution cave.

Structural characteristics of pore throat

The pore throat structure of the Ma55 subsegment is mainly microthroat (Table 5). The displacement pressure is 0.03–8.54 MPa (average 1.16 MPa). The median pressure is 1.6–191.4 MPa (average 45.01 MPa). The mercury removal efficiency is low, i.e., 10.7%–37.7% (average 26.5%). The sorting coefficient is 1.5–2.9 (average 2.4), mainly between 1 and 2.

Table 5 Structural parameters of the pore throat of the ma55 subsegment in East Sulige
Full size table

Based on the above analysis, the capillary pressure curve and pore structure parameter characteristics of the Ma55 submember are categorized into four types. Type I pore structure is dominated by fine medium pore throat, the capillary pressure curve is concave to the lower left, and there is a long approximate horizontal section in the middle (Fig. 10a), indicating that the pores are relatively uniform, well sorted with high drainage pressure, and belong to the type of good reservoir pore structure. Types II and III pore structures are mainly micropore throat type, and the capillary pressure curve has a certain concave convex section (Fig. 10b, c), which belongs to the general reservoir pore structure type. Type IV belongs to the worst reservoir pore structure type, and there is no obvious platform for the capillary pressure curve (Fig. 10d). See Table 6 for specific parameter characteristics.

Fig. 10
figure 10

Type of capillary pressure curve of the Ma55 submember reservoir in East Sulige

Full size image
Table 6 Classification of the pore structure of the Ma55 submember in East Sulige
Full size table

Fracture identification and model verification of the backpropagation neural network

Based on MATLAB, the model adopts a three-layer structure, namely, one input layer, one hidden layer, and one output layer. The number of input layer nodes is 5, which are the normalized five logging parameter values. According to experience, the number of hidden layer nodes is 1.5–2.5 times the input layer, and it is finally determined to be 10 through testing. The output layer has only one node, i.e., the normalized fracture density. The number of model training samples is 21. Through many tests, it is finally determined that the test results obtained after six iterations can better predict the results (Fig. 11).

Fig. 11
figure 11

Training error propagation curve of the constructed three-layer BP neural network

Full size image

Taking well SD38-60A as an example, the imaging logging image of fractures development shows a dark sine wave curve. The number of fractures can be identified quantitatively based on the imaging logging image (Zhang et al. 2018). The comparison verification shows that the BP neural network model identification result is good compared with the imaging logging image, and the curve response is obvious. The overall accuracy rate of identifying fractures is up to 80%, which is considerably higher than the accuracy rate of conventional logging interpretation (Fig. 12).

Fig. 12
figure 12

Comparison between fracture identification results and imaging logging

Full size image

For facilitating the application of reservoir evaluation, fracture identification was performed on 27 wells in the study area, and the contour map of fracture development probability in the whole area was drawn to intuitively display the fracture development probability and development degree in the study area (Fig. 13), providing a basis for later comprehensive reservoir prediction. The area with high fracture development probability is mainly concentrated in the middle and northwest of the study area, around SD38-60A and SD-ZC6 wells, up to 0.92, which is the basis for good reservoir conditions.

Fig. 13
figure 13

Contour map of fracture development probability in the study area

Full size image

Discussion

Determination of the synthetic weight of evaluation factors by analytic hierarchy process

Using core observation, physical property analysis, scanning electron microscopy, casting thin section, and other experimental techniques, the distribution characteristics of sedimentary microfacies, petrological characteristics, macrophysical and microstructural characteristics, seepage structure characteristics, and productivity phase distribution characteristics of the reservoir of interest are studied to judge the physical properties of the reservoir. Finally, the distribution characteristics of all parameters in the study area are summarized. A set of classification and evaluation system standards of the Ma55 subsegment in the study area was formulated. Based on the principle of the AHP, the evaluation indicators are divided into three first-level indicators, namely, sedimentary facies, physical parameters, and microscopic parameters, including nine second-level indicators (Table 7).

Table 7 Evaluation criteria for reservoir classification of the Ma55 submember
Full size table

By constructing the judgment matrix of each level and using the calculation method of the AHP, the weight of factors of each level can be obtained through the overall ranking of levels, as shown in Table 8. The composite weight of Fracture development probability is the highest, reaching 0.216. Next are porosity and permeability, with synthetic weights of 0.2. The Fracture development probability determines the distribution pattern of fractured oil and gas reservoirs and has a direct impact on the productivity of oil and gas wells. In tight reservoirs, fractures not only control the distribution of oil and gas reservoirs but also are the focus of research on oil and gas reservoir development plans. Porosity and permeability are the two most important parameters in the study of reservoir characteristics, which are also applicable to tight gas reservoirs. In addition, Subfacies and microfacies, pore structure types, pore filling types, and dolomite thickness are also important factors affecting reservoir quality, with composite weights of 0.128, 0.118, 0.072, and 0.057, respectively.

Table 8 Composite weights of reservoir evaluation indexes
Full size table

Distribution characteristics of the reservoir

A comprehensive evaluation map of the reservoirs of the three sublayers of the Ma55 subsegment is prepared from the above classification evaluation criteria and synthetic weights. A Class I reservoir is a high-quality reservoir in the study area and is mainly distributed in the middle and northwest of the study area. Its plane distribution is lenticular, and it is mainly distributed at 3113–3125 m vertically, represented by well SD 37-58. Sublayer M551 is the interval with the most exploration potential, and the area of the Class I reservoir is 11.86 km2 (Fig. 14). We have compiled and calculated the daily average gas production of 20 wells, and there is a clear correspondence between the production and evaluation results, indicating that the reservoir evaluation effect is good.

Fig. 14
figure 14

Comprehensive evaluation map of the sublayer Ma551 reservoir

Full size image

Summary and conclusions

In order to predict the high-quality reservoir of a tight sandstone, we applied the backpropagation neural network for fracture identification and the analytic hierarchy process for quantitative reservoir evaluation. After all, the following conclusions could be drawn:

  1. 1.

    Carbonate sediments are developed in the Ma55 submember in the eastern Sulige area composed of tidal flat facies and evaporative tidal flat facies as a whole. The medium crystal, fine crystal, and powder crystal dolomites are the best among all reservoir rock types. Reservoir space types are abundant, dominated by bird eye pores, intercrystalline pores, dissolution pores and structural fracture.

  2. 2.

    Five logging parameters, namely, AC, CNL, CAL, DEN, and RLLD, were selected to establish the BP neural network model and identify fractures in 27 wells. The results indicate that the areas with a high probability of fracture development are mainly concentrated in the central and northwest regions of the research area, around wells SD38-60A and SD-ZC6, with a maximum of 0.92. The logging identification result matches well with the imaging logging image, with an accuracy of 80%. Compared to conventional logging identification methods, the accuracy is significantly improved. This provides a basis for the later comprehensive reservoir prediction.

  3. 3.

    According to sedimentary microfacies, physical property characteristics, microporosity, and fracture characteristics, the reservoirs of the Ma5 submember in the eastern Sulige area are divided into four types. Reservoirs can be classified into four types according to their quality. According to the principle of the AHP, a set of classified evaluation system structures including three first-level indicators and nine second-level indicators are established. The results show that porosity, permeability, and fracture development probability are the most important evaluation parameters, and the synthetic weights are 0.2, 0.2, and 0.216, respectively. The high-quality reservoirs in the study area are mainly distributed in the central and northwestern parts of the study area.