Introduction

The high costs of drilling operations have led to a significant focus on the reduction in operation time and spending costs (Abbas et al. 2019). The rate of penetration (ROP) is significant in optimizing the drilling process of a well so that it can be accurately estimated to provide better planning of future well drilling and drastically minimize the additional costs (Ayoub et al. 2017). Rate of penetration is the speed at which the drill progresses to the ground layers, which is usually expressed in units of feet per hour (Al-AbdulJabbar et al. 2018b). The ROP is affected by various independent variables, which, solely by optimizing these independent parameters, the maximum rate of penetration can be achieved (Khosravanian et al. 2016). Some of these variables can be controlled during the operation, while others cannot be controlled due to economic and environmental issues. Important controllable variables include weight on bit, and rotary speed, which are usually considered in most drilling process optimization instances (Abbas et al. 2018). The complexity of the ROP estimation is due to the nonlinear impact of some variables. For example, the excessive elevation of some parameters such as weight on bit and rotary speed can cause rapid bit erosion, improper borehole cleaning, and drill string instability, which ultimately results in reduced ROP. Therefore, it is necessary to determine the optimum values of each of these parameters in order to avoid drilling problems, which can impede an ideal drilling scenario, while increasing the drilling speed (Yi et al. 2014).

In recent decades, major research has been done to achieve a comprehensive mathematical model of ROP. Most of the models presented in the research background use three variables of weight on bit, rotary speed, and pump flow rate in their calculations (Al-AbdulJabbar et al. 2018a). These models have constants that must be calculated for each formation, and assumptions that have to be considered such as complete borehole cleaning (Amer et al. 2017). Galle and Woods (1963) developed a mathematical model based on drilling bit rotation, weight on bit, type of formation, and bit erosion. Bingham (1965) presented his penetration rate model based on laboratory data, in which the ROP is considered a function of weight on bit, rotary speed, and bit diameter. Bourgoyne Jr and Young Jr (1974) model is one of the most comprehensive mathematical models for predicting ROP. This model is presented to determine the effect of different parameters on ROP by multiplying the eight different functions, which each has eight individual constants. Wiktorski et al. (2017) modified the Bourgoyne and Young model to account for dog leg severity (DLS) and the equivalent circulation density of the drilling fluid (ECD) and proved that the new model achieved higher accuracy than the classic model. Al-AbdulJabbar et al. (2018a) presented a new mathematical model for ROP estimation that used drilling operation parameters and drilling fluid properties for the development and evaluation of this model. The results showed that the model was developed with accuracy in estimating ROP. They also concluded that ROP is highly dependent on parameters such as weight on bit, rotary speed, torque, horsepower, and fluid properties such as: plastic viscosity, and density of drilling mud. Darwesh et al. (2020) used the Bourgoyne and Young model to optimize the values of controllable drilling parameters using data from 23 drilled oil wells in northern Iraq. They also mentioned the necessity of noise reduction and homogeneity assumptions elimination through clustering and averaging methods. Due to the limitations as well as the complexity of the relationship between the variables affecting ROP, so far, the mathematical models presented in the research background have not been able to estimate the penetration rate accurately (Yi et al. 2014). Nowadays, different methods of machine learning can be utilized as a powerful tool in ROP estimation as they are rapidly growing and expanding (Yang et al. 2007). These methods are also used in many different aspects of the oil and gas industry (Ahmadi et al. 2015; Rahmati and Tatar 2019; Fath et al. 2020; Khamis et al. 2020).

Elkatatny (2019) used a new artificial neural network (ANN) model combined with the self-adaptive differential evaluation (SaDE) method to estimate ROP. The proposed model had a structure with five inputs and thirty neurons in the hidden layer, which estimated ROP with mechanical drilling data and drilling fluid properties, which were collected from a well. Zhao et al. (2019) used neural networks combined with three Levenberg–Marquardt (LM), scaled conjugate (SG), and one-step secant (OSS) training functions to estimate penetration rates. Ultimately, the model obtained from neural networks was combined with a bee colony algorithm to determine the optimal value of each drilling parameters in order to achieve maximum ROP. Anemangely et al. (2018) used a combination of MLP neural networks with cuckoo optimization algorithm (COA) and particle swarm optimization (PSO) algorithm to estimate ROP. They collected the required data from a well drilled in the Karanj oil field, and after noise reduction and feature selection, used the data in model development process. The results of this study showed that the COA-MLP method has higher accuracy than PSO-MLP. Wang and Salehi (2015) investigated the estimation of pump pressure using a three-layer neural network with 12 input variables and 11 neurons in the hidden layer. They used data collected from three drilled wells after splitting them into three subsets of training (75%), validation (15%), and testing (10%) in the modeling process. Lashari et al. (2019) used the backpropagation neural network model to approximate ROP and proved that the developed model has good performance for monitoring and optimizing the drilling process.

In this paper, three computational intelligence (CI)-based models are used to estimate ROP. These models are multilayer perceptron neural network optimized by backpropagation algorithm (BP-MLPNN), cascade-forward neural network optimized by backpropagation algorithm (BP-CFNN), and radial basis function neural network optimized by biogeography-based optimization algorithm (BBO-RBFNN). The required data for developing the models are collected from the mud logging unit and the final reports of four drilled wells, which were combined into an integrated dataset. These wells are located in southwestern Iran, which consisted of Well 1 from Field A and Well 2, Well 3, and Well 4 from Field B. Before the modeling procedure, the collected data were analyzed to remove the outliers, and then Savitzky–Golay (SG) smoothing filter was applied to the remaining 7563 data points to reduce overall data noises. In the next stage, nine input variables were selected during a feature selection step by combining the BP-MLPNN and NSGA-II algorithm. Also, two mathematical ROP models including Bourgoyne and Young model (BYM) and Bingham model were used to broaden the comparisons. The results of this study can be contributed to the planning and optimizing of the drilling process in future wells.

Theoretical foundations of research

Multilayer perceptron neural network (MLPNN)

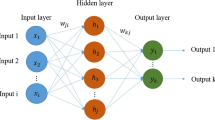
The human brain contains a large number of interconnected neurons that are responsible for learning and processing information. The complexity of the human brain is tremendous, so the construction of artificial neural network is only inspired by the structure of the connections between brain neurons. Thus, ANN is a data processing system that seeks to mimic the functional characteristics of the human nervous system and to create a computer model through which data patterns and correlations between variables can be found (Al-Azani et al. 2019). Multilayer perceptron neural networks are one of the types of feedforward neural networks consisting of three layers, including the input layer, the middle layer, and the output layer. Figure 1 shows the structure of an MLP neural network.

Fig. 1
figure 1

The structure of a three-layer neural network

Full size image

The mathematical equation of an MLP neural network, including n inputs and k neurons in the hidden layer can be written as shown in Eq. 1:

$$y = f^{o} \left( {\omega^{b} + \mathop \sum \limits_{i = 1}^{k} \omega_{j}^{o} f^{h} \left( {\omega_{j}^{b} + \mathop \sum \limits_{i = 1}^{n} \omega_{ji}^{h} x_{i} } \right)} \right)$$
(1)

In this equation, \(f^{o}\) is the activator function in the output layer, \(f^{h}\) is the activator function in each neuron of the hidden layer, \(\omega^{b}\) is the value of bias added to the output layer, and \(\omega_{j}^{b}\) is the value of bias added to the hidden layer. In multilayer perceptron neural network, each input is first multiplied by a certain weight and then transferred to the middle layer for necessary calculations. In the middle layer, neurons with nonlinear functions are deployed, which, after collecting the weighted values of inputs, transmit these values to a specified interval. Sigmoid activation function (Eq. 2) is one of the most commonly used functions in neural networks (Soofastaei et al. 2016).

$$f\left( x \right) = \frac{1}{{1 + e^{ - x} }}$$
(2)

The supervised learning method is used to train and update network weights. In the supervised learning method, the values of the network weights are randomly selected, and then the output value is calculated for each of the network inputs. The network weights and bias are updated as long as the stopping conditions are met, and the error between the actual and output values reaches a reasonable level. The network weights update function is presented in Eq. 3:

$$W_{{ij\left( {t + 1} \right)}} = W_{ij} \left( t \right) + \eta \frac{\partial f\left( e \right)}{{\partial W_{ij} }}$$
(3)

where \({W}_{ij}\) represents the weight parameter \(i\) in layer \(j\), \(t\) represents the iteration of training, \(\partial f(e)\) denotes the error function and \(\eta\) is the learning rate (Hordri et al. 2017).

Cascade-forward neural network (CFNN)

Today, the remarkable achievements of neural networks are used for modeling and forecasting in complex systems. Neural network techniques are used with almost identical architectures for processing and training the existing knowledge of the data. Cascade-forward neural network (CFNN) is a class of neural networks which is different and more complex than the conventional feedforward neural networks. In CFNN, weighted links from the input layer to the output layer and each hidden layer are added, which led to the possibility of learning the complex patterns of data and the consideration of the direct effect of inputs on outputs. For example, in a three-layer network, the output layer is directly attached to the input layer and the hidden layer. An optimal network structure can be achieved by incremental search method in hidden units and by considering the mean square error criterion. The equation derived from the structure of this network can be written as Eq. 4:

$$y = \mathop \sum \limits_{i = 1}^{n} f^{i} \omega_{i}^{i} x_{i} + f^{o} \left( {\omega^{b} + \mathop \sum \limits_{j = 1}^{k} \omega_{j}^{o} f^{h} \left( {\omega_{j}^{b} \mathop \sum \limits_{i = 1}^{n} \omega_{ji}^{h} x_{i} } \right)} \right)$$
(4)

In this equation, \(f^{i}\) and \(\omega_{i}^{i}\) are activation functions and weight values from the input layer to the output layer, respectively. \(f^{h}\) is the activation function of each neuron in the hidden layer, \(f^{o}\) is the activation function in the output layer, \(\omega^{b}\) is the amount of bias added to the output layer, and \(\omega_{j}^{b}\) is the amount of bias added to the hidden layer. Figure 2 shows the structure of a neural network (Warsito et al. 2018).

Fig. 2
figure 2

A simple structure of a cascade-forward neural network

Full size image

Radial basis function neural network (RBFNN)

Radial basis function neural network was first introduced by Moody and Darken (1989). RBFNN are similar to MLP neural network and differ only in how the input data is processed. This network is composed of a hidden layer, in which neurons with radial basis functions are based. The radial basis functions are responsible for mapping the data to the feature space. One of the most important factors that increase the efficiency of RBFNN is the absence of a high number of hidden layers, which in addition to reducing the complexity of computation, results in the determination of the effective number of neurons, based on the problem aspects (Aggarwal 2018). Figure 3 shows the structure of a radial basis neural network.

Fig. 3
figure 3

The structure of a radial basis function neural network

Full size image

Various radial basis functions have been presented so far; among those, the Gaussian activation function is one of the most widely used of these functions, which is presented in Eq. 5 (Rippa 1999).

$$\Phi \left( r \right) = e^{{ - \left( {\frac{{r^{2} }}{{\delta_{i}^{2} }}} \right)}}$$
(5)

In this equation, \(\delta\) is the function width, and \(r\) is the distance between the input \(X\) and the center \(C\). The Kth output from the RBF neural network is obtained in the form of an equation, which can be seen in Eq. 6 (Aggarwal 2018).

$$f\left( {X_{k} } \right) = \mathop \sum \limits_{i = 1}^{h} \Phi_{i} \left( r \right)W_{i} = \mathop \sum \limits_{i = 1}^{h} \Phi_{i}\left( \left\| {X - C_{i} } \right\| \right)W_{i}$$
(6)

where \(h\) is the number of neurons in the middle layers, and \({W}_{i}\) is the weight parameter of the radial basis neural network. After defining the initial centers, the base functions are applied to the intervals between the input vectors and the center of the functions to obtain the hidden layer output (Hordri et al. 2017). In order to calculate the network weights, Eq. 7 is used to minimize the sum of squared errors (SSE) (Chen et al. 2011).

$$SSE = \mathop \sum \limits_{K = 1}^{n} \left( {\mathop \sum \limits_{i = 1}^{n} \Phi \left(\left\| {\left\| X - C_{i}\right\|}\right\| \right)W_{i} - f\left( {X_{j} } \right)} \right)^{2}$$
(7)

Backpropagation algorithm (BP)

The backpropagation algorithm is a supervised learning algorithm that is widely used today to train neural networks. The way this algorithm works is that in each iteration, the input data is entered into the network, and the outputs corresponding to the input data are obtained. After the outputs are obtained, the difference is computed against the actual value and propagated back and forth across the network to update the weights and bias of the network to reduce the error. The algorithm in each iteration tries to reduce the error by changing the weights of the network until the stopping conditions are achieved (Puig-Arnavat and Bruno 2015).

Biogeography-based optimization (BBO)

Biogeography-based optimization algorithm was first introduced by Simon (2008). This algorithm is based on the scientific knowledge of migration and the distribution of species from one habitat to another. Based on the principles of this algorithm, each location has a habitat suitability index (HSI) that functions similarly to the fitness function in other population-centered algorithms. Also, independent variables that determine the suitability index of a settlement are called the suitability index variables (SIV) (Simon 2008). In this algorithm, there are two components of immigration and emigration for each habitat. The high HSI index results in low immigration due to the higher population and high emigration due to fierce competition and lack of resources. While the low HSI index, due to the lower population of the habitat, leads to the migration of other species to the habitat (Santosa and Safitri 2015). Figure 4 graphically shows the ratio of species population to emigration (in blue) and immigration (in red) of each island.

Fig. 4
figure 4

Species population ratio to emigration and immigration of each island (islands with a higher population have more emigration and islands with a lower population have more immigration)

Full size image

In the biogeography-based optimization algorithm, two migration and mutation operators are used to make the desired changes in each iteration. The emigration rate (μk), and immigration rate (λk) can be explained by Eq. 8 and Eq. 9, respectively:

$$\mu_{k} = E\left( \frac{k}{a} \right)$$
(8)
$$\lambda_{k} = I\left( {1 - \frac{k}{a}} \right)$$
(9)

In these equations, \(I\) and \(E\) are the maximum value of immigration and emigration rates, respectively, and \(K\) is the number of species. In the BBO algorithm, the mutation rate is defined as Eq. 10:

$$m\left( s \right) = m_{\max } \left( {1 - \frac{{p_{s} }}{{p_{\max } }}} \right)$$
(10)

In this equation, \(P_{s}\) is the probability of mutation in species causing variation and \(m_{\max }\) is the maximum mutation rate that is user-adjustable. Pschanges from time \(t\) to time (t+1) in the form of Eq. 11:

$$P_{s} \left( {t + 1} \right) = P_{s} \left( t \right)\left( {1 - \lambda_{s} \Delta t - \mu_{s} \Delta t} \right) + P_{s - 1} \lambda_{s - 1} \Delta t + P_{s + 1} \mu_{s + 1} \Delta t$$
(11)

In this equation, \(p_{s}\) is the probability of mutation, \(p_{s} \left( t \right)\) is the probability of the current population remaining without emigration and immigration, (s − 1) is the number of species at the time of t plus the addition of a new species to the habitat, \(\left( {s + 1} \right)\) is the number of species at the time of t plus one emigration or decrease in one species from the habitat. λs and μs, are the immigration rate and the emigration rate for the part s of species, respectively. Equation 11 can be written in the form of Eq. 12 to Eq. 14:

$$\dot{P}_{{\left( {s = 0} \right)}} = - \left( {\lambda_{s} + \mu_{s} } \right)p_{s} + \mu_{s + 1} p_{s + 1}$$
(12)
$$\dot{P}_{{\left( {1 \le s \le s_{\max } - 1} \right)}} = - \left( {\lambda_{s} + \mu_{s} } \right)p_{s} + \lambda_{s - 1} p_{s - 1} + \mu_{s + 1} p_{s + 1}$$
(13)
$$\dot{P}_{{\left( {s = s_{\max } } \right)}} = - \left( {\lambda_{s} + \mu_{s} } \right)p_{s} + \lambda_{s - 1} p_{s - 1}$$
(14)

It can also be written as p = AP where Matrix \(A\) is defined as Eq. 15 (Mao et al. 2019).

$$A = \left[ {\begin{array}{*{20}c} { - \left( {\lambda_{0} + \mu_{0} } \right)} & {\mu_{1} } & 0 & \cdots & 0 \\ {\lambda_{0} } & { - \left( {\lambda_{1} + \mu_{1} } \right)} & {\mu_{2} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & {\mu_{n - 2} } & { - \left( {\lambda_{n - 1} + \mu_{n - 1} } \right)} & {\mu_{n} } \\ 0 & \cdots & 0 & {\mu_{n - 1} } & { - \left( {\lambda_{n} + \mu_{n} } \right)} \\ \end{array} } \right]$$
(15)

NSGA-II algorithm

The NSGA-II algorithm, developed by Deb et al. (2002), is one of the most popular multi-objective optimization algorithms derived from the integration of classical genetic algorithms and non-dominating sorting approaches. The new population in this algorithm is selected based on non-dominating sorting, density estimating, and crowding comparison (Monsef et al. 2019). After creating an initial population, this algorithm applies the fit criterion to the population and calculates the value of the objective function for all the population. The population is then sorted by the predominance condition and congestion distance, and parents with lower rank and greater congestion distance are selected by multi-objective selection methods such as a binary tournament. After intersections and mutations to produce new offspring that speed up the algorithm’s convergence to the optimal solution, individuals from the initial population and the offspring population are merged and re-ranked based on non-dominating sorting and congestion distance. In the end, the highest-ranking people are eliminated, and the best of the population are passed on to the next generation based on the principle of elitism. These steps are repeated until the termination conditions are met (El-Hadidi et al. 2018).

Data collection

Providing appropriate data is one of the most important parts of the development of machine learning-based models; therefore, providing high-quality data with more samples can increase the reliability of these estimating tools (Ahmadi and Chen 2020). The data required for the development of the models were collected from four drilled wells in southwestern Iran. The collected data contained 13 independent variables and one dependent variable (ROP) related to the mud logging unit and the final reports of the wells. The statistical information of these variables is presented in Table 1. The variables included depth, bit diameter (d), weight on bit (WOB), hook load, bit rotation speed, torque (T), standpipe pressure (SSP), drilling mud flow rate (Q), lag time, mud weight (MW), equivalent circulating density (ECD), drilling mud temperature, bit working hours and rate of penetration (ROP). The collected data were first pre-processed with the aim of improving the quality and removing outliers. After removing the outliers, Well-1 from the first oil field contained 2220 data points and Well-2, Well-3, and Well-4 from the second oil field contained 5343 data points. In the next stage, to provide a unified view and form a larger dataset, all collected data from two fields were combined into one data set. After that, the feature selection method was used to improve the training performance of the models and also to prevent the creation of a larger model by reducing the number of inputs.

Table 1 Statistical details of the variables collected from the four drilled wells
Full size table

Data preprocessing

Since raw data has high noise and many outlier data, it is necessary to preprocess it before modeling (Wang et al. 1995). Failure to remove outliers and reduce noise, disrupts the model learning process and increases training time (Quinlan 1986). In this study, outlier data, duplicate data, and empty rows were identified and excluded. Then, to reduce noise, a Savitzky-Golay (SG) smoothing filter was used in the MATLAB software environment with a sgolayfilt function (Savitzky and Golay 1964). This filter performs data noise reduction with a polynomial function, and the smoothing performance depends on the order of polynomial and the frame length, which in this study, the values of these two parameters were selected as 3 and 11, respectively. One of the important advantages of SG smoothing filter is effective noise reduction while maintaining signal characteristics (Moosavi et al. 2018). To see the effect of deletion of outliers and data noise reduction, in Fig. 5, ROP of the total dataset is presented in three preprocessing stages. The noise reduction process was applied to all data collected from the two fields studied. Ultimately, the existing data were normalized by the mapminmax function in the MATLAB environment between values of -1 and 1. Data normalization improves the training process and is required for non-Gaussian distributed data to reduce the standard deviation and sensitivity of the models to the data scale (Tewari and Dwivedi 2020).

Fig. 5
figure 5

Comparison of rates of penetration at different preprocessing stages for the total dataset

Full size image

Feature selection

Selecting the feature or specifying input parameters to the model is one of the most important steps before the modeling process. Selecting a high number of inputs increases the complexity of the modeling. On the other hand, selecting the low number of inputs causes the modeling to be incorrect based on the available knowledge (Ansari et al. 2017). In this study, a combination of MLP neural network and NSGA-II metaheuristic algorithm was used to select inputs. The neural network used incorporates a hidden layer with 22 neurons in which the sigmoid activator function is used. The purpose of applying the NSGA-II algorithm is to solve a two-objective problem whose first purpose is to reduce the number of input variables to the network and the second to reduce the model approximation error (MSE). In each iteration of the NSGA-II algorithm, several variables are randomly selected, and then network training is performed with the backpropagation algorithm and the Levenberg–Marquardt function. At the end of each iteration, the variables that have the least error in a specified number of inputs are determined by the NSGA-II algorithm. The advantage of this method is the high speed and performance of selecting suitable inputs for model training, which significantly reduces the risk of an inappropriate choice.

Data collected from the four wells were used in the feature selection process, which included 13 independent variables and one dependent variable (rate of penetration). Details of the tuning parameters of the NSGA-II algorithm are presented in Table 2. After the 20th iteration, 600 different sets of inputs were selected, and the neural network was executed five times with these inputs so that after the 20th iteration, 3000 runs were obtained from the neural network to obtain the least error value for a given number of inputs. The results obtained in each iteration are shown graphically in Fig. 6. Finally, an appropriate decision must be made between the number of different inputs, and the risk of adding a new variable against a slight increase in model accuracy should be considered. As shown in Fig. 6, the error reduction process in the 20th iteration is prolonged after ten inputs. Also, the error difference between nine inputs and ten inputs is negligible. Therefore, the nine inputs in the 20th iteration of the NSGA-II algorithm are considered as optimal model inputs, namely depth, weight on bit (WOB), hook load, bit rotation speed, torque (T), standpipe pressure (SSP), lag time, drilling mud flow rate (Q), and equivalent circulating density (ECD). The statistical details of these variables are presented in Table 1.

Table 2 NSGA-II algorithm tuning parameters for feature selection
Full size table
Fig. 6
figure 6

The least amount of error in each iteration of neural network based on various inputs (The black line with red dots represents the last iteration of the algorithm, each of which points to a set of inputs that represents the minimum number of network errors in the number of inputs) (colour figure online)

Full size image

Model development

Multilayer perceptron neural network model with the backpropagation algorithm (BP-MLPNN)

The collected data were from the four drilled wells, after preprocessing and selecting nine input variables from them, were randomly divided into two sub-datasets of training (85%) and test (15%). Then, the training datasets with 6428 data points were used to develop and train the models, and the test datasets with 1135 data points were used to evaluate the approximation performance of the models.

After establishing the MLP neural network in MATLAB software, the network was trained by using the backpropagation algorithm with the Levenberg Marquardt function. The optimal number of hidden layers, neurons, and activator function types were determined by a trial-and-error approach based on model training and testing error rates to avoid overfitting. After examining the different structures, finally, a three-layer structure consisting of an input layer, a hidden layer with 25 neurons containing the sigmoidal transfer function, and a final layer with a linear function (Purelin) showed the most desirable performance in model training and testing. The neural network structure used in MATLAB software is shown in Fig. 7. Also, in Fig. 8, the flowchart illustrates how to develop penetration rate estimation models in this study.

Fig. 7
figure 7

Neural network structure developed in the MATLAB software environment

Full size image
Fig. 8
figure 8

Flowchart of the models developed in this study

Full size image

Cascade-forward neural network model with the backpropagation algorithm (BP-CFNN)

In developing the cascade-forward neural network model, a backpropagation algorithm with the Levenberg–Marquardt function was used. Afterward, the performance of different CFNN structures was evaluated during a trial-and-error process. Subsequently, a structure with two hidden layers and a number of 18 and 12 neurons, respectively, for the first layer and the second layer showed the best performance in model training and testing. The sigmoid activator function in the hidden layer, and the linear activator function in the output layer were also used. Figure 9 shows the structure of this network in the MATLAB software environment.

Fig. 9
figure 9

Cascade neural network structure developed in the MATLAB software environment

Full size image

Radial Basis function neural network optimized by biogeography-based optimization (BBO-RBFNN)

To develop the BBO-RBFNN model, the k-means algorithm was first used to determine the initial centers according to the input data distribution. The k-means algorithm assumes that the average of each input data belongs to a cluster with the least distance to the center of that cluster. After determining the initial centers and the number of hidden layer neurons, the tuning parameters and the weights of the output layer were determined in a supervised stage by the BBO algorithm. The optimization algorithms first consider the network-tuning parameters as the dimensions of each of its population members and then modify these parameters in order to reach the terminating condition according to the objective function (Hu et al. 2014). In Table 3, the tuning parameters of the biogeography-based algorithm that are used to optimize the RBFFNN model are presented. To develop the BBO-RBFNN model, the training datasets with 85% of the total data were used. After the training process, the accuracy of the model was evaluated by considering the remaining 15% of the total data.

Table 3 Biogeography-based optimization algorithm tuning parameters
Full size table

Results and discussion

Statistical analysis of the error of each model was evaluated by the average percent relative error (APRE), average absolute percent relative error (AAPRE), root-mean-square error (RMSE), and coefficient of determination (R2). These statistical parameters are defined using Eq. 16 to Eq. 19 (Karkevandi-Talkhooncheh et al. 2017; Zhao et al. 2019):

  • Average Percent Relative Error (APRE):

    $${\text{APRE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\frac{{{\text{ROP}}_{{{\text{field}}}} - {\text{ROP}}_{{{\text{predict}}}} }}{{{\text{ROP}}_{{{\text{field}}}} }}} \right) \times 100$$
    (16)

  • Average Absolute Percent Relative Error (AAPRE):

    $${\text{AAPRE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{{\text{ROP}}_{{{\text{field}}}} - {\text{ROP}}_{{{\text{predict}}}} }}{{{\text{ROP}}_{{{\text{field}}}} }}} \right| \times 100$$
    (17)

  • Root-Mean-Square Error (RMSE):

    $${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} ({\text{ROP}}_{{{\text{field}}}} - {\text{ROP}}_{{{\text{predict}}}} )^{2} }$$
    (18)

  • Coefficient of Determination (R2):

    $$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} ({\text{ROP}}_{{{\text{field}}}} - {\text{ROP}}_{{{\text{predict}}}} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} ({\text{ROP}}_{{{\text{field}}}} - (\frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} {\text{ROP}}_{{{\text{predict}}}} )^{2} }}$$
    (19)

In Table 4, the statistical results obtained from the developed models in this paper for three training, test, and total datasets are presented. In order to examine more accurately the performance of the models, in Fig. 10, regression plots of the real ROP versus predicted value for the two model training and test datasets are presented. Moreover, the comparison of real and predicted ROP values for training and test datasets are presented in Fig. 11.

Table 4 Statistical details of the results obtained from the models developed in this study
Full size table
Fig. 10
figure 10

Regression plots of the real penetration rate versus the predicted penetration rate for the training and testing datasets of developed models

Full size image
Fig. 11
figure 11

Comparison of predicted and real ROP among the BP-MLPNN, BP-CFNN, and BBO-RBFNN models for training and testing datasets

Full size image

One of the proper graphical tools in model error analysis is box plots provided by Tukey (1977). Through these plots, we can examine the distribution of data, the existence of outliers, and the symmetry of the data. Box plots of absolute error (E) for both training and testing sections of developed models are shown in Fig. 12.

Fig. 12
figure 12

Box plots of the absolute error value of the developed models for both training and testing datasets

Full size image

For the smaller values of APRE, AAPRE, and RMSE, it can be inferred that the desired model has higher accuracy in approximation. APRE values are varied in terms of the scale range and cannot be used alone to model error analysis. However, the AAPRE values compute an absolute value of the APRE, which the performance of the model can be well analyzed through this computation. Also, through R2, it can be determined what percentage of the model outputs can be defined by the fitted line on the data points, and the proximity of this index to one indicates that the model has good accuracy in approximation (Gholami et al. 2016; Karkevandi-Talkhooncheh et al. 2017). Accordingly, the BBO-RBFNN model with satisfying APRE, AAPRE, RMSE and R2values of  − 0.523, 5.380, 0.481, and 0.950 for the training dataset, respectively; and values of − 1.057, 6.388, 0.536, and 0.940 for the test dataset, respectively, can be considered as the best accurate model compared to the other two developed models. Also, it can be deduced from the regression plots that the BBO-RBFNN model has the highest correlation between the predicted and real values.

To broaden the comparisons, two mathematical ROP models of Bourgoyne and Young (BYM) and Bingham were used, which their mathematical relations are shown in Eq. 20 and Eq. 21, respectively. Further details of these models are provided in the research literature (Bingham 1965; Bourgoyne and Young 1974).

$${\text{ROP}} = a\left( {\frac{{{\text{WOB}}}}{Db}} \right)^{b}$$
(20)
$$\frac{{{\text{d}}f}}{{{\text{dt}}}} = e^{{\left( {a_{1} + \mathop \sum \limits_{j = 2}^{8} a_{j} x_{j} } \right)}}$$
(21)

In Fig. 13, the real ROP values from the total data set and the estimated values from the three developed models and the two mathematical models published in scientific journals are compared. Also, to compare the models in a more general view, a comparison between the calculated AAPRE values is shown in Fig. 14. AAPRE is a very important criterion for properly evaluating the performance of models (Karkevandi-Talkhooncheh et al. 2017).

Fig. 13
figure 13

A comparison of real and predicted ROP among the developed models and mathematical ROP models

Full size image
Fig. 14
figure 14

Comparison of average absolute percent relative error (AAPRE) calculated from the developed models and mathematical ROP models

Full size image

Based on Fig. 14, it can be concluded that the mathematical models are not very accurate compared to computational intelligence-based models. The mathematical models assume that the effect of some drilling variables on ROP has a linear and absolute incremental behavior, and consider the well in a constant cleaning condition, which at high drilling speeds can cause an error in ROP approximation. Therefore, it can be acknowledged that mathematical ROP models suitably estimate the penetration rate in areas where the involvement of other factors reducing the speed of drilling process is not yet intensified.

Conclusion

The optimization of the drilling process is directly related to the increase in the rate of penetration since it can increase the speed of drilling to a satisfying level and lead to cost-saving. Optimizing the drilling process requires understanding the relationship between the various parameters affecting this process so that a better estimation of the penetration rate factor can provide better planning for future wells by adjusting the controllable drilling parameters in their optimal values. In this study, three methods of computational intelligence were used to model and approximate the penetration rate through the collected data from four drilled wells. To broaden the comparisons, two published models in the literature were employed. The results of this study are described as the following:

  • Data preprocessing and feature selection are two of the most critical steps that must be considered precisely before the modeling process to increase the results reliability and the training process of the models to be performed with better performance. In this study, after removing the outliers and reducing the overall noise of data with Savitzky–Golay smoothing filter, nine independent variables (drilling parameters) and one dependent variable (ROP) were selected as suitable model inputs by using MLP neural networks and the NSGA-II algorithm.

  • An important aspect of data that affects machine learning performance is the number of sample points. The machine learning process will not promise improvement not before confronting large and broad amounts of data. On the other hand, if large datasets are available, better patterns can be expected to be discovered and more accurate predictions of the target variable can be made. In this study, all data collected from the four studied wells were combined to provide a unified view and form a larger dataset with 7563 data points.

  • Group analysis of models and comparison of developed models with published models in the literature confirms the fact that computational intelligence-based models have a much better performance compared to conventional ROP models. Also, statistical and graphical analyses confirmed that the BBO-RBFNN model had the highest accuracy in predicting ROP. The appropriate performance of BBO-RBFNN can be attributed to having only one hidden layer containing radial basis functions that prevent additional calculations and suitably make the learning of nonlinear patterns possible.

  • After BBO-RBFNN, BP-CFNN has higher accuracy in ROP approximation. The reason for the superiority of BP-CFNN over the conventional neural networks can be attributed to the additional connections from the input layer to the output layer and each of the hidden layers, which increases the network performance in recognizing the desired relationship between inputs and target variables.