Introduction

In recent years, tight sandstone gas reservoirs have shown promising resource prospects and have played an increasingly important role in compensating for the shortage of conventional oil and gas production. Tight sandstone reservoirs typically have poor petrophysical properties and are primarily developed through hydraulic fracturing techniques to achieve large-scale reservoir volume transformation and economic exploitation (Zheng et al. 2020; Feng et al. 2023; Wu et al. 2020; Ahammad et al. 2018). Hydraulic fracturing often results in complex fracture networks, and the degree of fracture network transformation is one of the main factors limiting the productivity of tight gas wells (Verdugo and Doster 2022; Vishkai and Gates 2019; Elputranto and Yucel 2020). Additionally, tight sandstone reservoirs generally have high initial water saturation, which can lead to gas–water two-phase flow characteristics during the development process, resulting in significant water production issues in some gas wells and affecting gas well productivity. Furthermore, tight sandstone reservoirs exhibit a certain degree of stress sensitivity, and the negative impact of stress sensitivity significantly affects the permeability of gas–water flow, directly influencing the stable production capacity of gas wells (Fu et al. 2022; Cui et al. 2020; Shen et al. 2022; Sun et al. 2020). Therefore, fracture network parameters, gas–water two-phase flow characteristics, and reservoir stress sensitivity are key factors that affect the accurate prediction of production capacity in tight gas wells and should be given careful consideration in production capacity evaluation models.

Currently, the methods for predicting production capacity in tight sandstone gas wells mainly include analytical, semi-analytical, and numerical simulation methods (Wang et al. 2022; Ruiz et al. 2022; Kuk and Stopa 2019; Stopa and Mikołajczak 2018). Analytical methods are typically based on steady-state flow theory and establish production capacity calculation models for tight gas wells. Production capacity calculation models are derived for tight fractured horizontal wells based on steady-state flow theory, using the point source method and the superposition principle of potentials. However, for tight sandstone gas reservoirs, the development process often occurs in the transient flow stage, and production capacity equations based on steady-state flow theory cannot accurately reflect the production process of the reservoir (Wu et al. 2019a, b; Bo et al. 2020; Wang et al. 2019; Sun et al. 2023). Semi-analytical methods are primarily based on the assumption of linear flow and effectively characterize the fracture network, while being computationally convenient and widely used. However, these analytical and semi-analytical methods are only applicable to the prediction of single-phase fluid production capacity. For the gas–water two-phase flow that occurs during tight gas development, these models are no longer suitable due to the severe nonlinearity of the mathematical models (Yao et al. 2021; Sun et al. 2019; Wang et al. 2021; Wu et al. 2022a). The equations can be linearized by introducing pseudo-pressures for gas and water phases and production capacity equations are derived for water-producing gas wells based on the principle of conformal transformation and the superposition principle of potentials, converting water production into gas production for evaluation. However, this method often simplifies the equations by introducing pseudo-pressures for the two-phase flow, neglecting the influence of nonlinear flow parameters (Zhang et al. 2019; Song et al. 2020; Zhang et al. 2023; Williams-Kovacs and Clarkson 2016), resulting in significant calculation errors. Numerical models for tight sandstone gas fracturing wells are developed, which can explicitly represent the characteristics of artificial fractures and handle multiphase fluid flow problems. However, the preprocessing process is complex, and to achieve high simulation accuracy, the fractures need to be refined, resulting in a large number of grids (Chen et al. 2019; Zhang and Sheng 2020; Wu et al. 2022b; Zhang et al. 2022). When analyzing thousands of cases, the computational efficiency is low. In summary, the main challenges in accurately predicting production capacity in tight sandstone gas wells are: difficulty in simulating fracture networks formed by hydraulic fracturing and difficulty in simulating gas–water two-phase flow and stress sensitivity.

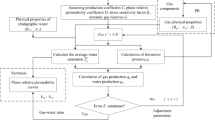
In this study, the fracture network was characterized using a trilinear flow model, and a predictive model for gas–water two-phase production capacity in tight fractured horizontal wells was established. An efficient solution method was developed to handle the nonlinear flow problems caused by gas–water two-phase flow and stress sensitivity. Comparing the conventional numerical simulation models, the proposed model incorporates fracture networks, gas–water two-phase flow as well as stress sensitivity simultaneously. Also, the calculation cost of the proposed semi-analytical model is much less than the existed numerical models. Firstly, the flow equations were normalized by introducing pseudo-pressures and pseudo-time, and analytical solutions for the initial moment of the model were obtained using Laplace transformation and other methods. Then, by combining material balance and Newton's iteration method, the nonlinear flow parameters of the model were updated using the average formation pressure and saturation at different times, gradually achieving the linearization of the flow model and obtaining a semi-analytical solution. The accuracy of the model was verified by comparing it with commercial numerical simulation software, and the effects of key flow parameters in the fracture network and reservoir on production capacity prediction were analyzed based on the developed semi-analytical model. Subsequently, production capacity prediction and analysis were carried out using case examples.

Model establishment

Physical model

The complex fracture network in tight reservoirs is treated as an equivalent stimulated reservoir volume (SRV) (Wu et al. 2019a, b; Li et al. 2020), which consists of an artificial main fracture, an inner stimulated zone, and an outer stimulated zone. The trilinear flow model is used to characterize the flow behavior in the SRV, which divides the fluid flow into three regions: linear flow along the fractures in the inner zone, vertical linear flow of reservoir fluids perpendicular to the fractures, and linear flow parallel to the fractures in the outer zone, as shown in Fig. 1. The inner zone considers the complex fracture network formed by hydraulic fracturing and is treated as a dual-porosity model. The outer zone, which is unaffected by the hydraulic fracturing, is treated as a single-porosity medium. It is assumed that the artificial hydraulic fractures are directly connected to the wellbore (Wang 2019; Fan et al. 2021; Yang and Liu 2019), and the fluid enters the production wellbore only through the hydraulic fractures, while the fluid continuously flows into the fractures from the matrix, providing energy supply. The co-production of gas and water is considered, and both gas and water phases flow in the reservoir and fracture network, following the assumption of isothermal Darcy flow. Other assumptions in the physical model include: (1) the top, bottom, and sides of the reservoir are impermeable boundaries; (2) the entire reservoir is fully opened, with symmetric artificial main fractures connected to the wellbore, and the half-length of the fractures is denoted as xF, and the fracture width is denoted as wF; (3) compared to gas, the compressibility of formation water is small and can be neglected; (4) the stress sensitivity of reservoir permeability is considered; (5) the effects of gravity and capillary forces are not taken into account.

Fig. 1
figure 1

Fractured horizontal well model in tight gas reservoir

Full size image

Mathematic model

Based on the assumptions of the physical model, mathematical flow models are established for each flow region. To facilitate the derivation, the mathematical models are simplified by introducing dimensionless variables. The dimensionless parameters are defined as follows:

$$\begin{aligned} & \psi_{{\text{D}}} = \frac{{\psi_{{\text{i}}} - \psi }}{{\psi_{{\text{i}}} - \psi_{{{\text{wf}}}} }};\;\;p_{{\text{D}}} = \frac{{p_{{\text{i}}} - p}}{{p_{{\text{i}}} - p_{{{\text{wf}}}} }}; \\ & q_{{{\text{gD}}}} = \frac{{1.291 \times 10^{ - 3} q_{{\text{g}}} T}}{{\left( {\psi_{{\text{i}}} - \psi_{{{\text{wf}}}} } \right)k_{{\text{r}}} H}};\;\;q_{{{\text{wD}}}} = \frac{{1.842q_{{\text{w}}} B_{{\text{w}}} \mu_{{\text{w}}} L_{{\text{r}}} }}{{k_{{\text{F}}} H\left( {p_{{\text{i}}} - p_{{{\text{wf}}}} } \right)}}; \\ & t_{{{\text{aD}}}} = \frac{{\eta_{{\text{r}}} }}{{L_{{\text{r}}}^{{2}} }}t_{{\text{a}}} ;\;\;t_{{\text{D}}} = \frac{{\eta_{{\text{r}}} }}{{L_{{\text{r}}}^{{2}} }}t;\;\;C_{{{\text{FD}}}} = \frac{{k_{{\text{F}}} w_{{\text{F}}} }}{{k_{{{\text{mi}}}} L_{{\text{r}}} }} \\ & x_{{\text{D}}} = \frac{x}{{L_{{\text{r}}} }};\;\;y_{{\text{D}}} = \frac{y}{{L_{{\text{r}}} }};\;\;z_{{\text{D}}} = \frac{z}{{L_{{\text{r}}} }};\;\;w_{{{\text{FD}}}} = \frac{{w_{{\text{F}}} }}{{L_{{\text{r}}} }}; \\ & k_{{{\text{FD}}}} = \frac{{k_{{\text{F}}} }}{{k_{{\text{r}}} }};\eta_{{{\text{jD}}}} = \frac{{\eta_{{\text{j}}} }}{{\eta_{{\text{r}}} }} = \frac{{k_{{\text{j}}} /(\mu \phi c_{{\text{t}}} )_{{\text{j}}} }}{{k_{{\text{r}}} /(\mu \phi c_{{\text{t}}} )_{{\text{r}}} }} \\ \end{aligned}$$
(1)

In the equation, pD represents dimensionless pressure, ψD represents dimensionless pseudo-pressure, tD represents dimensionless time, taD represents dimensionless pseudo-time, qgD represents dimensionless gas production rate, qwD represents dimensionless water production rate, ηD represents dimensionless drainage efficiency coefficient, CFD represents dimensionless fracture conductivity, xD, yD, zD represent dimensionless lengths in the x, y, and z coordinate directions, wFD represents dimensionless fracture width, kFD represents dimensionless fracture permeability, p represents pressure in MPa, pi represents initial reservoir pressure in MPa, pwf represents bottomhole flowing pressure in MPa, ψ represents pseudo-pressure in MPa2/(mPa·s), ψi represents initial reservoir pseudo-pressure in MPa2/(mPa·s), ψwf represents pseudo-bottomhole pressure in MPa2/(mPa·s), t represents time in days, ta represents pseudo-time in days, T represents temperature in Kelvin, kr represents reference permeability in mD, kF represents fracture permeability in mD, kmi represents initial matrix permeability in mD, qg represents gas production rate in 104 m3/d, qw represents water production rate in m3/d, Lr represents reference length in meters, H represents reservoir effective thickness in meters, wF represents fracture width in meters, Bw represents volume coefficient in m3/m3, μw represents water viscosity in mPa·s.

Introducing pseudo-pressure and pseudo-time, defined as follows:

$$\psi = 2\int\limits_{0}^{p} {\frac{p}{\mu Z}{\text{d}}p}$$
(2)
$$t_{{\text{a}}} = \int_{0}^{t} {\frac{{\mu_{{{\text{gi}}}} c_{{{\text{ti}}}} }}{{\mu_{{\text{g}}} (\hat{p})c_{{\text{t}}} (\hat{p})}}} {\text{d}}t$$
(3)

The dimensionless multiphase flow mathematical model for the outer region matrix system

The governing equation for gas phase flow is expressed using pseudo-pressure and pseudo-time, and it is given by:

$$\frac{{\partial^{2} \psi_{{{\text{mD}}}} }}{{\partial x_{{\text{D}}}^{2} }} = \frac{1}{{\eta_{{{\text{mD}}}} k_{{{\text{mrg}}}} }}\frac{{\partial \psi_{{{\text{mD}}}} }}{{\partial t_{{{\text{aD}}}} }}$$
(4)

In the equation, kmrg represents the dimensionless relative permeability of the gas phase in the matrix system, and ηmD represents the dimensionless pressure drawdown coefficient of the gas phase in the matrix system.

$${\text{Initial}}\;{\text{condition}}:\;\;\left. {\psi_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{{\text{aD}}}} )} \right|_{{t_{{{\text{aD}}}} = 0}} = 0$$
(5)
$${\text{Internal}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {\psi_{{{\text{fD}}}} (x_{{\text{D}}} ,t_{{{\text{aD}}}} )} \right|_{{x_{{\text{D}}} = 1}} = \left. {\psi_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{{\text{aD}}}} )} \right|_{{x_{{\text{D}}} = 1}}$$
(6)
$${\text{Outer}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {\frac{{\partial \psi_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{{\text{aD}}}} )}}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{{\text{eD}}}} }} = 0$$
(7)

The dimensionless governing equation and boundary conditions for the water phase flow, using real time, are as follows:

$$\frac{{\partial^{2} p_{{{\text{mD}}}} }}{{\partial x_{{\text{D}}}^{2} }} = \frac{1}{{\eta_{{{\text{mwD}}}} k_{{{\text{mrw}}}} }}\frac{{\partial p_{{{\text{mD}}}} }}{{\partial t_{{\text{D}}} }}$$
(8)
$${\text{Initial}}\;{\text{condition}}:\;\;\left. {p_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{t_{{\text{D}}} = 0}} = 0$$
(9)
$${\text{Internal}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {p_{{{\text{fD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{x_{{\text{D}}} = 1}} = \left. {p_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{x_{{\text{D}}} = 1}}$$
(10)
$${\text{Outer}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {\frac{{\partial p_{{{\text{mD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )}}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{{\text{eD}}}} }} = 0$$
(11)

In the equation, kmrw represents the dimensionless relative permeability of the water phase in the matrix system. ηmwD represents the dimensionless pressure drop coefficient of the water phase in the matrix system.

The dimensionless flow equations for the gas and water phases in the secondary fracture system within the internal region

$${\text{Gas - phase}}\;{\text{flow}}\;{\text{equation}}:\;\;\frac{{\partial^{2} \psi_{{{\text{fD}}}} }}{{\partial y_{{\text{D}}}^{2} }} + \frac{1}{{k_{{{\text{frg}}}} }}\left. {\frac{{\partial \psi_{{{\text{mD}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 1}} = \frac{1}{{\eta_{{{\text{fD}}}} k_{{{\text{frg}}}} }}\frac{{\partial \psi_{{{\text{fD}}}} }}{{\partial t_{{{\text{aD}}}} }}$$
(12)
$${\text{Initial}}\;{\text{condition}}:\;\;\left. {\psi_{{{\text{fD}}}} (y_{{\text{D}}} ,t_{{{\text{aD}}}} )} \right|_{{t_{{{\text{aD}}}} = 0}} = 0$$
(13)
$$\left. {\psi_{{{\text{fD}}}} (y_{{\text{D}}} ,t_{{{\text{aD}}}} )} \right|_{{y_{{\text{D}}} = {{w_{{{\text{FD}}}} } \mathord{\left/ {\vphantom {{w_{{{\text{FD}}}} } 2}} \right. \kern-0pt} 2}}} = \psi_{{{\text{FD}}}}$$
(14)
$${\text{Outer}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {\frac{{\partial \psi_{{{\text{fD}}}} (x_{{\text{D}}} ,t_{{{\text{aD}}}} )}}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = y_{{{\text{eD}}}} }} = 0$$
(15)
$${\text{Water - phase}}\;{\text{flow}}\;{\text{equation}}:\;\;\frac{{\partial^{2} p_{{{\text{fD}}}} }}{{\partial y_{{\text{D}}}^{2} }} + \frac{1}{{k_{{{\text{frw}}}} }}\left. {\frac{{\partial p_{{{\text{fD}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 1}} = \frac{1}{{\eta_{{{\text{fwD}}}} k_{{{\text{frw}}}} }}\frac{{\partial p_{{{\text{fD}}}} }}{{\partial t_{{\text{D}}} }}$$
(16)
$${\text{Initial}}\;{\text{condition}}:\;\;\left. {p_{{{\text{fD}}}} (y_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{t_{{\text{D}}} = 0}} = 0$$
(17)
$${\text{Internal}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {p_{{{\text{fD}}}} (y_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{y_{{\text{D}}} = {{w_{{{\text{FD}}}} } \mathord{\left/ {\vphantom {{w_{{{\text{FD}}}} } 2}} \right. \kern-0pt} 2}}} = p_{{{\text{FD}}}}$$
(18)
$${\text{Outer}}\;{\text{boundary}}\;{\text{condition}}:\;\;\left. {\frac{{\partial p_{{{\text{fD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )}}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = y_{{{\text{eD}}}} }} = 0$$
(19)

In the above equations, kfrg is relative permeability of the gas phase in the secondary fracture system; kfrw is relative permeability of the water phase in the secondary fracture system; ηfD is dimensionless pressure drop coefficient for the gas phase in the secondary fracture system; ηfwD is dimensionless pressure drop coefficient for the water phase in the secondary fracture system.

Mathematical model for two-phase flow (gas and water) in the artificial fracture system

$${\text{Gas - phase}}\;{\text{flow}}\;{\text{equation}}:\;\;\frac{{\partial^{2} \psi_{{{\text{FD}}}} }}{{\partial x_{{\text{D}}}^{2} }} + \frac{{2k_{{{\text{frg}}}} }}{{C_{{{\text{FD}}}} k_{{{\text{Frg}}}} }}\left. {\frac{{\partial \psi_{{{\text{fD}}}} }}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = w_{{{\text{FD}}}} /2}} = \frac{1}{{\eta_{{{\text{FD}}}} k_{{{\text{Frg}}}} }}\frac{{\partial \psi_{{{\text{FD}}}} }}{{\partial t_{{{\text{aD}}}} }}$$
(20)
$${\text{Initial}}\;{\text{condition}}:\;\;\left. {\psi_{{{\text{FD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )_{{t_{{\text{D}}} = 0}} } \right|$$
(21)
$${\text{Internal}}\;{\text{boundary}}\;{\text{condition}}\;{\text{with}}\;{\text{constant}}\;{\text{bottom - well}}\;{\text{pressure}}:\;\;\left. {\psi_{{{\text{FD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{x_{{\text{D}}} = 0}} = 1$$
(22)
$${\text{Closed}}\;{\text{condition}}\;{\text{at}}\;{\text{fracture}}\;{\text{ends}}:\;\left. {\frac{{\partial \psi_{{{\text{FD}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 1}} = 0$$
(23)
$${\text{Water - phase}}\;{\text{flow}}\;{\text{equation}}:\;\;\frac{{\partial^{2} p_{{{\text{FD}}}} }}{{\partial x_{{\text{D}}}^{2} }} + \frac{{2k_{{{\text{frg}}}} }}{{C_{{{\text{FD}}}} k_{{{\text{Frg}}}} }}\left. {\frac{{\partial p_{{{\text{fD}}}} }}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = w_{{{\text{FD}}}} /2}} = \frac{1}{{\eta_{{{\text{FD}}}} k_{{{\text{Frg}}}} }}\frac{{\partial p_{{{\text{FD}}}} }}{{\partial t_{{\text{D}}} }}$$
(24)
$${\text{Initial}}\;{\text{condition}}:\;\;\left. {p_{{{\text{FD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{t_{{\text{D}}} = 0}} = 0$$
(25)
$${\text{Internal}}\;{\text{boundary}}\;{\text{condition}}\;{\text{with}}\;{\text{constant}}\;{\text{bottom - well}}\;{\text{pressure}}:\;\;\left. {p_{{{\text{FD}}}} (x_{{\text{D}}} ,t_{{\text{D}}} )} \right|_{{x_{{\text{D}}} = 0}} = 1$$
(26)
$${\text{Closed}}\;{\text{condition}}\;{\text{at}}\;{\text{fracture}}\;{\text{ends}}:\left. {\frac{{\partial p_{{{\text{FD}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 1}} = 0$$
(27)

In the equation, kFrg and kFrw represent the relative permeabilities of the gas phase and water phase, respectively, in the artificial fracture system. ηFD and ηFwD represent the dimensionless pressure drop coefficients for the gas phase and water phase, respectively, in the artificial fracture system.

Semi-analytical solution for predicting two-phase gas–water productivity

The production time is discretized into multiple time steps. At each time step, the parameters related to pressure and saturation are replaced by the average pressure and average saturation within the operational range. Therefore, the nonlinear parameters in the above equations can be approximated as constant values at each time step. After addressing the nonlinear flow problem, the gas and water production at each time step can be directly obtained by solving the equations.

Solution to gas-phase flow equations

The gas-phase flow equation for each flow region is subjected to Laplace transformation with respect to the dimensionless pseudo-time. Similar to the single-phase model solving process, we first apply Laplace transformation to the gas-phase flow equation in the outer matrix system. The general solution is given by:

$$\overline{\psi }_{{{\text{mD}}}} = A\sinh \left( {\sqrt {\frac{s}{{\eta_{{{\text{mD}}}} k_{{{\text{mrg}}}} }}} \cdot x_{{\text{D}}} } \right) + B\cosh \left( {\sqrt {\frac{s}{{\eta_{{{\text{mD}}}} k_{{{\text{mrg}}}} }}} \cdot x_{{\text{D}}} } \right)$$
(28)

The gas-phase flow equation for the inner secondary fracture system is subjected to Laplace transformation, resulting in the following general solution:

$$\overline{\psi }_{{{\text{fD}}}} = C\sinh \left( {\sqrt \sigma \cdot y_{{\text{D}}} } \right) + D\cosh \left( {\sqrt \sigma \cdot y_{{\text{D}}} } \right)$$
(29)

The gas-phase flow equation for the artificial fracture system, subjected to Laplace transformation, yields the following general solution:

$$\overline{\psi }_{{{\text{FD}}}} = - \frac{1}{s}\left( {\tanh \sqrt \alpha \sinh \sqrt \alpha x_{{\text{D}}} - \cosh \sqrt \alpha x_{{\text{D}}} } \right)$$
(30)

where,

$$\alpha = \frac{s}{{\eta_{{{\text{FD}}}} k_{{{\text{Frg}}}} }} + \frac{{2k_{{{\text{frg}}}} }}{{C_{{{\text{FD}}}} k_{{{\text{Frg}}}} }}\sqrt \sigma \tanh \sqrt \sigma \left( {y_{{{\text{eD}}}} - \frac{{w_{{{\text{FD}}}} }}{2}} \right)$$
(31)
$$\sigma = \frac{s}{{\eta_{{{\text{fD}}}} k_{{{\text{frg}}}} }} + \frac{1}{{k_{{{\text{frg}}}} }}\sqrt {\frac{s}{{\eta_{{{\text{fD}}}} k_{{{\text{frg}}}} }}} \tanh \sqrt {\frac{s}{{\eta_{{{\text{fD}}}} k_{{{\text{frg}}}} }}} \left( {x_{{{\text{eD}}}} - 1} \right)$$
(32)

Gas production of a single well has the following expression.

$$\overline{q}_{{{\text{gD}}}} = \left. { - \frac{{k_{{{\text{FD}}}} k_{{{\text{Frg}}}} w_{{{\text{FD}}}} }}{\pi }\frac{{\partial \overline{\psi }_{{{\text{FD}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 0}}$$
(33)

Combining with Eq. (12), gas production yield.

$$\overline{q}_{{{\text{gD}}}} = - \frac{{k_{{{\text{FD}}}} k_{{{\text{Frg}}}} w_{{{\text{FD}}}} }}{\pi }\frac{1}{s}\sqrt \alpha \tanh \sqrt \alpha$$
(34)

The solution for gas production in Eq. (34) is obtained in the Laplace domain. To obtain the solution in the real space, the Stehfest numerical inversion method can be used.

Solution to water-phase flow equations

The Laplace transform of the water phase flow equation for the external matrix system, similar to the gas phase flow model, yields the general solution as follows:

$$\overline{p}_{{{\text{mD}}}} = A_{1} \sinh \left( {\sqrt {\frac{s}{{\eta_{{{\text{mwD}}}} k_{{{\text{mrw}}}} }}} \cdot x_{{\text{D}}} } \right) + B_{1} \cosh \left( {\sqrt {\frac{s}{{\eta_{{{\text{mwD}}}} k_{{{\text{mrw}}}} }}} \cdot x_{{\text{D}}} } \right)$$
(35)

The Laplace transform of the water phase flow equation for the internal secondary fracture system yields the general solution as follows:

$$\overline{p}_{{{\text{fD}}}} = C_{1} \sinh \left( {\sqrt \beta \cdot y_{{\text{D}}} } \right) + D_{1} \cosh \left( {\sqrt \beta \cdot y_{{\text{D}}} } \right)$$
(36)

The Laplace transform of the water phase flow equation for the artificial fracture system yields the general solution as follows:

$$\overline{p}_{{{\text{FD}}}} = - \frac{1}{s}\left( {\tanh \sqrt \xi \sinh \sqrt \xi x_{{\text{D}}} - \cosh \sqrt \xi x_{{\text{D}}} } \right)$$
(37)

where,

$$\xi = \frac{s}{{\eta_{{{\text{FwD}}}} k_{{{\text{Frw}}}} }} + \frac{{2k_{{{\text{frw}}}} }}{{C_{{{\text{FD}}}} k_{{{\text{Frw}}}} }}\sqrt \beta \tanh \sqrt \beta \left( {y_{{{\text{eD}}}} - \frac{{w_{{{\text{FD}}}} }}{2}} \right)$$
(38)
$$\beta = \frac{s}{{\eta_{{{\text{fwD}}}} k_{{{\text{frw}}}} }} + \frac{1}{{k_{{{\text{frw}}}} }}\sqrt {\frac{s}{{\eta_{{{\text{fD}}}} k_{{{\text{frw}}}} }}} \tanh \sqrt {\frac{s}{{\eta_{{{\text{fD}}}} k_{{{\text{frw}}}} }}} \left( {x_{{{\text{eD}}}} - 1} \right)$$
(39)

Combining above equations, the solution for the water phase production can be obtained as follows:

$$\overline{q}_{{{\text{wD}}}} = - \frac{{k_{{{\text{FD}}}} k_{{{\text{Frw}}}} w_{{{\text{FD}}}} }}{\pi }\frac{1}{u}\sqrt \xi \tanh \sqrt \xi$$
(40)

In above equations, there are still parameters related to pressure and saturation. Additionally, equation below provides an expression for permeability considering reservoir stress sensitivity. In this study, the stress sensitivity term is integrated into the dimensionless pressure coefficient and is treated as a function of average reservoir pressure. During the model solving process, the nonlinear parameters for each time step are updated using the average reservoir pressure and saturation within the dynamic region. The model solution is obtained through iterative calculations, where the average reservoir pressure and saturation are computed using the material balance method to achieve flow equilibrium.

$$k_{{\text{m}}} = k_{{{\text{mi}}}} e^{{ - \gamma \left( {p_{{\text{i}}} - \hat{p}} \right)}}$$
(41)

In the equation, km represents the reservoir permeability in millidarcies (mD), kmi represents the initial reservoir permeability in millidarcies (mD), γ represents the permeability modulus in megapascals per unit pressure (MPa-1), and represents the average reservoir pressure in megapascals (MPa).

Development of flowing material balance equation

The gas phase material balance equation is given by:

$$x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} \left( {\frac{{S_{{{\text{gi}}}} }}{{B_{{{\text{gi}}}} }}} \right) - x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} \left( {\frac{{\hat{S}_{{\text{g}}} }}{{\hat{B}_{{\text{g}}} }}} \right) = \int\limits_{0}^{t} {q_{{\text{g}}} {\text{d}}t}$$
(42)

In the equation, Sgi represents the initial gas saturation, \(\hat{S}_{{\text{g}}}\) represents the average gas saturation, Bgi represents the initial gas volume factor, \(\hat{B}_{{\text{g}}}\) represents the average gas volume factor, xinv represents the effective length along the fracture direction in the inner region (m), yinv represents the effective length along the vertical fracture direction (m), Φf represents the porosity of the secondary fractures.

Rearranging Eq. (42) yields:

$$\frac{{\hat{S}_{{\text{g}}} }}{{\hat{B}_{{\text{g}}} }} = \frac{{S_{{{\text{gi}}}} }}{{B_{{{\text{gi}}}} }} - \frac{{\int\limits_{0}^{t} {q_{{\text{g}}} {\text{d}}t} }}{{x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} }}$$
(43)

The effective ranges along the fracture direction and perpendicular to the fracture direction in the internal region are as follows:

$$x_{{{\text{inv}}}} = 0.5836\sqrt {\frac{{k_{{\text{f}}} t}}{{\phi_{{\text{f}}} \mu c_{{\text{t}}} }}} + x_{{\text{F}}} ,\;\;y_{{{\text{inv}}}} = 0.5836\sqrt {\frac{{k_{{\text{f}}} t}}{{\phi_{{\text{f}}} \mu c_{{\text{t}}} }}}$$
(44)

Water phase material balance equation is:

$$x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} \left( {\frac{{S_{{{\text{wi}}}} }}{{B_{{{\text{wi}}}} }}} \right) - x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} \left( {\frac{{\hat{S}_{{\text{w}}} }}{{\hat{B}_{{\text{w}}} }}} \right) = \int\limits_{0}^{t} {q_{{\text{w}}} {\text{d}}t}$$
(45)

Arranging Eq. (43) yields:

$$\frac{{\hat{S}_{{\text{w}}} }}{{\hat{B}_{{\text{w}}} }} = \frac{{S_{{{\text{wi}}}} }}{{B_{{{\text{wi}}}} }} - \frac{{\int\limits_{0}^{t} {q_{{\text{w}}} {\text{d}}t} }}{{x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} }}$$
(46)

In the equation, Swi represents the initial water saturation at a given time, expressed as a decimal fraction, and Sw represents the average water saturation, also expressed as a decimal fraction.

The saturation satisfies the following relationship:

$$\hat{S}_{{\text{w}}} + \hat{S}_{{\text{g}}} = 1$$
(47)

By combining Eqs. (45), (46), and (47), the average pressure function can be constructed as follows:

$$f\left( {\hat{p}} \right) = \frac{1}{{\hat{B}_{{\text{g}}} }} + \left( { - \frac{{\hat{B}_{{\text{w}}} }}{{\hat{B}_{{\text{g}}} }}} \right)A_{3} - B_{3}$$
(48)

where,

$$A_{3} = \frac{{S_{{{\text{wi}}}} }}{{B_{{{\text{wi}}}} }} - \frac{{\int\limits_{0}^{t} {q_{{\text{w}}} {\text{d}}t} }}{{x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} }};\,\;B_{3} = \frac{{S_{{{\text{gi}}}} }}{{B_{{{\text{gi}}}} }} - \frac{{\int\limits_{0}^{t} {q_{{\text{g}}} {\text{d}}t} }}{{x_{{{\text{inv}}}} Hy_{{{\text{inv}}}} \phi_{{\text{f}}} }}$$
(49)

To differentiate Eq. (49), we have:

$$f^{\prime}\left( {\hat{p}} \right) = - \frac{1}{{\hat{B}_{{\text{g}}}^{2} }}\frac{{{\text{d}}B_{{\text{g}}} }}{{{\text{d}}p}} + A_{1} \left( { - \frac{1}{{\hat{B}_{{\text{g}}} }}\frac{{{\text{d}}B_{{\text{w}}} }}{{{\text{d}}p}} + \frac{{B_{{\text{w}}} }}{{\hat{B}_{{\text{g}}}^{2} }}\frac{{{\text{d}}B_{{\text{g}}} }}{{{\text{d}}p}}} \right)$$
(50)

To construct the Newton iteration format for the average pressure based on Eq. (50), we have:

$$\hat{p}_{{{\text{k}} + 1}} = \hat{p}_{{\text{k}}} - \chi \frac{{f\left( {\hat{p}_{{\text{k}}} } \right)}}{{f^{\prime}\left( {\hat{p}_{{\text{k}}} } \right)}}$$
(51)

In the equation, “k” represents the previous time step, and “k + 1” represents the current time step. “Δ” is the iteration factor, typically chosen as a small value.

By applying the Newton iteration method, we can obtain the average pressure and then substitute it into the proposed equations to calculate the average saturation. The nonlinear parameters for each time step can be updated using the average pressure and saturation within the effective range. By iteratively solving the equations, we can obtain the solution for the gas–water two-phase flow mathematical model in tight gas reservoirs with horizontal wells fractured. This solution can be used to programmatically generate the gas–water production curve and predict the production dynamics.

Gas–water two-phase production data analysis

Model verification

To verify the accuracy of the established model, this paper validates the proposed semi-analytical model using the commercial numerical simulation software Eclipse, as shown in Fig. 2. The gas high-pressure thermophysical parameter relationship curve used in the model is illustrated in Fig. 3. Table 1 provides the reservoir and fracture parameters used in both methods, while Fig. 4 displays the relative permeability curves for gas and water in the reservoir. In this case study, both the matrix and fracture systems consider the presence of gas and water, resulting in two-phase flow occurring during the initial production stage.

Fig. 2
figure 2

Schematic of the fractured horizontal well model

Full size image
Fig. 3
figure 3

Schematic of the gas PVT properties

Full size image
Table 1 Input parameters for model validation
Full size table
Fig. 4
figure 4

Relative permeability of the matrix system

Full size image

The comparative results between the semi-analytical model and Eclipse are shown in Fig. 5. It can be observed that the production rate curves obtained from both methods exhibit some differences in the early production stage but converge towards the later stage. Under the same reservoir and fracture parameter conditions, the productivity under two-phase gas–water flow conditions is significantly lower than that under single-phase flow. This is mainly due to the significant pressure and saturation changes near the wellbore during the early production stage, and production is highly sensitive to parameters related to pressure and saturation. In the semi-analytical model, certain pressure-related parameters are implicitly handled using pseudo-pressure, while parameters related to saturation are explicitly handled. Therefore, the early-stage error in the single-phase flow model is less noticeable, whereas the error in the two-phase flow model is more prominent. However, the calculated average relative error is less than 10%, which falls within the acceptable engineering error range. This indicates that the proposed semi-analytical model can be used for production data analysis and forecasting. Compared to numerical simulation methods, the semi-analytical approach presented in this paper offers faster computation speed, making it more suitable for large-scale case analysis and application in mining fields.

Fig. 5
figure 5

Comparison of gas and water production rate between the semi-analytical method in this paper and numerical simulation method: (Left) Gas production; (Right) Water production

Full size image

There are two main limitations in this research. First of all, average saturation and average pressure over the whole formation are used to capture the variation of water saturation and pressure with production. However, saturation and pressure in each tiny element of the formation are unique and different, using the uniform average saturation or pressure inevitably leads to discrepancy, which becomes acceptable when the formation permeability is relatively large as reported. Additionally, the hydraulic fractures in the model established are assumed to follow symmetric distribution and have identical length, conflicting with that in realistic situations that fractures are complex. The model in this work would be further developed to overcome the mentioned limitations in the future.

Analysis of factors affecting production dynamics

Tight gas reservoirs have low natural productivity, and hydraulic fracturing is crucial for enhancing the productivity of tight gas wells. This study is based on a developed semi-analytical model. Firstly, it analyzes the influence of artificial fracture conductivity, fracture half-length, number of fracturing stages, and secondary fracture permeability on the productivity of tight gas wells. Then, based on experimental research results on reservoir flow mechanisms, the study analyzes the impact of reservoir stress sensitivity on the two-phase gas–water productivity. The basic input parameters of the model are presented in Table 1, while the range of sensitivity parameters is shown in Table 2.

Table 2 Range of values for sensitive parameters
Full size table

Figures 6 and 7 respectively illustrate the impact of fracture conductivity and fracture half-length on the productivity of hydraulic fractured horizontal wells in tight gas reservoirs. From Fig. 6, it can be observed that higher fracture conductivity leads to higher initial production and a slower decline in production over time. This is primarily because greater fracture conductivity results in higher production rates, and under constant bottomhole flowing pressure conditions, a smaller decrease in production is sufficient to maintain the production level.

Fig. 6
figure 6

Effects of fracture conductivity on gas production rate

Full size image
Fig. 7
figure 7

Effects of fracture half-length on gas production rate

Full size image

From Fig. 7, it is evident that the variation in fracture half-length affects the entire development stage, particularly during the early and middle production phases. Additionally, with increasing fracture half-length, gas production increases, albeit at a diminishing rate. This is mainly because the fracture half-length not only represents the size of the reservoir volume affected by the fracturing, but also reflects the well-controlled reserves and the drainage area. As the fracture half-length increases, the linear flow area of the fracture also increases, resulting in a larger drainage area and consequently higher production rates with a slower decline in production.

Figure 8 reflects the impact of the number of fracturing stages on the productivity of hydraulic fractured horizontal wells in tight gas reservoirs. It can be observed that as the number of fracturing stages increases, the contact area between the artificial fractures and the reservoir increases, resulting in higher production. However, the increase in productivity becomes less significant with an increasing number of fracturing stages.

Fig. 8
figure 8

Number of fracture stages on gas production rate

Full size image

Since tight gas reservoirs involve gas–water two-phase flow, the flow capacity is weaker compared to single-phase tight gas. Therefore, under the same reservoir properties, a larger number of fracturing stages should be employed for a horizontal section of the same length during the fracturing process.

Figure 9 illustrates the impact of secondary fracture permeability on the productivity of hydraulic fractured horizontal wells in tight gas reservoirs. The secondary fracture permeability represents the permeability of the fracture medium in the dual-porosity system. Increasing the permeability of the secondary fractures significantly enhances the flow capacity within the reservoir’s stimulated zone. Therefore, the permeability of the secondary fractures has a substantial influence on the productivity.

Fig. 9
figure 9

Effects of secondary fracture permeability on gas production rate

Full size image

During hydraulic fracturing operations, efforts should be made to enhance the support of the secondary fractures to increase their permeability. This can be achieved through appropriate design and execution techniques to optimize the conductivity of the secondary fractures.

Figure 10 depicts the impact of reservoir stress sensitivity on the productivity of hydraulic fractured horizontal wells in tight gas reservoirs. From Fig. 10, it can be observed that reservoir stress sensitivity affects the entire development process of the tight gas reservoir, particularly during the early and middle production stages. Moreover, as the production pressure differential increases, the loss of permeability becomes more severe, resulting in increased fluid flow resistance and ultimately leading to a decrease in production with an accelerated decline rate.

Fig. 10
figure 10

Effects of stress sensitivity of reservoir on gas production rate

Full size image

Therefore, for tight gas reservoirs, it is important to maintain a reasonable production pressure differential to mitigate the impact of stress sensitivity on productivity during the production process. This can help minimize the detrimental effects of stress-induced permeability reduction and ensure optimal production performance.

Field case study

This study demonstrates the application effectiveness of the model using a water-producing tight gas well in the Ordos Basin as an example. The horizontal section of the well is 1080 m in length, and it was hydraulically fractured and put into production in May 2015. The initial water saturation of the reservoir is approximately 50%. As of July 2022, the cumulative gas production is 1313 × 104 m3, and the cumulative water production is 1078 m3. The daily gas production is 3720 m3/d, and the daily water production is 0.3 m3/d. The basic data of the well are presented in Table 3, while the PVT relationship curve for gas and the gas–water relative permeability curve are shown in Figs. 3 and 4, respectively. Using the proposed semi-analytical model, the production data of the well for both gas and water phases are fitted and interpreted, as shown in Fig. 11. The theoretical curve aligns well with the measured curve, although there is a certain degree of deviation within the acceptable engineering error range. The fitted interpretation results for the well are summarized in Table 4, with a fracture half-length of 95 m, an inner zone fracture permeability of 0.87 mD, a reservoir permeability of 0.05 mD, and a reservoir stress sensitivity coefficient of 0.02 MPa−1, all of which are consistent with the actual gas reservoir. Based on the interpretation, the production forecast for the well indicates a gas recovery of 2470 × 104 m3 and a water recovery of 2.2 × 103 m3 over a 20-year production period.

Table 3 Input parameters for field case study
Full size table
Fig. 11
figure 11

Rate decline analysis and prediction of the studied tight gas well

Full size image
Table 4 The fitting results of the studied well
Full size table

Summary and conclusions

In this study, a theoretical model for calculating the production capacity of fractured horizontal wells in tight gas reservoirs was established, considering fracture network characteristics, reservoir stress sensitivity, and gas–water two-phase flow mechanisms. And, a semi-analytical solution method for predicting the production capacity of gas–water two-phase flow was developed, enabling fast and accurate predictions. The main conclusions are as follows:

  1. 1.

    Using the mass balance method to calculate the average pressure and average saturation of the reservoir and iteratively updating the nonlinear parameters in the flow model, the nonlinear flow problem of gas–water two-phase flow can be accurately solved. The verification work and its application in the field demonstrate the high prediction accuracy of the semi-analytical method proposed in this study.

  2. 2.

    The higher fracture conductivity leads to higher initial production and a slower decline in production over time. The variation in fracture half-length affects the entire development stage, particularly during the early and middle production stages. As the number of fracturing stages increases, contact area between the artificial fractures and the reservoir increases, resulting in higher production, however the increase becomes less significant with an increasing number of fracturing stages. During hydraulic fracturing operations, efforts should be made to enhance the support of the secondary fractures to increase their permeability.

  3. 3.

    The productivity of tight gas wells is adversely affected by the stress-sensitivity of the reservoir permeability. Moreover, the negative impact becomes evident during the early and middle production stages. In some cases, the impact could be as significant as 15.8% according to the calculations and field case study provided in this work. It is important to maintain a reasonable production pressure differential to mitigate the impact of stress sensitivity on productivity during the production process.