Introduction

Three-dimensional digital rock cores can provide a virtual representation of real rock samples, enabling researchers to study their physical and chemical properties without the need for physical experimentation. This technology can be used to simulate fluid flow and rock properties in oil and gas reservoirs, aiding in reservoir characterization, oil recovery prediction, and reservoir management. Furthermore, digital rock technology enables researchers to optimize drilling, hydraulic fracturing, and other extraction techniques, ultimately leading to more efficient and cost-effective oil and gas production. Currently, three-dimensional digital rock reconstruction methods are generally divided into two categories: (1) The 3D digital rock reconstruction based on physical experiments; (2) The 3D digital rock reconstruction based on numerical reconstruction (Linqi et al. 2019).

The 3D digital rock reconstruction method based on physical experiments involves scanning physical experimental samples, such as rock core samples, to obtain high-resolution images, which are then converted into 3D digital models using computer algorithms. This method requires the sample to be cut into standard sizes, which can result in waste and damage during the research process. However, the resulting digital rock model generated by this method is highly accurate and reliable, providing a visual representation of the real sample for analyzing its physical and chemical properties. The four main physical experimental methods for creating 3D digital cores include a series of two-dimensional slice stacking imaging (Tomutsa et al. 2007), focused ion beam scanning (Sok et al. 2010), X-ray computed tomography (Youssef et al. 2008), and confocal laser scanning (Rembe and Drabenstedt 2006; Yunhai et al. 2013).

The two-dimensional slice stacking imaging method cuts the rock sample parallelly and polishes to obtain flat surfaces and then obtains microscopic images of these polished rock surface to form a 3D core image. The disadvantage of this technique is that it is easy to generate static electricity on the rock sample surface and may damage the sample itself, which is not conducive to core imaging. The focused ion beam scanning method grinds the sample surface, which may cause loss of the sample's physical form during the grinding process, thus damaging the accuracy of the observation. The X-ray computed tomography method involves X-rays passing through the rock sample and being converted into electrical signals in a photodetector. The computer then reads these signals to obtain the three-dimensional data of the rock sample. This technique is currently the most widely used technology due to its high accuracy. However, it cannot simultaneously produce high-resolution and large-scale images. The confocal laser scanning method uses a confocal laser scanning microscope to capture the 3D distribution of pores and fissures in the rock sample. However, the maximum penetration depth of the confocal laser scanning microscope is limited, requiring a certain thickness of the rock sample. Furthermore, this method requires the injection of a staining agent into the rock sample, but it cannot be injected into small and independent pores, resulting in inaccurate pore distribution imaging. Therefore, this method is not widely used in practical research. In conclusion, the three-dimensional reconstruction method of obtaining rock core samples through physical experiments is difficult to industrialize due to cost issues and technical issues.

Currently, experts and scholars have developed various numerical reconstruction-based algorithms for digital core reconstruction and have made excellent progress in research. Different algorithm models can be applied according to different rock types, optimizing the generation effect for different rock properties. However, there are still several problems in this field that have not been completely solved. The main issues are: (1) poor universality of the reconstruction model. Most methods can only generate on homogeneous porous media, and it is difficult to capture the internal structural characteristics of heterogeneous porous media; (2) some methods require hard data constraints, resulting in increased parameters and longer reconstruction time. (3) The connectivity of the generation effect is poor and shows some differences from the actual microstructural characteristics of porous media.

The process of conventional 3D digital core reconstruction based on numerical reconstruction mainly involves the following steps: first, actual 3D digital core data is obtained as training samples. Then, using mathematical modeling, the information in 2D single images is mapped to the distribution characteristics of core images in the training samples. Finally, the 2D information is converted to 3D information based on the mapping information to reconstruct the 3D digital core. Common numerical reconstruction algorithms include the Gaussian field algorithm, Simulated Annealing algorithm, Sequential Indicator Simulation algorithm, Multi-point Geostatistics method, and Markov chain Monte Carlo algorithm.

The Gaussian field algorithm (Joshi 1974; Quiblier 1984) is based on statistical information of 2D rock core slices. Its advantages are that the reconstruction process is simple and computationally efficient, but its disadvantage is the poor connectivity reconstruction of digital cores. The Simulated Annealing algorithm (Hazlett 1997) has the advantage of effectively outputting constraint function information to the final reconstructed 3D digital core, showing the spatial structural characteristics of the pore space. This algorithm can introduce any statistical property as a constraint during the reconstruction process and is very effective for reconstructing rocks with high porosity and high permeability, and relatively simple pore structures. However, it can be easily limited by the modeling information, and as the constraints increase, the reconstruction process becomes slower. When reconstructing large rocks with complex pore structures, the speed and accuracy can be greatly reduced. Sequential Indicator Simulation (Keehm 2003) is a method that combines directional kriging interpolation with conditional stochastic simulation to create a probability distribution field for data. The algorithm's reconstructed 3D digital rock core is highly similar to the real rock core, but it falls short of fundamentally addressing the issue of reconstructing the connectivity of digital rock cores, and its accuracy in reconstruction can be easily influenced by the quality of the images. Additionally, due to the algorithm's relatively fixed evaluation function, the model's potential for improvement is limited. Multi-point geostatistics (Okabe and Blunt 2004, 2005) draws on the principles of multi-point statistics in geological modeling algorithms to consider the correlation between spatial multi-points. It uses a training image to represent the spatial structure of geological variables and then randomly reconstructs images with similar features. This method produces a digital core with good connectivity, which can effectively replicate 2D or 3D models of pore structure and reconstruct the long-distance connectivity of pore space. However, reconstructed rock samples have similar structural features in different directions, the calculation speed is slow, and hard data constraints need to be given in advance (Ting et al. 2010). The Markov Chain Monte Carlo algorithm (Keijan et al. 2004) is a method that creates a state sequence of a Markov chain. The state value at each position depends on a limited number of positions in front of it, and the probability of this state is called conditional probability. Wu et al. (2006) obtained the conditional probability of the neighborhood template under various conditions and introduced the concept of a 15-point neighborhood in 3D space for value reconstruction. This algorithm considers spatial structural information, resulting in a digital core with good connectivity, which is typically more accurate than the Sequential Indicator Simulation algorithm. However, it is not suitable for samples with strong heterogeneity (Chenchen et al. 2013), and the reconstructed digital core has weak heterogeneity and a concentrated pore radius distribution.

With the progress of deep learning, numerous data reconstruction issues have been effectively solved. In 2017, Mosser et al. (2017) introduced the deep convolutional generative adversarial network (3D-DCGAN) to digital core reconstruction. This algorithm employs 3D convolution to comprehend the three-dimensional data distribution, resulting in remarkable reconstruction outcomes on the Berea sandstone dataset. One notable advantage of this approach is its ability to generate multiple pore structures quickly by exploiting the implicit representation of the learned data distribution. However, this model also faces challenges, such as unstable training and convergence difficulties. Du et al. (2020) used a deep transfer learning algorithm to reconstruct porous media, extracting complex features of porous media with deep neural networks, and then replicating these features to obtain reconstruction results through transfer learning. This method shortens the reconstruction time and reduces the burden on the CPU. Zhang et al. (2021) used a model combining generative adversarial networks and variational autoencoders (VAE) to reconstruct 3D digital cores, proposing the VAE-GAN model. Combining GAN with VAE balances the advantages and disadvantages of both, improving reconstruction efficiency and quality. The aforementioned deep learning-based models require a large amount of sample data for training, and the high cost of obtaining rock slice data has led to some obstacles in their application and promotion. Li et al. (2022) based on the dimensionality enhancement concept in deep learning and super-dimension theory, designed a cascading progressive generative adversarial network to reconstruct 3D grayscale rock core images. The input object of this model is a two-dimensional grayscale image, so its advantages are: it requires less training samples, shorter training time, and strong generalizability. However, the model has the disadvantage of difficulty in convergence for reconstructing structurally complex and highly heterogeneous rock cores.

To overcome the difficulty of collecting large-scale datasets, this study was inspired by the Concurrent-Single-Image GAN (ConSinGAN) (Hinz et al. 2020) and replaced the 2D convolution kernels in the generator and discriminator with 3D ones, and modified the input 2D noise vector to 3D, resulting in a 3D input sample that preserves the texture information of the reconstructed structure and maintains the continuity and variability between the reconstruction layers. Several stages were trained simultaneously in a sequential multi-stage manner, which reduces the number of model parameters, speeds up training, and makes the model more stable. Compared with traditional reconstruction methods and existing GANs, our method demonstrates significant advantages in terms of reconstruction quality and stability.

Materials and methods

The model structure

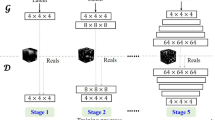
The 3D-Porous-GAN consisting of a 3D generator G and a 3D discriminator D. The generator learns the image distribution and produces samples, while the discriminator differentiates between the generated samples and real images. These two components are linked via forward and backward propagation and trained alternatively to achieve the objective of generating high-quality images. The network structure of the model is illustrated in Fig. 1.

Fig. 1
figure 1

The3D-Porous-GAN training process

Full size image

It is a gradual generator. The training of the generator includes six stages, from stage 0 to stage 5. Each stage consists of three convolution blocks, and each convolution block consists of one convolution layer and one LeakyReLU layer. Each layer of convolutional neural network has 64 convolution kernels with a size of 3 × 3 × 3, and the convolution step size is 1. The patch discriminator (Isola et al. 2017) limits attention to local image blocks and only punishes on the scale of the patches. The discriminator consists of five convolution blocks, and each convolution block of the middle three convolution blocks consists of a convolution layer with a convolution kernel size of 3 × 3 × 3 and a LeakyReLU layer except the head and tail.

We use the same loss function as the original SinGAN (Shaham et al. 2019). The receptive field related to the generated image size decreases with the increase in the number of stages. When the image resolution is low, the discriminator pays more attention to the global distribution of the image. When the image resolution is high, the discriminator pays more attention to the texture details of the image. In all stages, the weights of the discriminators in the previous stage are used to initialize the weights of the discriminators in the next stage. In a given stage n, the formula for optimizing the sum of the confrontation loss and the reconstruction loss is shown in Eq. (1):

$$ L = \min_{G_n } \max_{D_n } \mathcal{L}_{{\text{adv}}} (G_n ,D_n ) + \alpha \mathcal{L}_{{\text{rec}}} (G_n ) $$
(1)

Among them, \(\mathcal{L}_{{\text{adv}}} \left( {G_n ,D_n } \right)\) is the confrontation loss of WGAN-GP (Gulrajani et al. 2017) and \(\mathcal{L}_{{\text{rec}}} \left( {G_n } \right)\) is the reconstruction loss, which is used to improve the training stability of the model. \(\alpha\) is the weight factor of reconstruction loss. In all experiments, \(\alpha = 5\).

For the reconstruction loss, the generator \(G_n\), takes the downsampled image \(x_0\) of the original image \(x_n\) as input, and then trains to reconstruct the image at the resolution of stage N. The reconstruction loss in the stage N is the squared difference between the reconstructed image \(G_n \left( {x_0 } \right)\) and the original image \(x_n\), and the formula is Eq. (2):

$$ \mathcal{L}_{{\text{rec}}} \left( {G_n } \right) = \left\| {G_n \left( {x_0 } \right) - x_n } \right\|_2^2 $$
(2)

Model training process

  1. (1)

    The 3D rock sample \(X_N\) is downsampled for \(N - 1\) times, and \(N\) downsamples including rock sample \(X_N\) are obtained as the input of each stage discriminator. The down sampling ratio is calculated according to Eq. (3):

    $$ x_n = X_N \times r^{((N - 1)/{\text{log}}(N)){\text{*log}}(N - n) + 1} \quad {\text{for}} n = 0, \ldots ,N - 1 $$
    (3)

Among them, \(n\) is the current number of stages, and \(N\) is 6, which is the total number of stages. For example, the input \(x_0\) in stage 0 is substituted by Eq. (3) to get \(x_0 = X_N \times r^6\), and the input \(x_1\) in stage 1 is substituted by Eq. (3) to get \(x_1 = X_N \times r^{((5{\text{ log}}(6)){\text{*log}}(5) + 1)}\), and so on.

  1. (2)

    The following parameters are initialized: the number of iterations \(k\) of the discriminator D, the number of generated samples \(m\), the learning rate \(\eta\), the parameters \(\theta_D\), \(\theta_G\) of Gand D, the number of stages \(N\), the gradient penalty correlation coefficient \(\lambda\), and the weight factor \(\alpha\) of reconstruction loss. The training starts from stage 0, and the current stage number is \(n\). For the generator, the parameters of the last three stages are trained at the same time, and the parameters of the previous stage are fixed. For the discriminator, in all stages, the weight of the previous stage (stage \(n - 1\)) discriminator is used to initialize the weight of the given current stage.

  2. (3)

    Perform \(n\) stages of training, starting from stage 0, and when \(n < N\), perform steps (4) to (13).

  3. (4)

    When G does not converge, perform the following steps.

  4. (5)

    Perform steps (6), (7), (8), and (9) ktimes.

  5. (6)

    \(m\) three-dimensional noises \(\left\{ {z^{(1)} ,z^{(2)} , \ldots ,z^{(m)} } \right\}\) are extracted from the random vector that obeys the distribution \(p_z (z)\) and input into the generator.

  6. (7)

    Generate \(m\) rock generation samples \(\left\{ {\widetilde{x}^{(1)} ,\widetilde{x}^{(2)} ,\widetilde{x}^{(3)} , \ldots ,\widetilde{x}^{(m)} } \right\}\) by using the noise term input by generator \(\widetilde{x}^i = G\left( {z^i } \right)\).

  7. (8)

    Randomly select a weight \(\in\), \(\in \sim U[0,1]\) from the uniform distribution of 0–1 to obtain \(m\) weighted average samples \(\widehat{x}^{(i)} = \in x_n + (1 - \in )\widetilde{x}^{(i)} ,i = 1,2,3, \ldots ,m\).

  8. (9)

    The parameter \(\theta_D\) of the discriminator is updated by using the random gradient ascending method so that Eq. (4) gets the maximum value:

    $$ V = \frac{1}{n}\sum_{i = 1}^n {\left[ {D\left( {\widehat{x}^{(i)} } \right) - D(x^{(i)} ) + \lambda \left( {\left\| {_{\widehat{x}} D(\widehat{x})} \right\|\nabla_2 - 1} \right)^2 } \right]} ,\theta_D \leftarrow \theta_D + \eta \nabla V\left( {\theta_D } \right) $$
    (4)
  9. (10)

    Step (4) End of execution.

  10. (11)

    Randomly extract \(m\) noise vectors \(\left\{ {z^{(1)} ,z^{(2)} , \ldots ,z^{(m)} } \right\}\) from the noise distribution \(p_z (z)\) and input them into the generator.

  11. (12)

    Input noise vector with generator \(\widetilde{x}^i = G\left( {z^i } \right)\) to generate m shale samples \(\left\{ {\widetilde{x}^{(1)} ,\widetilde{x}^{(2)} ,\widetilde{x}^{(3)} , \ldots ,\widetilde{x}^{(m)} } \right\}\).

  12. (13)

    Use the random gradient drop algorithm to update the parameter \(\theta_G\) of the generator to get the minimum value.

    $$ \widetilde{V} = - \frac{1}{n}\sum_{i = 1}^n {\left[ {D\left( {\widetilde{x}^{(i)} } \right)} \right] - \alpha \left\| {\widetilde{x}^{(i)} - x_n } \right\|_2^2 ,\theta _G \leftarrow \theta _G - \eta \nabla V\left( {\theta _G } \right),{\text{~}}} $$
    (5)
  13. (14)

    Whenever the generator converges and the number of current training stages \(n < N\), it is supposed to enter the next training stage \( n = n + 1\). The generator adds 3 layers of convolution blocks on the basis of the previous stage and connects (Kaiming et al. 2016) the original up-sampled feature residual to the output of the newly added convolution layer. When the generator converges and the current number of training stages \(n = N\), the execution of step (3) ends, as shown in Fig. 1.

Training the last three stages at the same time is beneficial to the rapid training of the network, and the scaling factor of the learning rate \(\eta\) is set to make the previous stage use a smaller learning rate. The generator \(G_n\) uses learning rate \(\delta^0 \eta\) for training in stage \(n\), learning rate \(\delta^1 \eta\) for training in stage \( n - 1\) and learning rate \(\delta^2 \eta\) for training in stage \(n - 2\), which helps to reduce over-fitting. The process is shown in Fig. 2.

Fig. 2
figure 2

The 3D-Porous-GAN learning rate scaling diagram

Full size image

Model evaluation method

Dykstra-Parson coefficient

The Dykstra-Parson coefficient (Johnson 1956) is a measure used to describe the permeability of heterogeneous media. It is defined as the ratio of the total porosity of all connected pores in the media to the equivalent porosity. Porosity is the ratio of the total pore volume to the total volume of the media, while equivalent porosity is the ratio of the connected pore volume to the total volume of the media. Therefore, the Dykstra-Parson coefficient can be expressed as the porosity divided by the equivalent porosity. The significance of this expression lies in the fact that the Dykstra-Parson coefficient reflects the degree of pore connectivity in the media. When there are isolated areas between pores, the ratio of porosity to equivalent porosity decreases, resulting in a decrease in the Dykstra-Parson coefficient and vice versa.

When converting 3D sandstone and shale images into binary images with pixel values of 0 and 255, the equivalent porosity can be used to represent the proportion of pixels that truly represent pores. Therefore, in this study, the equivalent porosity was calculated as the sum of the porosity and the proportion of pixels with a value of 255. The principle of this calculation is that the pixels with a value of 255 after binary conversion represent pores, so the number of pixels with a value of 255 is equivalent to the number of pores. Then, for these pixels, their area, i.e., pixel size, can be calculated and expressed as the square root. By calculating the average of the square roots of all these pixels, the average pore size can be obtained. Finally, the equivalent porosity is the sum of the pore volume and the size of the remaining space, which is calculated based on the proportion of the average pore size. This method can more accurately estimate pores in rocks because it not only considers the number of pores in pixels but also takes into account the size distribution of pores.

Two-point correlation

The two-point probability function is one of the most commonly used evaluation methods in 3D pore structure reconstruction (Ghazavizadeh et al. 2012). By calculating a two-point probability function of the porous medium pore phase to characterize the second-order structure of the porous media (Lin et al. 2017). The two-point probability function of each direction is defined as the probability that any two points in the set \({{\mathbb{R}}}^d\) are in the same phase. Equation (6) represents the probability that two points \({\bf{x}}\) and \({\bf{x}} + {\bf{r}}\) separated by the separation distance \({\bf{r}}\) are both located in the pore phase \(P\).

$$ S_2 ({\bf{r}}) = {\bf{P}}({\bf{x}} \in P,{\bf{x}} + {\bf{r}} \in P){\rm{ for }}{\bf{x}},{\bf{r}} \in {{\mathbb{R}}}^d $$
(6)

When \({\bf{r}} = 0\), \(S_2 (0)\) is equal to the porosity \(\phi\), and when \({\bf{r}}\) approaches infinity, \(S_2 ({\bf{r}})\) is stable around \(\phi^2\). Because of the heterogeneity of pores, the average value of \(S_2 ({\bf{r}})\) is calculated along the three directions of x, y, and z in this paper.

Minkowski functional

The research shows that the flow characteristics at pore scale may be related to the morphological characteristics of the pore–solid interface of porous media (Joshi 1974). Hadwiger theorem shows that any continuous rigid body motion invariant estimation on compact convex subset \({{\mathbb{R}}}^d\) can be described by the linear combination of \({\text{d}} + 1\) independent parameters representing the object. Therefore, a set of morphological descriptors called Minkowski functional can be defined, which represent the topological structure of 3D objects and are stereological estimators that provide local and global morphological information related to the single-phase flow mechanism (Mecke and Arns 2005; Arns et al. 2010).

In three dimensions, there are four Minkowski functionals describing the geometric parameters of set \(X\) with smooth surface \(\partial (X)\), volume \(V(X)\), surface area \(S(X)\), integral \(b(X)\) of average curvature, and Euler characteristics \(\chi (X)\):

$$ V(X)\int_X {dx} $$
(7)
$$ S\left( X \right) = \int_{\partial X} {dx} $$
(8)
$$ b(X) = \frac{1}{2\pi }\int_{\partial X} {\frac{\kappa_1 (x) + \kappa_2 (x)}{2}} $$
(9)
$$ \chi \left( X \right) = \frac{1}{4\pi }\int_{\partial X} {\kappa_1 (x)\kappa_2 (x)dx} $$
(10)

Among them, \(\kappa_1 (x)\) and \(\kappa_2 (x)\) correspond to the curvatures of the maximum and minimum radii of curvature. Equations (7), (8), (9), and (10) correspond to zero-order, first-order, second-order, and third-order functional, respectively.

In this experiment, in order to evaluate the accuracy of the model, the zeroth-order functional is defined as porosity, that is, the ratio of pore phase space volume \(V_{\text{pore }}\) to sample volume \(V\). The porosity represents the ability to store fluids in porous media, which is represented by Eq. (11):

$$ \phi = \frac{{V_{\text{pore }} }}{V} $$
(11)

The first-order functional is defined as the specific surface area, which controls the adsorption and dissolution process of porous media, and is expressed by Eq. (12):

$$ S_v = \frac{1}{V}\int {dS} $$
(12)

The second-order functional is defined as the average width. In integral geometry, the integration of the average width and the average curvature is significantly different in any dimension. Although the average width is 1-dimensional and the integral of average curvature is \((n - 2)\)-dimensional, in the three-dimensional case, that is, when \(n = 3\), the integral of average width and average curvature is equivalent and is a constant. Meanwhile, the average width is proportional to the integral of the average curvature (Serra 1982; Ohser and Schladitz 2010). The average width is related to the curvature and indicates the flow resistance in the tubular network (Barbosa et al. 2019). In three dimensions, for a given direction \(\theta\), which is perpendicular to the normal \(\theta\) of the convex set \(K\) and completely surrounds the convex set \(K\), the maximum distance between two mutually parallel hyperplanes is the width \(b\) of the convex set \(K\) in the direction \(\theta\). Now, the average width \(\overline{b}\) of the convex set \(K\) is defined as the average width in all directions \(\theta_{all}\). In the special case of polyhedron \(P\) in \({{\mathbb{R}}}^3\), the average width can be calculated by Eq. (13):

$$ \overline{b}(P) = \frac{1}{4\pi }\sum_{i = 1}^m {\ell_i \gamma_i } $$
(13)

Among them, \(m\) is the number of edges, \(\ell_i\) is the length of the \(i\)-th edge, and \(\gamma_i\) is the angle between the outer normal of two surfaces touching on the \(i\)-th edge.

The third-order functional is defined as the Euler characteristic \(\chi\) normalized by the sample volume \(V\), which is expressed by Eq. (14):

$$ \chi v = \frac{\chi }{V} $$
(14)

When calculating the Euler characteristics \(\chi\), instead of directly calculating the integral in Eq. (10), the Euler eigen relation of any polyhedron is used, which is expressed as follows:

$$ \chi = {\text{D}} - E + F - O $$
(15)

Among them, \(D\) is the number of vertices, \(E\) represents the number of edges, \(F\) represents the number of faces, and \(O\) represents the number of entities (Blunt 2017). This expression is the basis of an efficient algorithm for calculating Minkowski functional of arbitrary geometry expressed as volume voxel domain (Lang et al. 2001). In the calculation, this paper calculates the sum of the number of vertices, edges, faces, and entities using a 6-adjacency system considering only the three main directions.

The Euler characteristics describes the connectivity of the volume. For the pore network, the region with positive Euler characteristics has more connected skeletons and less connected pores, indicating that the pore connectivity in this region is small. The area with negative Euler characteristics has more connected pores, so the pores in this area have greater connectivity.

Although porosity indicates the ability to store fluid in porous media, the adsorption and dissolution processes are controlled by specific surface area. The Euler property describes the connectivity of porous media and characterizes the flow ability of fluid in porous media. Therefore, the reconstructed porous media should be consistent with the Minkowski functional of real samples to simulate the properties of relevant physical processes at the pore scale.

Dataset

To verify the reconstruction effect of this algorithm on homogeneous and heterogeneous cores, a set of Berea sandstone dataset (Mosser et al. 2017) is used as the homogeneous core sample set, and a set of shale samples scanned by focused ion beam scanning electron microscope (FIB-SEM) is used as the heterogeneous core sample set for training and verification.

Shale dataset

Shale is a typical heterogeneous porous medium. In order to verify the expression ability of the model on heterogeneous porous medium, a group of real shale samples scanned by focused ion beam scanning electron microscope were sampled for training and verification. Figure 3a shows a section in the scanned image of the shale sample. Figure 3b shows the label image of the real shale image, in which green is the pore label, blue is the organic matter label, and gray is the rock skeleton label. In this paper, gray and blue labels are considered as skeleton phase. The real shale image is marked, cut, and its pores are extracted, i.e., skeletal binary features and then make the image into binary form. Black is the skeleton and white is the pore, as shown in Fig. 3c. The shale sample used for training is a binary three-dimensional image with size 250 × 250 × 250 (pixels). Figure 4 shows the three-dimensional display of the dataset.

Fig. 3
figure 3

Shale data

Full size image
Fig. 4
figure 4

Three-dimensional pore structure of shale

Full size image

Berea sandstone dataset

Berea sandstone is a typical homogeneous porous medium. In order to verify the expression ability of the model in homogeneous porous medium, a group of Berea sandstone from a quarry near Berea, Ohio, was sampled for training and verification. The size of the dataset is 400 × 400 × 400 (pixels). Figure 5a shows the two-dimensional image display of the training sample, and Fig. 5b shows the three-dimensional image display of the training sample.

Fig. 5
figure 5

Berea sandstone dataset

Full size image

Experiment results

In this experiment, the dataset used by 3D-DCGAN is as follows. For the experimental comparison under the size of 1003 (pixels), the shale dataset of this experiment is made by cutting 1000 3D shale images with the size of 100 × 100 × 100 (pixels) layer by layer with the size of 250 × 250 × 250 (pixels) 3D shale images as the step size of 16. The Berea sandstone dataset with the size of 400 × 400 × 400 (pixels) is divided into 6,859 3D images with the size of 100 × 100 × 100 (pixels) layer by layer with the step size of 16 as the Berea sandstone dataset of this experiment. For the experimental comparison under the size of 643 (pixels), a total of 1680 3D shale images of size of 64 × 64 × 64 (pixels) were cut layer by layer with the size of 250 × 250 × 250 (pixels) as step 16 and used as the shale dataset in this experiment. The Berea sandstone dataset with the size of 400 × 400 × 400 (pixels) is divided into 10,648 3D images with the size of 64 × 64 × 64 (pixels) layer by layer with the step size of 16 as the Berea sandstone dataset of this experiment.

In this experiment, the dataset used by 3D-Porous-GAN is as follows. For the experimental comparison under the size of 1003 (pixels), the 3D shale image with the size of 250 × 250 × 250 (pixels) was downsampled to the size of 100 × 100 × 100 (pixels) as the shale dataset of this experiment. A 100 × 100 × 100 (pixels) 3D image randomly cut from the 400 × 400 × 400 (pixels) Berea sandstone dataset was used as the Berea sandstone dataset of this experiment. For the experimental comparison under the size of 643 (pixels), the 3D shale image with the size of 250 × 250 × 250 (pixels) was downsampled to the size of 64 × 64 × 64 (pixels) as the shale dataset. A 3D image of size 64 × 64 × 64 (pixels) randomly cut from the 400 × 400 × 400 (pixels) Berea sandstone dataset was used as the Berea sandstone dataset. The traditional methods, Sequential Indicator Simulation (SIS) and Multi-point Geostatistics (MPS), were used on datasets from the aforementioned 250 × 250 × 250 (pixels) shale and 400 × 400 × 400 (pixels) Berea sandstone datasets.

The training stage of 3D-Porous-GAN model is set as 6, and each stage is composed of three convolutional layers plus LeakyReLU activation function, and the residual connects the input and output of each stage. Among them, LeakyReLU's negative slope = 0.05; The weight factor of reconstruction loss \(\alpha = 5\), the maximum size is 100 pixels, the minimum size is 50 pixels, the weight of superimposed noise is 0.1, the learning rate adjustment weight of lower stage is 0.01, the gradient penalty weight is 0.1, the learning rate of generator and discriminator is 0.0001, and the optimizer is Adam optimizer. Table 1 shows the main architectural configurations of the 3D-Porous-GAN model.

Table 1 The 3D-Porous-GAN network structure configuration
Full size table

Discussion

Compared with SIS and MPS methods

In this study, we first created datasets using traditional methods. The 400 × 400 × 400 (pixels) sandstone and 250 × 250 × 250 (pixels) shale datasets were reduced in dimension and transformed into 400 2D sandstone images of size 400 × 400 (pixels) and 250 2D shale images of size 250 × 250 (pixels), respectively. The 3D-Porous-GAN method was then applied to the original 400 × 400 × 400 (pixels) sandstone and 250 × 250 × 250 (pixels) shale datasets. The original images and 3D display images generated using these three methods are shown in Figs. 6 and 7.

Fig. 6
figure 6

a shows the real 3D display of shale, b shows the 3D reconstructed porosity using the SIS method, c shows the 3D reconstructed porosity using the MPS method, and d shows the 3D reconstructed porosity using 3D-Porous-GAN for shale

Full size image
Fig. 7
figure 7

a shows the 3D display of the real Berea sandstone image, b displays the 3D pore reconstruction of the Berea sandstone using the SIS method, c displays the 3D pore reconstruction of the Berea sandstone using the MPS method, and d shows the 3D pore reconstruction of the Berea sandstone using the 3D-Porous-GAN method

Full size image

To our surprise, the image quality generated by the two traditional methods was not as poor as expected. The overall reconstruction effect was good, but there were differences in local reconstruction, and the internal structural features could not be reconstructed, resulting in differences in connectivity. From the perspective of the images, our method outperformed the traditional methods in both overall and local reconstruction of sandstone and shale. Both SIS and MPS algorithms have limitations in reconstructing pixels with significant differences from the original pixels due to the randomness of the algorithm and inherent restrictions. This can result in blurred spherical particles and protrusions on the surface of the shale in local areas. Similar problems arise when reconstructing three-dimensional sandstone images, where the compact structure of the sandstone leads to the generation of many blocky protrusions on the surface, and longer rock bodies are segmented during reconstruction, resulting in blurred local areas.

As shown in Table 2, regarding the indicators of rock heterogeneity, we calculated that the sandstone images reconstructed by MPS, SIS, and 3D-Porous-GAN differ from the real images by 0.190, 0.133, and 0.005, respectively, in terms of porosity. The shale images reconstructed by MPS, SIS, and 3D-Porous-GAN differ from the real images by 0.291, 0.298, and 0.032, respectively, in terms of porosity. Regarding the Dykstra-Parson coefficient, the sandstone images reconstructed by MPS, SIS, and 3D-Porous-GAN differ from the real images by 0.097, 0.062, and 0.004, respectively, while the shale images reconstructed by MPS, SIS, and 3D-Porous-GAN differ from the real images by 0.228, 0.249, and 0.022, respectively. The experimental results show that the porosity and Dykstra-Parson coefficient of the two rocks reconstructed by 3D-Porous-GAN are closest to the original images, indicating that our method outperforms traditional methods in terms of reconstructing heterogeneity indicators.

Table 2 Comparison table of porosity and Dykstra-Parson coefficient generated by different methods for sandstone and shale
Full size table

Comparison with 3D-DCGAN

We conducted experiments comparing the performance of 3D-Porous-GAN and 3D-DCGAN in reconstructing sandstone and shale to demonstrate their distinct reconstruction abilities. Through visual comparison of the generated sample slices from both models, the experimental results showed that 3D-Porous-GAN could produce convergent samples with good reconstruction quality. Therefore, the accuracy of the reconstruction was evaluated using two-point correlation function, porosity, Minkowski functionals, and Dykstra-Parson coefficient and compared with real samples. However, due to the complex convolutional network structure of 3D-DCGAN, the model parameters increased significantly, causing it to fail to converge, resulting in poor core reconstruction performance. Therefore, the relevant statistical information of 3D-DCGAN was not calculated. In each experiment, a real sample was used as the target, and 20 randomly generated samples were tested and compared. The results are presented below.

The reconstructed sandstone results are shown in the central slice of Fig. 8, demonstrating the generated results for homogeneous porous media of varying sizes and iteration numbers. Both 3D-DCGAN and the proposed model produce high-quality 643 (pixels) images. However, as the size of the training image is increased to 1003 (pixels), the complex convolutional layer structure of 3D-DCGAN leads to a higher number of parameters, making it challenging to capture the intrinsic structure of the training image and converge within the same number of iterations. Conversely, our model's parallel multi-stage network structure design significantly reduces the number of parameters, allowing it to learn the distribution characteristics of homogeneous porous media more quickly and reliably within the same number of iterations, resulting in superior reconstruction results.

Fig. 8
figure 8

Comparison of Berea samples with size 643(pixels) and size 1003(pixels) reconstructed by different methods, and generated sample center slices under different iterations

Full size image

The image in Fig. 9 depicts the central slice of the reconstructed shale. It presents the generated results of heterogeneous porous media under different sizes and iteration numbers. In comparison with the proposed model, the 3D-DCGAN exhibits a poorer fitting ability for heterogeneous porous media due to its complex convolutional layer structure. Regardless of the image size, 643 (pixels) or 1003 (pixels), the 3D-DCGAN cannot reconstruct a reasonable three-dimensional structure. In contrast, the proposed model has excellent reconstruction ability for heterogeneous porous media and greater versatility.

Fig. 9
figure 9

Comparison of shale samples with size 643 (pixels) and size 1003 (pixels)in different methods and generating sample center slices under different iterations

Full size image

As shown in Figs. 10 and 11, the 3D digital cores reconstructed by the proposed model have similar global distribution with real shale samples and real Berea samples, but from a visual perspective, they are not completely consistent locally, indicating the diversity of the generated 3D digital cores.

Fig. 10
figure 10

The figures a, b, c, and d show four different samples selected from the Berea dataset, and the corresponding pore-throat network structures and orthogonal section images in three directions generated by the 3D-Porous-GAN model

Full size image
Fig. 11
figure 11

Figures a, b, c, and d show four different samples selected from the shale dataset, and the corresponding pore-throat network structures and orthogonal section images in three directions generated by the 3D-Porous-GAN model

Full size image

As shown in Fig. 13, the average porosity of the generated samples using the \(\phi_{3{\text{D}} - {\text{Porous}} - {\text{GAN}}} = 0.184{ } \pm { }0.012\), which is very close to the porosity value of the real sample \(\phi = 0.185\). The porosity values and their differences between the real and generated samples demonstrate excellent consistency. In Fig. 12, we compare the two-point correlation functions in the x, y, and z directions between the real samples and the samples generated by our proposed model on the Berea dataset. Figure 13 presents the comparison of radial mean two-point correlation functions between the real and generated samples on the Berea dataset. Figure 14 shows the comparison of Minkowski functionals between the real and generated samples on the same dataset. The two-point correlation function, radial average two-point correlation function, and Minkowski functional of the generated samples in all three directions exhibit excellent consistency with the real samples. These results once again prove the capability of our proposed model to reconstruct homogeneous porous media.

Fig. 12
figure 12

Comparison of the two-point correlation functions in the x, y, and z directions between real Berea samples and samples generated by 3D-Porous-GAN

Full size image
Fig. 13
figure 13

Comparison of radial average two-point correlation functions between real Berea samples and samples generated by 3D-Porous-GAN

Full size image
Fig. 14
figure 14

Comparison of the Minkowski functionals between real Berea samples and 3D-Porous-GAN generated samples

Full size image

As shown in Fig. 16, the average porosity of the generated sample is \(\phi_{3{\text{D}} - {\text{Porous}} - {\text{GAN}}} = 0.091{ } \pm { }0.022\), and the real sample is \(\phi = 0.083\). The size and porosity difference between the real and generated samples are in excellent agreement. Figure 15 illustrates the comparison of two-point correlation functions in the x, y, and z directions between the real samples and the model-generated samples proposed in this paper on the shale dataset. Additionally, Fig. 16 compares the radial average two-point correlation function between the real sample and the sample generated by the proposed model on the shale dataset. Furthermore, Fig. 17 shows the comparison of the Minkowski functional between the real sample and the sample generated by the proposed model on the shale dataset. The two-point correlation function, radial average two-point correlation function, and Minkowski functional of the generated samples in all three directions show good consistency with the real samples. This provides further evidence that the proposed model can effectively reconstruct heterogeneous porous media.

Fig. 15
figure 15

Comparison of the two-point correlation functions in the x, y, and z directions between real shale samples and samples generated by 3D-Porous-GAN

Full size image
Fig. 16
figure 16

Comparison of radial average two-point correlation functions between real shale samples and samples generated by 3D-Porous-GAN

Full size image
Fig. 17
figure 17

Comparison of the Minkowski functionals between real shale samples and 3D-Porous-GAN generated samples

Full size image

Analysis of results

As presented in Table 3, the 3D-Porous-GAN utilizes only one 3D data as the training dataset, whereas 3D-DCGAN demands a considerable amount of data for training. Given the challenging and expensive nature of rock sample acquisition, employing the 3D-Porous-GAN model for training requires fewer samples, leading to a significant reduction in sample acquisition costs. The experimental findings indicate that 3D-DCGAN can effectively reconstruct the Berea sandstone sample at the size of 643 (pixels); however, the model fails to converge and the reconstruction quality deteriorates when the size is increased to 1003 (pixels). Conversely, the 3D-Porous-GAN can generate high-quality reconstructions at both 643 (pixels) and 1003 (pixels) sizes. Additionally, the 3D-Porous-GAN achieves favorable reconstruction outcomes for both shale samples at the two scales, while 3D-DCGAN struggles to converge. By using a loss function with gradient penalty to enhance the stability of training, 3D-Porous-GAN adopts a multi-scale, multi-stage parallel training strategy in which the training image is down sampled to the minimum size at the low stage and the model focuses on the global image information. At the high stage, the training image size gradually increases, enabling the model to capture the local image details. Therefore, the 3D-Porous-GAN outperforms 3D-DCGAN in terms of model generalization and can reconstruct more types of rock samples. Moreover, 3D-Porous-GAN is more efficient as it requires less training time.

Table 3 Comparison of performance and heterogeneity indicators of 3D-DCGAN and Porous3D-GAN
Full size table

We have calculated and compared the heterogeneity indices of 3D-DCGAN and 3D-Porous-GAN, and also determined the porosity and Dykstra-Parson coefficient of the real sandstone and shale images at two different sizes, as presented in Table 3. For 3D-DCGAN, only the images reconstructed from the sandstone dataset of size 64 × 64 × 64 (pixels) were considered for calculation, as the models failed to converge for other datasets. Conversely, for 3D-Porous-GAN, all datasets of both rock types were included in the calculation. Therefore, we calculated that the 643-size sandstone images reconstructed by 3D-DCGAN differ from the real images by 0.215 and 0.149 in terms of porosity and Dykstra-Parson coefficient, respectively. For 3D-Porous-GAN, the minimum difference in porosity between the reconstructed images at two sizes and the real images was 0.001, and the maximum difference was 0.06. The minimum and maximum differences in Dykstra-Parson coefficient were 0.002 and 0.027, respectively. The experimental results indicate that our model's reconstructed images are closer to the real images in terms of porosity and Dykstra-Parson coefficient, demonstrating better reconstruction performance.

Conclusions

To address the challenges of acquiring difficult and costly samples, the limited generalizability of existing models, and the instability and convergence issues in training porous media, this paper enhances the generator, discriminator, and noise vector components of the ConSinGAN network structure. It introduces a loss function with gradient penalty and adopts a multi-scale, multi-stage parallel training strategy. The proposed algorithm is applied in an innovative manner to reconstruct 3D digital rock cores. Comparative experiments are conducted on the Berea sandstone dataset and shale dataset, comparing against traditional methods and the 3D-DCGAN approach. The results lead to the following conclusions:

  • Superior results in reconstructing 3D rock cores using a smaller amount of training data are achieved by the developed model in this study.

  • The 3D-Porous-GAN model excels in reconstructing both anisotropic and isotropic porous media, showcasing its high level of generalizability. Furthermore, it effectively reduces the number of parameters, lowers the complexity of training, and facilitates rapid convergence.

  • Reconstructed images produced by the 3D-Porous-GAN closely resemble real images in terms of heterogeneity index, two-point correlation function, Minkowski function, and visual display.