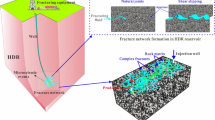
Abstract
Understanding fluid flow in fractured porous media under coupled thermal–hydrological–mechanical (THM) conditions is a fundamental aspect of geothermal energy extraction. In this study, we developed a fully coupled THM model, incorporating porosity and permeability variations, to scrutinize the process of geothermal energy extraction within fractured porous reservoirs. Moreover, we accentuated the significance of natural fracture orientation and hydraulic fracture permeability on fluid trajectories and heat extraction efficiency. Simulation results revealed that hydraulic fractures predominantly govern fluid channels and thermal exchange between injected water and the reservoir. Interconnected natural fractures bolster water migration into the reservoir, while detached fractures exert minimal influence on fluid dynamics, underscoring the crucial role of fracture connectivity in optimizing heat extraction efficiency. The sensitivity analysis indicated that larger fracture angles marginally hinder pressure and cool-water dispersion into the fractured reservoir, resulting in subtle enhancements in heat extraction rates and average production temperatures. An upsurge in hydraulic fracture permeability augments fluid velocity and thermal exchange, thereby fostering heat extraction efficiency. The THM model developed in this study offers a comprehensive insight into fluid flow within fractured porous media and its implications on geothermal energy extraction.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Geothermal energy is a promising source of renewable energy that can be used to generate electricity and heat. In deep subsurface reservoirs, the geothermal resources are present in the form of hot, dry rock (Kazemi et al. 2019). However, the permeability of these rocks is usually low, which limits the extraction of the geothermal energy (Li and Lior 2015; Han et al. 2020; Zhang et al. 2020). To overcome this limitation, an Enhanced Geothermal System (EGS) is used, which involves the injection of cold water into the reservoir at high pressure (Blackwell et al. 2006; Feng et al. 2014; Lu 2018). The water is circulated through the reservoir to extract the geothermal energy and then, returned to the surface for reheating and recirculation.
Heat extraction from porous or fractured porous reservoirs is believed to be a coupled Thermal–Hydraulic-Mechanical (THM) process (Jeanne et al. 2014; Zhao et al. 2015; Song et al. 2018; Aliyu and Chen 2018). Over the past few decades, numerous simulation models have been developed to investigate and comprehend the coupled THM phenomenon in the process of heat extraction (Ma et al. 2020a, 2021). Chen et al. (2014) presented a discrete fracture modeling strategy for examining flow and heat transmission in fractured reservoirs, while Bower et al. implemented a dual-porosity model into the FEHM finite element code to study groundwater flow dynamics in a saturated reservoir with thermal sources. Pandey et al. (2017) extended the FEHM code to three-dimensional numerical simulation cases, focusing on the reservoir deformation-induced hydraulic transmissivity during heat extraction. Gutierrez and Makurat (1997) presented a THM modeling approach for analyzing cold water injection into the fractured reservoir, and Koh et al. (2011) simulated cold water injection into the fractured reservoir using a thermo-poroelastic model that considers the closure and opening of fractures due to the effective stress. Ghassemi and Zhou (2011) proposed a three-dimensional coupled poro-thermo-chemo-mechanical model, where FEM and boundary integral equation methods are utilized to represent flow and heat transfer in fracture and matrix, respectively. The model was expanded by Rawal and Ghassemi (2014) to include reactive solute transport in the fracture. De Simone et al. (2013) performed a coupled THM model to investigate the cold water injection-induced seismicity in a fractured zone within a multi-layer system, while Taron and Elsworth (2009) developed a new approach and TOUGHREACT-FLAC simulator to model coupled THMC processes in dual-porosity geothermal reservoirs.
Recent experiments conducted by Shu et al. (2022) investigated the heat transport properties of a single geothermal fracture at varying reservoir temperatures and in situ stress conditions, while Zhang et al. (2022) investigated the evolution of fractures in EGS using fractal theory. Additionally, numerous researchers employ random methods to construct a fracture network and then, conduct numerical simulation research to examine fluid flow and heat transfer in the fracture network (Yao et al. 2018; Guo et al. 2019; Nadimi et al. 2020). (Ma et al. 2020b) developed a two-dimensional random fracture model to investigate the relationship between the optimal well layout and fracture parameters. The results indicate that increasing the number of fractures could improve the performance of heat extraction, but excessive fractures could exacerbate the interference between fractures, resulting in negative impacts. (Ma et al. 2020c) investigated the influence of intersecting fractures with different angles on the heat extraction of a three-dimensional EGS model. The results indicate that the heat transfer rate of the fluid increases according to the uniformity of fracture distribution in the reservoir. Overall, these simulation models and experiments provide valuable insights into the complex THM processes involved in heat extraction from fractured porous reservoirs, which can inform the design and optimization of EGS.
Previous studies on heat extraction from fractured porous reservoirs have mainly focused on the effect of fluid flow in a single fracture or a random fracture network on heat extraction performance, while ignoring the impact of hydraulic fractures. However, hydraulic fractures are crucial pathways for seepage and heat transmission, and their properties are essential for successful exploitation of Hot Dry Rock (HDR) resources (Legarth et al. 2005; Julian et al. 2010; Li et al. 2021). To simulate heat energy extraction from fractured porous reservoirs in a coupled Thermo-Hydro-Mechanical (THM) model, this study constructs an Enhanced Geothermal System (EGS) model with a random fracture network. The study aims to examine the influence of hydraulic fractures on heat extraction performance. By considering hydraulic fractures, this study can provide a more comprehensive understanding of the complex THM processes involved in heat extraction from fractured porous reservoirs.
The paper is structured as follows: Firstly, we present the governing equations of the coupled THM model. Next, we describe the model setup, including details about the geometry, initial and boundary conditions and other relevant factors. Then, we present the simulation results of the base case and investigate the influence of natural fracture orientations and fracture permeability on heat extraction. Finally, we provide a summary and conclusion.
Governing equations of coupled THM model
To obtain mathematical models that describe the coupled process during heat extraction from fractured reservoirs, the following assumptions are made(Tian et al. 2023):
-
(1)
The strains of the reservoir are infinitesimal.
-
(2)
Water viscosity remains constant.
-
(3)
The influence of gravity is neglected.
-
(4)
The effect of solid deformation on fracture aperture and permeability is ignored.
The governing equations for the coupled Thermo-Hydro-Mechanical (THM) model in the matrix and fracture systems are described by Rutqvist et al. (2001) and Lei et al. (2021). These equations take into account the coupled processes of fluid flow, heat transfer, and rock deformation, providing a comprehensive understanding of the complex THM processes involved in heat extraction from fractured reservoirs. By utilizing the aforementioned assumptions, this study can derive a mathematical model for simulating heat extraction from fractured reservoirs, which is described as follows:
The mass and energy balance equations are represented by Eqs. (1) and (2), respectively. Equation (3) represents the solid deformation equation, where \({\rho }_{\mathrm{w}}\) and \({\mu }_{\mathrm{w}}\) denote the density and viscosity of water. Subscripts \(\theta =m\) and \(f\) represent the variables in matrix and fractures, respectively. \({S}_{\theta }\) is the storage coefficient, \(\beta\) is thermal compressibility, \(\alpha\) is Biot’s coefficient, \({\left(\rho C\right)}_{\mathrm{b}}\) is the bulk specific heat, \({T}_{0}\) is initial temperature, \({\lambda }_{\theta }\) is the thermal conductivity, \(G\) is the shear modulus of porous media, \(u\) is displacement, \(\nu\) is Poisson’s ratio, \(p\) is the pore pressure, \(T\) is the temperature, and \({\varepsilon }_{\mathrm{v}}\) denotes for volumetric strain.
The model presented in this study disregards variations in fracture porosity and assumes that the fracture porosity is a constant value of 1. Additionally, the aperture and permeability of the fracture are assumed to be constant throughout the process of thermal extraction. However, solid deformation induced by pore pressure and temperature can lead to changes in the structures of pores, resulting in variations in the porosity and permeability of the matrix. To account for these changes, a stress-dependent porosity model is adopted in this study, which is expressed as follows:
where \({\phi }_{m0}\) represents the fracture porosity at the initial stress condition; \(\Delta {\upsigma }^{^{\prime}}\) represents the effective stress difference between the current average effective stress \({\upsigma }^{^{\prime}}=\frac{1}{3}({\sigma }_{1}^{^{\prime}}+{\sigma }_{2}^{^{\prime}}+{\sigma }_{3}^{^{\prime}})\) and initial effective stress \({\sigma }_{0}^{^{\prime}}=\frac{1}{3}({\sigma }_{10}^{^{\prime}}+{\sigma }_{20}^{^{\prime}}+{\sigma }_{30}^{^{\prime}})\).
The effective principal stresses, with compression stress being represented as a negative quantity, can be expressed as follows(Tian et al. 2022):
where the total principal stresses are denoted by \({\sigma }_{1}\), \({\sigma }_{2}\), and \({\sigma }_{3}\), respectively.
The relationship between matrix porosity and permeability in this study is assumed to follow the cubic law, which is expressed as follows (Ma et al. 2017):
where \({k}_{m0}\) represents the initial permeability of the matrix system.
Model setup
To investigate the influence of discrete fracture networks on heat recovery, two cases are considered in this study: one with randomly distributed natural fractures, and the other without. The geometry of both cases is depicted in Fig. 1, with the simulation domain measuring 500 m by 300 m in size.
Figure 1b shows two types of fractures: hydraulic fractures and randomly distributed natural fractures. Nine cracks are evenly dispersed in the vertical direction, with a spacing of 50 m between them. The lengths of natural fractures adhere to a normal distribution with an expected value and variance of 25 and 1, respectively. The aperture and permeability of the hydraulic fractures are set to 2 mm and \(3\times {10}^{-13}\) m2, respectively. The width and permeability of the natural fractures are adjusted to 0.5 mm and \(7.5\times {10}^{-14}\) m2, respectively. These parameters are chosen to represent a typical fractured reservoir, and the two cases are used to analyze the impact of natural fractures on heat recovery in a hydraulic fracture-dominated system.
To obtain the initial pore pressure, temperature, and stress state at the start of thermal extraction, a steady-state model is simulated. It is assumed that the reservoir is initially saturated with water, with an initial temperature and pressure of 420 K and 2 MPa, respectively. The upper and lower boundaries of the simulation domain are assigned as injection and production wells, respectively, with Dirichlet boundary conditions. The pressure and temperature of the injection well are set to 8 MPa and 290 K, while the production well has the same pressure and temperature values as the initial conditions. The remaining boundaries are enforced by thermal insulation and no-flow conditions. For the mechanical boundaries, the left and upper boundaries of the domain are subjected to boundary loadings of 10 MPa, while the lower and right boundaries are constrained with zero-displacements. The specific simulation parameters are listed in Table 1. These conditions are chosen to represent a typical geothermal reservoir, and the steady-state model is used to provide the initial conditions for the subsequent thermal extraction simulations.
The final governing equations for fluid flow, heat transfer, and solid deformation are represented by Eqs. (1)–(3). To solve these equations, we employ the finite element software COMSOL Multiphysics. We utilize a preconfigured COMSOL porous media and subsurface flow module to address the flow component in Eq. (1). Meanwhile, Eqs. (2) and (3) are computed using the heat transfer in solids and geomechanics modules, respectively. For solving the differential equations, we opt for the Time-Dependent Solver technique, which incorporates implicit time-stepping methods based on the backward differentiation formula (BDF). The BDF order ranges from 1 to 5, and we assign the default value of 2. The nonlinear solver implements a dampened version of Newton's method, which manages parameters for a fully coupled approach to the solution. The convergence criterion is verified when the damping factor for the current iteration equals 1. Consequently, the solution proceeds as long as the damping factor does not equal 1, even if the estimated error is less than the specified relative tolerance. To enhance the accuracy of our results, we establish a relative tolerance of 0.001.
Results and discussion
Figure 2 displays the pressure distribution after 5, 15, and 20 years for both cases. The simulation results reveal that pore pressure generally propagates along the hydraulic fractures, leading to higher pressure in their vicinity compared to areas further away. Consequently, hydraulic fractures predominantly influence the flow path due to their higher permeability and porosity compared to the surrounding matrix. A noticeable pressure change is observed around natural fractures connected to hydraulic fractures in Case B, indicating that connected fractures significantly impact fluid flow, while isolated fractures have a negligible effect on flow channels.
Figure 3 illustrates the temporal evolution of pore pressure at monitoring points A1, A2, and A3 along the y-direction. After 20 years of extraction, the pressures at Points A1, A2, and A3 are approximately 2.25 MPa, 3.02 MPa, and 4.60 MPa in Case B, while the pressures at Points A1, A2, and A3 are approximately 2.27 MPa, 3.07 MPa, and 4.76 MPa in Case A. The simulation results indicate that pore pressure increases as high-pressure water is continuously injected into the reservoir. In the early stages, the pressures at monitoring points in Case A are lower due to isolated fractures, which reduce the amount of fluid entering the hydraulic fractures. Case A exhibits higher pressures at points than Case B because non-isolated natural fractures impact flow patterns.
Figure 4 presents the temperature distribution after 5, 15, and 20 years for both cases. As cold water is injected, heat exchange occurs between the reservoir and water, lowering the temperature within the fracture. Along the hydraulic fractures, their high thermal conductivity coefficient causes significant temperature fluctuations. Furthermore, heat in the area surrounding a fracture is transferred into the fracture, resulting in the cooling of the adjacent area.
Figure 5 illustrates the evolution of temperature at Points B1, B2, and B3. The results indicate a temperature decrease for both cases, with Case B exhibiting a lower temperature than Case A due to the increased heat conductivity of the fracture in Case A. The temperatures are approximately 325 K in Case A and 322 K in Case B, respectively.
Figure 6 displays the evolution of average production temperature, output thermal power, and heat extraction rate for the two cases. The average production temperature (\({T}_{\mathrm{a}}\)) is defined as follows:
where \(T\left(t\right)\) represents the temperature on the well surface at different times, and A is the production well surface area.
The output thermal power \({p}_{\mathrm{out}}\) is calculated by:
where \(q\) is the average flow rate through the production well, and \({T}_{\mathrm{inj}}\) and \({T}_{\mathrm{pro}}\) are the temperatures at the injection and production wells, respectively.
The heat exchange rate \({h}_{\mathrm{r}}\) is defined as follows:
where \({\eta }_{1}\) is the output thermal energy, and \({\eta }_{2}\) is the total stored thermal energy.
At the early stage, the average production temperature in Case A is similar to that in Case B. After 8 years of injection, the average production temperature in Case B becomes greater than that in Case A, which can be attributed to the natural fractures that increase flow velocity and enhance heat extraction efficiency. Case B offers higher output thermal power due to its increased permeability, which provides more flow channels. The heat extraction rate is slightly larger in Case B than in Case A, which can be explained by the fact that considerable portions of natural fractures are separated. This demonstrates that the connection of fractures has a significant effect on improving heat extraction rate efficiency.
Influence of the orientations of natural fractures on heat extraction
In this section, we conduct three cases to examine the impact of natural fracture orientations on heat extraction. Figure 7 displays the fracture configurations for each case, where the angles \(\theta\) between natural fractures and hydraulic fractures are set to 30°, 60°, and 90°, respectively. The length and aperture remain consistent across all cases.
The distributions of pressure and temperature for the five cases with different fracture angles after 20 years of coal-water injection are shown in Figs. 8 and 9. The simulation results demonstrate that the orientation of natural fractures influences fluid flow routes and temperature fields across the entire region.
Figure 10 displays the evolution of pressure at Points A1, A2, and A3, while Fig. 11 illustrates the changes in temperature at Points B1, B2, and B3. As the fracture angle increases, both pressure and temperature at the monitoring points decrease. Fluids tend to flow along the x-direction, leading to reduced pressure and heat propagation into the fractured reservoir. Among the cases, the one with a fracture angle of 30° exhibits the highest pore pressure values, reaching 2.08 MPa, 2.48 MPa, and 3.08 MPa at Points A1, A2, and A3, respectively, after 20 years of thermal extraction.
Figure 12 illustrates the average extraction temperature and heat rate for cases with different fracture angles. In cases where fracture angles are 30 degrees, heat extraction is least effective. As the fracture angles increase, the heat extraction rate and average production temperature experience a slight rise. From these results, it can be inferred that isolated fractures do not significantly contribute to enhancing heat extraction performance.
Influence of the permeability of hydraulic fractures on heat extraction
This section examines the effect of hydraulic fracture permeability on heat extraction through four different cases. The permeabilities of hydraulic fractures in these cases are \(5\times {10}^{-14} {\mathrm{m}}^{2}\), \(1\times {10}^{-13} {\mathrm{m}}^{2}\), \(2\times {10}^{-13}\) and \(4\times {10}^{-13}\), respectively. Figures 13 and 14 display the distribution of pore pressure and temperature after 20 years of injection for each case. As the permeability of hydraulic fractures increases, fluid migration into the reservoir accelerates, leading to enhanced heat exchange between cold water and hot rock. This causes the heat exchange zone to expand gradually toward the production well. It is noteworthy that as the permeability increases from \(2\times {10}^{-13} {\mathrm{m}}^{2}\) and \(4\times {10}^{-13} {\mathrm{m}}^{2}\), the expansion trend of the pressure range slows down.
Temperature distribution after 20 years of heat extraction for the four cases with different hydraulic fracture permeability of a \(5\times {10}^{-14} {\mathrm{m}}^{2}\), b \(1\times {10}^{-13} {\mathrm{m}}^{2}\), c \(2\times {10}^{-13}{\mathrm{m}}^{2}\), and d \(4\times {10}^{-13}{\mathrm{m}}^{2}\)
Figure 15 displays the relationship between water pressure and time at Point A1. An increase in permeability leads to a rise in water pressure. Figure 16 illustrates the evolution of average production temperature, heat extraction rate, and cumulative heat extraction for the four cases. The cumulative heat extraction (\({h}_{t}\)) is calculated using the following equation:
After 20 years of extraction, the maximum and minimum pressure values are approximately 5.94 MPa and 3.50 MPa for fracture permeabilities of \(4\times {10}^{-13} {\mathrm{m}}^{2}\) and \(5\times {10}^{-14} {\mathrm{m}}^{2}\), respectively. An increase in fracture permeability tends to raise the pore pressure within the reservoir. A significant reduction in average production temperature is observed with increasing hydraulic fracture permeability, facilitating heat exchange and enhancing both the heat extraction rate and cumulative heat extraction. As fracture permeability increases from \(5\times {10}^{-14} {\mathrm{m}}^{2}\) to \(4\times {10}^{-13} {\mathrm{m}}^{2}\), the heat extraction rate rises from 40.1 to 78.0%, and heat extraction grows from \(1.0\times {10}^{12}\) to \(3.1\times {10}^{13}\) J.
Summary and conclusions
In this study, we explored the extraction of geothermal energy from fractured porous reservoirs using a coupled thermal–hydrological–mechanical (THM) model, where porosity and permeability relate to effective stress changes. We focused on the impact of natural fracture orientation and hydraulic fracture permeability on fluid pathways and heat extraction efficiency. The following conclusions are derived:
-
(1)
The influence of hydraulic fracture is significant on the fluid pathway and the thermal interchange between the injected water and the reservoir. Augmented by natural fractures intersecting the primary fracture, the area available for fluid migration expands, while isolated fractures exert minimal influence on fluid dynamics. This observation underscores the premise that fracture connectivity enhancement optimizes both heat extraction efficiency and overall performance.
-
(2)
Fluids exhibit a propensity to flow along the x-axis as the fracture angle enlarges, thereby attenuating pressure and thermal propagation into the fractured reservoir. Subtle improvements in the heat extraction rate and mean production temperature are observed with escalating fracture angles. Enhanced hydraulic fracture permeability amplifies the fluid velocity and thermal exchange between cool water and heated rock strata. This surge in permeability results in a decrease in reservoir temperature, facilitating increased heat extraction efficiency and overall performance.
This current investigation utilized a two-dimensional geometry model, but future research will concentrate on heat extraction and water migration efficiency using a more realistic three-dimensional geometry model during geothermal energy extraction.
Data availability
The data used to support the findings of this study are available from the first author upon request.
Abbreviations
- \({C}_{s}\) :
-
Specific heat of matrix, J kg−1 K−1
- \({C}_{\mathrm{w}}\) :
-
Specific heat of water, J kg−1 K−1
- \(E\) :
-
Young’s modulus, Pa
- \(G\) :
-
Shear modulus of porous media, Pa
- \({h}_{\mathrm{r}}\) :
-
Heat exchange rate, %
- \({h}_{t}\) :
-
Cumulative heat extraction, J
- \({k}_{\mathrm{m}0}\) :
-
Initial permeability of matrix, m2
- \({k}_{\mathrm{m}}\) :
-
Permeability of matrix, m2
- \({K}_{\mathrm{s}}\) :
-
The bulk modulus of rock skeleton, Pa
- \(p\) :
-
Pore pressure, Pa
- \(q\) :
-
Average flow rate, m3 s−1
- \({S}_{\theta }\) :
-
Storage coefficient, 1 Pa−1
- \(t\) :
-
Time, s
- \({T}_{0}\) :
-
Initial temperature, K
- \(T\) :
-
Temperature, K
- \({T}_{\mathrm{a}}\) :
-
Average production temperature, K
- \({T}_{\mathrm{inj}}\) :
-
Temperatures at the injection well, K
- \({T}_{\mathrm{pro}}\) :
-
Temperatures at production well, K
- \(\alpha\) :
-
Biot’s coefficient
- \({\alpha }_{\mathrm{T}}\) :
-
Thermal expansion coefficient, 1/°C
- \({\varepsilon }_{\mathrm{v}}\) :
-
Volumetric strain
- \({\lambda }_{\theta }\) :
-
Thermal conductivity, W m−1 K−1
- \({\mu }_{\mathrm{w}}\) :
-
Viscosity of water, Pa s
- \({\rho }_{s}\) :
-
The density of matrix, kg m−3
- \({\rho }_{\mathrm{w}}\) :
-
Density of water, kg m−3
- \(\Delta \sigma^{\prime }\) :
-
Effective stress change, Pa
- \({\phi }_{m0}\) :
-
Initial fracture porosity
- \({\phi }_{m}\) :
-
Fracture porosity
References
Aliyu MD, Chen H-P (2018) Enhanced geothermal system modelling with multiple pore media: thermo-hydraulic coupled processes. Energy 165:931–948. https://doi.org/10.1016/j.energy.2018.09.129
Blackwell DD, Negraru PT, Richards MC (2006) Assessment of the enhanced geothermal system resource base of the United States. Nat Resour Res 15:283–308. https://doi.org/10.1007/s11053-007-9028-7
Chen BG, Song EX, Cheng XH (2014) A numerical method for discrete fracture network model for flow and heat transfer in two-dimensional fractured rocks. Chin J Rock Mech Eng 33:43–51
De Simone S, Vilarrasa V, Carrera J et al (2013) Thermal coupling may control mechanical stability of geothermal reservoirs during cold water injection. Phys Chem Earth Parts A/B/C 64:117–126. https://doi.org/10.1016/j.pce.2013.01.001
Feng Y, Chen X, Xu XF (2014) Current status and potentials of enhanced geothermal system in China: a review. Renew Sustain Energy Rev 33:214–223. https://doi.org/10.1016/j.rser.2014.01.074
Ghassemi A, Zhou X (2011) A three-dimensional thermo-poroelastic model for fracture response to injection/extraction in enhanced geothermal systems. Geothermics 40:39–49. https://doi.org/10.1016/j.geothermics.2010.12.001
Guo T, Gong F, Wang X et al (2019) Performance of enhanced geothermal system (EGS) in fractured geothermal reservoirs with CO2 as working fluid. Appl Therm Eng 152:215–230. https://doi.org/10.1016/j.applthermaleng.2019.02.024
Gutierrez M, Makurat A (1997) Coupled HTM modelling of cold water injection in fractured hydrocarbon reservoirs. Int J Rock Mech Min Sci 34:62.e1-62.e15. https://doi.org/10.1016/S1365-1609(97)00177-9
Han S, Cheng Y, Gao Q, Yan C, Zhang J (2020) Numerical study on heat extraction performance of multistage fracturing Enhanced Geothermal System. Renew Energy 149:1214–1226
Jeanne P, Rutqvist J, Vasco D et al (2014) A 3D hydrogeological and geomechanical model of an enhanced geothermal system at The Geysers, California. Geothermics 51:240–252. https://doi.org/10.1016/j.geothermics.2014.01.013
Julian BR, Foulger GR, Monastero FC, Bjornstad S (2010) Imaging hydraulic fractures in a geothermal reservoir. Geophys Res Lett. https://doi.org/10.1029/2009GL040933
Kazemi AR, Mahbaz SB, Dehghani-Sanij AR et al (2019) Performance evaluation of an enhanced geothermal system in the Western Canada Sedimentary Basin. Renew Sustain Energy Rev 113:109278. https://doi.org/10.1016/j.rser.2019.109278
Koh J, Roshan H, Rahman SS (2011) A numerical study on the long term thermo-poroelastic effects of cold water injection into naturally fractured geothermal reservoirs. Comput Geotech 38:669–682. https://doi.org/10.1016/j.compgeo.2011.03.007
Legarth B, Huenges E, Zimmermann G (2005) Hydraulic fracturing in a sedimentary geothermal reservoir: results and implications. Int J Rock Mech Min Sci 42:1028–1041. https://doi.org/10.1016/j.ijrmms.2005.05.014
Lei Q, Gholizadeh Doonechaly N, Tsang C-F (2021) Modelling fluid injection-induced fracture activation, damage growth, seismicity occurrence and connectivity change in naturally fractured rocks. Int J Rock Mech Min Sci 138:104598. https://doi.org/10.1016/j.ijrmms.2020.104598
Li M, Lior N (2015) Analysis of hydraulic fracturing and reservoir performance in enhanced geothermal systems. J Energy Resour Technol 137(4):041203.
Li N, Xie H, Hu J, Li C (2021) A critical review of the experimental and theoretical research on cyclic hydraulic fracturing for geothermal reservoir stimulation. Geomech Geophys Geo-Energy Geo-Resour 8:7. https://doi.org/10.1007/s40948-021-00309-7
Lu S-M (2018) A global review of enhanced geothermal system (EGS). Renew Sustain Energy Rev 81:2902–2921. https://doi.org/10.1016/j.rser.2017.06.097
Ma T, Rutqvist J, Oldenburg CM et al (2017) Fully coupled two-phase flow and poromechanics modeling of coalbed methane recovery: impact of geomechanics on production rate. J Nat Gas Sci Eng 45:474–486. https://doi.org/10.1016/j.jngse.2017.05.024
Ma T, Xu H, Guo C et al (2020a) A discrete fracture modeling approach for analysis of coalbed methane and water flow in a fractured coal reservoir. Geofluids 2020:8845348. https://doi.org/10.1155/2020/8845348
Ma Y, Li S, Zhang L et al (2020) Study on the effect of well layout schemes and fracture parameters on the heat extraction performance of enhanced geothermal system in fractured reservoir. Energy 202:117811. https://doi.org/10.1016/j.energy.2020.117811
Ma Y, Zhang Y, Hu Z et al (2020c) Numerical investigation of heat transfer performance of water flowing through a reservoir with two intersecting fractures. Renew Energy 153:93–107. https://doi.org/10.1016/j.renene.2020.01.141
Ma T, Zhang K, Shen W et al (2021) Discontinuous and continuous Galerkin methods for compressible single-phase and two-phase flow in fractured porous media. Adv Water Resour 156:104039. https://doi.org/10.1016/j.advwatres.2021.104039
Nadimi S, Forbes B, Moore J et al (2020) Utah FORGE: hydrogeothermal modeling of a granitic based discrete fracture network. Geothermics 87:101853. https://doi.org/10.1016/j.geothermics.2020.101853
Pandey SN, Chaudhuri A, Kelkar S (2017) A coupled thermo-hydro-mechanical modeling of fracture aperture alteration and reservoir deformation during heat extraction from a geothermal reservoir. Geothermics 65:17–31. https://doi.org/10.1016/j.geothermics.2016.08.006
Rawal C, Ghassemi A (2014) A reactive thermo-poroelastic analysis of water injection into an enhanced geothermal reservoir. Geothermics 50:10–23. https://doi.org/10.1016/j.geothermics.2013.05.007
Rutqvist J, Börgesson L, Chijimatsu M et al (2001) Thermohydromechanics of partially saturated geological media: governing equations and formulation of four finite element models. Int J Rock Mech Min Sci 38:105–127. https://doi.org/10.1016/S1365-1609(00)00068-X
Shu B, Wang Y, Zhu R et al (2022) Experimental study of the heat transfer characteristics of single geothermal fracture at different reservoir temperature and in situ stress conditions. Appl Therm Eng 207:118195. https://doi.org/10.1016/j.applthermaleng.2022.118195
Song X, Shi Y, Li G et al (2018) Numerical simulation of heat extraction performance in enhanced geothermal system with multilateral wells. Appl Energy 218:325–337. https://doi.org/10.1016/j.apenergy.2018.02.172
Taron J, Elsworth D (2009) Thermal–hydrologic–mechanical–chemical processes in the evolution of engineered geothermal reservoirs. Int J Rock Mech Min Sci 46:855–864. https://doi.org/10.1016/j.ijrmms.2009.01.007
Tian J, Liu J, Elsworth D et al (2022) Shale gas production from reservoirs with hierarchical multiscale structural heterogeneities. J Pet Sci Eng 208:109380. https://doi.org/10.1016/j.petrol.2021.109380
Tian J, Liu J, Elsworth D, Leong Y-K (2023) A 3D hybrid DFPM-DFM Model for gas production from fractured shale reservoirs. Comput Geotech 159:105450. https://doi.org/10.1016/j.compgeo.2023.105450
Yao J, Zhang X, Sun Z et al (2018) Numerical simulation of the heat extraction in 3D-EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model. Geothermics 74:19–34. https://doi.org/10.1016/j.geothermics.2017.12.005
Zhang H, Huang Z, Zhang S, Yang Z, Mclennan JD (2020) Improving heat extraction performance of an enhanced geothermal system utilizing cryogenic fracturing. Geothermics 85:101816
Zhang P, Zhang Y, Huang Y, Xia Y (2022) Experimental study of fracture evolution in enhanced geothermal systems based on fractal theory. Geothermics 102:102406. https://doi.org/10.1016/j.geothermics.2022.102406
Zhao Y, Feng Z, Feng Z et al (2015) THM (Thermo-hydro-mechanical) coupled mathematical model of fractured media and numerical simulation of a 3D enhanced geothermal system at 573 K and buried depth 6000–7000 M. Energy 82:193–205. https://doi.org/10.1016/j.energy.2015.01.030
Acknowledgements
Technical review comments by Prof. Weiqun Liu are greatly appreciated. We would like to thank the anonymous reviewers for their thorough reviews and very useful comments.
Funding
This work was supported by the Liaoning Natural Science Foundation (No. 2020-KF-23-03), Chinese Geological Survey (No. DD20201165), National Natural Science Foundation of China (No. 42002255 and 41902310), and the Fund from SinoProbe Laboratory (SinoProbe Lab 202210) and China Postdoctoral Science Foundation (No. 2022M713374).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest regarding the publication of the paper.
Ethical approval
This paper is the authors’ own original work, which has not been published elsewhere.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fang, T., Feng, Q., Zhou, R. et al. A coupled thermal–hydrological–mechanical model for geothermal energy extraction in fractured reservoirs. J Petrol Explor Prod Technol 13, 2315–2327 (2023). https://doi.org/10.1007/s13202-023-01665-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-023-01665-8