A productivity prediction method for multi-fractured horizontal wells in tight oil reservoirs considering fracture closure

Abstract

The closure fracture phenomenon increases the complexity of well testing and reduces the accuracy of productivity forecasts when tight oil reservoirs are exploited. However, most existing productivity models tend to ignore this. Therefore, a productivity prediction model for multi-fractured horizontal wells in tight oil reservoirs considering fracture closure has been developed by considering the stress sensitivity in the formation and combining the physical parameters of actual production. The model is solved by the Laplace transform, perturbation transform, Pedrosa transform, and Stehfest numerical inversion. Drawing productivity impact curves and discussing productivity influence factors based on the model results from this study show that the model is reasonable. In the actual production process, the hydraulic fracture parameter values are not as high as possible, and they have a reasonable range of values. The fracture closure pressure has a significant impact on the production of tight oil reservoirs. The higher the fracture closure pressure is, the greater the fracture conductivity decreases sharply, and the larger the proppant elastic modulus is, the stronger the fracture conductivity. The influence of fracture conductivity on the production in tight oil reservoirs has an obvious point, and when the value is less than the point, the production effect is good. Improved production can be achieved by balancing the relationship between fracture parameters. The findings of this study can help to better understand the influence of fracture parameters on productivity and contribute to increasing well production and improved development of tight oil reservoirs.

Introduction

Tight oil is a significant unconventional resource, the global reserves are approximately 9691.43 × 10⁸t, and the workable reserves are approximately 480.28 × 10⁸t (Qin et al. 2018; Shen et al. 2019; Weiyao et al. 2019; Suyun et al. 2018; Junfeng et al. 2015; Bing et al. 2021). Tight oil resources are rich and have a high demand for extraction. In development, staged fracturing technologies for horizontal wells are usually used to improve the production of tight oil reservoirs with low porosity and low permeability (Sun et al. 2020; Naizhen et al. 2018; Feng et al. 2019; Ming et al. 2020; Asadi et al. 2020). A series of fracture networks in tight reservoirs are formed by hydraulic fracturing. One of the fractures is filled with proppant near the wellbore, and the other is a natural fracture that stays away from the wellbore (Cong et al. 2022). In actual production, production declines rapidly, which is influenced by fracturing.

In the 1980s, researchers concentrated on the differences in production between horizontal wells and straight wells. The problem of fractured horizontal well production in low-permeability reservoirs was initially researched by (Giger 1985). In the 1990s, some researchers began to focus on the production dynamics of horizontal wells, researching the relationship between fracture conductivity and production and the influence of fracture parameters on production (Soliman et al. 1990; Soliman et al. 1996; Mukherjee and Economides 1991). Hegre (1994) established a productivity prediction model considering transverse and longitudinal fractures and analyzed the influence of fracture parameters on effective wellbore radius and production (Guo et al. 1993). Since 2000, the flow model is no longer limited by finite conductivity. Models become more relevant to reality. Researchers have established a new productivity prediction model considering various fracture parameters (Zerzar et al. 2004; Yanbo et al. 2006; Yiping et al. 2008; Restrepo and Tiab 2009). In 2010, researchers first focused on the fracture closure phenomenon, but the accuracy was low (Rbeawi and Tiab 2013; Youwei et al. 2017; Qin et al. 2018, 2019). For the first time, (Qin et al. 2018) modeled a multi-fractured horizontal well model considering infinite conductivity and explained the partial fracture closure phenomenon to a degree. Since 2021, researchers have begun to pay attention to the influence of fracture closure parameters on production capacity. Di et al. (2021) proposed a two-segment nonplanar asymmetric fracture model, researched the influence of two-segment nonplanar asymmetric fractures on production, and analyzed the influence of closed section length and conductivity on production (Di et al. 2021).

The previous research has the following shortcomings: (1) The production model assumptions had a general problem of idealization and simplification, and the flow characteristics were simplified. (2) For fracture parameters in fractured wells, equal parameters are often used to simplify the calculation, but this method will cause errors in the later calculation. (3) For the production factors, previous research generally focused on single-factor analysis, but lacked research on multiple factors' influences on production, ignoring the complex relations among multiple factors in the actual process. (4) In the process of solving the formula, the superposition principle, complex potential theory, and conformal transformation are mostly used, which lacks innovation and the combination with a computer. Therefore, it is necessary to establish a better capacity model by considering the influence of various factors.

Fracture closure is caused by various factors, such as the force between mechanical closure, multiphase flow, and proppant–rock interaction, which directly influences the fluid conductivity and indirectly influences the oil well production. From some actual production data and physical models, it can be concluded that fracture closure is the main reason for the rapid decline in fracturing well production. As the effective stress of the proppant is increased, the fracture width decreases and the fracture conductivity decreases with decreasing formation stress (Wang et al. 2016; Jiang et al. 2020; Yongzan et al. 2018). Finally, the fracture will be closed. It is not difficult to find that previously proposed productivity prediction equations ignored the influence of fracture closure on production. In addition, in the reservoir, the fractures are complex. In the reservoir, the change in stress sensitivity is directly reflected by fracture closure. Stress sensitivity is also a key factor affecting production. However, previous research has not proposed a productivity prediction model that incorporates stress sensitivity and fracture closure.

The purpose of this research article is to focus on the influence of this dynamic characteristic of fracture closure on productivity and to provide some guidelines for tight oil recovery in later stages. Therefore, after concluding the shortcomings of previous research, a new productivity prediction model for multi-fractured horizontal wells in tight oil reservoirs considering fracture closure was established by combining stress sensitivity with the dynamic characteristic of fracture closure and taking into account the mechanical characteristics of the reservoir and the influences of proppant in actual construction. The Laplace transform, perturbation transform, Pedrosa transform, and Stehfest numerical inversion are used to solve the models, and the influences of the formation permeability, closing pressure, and relevant fracture closure parameters on production are discussed. This model pays more attention to the actual production situation, such as different fracture conductivities, different fracture numbers, different fracture lengths, different fracture spacings, and different fracture shapes. It is more similar to the actual situation of real reservoirs and can be used for accurate prediction of the production in actual construction. However, this research lacks a model validation component, and the difference between it and the classical productivity prediction model is open to debate.

The organization for this article is as follows (Fig. 1). First, the model is developed. Then the results and discussion are presented. Finally, the summary and conclusions are highlighted.

Fig. 1

Framework of the research topic

Model construction and solution

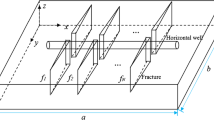
After stimulating the reservoir, a series of fractures are formed in the fractured area. These increased contact areas and improved conductivity in tight oil reservoirs (Yuliang et al. 2015; Sang et al. 2014). Fracture shape is controlled by fracturing technology, the ground stress field, and petrophysics (Hongen et al. 2016). According to the permeability of reservoirs, after stimulation, the reservoir can be divided into two areas: fractured areas and unfractured areas (Dejam 2019). The assumptions are as follows: (1) A fractured horizontal well is in the center of a confined reservoir. (2) Fractures with different shapes and directions, and heights that are equal to the reservoir thickness. (3) Isothermal flow, ignoring capillary force and gravity. (4) Fluid through fractures flows into the wellbore. According to assumptions, a multi-fractured horizontal well production model is modeled (Fig. 2).

Fig. 2

Flow model for multi-fractured horizontal wells in tight oil reservoirs

Construction of the stress sensitivity model in the reservoir

The pore structure is complex, and the pore throat radius is small in tight reservoirs. As the effective stress increases, the pore deforms and the formation permeability decreases. Compared with conventional reservoirs, tight reservoirs have stronger stress sensitivity. In tight reservoirs, as formation pressure decreases, the formation permeability also decreases (Pedrosa 1986). This phenomenon is called stress sensitivity. It can be written as (Chen et al. 2016, Chen et al. 2017):

$$k = k_{{\text{i}}} e^{{ - \gamma \left( {p_{{\text{i}}} - p} \right)}}$$

(1)

where k is the permeability, mD, γ is the stress sensitivity coefficient, MPa⁻¹, and i is the initial formation condition.

David et al. proposed a mathematical relationship between the stress sensitivity coefficient and the compression coefficient. It can be expressed as (David et al. 1994):

$$\gamma = \alpha C_{{\text{p}}}$$

(2)

where α is the constant, and C_p is the compression coefficient, MPa⁻¹.

Based on the capillary model, Al-Wardy et al. built a mathematical model among the compression coefficient, the elastic modulus, and Poisson's ratio. It can be expressed as:

$$C_{{\text{p}}} = \frac{{2\left( {1 - \nu } \right)}}{E}$$

(3)

where E is the elastic modulus, MPa, and ν is the Poisson’s ratio.

Poisson’s ratio slightly affects the compression coefficient. Therefore, for the pore, the compression coefficient is determined by the Young’s model. Wang and Cheng et al. used the exponential model between permeability and effective stress to simplify the pore reservoir into a capillary model (Fig. 3) and introduced fractal theory to obtain the expression of effective permeability during rock compression (Wang and Cheng 2020). α can be expressed as:

$$\alpha = \frac{{3 + D_{{{\text{Tm}}}} }}{2}$$

(4)

where D_Tm is the tortuosity of the capillary channel, and in the ideal capillary model, D_Tm = 1. Therefore, the stress sensitivity coefficient can be written as:

$$\gamma = \alpha C_{{\text{p}}} = \frac{{\left( {3 + D_{{{\text{Tm}}}} } \right)\left( {1 - \nu } \right)}}{E}$$

(5)

Fig. 3

Diagram of the stress sensitivity in the capillary bundle model (Fuyong Wang et al. 2020)

Construction of the flow model in the reservoir

Considering the stress sensitivity, the fluid flow velocity in the reservoir can be expressed as:

$$v_{{\text{x}}} = \frac{{k_{{\text{x}}} }}{\mu }e^{{ - \gamma \left( {p_{{\text{i}}} - p} \right)}} \frac{{{\text{dp}}}}{{{\text{d}}x}}$$

(6)

where ν_x is the seepage velocity in the x-direction, cm/s, k_x is the permeability in the x-direction in the initial state, mD, and μ is the viscosity in the initial state, mPa·s.

The formation and the formation fluid are considered compressible fluids and anisotropy. The flow equation in space can be expressed as:

$$\frac{\partial }{\partial x}\left( {\frac{{k_{{\text{x}}} }}{\mu }\frac{\partial p}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {\frac{{k_{{\text{y}}} }}{\mu }\frac{\partial p}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {\frac{{k_{{\text{z}}} }}{\mu }\frac{\partial p}{{\partial z}}} \right) = \phi C_{{\text{t}}} \frac{\partial p}{{\partial t}}$$

(7)

where ϕ is the reservoir porosity, decimal, C_t is the reservoir composite compressibility, 1/MPa, and t is the time, s.

Assuming:

$$r^{2} = x^{2} + y^{2}$$

(8)

The flow equation is nonlinear. Due to the stress sensitivity, the fluid in reservoirs shows a stronger influence on the flow equation. Therefore, it is necessary to transform the nonlinear equation into a linear equation by the Pedrosa transform (Pedrosa 1986). Assuming:

$$p_{{\text{D}}} = - \frac{1}{{\gamma_{{\text{D}}} }}\ln (1 - \gamma_{{\text{D}}} \xi_{{\text{D}}} )$$

(9)

where $\xi_{{\text{D}}}$ is the dimensionless variable.

Due to the extremely small value of γ_D, using zero-order perturbations can obtain the exact result (Kidder et al. 1957; Wang et al. 2016). The flow equation after perturbation transformation can be expressed as:

$$\frac{{\partial^{2} \xi_{{\text{D}}} }}{{\partial r_{{\text{D}}}^{2} }} + \frac{1}{{r_{{\text{D}}} }}\frac{{\partial \xi_{{\text{D}}} }}{{\partial r_{{\text{D}}} }} = \frac{{\partial \xi_{{\text{D}}} }}{{\partial t_{{\text{D}}} }}$$

(10)

where the superscript is the Laplace spatial variable.

Because the flow equation is a stronger nonlinear equation, to simplify operations, the flow equation is transformed with the Laplace transform. It can be expressed as:

$$\frac{{\partial^{2} \overline{\xi }_{{\text{D}}} }}{{\partial r_{{\text{D}}}^{2} }} + \frac{1}{{r_{{\text{D}}} }}\frac{{\partial \overline{\xi }_{{\text{D}}} }}{{\partial r_{{\text{D}}} }} = s\overline{\xi }_{{\text{D}}}$$

(11)

Construction of the stress sensitivity model in the hydraulic fracture

In hydraulic fractures, the closure stress compresses or sinks proppants into the formation, and this phenomenon is called fracture closure (Fig. 4). Jike Wu (2001) based on the formula of spherical center distance, assumed sphere 1 as the proppant, and when R₂ → ∞, assumed sphere 2 as a fracture surface, obtained the variation of the center distance between the two spheres:

$$\alpha^{\prime} = \frac{{\left[ {\frac{3}{4}PR_{1} \left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }}} \right)} \right]^{\frac{2}{3}} }}{{R_{1} }}$$

(12)

where α´ is the variation of the center distance between two spheres center, mm, P is the force between two spheres, N, R₁ is the radius of sphere 1, mm, ν₁ is the Poisson’s ratio of sphere 1, dimensionless, ν₂ is the Poisson’s ratio of sphere 2, dimensionless, E₁ is the elastic modulus of sphere 1, MPa, and E₂ is the elastic modulus of sphere 2, MPa.

Fig. 4

Force analysis of the rock–proppant system

Two important influencing factors are proppant deformation and the depth of proppant embedded in the formation. According to formula (12), when E₂ → ∞, amused sphere 1 just deformed and was not embedded in the formation. The deformation of sphere 1 is written as:

$$\beta = \frac{{\left( {\frac{3}{4}PR_{1} } \right)^{\frac{2}{3}} }}{{R_{1} }}\left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}}$$

(13)

where β is the deformation of sphere 1, mm.

Assuming sphere 2 is an elastomer, the depth of proppant embedded into the fracture surface (depth of sphere 1 embedded into sphere 2) can be written as:

$$h = \frac{{\left( {\frac{3}{4}PR_{1} } \right)^{\frac{2}{3}} }}{{R_{1} }}\left[ {\left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }}} \right)^{\frac{2}{3}} - \left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} } \right]$$

(14)

where h is the depth of proppant embedded in the reservoir (depth of sphere 1 embedded into sphere 2), mm.

The fracture width in the case of multilayer sanding can be expressed as (Li et al. 2010):

$$\alpha^{\prime} = 1.04w\left( {K^{2} p} \right)^{\frac{2}{3}} \left\{ {\left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} + \frac{{2R_{1} }}{w}\left[ {\left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }} + \frac{{1 - v_{2}^{2} }}{{E_{2} }}} \right)^{\frac{2}{3}} - \left( {\frac{{1 - v_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} } \right]} \right\}$$

(15)

where w is the fracture width in the case of multilayer proppants, mm.

In the actual reservoir, minerals are heterogeneous and proppants have different sizes. Li et al. modified the fracture closure width by presenting relevant parameters. The modified formula for the fracture closure width can be written as:

$$\alpha^{\prime} = b_{2} + 1.04b_{3} w\left( {K^{2} p} \right)^{\frac{2}{3}} \left\{ {\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} + \frac{{2R_{1} }}{w}\left[ {\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}} \right)^{\frac{2}{3}} - \left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} } \right]} \right\}$$

(16)

When the hydraulic fracture is filled by proppants, the fluid flow in the reservoir can be regarded as fluid flow in the porous media. The representation relationship between permeability and stress can be expressed as:

$$k_{{\text{f}}} = k_{{{\text{fi}}}} e^{{ - 3C_{{{\text{fp}}}} (p_{{\text{f}}} - p_{{{\text{fi}}}} )}}$$

(17)

where k_f is the sand-filled fracture permeability, mD, C_fp is the compression coefficient in fractures, 1/MPa, P_f is the effective stress of fractures, MPa, and i is the initial state.

Based on the Waren & Root model, the compression coefficient of the fracture model has a relationship to Young’s model and the fracture aspect. The lower the fracture aspect, the higher the compression coefficient. In addition, it can be written as:

$$C_{{{\text{fp}}}} = \frac{2(1 - \nu )}{{\varepsilon E}}$$

(18)

where ε is the fracture aspect

In the initial state, the fracture conductivity is the product of the fracture permeability and the fracture width. It can be written as:

$$F_{{\text{i}}} = k_{{{\text{fi}}}} w_{{{\text{fi}}}}$$

(19)

When the stress is p in the hydraulic fracture, the fracture conductivity can be expressed as:

$$F = k_{fi} w_{fi} e^{{ - C_{{fp\left( {p_{i} - p} \right)}} }} \left\{ {1 - 1.04b_{3} \left[ {K^{2} \left( {p_{{\text{i}}} - p} \right)} \right]^{\frac{2}{3}} \left[ {\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} + \frac{{2R_{1} }}{{w_{{{\text{f}}_{{0}} }} }}\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu_{2}^{2} }}{{E_{2} }}} \right)^{\frac{2}{3}} - \frac{{2R_{1} }}{{w_{{{\text{f}}_{{0}} }} }}\left( {\frac{{1 - \nu_{1}^{2} }}{{E_{1} }}} \right)^{\frac{2}{3}} } \right]} \right\} - b_{2}^{\,\prime }$$

(20)

Construction of the flow model in the hydraulic fracture

Ignoring the density change during the fluid flow and the pore volume after fracturing, the flow equation can be simplified as:

$$\frac{\partial }{{\partial l_{{\text{f}}} }}\left( {\frac{{k_{{\text{f}}} w_{{\text{f}}} }}{\mu }\frac{{\partial p_{{\text{f}}} }}{{\partial l_{{\text{f}}} }}} \right) + q_{{\text{f}}} \left( {l_{{\text{f}}} } \right) = 0$$

(21)

where l_f is the fracture length, k_fw_f is the fracture conductivity, p_f is the stress inside the hydraulic fracture, and q_f(l_f) is the hydraulic fracture microelement l_f production.

As the formation stress decreases, the stress on the hydraulic fracture increases, and the fracture closes. Considering the influences of stress sensitivity on fractures (Fig. 5), the flow equation is made dimensionless. The dimensionless model can be written as:

$$\frac{\partial }{{\partial l_{{{\text{fD}}}} }}\left[ {C_{{{\text{fD}}}} \frac{{\partial p_{{{\text{fD}}}} }}{{\partial l_{{{\text{fD}}}} }}} \right] + 2\pi L_{{{\text{ref}}}} q_{{{\text{fD}}}} \left( {l_{{{\text{fD}}}} } \right) = 0$$

(22)

Fig. 5

Diagram of fracture stress sensitivity in the plate model

Inside the hydraulic fracture, the fluid flow is different. In different places, the hydraulic fracture stress is different. After discretizing the formula (40), the stress sensitivity is calculated by the stress with the previous step time. It can be expressed as:

$$p_{{{\text{fDm}}}} - p_{{{\text{wD}}}} = \sum\limits_{k = 1}^{m} {\frac{{2\pi L_{{{\text{ref}}}} q_{{{\text{fDk}}}} l_{{{\text{fD}}}} }}{{C_{{{\text{fDk}}}} }}}$$

(23)

Model solution

The fracture system and the reservoir are continuous at the fracture surface. According to the continuity boundary conditions, we have:

$$p_{{{\text{fD}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right) = p_{{\text{D}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right)$$

(24)

$$p_{{{\text{fD}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right) = \frac{{2\pi k_{{\text{i}}} h}}{qB\mu }\left( {p_{{\text{i}}} - p} \right)\left( {\frac{x}{{L_{{{\text{ref}}}} }},\frac{y}{{L_{{{\text{ref}}}} }},t} \right)$$

(25)

$$q_{{{\text{fD}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right) = q_{{\text{D}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right)$$

(26)

Amusing a flow rate, the pseudopressure of the fracture surface is obtained by using a flow model of the reservoir. The Laplace space calculation result is transformed into pseudopressure in real space by using the numerical inversion of Stehfest (Stehfest 1970).

The solution of the reservoir flow model is achieved by using the perturbation transformation and the Pedrosa transformation. The pseudopressure in real space can be expressed as:

$$p_{{{\text{fD}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right) = - \frac{1}{{\gamma_{{\text{D}}} }}\ln \left[ {1 - \gamma_{{\text{D}}} p_{{{\text{fD}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} ,t} \right)} \right]$$

(27)

When the bottom hole pressure is a certain value, the pseudopressures of $p_{{\text{D}}} (x_{{\text{D}}} ,y_{{\text{D}}} ,t)$ and $p_{{{\text{fD}}}} (x_{{\text{D}}} ,y_{{\text{D}}} ,t)$ are calculated using reservoir and fracture flow models. Based on the difference in stress, taking overrelaxation to adjust the trial production, accelerated coupling of the pseudopressures of $p_{{\text{D}}} (x_{{\text{D}}} ,y_{{\text{D}}} ,t)$ and $p_{{{\text{fD}}}} (x_{{\text{D}}} ,y_{{\text{D}}} ,t)$. The pseudopressures are in a reasonable range. Therefore, we can obtain the oil production $q_{{{\text{fD}}}} (x_{{\text{D}}} ,y_{{\text{D}}} ,t)$ of the fracture point:

$$q_{{\text{D}}} (t_{{\text{D}}} ) = \sum\limits_{{{\text{i}} = 1}}^{M} {\sum\limits_{{{\text{j}} = 1}}^{NN} {q_{{{\text{Dij}}}} } } \left( {t_{{\text{D}}} } \right)$$

(28)

where M is the fracture strip number and NN is the number of discrete segments per fracture.

Analysis and discussion

In this section, we use the capacity model to discuss the influence of closing pressure and fracture parameters on fracture conductivity and production, and we draw relevant curves. On the basis of certain physical parameters and fracture parameters in the tight oil reservoir, we discuss the fracture conductivity change and the capacity change. The tight oil physical parameters used in the discussion are as follows Table 1:

Table 1 Table of tight oil physical parameters

Influence of formation permeability on production

After fracturing, the formation permeability is the basis for fracturing effect evaluation and construction parameter optimization. With increasing formation permeability, the daily production also increases (Fig. 6). Using the average of the experimental data, when the formation permeability increases from 0.01 md to 0.05 md, it increases by 65.85%, when it increases from 0.1 md to 0.5 md, it increases by 65.89%, and the difference between the two increases is not significant. However, when the formation permeability increases from 0.05 md to 0.1 md, it increases by 25.17%. The hydraulic fractures are not infinite conductivity fractures, so the production increases are not significant. When the formation permeability increases to a certain value in the fractured area, limited by the infinite conductivity, increases in the formation permeability have little influence on production. Therefore, when the formation permeability is 0.1 md, the best productivity outcomes are achieved.

Fig. 6

Well production curves for various formation permeabilities

Influence of closing pressure on hydraulic fracture conductivity

The hydraulic fracture effect is determined by the fracture conductivity, and the fracture conductivity is directly influenced by the closure pressure. For a simulated well, assuming the fracture width is 1 mm and other parameters in a tight oil reservoir are a certain value, the production change curves of different proppant elastic modulus are 2000 MPa, 4000 Mpa, 6000 Mpa, and 8000 Mpa (Fig. 7). When the proppant elastic modulus is a certain value, from the characteristics of a single curve, with increasing the closure pressure, the fracture conductivity decreases. In particular, the fracture conductivity curve when the closure pressure is 2000 MPa has a large drop, and in the other cures of high proppant elastic modulus, their fracture conductivity drop is not significant. On the whole, the larger the proppant elastic modulus, the stronger the fracture conductivity. When the proppant elastic modulus increases from 2000 to 4000 Mpa, it increases by 16.52%. When it increases from 4000 to 6000 Mpa and from 6000 to 8000 Mpa, its fracture conductivity increases by 5.54% and 2.88%, respectively, and the difference between the two increases is not significant.

Fig. 7

Variation curves of fracture conductivity under different closure pressures

According to the analysis, a closure pressure that is too high will result in proppant embedding in the formation and severe crushing. This phenomenon will cause the hydraulic fracture to be filled and the proppant chips to be transported difficultly. Therefore, the fracture conductivity decreases sharply, especially when the proppant elastic modulus is 2000 Mpa. The proppant elastic modulus from 4000 to 8000 Mpa is an ideal range to improve the hydraulic fracture effect. The larger the proppant elastic modulus is, the stronger the fracture conductivity, so 8000 MPa is the best value for the proppant elastic modulus to improve production.

Influence of hydraulic fracture conductivity on production

In tight reservoirs, hydraulic fractures are the main flow channel, and fracture conductivity has a significant influence on production in tight oil reservoirs. The fracture conductivity is determined by the fracture width and fracture permeability. Formation stress will cause the proppant to be embedded in the formation, causing fracture closure, which will make the fracture conductivity decrease rapidly and finally influence the production.

The well production curves for different fracture conductivities are shown in Fig. 8. With increasing the fracture conductivity, the daily production also increases, and this phenomenon occurs especially at the beginning and middle of oil well production. When the fracture conductivity is increased from 10 md·cm to 250 md·cm, the production increases significantly, but when the fracture conductivity increases to 1000 md·cm, the daily production increase decreases from 81.95% to 29.09%. This is an obvious point when the fracture conductivity is 250 md·cm. When the value is less than the point, the production effect is good. When the value is more than the point, the production effect is not significant. Therefore, 250 md·cm is the best value for the fracture conductivity to improve production.

Fig. 8

Well production curves with different hydraulic fracture conductivities

Influence of hydraulic fracture numbers on well production

In actual production, reasonable optimization fracture series and control fracture numbers can improve production and save exploitation expenses. The relationship with oil production at different fracture numbers is shown in Fig. 9. When the fracture numbers increase from 6 to 8, the daily production increases by 33.06%, and when it increases from 10 to 12, the daily production increases by 15.78%. As the fracture numbers increase, the oil-accumulating area expands, and the daily production also increases. During the same production time, has the fracture numbers increase, the increase in daily well production gradually decreases. This phenomenon occurs especially in the late stages of oil well production, because when the fracture numbers increase and the fracture spacing decreases, the interference between fractures is enhanced, finally causing the production to decrease. Therefore, it is important to select a reasonable fracture number for oil well development.

Fig. 9

Well production curves with different fracture numbers

Influence of hydraulic fracture length on production

Due to the difference in formation stress distribution and fracturing methods, the fracture length will be different (Zhanqing et al. 2014). The production is influenced by the fracture length. Theoretically, on the one hand, increasing the fracture length can increase the fractured areas and allow fluids in the reservoir to more easily flow to hydraulic fractures, but on the other hand, too long a fracture length will cause high flow resistance, and it is not beneficial to increase the production of oil wells. The well production curves for different fracture numbers are shown in Fig. 10. The average daily production increases by 17.59% when the fracture length is increased from 60 to 80 m. When the fracture length is increased from 100 to 120 m, the average daily production increases by 7.09%. The average daily production increase has slowed. With the increase in hydraulic fractures, the production and production increase, but a fracture length that is too long will cause the production increase to slow. Therefore, there is an optimal interval for the selection of the fracture length.

Fig. 10

Well production curves for different hydraulic fracture slit lengths

Effect of hydraulic fracture spacing on production

The hydraulic fracture spacing is one of the controllable parameters during the development of tight oil reservoirs. The distribution of the hydraulic fracture spacing is divided into uniform distribution, sparse to dense distribution, dense to sparse distribution, external sparse and internal dense distribution, and external dense and internal sparse distribution. The uniform distribution can increase the fractured area and decrease the well interference phenomenon, which is beneficial for tight oil production. For a simulated well, the uniform distribution is used to obtain the production change curves of different hydraulic fracture spacings of 20 m, 40 m, 60 m, and 80 m (Fig. 11). At the beginning of production, the daily production under different hydraulic fracture spacings is not much different, but this does not last too long. In the middle of production, has the hydraulic fracture spacing increases, the daily production increases. During the late stages of production, the influence of the hydraulic fracture spacing on production is not significant. The fracture length directly influences the hydraulic fracture spacing. Improved production can be achieved by balancing the relationship between fracture length and hydraulic fracture spacing.

Fig. 11

Well production curves with different hydraulic fracture spacing

Effect of hydraulic fracture shape on production

The different hydraulic fracture shapes are influenced by the petrophysics, formation stress, fracturing fluid characteristics, and hydraulic parameters. The different flow fields of different hydraulic fracture shapes cause the swept volume to be different, which finally influences the stimulated reservoir volume and the production (Weidong et al. 2015). Therefore, three common types of fractures were selected to research the influence of each on production, similar to equal-length cloth fractures, spindle-shaped fractures, and dumbbell-shaped fractures (Fig. 12). Ranking the total daily production from highest to lowest, the production under the influence of equal-length cloth fractures is the highest, the production under the influence of dumbbell-shaped fractures is in the middle, and the production under the influence of spindle-shaped fractures is the lowest. During the late stages of production, the influence of the hydraulic fracture shapes on production is not significant.

Fig. 12

Well production curves for different hydraulic fracture shapes

Summary and conclusions

• 1. Considering fracture closure, we propose a productivity prediction method for multi-fractured horizontal wells in tight oil reservoirs and discuss the influence of closing pressure and fracture parameters on fracture conductivity and production.

• 2. A reasonable range of values is crucial to increasing production of the actual production process. This is particularly evident in the parameter values of fracture number, fracture length, fracture spacing, and formation permeability.

• 3. According to the analysis, a closure pressure that is too high will result in proppant embedding in the formation and severe crushing. The larger the proppant elastic modulus is, the stronger the fracture conductivity.

• 4. The influence of fracture conductivity on the production of tight oil reservoirs has a clear value, and when the value is less than the point, the production is good.

• 5. Production can be influenced by single factors. Improved production can be achieved by balancing the relationship between fracture parameters.

Appendix

Dimensionless definition

Dimensionless pressure:

$$p_{{\text{D}}} = \frac{{2\pi k_{{\text{i}}} h}}{qB\mu }\Delta p\quad \Delta p = p_{{\text{i}}} - p$$

(29)

Dimensionless production:

$$q_{{\text{D}}} = \frac{q}{{q_{{{\text{ref}}}} }}$$

(30)

Dimensionless time:

$$t_{{\text{D}}} = \frac{{k_{{\text{i}}} }}{{\phi_{{\text{i}}} C_{{\text{t}}} \mu L_{{{\text{ref}}}}^{2} }}t$$

(31)

Dimensionless permeability modulus:

$$\gamma_{{\text{D}}} = \frac{qB\mu }{{2\pi k_{{\text{i}}} h}}\gamma$$

(32)

Dimensionless x coordinate:

$$x_{{\text{D}}} = \frac{x}{{L_{{{\text{ref}}}} }}$$

(33)

Dimensionless y coordinate:

$$y_{{\text{D}}} = \frac{y}{{L_{{{\text{ref}}}} }}$$

(34)

Dimensionless distance:

$$r_{{\text{D}}} = \frac{r}{{L_{{{\text{ref}}}} }}$$

(35)

Dimensionless fracture half-length:

$$L_{{{\text{fD}}}} = \frac{{L_{{\text{f}}} }}{{L_{{{\text{ref}}}} }}$$

(36)

Dimensionless conductivity:

$$C_{{{\text{fD}}}} = \frac{{k_{{\text{f}}} w_{{\text{f}}} }}{{k_{{\text{i}}} L_{{{\text{ref}}}} }}$$

(37)

Derivation of the flow model in the reservoir

To simplify operations, the fluid flow in the vertical direction is ignored, and the reservoir anisotropy is assumed to be the same. The flow equation in the reservoir can be expressed as:

$$\frac{{\partial^{2} p}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial p}{{\partial r}} + \gamma \left( {\frac{\partial p}{{\partial r}}} \right)^{2} = e^{{\gamma \left( {p_{{\text{i}}} - p} \right)}} \frac{{\phi \mu C_{{\text{t}}} }}{{k_{{\text{i}}} }}\frac{\partial p}{{\partial t}}$$

(38)

To simplify operations, the dimensionless definition in Appendix 1 is introduced into the flow equation in the reservoir to make it dimensionless. It can be written as:

$$\frac{{\partial^{2} p_{{\text{D}}} }}{{\partial r_{{\text{D}}}^{2} }} + \frac{1}{{r_{{\text{D}}} }}\frac{{\partial p_{{\text{D}}} }}{{\partial r_{{\text{D}}} }} + \gamma_{D} \left( {\frac{{\partial p_{{\text{D}}} }}{{\partial r_{{\text{D}}} }}} \right)^{2} = e^{{\gamma_{{\text{D}}} p_{{\text{D}}} }} \frac{{\partial p_{{\text{D}}} }}{{\partial t_{{\text{D}}} }}$$

(39)

Derivation of the flow model in the hydraulic fracture

The dimensionless flow equation is a function of fracture length, an integral of formula (22) from 0 to l_fD. It can be written as:

$$C_{{{\text{fD}}}} \frac{{\partial p_{{{\text{fD}}}} }}{{\partial l_{{{\text{fD}}}} }} + \int_{0}^{{L_{{{\text{fD}}}} }} {2\pi L_{{{\text{ref}}}} q_{{{\text{fD}}}} \left( {l_{{{\text{fD}}}} } \right)dl_{{{\text{fD}}}} } = 0$$

(40)