Introduction

The rapid increase in exploitation of unconventional resources has reshaped the global oil-gas market. Tight oil and shale oil constitute the main sources of unconventional oil supply (Jia et al. 2012). Unconventional resources are playing increasingly important roles in the energy industry (Cheng et al. 2010). China is rich in tight oil and gas resources, with reserves of about 50 × 108 t, which has great potential for exploitation. Owing to tight reservoirs’ extremely low permeability (Wang and Sheng 2017), there is almost no natural productivity via conventional technology. At present, multi-stage fractured horizontal well (MFHW) is an efficient technique in the exploitation of unconventional resources (Mason 2012; Hughes 2013; Wu et al. 2012). MFHW technology optimizes the field development and increases the oil well productivity by improving the flow condition of near-wellbore area and increasing the oil drainage area of the tight reservoir (Zhao et al. 2015; Abbasi et al. 2014; Schneising et al. 2015).

The studies of MFHW have been carried on by a large number of scholars and institutes in recent years. In terms of analytical and semi analytical models, Gringarten firstly established the flow model of multi-stage fractured horizontal wells by using Green function and Newman product method (Gringarten and Ramey 1973). On this basis, the flow model is established under Laplace space, and the three-linear flow model of fractured horizontal well is established by Ozkan (Ozkan et al. 2011). In terms of numerical model, Sun et al. established a horizontal well model of complex fracture system based on discrete fracture network (Sun et al. 2014). Ren et al. (2015) studied the flow model of SRV-fractured horizontal well based on different stimulated patterns. Yin et al. (2016) carried on the correlation research to the reasonable production test method of multi-stage fractured horizontal well in tight oil reservoir.

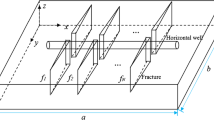
Although the studies of MFHW have been carried on by a large number of scholars in recent years, there are few studies on the reasonable production pressure drop of MFHW in tight oil reservoirs. In the exploitation of tight oil reservoir, the characteristic decline in reservoir pressure has caused the change of reservoir properties, resulting in the decline in well productivity, as it is crucial to optimize the pressure drop. Deng (2017) modified permeability by introducing dynamic permeability theory and pressure-sensitive effect into numerical simulation, and obtained the range of reasonable production pressure drop of fractured horizontal well; however, the primary fractures closure and complex fracture network system has not taken (shown in Fig. 1a) into account. In this work, a matrix system is established to account for the threshold pressure gradient (TPG) and stress-sensitive effect. The secondary fractures, natural fractures and matrix system near the primary fractures is set as the stimulated area (SA) whose permeability is modified (shown in Fig. 1b), and the primary fractures system is established to account for the dynamic fracture closure. Then we takes all factors into consideration and establishes a reasonable numerical simulation model with the production data of a long fractured horizontal well in a tight oil reservoir in Xinjiang oilfield to optimize the range of reasonable production pressure drop. It provides the theoretical basis and applicable value for the economic exploitation and long-term planning of the tight oil reservoirs.

Fig. 1
figure 1

a Microseismic data showing the complex fractures in Jimsar sag, Xinjiang oilfield; b schematic of a fracture network

Full size image

Physical model of MFHW

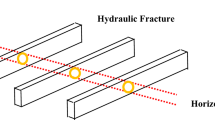
The initial matrix permeability of tight reservoir is extremely low. In order to improve the stimulation effect, the fractured horizontal well is often deployed in the direction of the minimum horizontal main stress. In the fractures network, the primary fractures is perpendicular to the horizontal wellbore and extend to the reservoir; the secondary fractures are generally perpendicular to the primary fracture and parallel to the horizontal wellbore. The conductivity of primary fracture, which cannot be regarded as infinite conductivity, has a significant effect on productivity of MFHW (Raghavan and Chen 2013). Furthermore, during the oil production, the primary fractures may be gradually closed, while the permeability of the primary fracture decreases and the fracture width is reduced. Therefore, the fracture conductivity is declining, thereby affecting the productivity of horizontal wells (Feng et al. 2017).

According to the above analysis, a physical model of multi-stage fractured horizontal wells in tight oil reservoir is established (shown in Fig. 1b), including primary fractures, horizontal well bore, stimulated area and unstimulated area (shown in Fig. 1b): (1) primary fracture, (2) horizontal well bore, (3) stimulated area, (4) unstimulated area. Besides, the stimulated area is mainly composed of secondary fractures, natural fractures and the matrix around the primary fractures. The flow of the reservoir fluid consists of four processes: from the unstimulated area to the stimulated area, from the stimulated area to the primary fractures in the direction perpendicular to the wellbore direction, from the primary fractures to the horizontal wellbore, and the flow in the horizontal wellbore.

The assumptions of the model: (1) the reservoir is homogeneous isotropic with upper and lower layers; (2) the horizontal section is in the middle of equal thickness horizontal reservoir; (3) single-phase flow in the reservoir and fracture; (4) the fluid is slightly compressible, and the flow is isothermal and unsteady; (5) the primary fracture is perpendicular to the horizontal wellbore. The fluid flows firstly into the fracture along the wall from the matrix, and then flows to the wellbore, neglecting the flow of fluid directly into the wellbore from the matrix.

The establishment of mathematical model

Based on the basic assumptions and the physical model established above, we develop a mathematical model of complex fracture network in consideration of the characteristics of tight reservoir including threshold pressure gradient, stress-sensitive effect and dynamic fracture closure.

Matrix system

Due to the existence of threshold pressure gradient in the tight oil reservoir, the flow in matrix no longer satisfies Darcy’s Law. Instead, it obeys the quasi-threshold pressure gradient model as follows (Liu 2017):

$$\nu =\left\{ \begin{gathered} 0 \left| {\Delta p} \right| \leqslant G \hfill \\ - \frac{K}{\mu }\Delta p\left( {1 - G/\left| {\Delta p} \right|} \right) \quad \left| {\Delta p} \right|>G \hfill \\ \end{gathered} \right.,$$
(1)

where v is the flow velocity, p is the pressure, G is the threshold pressure gradient, K is the permeability, and µ is the viscosity. According to the equation, only when |Δp| ≥ G can the velocity be calculated and the fluid flow. The effect of TPG can be simulated in IMEX simulator. Define the threshold pressure gradient of the flow boundary between grids, below which the fluid cannot flow.

Due to the more compact reservoir matrix, the thinner capillary of porous medium, the permeability of matrix system is very sensitive to the change of pressure, thus affecting the productivity. The experimental results show that permeability of varies exponentially with pressure (Ozkan et al. 2010).

$${K_{\text{m}}}={K_{\text{i}}}{{\text{e}}^{ - {\alpha _{\text{k}}}({p_{\text{i}}} - p)}},$$
(2)

where Km is the permeability of matrix, Ki is the initial permeability of matrix, αk is the coefficient of stress-sensitive, pi is the initial formation pressure, and p is the formation pressure.

Fracture network system

In tight oil reservoirs, there are many secondary fractures near the primary fractures. The interactions between secondary fractures and natural fractures lead to a more complex fracture network system. Firstly, the fracture network system is simplified as a stimulated area (Yang et al. 2017a), which includes not only the matrix system but also the secondary fracture and natural fracture. Thus, the equivalent characterization of the permeability of stimulated area is necessary. According to Darcy’s law, the flow rate of the stimulated area (SA) is as follows:

$$q=\frac{{{K_{\text{b}}}A({p_1} - {p_2})}}{{\mu L}},$$
(3)

where q is the flow rate of SA, L is the Length of SA, A is the sectional area, µ is the viscosity, Kb is the equivalent permeability of SA, p1 is the inlet pressure of SA, and p2 is the outlet pressure of SA.

According to the principle of equivalent flow:

$$\frac{{{K_{\text{b}}}A}}{L}=\frac{{{K_{\text{m}}}{A_{\text{m}}}}}{{{L_{\text{m}}}}}+\frac{{{K_{{\text{f}}1}}{A_{{\text{f}}1}}}}{{{L_{{\text{f}}1}}}}+\frac{{{K_{{\text{f}}2}}{A_{{\text{f}}2}}}}{{{L_{{\text{f}}2}}}},$$
(4)

where subscript m represents matrix system, f1 represents secondary fracture system, and f2 represents natural fracture system.

As shown in Eq. 4, equivalent permeability of stimulated area can be calculated as the weighted average of the volume of fracture network, the permeability of fracture network, the volume of matrix and the permeability of matrix. Therefore, we simplify the complex fracture network into an area with high permeability. Threshold pressure gradient and stress-sensitive effect should also be taken into consideration in this area.

Primary fracture system

The local grid refinement (LGR) approach is utilized to model hydraulic fracture explicitly, which can accurately capture the fluid transport behavior from shale matrix to fracture, as shown in Fig. 2. The fracture grid has a small fracture width but a large permeability. The ability of a fracture to supply the flow of a liquid depends mainly on the fracture conductivity which is defined as the product of fracture width and fracture permeability (Moinfar et al. 2013; Liu et al. 2013). The equation is represented as follows:

Fig. 2
figure 2

Enlarged zone with LGR used to model hydraulic fracture

Full size image
$${C_{\text{f}}}={w_{\text{f}}}{K_{\text{f}}},$$
(5)

where Cf is the fracture conductivity, wf is the fracture width, and Kf is the fracture permeability.

With the decrease of pore pressure, the primary fracture will be closed gradually during the production process, and the primary fracture conductivity will be gradually reduced, while the fracture conductivity is mainly reflected in the fracture width and the fracture permeability. According to research of Ozkan and RaghaVanM (Ozkan et al. 2010), the equation of fracture permeability with pore pressure is given by Eq. 6. Based on the research of Yuhang and Saman Aryana (Wang and Aryana 2016), we derive an expression for fracture width in terms of pore pressure through regression given by Eq. 7.

$${K_{\text{f}}}={K_{{\text{fi}}}}{{\text{e}}^{ - {\alpha _{\text{k}}}({p_{{\text{fi}}}} - {p_{\text{f}}})}},$$
(6)
$${w_{\text{f}}}={w_{{\text{fi}}}}{{\text{e}}^{ - {c_{\text{k}}}({p_{{\text{fi}}}} - {p_{\text{f}}})}},$$
(7)

where Kfi is the initial permeability of primary fracture, pfi is the initial pressure of primary fracture, pf is the pressure of primary fracture, primary fracture wfi is the initial width of primary fracture, and ck is the sensitive coefficient of fracture width.

Through Eqs. 5–7, the variation of fracture conductivity with pressure can be obtained:

$$\frac{{{C_{\text{f}}}}}{{{C_{{\text{fi}}}}}}=\frac{{{w_{\text{f}}}{K_{\text{f}}}}}{{{w_{{\text{fi}}}}{K_{{\text{fi}}}}}}.$$
(8)

Suppose that the ratio of wf to wfi is b, the Kf to Kfi is d; Eq. 8 can be simplified to:

$${C_{\text{f}}}={C_{{\text{fi}}}}bd.$$
(9)

The establishment of a numerical simulation model

Based on the actual parameters of a long fractured horizontal well in a tight oil reservoir in Xinjiang oilfield, we utilize the numerical Simulation Software CMG to establish a theoretical Model of MFHW with the size of 1500 m × 400 m × 20 m adopting the method of local grid refinement. Reservoir and fluid properties are presented in Table 1. The parameters of multi-stage fracturing horizontal well are presented in Table 2. The total number of effective hydraulic fracture is 24 for the horizontal well, and we take the first effective fracture as an example.

Table 1 Parameters of reservoir and fluid properties
Full size table
Table 2 Parameters of the first fracturing
Full size table

Results and discussion

The impact of threshold pressure gradient

Due to the characteristic of tight reservoir in consideration of the compact reservoir matrix and the thinner capillary, a high threshold pressure gradient exists in the flow process. The formation fluids can flow only when the formation pressure gradient is greater than threshold pressure gradient. Furthermore, the effect of threshold pressure gradient on productivity is analyzed as below. In the tight oil reservoir of Xinjiang oilfield, the threshold pressure gradient is usually between 0.1 ~ 1 MPa/m (Zheng et al. 2016; Fan et al. 2014). The different values of threshold pressure gradient are selected, respectively, in the numerical simulation model for calculation: 0.2 MPa/m, 0.4 MPa/m, 0.6 MPa/m, 0.8 MPa/m. Figure 3 shows the cumulative oil production curve and daily oil production curve under different threshold pressure gradient. As shown in Fig. 3a, the well production is inversely proportional to the threshold pressure gradient. With the increase of threshold pressure gradient, the oil production will decrease. Besides, the changes of threshold pressure gradient has little effect on productivity. When the threshold pressure gradient changes from 0.2 to 0.8 MPa/m, the productivity of the horizontal well is reduced by 8%. Figure 3b shows that the impact of threshold pressure gradient on productivity is mainly in the early stage of production. The daily oil production under different threshold pressure gradient is different in the early stage, and the daily oil production in the middle and late stage is almost the same. Because of the existence of threshold pressure gradient (TPG), the pressure drop cannot spread to the whole reservoir in time in the early stage of production, resulting in the fluid cannot flow. As the TPG increases, the propagation of pressure drop will be slowed down and the spikes will become more significant. However, in the middle–late stage, with the pressure drop propagating to the entire reservoir, this phenomenon is no longer obvious.

Fig. 3
figure 3

a Cumulative oil production curve; b daily oil production curve

Full size image

The pressure field maps at 4000 days are obtained under different threshold pressure gradients of 0 MPa/m; 0.2 MPa/m; 0.8 MPa/m, respectively, to analyze the dynamic changes of pressure in tight reservoir. As shown in Fig. 4, the existence of threshold pressure gradient has little effects on pressure system of tight oil reservoir. With the increasing of threshold pressure gradient, the employed range of pressure system is gradually reduced.

Fig. 4
figure 4

Pressure maps at 4000 days

Full size image

The impact of stress-sensitive effect

With further exploitation of oil fields, the formation fluid is discharged and the pore pressure decreases, the reservoir matrix will show a strong stress-sensitive effect due to the formation fluid outflow and pore pressure drop. Therefore, considering the stress-sensitive effect of matrix on oil well productivity is necessary for the oil production. Compared with low-permeability and ultra-low-permeability reservoirs, the stress-sensitive effect in tight reservoirs is more significant and causes the lower productivity. Based on the previous research results and field experimental data, the different values of stress-sensitive coefficient, 0.01; 0.02; 0.03; 0.04; 0.05, respectively, are adopted in the numerical simulation model for calculation (Yang et al. 2017b). Figure 5 shows the cumulative oil production curves (Fig. 5a) and daily oil production curves (Fig. 5b) under different stress-sensitive coefficient. As shown in Fig. 5a, the well production is inversely proportional to the stress-sensitive effect with the increase of stress-sensitive effect, production capacity will decrease. Besides, compared with the effect of the threshold pressure gradient on the productivity, the change of the stress-sensitive effect has greater effect on the productivity. When the stress-sensitive coefficient is increased from 0.01 to 0.05, the productivity of the horizontal well is reduced by 75%. Figure 5b shows that the impact of stress-sensitive effect on productivity is mainly in the whole stage of production, which is different from the threshold pressure gradient. The daily oil production under different stress-sensitive coefficients is quite different in the early–mid stage, and the daily oil production in the late stage is almost the same.

Fig. 5
figure 5

a Cumulative oil production curve; b daily oil production curve

Full size image

For different stress-sensitive coefficients, 0; 0.01; 0.05, respectively, we obtain the pressure field maps (shown in Fig. 6) at 4000 days to analyze the dynamic change of pressure system in tight reservoir. As shown in Fig. 6, it shows that the existence of stress-sensitive coefficient has greater effect on the pressure system of the tight oil reservoir development, and with the increase of stress-sensitive coefficient, the range of pressure system is rapidly decreasing. It can be seen that when the stress-sensitive coefficient reaches 0.05, the range and degree for development of the pressure system are obviously decreased.

Fig. 6
figure 6

Pressure maps at 4000 days

Full size image

Reasonable production pressure drop

According to the calculation and analysis above, the productivity is affected by both threshold pressure gradient and stress-sensitive effects. We analyze the oil well productivity under different bottom-hole pressure based on aforementioned two influencing factors. Figure 7 shows the relationship between productivity and bottom-hole pressure only considering the effects of threshold pressure gradient. In the reasonable range of bottom-hole pressure, a larger production pressure difference leads to a smaller bottle-hole pressure, which represents a better productivity. Therefore, the threshold pressure gradient has no effect on the reasonable bottom-hole flow pressure. Due to the strong stress-sensitive effect of oil reservoir, however, the matrix permeability will be affected by the extremely low bottom-hole pressure. We obtain the curve of productivity varying with production pressure drop in consideration of the threshold pressure gradient and the stress-sensitive effect (shown in Fig. 8). Figure 8 shows that when the stress-sensitive coefficient is low, there is no optimum point of the bottom-hole pressure. However, when αk is increasing, the stress-sensitive effect is stronger, the productivity curve gradually becomes slow as the production pressure drop increases. When αk is 0.03, the reasonable production pressure drop exists, which is about 4 ~ 6 MPa. When the αk is 0.04, the reasonable hole bottom flow pressure is about 14 ~ 17 MPa. We can draw a conclusion that in the reasonable bottom-hole flow pressure range, with the increase of the stress-sensitive effect, the reasonable bottom-hole flow pressure increases gradually, that is, the reasonable production pressure difference decreases gradually.

Fig. 7
figure 7

Cumulative oil production versus pressure drop for different threshold pressure gradients

Full size image
Fig. 8
figure 8

Cumulative oil production versus pressure drop for different stress-sensitive coefficients

Full size image

The primary fracture is the main channel of flow in the development of tight reservoir. The change of the conductivity of the primary fracture has great effect on the productivity (shown in Fig. 9). Based on the threshold pressure gradient and stress-sensitive effect, through Eq. 9, the effect of dynamic change of primary fracture on productivity is introduced into the numerical simulation model to optimize the reasonable pressure drop. We obtain the curve of productivity varying with production pressure drop in consideration of the primary fracture closure (shown in Fig. 10). The black curve shows the change of productivity with pressure drop when the primary fracture is unclosed (αk = 0.03, TPG = 0.4 MPa/m) and the red curve is the change of productivity with pressure drop considering the closure of primary fracture.

Fig. 9
figure 9

Cumulative oil production curve

Full size image
Fig. 10
figure 10

Cumulative oil production versus pressure drop for fracture closure

Full size image

It is evident that when the pressure drop is small, the primary fracture closure has little effect on the productivity, and the two curves almost coincide. As the bottom-hole flow pressure decreasing, the pressure difference gradually increases. The two curves are separated obviously, and the red curve reaches the maximum productivity when the bottom-hole flow pressure is 20 ~ 25 MPa while black curve reaches the maximum productivity under the bottom-hole flow pressure of 4 ~ 6 MPa (shown in Fig. 10). The reasonable range of bottom-hole flow pressure is obviously increasing in consideration of the dynamic change of the primary fracture. The amplitude of increase depends on the sensitivity coefficient of the primary fracture (the fitting values of the sensitivity coefficient are 0.03).

Conclusion

In this study, the reasonable production pressure drop range of the multi-stage fracturing horizontal well has been investigated to account for the threshold pressure gradient, the matrix stress-sensitive effect and fractures closure. The following conclusions can be drawn from the results:

(1) Pressure drop cannot spread quickly to the boundary in the early stage of production due to its existence. The TPG has an effect on the productivity, but has no obvious effect on the optimization of reasonable production pressure drop.

(2) Stress-sensitive effect not only affects oil production rate, but also the optimization of reasonable production pressure drop. With the stress-sensitive coefficient increasing, the range of reasonable production pressure drop is smaller.

(3) The phenomenon of fractures closure has obvious effect on the optimization of reasonable production pressure drop, and when the fracture is gradually closed, the reasonable production pressure drop will become smaller.

(4) The stress-sensitive effect and fracture closure are the major factors for the optimization of reasonable production pressure drop.